Distributed Systematic Network Coding for Reliable Content Uploading in Wireless Multimedia Sensor Networks
Abstract
:1. Introduction
- The proposed DSNC enables to enhance the efficient multimedia content uploading and to solve the issue of heavy feedback signaling and retransmission caused by retransmission-based protocols in WMSNs.
- We propose a bandwidth-efficient and channel-aware error control algorithm to enhance the bandwidth-efficient utilization. Our proposed DSNC can be simply embedded on application layer. In the practical point of view, DSNC can take a significant step towards realistic deployment integrated into WMSNs.
- We derive the closed-form equations of decoding probability that are validated by various simulations. We evaluate the effectiveness in terms of three performance metrics: decoding probability, redundancy, and image quality measurement using peak signal-to-noise ratio (PSNR). The experimental results demonstrate that the performance of the proposed DSNC outperforms the existing uploading schemes.
2. Related Work
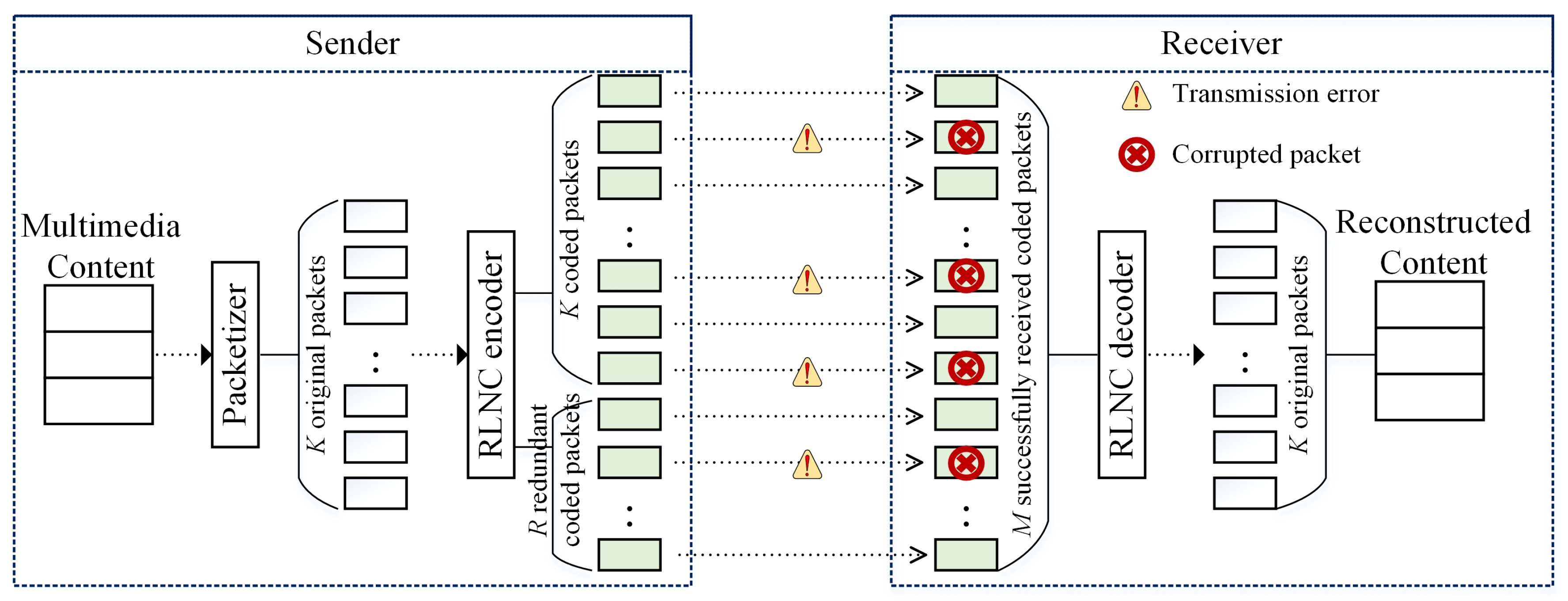
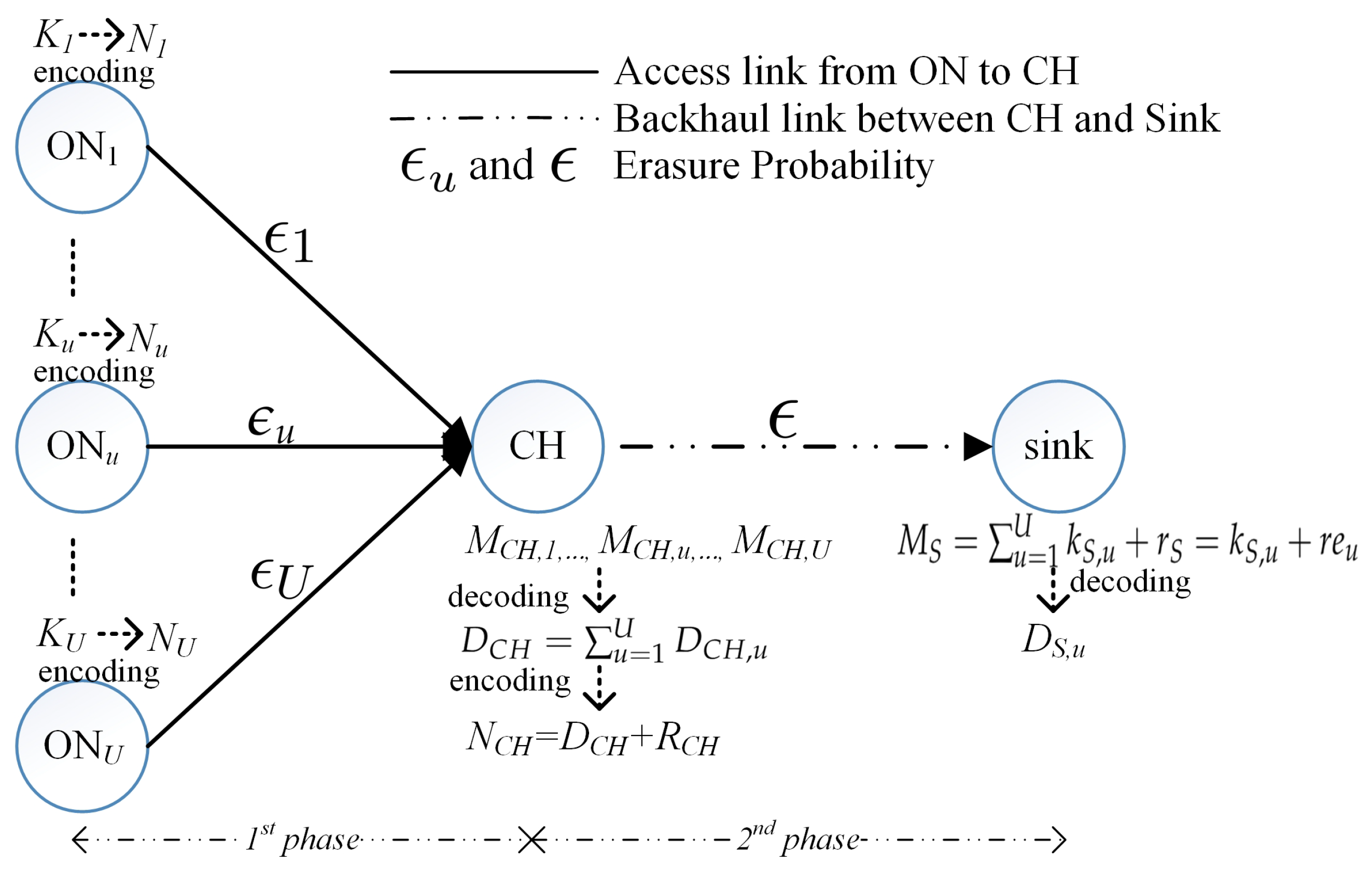
3. Proposed DSNC
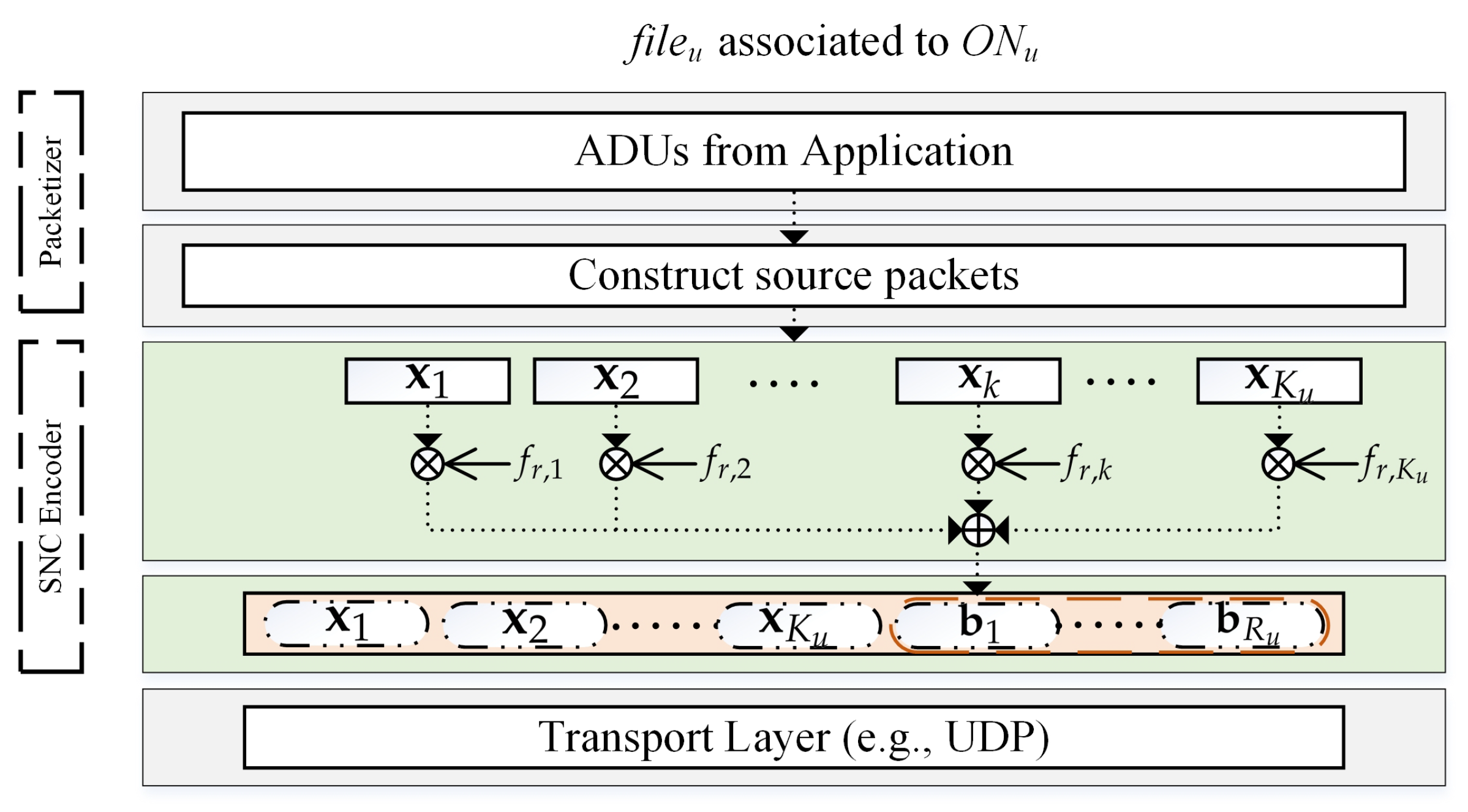
3.1. Multimedia Content Encoding at Multiple ONs in the First Phase
| Algorithm 1: Proposed bandwidth-efficient and channel-aware error control algorithm. |
| Input: Given , , , Output:
|
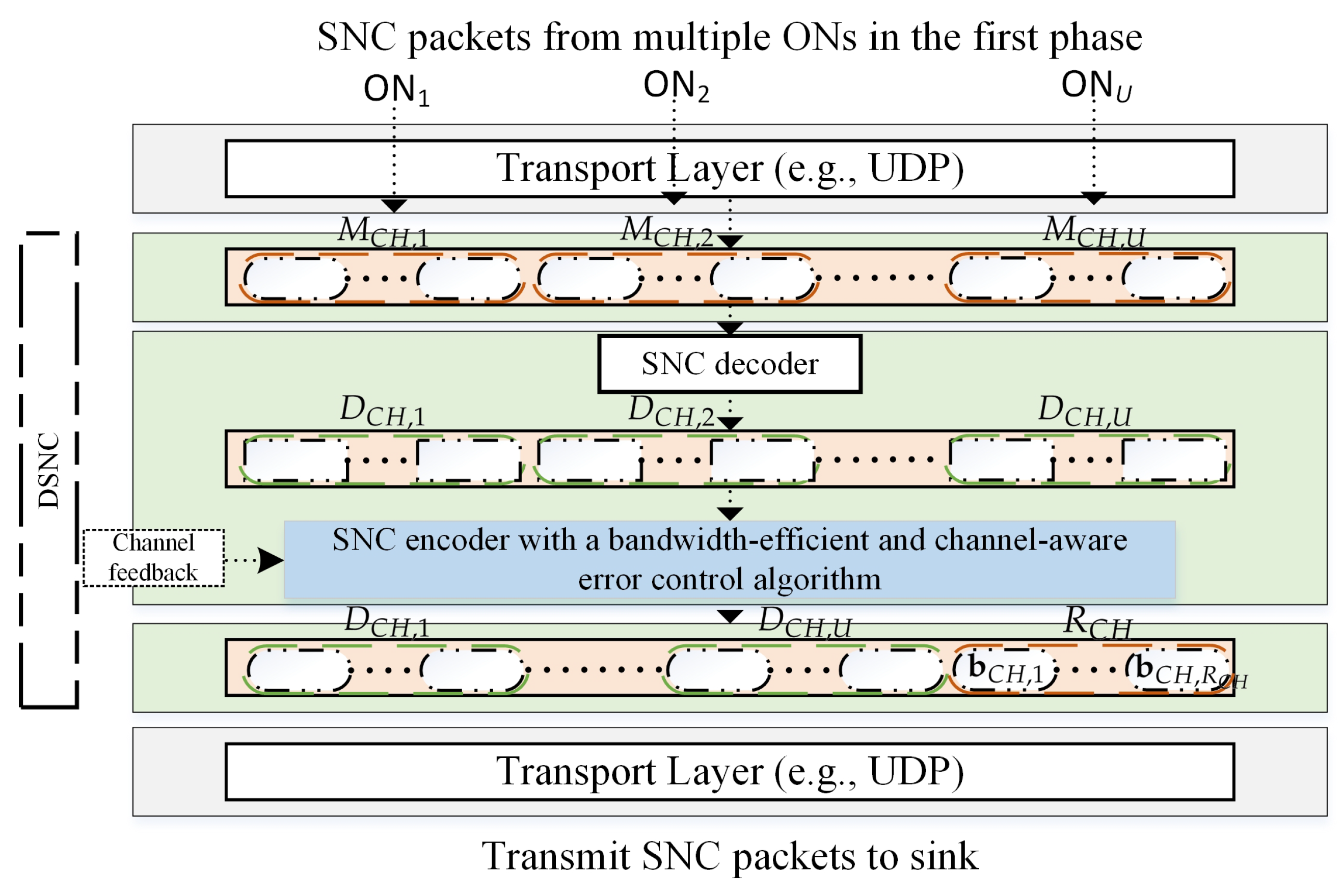
3.2. DSNC Execution at CH in the Second Phase
4. Performance Analysis
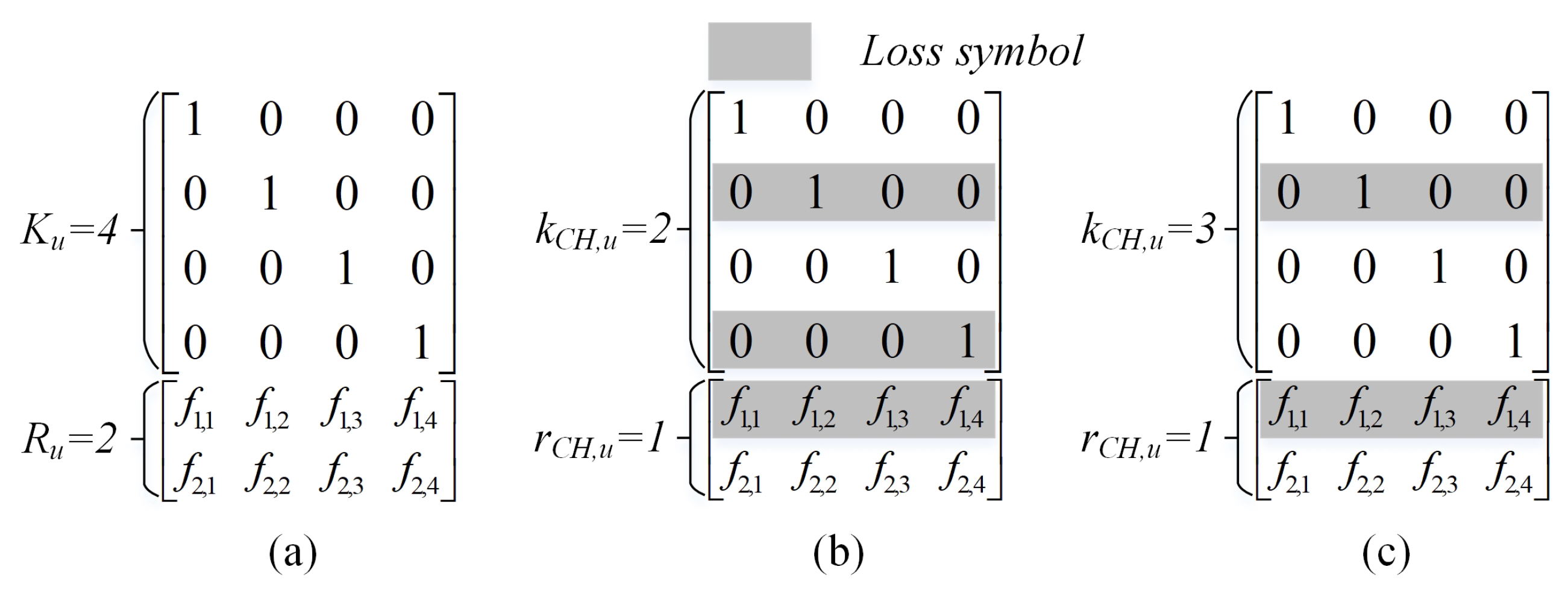
4.1. A Single ON over One-Hop Transmission
- In the case of (i.e., example shown in Figure 5b): CH only can decode successfully uncoded packets (i.e., ) and the coefficient coding vectors of all the received packets cannot achieve the rank of .where is the number of RLNC packets used for transmission, in which and represent the ranks of coefficient matrix and redundant packets, respectively; is the probability that the coefficient coding matrix achieves the rank of derived in [22].
- In the case of (i.e., example shown in Figure 5c): obviously, CH can decode all source packets as the matrix of received coefficient coding vectors achieves the rank of . The can be simply expressed as follows:Finally, the for a single-hop wireless transmission can be derived as follows:
4.2. A Single ON over Two-Hop Transmission
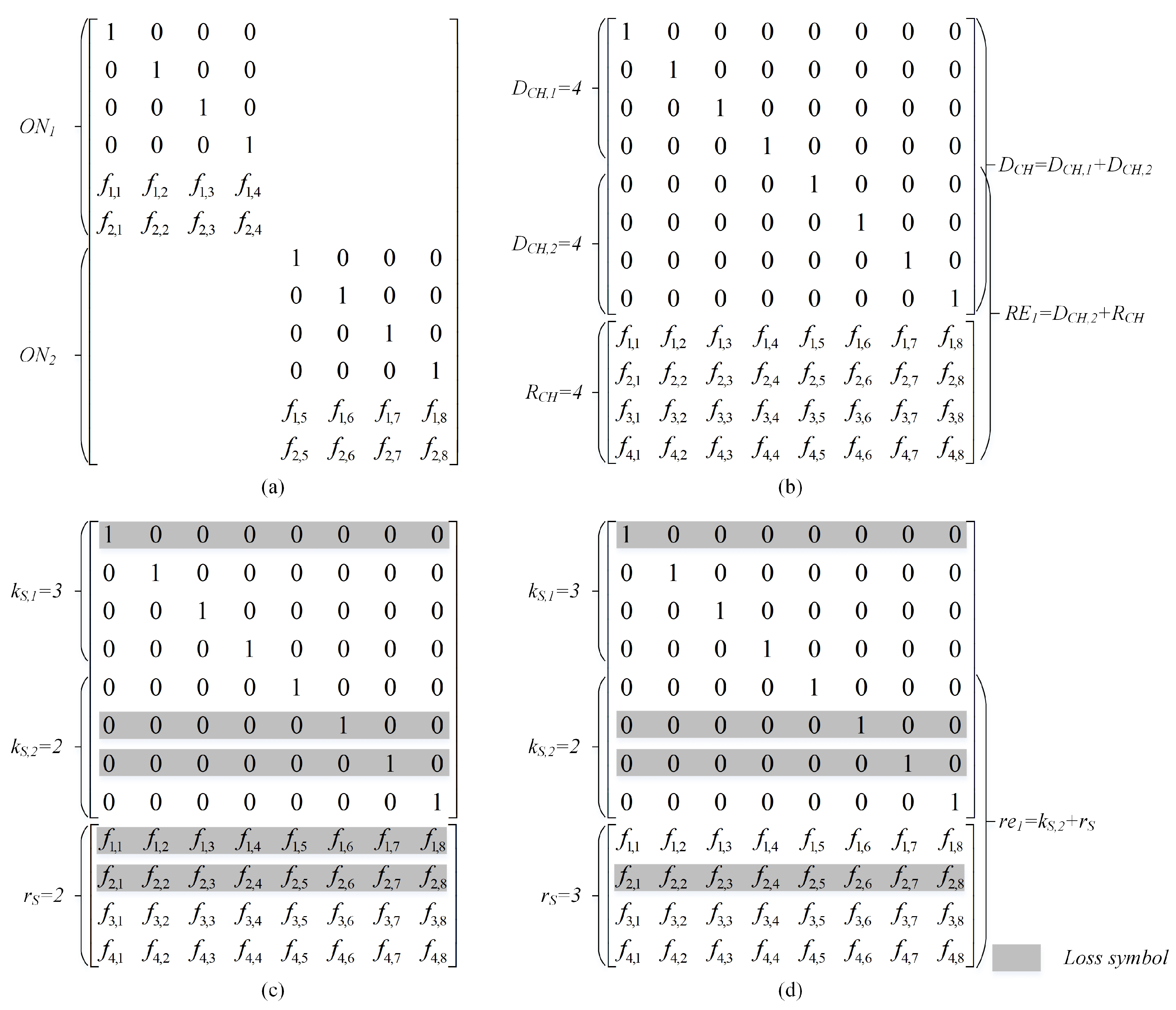
4.3. Analysis of DSNC with Multiple Source Senders
- The case of (i.e., example shown in Figure 6c): sink only can decode successfully uncoded packets (i.e., ) and the coefficient coding vectors of uncoded and RLNC packets are not linearly independent.where is treated as the number of redundant packets of the 1st ON. Each ON treats the received packets of other ONs as redundancy. Examples of the and are presented in Figure 6b.
- The case of (i.e., example shown in Figure 6d): obviously, CH can decode all source packets as the matrix of received coefficient coding vectors achieves the rank of .
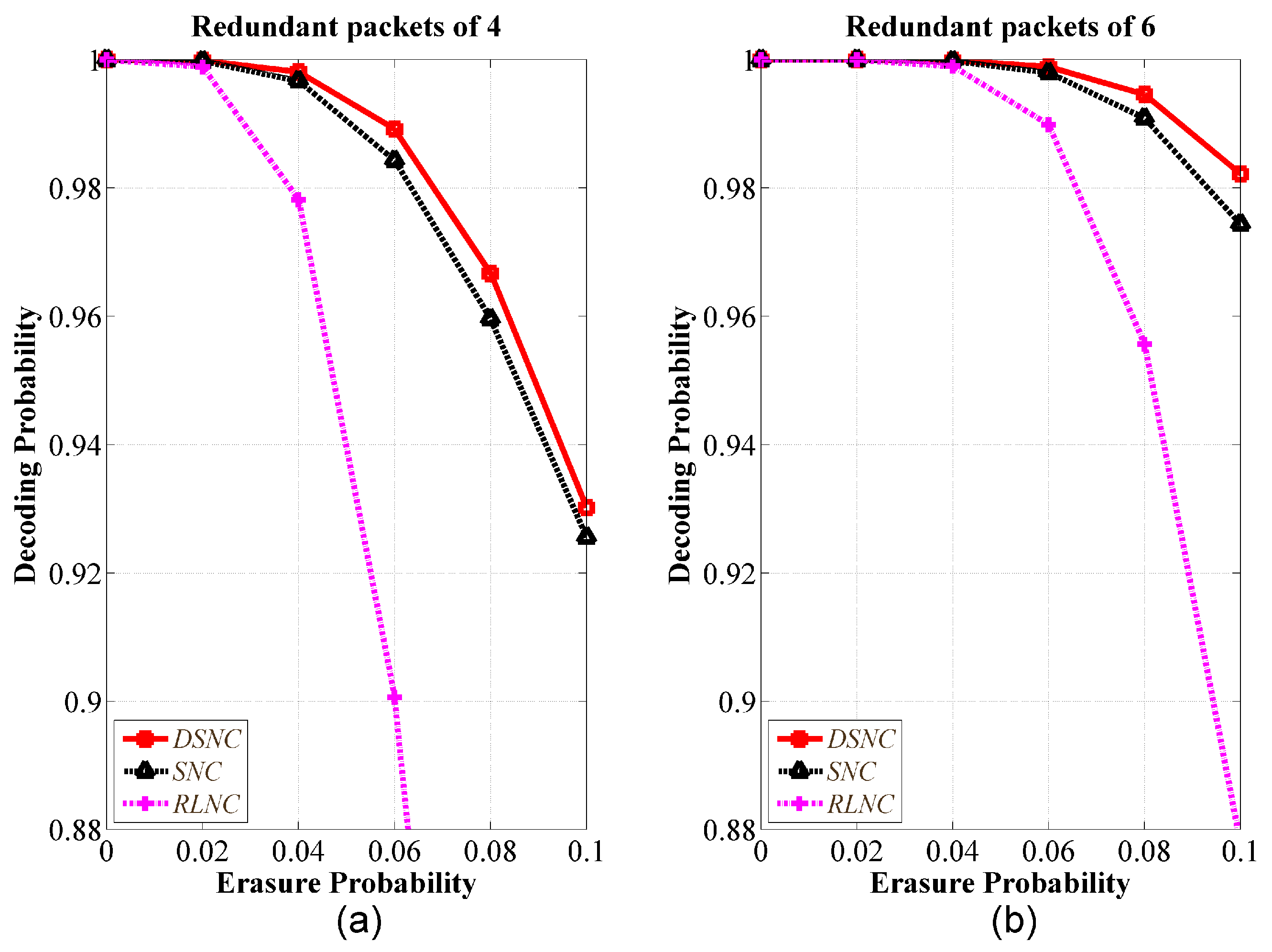
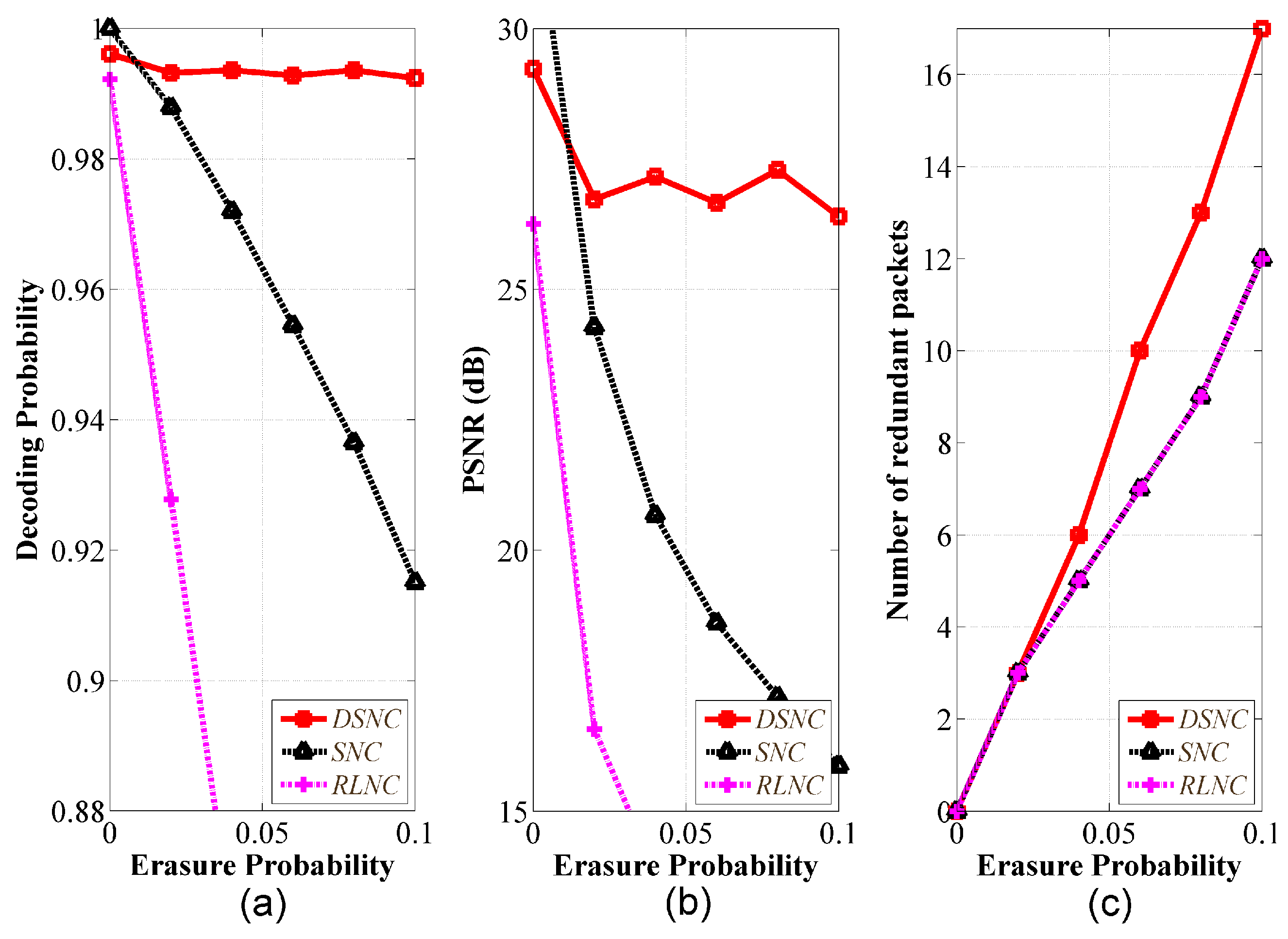
5. Performance Evaluation
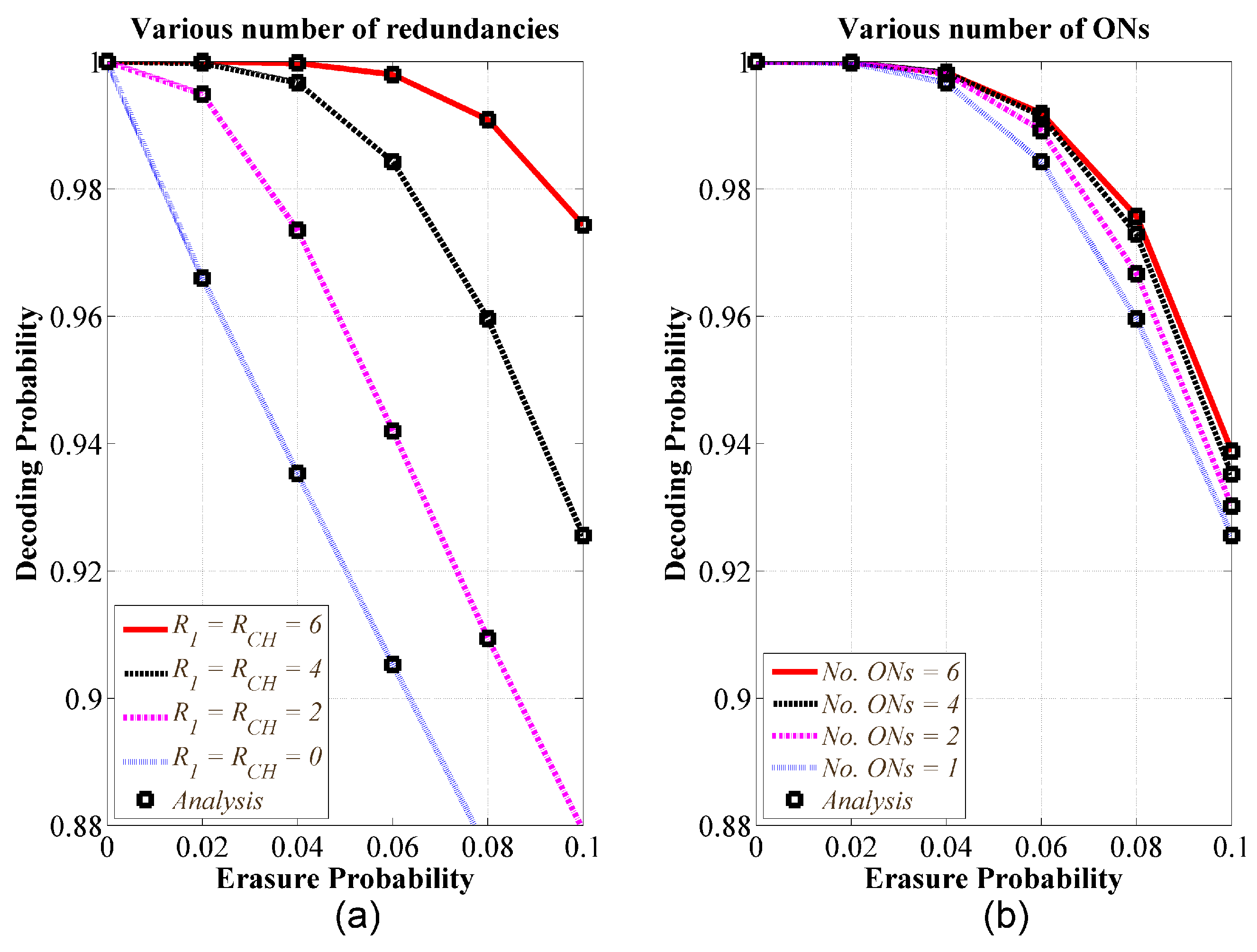
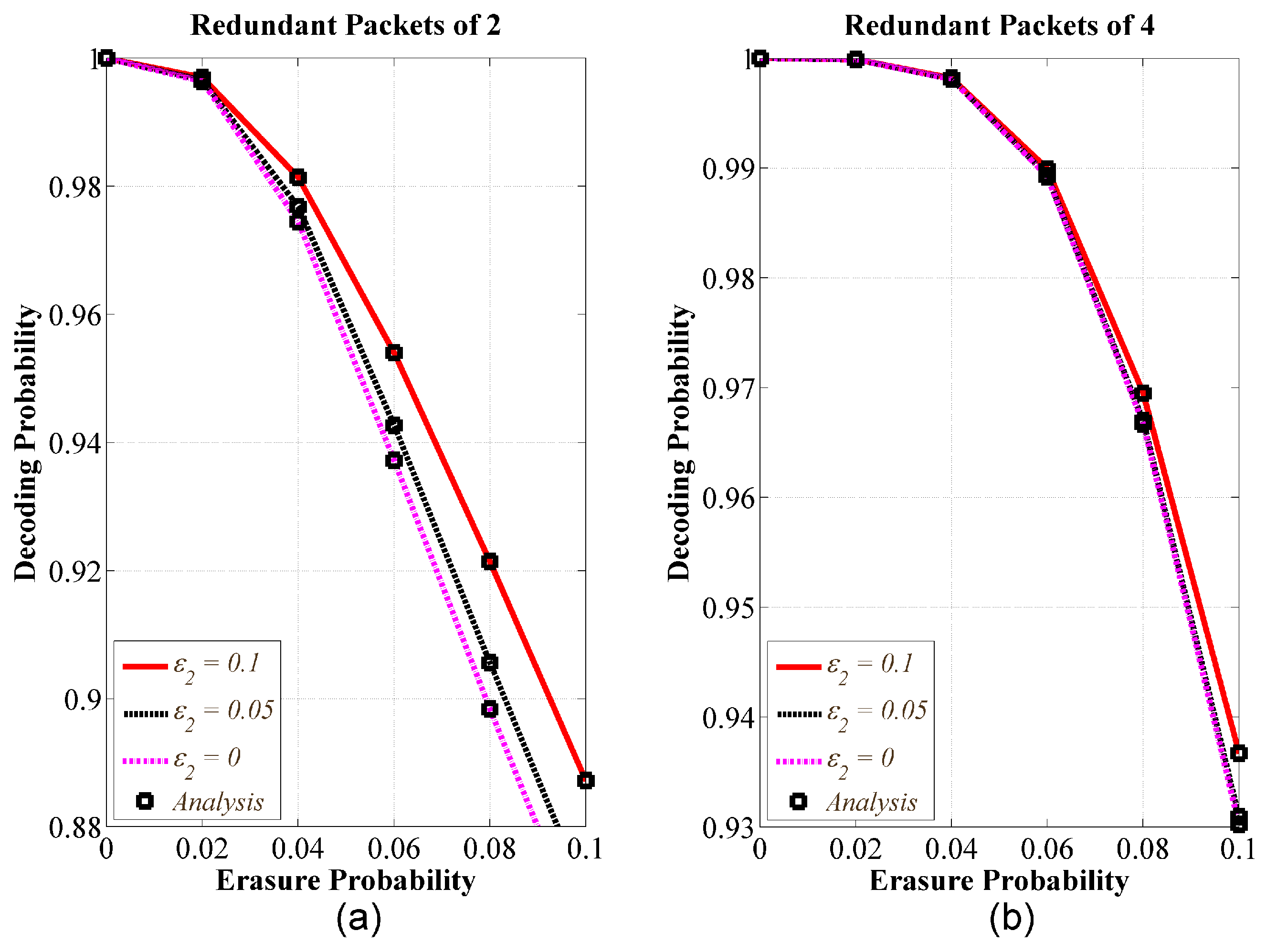
5.1. Validation of Theoretical Analysis
5.2. Comparative Performance Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADUs | Application data units |
| BP | Brief propagation |
| CH | Cluster head |
| DSNC | Distributed systematic network coding |
| GE | Gaussian Elimination |
| ON | Ordinary node |
| PHY | Physical layer |
| PLR | Packet loss ratio |
| QoS | Quality of service |
| RLNC | Random linear network coding |
| RSSI | Received Signal Strength Indicator |
| SNC | Systematic network coding |
| WMSNs | Wireless multimedia sensor networks |
References
- Akyildiz, I.F.; Melodia, T.; Chowdury, K.R. Wireless multimedia sensor networks: A survey. IEEE Wirel. Commun. 2007, 14. [Google Scholar] [CrossRef]
- Rezvani, M.; Ignjatovic, A.; Bertino, E.; Jha, S. Secure data aggregation technique for wireless sensor networks in the presence of collusion attacks. IEEE Trans. Dependable Secure Comput. 2015, 12, 98–110. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, S.; Guo, K.; Wang, J. A secure data collection scheme based on compressive sensing in wireless sensor networks. Ad Hoc Netw. 2018, 70, 73–84. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Lai, C.F.; Chao, H.C. A green data transmission mechanism for wireless multimedia sensor networks using information fusion. IEEE Wirel. Commun. 2014, 21, 14–19. [Google Scholar] [CrossRef]
- Mostafaei, H.; Shojafar, M. A new meta-heuristic algorithm for maximizing lifetime of wireless sensor networks. Wirel. Pers. Commun. 2015, 82, 723–742. [Google Scholar] [CrossRef]
- Shojafar, M.; Canali, C.; Lancellotti, R.; Abawajy, J. Adaptive computing-plus-communication optimization framework for multimedia processing in cloud systems. IEEE Trans. Cloud Comput. 2016. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.J.; Tsai, P.W.; Zou, F.M.; Ji, X.R. Directional virtual backbone based data aggregation scheme for Wireless Visual Sensor Networks. PLoS ONE 2018, 13, 0196705. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.; Zhou, Y.; Liu, M. Fault tolerant scheduling algorithm in distributed sensor networks. J. Inf. Hiding Multimed. Signal Process. 2017, 8, 127–137. [Google Scholar]
- Kong, L.; Pan, J.S.; Sung, T.W.; Tsai, P.W.; Snášel, V. An energy balancing strategy based on Hilbert curve and genetic algorithm for wireless sensor networks. Wirel. Commun. Mob. Comput. 2017, 2017. [Google Scholar] [CrossRef]
- Mekonnen, T.; Porambage, P.; Harjula, E.; Ylianttila, M. Energy consumption analysis of high quality multi-tier wireless multimedia sensor network. IEEE Access 2017, 5, 15848–15858. [Google Scholar] [CrossRef]
- Abu-Ali, N.; Taha, A.E.M.; Salah, M.; Hassanein, H. Uplink scheduling in LTE and LTE-advanced: Tutorial, survey and evaluation framework. IEEE Commun. Surv. Tutor. 2014, 16, 1239–1265. [Google Scholar] [CrossRef]
- Sarvi, B.; Rabiee, H.R.; Mizanian, K. An adaptive cross-layer error control protocol for wireless multimedia sensor networks. Ad Hoc Netw. 2017, 56, 173–185. [Google Scholar] [CrossRef]
- Mahmood, M.A.; Seah, W.K.; Welch, I. Reliability in wireless sensor networks: A survey and challenges ahead. Comput. Netw. 2015, 79, 166–187. [Google Scholar] [CrossRef]
- Naderi, M.Y.; Rabiee, H.R.; Khansari, M.; Salehi, M. Error control for multimedia communications in wireless sensor networks: A comparative performance analysis. Ad Hoc Netw. 2012, 10, 1028–1042. [Google Scholar] [CrossRef]
- Khirallah, C.; Vukobratovic, D.; Thompson, J. Performance analysis and energy efficiency of random network coding in LTE-advanced. IEEE Trans. Wirel. Commun. 2012, 11, 4275–4285. [Google Scholar] [CrossRef]
- Rezende, C.; Boukerche, A.; Almulla, M.; Loureiro, A.A. The selective use of redundancy for video streaming over Vehicular Ad Hoc Networks. Comput. Netw. 2015, 81, 43–62. [Google Scholar] [CrossRef]
- Tassi, A.; Khirallah, C.; Vukobratović, D.; Chiti, F.; Thompson, J.S.; Fantacci, R. Resource allocation strategies for network-coded video broadcasting services over LTE-advanced. IEEE Trans. Veh. Technol. 2015, 64, 2186–2192. [Google Scholar] [CrossRef]
- Chau, P.; Shin, J.; Jeong, J.P. Efficient scalable video multicast based on network-coded communication. Wirel. Netw. 2016, 1–14. [Google Scholar] [CrossRef]
- Tassi, A.; Chatzigeorgiou, I.; Vukobratović, D. Resource-allocation frameworks for network-coded layered multimedia multicast services. IEEE J. Sel. Areas Commun. 2015, 33, 141–155. [Google Scholar] [CrossRef]
- Moritz, G.L.; Rebelatto, J.L.; Souza, R.D.; Uchôa-Filho, B.F.; Li, Y. Time-switching uplink network-coded cooperative communication with downlink energy transfer. IEEE Trans. Signal Process. 2014, 62, 5009–5019. [Google Scholar] [CrossRef]
- Yang, T.; Sun, Q.T.; Zhang, J.A.; Yuan, J. A linear network coding approach for uplink distributed MIMO systems: Protocol and outage behavior. IEEE J. Sel. Areas Commun. 2015, 33, 250–263. [Google Scholar] [CrossRef]
- Shrader, B.; Jones, N.M. Systematic wireless network coding. In Proceedings of the 2009 IEEE Military Communications, Boston, MA, USA, 18–21 October 2009; pp. 1–7. [Google Scholar]
- Li, Y.; Blostein, S.; Chan, W.Y. Systematic network coding for two-hop lossy transmissions. EURASIP J. Adv. Signal Process. 2015, 2015, 93. [Google Scholar] [CrossRef]
- Jones, A.L.; Chatzigeorgiou, I.; Tassi, A. Binary systematic network coding for progressive packet decoding. In Proceedings of the IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 4499–4504. [Google Scholar]
- Park, S.; Daniels, R.C.; Heath, R.W. Optimizing the target error rate for link adaptation. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Nafaa, A.; Taleb, T.; Murphy, L. Forward error correction strategies for media streaming over wireless networks. IEEE Commun. Mag. 2008, 46. [Google Scholar] [CrossRef]
- Agrawal, D.P.; Zeng, Q.A. Introduction to Wireless and Mobile Systems; Cengage Learning: Boston, MA, USA, 2015. [Google Scholar]
- Chau, P.; Lee, Y.; Bui, T.; Shin, J. Analysis of decoding probability for systematic wireless network coding. Electron. Lett. 2017, 53, 964–966. [Google Scholar] [CrossRef]
- Chou, P.A.; Wu, Y. Network coding for the internet and wireless networks. IEEE Signal Process. Mag. 2007, 24, 77–85. [Google Scholar] [CrossRef]
- Zhang, X.; Jing, C.; Tang, F.; Fowler, S.; Cui, H.; Dong, X. Joint redundant and random network coding for robust video transmission over lossy networks. Mob. Inf. Syst. 2012, 8, 213–230. [Google Scholar] [CrossRef]
- Ji, X.; Zheng, B.; Cai, Y.; Zou, L. On the study of half-duplex asymmetric two-way relay transmission using an amplify-and-forward relay. IEEE Trans. Veh. Technol. 2012, 61, 1649–1664. [Google Scholar] [CrossRef]
| Notation | Definition |
|---|---|
| U | The number of ONs |
| The number of original packets used for a frame transmission of the uth ON | |
| The number of RLNC packets of the uth ON used for a frame transmission | |
| The maximum number of RLNC packets of the uth ON used for transmission | |
| The total number of SNC packets used for transmission of the uth ON, note that | |
| The total number of received SNC packets of the uth ON at CH, note that | |
| The number of received uncoded packets of the uth ON at CH | |
| The number of received RLNC packets of the uth ON at CH | |
| The number of successfully decoded packets of the uth ON at CH | |
| The total number of successfully decoded packets at CH, note that | |
| The number of RLNC packets used for transmission of the uth ON from CH to sink | |
| The total number of RLNC packets used for transmission from CH to sink, note that | |
| The number of SNC packets used for transmission of the uth ON from CH to sink, note that | |
| The total number of SNC packets used for transmission from CH to sink, note that | |
| The total number of received packets at sink | |
| The number of successfully decoded packets of the uth ON at sink | |
| The number of received uncoded packets of the uth ON at sink | |
| The total number of received RLNC packets at sink | |
| Decoding probability of the uth ON at sink | |
| Decoding probability threshold of the uth ON | |
| Expected decoding probability of the uth ON at sink | |
| Erasure probability of access link from the uth ON to CH | |
| Erasure probability of the backhaul link from CH to sink |
| Parameter | Value |
|---|---|
| Galois Field size q | 256 |
| Generation size | 30 |
| Packet size | 1500 bytes |
| Transmission rate | 480 Kbps |
| Image used for transmission | Lena |
| Size of Lena Image | 501 KB |
| Generation size for image transmission | 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chau, P.; Shin, J.; Jeong, J. Distributed Systematic Network Coding for Reliable Content Uploading in Wireless Multimedia Sensor Networks. Sensors 2018, 18, 1824. https://doi.org/10.3390/s18061824
Chau P, Shin J, Jeong J. Distributed Systematic Network Coding for Reliable Content Uploading in Wireless Multimedia Sensor Networks. Sensors. 2018; 18(6):1824. https://doi.org/10.3390/s18061824
Chicago/Turabian StyleChau, Phuc, Jitae Shin, and Jaehoon (Paul) Jeong. 2018. "Distributed Systematic Network Coding for Reliable Content Uploading in Wireless Multimedia Sensor Networks" Sensors 18, no. 6: 1824. https://doi.org/10.3390/s18061824
APA StyleChau, P., Shin, J., & Jeong, J. (2018). Distributed Systematic Network Coding for Reliable Content Uploading in Wireless Multimedia Sensor Networks. Sensors, 18(6), 1824. https://doi.org/10.3390/s18061824





