Energy Harvesting over Rician Fading Channel: A Performance Analysis for Half-Duplex Bidirectional Sensor Networks under Hardware Impairments
Abstract
1. Introduction
- The exact form expression of outage probability and achievable throughput at each destination node with imperfect hardware and in Rician fading environment are derived mathematically.
- We derive the exact-form cumulative distribution function (CDF) of the SNR at each destination node, and use this result to derive the integral exact-form of the SER at destination nodes.
- We also conduct the asymptotic analysis and provide the approximation of all performance factors mentioned above at high regime.
- The analytical results are all confirmed by Monte Carlo simulations. Using the simulation results, the effect of various system parameters on the system performance is carefully studied.
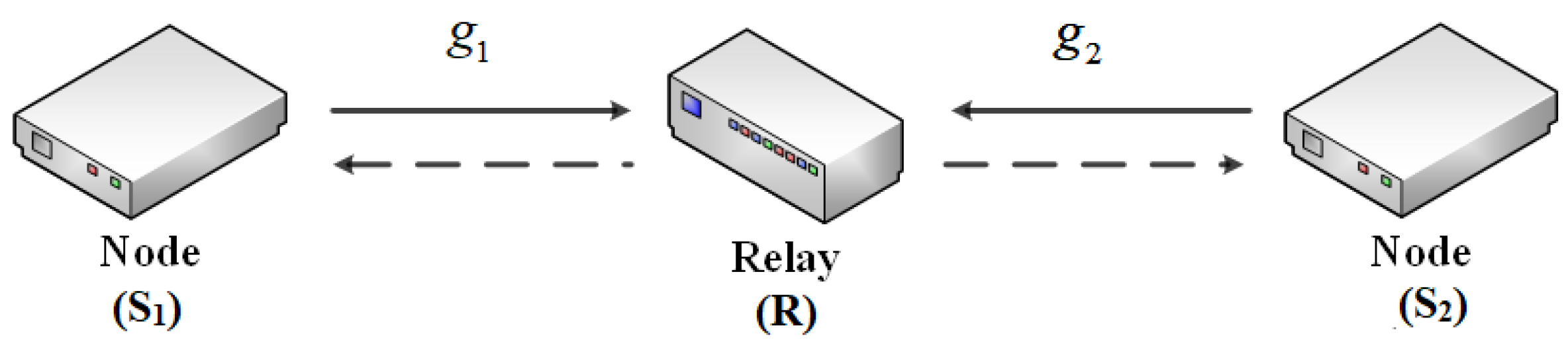
2. System Model
2.1. System Model Description
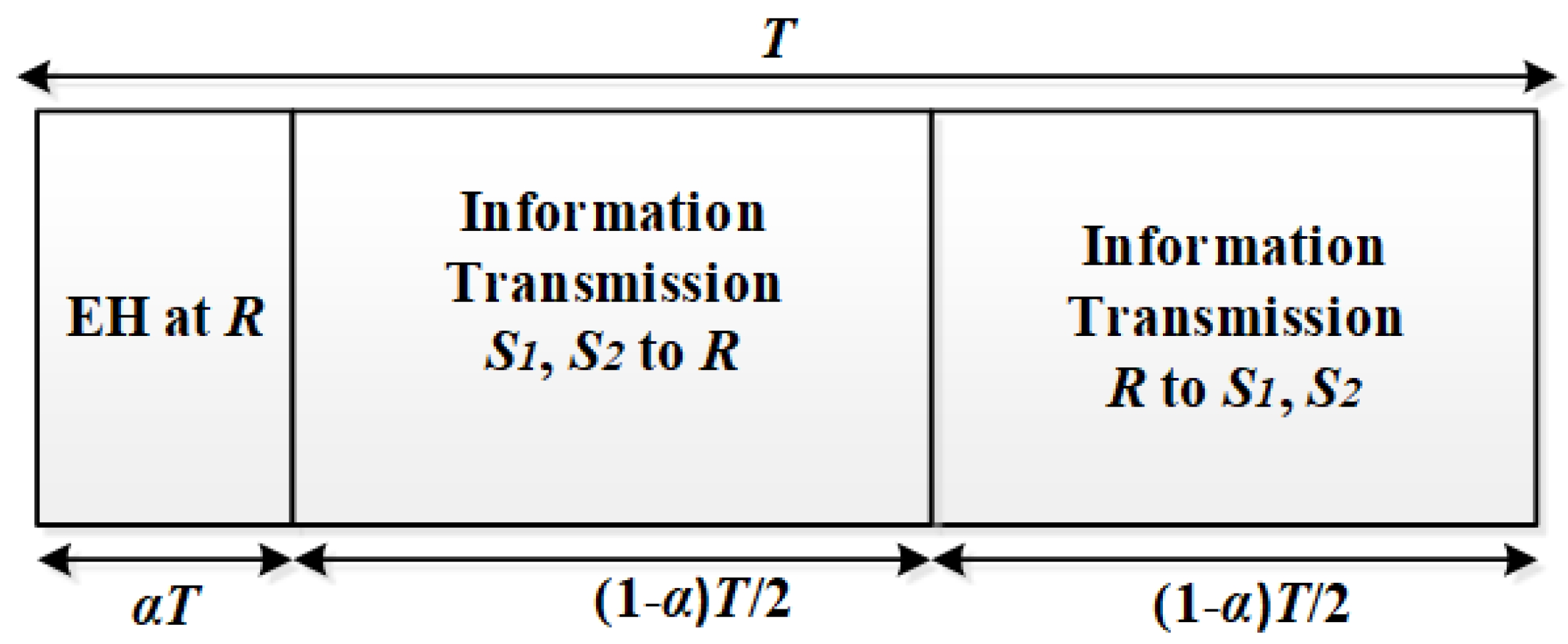
2.2. Energy Harvesting and Information Transfer Protocols
- denotes the hardware distortion noise at with zero mean and variance . Here, is sufficient to characterize the aggregate level of impairments of the channel [1].
- is the additive white Gaussian noise (AWGN) at R with zero mean and variance .
3. System Performance
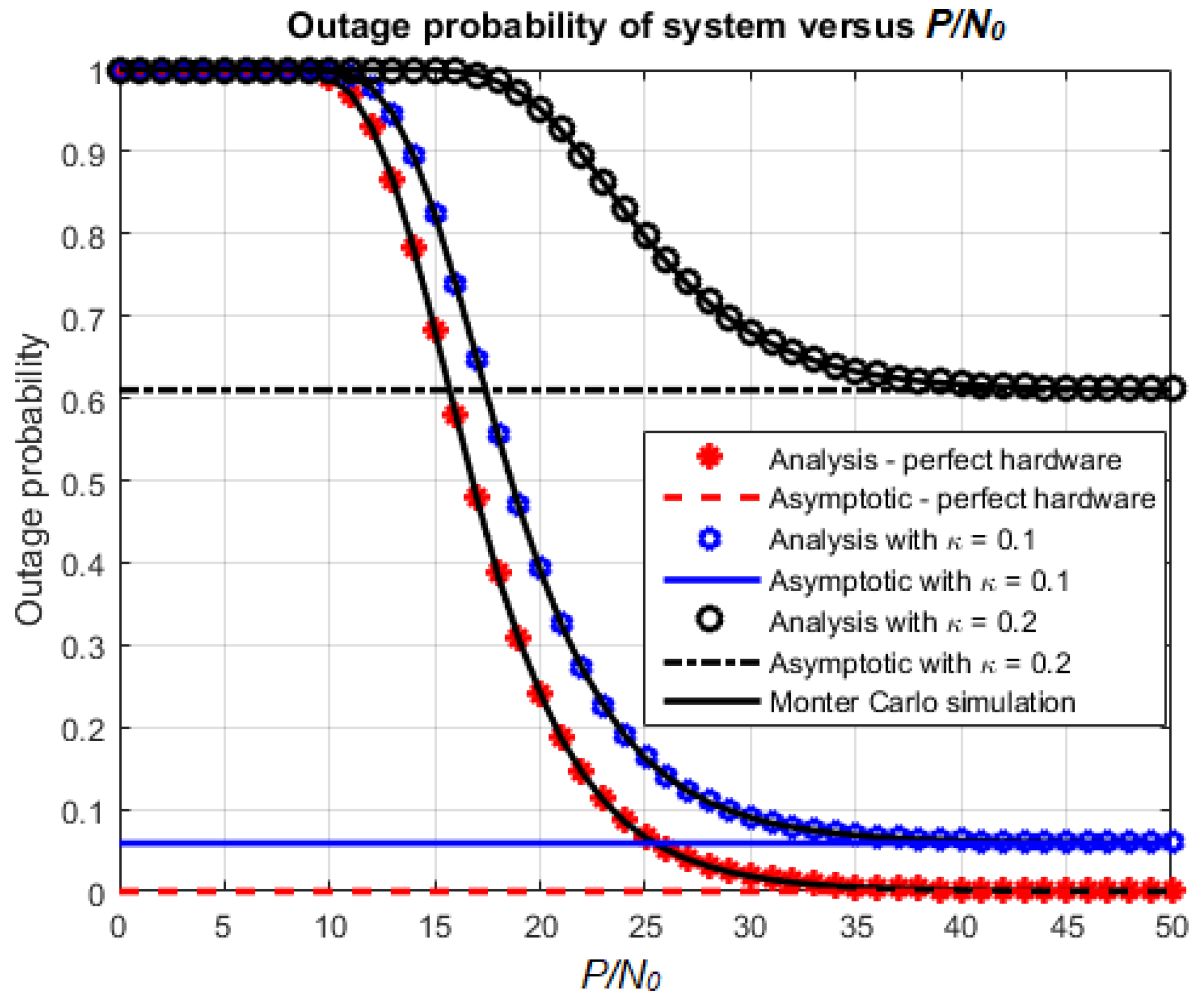
3.1. Outage Probability
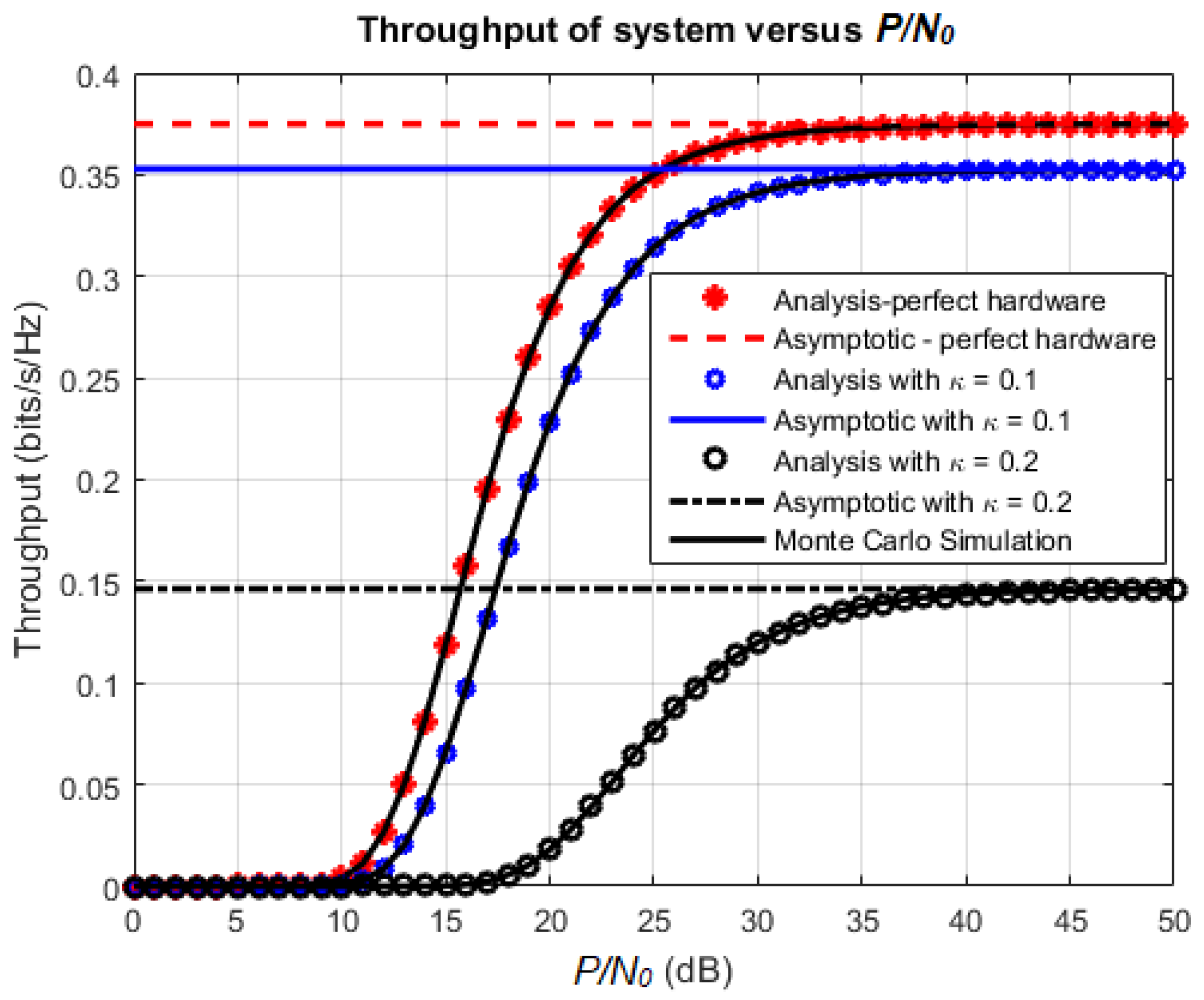
3.2. Achievable Throughput
3.3. SER Analysis
3.4. Asymptotic Analysis
3.4.1. Outage Probability
3.4.2. SER Analysis
- If :
- If :
3.5. Optimal Time-Switching Factor
4. Numerical Results and Discussion
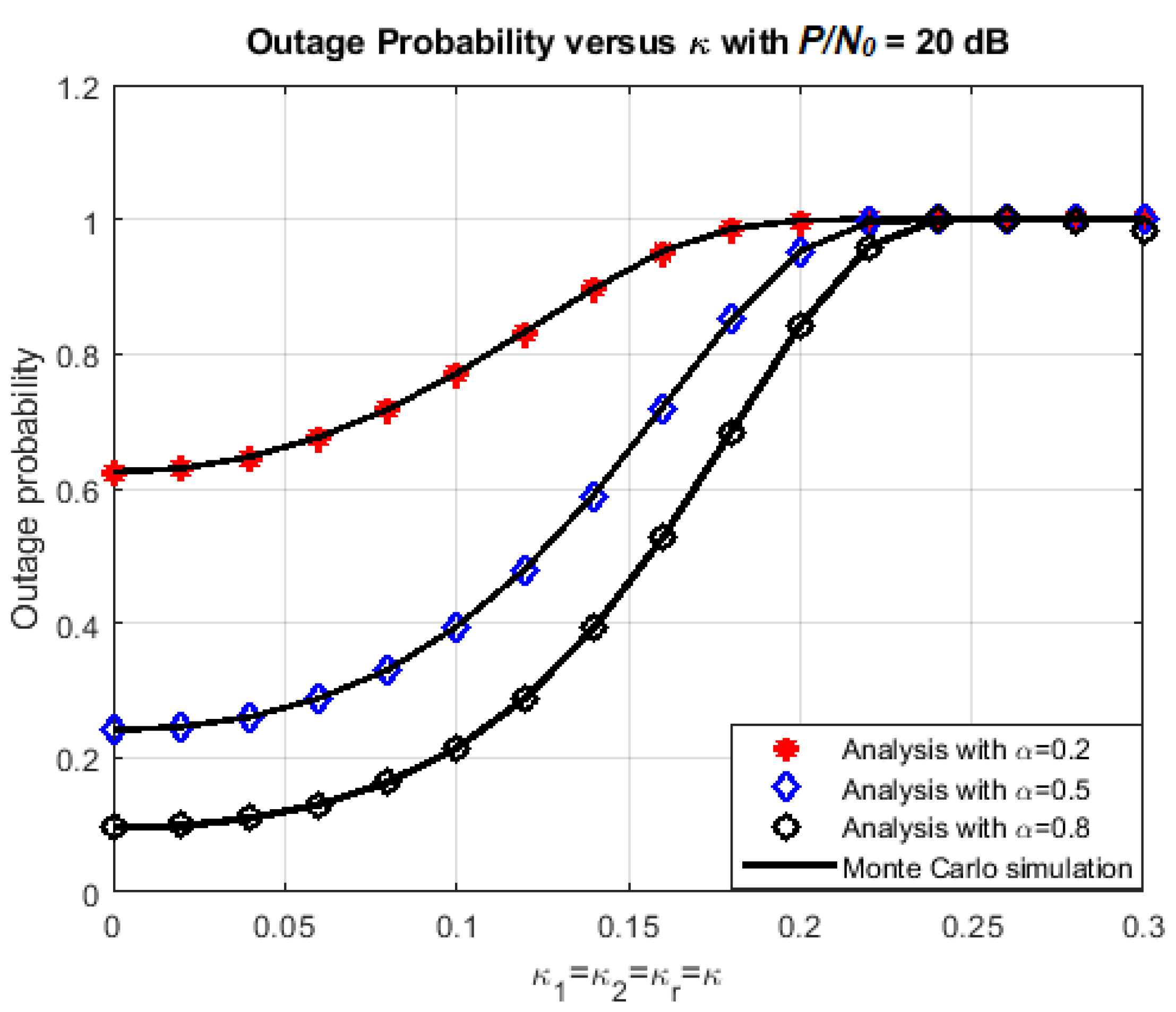
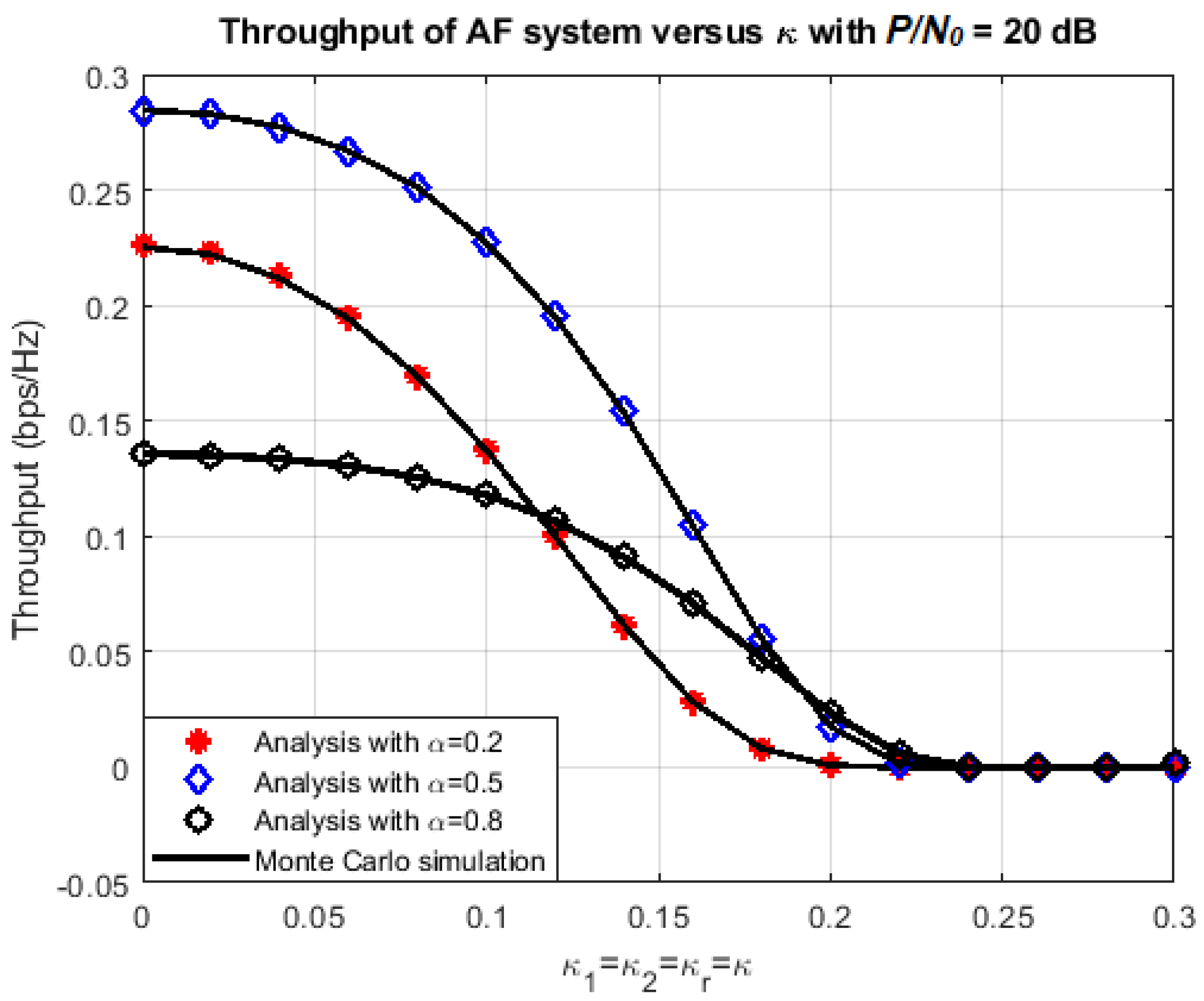
4.1. Effects of Various Parameters on the System Performance
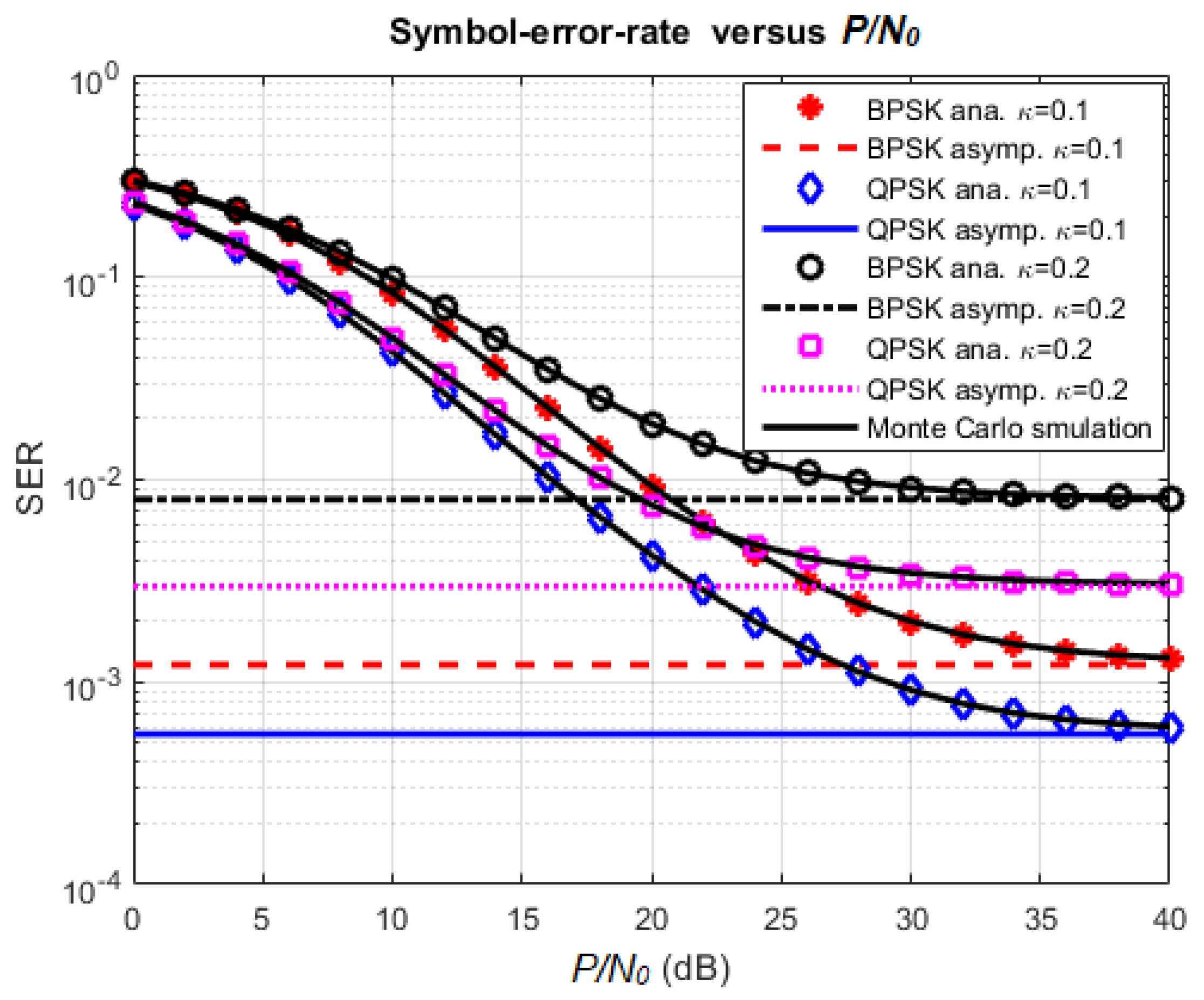
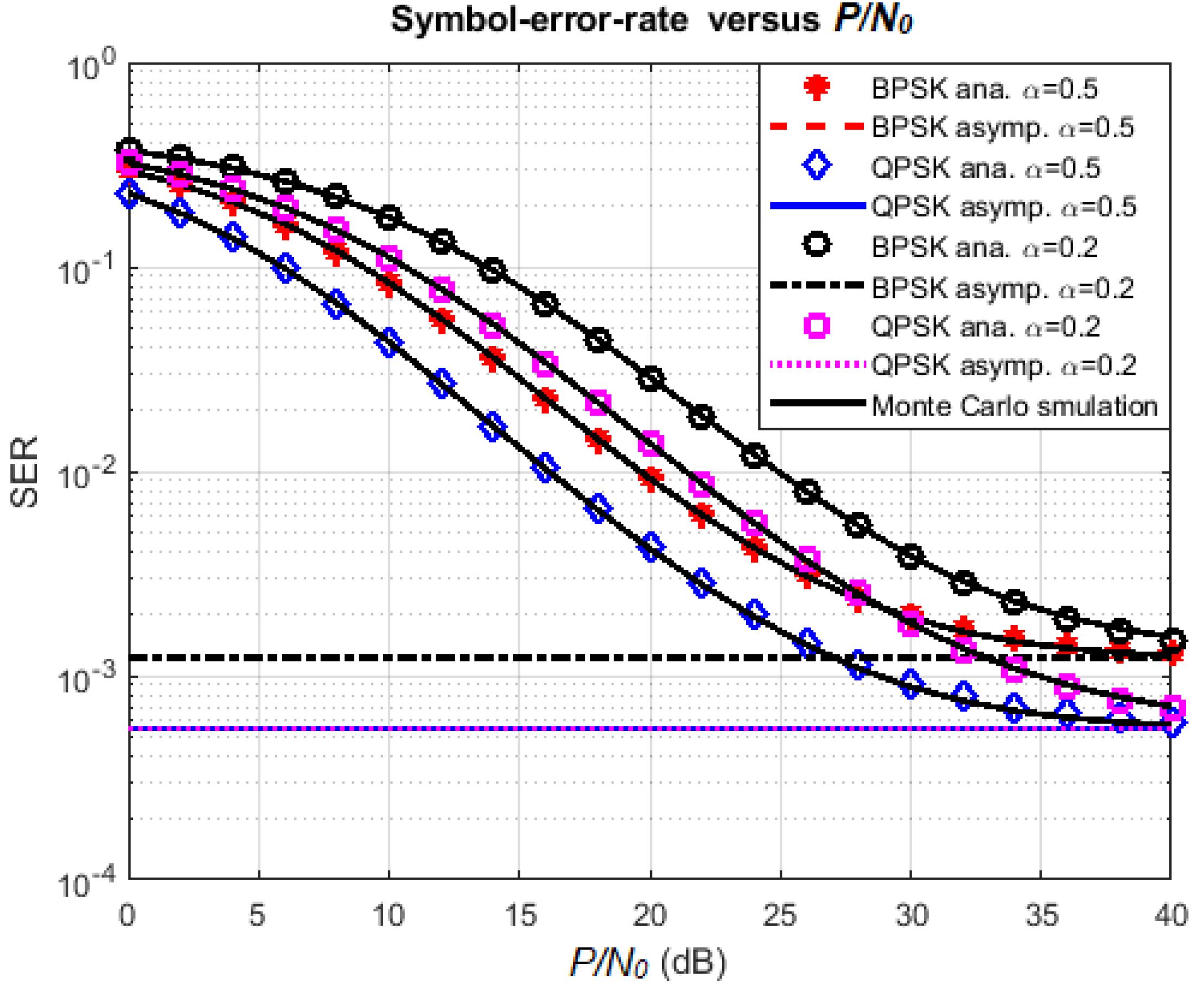
4.2. Effect of Various Parameters on SER
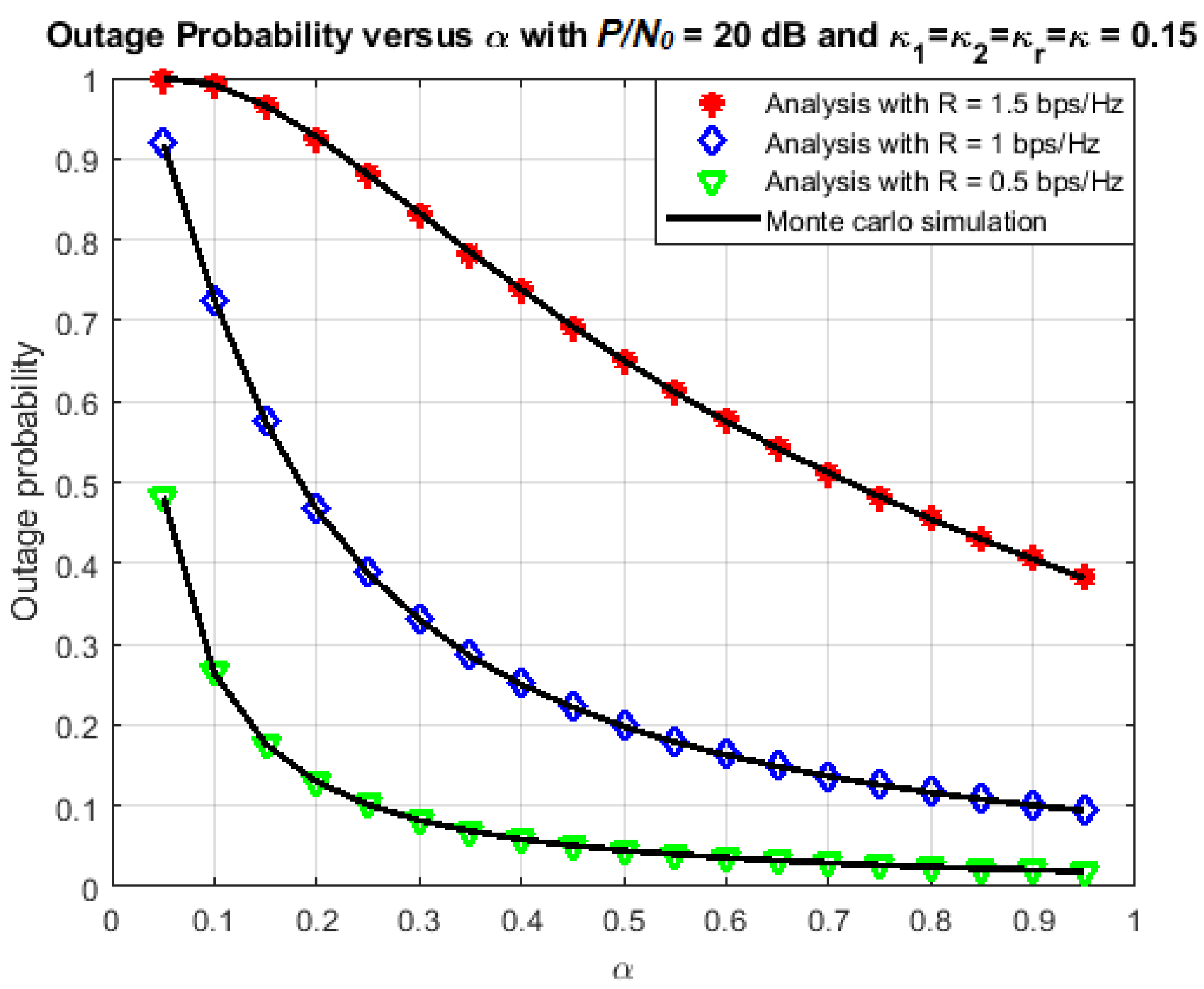
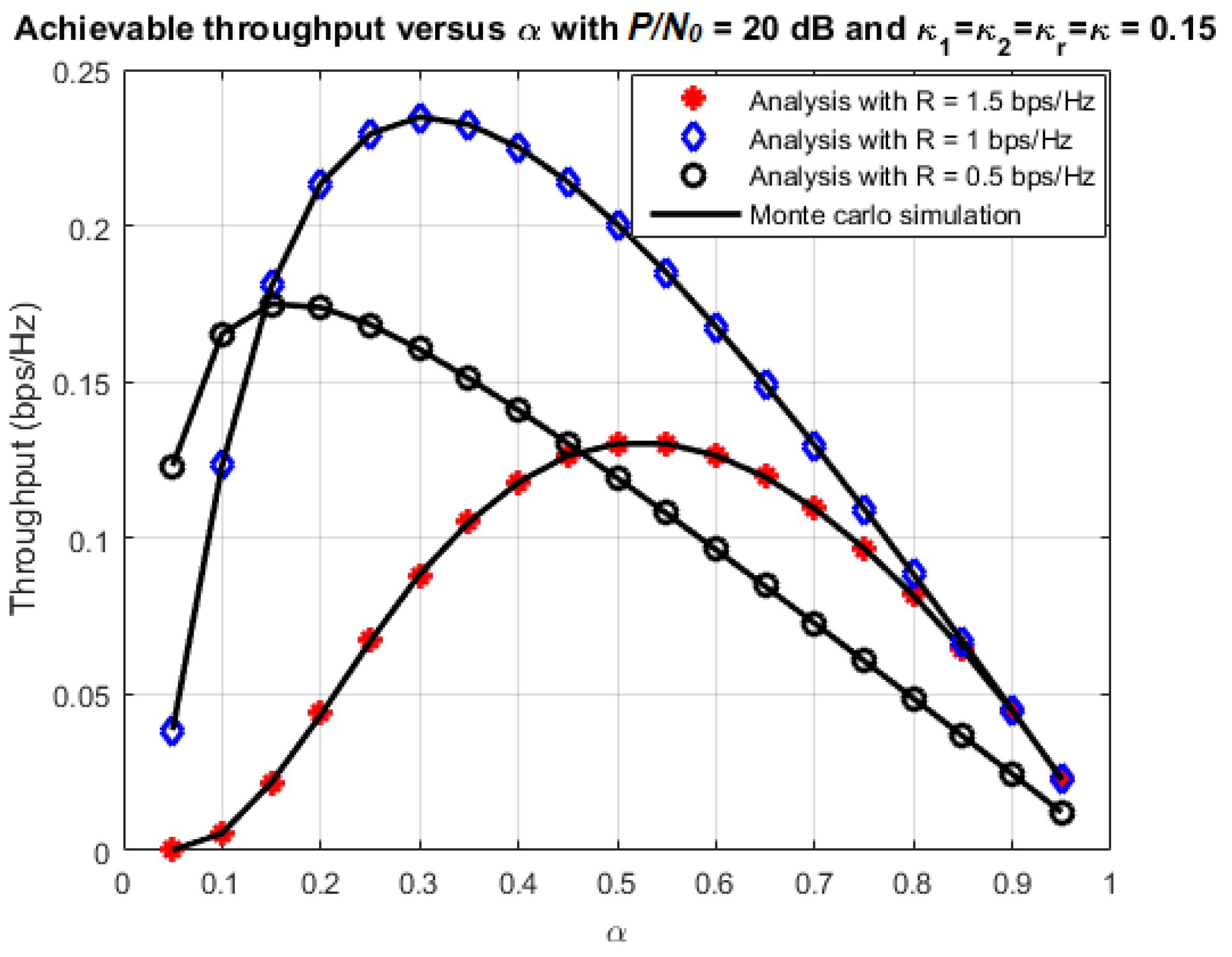
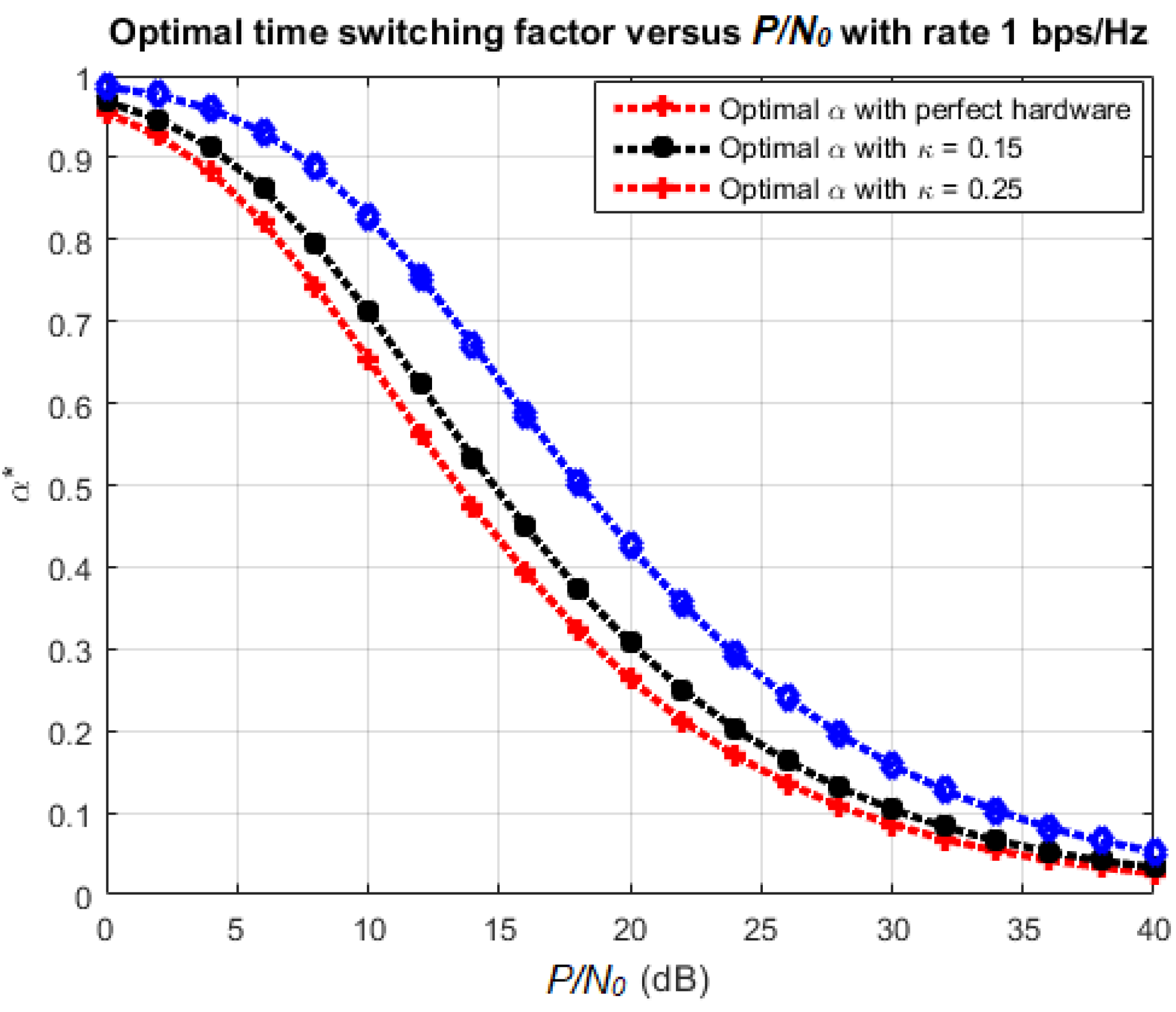
4.3. Optimal Time-Switching Factor
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AF | amplify-and-forward |
| AWGN | additive white Gaussian noise |
| BPSK | binary phase shift keying |
| CDF | cumulative distribution function |
| EH | energy harvesting |
| I/Q | In-phase/Quadrature |
| LOS | line-of-sight |
| probability density function | |
| PS | power splitting |
| QPSK | quadrature phase shift keying |
| RF | radio frequency |
| RV | random variable |
| SER | symbol-error-rate |
| SNR | signal-to-noise ratio |
| SWIPT | simultaneous wireless information and power transfer |
| TS | time switching |
| TWRN | two-way relay network |
| WSN | wireless sensor network |
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
Appendix C. Proof of Theorem 3
Appendix D. Proof of Theorem 4
References
- De Rango, F.; Lonetti, P.; Marano, S. MEA-DSR: A multipath energy-aware routing protocol for wireless Ad Hoc Networks. IFIP Int. Fed. Inf. Process. 2008, 265, 215–225. [Google Scholar] [CrossRef]
- Nguyen, H.S.; Do, D.T.; Voznak, M. Two-way relaying networks in green communications for 5G: Optimal throughput and trade-off between relay distance on power splitting-based and time switching-based relaying SWIPT. AEU-Int. J. Electron. Commun. 2016, 70, 1637–1644. [Google Scholar] [CrossRef]
- Nguyen, H.S.; Bui, A.H.; Do, D.T.; Voznak, M. Imperfect channel state information of AF and DF energy harvesting cooperative networks. China Commun. 2016, 13, 11–19. [Google Scholar] [CrossRef]
- Chu, Z.; Zhou, F.; Zhu, Z.; Hu, R.Q.; Xiao, P. Wireless Powered Sensor Networks for Internet of Things: Maximum Throughput and Optimal Power Allocation. IEEE Internet Things J. 2018, 5, 310–321. [Google Scholar] [CrossRef]
- Mekikis, P.V.; Lalos, A.S.; Antonopoulos, A.; Alonso, L.; Verikoukis, C. Wireless Energy Harvesting in Two-Way Network Coded Cooperative Communications: A Stochastic Approach for Large Scale Networks. IEEE Commun. Lett. 2014, 18, 1011–1014. [Google Scholar] [CrossRef]
- Sudevalayam, S.; Kulkarni, P. Energy Harvesting Sensor Nodes: Survey and Implications. IEEE Commun. Surv. Tutor. 2011, 13, 443–461. [Google Scholar] [CrossRef]
- Guo, S.; Wang, F.; Yang, Y.; Xiao, B. Energy-Efficient Cooperative Tfor Simultaneous Wireless Information and Power Transfer in Clustered Wireless Sensor Networks. IEEE Trans. Commun. 2015, 63, 4405–4417. [Google Scholar] [CrossRef]
- Fotino, M.; Gozzi, A.; Cano, J.C.; Calafate, C.; Rango, F.; Manzoni, P.; Marano, S. Evaluating energy consumption of proactive and reactive routing protocols in a MANET. IFIP Int. Fed. Inf. Process. 2007, 248, 119–130. [Google Scholar] [CrossRef]
- Mekikis, P.V.; Antonopoulos, A.; Kartsakli, E.; Lalos, A.S.; Alonso, L.; Verikoukis, C. Information Exchange in Randomly Deployed Dense WSNs with Wireless Energy Harvesting Capabilities. IEEE Trans. Wirel. Commun. 2016, 15, 3008–3018. [Google Scholar] [CrossRef]
- Wang, C.; Li, J.; Yang, Y.; Ye, F. Combining Solar Energy Harvesting with Wireless Charging for Hybrid Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2018, 17, 560–576. [Google Scholar] [CrossRef]
- Kosunalp, S. An energy prediction algorithm for wind-powered wireless sensor networks with energy harvesting. Energy 2017, 139, 1275–1280. [Google Scholar]
- Prijić, A.; Vračar, L.; Vučković, D.; Milić, D.; Prijić, Z. Thermal Energy Harvesting Wireless Sensor Node in Aluminum Core PCB Technology. IEEE Sens. J. 2015, 15, 337–345. [Google Scholar] [CrossRef]
- Guo, S.; Wang, C.; Yang, Y. Joint Mobile Data Gathering and Energy Provisioning in Wireless Rechargeable Sensor Networks. IEEE Trans. Mob. Comput. 2014, 13, 2836–2852. [Google Scholar] [CrossRef]
- Perera, T.D.P.; Jayakody, D.N.K.; Sharma, S.K.; Chatzinotas, S.; Li, J. Simultaneous Wireless Information and Power Transfer (SWIPT): Recent Advances and Future Challenges. IEEE Commun. Surv. Tutor. 2018, 20, 264–302. [Google Scholar] [CrossRef]
- Nguyen, H.S.; Nguyen, T.S.; Voznak, M. Relay selection for SWIPT: Performance analysis of optimization problems and the trade-off between ergodic capacity and energy harvesting. AEU-Int. J. Electron. Commun. 2018, 85, 59–67. [Google Scholar] [CrossRef]
- Varshney, L.R. Transporting information and energy simultaneously. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1612–1616. [Google Scholar]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless Information and Power Transfer: Architecture Design and Rate-Energy Tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying Protocols for Wireless Energy Harvesting and Information Processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Peng, C.; Li, F.; Liu, H. Wireless Energy Harvesting Two-Way Relay Networks with Hardware Impairments. Sensors 2017, 17, 2604. [Google Scholar] [CrossRef]
- Mouapi, A.; Hakem, N. A New Approach to Design Autonomous Wireless Sensor Node Based on RF Energy Harvesting System. Sensors 2018, 18, 133. [Google Scholar] [CrossRef]
- Le, Q.N.; Bao, V.N.Q.; An, B. Full-duplex distributed switch-and-stay energy harvesting selection relaying networks with imperfect CSI: Design and outage analysis. J. Commun. Netw. 2018, 20, 29–46. [Google Scholar] [CrossRef]
- Nguyen, D.K.; Jayakody, D.N.K.; Chatzinotas, S.; Thompson, J.S.; Li, J. Wireless Energy Harvesting Assisted Two-Way Cognitive Relay Networks: Protocol Design and Performance Analysis. IEEE Access 2017, 5, 21447–21460. [Google Scholar] [CrossRef]
- Olofsson, T.; Ahlén, A.; Gidlund, M. Modeling of the Fading Statistics of Wireless Sensor Network Channels in Industrial Environments. IEEE Trans. Signal Process. 2016, 64, 3021–3034. [Google Scholar] [CrossRef]
- Zhao, F.; Lin, H.; Zhong, C.; Hadzi-Velkov, Z.; Karagiannidis, G.K.; Zhang, Z. On the Capacity of Wireless Powered Communication Systems over Rician Fading Channels. IEEE Trans. Commun. 2018, 66, 404–417. [Google Scholar] [CrossRef]
- Hu, Y.; Cao, N.; Chen, Y. Analysis of Wireless Energy Harvesting Relay Throughput in Rician Channel. Mob. Inf. Syst. 2016, 2016. [Google Scholar] [CrossRef]
- Mishra, D.; De, S.; Chiasserini, C.F. Joint Optimization Schemes for Cooperative Wireless Information and Power Transfer over Rician Channels. IEEE Trans. Commun. 2016, 64, 554–571. [Google Scholar]
- Schenk, T. RF Imperfections in High-Rate Wireless Systems: Impact and Digital Compensation, 1st ed.; Springer: New York, NY, USA, 2008; ISBN 978-1-4020-6903-1. [Google Scholar]
- Bjornson, E.; Matthaiou, M.; Debbah, M. A New Look at Dual-Hop Relaying: Performance Limits with Hardware Impairments. IEEE Trans. Commun. 2013, 61, 4512–4525. [Google Scholar]
- Nguyen, T.N.; Duy, T.T.; Luu, G.T.; Tran, P.T.; Voznak, M. Energy Harvesting-based Spectrum Access with Incremental Cooperation, Relay Selection and Hardware Noises. Radioengineering 2017, 10, 240–250. [Google Scholar] [CrossRef]
- Katti, S.; Gollakota, S.; Katabi, D. Embracing Wireless Interference: Analog Network Coding. SIGCOMM Comput. Commun. Rev. 2007, 37, 397–408. [Google Scholar] [CrossRef]
- Qin, J.; Zhu, Y.; Zhe, P. Broadband Analog Network Coding with Robust Processing for Two-Way Relay Networks. IEEE Commun. Lett. 2017, 21, 1115–1118. [Google Scholar] [CrossRef]
- Zwillinger, D.; Moll, V.; Gradshteyn, I.; Ryzhik, I. Table of Integrals, Series, and Products, 8th ed.; Zwillinger, D., Ed.; Academic Press: Boston, MA, USA, 2015; ISBN 978-0-12-384933-5. [Google Scholar]
- Bhatnagar, M.R. On the Capacity of Decode-and-Forward Relaying over Rician Fading Channels. IEEE Commun. Lett. 2013, 17, 1100–1103. [Google Scholar] [CrossRef]
- McKay, M.R.; Grant, A.J.; Collings, I.B. Performance Analysis of MIMO-MRC in Double-Correlated Rayleigh Environments. IEEE Trans. Commun. 2007, 55, 497–507. [Google Scholar] [CrossRef]
- Duong, T.Q.; Duy, T.T.; Matthaiou, M.; Tsiftsis, T.; Karagiannidis, G.K. Cognitive cooperative networks in dual-hop asymmetric fading channels. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 955–961. [Google Scholar]
- Chong, E.K.P.; Zak, S.H. An Introduction to Optimization, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 978-1-118-27901-4. [Google Scholar]
- Morosi, C.; Pizzocchero, L. On the expansion of the Kummer function in terms of incomplete Gamma functions. Arch. Inequal. Appl. 2004, 2, 49–72. [Google Scholar]
| Symbol | Parameter Names | Values |
|---|---|---|
| Energy harvesting efficiency | 0.7 | |
| Mean of | 0.5 | |
| Mean of | 0.5 | |
| K | Rician K-factor | 3 |
| Source-power-to-noise ratio | 0–50 dB | |
| Hardware impairment levels | 0, 0.15, 0.25 | |
| R | Source transmission rate | 1.5 bps/Hz |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.N.; Quang Minh, T.H.; Tran, P.T.; Vozňák, M. Energy Harvesting over Rician Fading Channel: A Performance Analysis for Half-Duplex Bidirectional Sensor Networks under Hardware Impairments. Sensors 2018, 18, 1781. https://doi.org/10.3390/s18061781
Nguyen TN, Quang Minh TH, Tran PT, Vozňák M. Energy Harvesting over Rician Fading Channel: A Performance Analysis for Half-Duplex Bidirectional Sensor Networks under Hardware Impairments. Sensors. 2018; 18(6):1781. https://doi.org/10.3390/s18061781
Chicago/Turabian StyleNguyen, Tan N., Tran Hoang Quang Minh, Phuong T. Tran, and Miroslav Vozňák. 2018. "Energy Harvesting over Rician Fading Channel: A Performance Analysis for Half-Duplex Bidirectional Sensor Networks under Hardware Impairments" Sensors 18, no. 6: 1781. https://doi.org/10.3390/s18061781
APA StyleNguyen, T. N., Quang Minh, T. H., Tran, P. T., & Vozňák, M. (2018). Energy Harvesting over Rician Fading Channel: A Performance Analysis for Half-Duplex Bidirectional Sensor Networks under Hardware Impairments. Sensors, 18(6), 1781. https://doi.org/10.3390/s18061781







