Registration of Aerial Optical Images with LiDAR Data Using the Closest Point Principle and Collinearity Equations
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
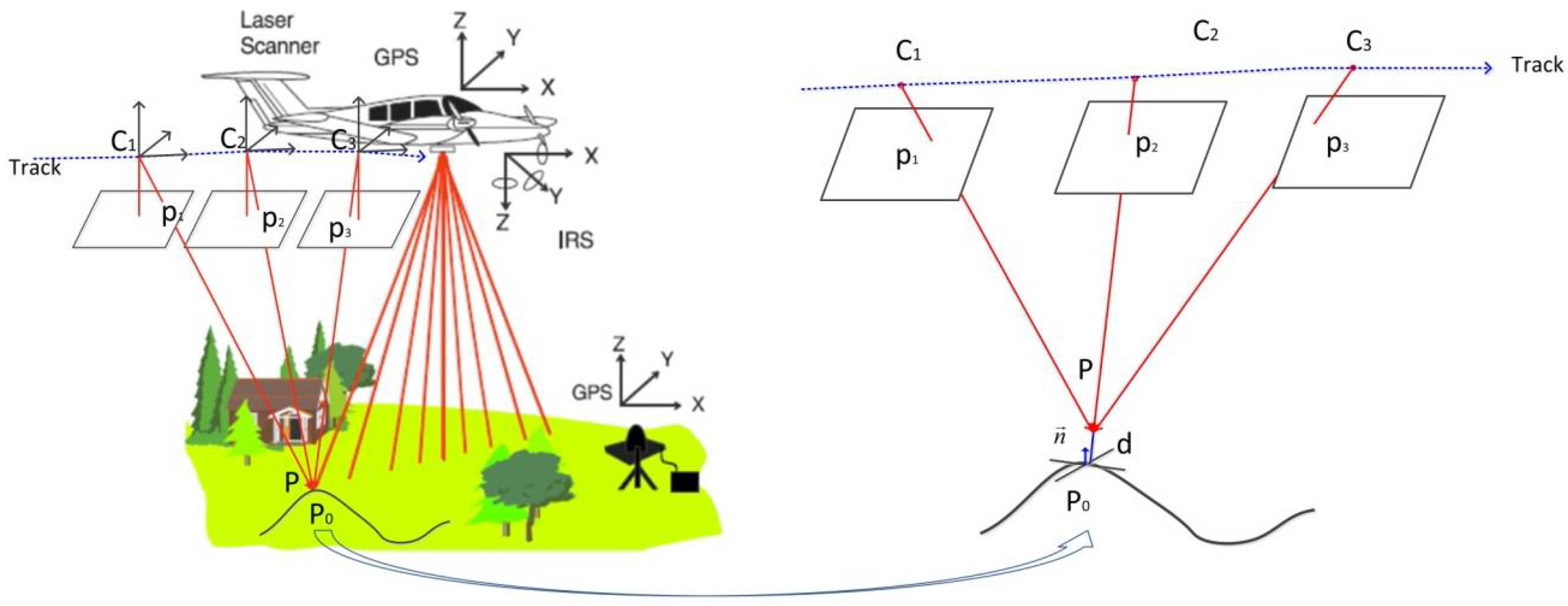
2.2. Fundamental Geometric Relationship
2.3. Parameterization of the Geometric Relationship
2.4. Bundle Adjustment Model and Solution
3. Implementation
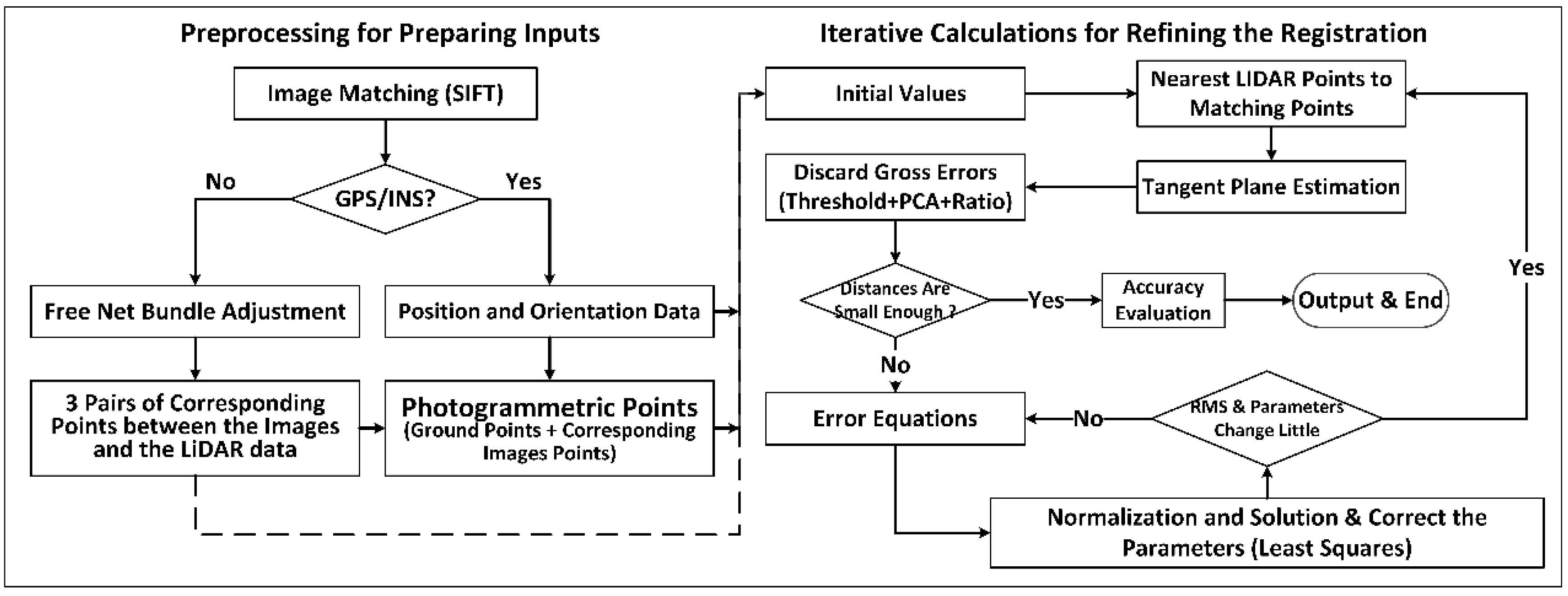
3.1. Implementation Flow
- (1)
- Preprocess the data for estimating the initial values, i.e., the exterior orientation parameters, the object point coordinates, and the intrinsic parameters;
- (2)
- Find the closest 3D point to the photogrammetric matching point from the LiDAR data, and fit a local plane to estimate the normal vector using the surrounding LiDAR points;
- (3)
- Discard the gross 3D points and check if the distances from the photogrammetric matching points to the corresponding tangent planes are all small enough to go to step 8. Otherwise, go to step 4.
- (4)
- Construct the error equations and normal equations with the initial parameters, and then reduce the structure parameters (the corrections of the coordinates of the 3D points) of the normal equations;
- (5)
- Solve the reduced normal equations for acquiring the corrections of the exterior orientation parameters and the intrinsic parameters, and further obtain the corrections of the ground point coordinates with back-substitution;
- (6)
- Correct the parameters and estimate the unit weighted root mean square error (RMSE);
- (7)
- Check if the RMSE or the corrections are small enough to go to step 2. Otherwise, go to step 4, using the corrected parameters as the initial parameters;
- (8)
- Evaluate the accuracy and output the results.
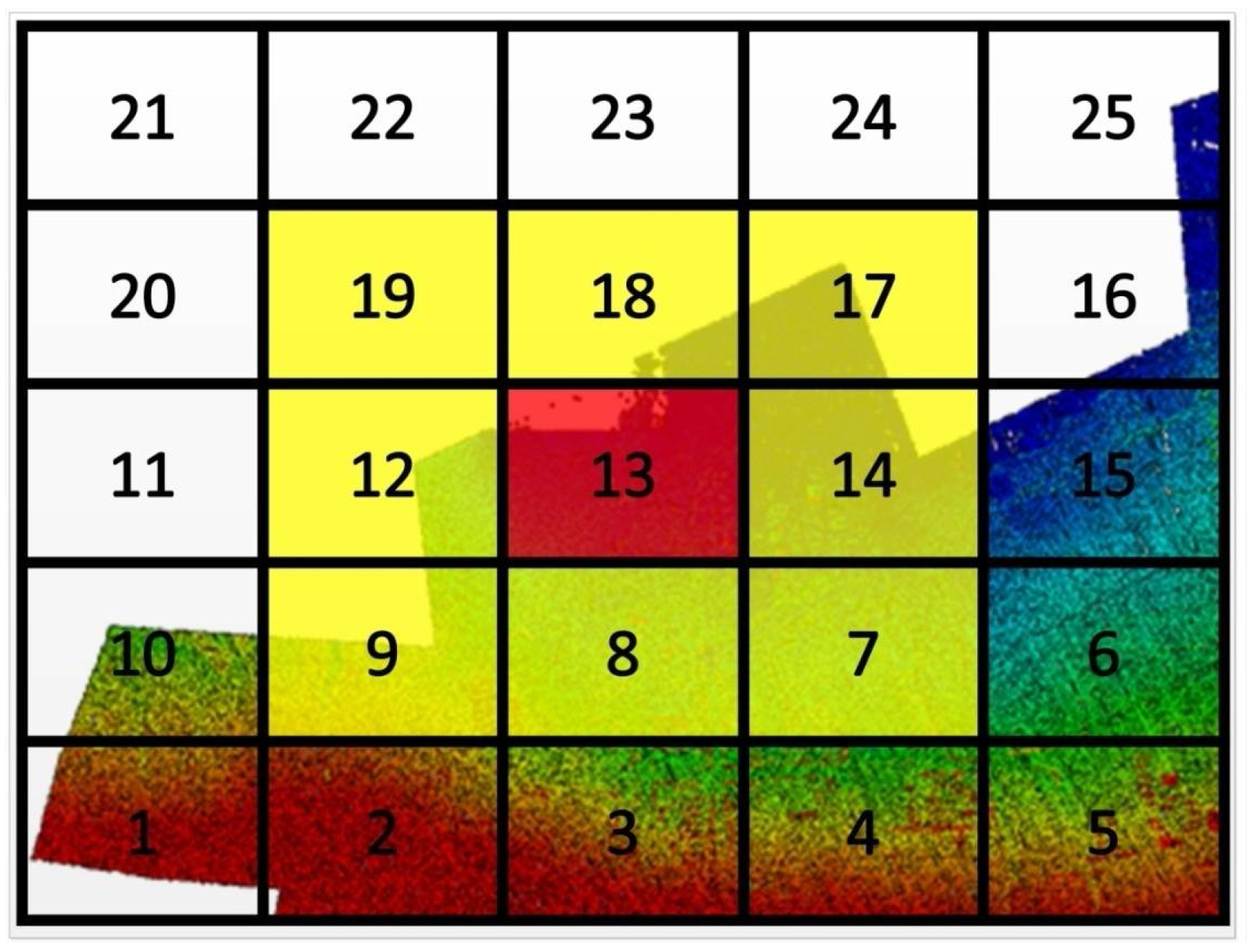
3.2. Organization Structure of the LiDAR Data
3.3. Discard the Gross Points
3.4. Assess the Registration
- (1)
- Measure the 3D coordinates corresponds to the CPs from the aerial optical images by using forward intersection, (, and is the number of the CPs);
- (2)
- Calculate the errors by comparing the measured with the coordinates of the corresponding CP ,where:
- (3)
- Calculate the statistics of the errors of CPs, for example, the minimum error (MIN), the maximum error (MAX), the mean of the errors (), and the root mean square errors (),
4. Results
4.1. Results of Unit Weighted RMS
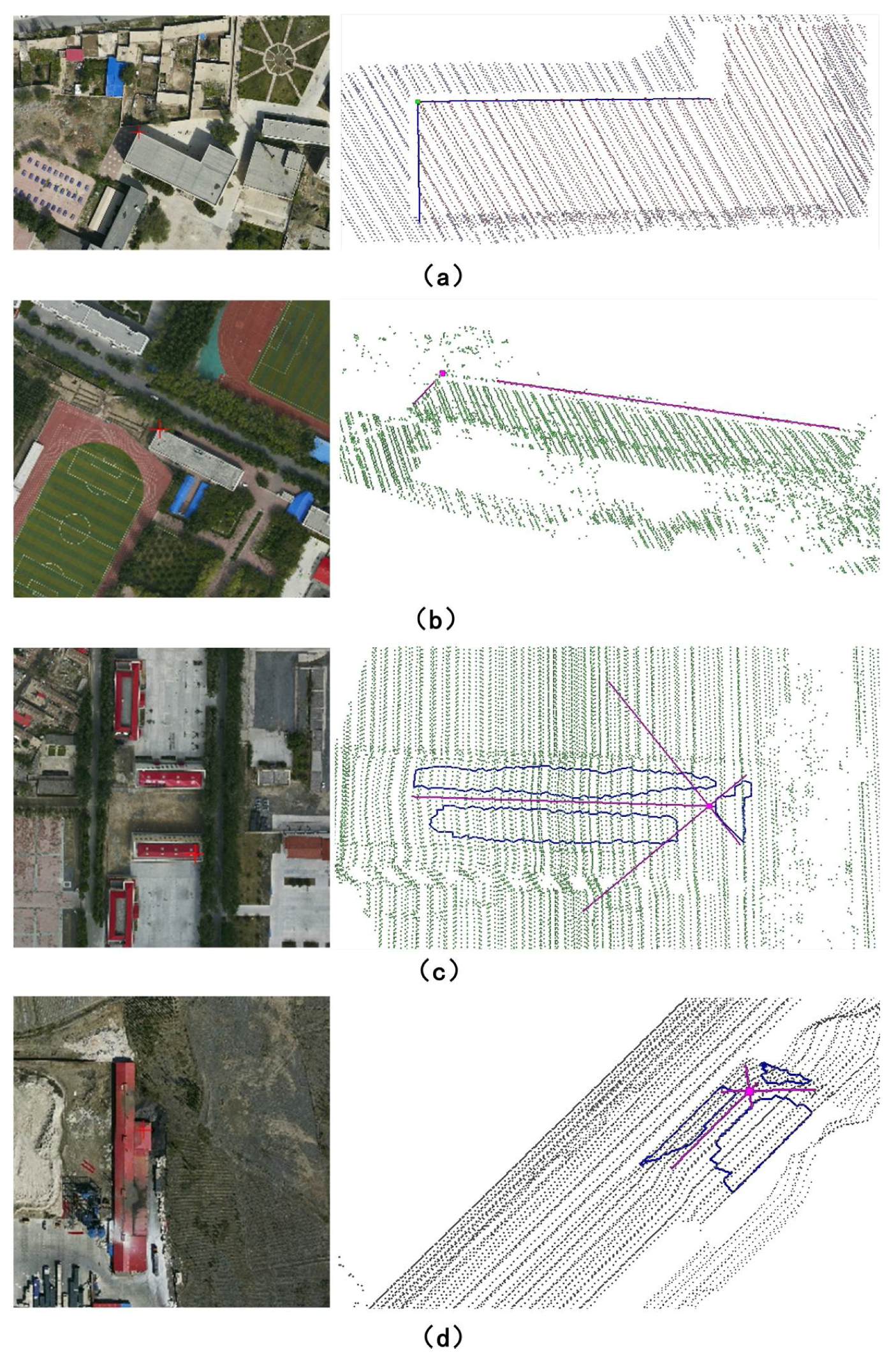
4.2. Re-Projection of the LiDAR Data
4.3. Statistics of the Check Point Errors
5. Discussion
5.1. Discussion on the Accuracy
5.2. Discussion on the Efficiency
5.3. Discussion on Some Supplementary Notes
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ackermann, F. Airborne laser scanning—Present status and future expectations. ISPRS J. Photogramm. 1999, 54, 64–67. [Google Scholar] [CrossRef]
- Baltsavias, E.P. A comparison between photogrammetry and laser scanning. ISPRS J. Photogramm. 1999, 54, 83–94. [Google Scholar] [CrossRef]
- Rönnholm, P.; Haggrén, H. Registration of laser scanning point clouds and aerial images using either artificial or natural tie features. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 3, 63–68. [Google Scholar] [CrossRef]
- Schenk, T.; Csathó, B. Fusion of LiDAR data and aerial imagery for a more complete surface description. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 310–317. [Google Scholar]
- Leberl, F.; Irschara, A.; Pock, T.; Meixner, P.; Gruber, M.; Scholz, S.; Wiechert, A. Point Clouds: LiDAR versus 3D Vision. Photogramm. Eng. Remote Sens. 2010, 76, 1123–1134. [Google Scholar] [CrossRef]
- Secord, J.; Zakhor, A. Tree detection in urban regions using aerial LiDAR and image data. IEEE Geosci. Remote Sens. Lett. 2007, 4, 196–200. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Fusion of hyperspectral and LiDAR remote sensing data for classification of complex forest areas. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1416–1427. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Zhang, C.; Fraser, C.S. Building detection in complex scenes thorough effective separation of buildings from trees. Photogramm. Eng. Remote Sens. 2012, 78, 729–745. [Google Scholar] [CrossRef]
- Murakami, H.; Nakagawa, K.; Hasegawa, H.; Shibata, T.; Iwanami, E. Change detection of buildings using an airborne laser scanner. ISPRS J. Photogramm. 1999, 54, 148–152. [Google Scholar] [CrossRef]
- Zhong, C.; Li, H.; Huang, X. A fast and effective approach to generate true orthophoto in built-up area. Sens. Rev. 2011, 31, 341–348. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Jansa, J. Automatic extraction of buildings from LiDAR data and aerial images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 569–574. [Google Scholar]
- Chen, L.C.; Teo, T.; Shao, Y.; Lai, Y.; Rau, J. Fusion of LiDAR data and optical imagery for building modeling. Int. Arch. Photogramm. Remote Sens. 2004, 35, 732–737. [Google Scholar]
- Demir, N.; Poli, D.; Baltsavias, E. Extraction of buildings and trees using images and LiDAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 313–318. [Google Scholar]
- Poullis, C.; You, S. Photorealistic large-scale urban city model reconstruction. IEEE Trans. Vis. Comput. Graph. 2009, 15, 654–669. [Google Scholar] [CrossRef] [PubMed]
- Rottensteiner, F.; Trinder, J.; Clode, S.; Kubik, K. Using the Dempster–Shafer method for the fusion of LiDAR data and multi-spectral images for building detection. Inf. Fusion 2005, 6, 283–300. [Google Scholar] [CrossRef]
- Smith, M.J.; Asal, F.; Priestnall, G. The use of photogrammetry and LiDAR for landscape roughness estimation in hydrodynamic studies. In Proceedings of the International Society for Photogrammetry and Remote Sensing XXth Congress, Istanbul, Turkey, 12–23 July 2004; p. 6. [Google Scholar]
- Postolov, Y.; Krupnik, A.; McIntosh, K. Registration of airborne laser data to surfaces generated by photogrammetric means. Int. Arch. Photogramm. Remote Sens. 1999, 32, 95–99. [Google Scholar]
- Habib, A.; Schenk, T. A new approach for matching surfaces from laser scanners and optical scanners. Int. Arch. Photogramm. Remote Sens. 1999, 32, 3–14. [Google Scholar]
- Habib, A.F.; Bang, K.I.; Aldelgawy, M.; Shin, S.W.; Kim, K.O. Integration of photogrammetric and LiDAR data in a multi-primitive triangulation procedure. In Proceedings of the ASPRS 2007 Annual Conference, Tampa, FL, USA, 7–11 May 2007. [Google Scholar]
- Skaloud, J. Reliability of Direct Georeferencing Phase 1: An Overview of the Current Approaches and Possibilities, Checking and Improving of Digital Terrain Models/Reliability of Direct Georeferencing; Infoscience EPFL: Lausanne, Switzerland, 2006. [Google Scholar]
- Vallet, J. GPS/IMU and LiDAR Integration to Aerial Photogrammetry: Development and Practical Experiences with Helimap System. Available online: http://www.helimap.eu/doc/HS_SGPBF2007.pdf (accessed on 30 May 2018).
- Kraus, K. Photogrammetry: Geometry from Images and Laser Scans; Walter de Gruyter: Berlin, Germany, 2007. [Google Scholar]
- Wu, H.; Li, Y.; Li, J.; Gong, J. A two-step displacement correction algorithm for registration of LiDAR point clouds and aerial images without orientation parameters. Photogramm. Eng. Remote Sens. 2010, 76, 1135–1145. [Google Scholar] [CrossRef]
- Kurz, T.H.; Buckley, S.J.; Howell, J.A.; Schneider, D. Integration of panoramic hyperspectral imaging with terrestrial LiDAR data. Photogramm. Rec. 2011, 26, 212–228. [Google Scholar] [CrossRef]
- Hu, J.; You, S.; Neumann, U. Integrating LiDAR, Aerial Image and Ground Images for Complete Urban Building Modeling. In Proceedings of the Third International Symposium on 3D Data Processing, Visualization and Transmission, Chapel Hill, NC, USA, 14–16 June 2006; pp. 184–191. [Google Scholar]
- Lee, S.C.; Jung, S.K.; Nevatia, R. Automatic integration of facade textures into 3D building models with a projective geometry based line clustering. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2002; pp. 511–519. [Google Scholar]
- Wang, L.; Niu, Z.; Wu, C.; Xie, R.; Huang, H. A robust multisource image automatic registration system based on the SIFT descriptor. INT J. Remote Sens. 2012, 33, 3850–3869. [Google Scholar] [CrossRef]
- Cen, M.; Li, Z.; Ding, X.; Zhuo, J. Gross error diagnostics before least squares adjustment of observations. J. Geodesy 2003, 77, 503–513. [Google Scholar] [CrossRef]
- Li, H.; Zhong, C.; Zhang, Z. A comprehensive quality evaluation system for coordinate transformation. In Proceedings of the IEEE 2010 Second International Symposium on Data, Privacy and E-Commerce (ISDPE), Buffalo, NY, USA, 13–14 September 2010; pp. 15–20. [Google Scholar]
- Toth, C.; Ju, H.; Grejner-Brzezinska, D. Matching between different image domains. In Photogrammetric Image Analysis; Springer: Berlin/Heidelberg, Germany, 2011; pp. 37–47. [Google Scholar]
- Kwak, T.S.; Kim, Y.I.; Yu, K.Y.; Lee, B.K. Registration of aerial imagery and aerial LiDAR data using centroids of plane roof surfaces as control information. KSCE J. Civ. Eng. 2006, 10, 365–370. [Google Scholar] [CrossRef]
- Mitishita, E.; Habib, A.; Centeno, J.; Machado, A.; Lay, J.; Wong, C. Photogrammetric and LiDAR data integration using the centroid of a rectangular roof as a control point. Photogramm. Rec. 2008, 23, 19–35. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, X.; Shen, X. Automatic registration of urban aerial imagery with airborne LiDAR data. J. Remote Sens. 2012, 16, 579–595. [Google Scholar]
- Xiong, X. Registration of Airborne LiDAR Point Cloud and Aerial Images Using Multi-Features; Wuhan University: Wuhan, China, 2014. [Google Scholar]
- Habib, A.; Ghanma, M.; Morgan, M.; Al-Ruzouq, R. Photogrammetric and LiDAR data registration using linear features. Photogramm. Eng. Remote Sens. 2005, 71, 699–707. [Google Scholar] [CrossRef]
- Kim, H.; Correa, C.D.; Max, N. Automatic registration of LiDAR and optical imagery using depth map stereo. In Proceedings of the IEEE International Conference on Computational Photography (ICCP), Santa Clara, CA, USA, 2–4 May 2014. [Google Scholar]
- Zhao, W.; Nister, D.; Hsu, S. Alignment of continuous video onto 3D point clouds. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1305–1318. [Google Scholar] [CrossRef] [PubMed]
- Besl, P.J.; McKay, N.D. A Method for registration of 3-D shapes. IEEE Trans. Pattern Anal. 1992, 2, 239–256. [Google Scholar] [CrossRef]
- Pothou, A.; Karamitsos, S.; Georgopoulos, A.; Kotsis, I. Assessment and comparison of registration algorithms between aerial images and laser point clouds. In Proceedings of the ISPRS, Symposium: From Sensor to Imagery, Paris, France, 4–6 July 2006. [Google Scholar]
- Teo, T.; Huang, S. Automatic Co-Registration of Optical Satellite Images and Airborne LiDAR Data Using Relative and Absolute Orientations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2229–2237. [Google Scholar] [CrossRef]
- Habib, A.F.; Ghanma, M.S.; Mitishita, E.A.; Kim, E.; Kim, C.J. Image georeferencing using LiDAR data. In Proceedings of the 2005 IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS’05), Seoul, Korea, 29 July 2005; pp. 1158–1161. [Google Scholar]
- Shorter, N.; Kasparis, T. Autonomous Registration of LiDAR Data to Single Aerial Image. In Proceedings of the 2008 IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS 2008), Boston, MA, USA, 7–11 July 2008; pp. 216–219. [Google Scholar]
- Deng, F.; Hu, M.; Guan, H. Automatic registration between LiDAR and digital images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 7, 487–490. [Google Scholar]
- Ding, M.; Lyngbaek, K.; Zakhor, A. Automatic registration of aerial imagery with untextured 3D LiDAR models. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Wang, L.; Neumann, U. A robust approach for automatic registration of aerial images with untextured aerial LiDAR data. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, FL, USA, 20–25 June 2009; pp. 2623–2630. [Google Scholar]
- Choi, K.; Hong, J.; Lee, I. Precise Geometric Resigtration of Aerial Imagery and LiDAR Data. ETRI J. 2011, 33, 506–516. [Google Scholar] [CrossRef]
- Yang, B.; Chen, C. Automatic registration of UAV-borne sequent images and LiDAR data. ISPRS J. Photogramm. 2015, 101, 262–274. [Google Scholar] [CrossRef]
- Safdarinezhad, A.; Mokhtarzade, M.; Valadan Zoej, M. Shadow-based hierarchical matching for the automatic registration of airborne LiDAR data and space imagery. Remote Sens. 2016, 8, 466. [Google Scholar] [CrossRef]
- Javanmardi, M.; Javanmardi, E.; Gu, Y.; Kamijo, S. Towards High-Definition 3D Urban Mapping: Road Feature-Based Registration of Mobile Mapping Systems and Aerial Imagery. Remote Sens. 2017, 9, 975. [Google Scholar] [CrossRef]
- Zöllei, L.; Fisher, J.W.; Wells, W.M. A unified statistical and information theoretic framework for multi-modal image registration. In Proceedings of the Information Processing in Medical Imaging, Ambleside, UK, 20–25 July 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 366–377. [Google Scholar]
- Le Moigne, J.; Netanyahu, N.S.; Eastman, R.D. Image Registration for Remote Sensing; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Suri, S.; Reinartz, P. Mutual-information-based registration of TerraSAR-X and Ikonos imagery in urban areas. IEEE Trans. Geosci. Remote Sens. 2010, 48, 939–949. [Google Scholar] [CrossRef]
- Mastin, A.; Kepner, J.; Fisher, J. Automatic registration of LiDAR and optical images of urban scenes. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, FL, USA, 20–25 June 2009; pp. 2639–2646. [Google Scholar]
- Parmehr, E.G.; Zhang, C.; Fraser, C.S. Automatic registration of multi-source data using mutual information. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 7, 303–308. [Google Scholar] [CrossRef]
- Parmehr, E.G.; Fraser, C.S.; Zhang, C.; Leach, J. Automatic registration of optical imagery with 3D LiDAR data using local combined mutual information. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 5, W2. [Google Scholar] [CrossRef]
- Parmehr, E.G.; Fraser, C.S.; Zhang, C.; Leach, J. Automatic registration of optical imagery with 3D LiDAR data using statistical similarity. ISPRS J. Photogramm. Remote Sens. 2014, 88, 28–40. [Google Scholar] [CrossRef]
- Zheng, S.; Huang, R.; Zhou, Y. Registration of Optical Images with LiDAR Data and Its Accuracy Assessment. Photogramm. Eng. Remote Sens. 2013, 79, 731–741. [Google Scholar] [CrossRef]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle adjustment—A modern synthesis. In Vision Algorithms: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2000; pp. 298–372. [Google Scholar]
- Mikhail, E.M.; Bethel, J.S.; McGlone, J.C. Introduction to Modern Photogrammetry; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Z.; Ke, T.; Zhang, Y.; Duan, Y. Digital Photogrammetry GRID (DPGRID) and its application. In Proceedings of the ASPRS 2011 Annual Conference, Milwaukee, WI, USA, 1–5 May 2011. [Google Scholar]
- De Berg, M.; Van Kreveld, M.; Overmars, M.; Schwarzkopf, O.C. Computational Geometry: Algorithms and Applications; Springer: New York, NY, USA, 2000. [Google Scholar]
- Weingarten, J.W.; Gruener, G.; Siegwart, R. Probabilistic plane fitting in 3D and an application to robotic mapping. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (ICRA’04), New Orleans, LA, USA, 26 April–1 May 2004; pp. 927–932. [Google Scholar]
- Kaartinen, H.; Hyyppä, J.; Gülch, E.; Vosselman, G.; Hyyppä, H.; Matikainen, L.; Hofmann, A.D.; Mäder, U.; Persson, Å.; Söderman, U.; et al. Accuracy of 3D city models: EuroSDR comparison. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2005, 36, 227–232. [Google Scholar]





| Data | I | II | III | IV | |
|---|---|---|---|---|---|
| Images | Pixel Size (mm) | 0.006 | 0.006 | 0.012 | 0.012 |
| Frame Size (pixel) | 6732 × 8984 | 6732 × 8984 | 7680 × 13,824 | 7680 × 13,824 | |
| Focal Length (mm) | 51.0 | 51.0 | 120.0 | 120.0 | |
| Flying Height (m) | 900 | 700 | 1800 | 1700 | |
| GSD (m) | 0.10 | 0.09 | 0.18 | 0.17 | |
| Forward Overlap | 80% | 60% | 80% | 65% | |
| Side Overlap | 75% | 30% | 35% | 20% | |
| Image Number | 1432 | 222 | 270 | 108 | |
| Stripe Number | 26 | 6 | 8 | 4 | |
| LiDAR Data | Point Distance (m) | 0.5 | 0.5 | 0.9 | |
| Point Density (pts/m2) | 4.0 | 4.8 | 1.3 | ||
| Point Number | 183,062,176 | 251,893,187 | 273,780,202 | ||
| Stripe Number | - | 6 | 12 | ||
| File Number | 424 | 6 | 12 | ||
| Data | RMS0 | RMSI (mm) | RMSd (m) |
|---|---|---|---|
| I | 0.0022 | 0.0027 | 0.18 |
| II | 0.0026 | 0.0037 | 0.20 |
| III | 0.0036 | 0.0052 | 0.34 |
| IV | 0.0033 | 0.0062 | 0.24 |
| Data | Before the Iterative Calculations | After the Iterative Calculations | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MIN | MAX | MIN | MAX | ||||||||
| Ⅰ | −12.86 | 36.92 | −3.175 | 9.270 | 13.86 | −0.375 | 0.400 | −0.020 | 0.192 | 0.270 | |
| −24.38 | 30.69 | −3.982 | 10.30 | −0.445 | 0.355 | −0.004 | 0.189 | ||||
| −93.31 | 355.9 | 24.747 | 97.13 | −0.293 | 0.286 | −0.012 | 0.134 | ||||
| Ⅱ | −0.750 | 0.964 | 0.080 | 0.369 | 0.437 | −0.205 | 0.282 | 0.027 | 0.126 | 0.165 | |
| −0.489 | 0.499 | 0.061 | 0.235 | −0.185 | 0.199 | −0.008 | 0.107 | ||||
| −7.049 | 1.592 | −2.160 | 3.035 | −0.130 | 0.196 | 0.031 | 0.096 | ||||
| Ⅲ | −0.508 | 0.271 | −0.081 | 0.219 | 0.585 | −0.271 | 0.241 | −0.053 | 0.159 | 0.225 | |
| −0.434 | 1.048 | 0.389 | 0.542 | −0.225 | 0.290 | 0.063 | 0.158 | ||||
| −0.984 | 1.617 | 0.237 | 0.710 | −0.147 | 0.230 | 0.066 | 0.150 | ||||
| Ⅳ | −0.299 | 1.136 | 0.518 | 0.644 | 0.806 | −0.161 | 0.289 | 0.038 | 0.147 | 0.218 | |
| −0.183 | 0.917 | 0.393 | 0.486 | −0.276 | 0.227 | −0.040 | 0.161 | ||||
| −1.746 | 2.207 | 0.014 | 0.937 | −0.179 | 0.246 | 0.024 | 0.120 | ||||
| Author | Image GSD (m) | Image Number | LiDAR Point Distance (m) | CP Number | Method |
|---|---|---|---|---|---|
| Kwak et al. [31] | 0.25 | - 4 | 0.68 | 13 | Bundle adjustment with centroids of plane roof surfaces as control points. |
| Mitishita et al. [32] | 0.15 | 3 | 0.70 | 19 | Bundle adjustment with the centroid of a rectangular building roof as a control point. |
| Zhang et al. [33] 2 | 0.14 | 8 | 1.0 | 9 | (1) Bundle adjustment with control points extracted by using image matching between the LiDAR intensity images and the optical images; (2) Bundle adjustment with building corners as control points |
| Xiong [34] | 0.09 | 84 | 0.5 | 109 3 | Bundle adjustment with multi-features as control points. |
| Author | ||||
|---|---|---|---|---|
| Kwak et al. [31] | 0.76 | 0.98 | 1.24 | 1.06 |
| Mitishita et al. [32] | 0.21 | 0.31 | 0.37 | 0.36 |
| Zhang et al. [33] 1 | 0.24 | 0.28 | 0.37 | 0.23 |
| Zhang et al. [33] 2 | 0.16 | 0.19 | 0.25 | 0.13 |
| Xiong [34] | 0.23 | 0.22 | 0.33 | 0.13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, R.; Zheng, S.; Hu, K. Registration of Aerial Optical Images with LiDAR Data Using the Closest Point Principle and Collinearity Equations. Sensors 2018, 18, 1770. https://doi.org/10.3390/s18061770
Huang R, Zheng S, Hu K. Registration of Aerial Optical Images with LiDAR Data Using the Closest Point Principle and Collinearity Equations. Sensors. 2018; 18(6):1770. https://doi.org/10.3390/s18061770
Chicago/Turabian StyleHuang, Rongyong, Shunyi Zheng, and Kun Hu. 2018. "Registration of Aerial Optical Images with LiDAR Data Using the Closest Point Principle and Collinearity Equations" Sensors 18, no. 6: 1770. https://doi.org/10.3390/s18061770
APA StyleHuang, R., Zheng, S., & Hu, K. (2018). Registration of Aerial Optical Images with LiDAR Data Using the Closest Point Principle and Collinearity Equations. Sensors, 18(6), 1770. https://doi.org/10.3390/s18061770





