Abstract
Inspired by the problem that the current spatial registration methods are unsuitable for three-dimensional (3-D) sensor on high-dynamic platform, this paper focuses on the estimation for the registration errors of cooperative missiles and motion states of maneuvering target. There are two types of errors being discussed: sensor measurement biases and attitude biases. Firstly, an improved Kalman Filter on Earth-Centered Earth-Fixed (ECEF-KF) coordinate algorithm is proposed to estimate the deviations mentioned above, from which the outcomes are furtherly compensated to the error terms. Secondly, the Pseudo Linear Kalman Filter (PLKF) and the nonlinear scheme the Unscented Kalman Filter (UKF) with modified inputs are employed for target tracking. The convergence of filtering results are monitored by a position-judgement logic, and a low-pass first order filter is selectively introduced before compensation to inhibit the jitter of estimations. In the simulation, the ECEF-KF enhancement is proven to improve the accuracy and robustness of the space alignment, while the conditional-compensation-based PLKF method is demonstrated to be the optimal performance in target tracking.
1. Introduction
The spatial registration is vital for current and near-future cooperative combat missions through the vehicle network to estimate and compensate the sensor errors by measuring the common target [1,2,3].
Depending on the dimension of the error model, the algorithm is usually divided into a two-dimensional (2-D) system and a three-dimensional (3-D) system [4]. Many typical 2-D algorithms have been proposed in literatures. e.g., Real Time Quality Control (RTQC) [5], Least Square (LS) [6], Generalized Least Square (GLS) [7], Exact Maximum Likelihood (EML) [8]. Compared to 3-D algorithms, the former wherein has relatively lower computational complexity at the expense of accuracy. Meanwhile, a number of online registration algorithms for 3-D sensors have been put forward. Unfortunately, there are few approaches taking both measurement errors and orientation errors into consideration. The traditional Earth-Centered Earth-Fixed coordinate (ECEF) method [9] capable of solving the spatial registration problem concentrates on the measurement biases, yet ignores the attitude errors of sensors themselves when the measurement states are transformed from separate reference frame to public system. The neglect of measurement deviations in the Kalman-filter-based method [10] proposed for attitude biases makes it deficient way as well. Although the algorithm [11] combines the two types of errors for estimation, it only fits for the situation where the attitude angles are small and the sensors are close to each other.
Besides, there is another branch of research that integrates the registration with target tracking. The paper [12] presents an improved method based on the state value and space deviation of federated filtering of unscented Kalman filter and standard Kalman filter, conducting registration and tracking simultaneously. However, this method is thought to accounts for more computation [13]. For this reason, the processes of those two are usually performed separately in current investigation. Moreover, most methods referred above are only suitable for sensors on stationary base which would be deemed points in the relative motion between them and targets. Failure of them to adapts for the sensors having their own attitude and position changes (e.g., radar seeker on high-speed moving and turning missiles) is considered as the deficiency.
Target tracking, based on sensor measurement information, is a technique for estimation of the state (position, speed) of a moving target at the current or future time [14,15]. Filtering is the cornerstone of tracking algorithm with the existence of systematic and measured noise. The typical filters have been greatly adopted for more than half a century: Kalman Filter (KF) is first exploited by [16] to solve the problem of tracking for linear system. Extended Kalman Filter (EKF) [17] transforms nonlinear model to linear one and then takes KF to estimate the states, which easily diverges under strongly nonlinearity. On this basis, [18] puts forwards Unscented Kalman Filter (UKF) which is apt for both linear and nonlinear tracking, but compromised by the heavy computation. To make up the disadvantage of the methods above, the Pseudo Linear Kalman Filter (PLKF) [19] which takes the models in [20] preserves the nonlinearity in the system. With the development of computers and data links during the last ten years, tracking performance is increased through the design and implementation of systems using data collected by a network of spatially distributed sensors. Consequently, the spatial registration has gradually become the pre-requisite for information process and data fusion for multiple sensors.
In the case of two missiles cooperative target tracking, this paper employs an improved Kalman Filter on Earth-Centered Earth-Fixed coordinate (ECEF-KF) algorithm which transforms the measurements to public target from body systems into the ECEF system so as to isolate the motion of sensors. Taking advantage of the difference of transformed values, the systemic biases and the attitude errors are estimated simultaneously. Subsequently, the results of registration algorithm adopted are fed back to compensate the inputs of linear PLKF and nonlinear UKF which are used for target tracking. It is found in this paper that the convergence of ECEF-KF and the effectiveness of compensation depend on the quality of the 3-D measurement data that can be adversely affected by the movement of missiles and target. More specifically, the 3-D information may loses one degree of freedom on any dimension and turns to be 2-D with the approach of vehicles, ruining the registration results. For sake of the possible divergence, a Low-pass First Order Filter (LFOF) with position-judgement condition is introduced to detect and inhibit divergent trend, furtherly improves the accuracy of the target tracking. The paper researches theoretically in the information processing methods, which conduces furtherly to the application of sensor in the engineering problems.
The main contributions are listed below:
- A new spatial registration algorithm is first proposed for sensors on high-speed moving vehicles, realizing the simultaneous estimation for system and attitude biases which are compensated to the biased measurements of the tracking schemes. The accuracy and robustness of the estimation of target state are effectively improved.
- Inspired by the ideal of integral controller, a Low-pass filter is used when the position relationship between missiles and target meets the special condition to inhibit the jitter of estimations. This skill improve the adaptability of tracking system without time-delay caused by the common integral controllers.
This paper is organized as follows. The definition of each coordinate system and their transform relationships are given in Section 2. Section 3 develops the model of original and improved ECEF-KF algorithm. The compensation-based PLKF and UKF methods with strategies of divergence detection and inhibition is introduced in Section 4. Section 5 presents the performance of improved ECEF-KF under two cases of motion of missiles and compares PLKF methods and UKF methods. The concluding remarks are given in Section 6.
2. Coordinate Defination and Transformation
Before the model development, the reference frames will be introduced in this section.
2.1. Definition of Coordinate System
In the spatial alignment of multiple missiles, each member has its own reference frame or coordinate system. Among which, the measurements of sensors on the platform are obtained in the body coordinate system, the attitude angles and the position are usually described in the Local East, North, Up system and ECEF coordinate system respectively. The definition of these coordinate systems referred are listed as follows (see in Figure 1).
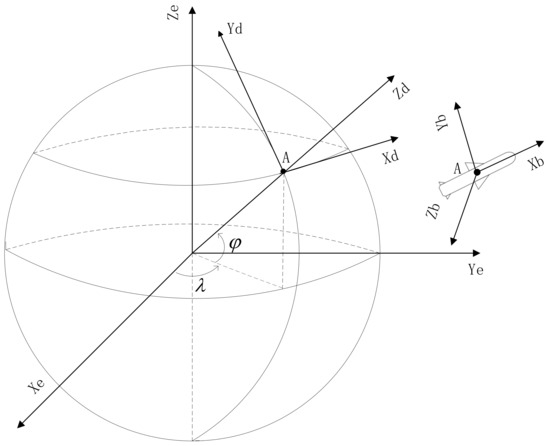
Figure 1.
The definition of coordinate systems.
(1) ECEF Coordinate : As defined in WGS-84 coordinate [21], the origin is located in the earth’s Center of Mass (CM). The axis points to the direction of Conventional Terrestrial Pole (CTP). The axis points to the intersection point of the zero-meridian plane and the CTP equator defined in Bureau International deI’Heure (BIH) 1984 [22]. The axis and the axis are perpendicular to the axis, forming the right-hand coordinate system.
(2) Local East, North and Up (LENU) Coordinate : The origin is the projection of the platform’s CM to the surface of the earth, the , and axis points to the east, north and up respectively [23].
(3) Body Coordinate : The origin is located in the CM of platform. The axis coincides with the longitudinal axis of platform, pointing to the head as positive. The axis coincides with the vertical axis of platform, pointing to the up as positive. And the is determined by the right-hand rule.
2.2. Transformation between Reference Frames
(1) ECEF and LENU Coordinate: Let the column vectors and (the superscript T denotes matrix transposition) represent the ECEF coordinate and LENU coordinate respectively. The transformation from the later to the former is given by
where is the orthogonal matrix given by [24]
and denote the longitude and latitude of platform. Besides, if the longitude , latitude and height h are known, its ECEF coordinate can be calculated by [25]
where is the equatorial radius, e is the eccentricity of the earth.
(2) LENU and Body Coordinate: Let the column vectors represents the body coordinates. Likewise, the transformation from the body coordinate to the LENU coordinate is represented by a matrix in [26]
where , and are the yaw, pitch and roll angle of the platform respectively.
3. Registration Algorithm
The algorithm is based on the following assumptions:
- The attitude biases and the measured deviations are considered as constant and the attitude biases are assumed as small values.
- The coupling between biases is ignored.
- The position errors of sensors are not considered. It means the positions are known exactly with other possible assistant device (e.g., GPS).
3.1. Attitude and Sensor Measurement Errors
The ECEF-KF algorithm is introduced to estimate attitude and sensor measurement biases which are modeled as additive constant biases to the reported values. That is
where , , are the reported values of the k th sensor’s yaw, pitch and roll angles. , , are the true values and , , are the bias errors of these angles. Likewise, the measurement erros are modeled as
where , , represent the true values of the kth sensor’s slope distance (range), the elevation and azimuth angle of line of sight respectively. It is notable that the measurement errors include constant biases and random noises, that is
where , , are the constant biases, and , , denote the random noises.
3.2. Traditional ECEF-KF Algorithm
Given the true measurements of range r, elevation and azimuth of radar sensor which are defined under body system, the non-linear relationship between target state and measurement is (see in Figure 2)
then the coordinate of target can be written as
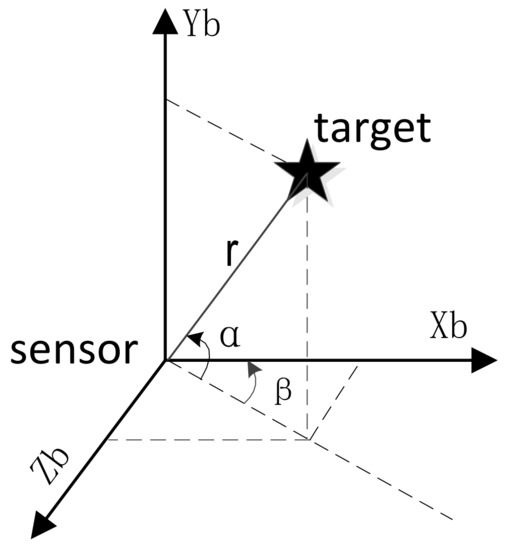
Figure 2.
Measurement of target in body coordinate system.
Substitute (6) in (9)
Let , . Since the measurement errors are small values as assumed, the Equation (10) can be expressed as the first-order linearity of the errors
where is the reported coordinate of target, is the Jacobian matrix of with respect to given by
Now, here are two sensors A and B. (,,) and (,,) are their longitude, latitude and height coordinates. Let and be the ECEF coordinates of two sensors respectively and represents the ECEF coordinate of target. and are the body coordinates of target from two sensors respectively. Thus, the following relationships are given.
From the two equations above, we obtain the following equality
where and denote the rotational matrices in (13) and (14). and can be expanded to the linear form like (11), that is
where and represent the ECEF coordinates of target reported by sensors A and B. In order to estimate the measurement errors of sensors A and B, the state vector is developed as
where , , and are the measurment biases of sensor A, , , denote the measurment biases of sensor B. Since these terms are constant, the discrete equation of the state can be written as
where is zero mean white Gaussian process noise with covariance . is the state transition matrix. In (16), let , , , . Therefore, the measurement equation can be expressed as
where is zero mean white Gaussian process noise with covariance . Kalman filtering techniques [27] using (18) and (19) can be applied to estimate sensor errors online.
3.3. Improved ECEF-KF Algorithm
From the above derivation, it can be seen that the traditional ECEF-KF method only fits for sensors on stationary base without attitude errors. For the sensors on high-speed moving missiles, the position’s and attitude’s change of missiles will influence the actual measurements, and the oriented biases of each partner which may cause the misalignment of tracking or even the loss of target must not be ignored. Considering this situation, an improved method making minor modifications on the original algorithm, is proposed to realize the simultaneous estimation of attitude and measurement errors.
Here assuming two missiles A and B as well. Considering the attitude change, (13) and (14) are modified as
where and equal with and in (15) are rotation matrices from the LENU coordinate system to the ECEF coordinate system (2) of missiles A and B. and represent rotation matrices from the body coordinate system to the LENU coordinate system (4). Combining the two equations above, there is
Since the rotation matrix is orthogonal [28], (for one orthogonal matrix , there is ), (22) is transformed to
When attitude errors are small values, the rotation matrix from body coordinate system to LENU system can be written as [29]
Thus
Both sides of (26) are multiplied by
Expand and into the form of first-order linearity as (11). Since the item and are both small values, their product is ignored. Therefore, (27) becomes
In the above formula, the left part of the equation is labeled as . Let , and the last term in the right part of the equation is represented as , we arrive at
The following work is to transform to the linear form of attitude errors. The matrix is written as the following
where
and are the column vectors of A and B respectively.
Remark 1.
Here giving an equality:
Proof of Remark 1.
So, the Theorem 1 is true. ☐
Likewise
Let
Let (34) in (29)
where are constant measurment biases of missile A and B respectively, are random noises added to these measurements.
Considering the terms of attitude errors, we redefine
to be the 12-dimensional state vector. The corrected discrete equation of the state is
Since the attitude and measurement biases are all considered as constant values.
4. Target Tracking with Error Compensation
4.1. Compensation PLKF Algorithm
In Section 3, the coordinate of target in the body coordinate system has been given in (10):
where .
In order to improve the accuracy of target tracking, the error compensation method is introduced.The estimation of registration errors including range , elevation angle , azimuth angle and attitude errors , , are obtained through ECEF-KF. These estimated values are compensated to the error terms of the equation above and the rotation matrix in (24), that is
Let , , , (39) becomes
Considering that are small values, there are , , , . While, ignore the high-level small quantities, which means , , . Then, the equation above turns to the following pseudo measurement:
where are pseudo measurement noises, here are
The covariance of these measurement noises is
where
Representing as the state vector, the continuous equation is
where is zero-mean white noise with covariance , and is the transition matrix. The CV (Constant Velocity) model [30] is chosen as the target motion model, that is
The discrete-time state function is
where is discrete-time process noise, and the state transition matrix at time over time interval is given by
The covariance of the discrete-time process noise is
Let denotes the measurement vector. Therefore, the measurement equation is transformed to the linear function of the target state.
where is zero-mean Gaussian noise.
4.2. Conpensation UKF Algorithm
If we directly take the compensation inputs as the measurements of filter , then the measurement equation will be changed as the non-linear form (8)
where is measurement noise with as variance. Combined with (46) and (48), the UKF algorithm for nonlinear system state estimation is exactly required. The formulas of UKF are directly given as follows.
Initializing:
Computing sigma point set:
Prediction updating:
Measurement updating:
4.3. Compensation Condition and Strategy
Remark 2.
Considering the situation where two missiles and target are on the same latitude or longitude plane during their fight, the 3-D tracking problem will become 2-D.
As shown in the Figure 3, coordinate system is the longitude, latitude and height coordinate system. The axes , , denote longitude, height and latitude respectively. In this moment, the two missiles and the target are on the same latitude plane and the track plane is parallel to the plane , which means the measurement of space registration will lost the measurements on axis and the tracking problem in 3-D space turns to be on the plane . If two missiles keep flying on this plane for some time, the estimation of errors may be divergent, which will worsen the compensation effect.
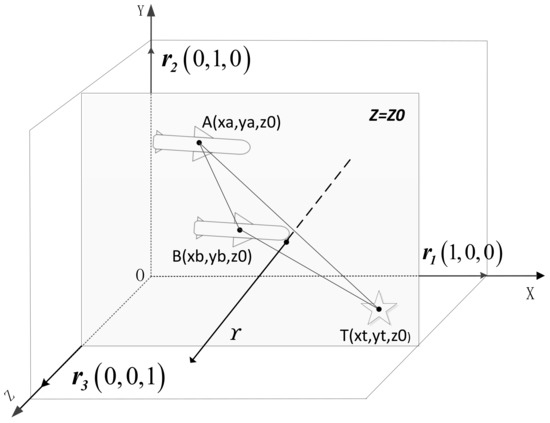
Figure 3.
Judge on spatial relationship.
A judging condition is presented here: Assume is the normal vector of the tracking plane , is the unit vector parallel to the axes, is the vectorial angle between and .
where is a sufficiently small value, is the Euclidean metric of vector [31]. If the inequality satisfies, the situation in Remark 2 will happen.
To avoid the decreasing precision of compensation tracking, the estimation of registration errors will be introduced to a LFOF when (53) is true, that is
where u is the error items, y is the output of the filter, is the propotionality coefficient. The fourth-order Runge-Kutta algorithm [32,33] can be used to solve the above differential equation.
Figure 4 shows the flow of whole algorithms. Before target tracking, the ECEF-KF is introduced to obtain registration errors of measurements of missiles. The errors acquired are furtherly introduced to the tracking system through the conditional compensation. When the tracking plane is parallel to one of three coordinate planes, the LFOF is taken to inhibit the divergence of error estimations.
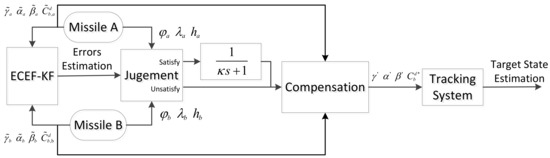
Figure 4.
Arcitecture of registration and tracking algorithm.
The compensation PLKF method with LFOF is called the CCPLKF (Conditional Compensation Pseudo Linear Kalman Filter), otherwise, called UCPLKF (Unconditional Compensation Pseudo Linear Kalman Filter). Accordingly, the compensation UKF method is divided to CCUKF and UCUKF.
5. Simulation
In this section, the performance of the proposed algorithm in spatial registration compared with traditional ECEF-KF is demonstrated. And the target tracking scheme is proved effective through the comparison of linear filters and nonlinear filters.
In the simulation, the ground target on curvilinear motion with variable velocity is considered. The velocity of target is (N 10 sin, E 5m/s), wherein t is the current time and T is the total simulation time.
The initial position of target is (longitude , latitude , height 0 m). The same terms of 1th and 2th missiles are (longitude , latitude , height 300 m) and (longitude , latitude , height 200 m) respectively. There are two motion situations of missiles being considered:
Case 1: Both two missiles make uniform linear flight to the east, the velocity are (N 0 m/s, E 120 m/s) and (N 0 m/s, E 100 m/s) respectively.
Case 2: The missiles make uniform linear flight as well, the velocity are (N 5 m/s, E 120 m/s) and (N −7 m/s, E 100 m/s) respectively. Figure 5 shows the absolute trajectories of missiles and target in the longitude, latitude and height coordinate system under the cases above.
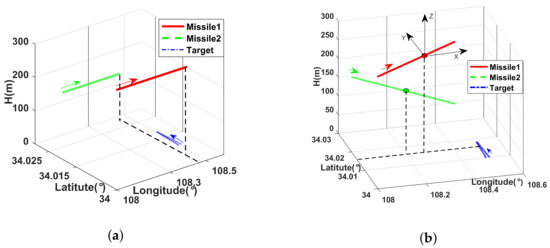
Figure 5.
(a) Trajectories of missiles and target under case 1; (b)Trajectories of missiles and target under case 2.
The 1th sensor offset error is (range 200 m, elevation angle , azimuth angle ) and the 2th sensor offset error is (range 300 m, elevation angle , azimuth angle ). Both two sensors’ standard deviation of measurement noises is (5 m, , ) All the measurement errors and noises are added to ideal measurements to create reported values. Both two platforms’ initial attitudes are (yaw , pitch , roll ) and offset errors of these angles are , which are added to initial attitudes to create deviated values. The sampling interval is 0.1 s. All the simulation results are obtained over 100 Monte Carlo trials. The performance of improved ECEF-KF algorithm proposed in the paper is compared with the method based on ECEF-LS in [24] and the standard Kalman filter, which is called traditional ECEF-KF.
The estimations of sensor errors are proposed in Figure 6, wherein the left column is about missile 1 and the right column presents the outcome of missile 2. The results of two cases are compared in one figure. It is obvious that the curves of case 2 jitter severely during 100∼200 s, which does not appear in the case 1. As mentioned in Section 4.2, the jitter is caused by the approach of latitudes of two missiles and target (see in Figure 5b). At 150 s, the two missiles move to nearly the same latitude (about ), the latitude of target is about , they are almost on the same latitude plane. That means the measurements of ECEF-KF become two dimensional, which causes the divergence during this time and converge gradually with the continual motion of missiles.
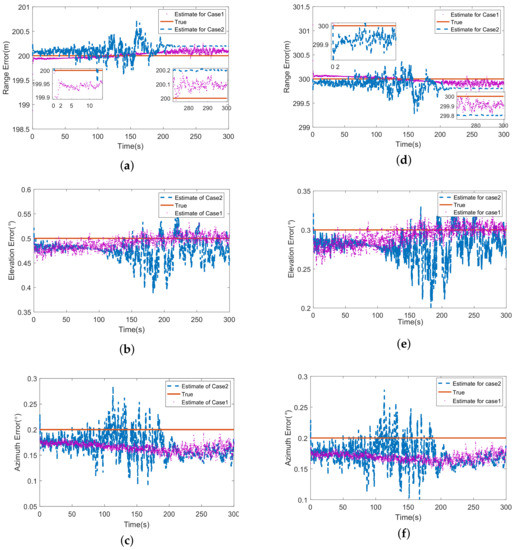
Figure 6.
(a) The estimation of range error of missile 1; (b) The estimation of elevation error of missile 1; (c) The estimation of azimuth error of missile 1; (d) The estimation of range error of missile 2; (e) The estimation of elevation error of missile 2; (f) The estimation of azimuth error of missile 2.
The Figure 7 shows the estimations of attitude biases. The divergency during 100∼200 s appears similarly under case 2. Besides, it is found in Figure 7c,f that the roll error increases after 200 s. This is because the longitudes of missiles come close to the targets’ at the end of track, which leads to the same phenomenon caused by the approach of latitude. Since the measurement equation of ECEF-KF is a first-order linear function of state, the estimations converge quickly from beginning (about 2 s in Figure 7a) and jitter near the truth.
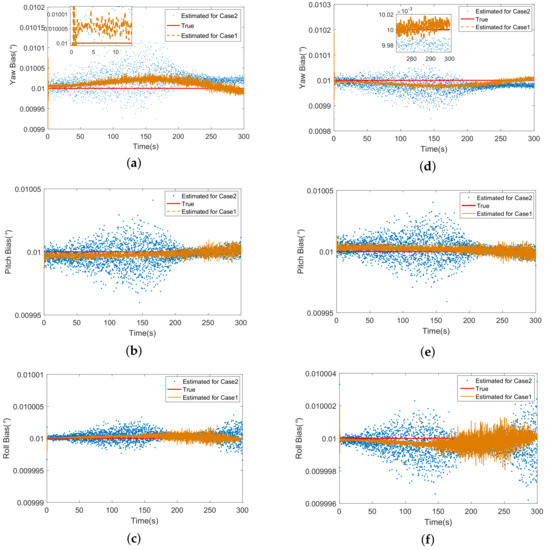
Figure 7.
(a) The estimation of yaw bias of missile 1; (b) The estimation of pitch bias of missile 1; (c) The estimation of roll bias of missile 1; (d) The estimation of yaw bias of missile 2; (e) The estimation of elevation error of pitch bias of missile 2; (f) The estimation of roll bias of missile 2.
To demonstrate the priority of proposed registration method for sensors on motivated platforms, Figure 8 illustrates the bias estimates of traditional ECEF-KF and improved one under case 1. The overlook of attitudes of orientated frames makes the former deviate from the truth as well as the disability to estimate the align errors. On the contrary, the latter which follows the truth closely gives better performance on the results. The reason causing the disappointment of traditional one is that the attitudes of missiles lead to the noncoincidence of LENU system and missile body system and influence the measurement obtained from sensors. For instance, the positive yaw value would increase the measurement of azimuth angle which is actually invariant in LENU system. However, the item of improved method transform the measurement from body system to LENU system, isolating the disturbance of frame angles.
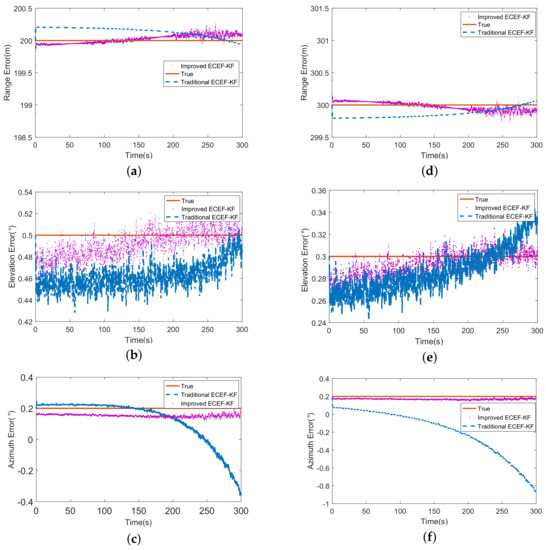
Figure 8.
(a) The comparison of range error of missile 1; (b) The comparison of elevation error of missile 1; (c) The comparison of azimuth error of missile 1; (d) The comparison of range error of missile 2; (e) The comparison of elevation error of missile 2; (f) The comparison of azimuth error of missile 2.
The RMSE (Root Mean Square Error) of the estimation of two methods is listed in Table 1. Obviously, the improved ECEF-KF outperforms the original strategy in all terms, especially for the azimuth because of the relatively large value of yaw angle, which demonstrates the proposed algorithm has more advantage in spatial registration for mobile sensors.

Table 1.
RMSE of registration errors.
Take case 2 for example, the target tracking is conducted on missile 1. Figure 9 compares the estimations of different schemes, wherein the left column presents the results of linear filters and the nonlinear filters are illustrated in the right list. The trajectory of target is estimated in the LENU coordinate system of missile 1 (see in Figure 5b). The parameters are given .
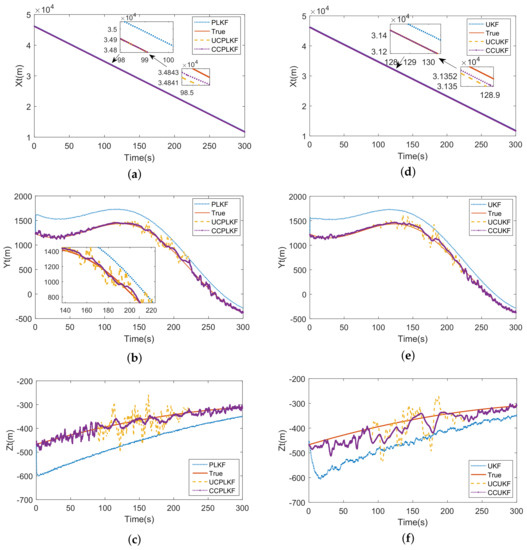
Figure 9.
(a) Linear estimation of x coordinate of target; (b) Linear estimation of y coordinate of target; (c) Linear estimation of z coordinate of target; (d) Nonlinear estimation of x coordinate of target; (e) Nonlinear estimation of y coordinate of target; (f) Nonlinear estimation of z coordinate of target.
Remark 3.
It is notable that ε is the limit of (53) and κ is the scale factor of integrator in (54). The former wherein will influence the time of error compensation (the lager ε is, the longer the LFOF will be taken) and the latter wherein will enhance the stability of error estimations (the lager κ is, the smoother the estimation through LFOF will be).
Seen from the left column of Figure 9, the accuracy of estimation dramatically improved after compensation (the estimation of UCPLKF is much closer to the truth value than PLKF). This is because the constant biases are subtracted from the input of UCPLKF. But during 100∼200 s, the estimations of these biases deviate from the truth, resulting to the unsatisfactory performance of UCPLKF in this period. The CCPLKF which can effectively inhibit the jitter of curves through a condition-based LFOF is prior to UCPLKF. Since the LFOF only works when (53) satisfies, so it does not cause the time delay to the whole tracking process. In the right column, likewise, the CCUKF is the optimal method among the nonlinear tracking schemes.
The RMSE of the estimation of target state is listed in Table 2. Seen from the results, the accuracy of tracking system can be greatly improved through compensation and the conditional compensation methods (CCPLKF and CCUKF) have nearly the same and the smallest errors. The CCUKF although has slight edge over CCPLKF in the items RMSEx and RMSEy, but suffer from more error in RMSEz, which turns the advantage to disadvantage in joint distance. This result can be explained through the comparison of Figure 9c,f. As mentioned, the registration errors jitter severely during 100∼200 s, which are compensated directly to the measurement inputs of UKF yet indirectly introduced to PLKF. Thus, the latter has the better input-jitter tolerance, which can also be proved in Figure 10.

Table 2.
RMSE of tracking errors.
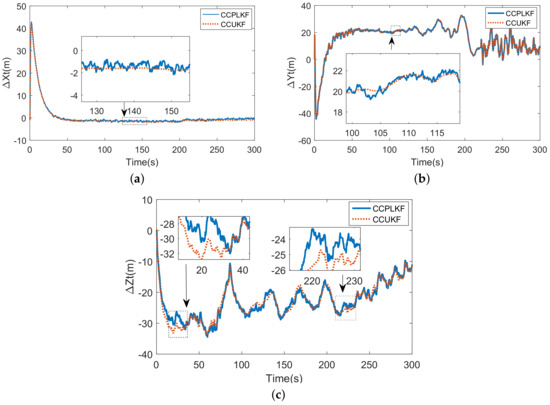
Figure 10.
(a) Estimation Error of x coordinate of target; (b) Estimation Error of y coordinate of target. (c) Estimation Error of z coordinate of target.
The estimations of CCPLKF and CCUKF are compared in Figure 10. Although the local magnifications in Figure 10a,b show the smoother curves of CCUKF than those of CCPLKF, but the Figure 10c exposes its flaw when the inputs jitter more severely. Moreover, the another fatal weakness of CCUKF is its relatively large computation. Given from simulation, the operation time caused by CCPLKF is 2.32 s, whereas CCUKF takes 5.62 s. In summary, the CCPLKF method keeps the best performance in target tracking.
6. Conclusions
In this paper, a novel spatial registration algorithm is proposed to estimate biases of measurements and orientation angles simultaneously. The linear and nonlinear filtering algorithms are introduced to solve the three-dimensional maneuvering target tracking problem. The estimations of registration method are used to modify the inputs of tracking scheme. In addition, a low pass first order filter is selectively taken to inhibit the jitter of estimation without the time delay. Simulation shows the good performance and robustness of the registration approach and the advantage of linear tracking method with modified inputs. Research results of this paper can also be extended to solve the registration and tracking of a dynamic network consisted of large quantities of sensors and multi-maneuvering targets [34,35].
Author Contributions
X.L. and Y.X. conceived and designed the experiments; Y.X. derived the mathmatical expression. All the authors contributed to the writing of the paper.
Acknowledgments
This work was supported by “the Fundamental Research Funds for the Central Universities” No. 61703339 and No. 3102016ZB021. The authors would like to thank the associate editor and anonymous reviewers for their valuable comments and suggestions to improve this paper.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Li, M.; Jing, Z.; Hu, M.; Dong, P. Exact Joint Estimation of Registration Error and Target States Based on GLMB Filter. In Proceedings of the 20th International Conference on Information Fusion, Xi’an, China, 10–13 July 2017. [Google Scholar]
- Xiu, J.; Dong, K.; He, Y. Systematic error real-time registration based on modified input estimation. Syst. Eng. Electron. 2016, 27, 986–992. [Google Scholar] [CrossRef]
- Zhang, F.; Christian, B.; Alois, K. Multiple Vehicle Cooperative Localization with Spatial Registration Based on a Probability Hypothesis Density Filter. Sensors 2014, 14, 995–1009. [Google Scholar] [CrossRef] [PubMed]
- Song, W. Research progress of spatial registration algorithms for sensor data. Trans. Microsyst. Technol. 2012, 8, 5–8. [Google Scholar]
- He, Y.; Xiu, J.; Guan, X. Radar Network Error Registration Algorithm. Radar Data Processing with Applications; John Wiley & Sons Singapore Pte. Ltd.: Singapore, 2016. [Google Scholar]
- Zheng, Z.; Zhu, Y. New least squares registration algorithm for data fusion. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1410–1416. [Google Scholar] [CrossRef]
- Dong, Y.; He, Y.; Wang, G. A Generalized Least Squares Registration Algorithm with Earth-Centered Earth-Fixed (ECEF) Coordinate System [Radar Sensor Fusion Applications]. In Proceedings of the International Conference on Computational Electromagnetics and ITS Applications, Beijing, China, 1–4 November 2004. [Google Scholar]
- Yang, X.; Wang, Y.; Shan, X. Ill-Condition Controlled Maximum Likelihood Registration for Multiple Sensors. Adv. Mater. Res. 2014, 898, 797–801. [Google Scholar]
- Han, C.; Zhu, H.; Duan, Z. Time and Spatial Registration. In Multi-Source Information Fusion, 2nd ed.; Tsinghua University Press: Beijing, China, 2010; pp. 198–202. [Google Scholar]
- Liu, Y.; Yang, Z.; Han, C. A study on space registration algorithm of sensor attitude bias. Mod. Radar 2009, 31, 29–31. [Google Scholar]
- Helmick, R.E.; Rice, T.R. Removal of alignment errors in an integrated system of two 3-d sensors. IEEE Trans. Aerosp. Electron. Syst. Aes. 1993, 29, 1333–1343. [Google Scholar] [CrossRef]
- Bo, Y.; Chen, Z.; Yin, M.; Wang, T. Improved different dimensional sensors combined space registration algorithm. Math. Prob. Eng. 2015, 2015, 1–9. [Google Scholar] [CrossRef]
- Van Doorn, B.A.; Blom, H.A. Systematic Error Estimation in Multisensor Fusion Systems. In Proceedings of the SPIE—Conference on Signal and Data Processing of Small Targets, Orlando, FL, USA, 22 October 1993; pp. 450–461. [Google Scholar]
- Li, S. Research on the Method of Locating and Tracking Based on Multi-Source Information Fusion Technology. Master’s Degree, Henan University, Kaifeng, China, May 2014. [Google Scholar]
- Doulamis, A. Dynamic tracking re-adjustment: A method for automatic tracking recovery in complex visual environments. Multimed. Tool. Appl. 2010, 50, 49–73. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Bucy, R.S.; Senne, K.D. Digital Synthesis of Non-linear Filters. Autimatica 1971, 7, 287–298. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. New Extension of the Kalman Filter to Nonlinear Systems. Int. Soc. Opt. Photonics 1997, 182–193. [Google Scholar] [CrossRef]
- Pathiranage, C.D.; Watanabe, K.; Jayasekara, B.; Izumi, K. Simultaneous Localization and Mapping: A Pseudolinear Kalman Filter (PLKF) Approach. In Proceedings of the International Conference on Information and Automation for Sustainability, Colombo, Sri Lanka, 12–14 December 2008; pp. 61–66. [Google Scholar]
- Li, X.R.; Jikov, V.P. A Survey of Maneuvering Target Tracking-part III Measurement Models. In Proceedings of the Conference on Signal and Date Processing of Small Targets, San Diego, CA, USA, 26 November 2001. [Google Scholar]
- Li, W.; Peng, W.; Peng, L.; Li, Y. Semidefinite programming algorithm with TDOA and FDOA measurements based on WGS-84 earth model. Acta Aeronaut. ET Astronaut. Sin. 2017, 38, 283–290. [Google Scholar]
- Guinot, B.; Feissel, M. Bureau International de l’Heure. Annual Report 1984; Observatoire de Paris: Paris, France, 1985; p. 22. [Google Scholar]
- Crespi, M.; Baiocchi, V.; De Vendictis, L.; Giannone, F. A New Rigorous Model for the Orthorectification of Syncronous and Asyncronous High Resolution Imagery. In Proceedings of the 24th EARSeL Symposium, Dubrovnik, Croatia, 25–27 May 2004; pp. 461–468. [Google Scholar]
- Zhou, Y.; Leung, H.; Blanchette, M. Sensor alignment with Earth-centered Earth-fixed (ECEF) coordinate system. IEEE Trans. Aerosp. Electron. Syst. 2002, 35, 410–418. [Google Scholar] [CrossRef]
- Carlson, G.E.; Bott, M.E. Tilt-Table Alignment for Inertial-Platform Maintenance without a Surveyed Site. IEEE Trans. Aerosp. Electron. Syst. 1973, AES-9(3), 406–411. [Google Scholar] [CrossRef]
- Lo, J.; Ma, W.; Yuan, J. Inertial Navigation. In Principle and Application of Integrated Navigation, 1st ed.; NWPU Press: Xi’an, China, 2012; p. 61. [Google Scholar]
- Qin, Y.; Zhang, H.; Wang, S. Discrete Kalman Filter. In Kalman Filter and Integrated Navigation Principle, 2nd ed.; NWPU Press: Xi’an, China, 2012; p. 34. [Google Scholar]
- Xu, Y. The Concept and Some Conclusion of Rotation Matrix. J. Jiangsu Open Univ. 1997, 1997, 81–83. [Google Scholar]
- Qin, Y. Strapdown inertial navigation system. In Inertial Navigation, 1st ed.; Science Press: Beijing, China, 2006; p. 356. [Google Scholar]
- Liu, C. Study on Motion Model and Tracking Algorithm of Radar Maneuvering Target. Ph.D. Thesis, Xidian University, Xi’an, China, April 2014. [Google Scholar]
- Guo, Z.; Zhou, J.; Guo, J.; Cieslak, J.; Chang, J. Coupling characterization-based robust attitude control scheme for hypersonic vehicles. IEEE Trans. Ind. Electron. 2017, 64, 6350–6361. [Google Scholar] [CrossRef]
- Yang, H.; Gao, Y. GPS Satellite Orbit Prediction at User End for Real-Time PPP System. Sensors 2017, 17, 1981. [Google Scholar] [CrossRef] [PubMed]
- Abadi, M.A.H.; Cao, B.Y. Solving First Order Fuzzy Initial Value Problem by Fourth Order Runge-Kutta Method Based on Different Means. Fuzzy Inf. Eng. Decis. 2018. [Google Scholar] [CrossRef]
- Nillius, P.; Sullivan, J.; Carlsson, S. Multi-Target Tracking-Linking Identities Using Bayesian Network Inference. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; pp. 2187–2194. [Google Scholar]
- Andriyenko, A.; Schindler, K.; Roth, S. Discrete-Continuous Optimization for Multi-Target Tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 1926–1933. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).