1. Introduction
With the continuous global depletion of petroleum energy, the development and utilization of clean wind energy have become a hot topic in recent decades. Offshore wind energy has been the focus of researchers due to the vast area of marine resources. Measurements of offshore wind information also contribute to oil spill monitoring, weather forecasting and understanding of air-sea interactions [
1,
2,
3]. Spaceborne active microwave scatterometer such as QuickSCAT and ASCAT have provided mature wind products for National Oceanic and Atmospheric Administration (NOAA) [
4,
5]. However, the wind fields acquired by scatterometer cannot be applied to fine scale marine products due to the course spatial resolution (12.5 km~25 km) [
6]. Because of features like imaging in all-weather conditions and high spatial resolution, synthetic aperture radar (SAR) has been widely used in military, economics, and science applications, and plays an important role in the retrieval of ocean surface wind fields, especially for C-band (~5.3 GHz) SAR [
7].
Numerous studies have revealed that ocean surface normalized radar cross-section (NRCS) obtained from C-band SAR is mainly dominated by resonant Bragg backscattering at the centimeter scale wavelength [
8,
9,
10]. This scale roughness is predominantly influenced by local wind and therefore ocean wind information may be extracted from SAR images [
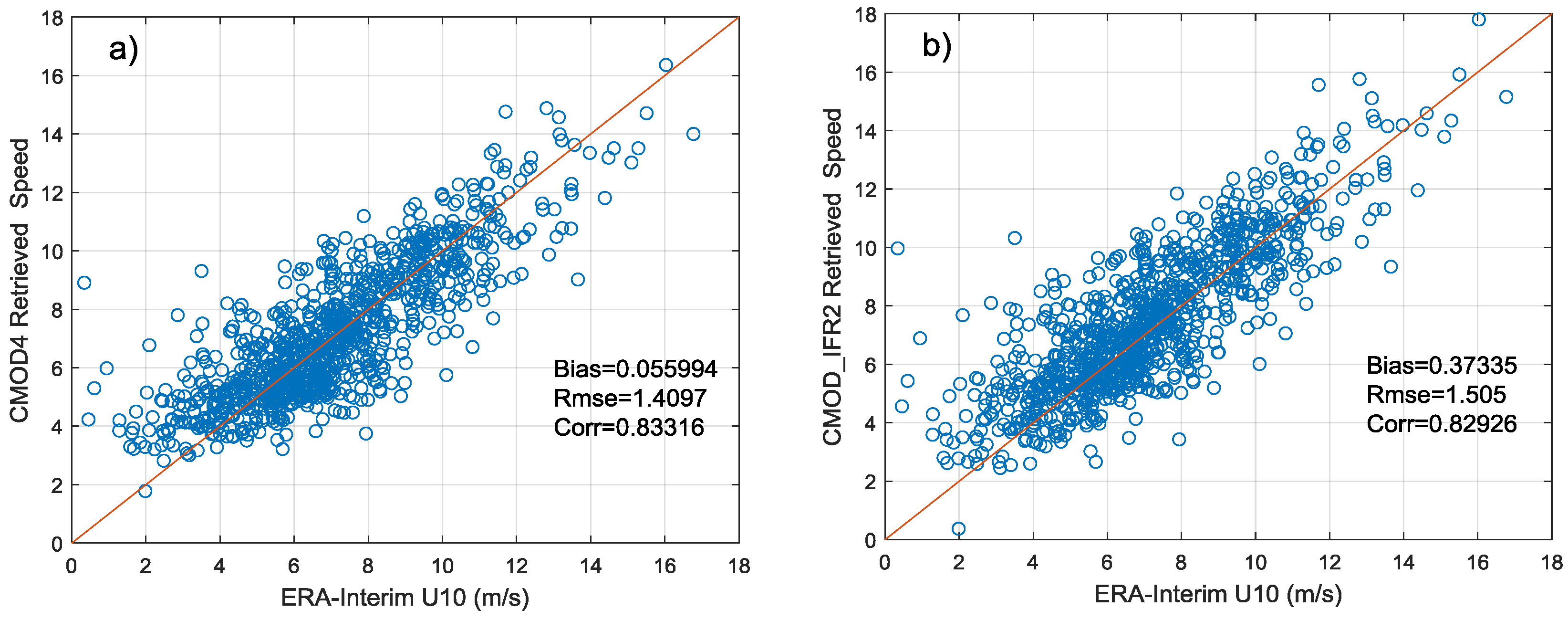
11]. In recent decades, several empirical geophysical model functions (GMFs), such as CMOD4 [
12], CMOD_IFR2 [
13], CMOD5 [
14] and CMOD5.N [
15] have been proposed to perform ocean surface wind retrieval. These GMFs relate the NRCS to the incidence angle, wind speed at a height of 10 m above sea level, and azimuth angle (radar look angle with respect to wind direction). Not only from scatterometers, such as QuickSCAT [
16,
17] and ASCAT [
18], they can also accurately retrieve the wind speed from SAR images (within about 2 m/s), e.g., ENVISAT [
19], RADARSAT-1/2 [
20,
21,
22] and Sentinel-1A/B [
23]. However, such GMFs are only suitable for VV-polarized NRCS, and no similar models exist to retrieve wind speed from images in HH-polarization. Therefore, it is necessary to convert HH-polarized NRCS to VV-polarization using polarization ratio (PR), denoted as
[linear units], before retrieving wind speed [
24,
25,
26,
27,
28]. In traditional research, it is generally believed that the PR is only relevant to incidence angle [
24]. Recent studies in [
27,
28] show that the PR is also dependent on speed and azimuth. These results reveal that different satellites have their own optimal PR and GMF. Thus, the choice of suitable hybrid model is critical for Gaofen-3 satellite [
29].
Recent decades, wind speed retrieval from cross polarized (cross-pol) NRCS has become a research focus due to the saturation of co-pol data at high wind speed. Some studies of cross-pol images have been conducted for RADARSAT-1/2 quad-polarization and dual-polarization [
30,
31,
32,
33,
34,
35,
36,
37]. Hwang and Zhang et al. [
30,
31] revealed the breaking contribution of cross-pol NRCS and emphasized the advantages of wind retrieval with cross-pol data at high wind speeds. Vachon and Zhang et al. [
32,
33] proposed a cross-pol wind retrieval model which is only relevant to wind speed and independent on incidence angle as well as wind direction, respectively. In [
34,
35,
36], Hwang and Shen proposed that the VH NRCS of RADARSAT-2 dual-polarization mode is also relevant to incidence angle and the noise floor must be considered before wind retrieval. Moreover, Huang et al. [
38] conducted an evaluation on cross-pol NRCS in Sentinel-1 IW mode and proposed a wind retrieval algorithm related to incidence angle and wind direction. The above studies show that the cross-pol NRCS has potential to retrieve high wind speeds, e.g., hurricanes and typhoons.
The accuracy of the retrieved wind vector is strongly affected by the absolute radiometric calibration accuracy of NRCS. Accurate wind speed can be obtained from refined NRCS. Therefore, it is possible to assess the accuracy of the calibration by using GMFs and known wind information. Horstmann et al. [
39] propose a method for estimating ERS SAR calibration constants using C-band models and ocean surface wind fields. Stoffelen et al. [
40] obtained an accurate calibration of a scatterometer over the ocean using CMOD4 and wind fields from European Centre for Medium-Range Weather Forecasts (ECMWF). This method achieves a calibration accuracy of 0.1 dB. Verspeek et al. [
41] proposed an estimation correction table based on CMOD5.N to improve ASCAT wind retrieval. Zhu et al. [
42] used Numerical Ocean Calibration (NOC) to calibrate HY-2 SCAT and the retrieved winds were in good agreement with winds from ECMWF.
The Gaofen-3 (GF-3) satellite, which was launched on 10 August 2016 by the China Academy of Space Technology (CAST), is the first C-band multi-polarization SAR in China with a highest resolution of 1 m. It has characteristics such as high resolution, large coverage, long-life operation and multiple imaging modes, including Wave Mode [
43]. To date, some preliminary evaluations of ocean application have been carried out. Shao et al. [
44] collected 244 Stander Stripmap (SS) and Quad-Polarization Stripmap (QPSI and QPSII) mode images to complete wind and wave retrieval firstly. In [
29], Wang et al. validated the GF-3-derived winds against NDBC measurements using SS, QPSI, QPSII, FSI and NSC mode data. Ren et al. [
45] conducted a comprehensive analysis of QPSI and QPSII mode data in each polarization. Several empirical algorithms for significant wave height in Wave Mode data and wind retrieval from cross-polarization in typhoons are also discussed in [
46,
47], which uses GF-3 images acquired in Global Observation (GLO) and Wide ScanSAR (WSC) mode.
The remainder of this paper is organized as follows:
Section 2 describes the GF-3 Wave Mode SAR images and other validated data, including ECMWF ERA-Interim re-analysis wind fields and Amazon rainforest images. Methodologies for correcting calibration constants, fitting PR models and cross-pol wind speed retrieval formula are introduced in
Section 3.
Section 4 shows results of calibration, polarization conversion and wind speed retrieval accuracy. Finally, discussion and conclusion are presented in
Section 5 and
Section 6.
5. Discussion
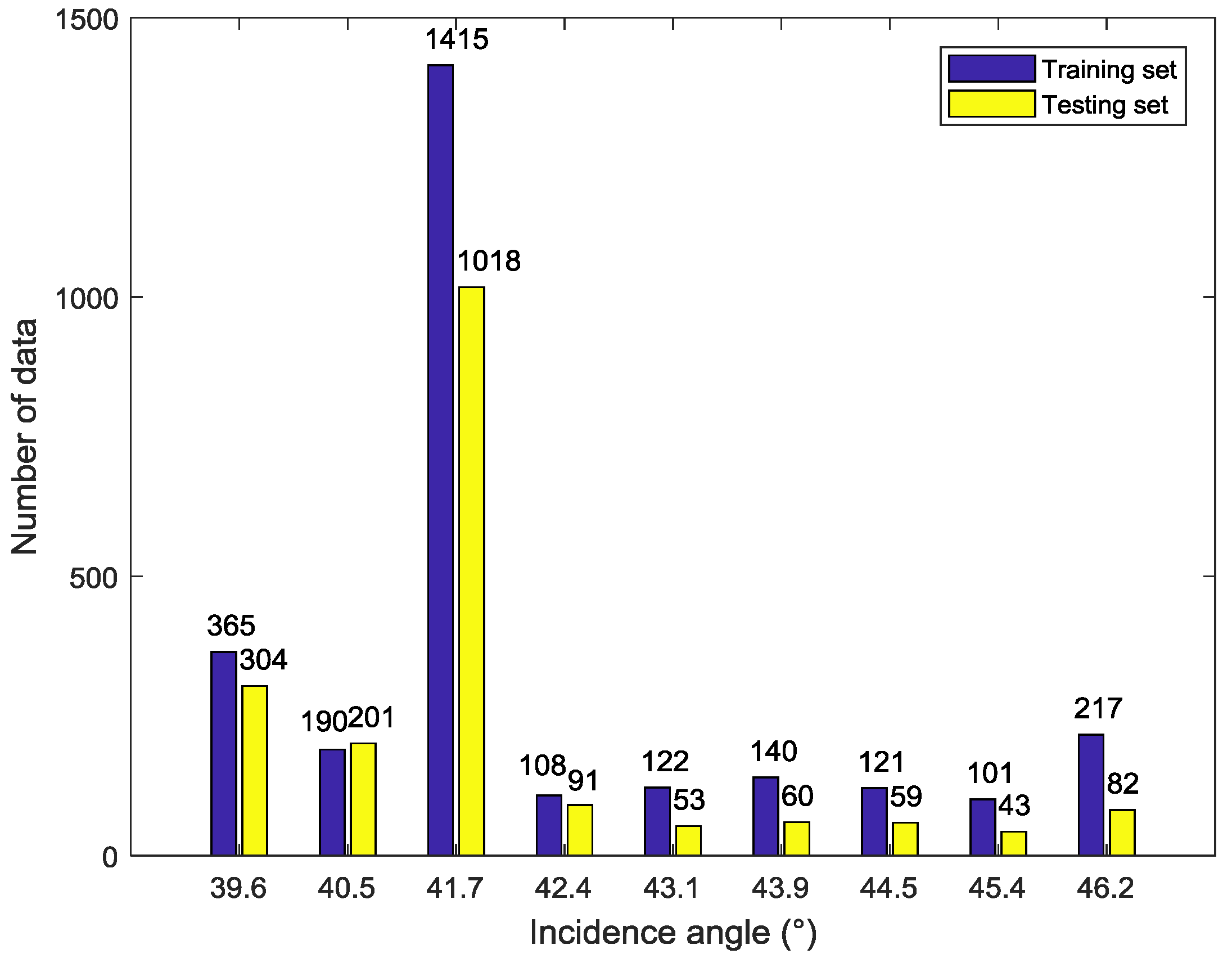
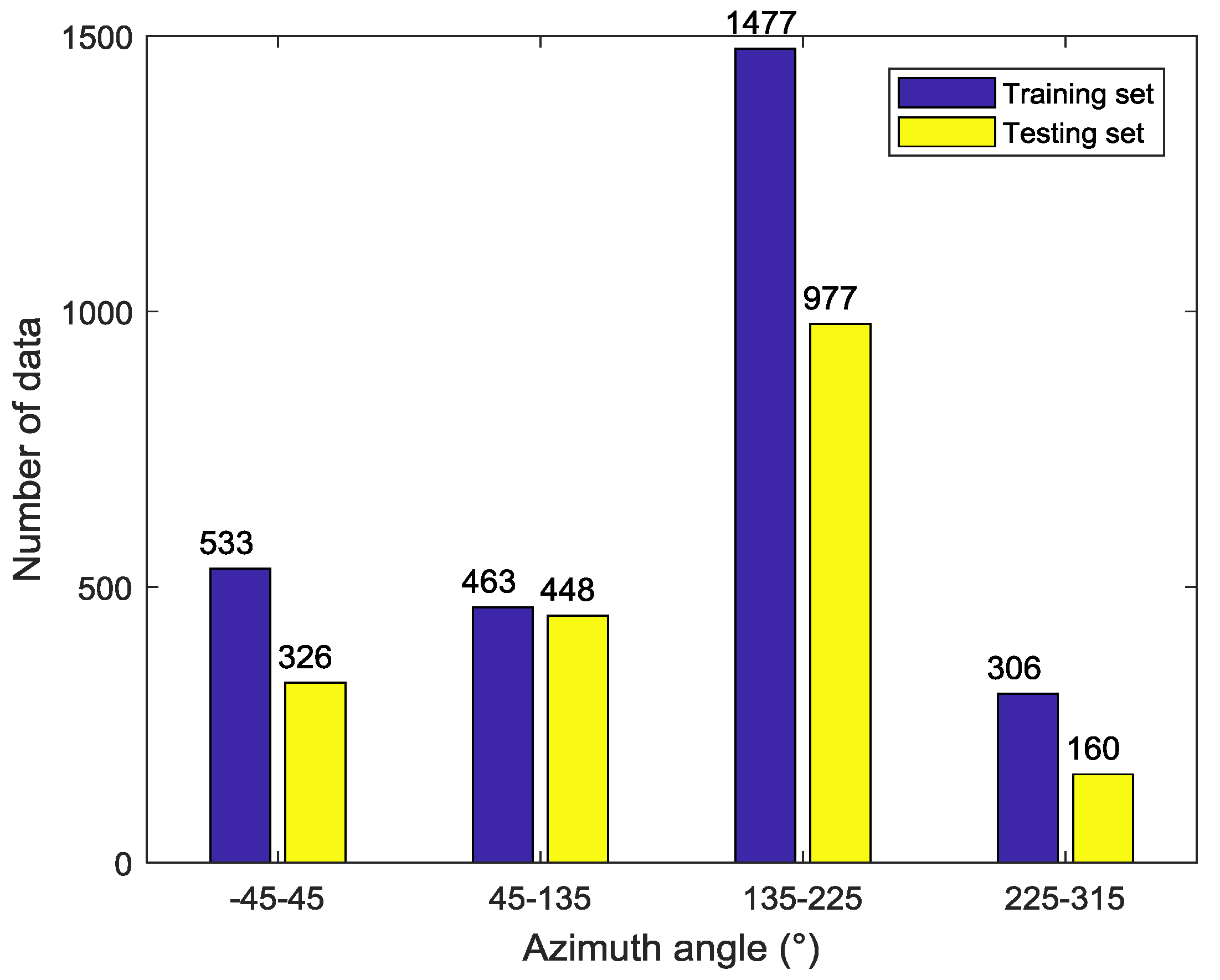
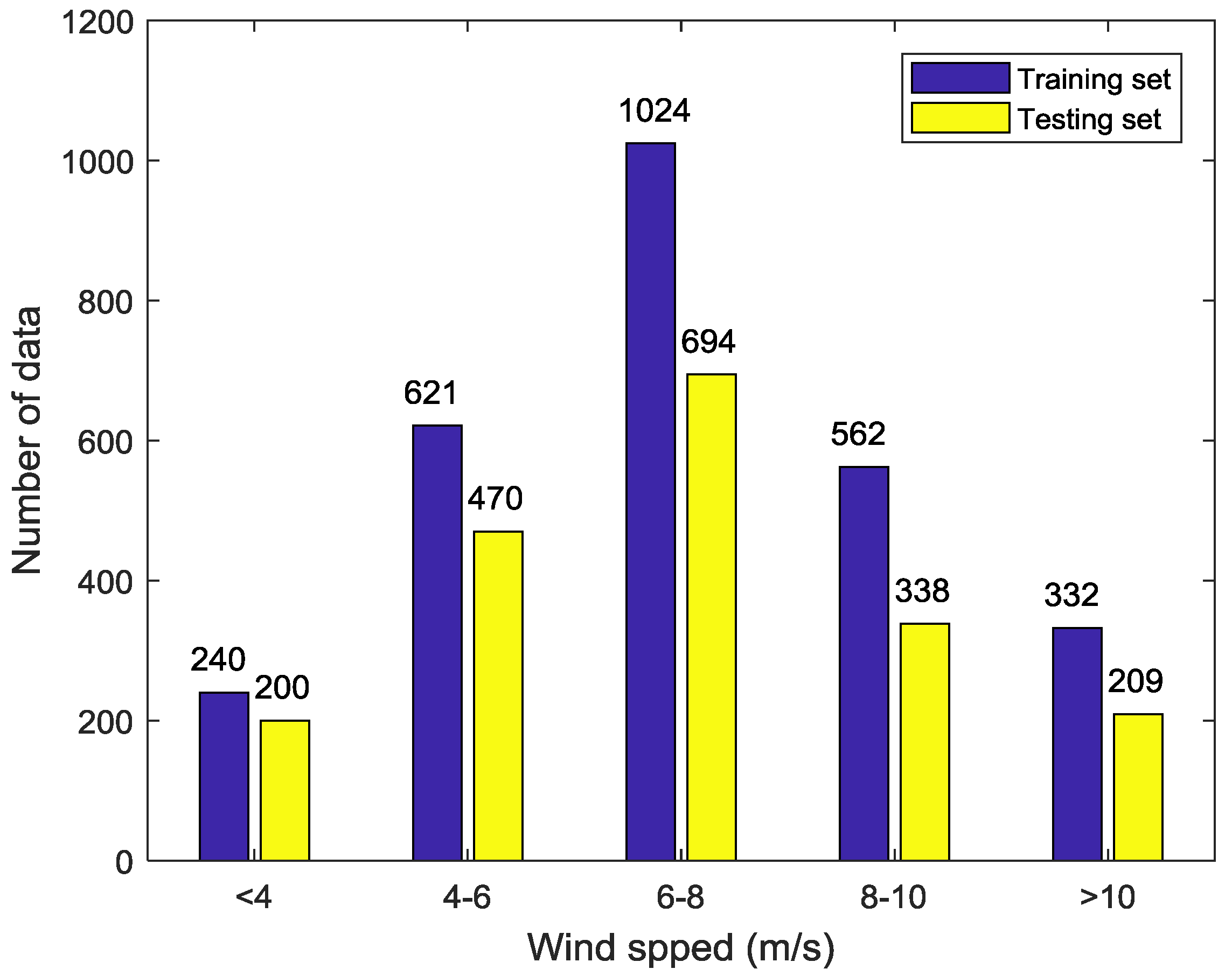
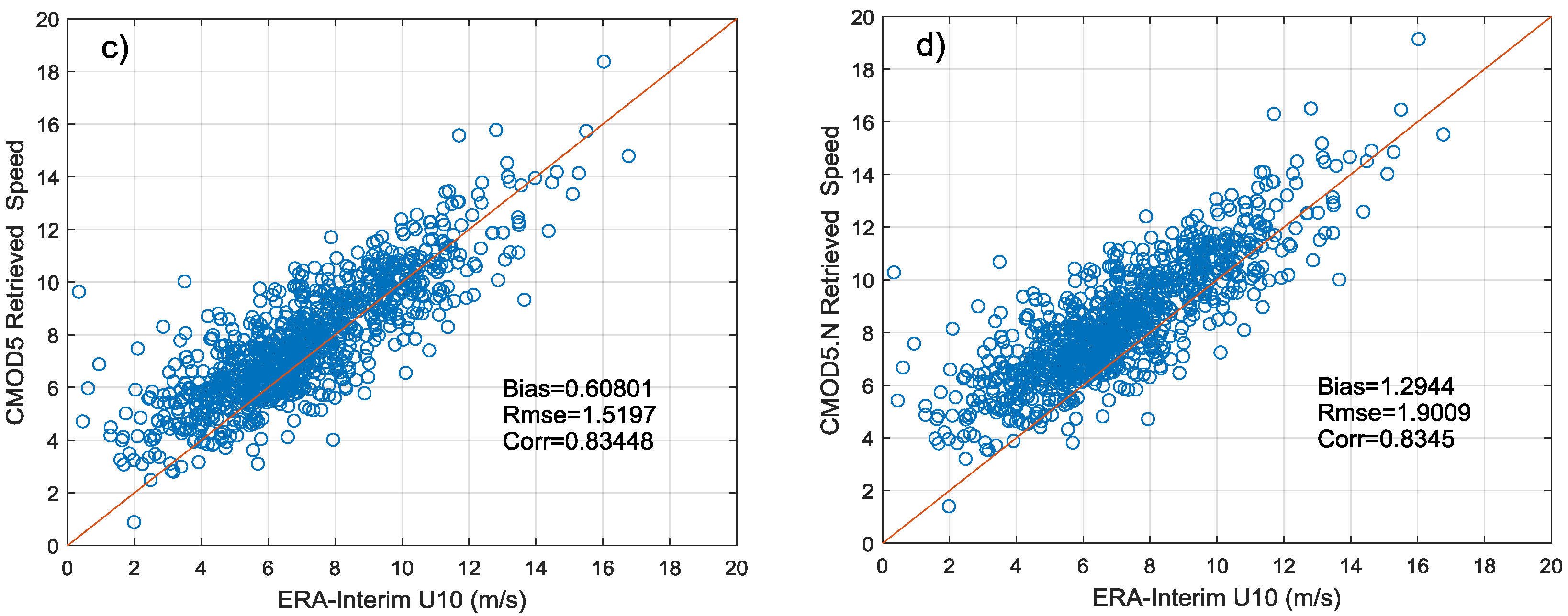
In this paper, we conduct a preliminary analysis of SAR images in Wave Mode for GF-3 satellite. 2779 GF-3 Wave Mode NRCS and wind vectors for the corresponding location are collected as training set and additional 1911 match-ups are as testing set. To reduce the effect of speckle noise and improve the matching precision of the data set, the NRCS is first sampled from 10 m pixel spacing to 5 km firstly, then the wind field interval is interpolated to 1 h and the wind vectors of the center of each SAR image is calculated using bilinear interpolation.
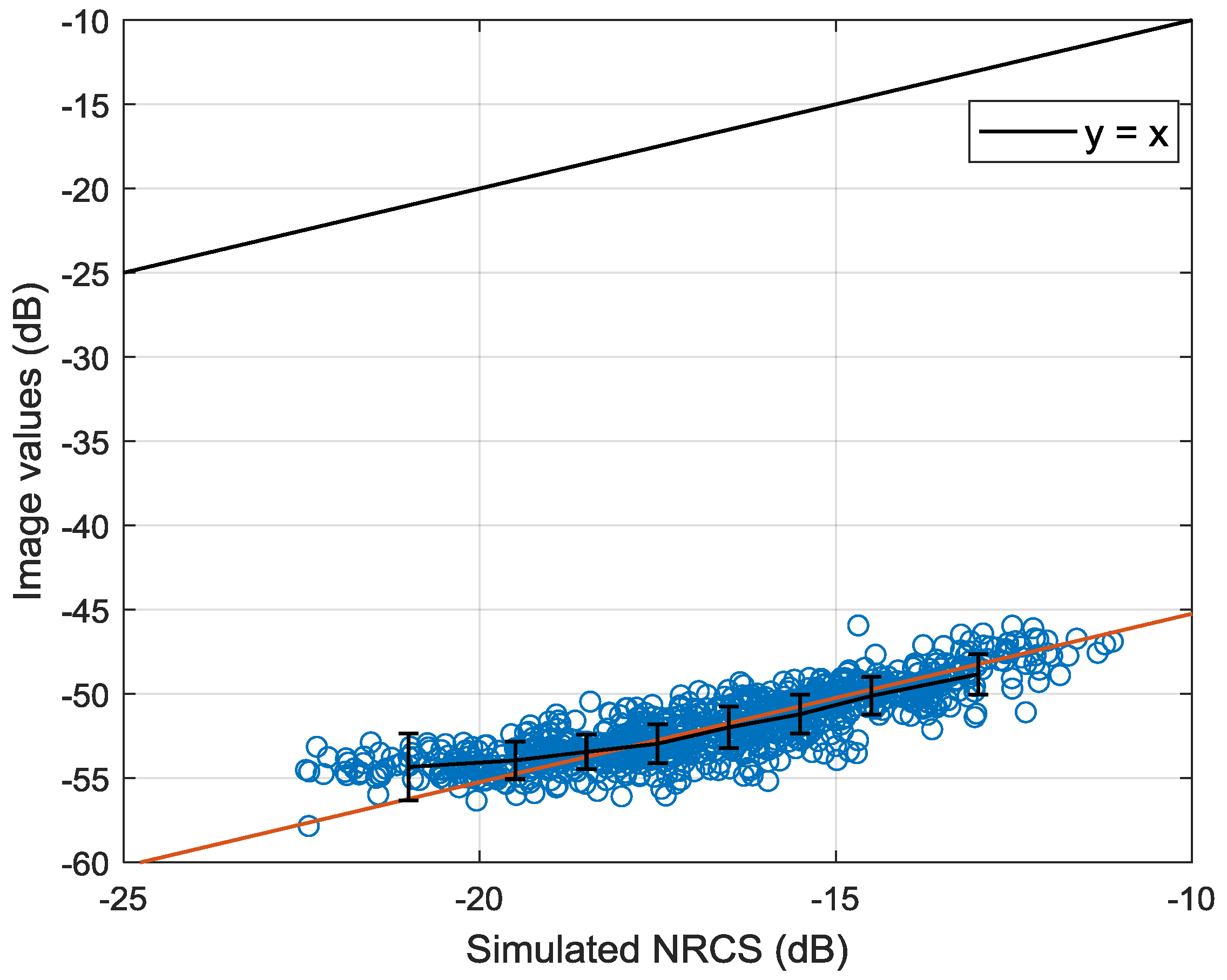
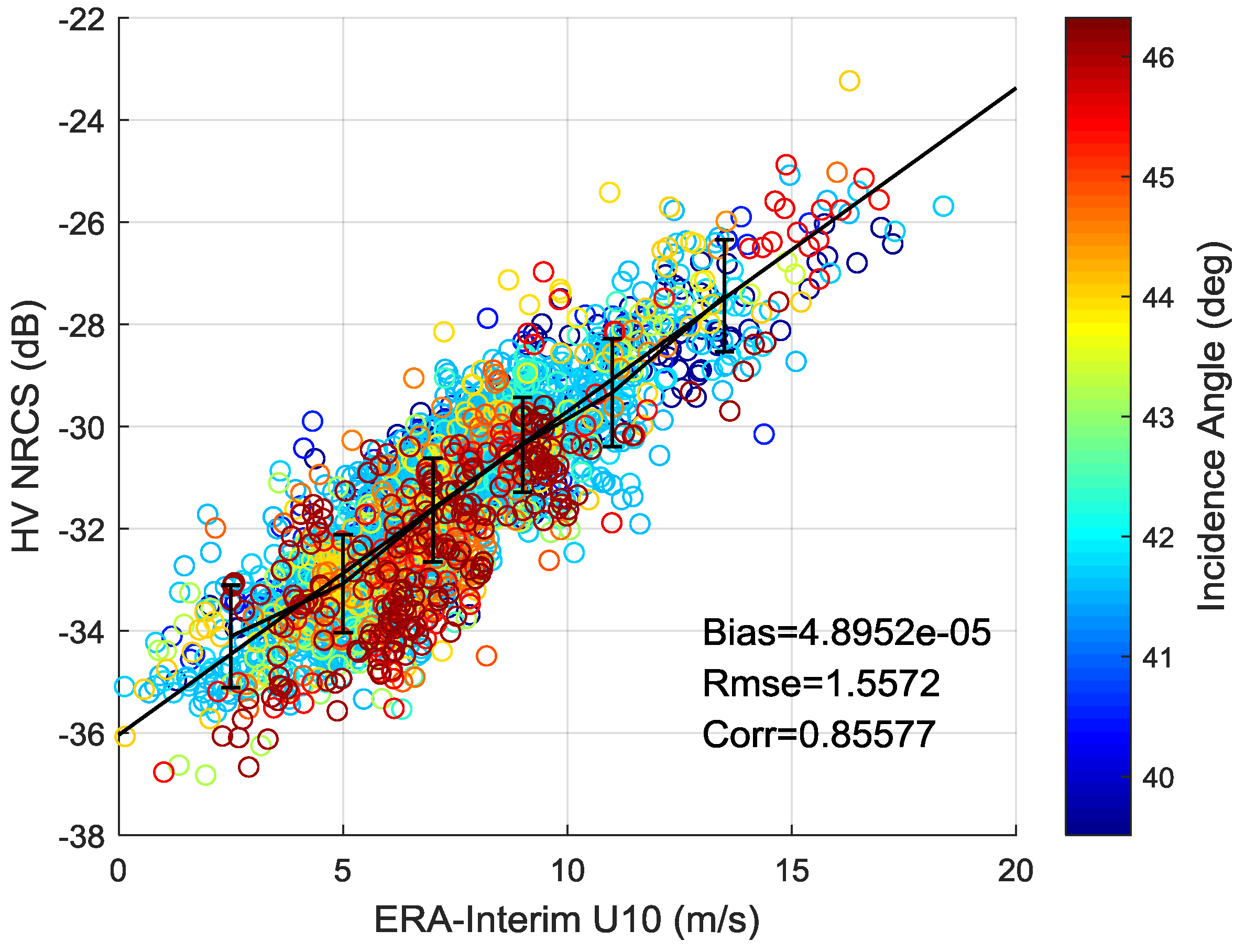
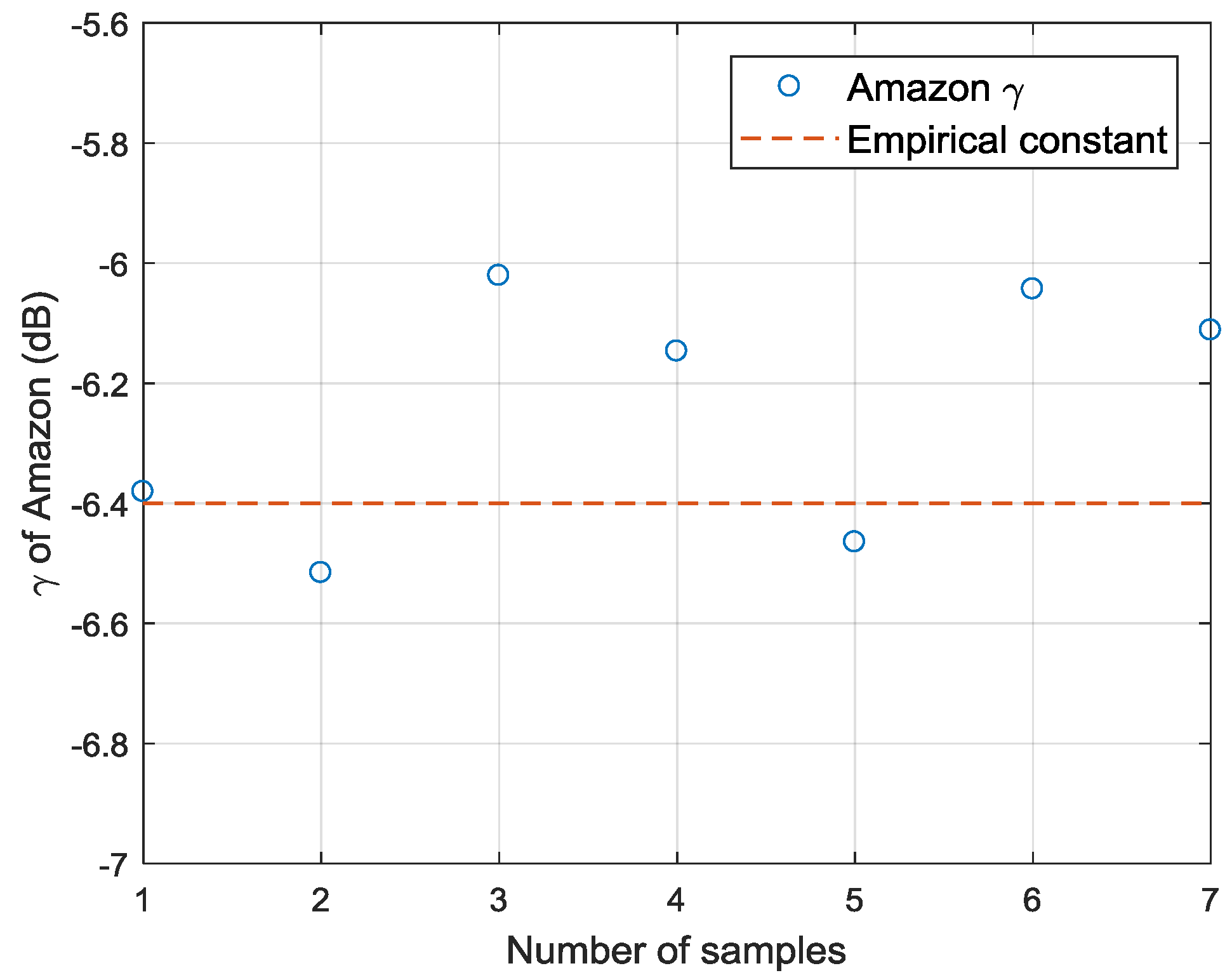
A simple method for absolute radiometric calibration using ocean surface wind fields and CMOD4 is introduced and tested. Due to the linear relationship between NRCS and calibration constant, an estimator of calibration constant can be obtained by calculating the difference between the simulated NRCS and image value. Since the calibration constant given by China Centre for Resources Satellite Data and Application is only calculated by combing system bandwidth and antenna pattern, this experiment also verifies the constant using Amazon rainforest data. The result shows the obtained Amazon rainforest using estimated calibration constant is in good agreement with empirical . This normalized calibration method provides a more convenient and affordable way for future absolute radiometric calibration. It saves the expensive cost of calibration using corner reflector and can obtain an accurate calibration constant continuously.
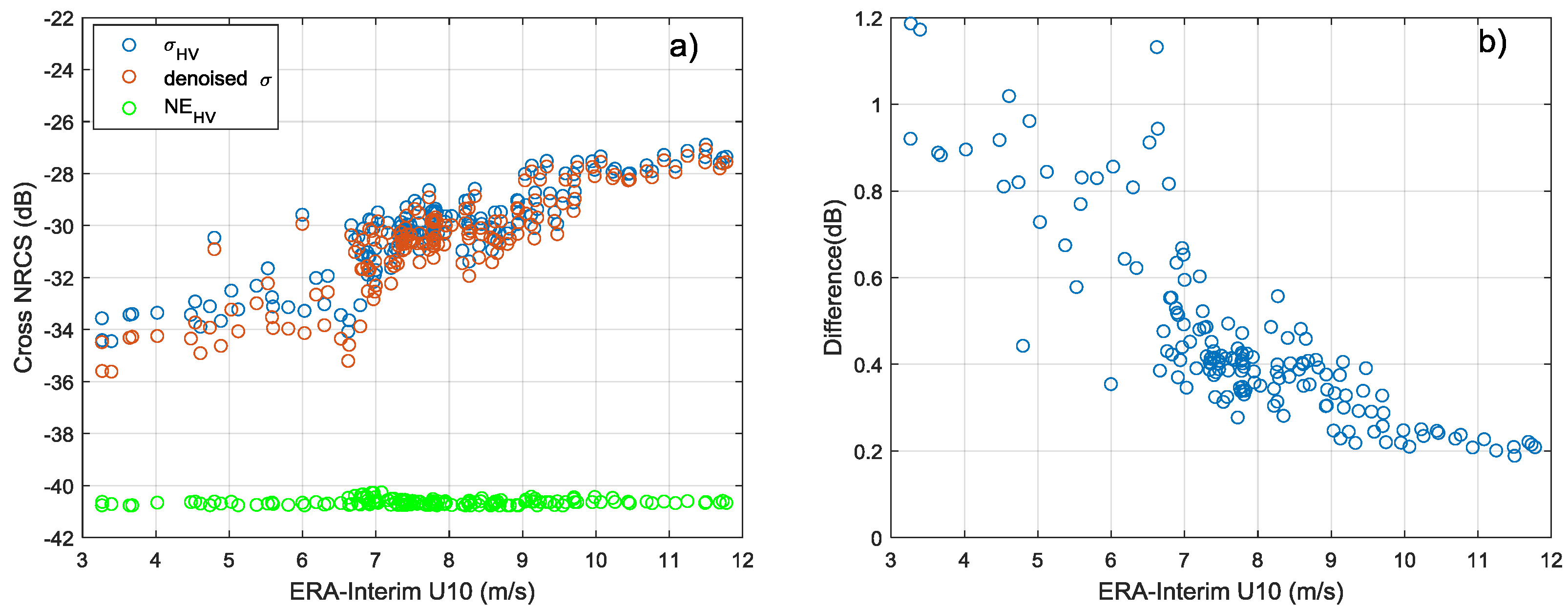
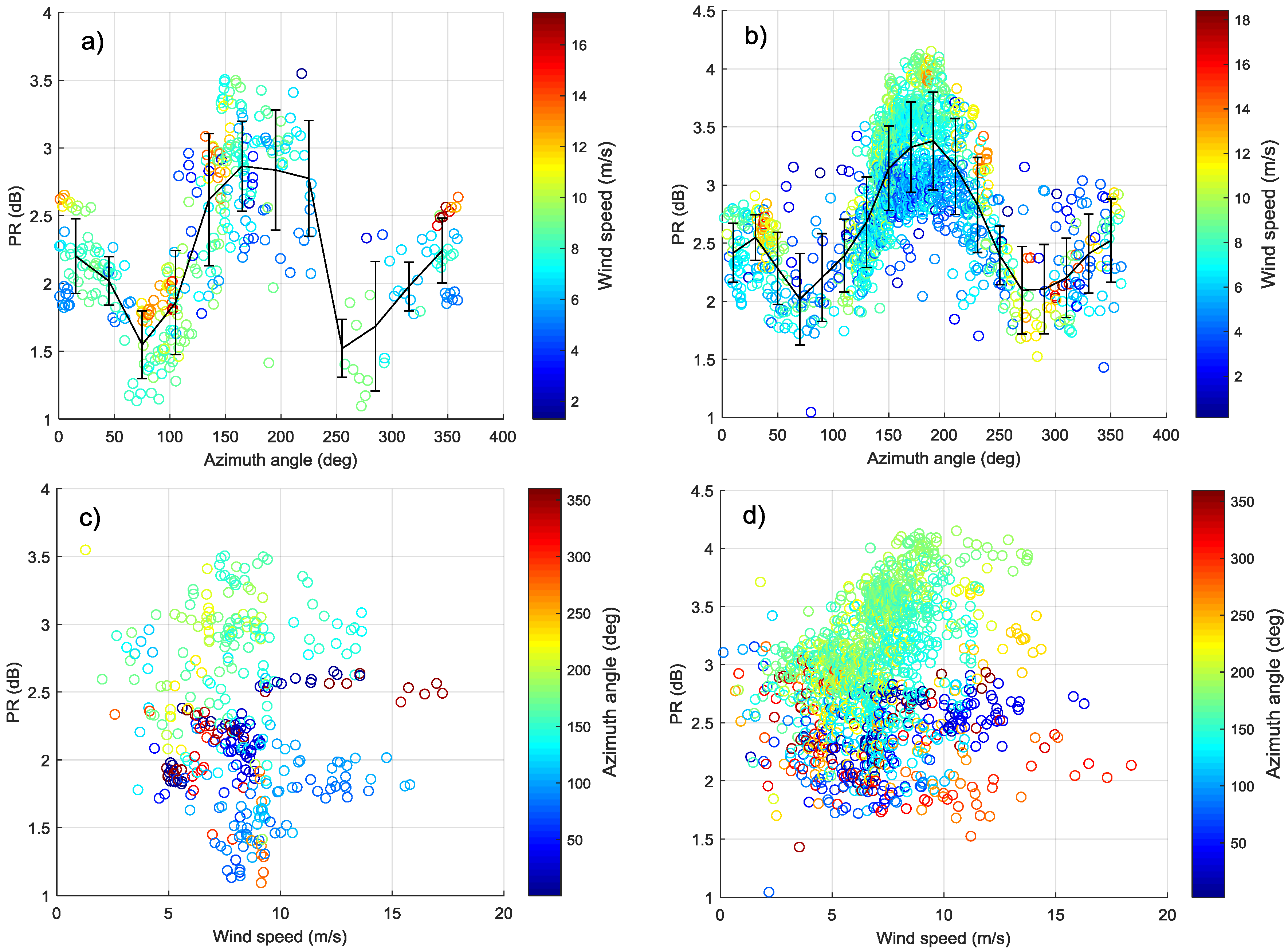
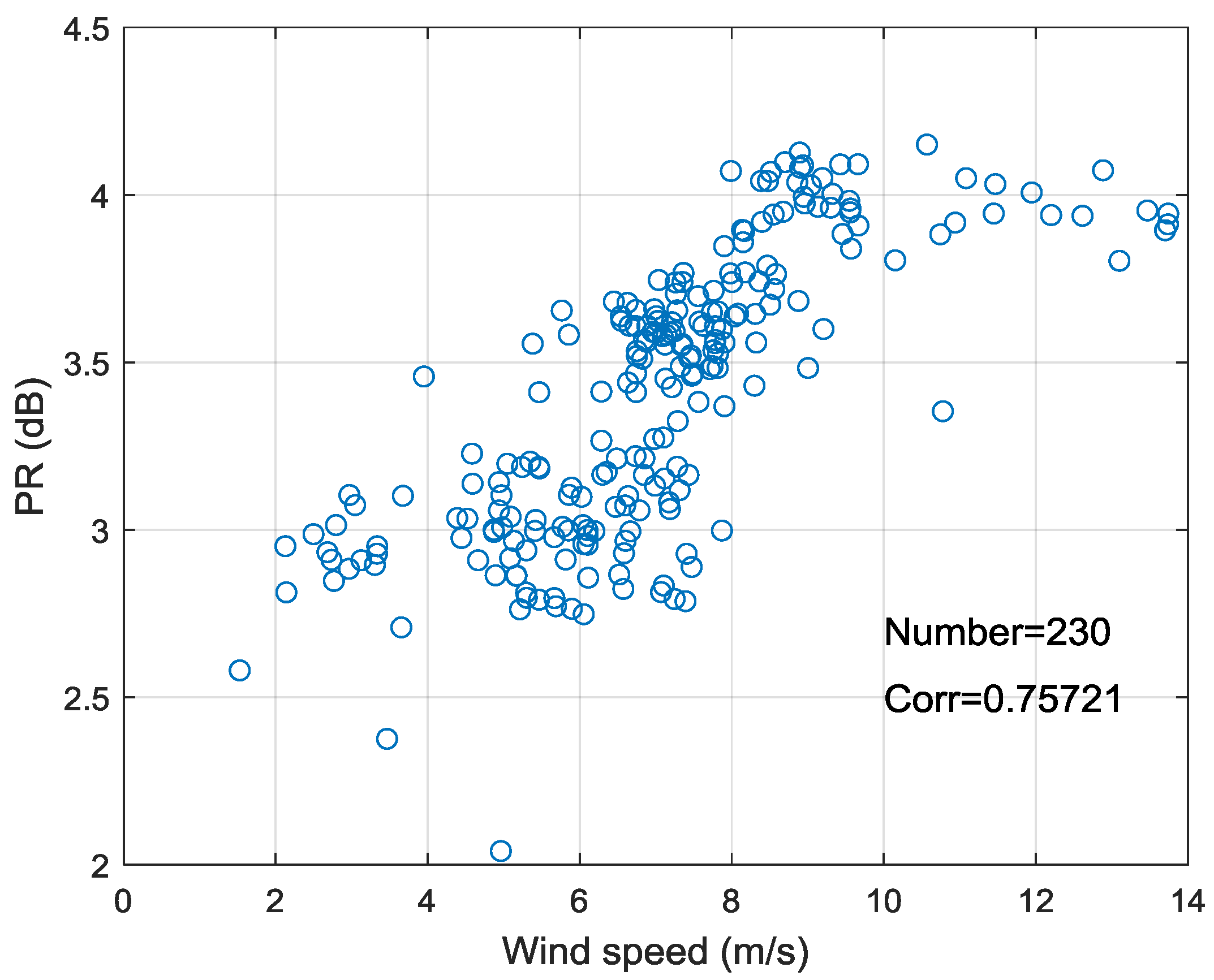
The relationship between cross-pol images of Wave Mode and system noise floor, wind vectors and satellite geometry parameters is also investigated. The experiment indicates that the system noise floor of cross polarization is about −40 dB. It is low enough and stable. There is a clear linear relationship between cross-pol NRCS and wind speeds in the case of ignoring noise floor effects, and the cross-pol NRCS is independent on incidence angle. As the wind speed increase, the cross-pol NRCS is more affected by azimuth angle. Therefore, it is necessary to consider the azimuth angle when retrieving high wind speed in the future.
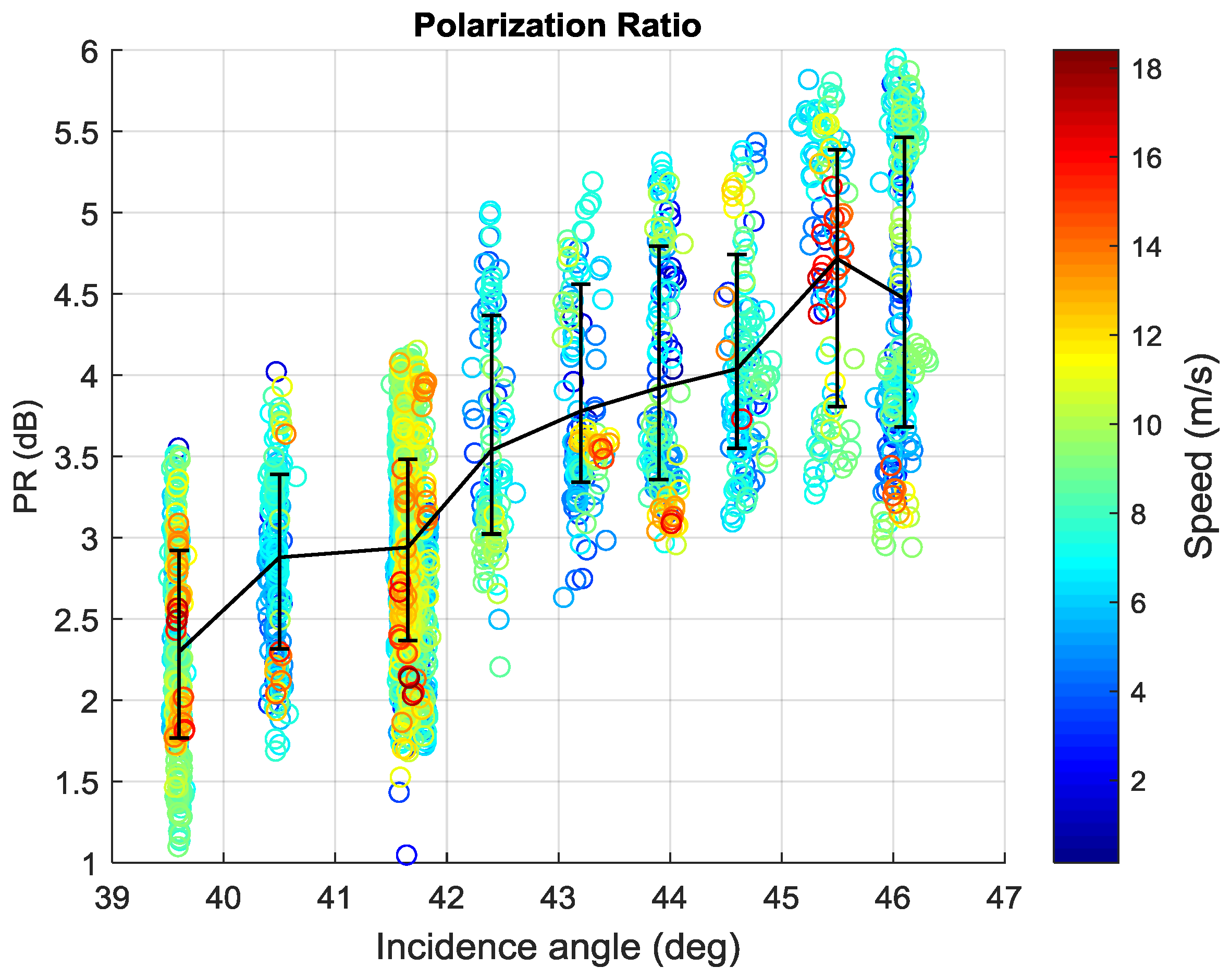
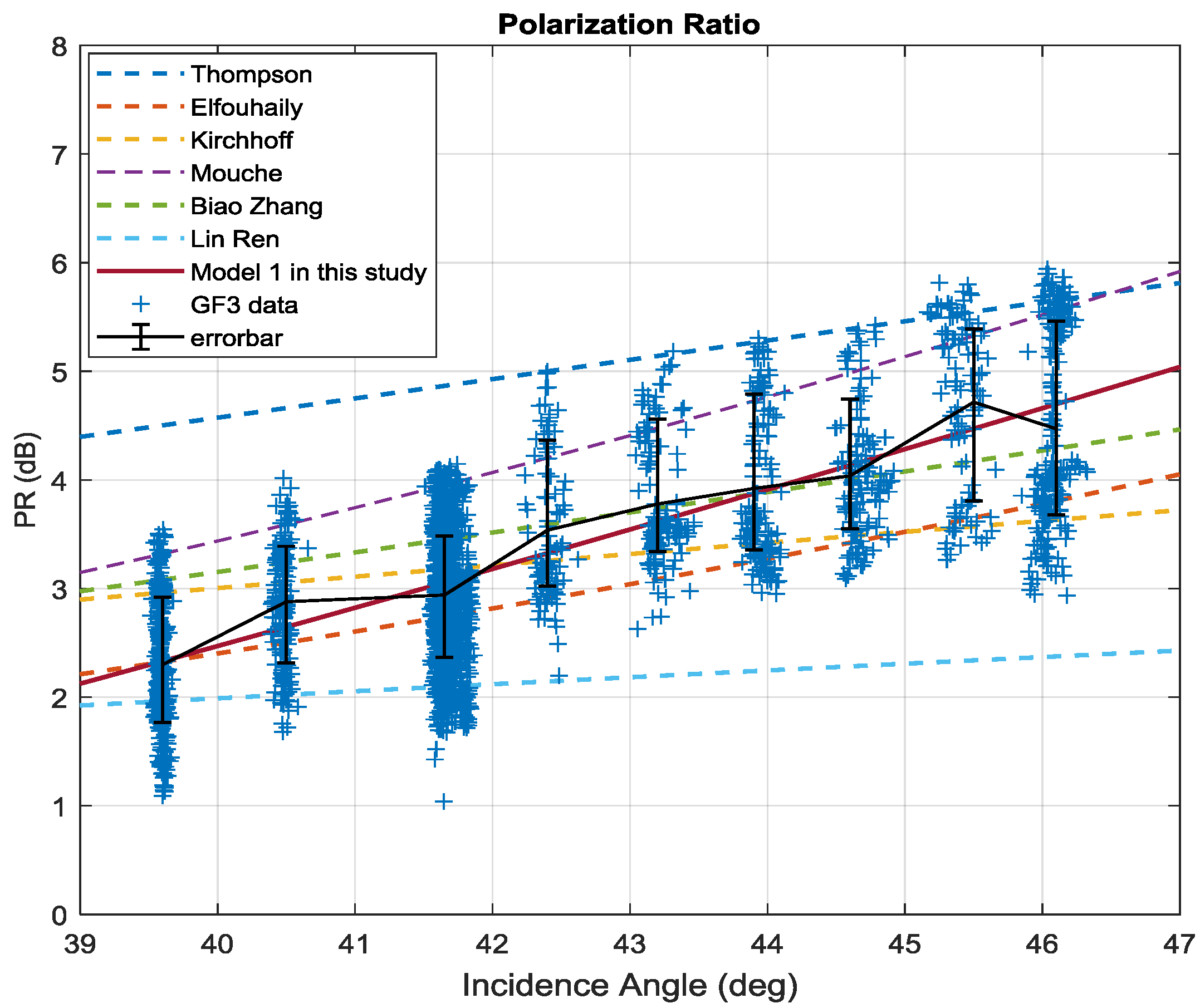
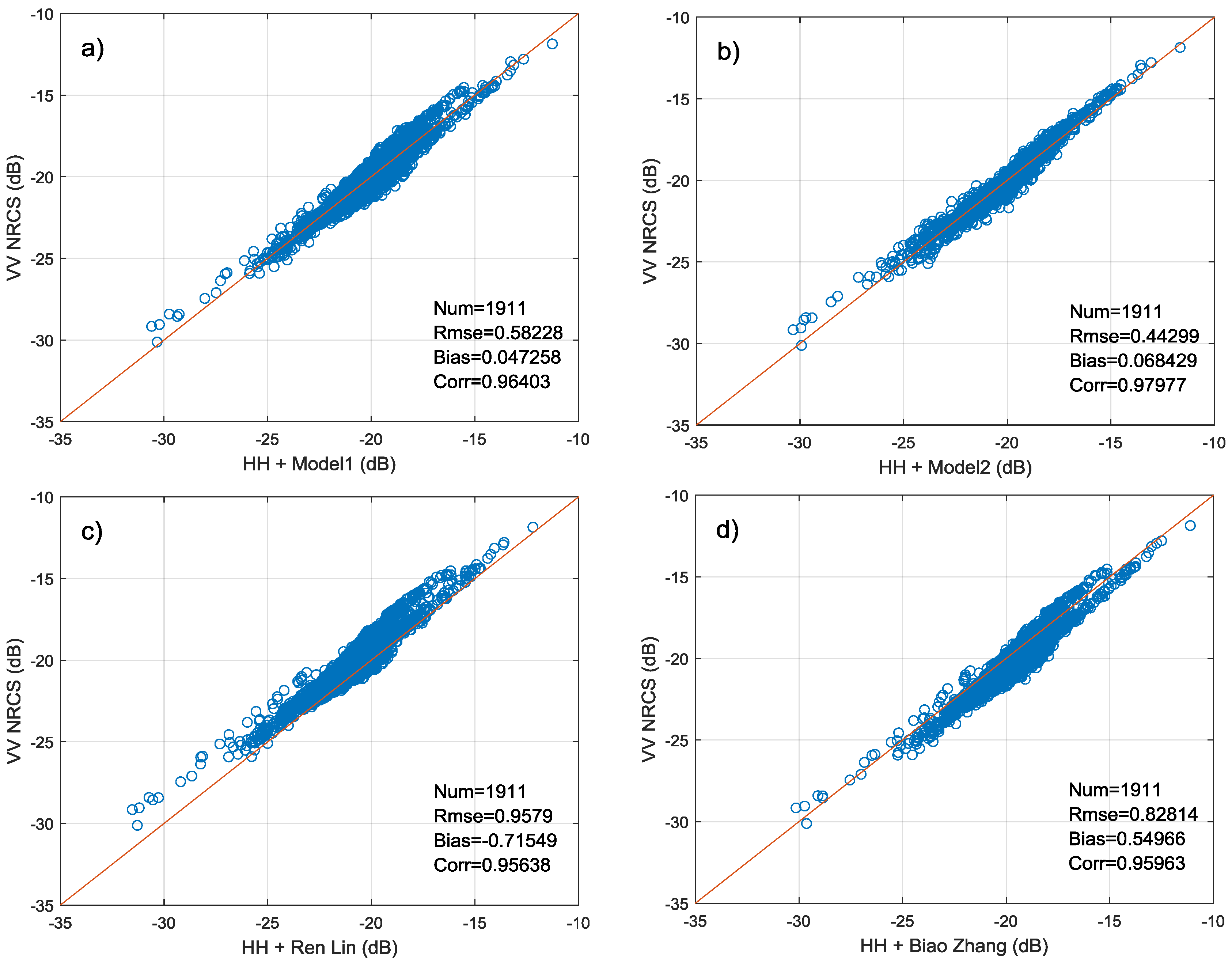
The PR of Wave Mode is not only dependent on incidence angle but also modulated by the azimuth angle. Its first maximum corresponds to downwind direction, the second maximum in the upwind, and two minima appear in the crosswind direction. Moreover, when speed is lower than 10 m/s, the PR presents a linear increase trend with wind speed in the downwind while it is independent on wind speed in other wind directions. Therefore, we fit two PR models which are suitable for large incidence angle using training set. The first is only dependent on incidence angle (Model 1) and the other one adds additional azimuth angle variable (Model 2). The results of two models on the testing set show that the PR models fitted in this paper are superior to models given in previous studies [
24,
25,
26,
27,
28,
45]. The Model 2 has higher polarization conversion accuracy than Model 1, with RMSE 0.443 dB and correlation coefficient 0.98.