Use of the Stockwell Transform in the Detection of P300 Evoked Potentials with Low-Cost Brain Sensors
Abstract
1. Introduction
2. Related Work
3. Stockwell Transform
4. Materials and Methods
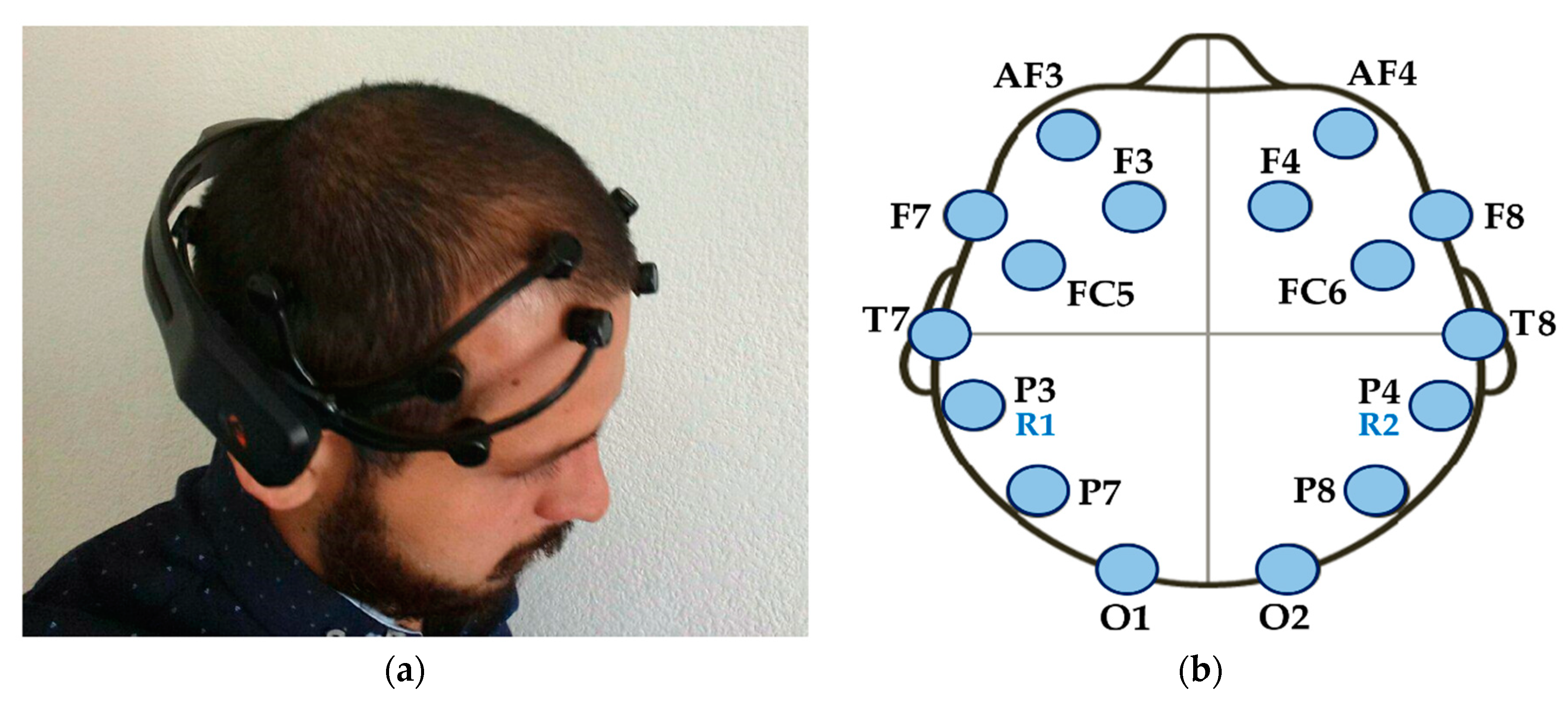
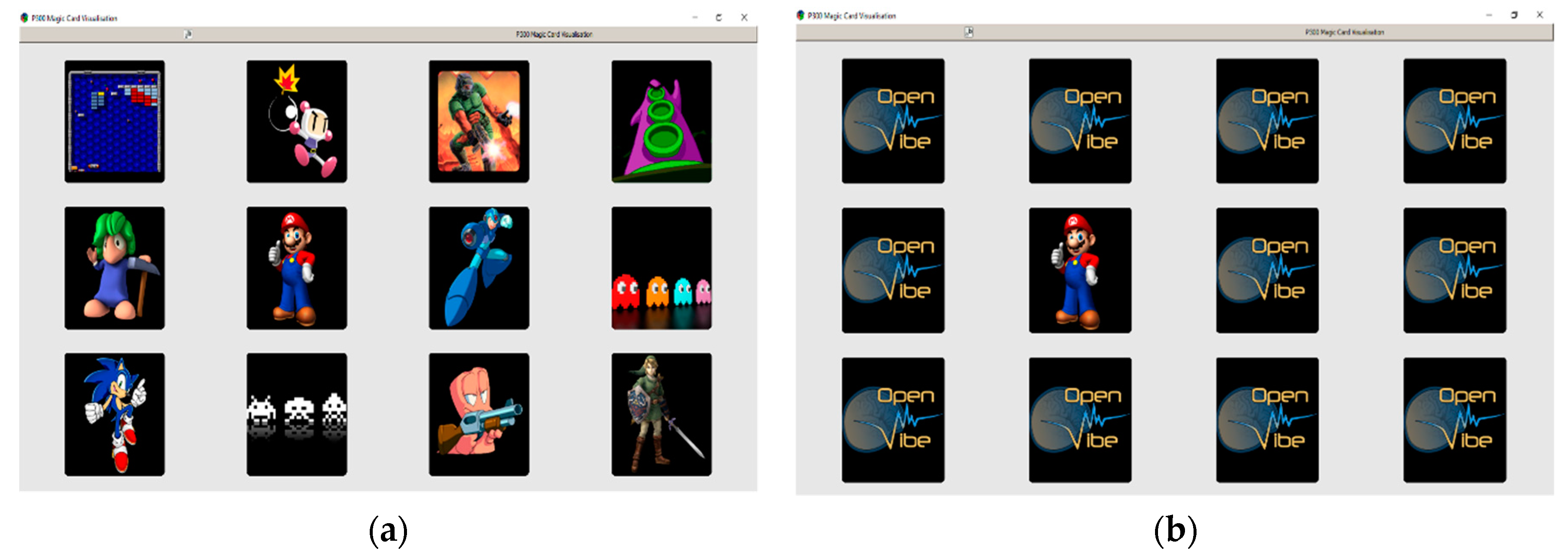
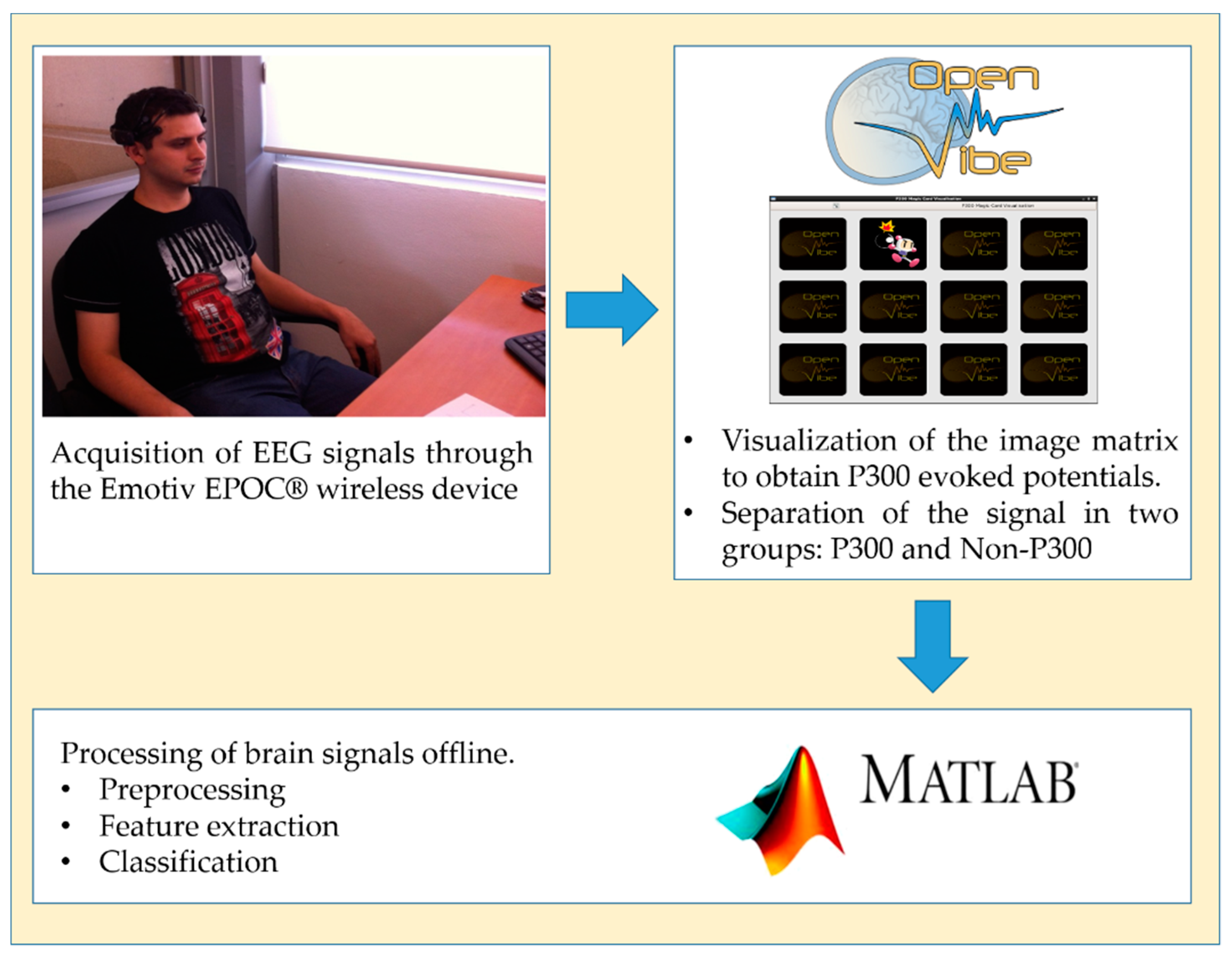
4.1. Data Acquisition
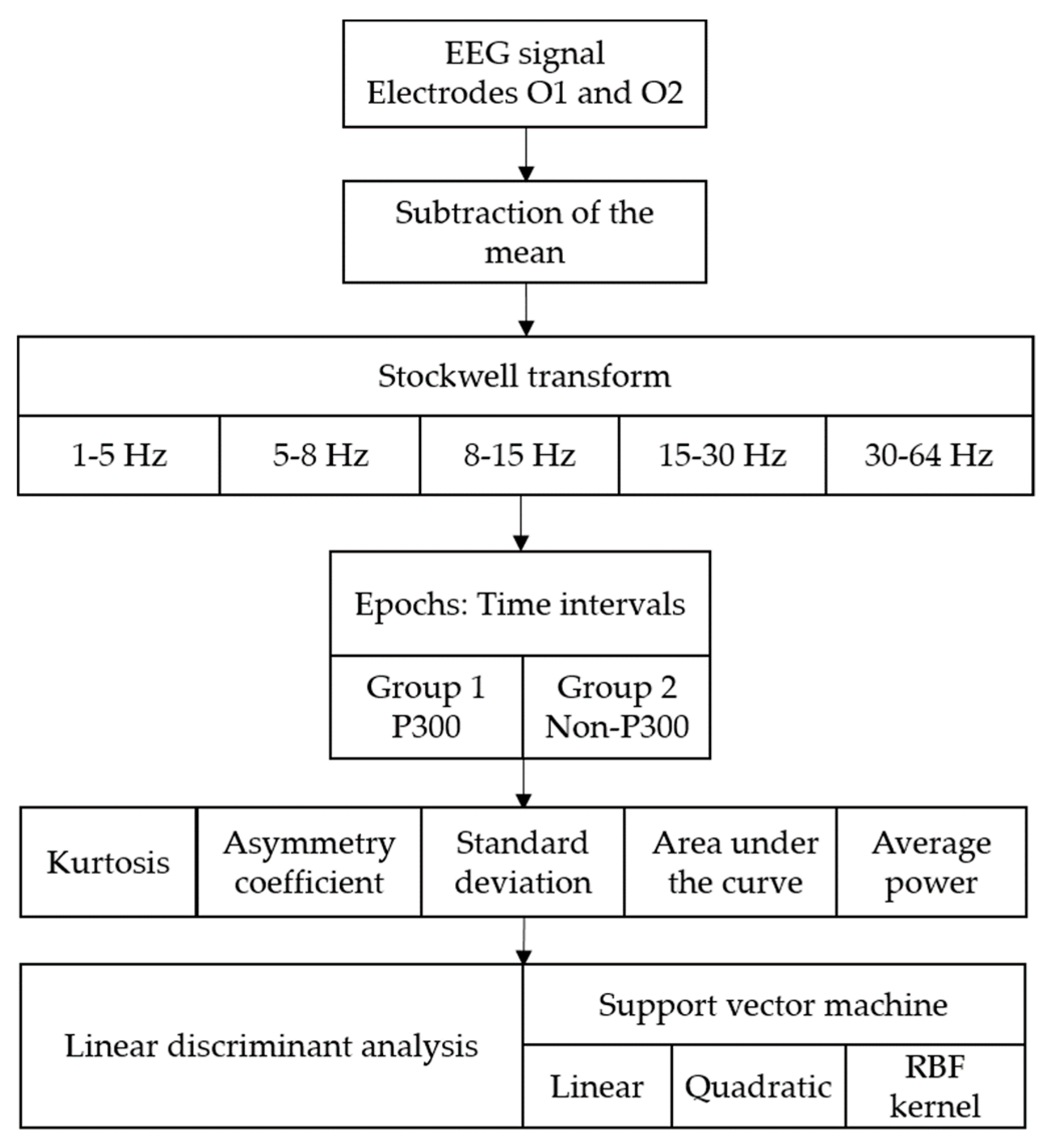
4.2. Feature Extraction
4.3. Classification
- Radial Basis Function,
- Polynomial,
- Sigmoidal,
- Cauchy,
- Logarithmic,
5. Results
6. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Li, J.; Liu, Y.; Zhang, Z.; Wang, Z.; Luo, D.; Zhou, X.; Zhu, M.; Salman, W.; Hu, G.; et al. Design of a fatigue detection system for high-speed trains based on driver vigilance using a wireless wearable EEG. Sensors 2017, 17, 486. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Chung, W.Y. A context-aware EEG headset system for early detection of driver drowsiness. Sensors 2015, 15, 20873–20893. [Google Scholar] [CrossRef] [PubMed]
- Marquez, L.A.P.; Munoz, G.R. Analysis and classification of electroencephalographic signals (EEG) to identify arm movements. In Proceedings of the 10th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 30 September–4 October 2013; pp. 138–143. [Google Scholar]
- Liu, Y.-H.; Huang, S.; Huang, Y.-D. Motor Imagery EEG Classification for Patients with Amyotrophic Lateral Sclerosis Using Fractal Dimension and Fisher’s Criterion-Based Channel Selection. Sensors 2017, 17, 1557. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Park, S.H.; Lee, S.G. Improving the accuracy and training speed of motor imagery brain-computer interfaces using wavelet-based combined feature vectors and gaussian mixture model-supervectors. Sensors 2017, 17, 2282. [Google Scholar] [CrossRef] [PubMed]
- Lo, C.C.; Chien, T.Y.; Chen, Y.C.; Tsai, S.H.; Fang, W.C.; Lin, B.S. A wearable channel selection-based brain-computer interface for motor imagery detection. Sensors 2016, 16, 213. [Google Scholar] [CrossRef] [PubMed]
- Vijean, V.; Hariharan, M.; Saidatul, A.; Yaacob, S. Mental tasks classifications using S-transform for BCI applications. In Proceedings of the IEEE Conference on Sustainable Utilization and Development in Engineering and Technology (STUDENT), Piscataway, NJ, USA, 20–21 October 2011; pp. 69–73. [Google Scholar]
- Chai, X.; Wang, Q.; Zhao, Y.; Li, Y.; Liu, D.; Liu, X.; Bai, O. A fast, efficient domain adaptation technique for cross-domain electroencephalography(EEG)-based emotion recognition. Sensors 2017, 17, 1014. [Google Scholar] [CrossRef] [PubMed]
- Korik, A.; Sosnik, R.; Siddique, N.; Coyle, D. Imagined 3D hand movement trajectory decoding from sensorimotor EEG rhythms. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 4591–4596. [Google Scholar]
- Makary, M.M.; Bu-Omer, H.M.; Soliman, R.S.; Park, K.; Kadah, Y.M. Spectral Subtraction Denoising Preprocessing Block to Improve Slow Cortical Potential Based Brain–Computer Interface. J. Med. Biol. Eng. 2017, 38, 87–98. [Google Scholar] [CrossRef]
- Kim, K.; Lim, S.H.; Lee, J.; Choi, J.W.; Kang, W.S.; Moon, C. Joint maximum likelihood time delay estimation of unknown event-related potential signals for EEG sensor signal quality enhancement. Sensors 2016, 16, 891. [Google Scholar] [CrossRef] [PubMed]
- Floriano, A.; Diez, P.F.; Freire Bastos-Filho, T. Evaluating the Influence of Chromatic and Luminance Stimuli on SSVEPs from Behind-the-Ears and Occipital Areas. Sensors 2018, 18, 615. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Lin, S.; Huang, Z. Feature extraction of P300s in EEG signal with discrete wavelet transform and fisher criterion. In Proceedings of the 8th International Conference on BioMedical Engineering and Informatics (BMEI), Shenyang, China, 14–16 October 2015; pp. 200–204. [Google Scholar]
- Schürmann, M.; Başar-Eroglu, C.; Kolev, V.; Başar, E. Delta responses and cognitive processing: Single-trial evaluations of human visual P300. Int. J. Psychophysiol. 2000, 39, 229–239. [Google Scholar] [CrossRef]
- Yordanova, J.; Rosso, O.A.; Kolev, V. A transient dominance of theta event-related brain potential component characterizes stimulus processing in an auditory oddball task. Clin. Neurophysiol. 2003, 114, 529–540. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Z.; Hu, D. Comparison of stimulus types in visual P300 speller of brain-computer interfaces. In Proceedings of the 9th IEEE International Conference on Cognitive Informatics (ICCI), Beijing, China, 7–9 July 2010; pp. 273–279. [Google Scholar]
- Chang, M.; Makino, S.; Rutkowski, T.M. Classification improvement of P300 response based auditory spatial speller brain-computer interface paradigm. In Proceedings of the IEEE Region 10 Conference on TENCON, Xi’an, China, 22–25 October 2013; pp. 1–4. [Google Scholar]
- Kodama, T.; Makino, S. Convolutional Neural Network Architecture and Input Volume Matrix Design for ERP Classifications in a Tactile P300—Based Brain—Computer Interface. In Proceedings of the 39th IEEE International Conference on Engineering in Medicine and Biology Society (EMBC), Jeju, Korea, 11–15 July 2017; pp. 3814–3817. [Google Scholar]
- Nicolas-Alonso, L.F.; Gomez-Gil, J. Brain computer interfaces, a review. Sensors 2012, 12, 1211–1279. [Google Scholar] [CrossRef] [PubMed]
- Jones, K.A.; Porjesz, B.; Chorlian, D.; Rangaswamy, M.; Kamarajan, C.; Padmanabhapillai, A.; Stimus, A.; Begleiter, H. S-transform time-frequency analysis of P300 reveals deficits in individuals diagnosed with alcoholism. Clin. Neurophysiol. 2006, 117, 2128–2143. [Google Scholar] [CrossRef] [PubMed]
- Farwell, L.A.; Donchin, E. Talking off the top of your head: Toward a mental prothesis utilizing event-relatedpotencials. Electroencephalogr. Clin. Neurophysiol. 1988, 70, 510–523. [Google Scholar] [CrossRef]
- Alvarado-Gonzalez, M.; Garduno, E.; Bribiesca, E.; Yanez-Suarez, O.; Medina-Banuelos, V. P300 Detection Based on EEG Shape Features. Comput. Math. Methods Med. 2016, 2016, 2029791. [Google Scholar] [CrossRef] [PubMed]
- Maddula, R.K.; Stivers, J.; Mousavi, M.; Ravindran, S.; de Sa, V.R. Deep Recurrent Convolutional Neural Networks for Classifying P300 Bci Signals. In Proceedings of the 7th Graz Brain-Computer Interface Conference, Graz, Austria, 18–22 September 2017. [Google Scholar]
- Onishi, A.; Takano, K.; Kawase, T.; Ora, H.; Kansaku, K. Affective stimuli for an auditory P300 brain-computer interface. Front. Neurosci. 2017, 11, 522. [Google Scholar] [CrossRef] [PubMed]
- Tayeb, S.; Mahmoudi, A.; Regragui, F.; Himmi, M.M. Efficient detection of P300 using Kernel PCA and support vector machine. In Proceedings of the Second World Conference on Complex Systems (WCCS), Agadir, Morocco, 10–12 November 2014; pp. 17–22. [Google Scholar]
- Hariharan, M.; Vijean, V.; Sindhu, R.; Divakar, P.; Saidatul, A.; Yaacob, S. Classification of mental tasks using stockwell transform. Comput. Electr. Eng. 2014, 40, 1741–1749. [Google Scholar] [CrossRef]
- Grubov, V.V.; Sitnikova, E.Y.; Pavlov, A.N.; Khramova, M.V.; Koronovskii, A.A.; Hramov, A.E. Time-frequency analysis of epileptic EEG patterns by means of empirical modes and wavelets. Proc. SPIE 2014, 9448, 94481Q. [Google Scholar] [CrossRef]
- Sarker, T.; Paul, S.; Rayhan, A.; Zabir, I.; Shahnaz, C. Bi-spectral higher order statistics and time-frequency domain features for arithmetic task classification from EEG signals. In Proceedings of the IEEE International Conference on Imaging, Vision and Pattern Recognition (icIVPR), Dhaka, Bangladesh, 13–14 February 2017; pp. 1–4. [Google Scholar]
- Güneysu, A.; Akin, H.L. An SSVEP based BCI to control a humanoid robot by using portable EEG device. In Proceedings of the 35th Annual International Conference of the IEEE on Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 6905–6908. [Google Scholar]
- Swee, S.K.; You, L.Z. Fast fourier analysis and EEG classification brainwave controlled wheelchair. In Proceedings of the 2nd International Conference on Control Science and Systems Engineering (ICCSSE), Singapore, 27–29 July 2016; pp. 20–23. [Google Scholar]
- Phothisonothai, M.; Watanabe, K. Time-frequency analysis of duty cycle changing on steady-state visual evoked potential: EEG recording. In Proceedings of the Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA), Chiang Mai, Thailand, 9–12 December 2014; pp. 2010–2013. [Google Scholar]
- Motlagh, F.E.; Tang, S.H.; Motlagh, O. Combination of continuous and discrete wavelet coefficients in single-trial P300 detection. In Proceedings of the IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES), Langkawi, Malaysia, 17–19 December 2012; pp. 954–959. [Google Scholar]
- Costagliola, S.; Dal Seno, B.; Matteucci, M. Recognition and classification of P300s in EEG signals by means of feature extraction using wavelet decomposition. In Proceedings of the International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009; pp. 597–603. [Google Scholar]
- Chen, L.; Zhao, E.; Wang, D.; Han, Z.; Zhang, S.; Xu, C. Feature extraction of EEG signals from epilepsy patients based on Gabor Transform and EMD decomposition. In Proceedings of the Sixth International Conference on Natural Computation (ICNC), Yantai, China, 10–12 August 2010; Volume 3, pp. 1243–1247. [Google Scholar]
- Brown, R.A.; Frayne, R. A fast discrete S-transform for biomedical signal processing. In Proceedings of the 30th Annual International Conference on Engineering in Medicine and Biology Society (EMBS), Vancouver, BC, Canada, 20–24 August 2008; Volume 2008, pp. 2586–2589. [Google Scholar]
- Senapati, K.; Kar, S.; Routray, A. A new technique for removal of ocular artifacts from EEG signals using S-transform. In Proceedings of the International Conference on Systems in Medicine and Biology (ICSMB), Kharagpur, India, 16–18 December 2010; pp. 113–116. [Google Scholar]
- Upadhyay, R.; Padhy, P.K.; Kankar, P.K. Ocular artifact removal from EEG signals using discrete orthonormal stockwell transform. In Proceedings of the Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–5. [Google Scholar]
- Shekar, B.H.; Rajesh, D.S. Stockwell Transform based Face Recognition: A Robust and an Accurate Approach. In Proceedings of the International Conference on Advances in Computing, Communications and Informatics (ICACCI), Jaipur, India, 21–24 September 2016; pp. 168–174. [Google Scholar]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Stockwell, R.G. A basis for efficient representation of the S-transform. Digit. Signal Process. A Rev. J. 2007, 17, 371–393. [Google Scholar] [CrossRef]
- Renard, Y.; Lotte, F.; Gibert, G.; Congedo, M.; Maby, E.; Delannoy, V.; Bertrand, O.; Lécuyer, A. OpenViBE: An Open-Source Software Platform to Design, Test, and Use Brain–Computer Interfaces in Real and Virtual Environments. Presence Teleoper. Virtual Environ. 2010, 19, 35–53. [Google Scholar] [CrossRef]
- P300: Magic Card. Available online: http://openvibe.inria.fr/openvibe-p300-magic-card/ (accessed on 19 March 2018).
- Perez Vidal, A.F.; Oliver Salazar, M.A.; Salas Lopez, G. Development of a Brain-Computer Interface Based on Visual Stimuli for the Movement of a Robot Joints. IEEE Lat. Am. Trans. 2016, 14, 477–484. [Google Scholar] [CrossRef]
- Robinson, N.; Vinod, A.P. Bi-Directional Imagined Hand Movement Classification Using Low Cost EEG-Based BCI. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Hong Kong, China, 9–12 October 2015; pp. 3134–3139. [Google Scholar]
- Wu, S.-L.; Wu, C.-W.; Pal, N.R.; Chen, C.-Y.; Chen, S.-A.; Lin, C.-T. Common spatial pattern and lnear discriminant analysis for motor imagery classification. In Proceedings of the IEEE Symposium on Computational Intelligence, Cognitive Algorithms, Mind, and Brain (CCMB), Singapore, 6–19 April 2013; pp. 146–151. [Google Scholar]
- Bang, J.W.; Choi, J.S.; Park, K.R. Noise reduction in brainwaves by using both EEG signals and frontal viewing camera images. Sensors 2013, 13, 6272–6294. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Chen, M.; Zhao, S.; Hu, S.; Shi, Z.; Cao, Y. ReliefF-based EEG sensor selection methods for emotion recognition. Sensors 2016, 16, 1558. [Google Scholar] [CrossRef] [PubMed]
- Quitadamo, L.R.; Cavrini, F.; Sbernini, L.; Riillo, F.; Bianchi, L.; Seri, S.; Saggio, G. Support vector machines to detect physiological patterns for EEG and EMG-based human-computer interaction: A review. J. Neural Eng. 2017, 14, 11001. [Google Scholar] [CrossRef] [PubMed]
- Krusienski, D.J.; Sellers, E.W.; McFarland, D.J.; Vaughan, T.M.; Wolpaw, J.R. Toward enhanced P300 speller performance. J. Neurosci. Methods 2008, 167, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Mautner, P.; Vareka, L. Off-line Analysis of the P300 Event-Related Potential using Discrete Wavelet Transform. In Proceedings of the 36th International Conference on Telecommunications and Signal Processing (TSP), Rome, Italy, 2–4 July 2013; pp. 569–572. [Google Scholar]
- Shi, K.; Gao, N.; Li, Q.; Bai, O. A P300 brain-computer interface design for virtual remote control system. In Proceedings of the 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 August 2017; pp. 326–329. [Google Scholar]
- Guger, C.; Ortner, R.; Dimov, S.; Allison, B. A comparison of face speller approaches for P300 BCls. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 4809–4812. [Google Scholar]
- Kolev, V.; Demiralp, T.; Yordanova, J.; Ademoglu, A.; Isoglu-Alkaç, U. Time-frequency analysis reveals multiple functional components during oddball P300. Neuroreport 1997, 8, 2061–2065. [Google Scholar] [CrossRef] [PubMed]
- Yordanova, J.; Devrim, M.; Kolev, V.; Ademoglu, A.; Demiralp, T. Multiple time-frequency components account for the complex functional reactivity of P300. Neuroreport 2000, 11, 1097–1103. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Thulasidas, M.; Guan, C.; Wu, J. Robust classification of EEG signal for brain-computer interface. IEEE Trans. Neural Syst. Rehabil. Eng. 2006, 14, 24–29. [Google Scholar] [CrossRef] [PubMed]
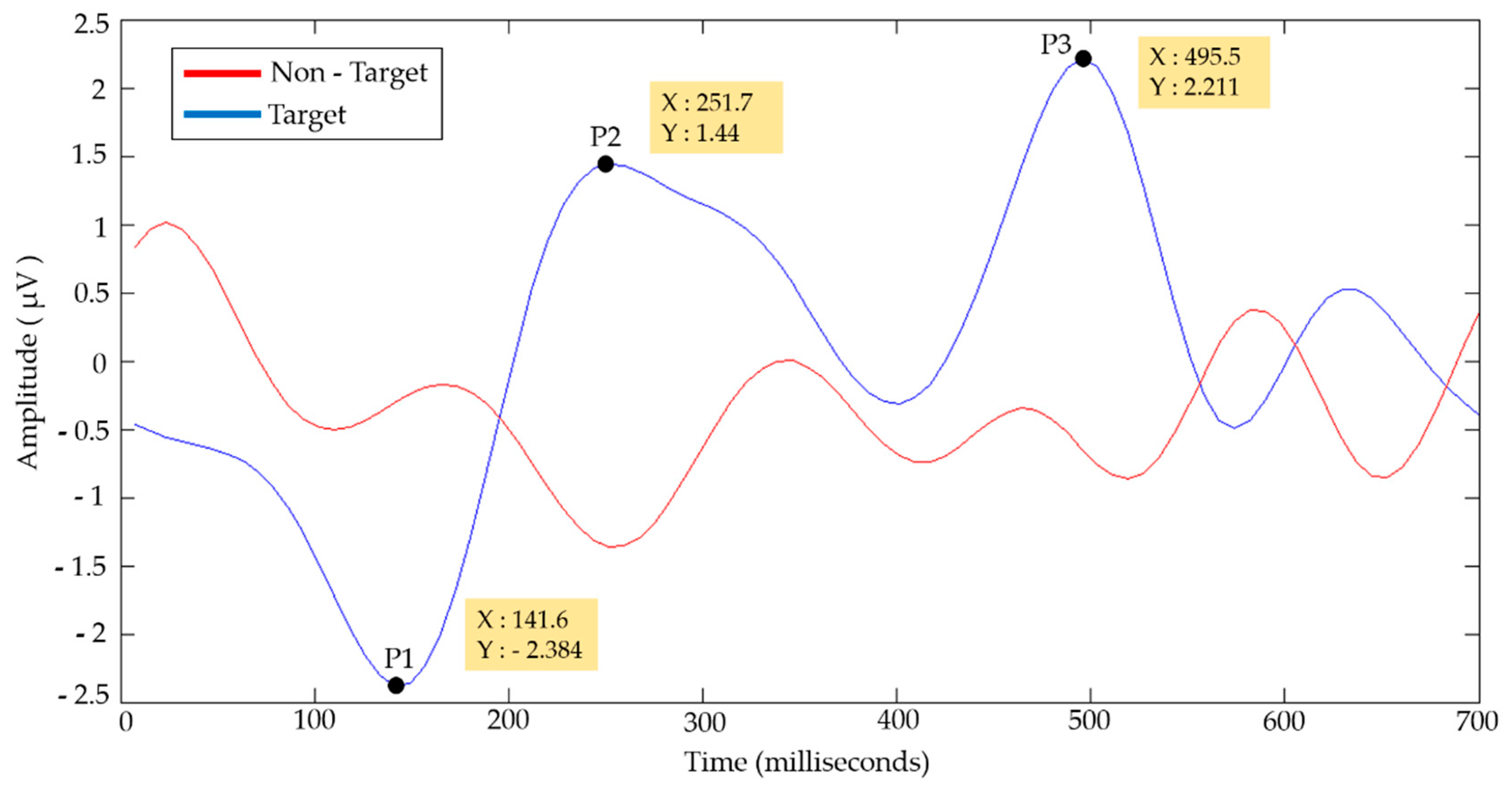
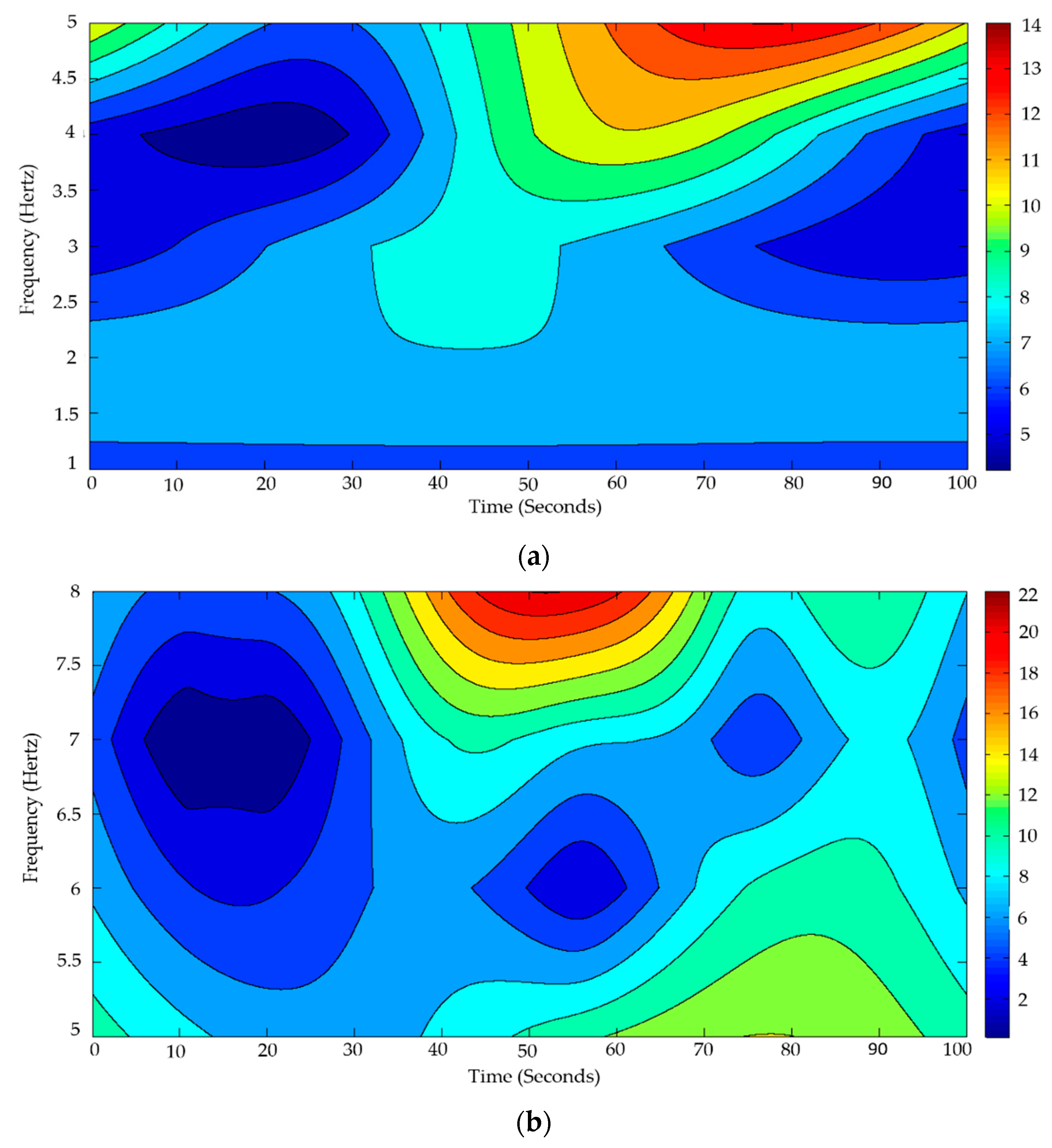
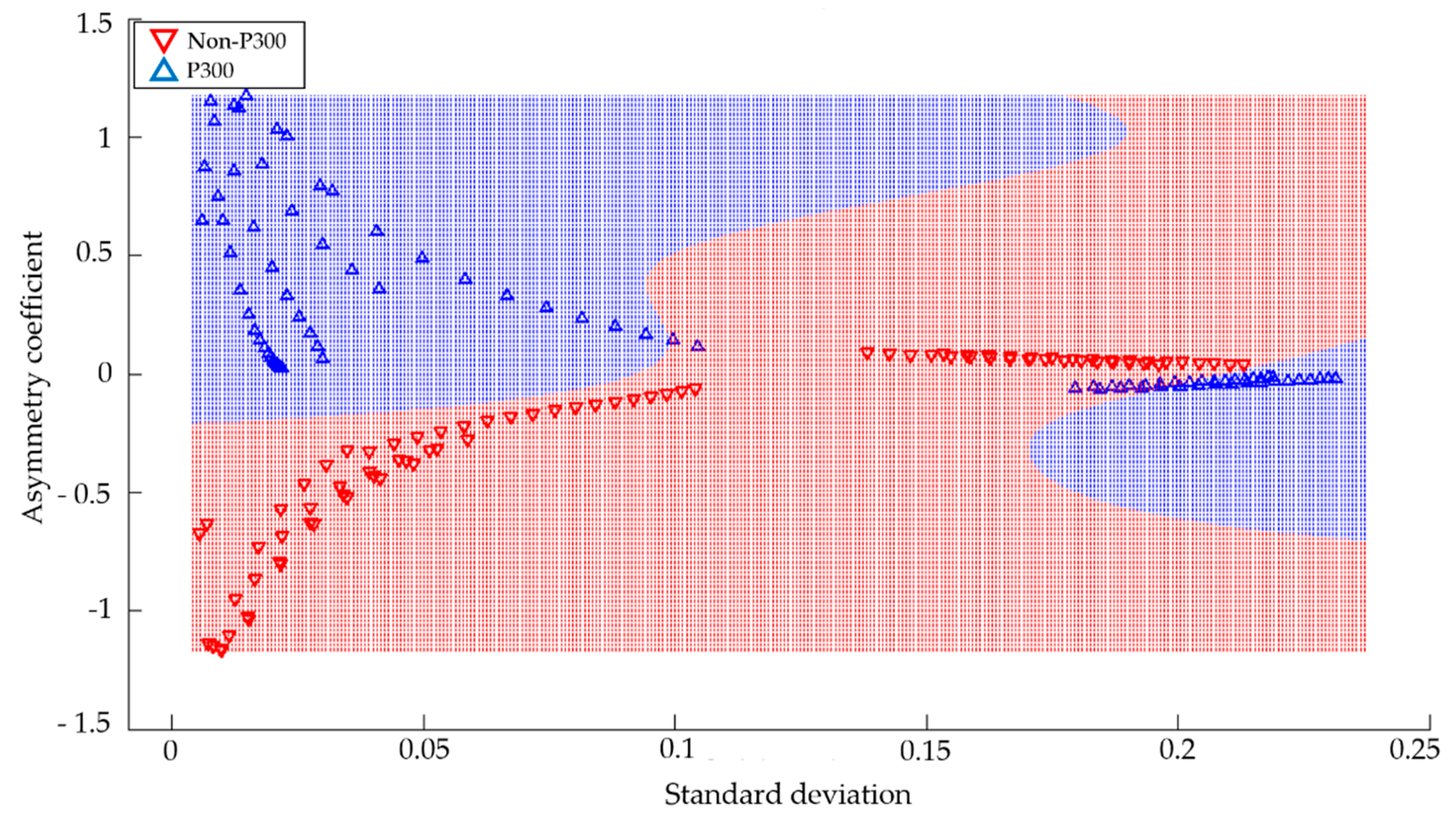
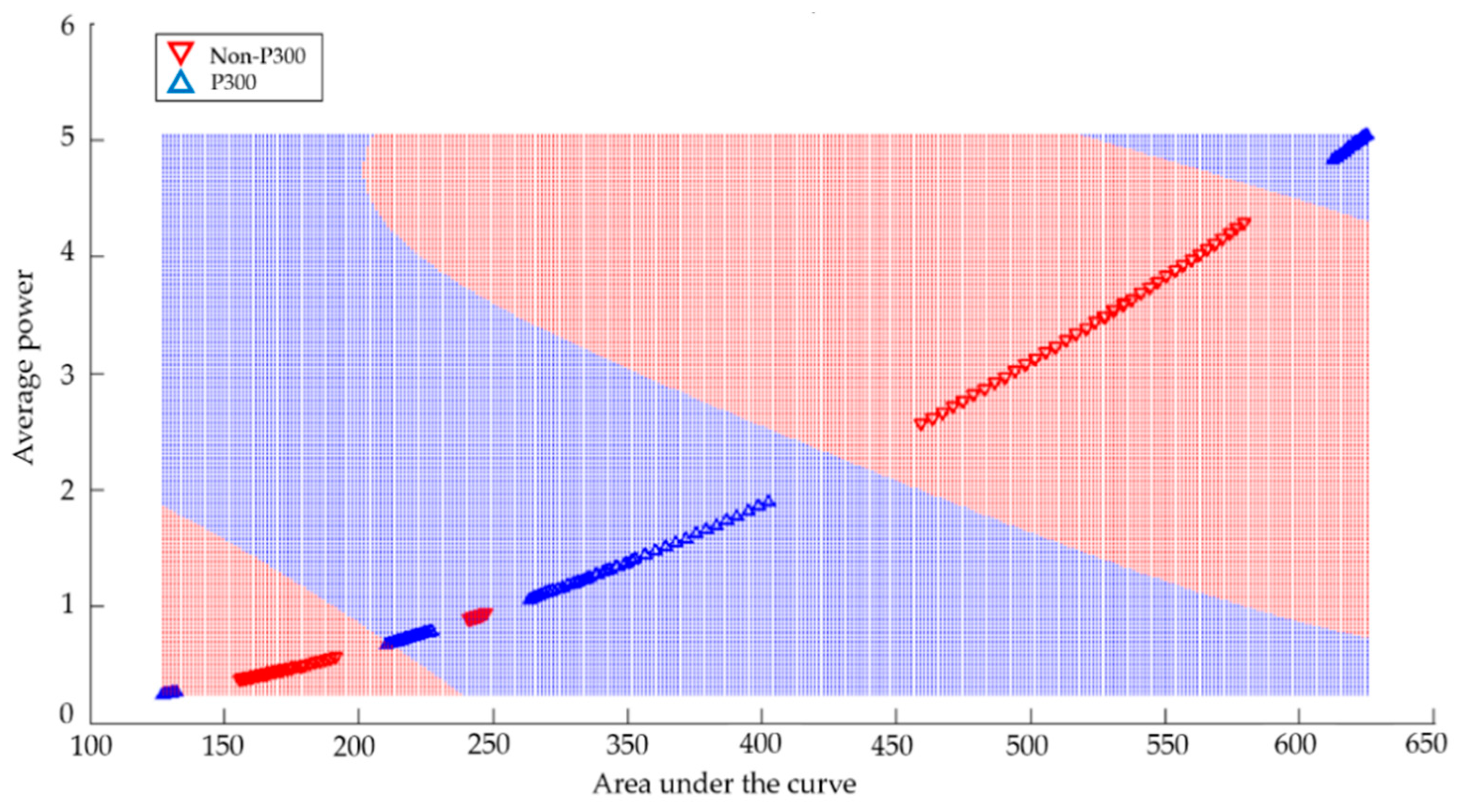
| Component | Amplitude (µV) | Time (ms) | ||
|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | |
| P1 | −6.29 | 4.03 | 159.26 | 45.98 |
| P2 | 5.62 | 3.26 | 266.17 | 63.03 |
| P3 | 8.72 | 4.17 | 478.65 | 76.53 |
| Subject | Average Power—Area under the Curve | Asymmetry Coefficient—Standard Deviation | ||
|---|---|---|---|---|
| 1–5 Hz | 5–8 Hz | 1–5 Hz | 5–8 Hz | |
| S1 | 85 | 81 | 84 | 85 |
| S2 | 81 | 80 | 82 | 90 |
| S3 | 84 | 84 | 80 | 92 |
| S4 | 75 | 76 | 87 | 78 |
| S5 | 77 | 80 | 83 | 82 |
| S6 | 78 | 81 | 86 | 81 |
| S7 | 80 | 75 | 82 | 80 |
| S8 | 79 | 83 | 84 | 86 |
| S9 | 75 | 82 | 81 | 82 |
| S10 | 81 | 83 | 82 | 85 |
| Average | 79.5 | 80.5 | 83.1 | 84.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Vidal, A.F.; Garcia-Beltran, C.D.; Martínez-Sibaja, A.; Posada-Gómez, R. Use of the Stockwell Transform in the Detection of P300 Evoked Potentials with Low-Cost Brain Sensors. Sensors 2018, 18, 1483. https://doi.org/10.3390/s18051483
Pérez-Vidal AF, Garcia-Beltran CD, Martínez-Sibaja A, Posada-Gómez R. Use of the Stockwell Transform in the Detection of P300 Evoked Potentials with Low-Cost Brain Sensors. Sensors. 2018; 18(5):1483. https://doi.org/10.3390/s18051483
Chicago/Turabian StylePérez-Vidal, Alan F., Carlos D. Garcia-Beltran, Albino Martínez-Sibaja, and Rubén Posada-Gómez. 2018. "Use of the Stockwell Transform in the Detection of P300 Evoked Potentials with Low-Cost Brain Sensors" Sensors 18, no. 5: 1483. https://doi.org/10.3390/s18051483
APA StylePérez-Vidal, A. F., Garcia-Beltran, C. D., Martínez-Sibaja, A., & Posada-Gómez, R. (2018). Use of the Stockwell Transform in the Detection of P300 Evoked Potentials with Low-Cost Brain Sensors. Sensors, 18(5), 1483. https://doi.org/10.3390/s18051483





