Least Squares Neural Network-Based Wireless E-Nose System Using an SnO2 Sensor Array
Abstract
1. Introduction
2. Materials and Methods
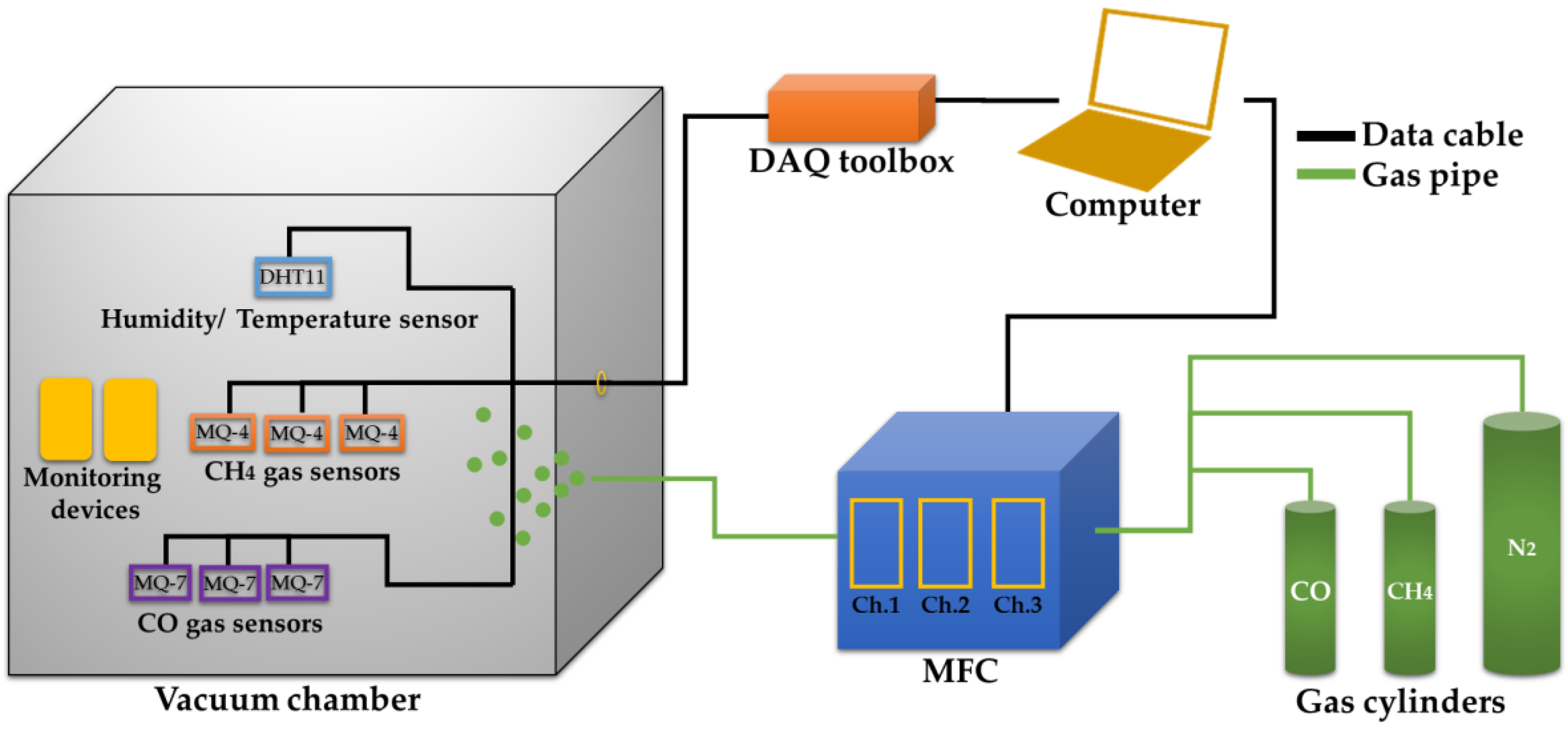
2.1. Experimental Setup
2.1.1. Gas Sensor Setup
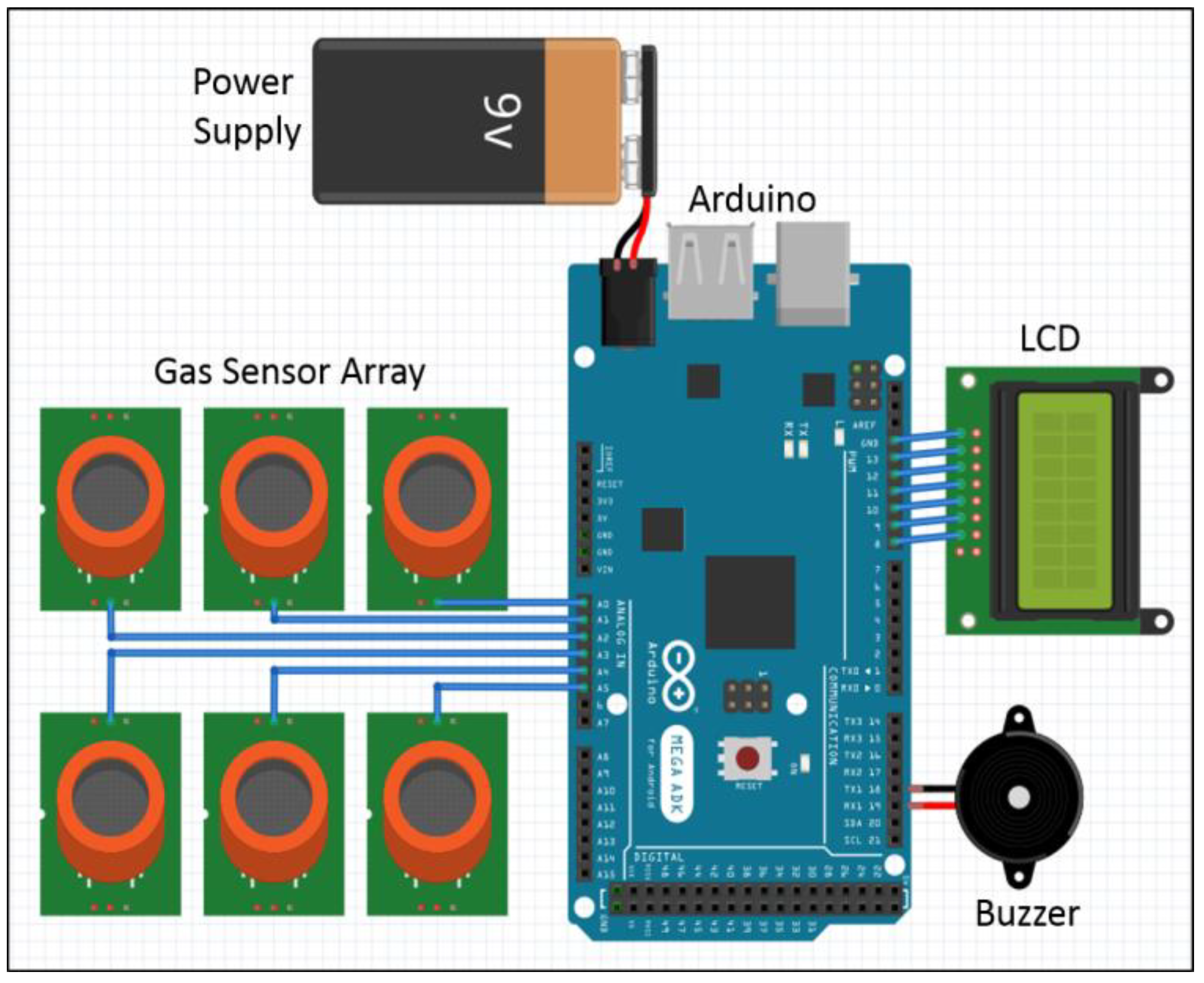
2.1.2. System Setup
2.2. Sample Preparation
2.3. Data Acquisition and Preprocessing
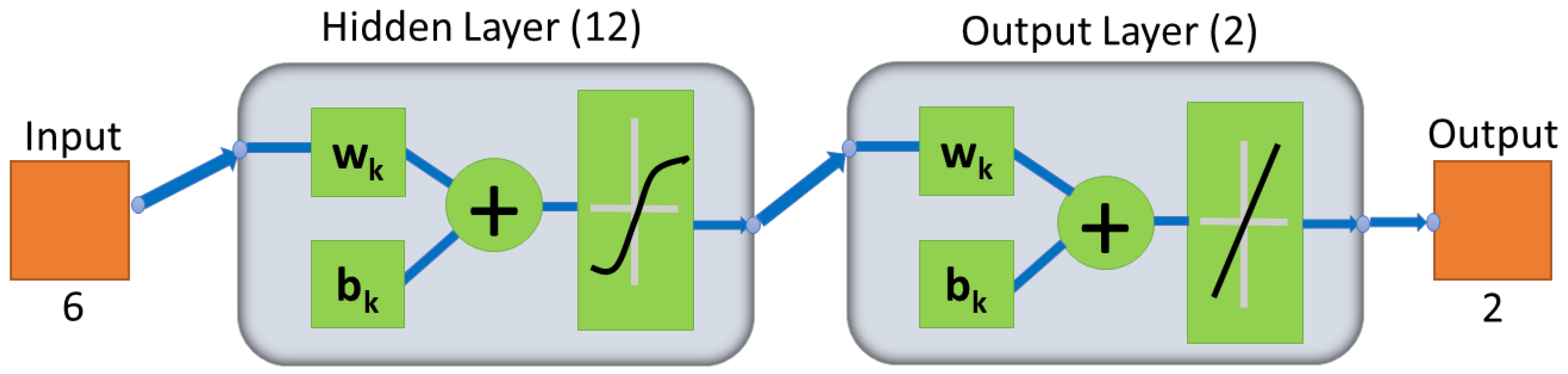
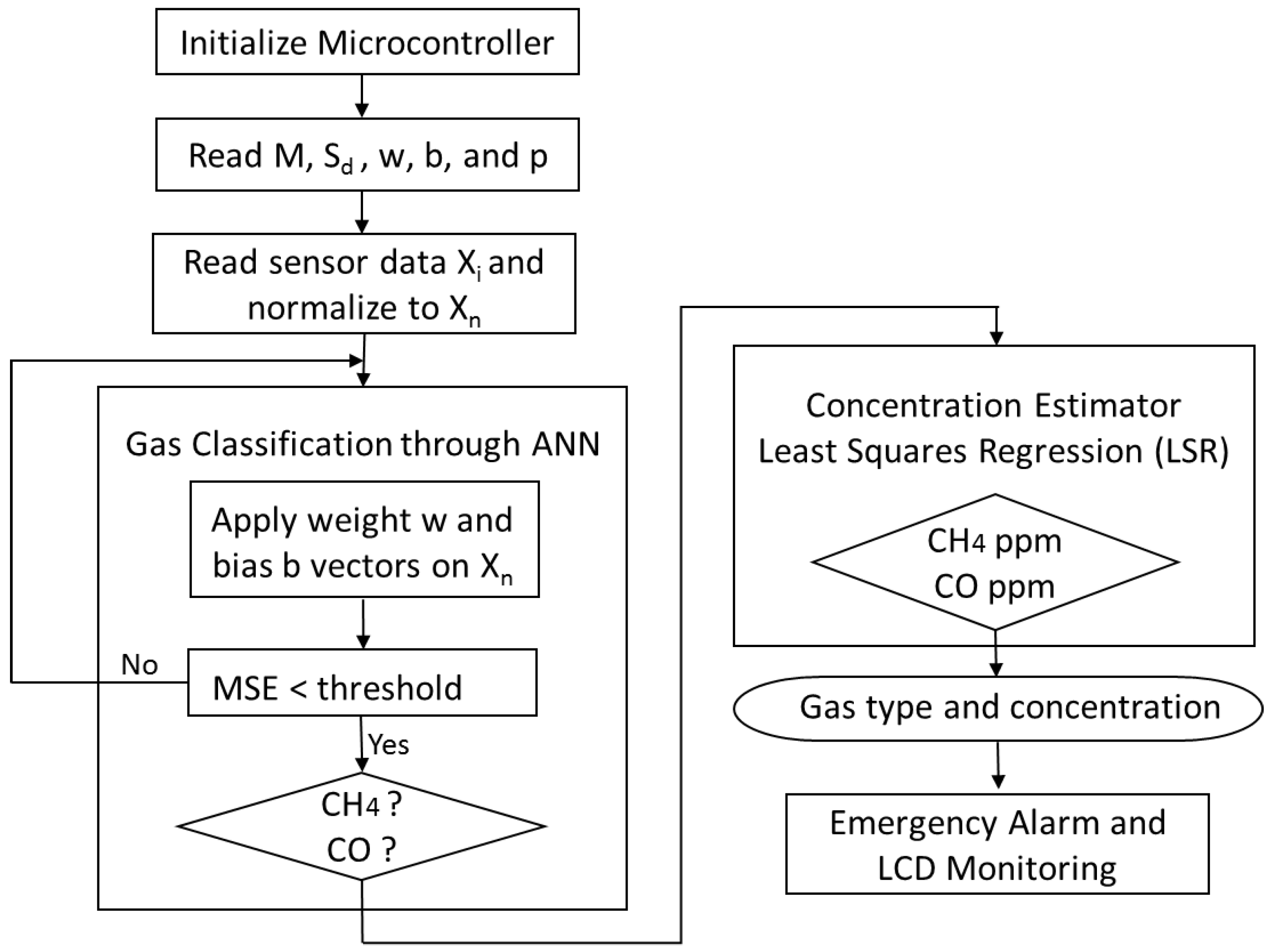
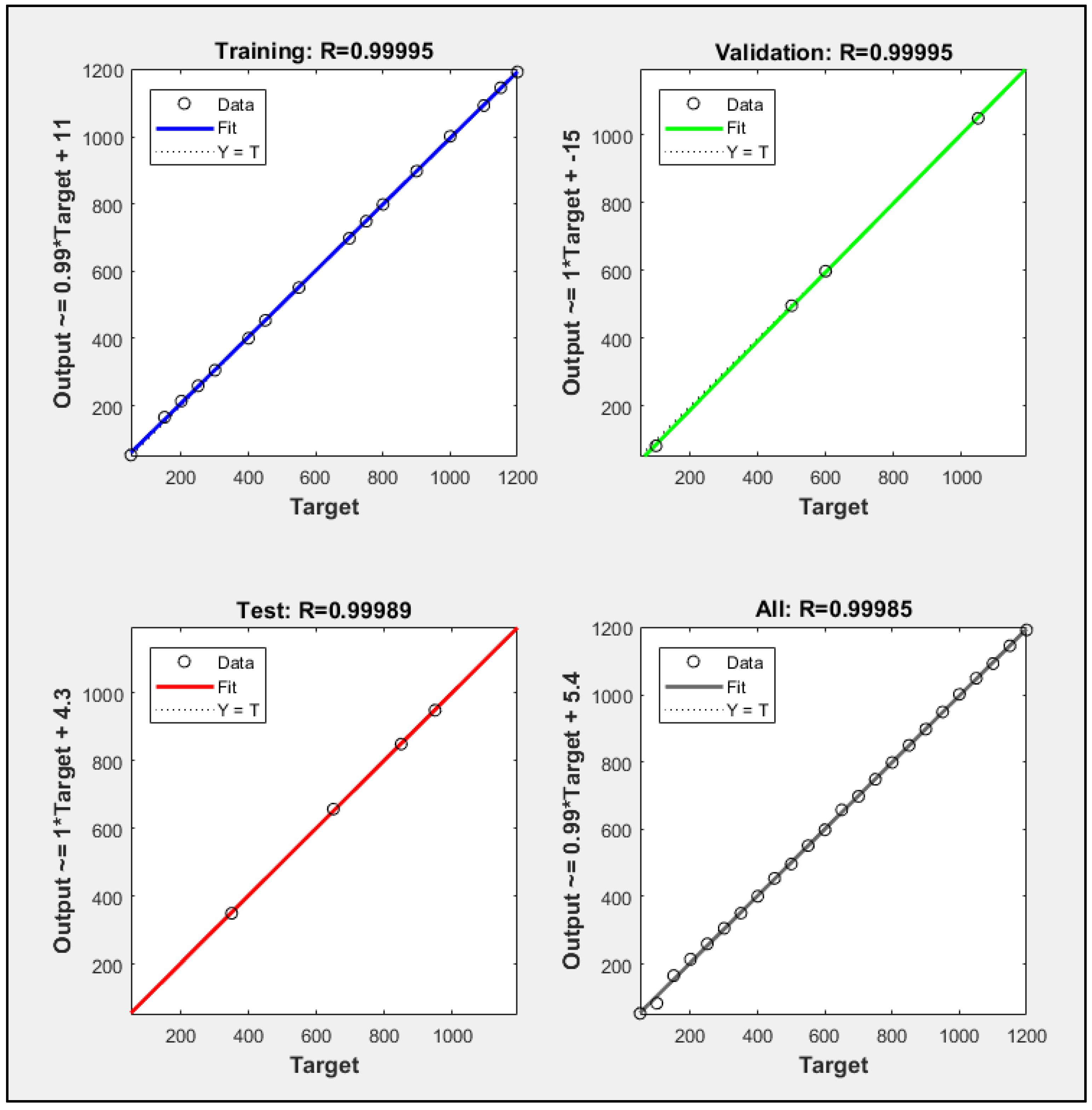
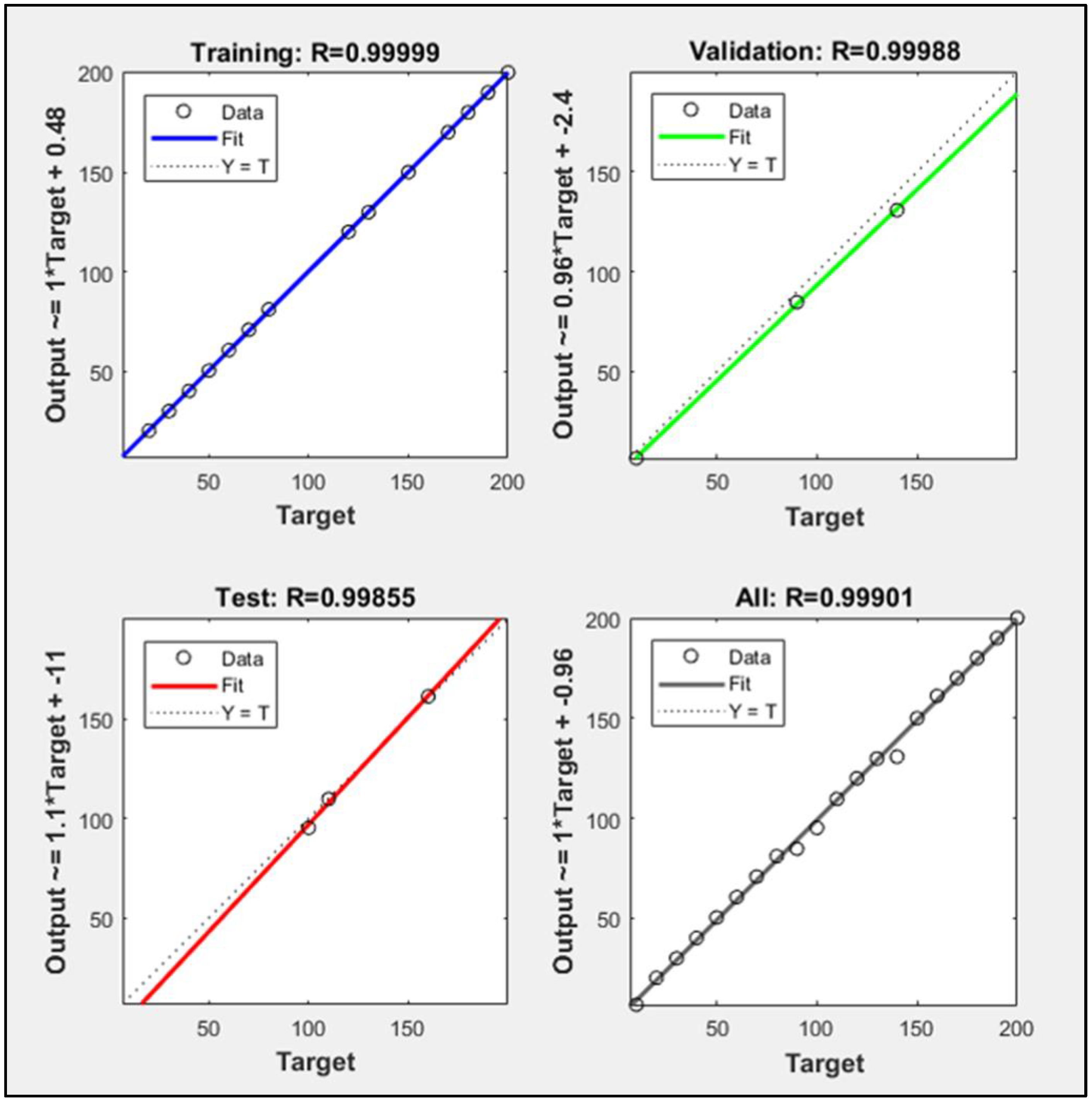
2.4. Artificial Neural Network for Classification
2.5. Least Squares Regression to Estimate Concentrations
2.6. Emergency Alarm System
3. Results and Discussion
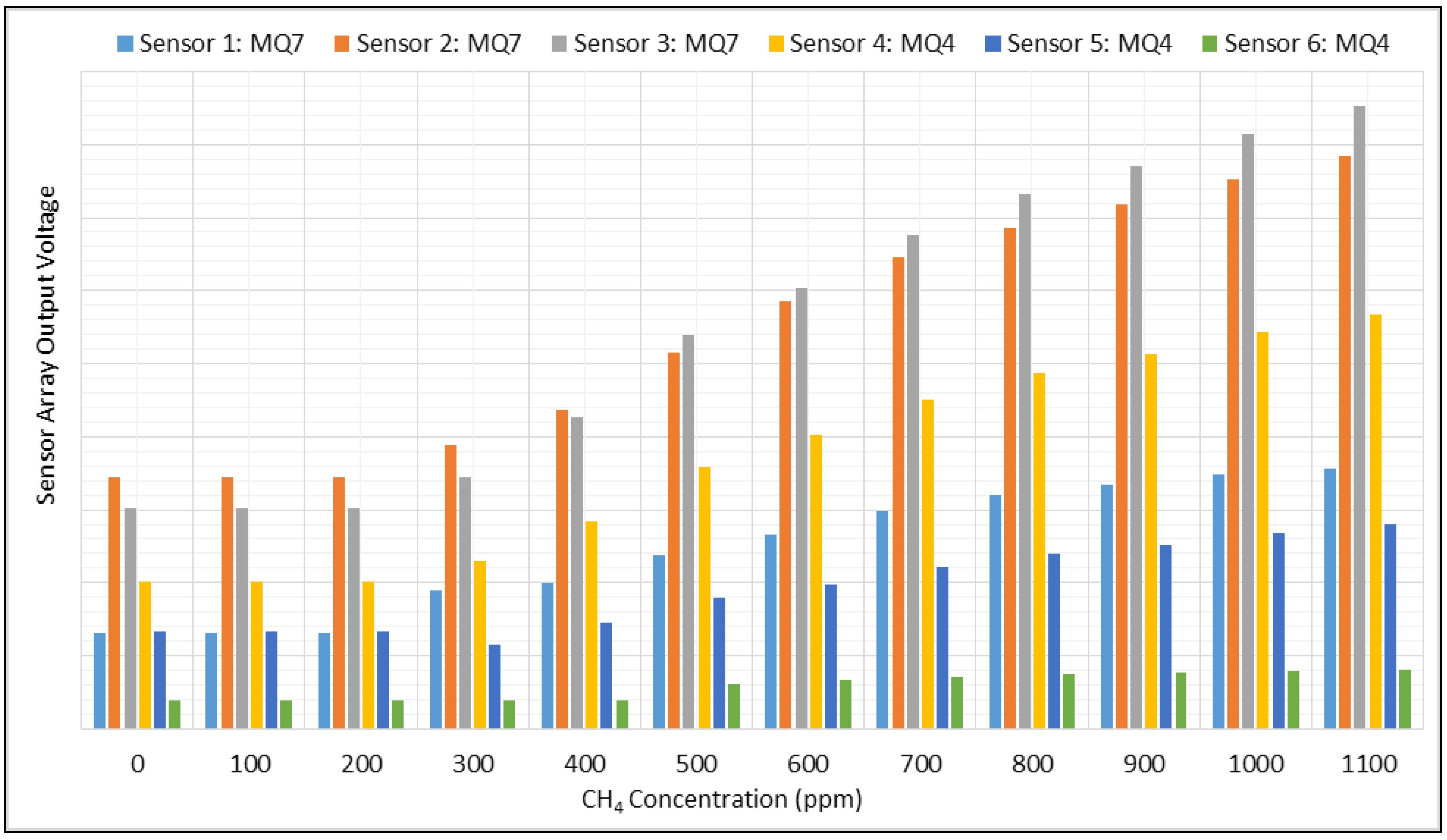
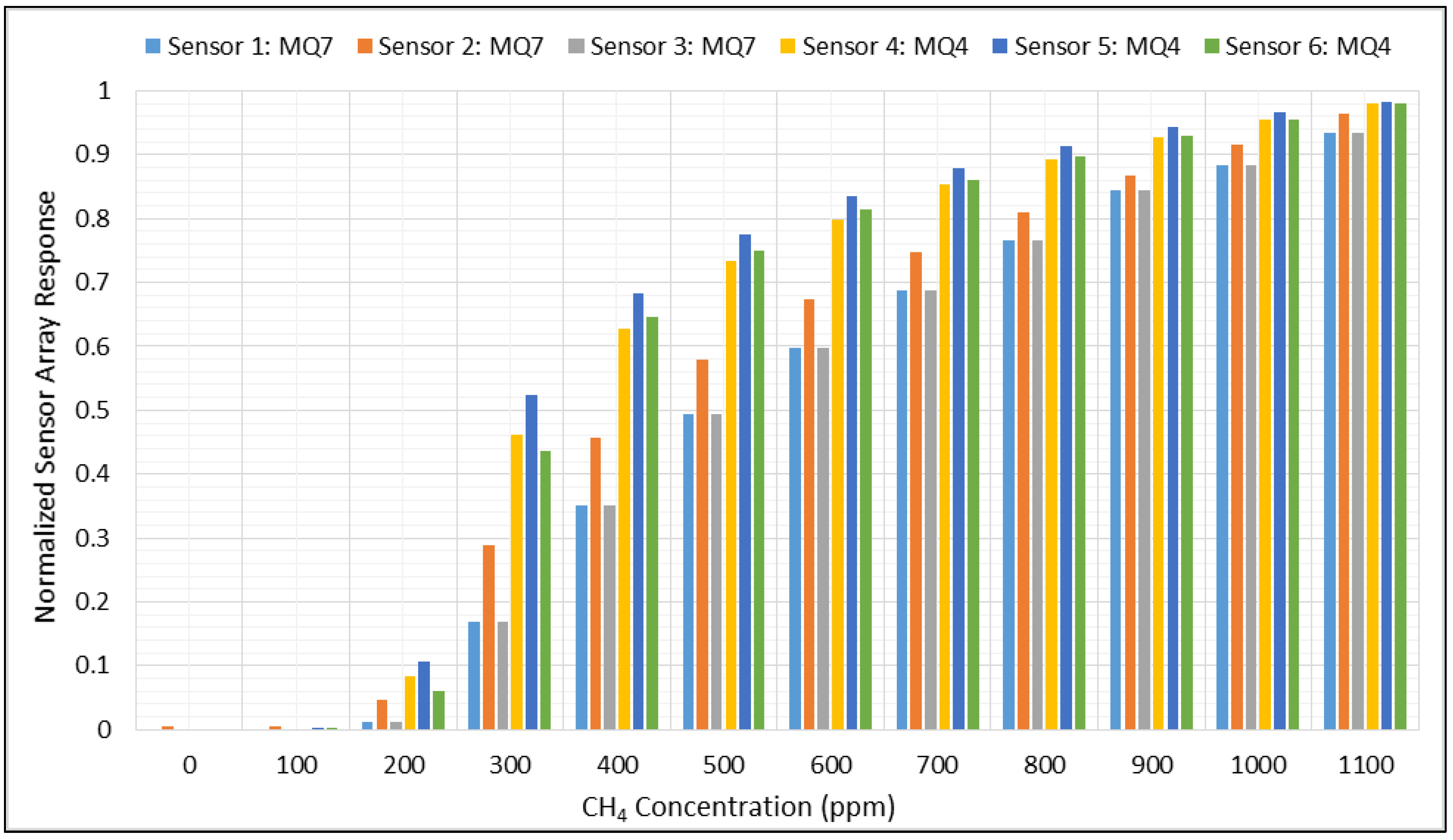
3.1. Normalizing and Mean Centering
3.2. Feature Extraction and Classification
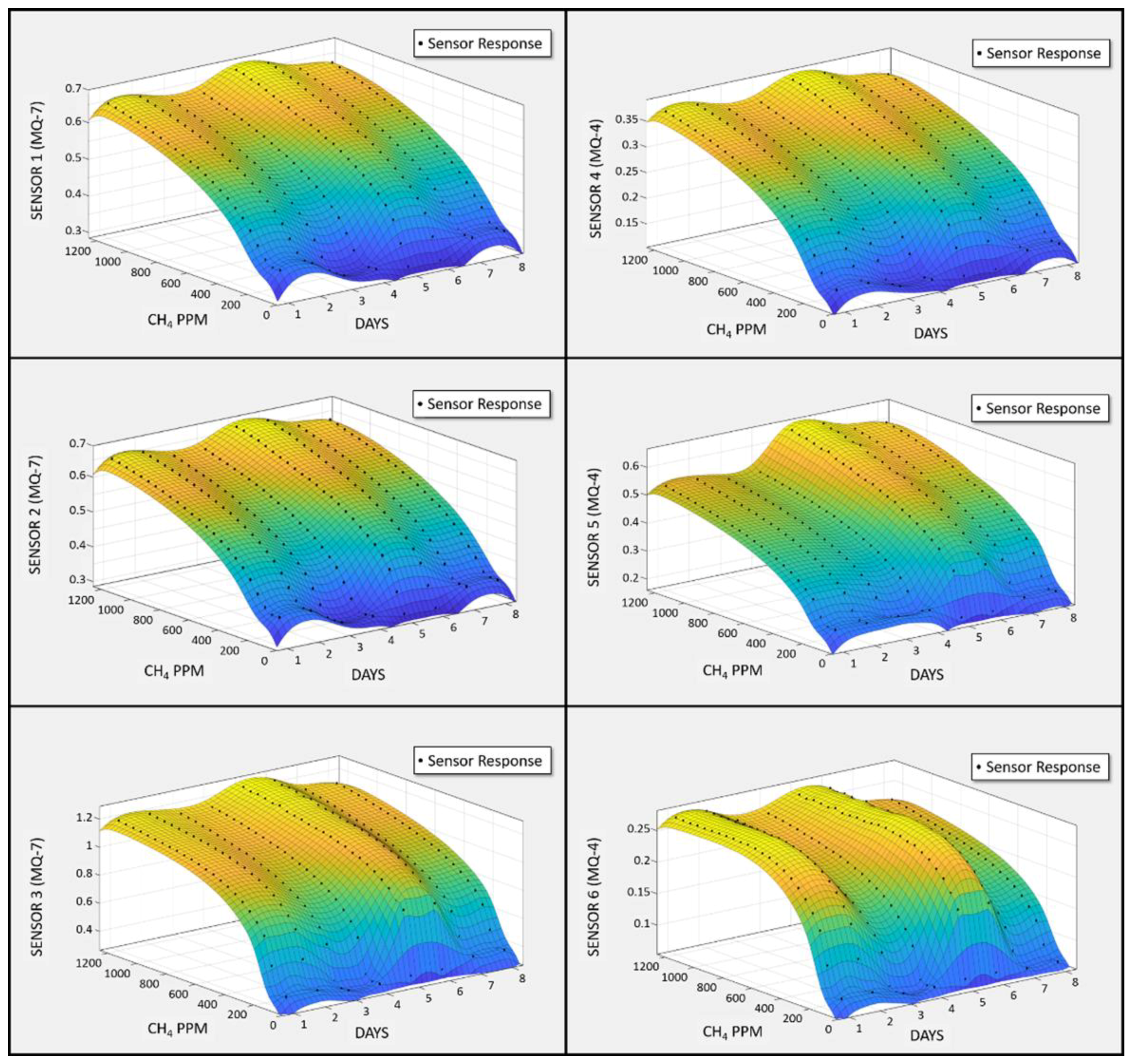
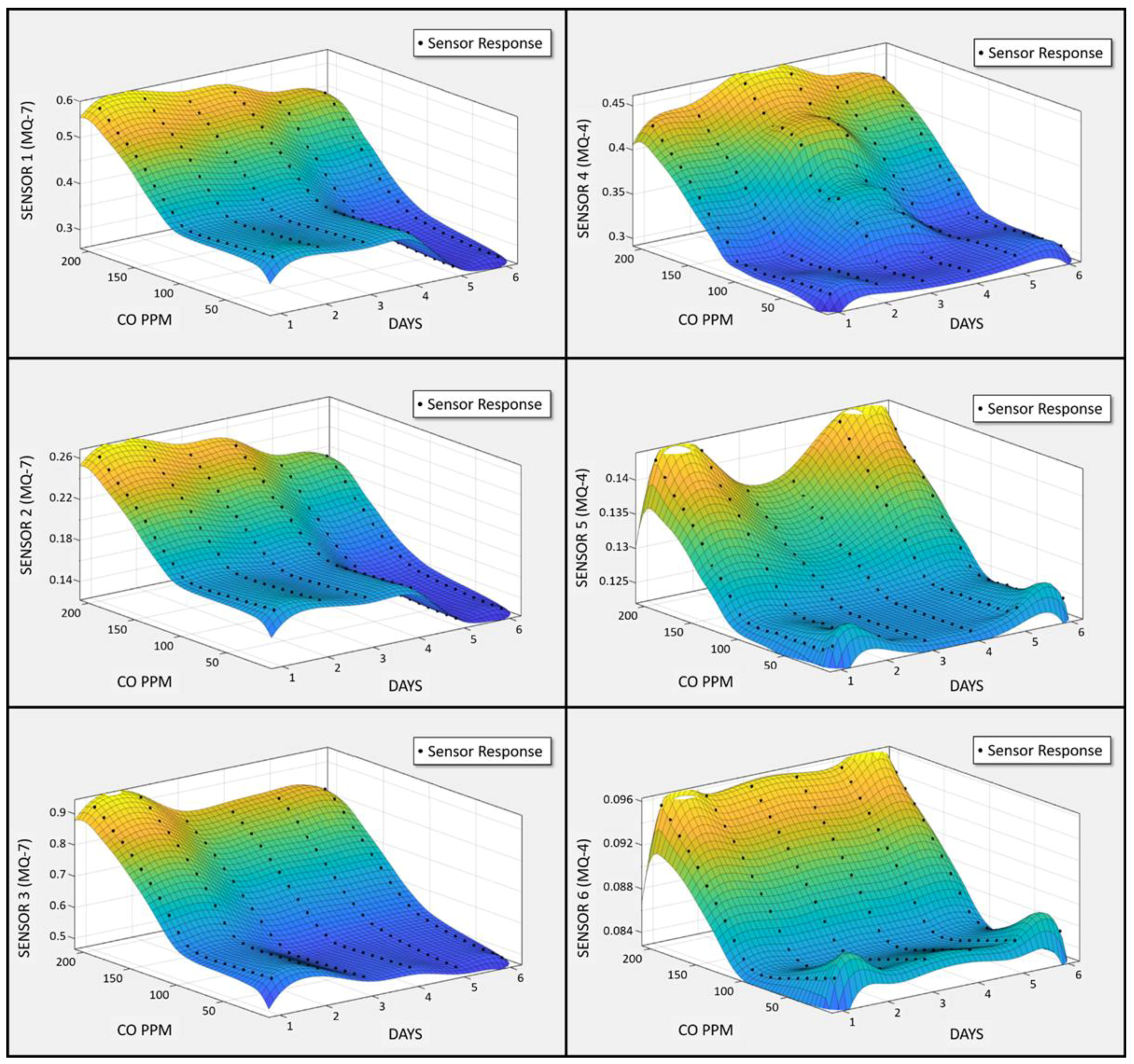
3.3. Quality Assurance/Quality Control
3.4. Estimated Gas Concentrations Using Least Squares Regression
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Llobet, E.; Hines, E.L.; Gardner, J.W.; Franco, S. Non-destructive banana ripeness determination using a neural network-based electronic nose. Meas. Sci. Technol. 1999, 10, 538–548. [Google Scholar] [CrossRef]
- Casalinuovo, I.; Pierro, D. Application of Electronic Noses for Disease Diagnosis and Food Spoilage Detection. Sensors 2006, 6, 1428–1439. [Google Scholar] [CrossRef]
- Hanson, C.W., III. Method and System of Diagnosing Intrapulmonary Infection using an Electronic Nose. U.S. Patent 6,620,109, 19 September 2003. [Google Scholar]
- Turner, A.P.; Magan, N. Electronic noses and disease diagnostics. Nat. Rev. Microbiol. 2004, 2, 161–166. [Google Scholar] [CrossRef] [PubMed]
- Hong, H.K.; Shin, H.W.; Park, H.S.; Yun, D.H.; Kwon, C.H.; Lee, K.; Kim, S.T.; Moriizumi, T. Gas identification using micro gas sensor array and neural-network pattern recognition. Sens. Actuators B Chem. 1996, 33, 68–71. [Google Scholar] [CrossRef]
- Zakrzewska, K. Mixed oxides as gas sensors. Thin Solid Films 2001, 391, 229–238. [Google Scholar] [CrossRef]
- Keith, F.E. Resolving combustible gas mixtures using gas sensitive resistors with arrays of electrodes. J. Chem. Soc. Faraday Trans. 1996, 92, 4497–4504. [Google Scholar]
- Rana, A.S.; Kang, M.; Kim, H.S. Microwave-assisted facile and ultrafast growth of ZnO nanostructures and proposition of alternative microwave-assisted methods to address growth stoppage. Sci. Rep. 2016, 6, 24870. [Google Scholar] [CrossRef] [PubMed]
- Bielanski, A.; Deren, J.; Haber, J. Electric conductivity and catalytic activity of semiconducting oxide catalysts. Nature 1957, 179, 668–669. [Google Scholar] [CrossRef]
- Nissha FIS, Inc. Available online: http://www.fisinc.co.jp (accessed on 29 January 2018).
- City Technology Ltd. Global Leaders in Gas Sensor Technology. Available online: http://www.citytech.com (accessed on 29 January 2018).
- MicroChem: Innovative Chemical Solutions for MEMS and Microelectronics. Available online: http://www.microchem.com (accessed on 29 January 2018).
- Harrison, P.G.; Willett, M.J. The mechanism of operation of tin (IV) oxide carbon monoxide sensors. Nature 1988, 332, 337–339. [Google Scholar] [CrossRef]
- Barsan, N.; Schweizer-Berberich, M.; Gopel, W. Fundamental and practical aspects in the design of nanoscaled SnO2 gas sensors: A status report. Fresenius J. Anal. Chem. 1999, 365, 287–304. [Google Scholar] [CrossRef]
- Ihokura, K.; Watson, J. The Stannic Oxide Gas Sensor: Principles and Applications; CRC Press: Boca Raton, FL, USA, 1994; ISBN 0849326044. [Google Scholar]
- Batzill, M.; Diebold, U. The surface and materials science of tin oxide. Prog. Surf. Sci. 2005, 79, 47–154. [Google Scholar] [CrossRef]
- Wang, C.; Yin, L.; Zhang, L.; Xiang, D.; Gao, R. Metal oxide gas sensors: Sensitivity and influencing factors. Sensors 2010, 10, 2088–2106. [Google Scholar] [CrossRef] [PubMed]
- SparkFun Electronics. (Model:MQ-4). Available online: https://cdn.sparkfun.com/datasheets/Sensors/Biometric/MQ-4%20Ver1.3%20-%20Manual.pdf (accessed on 29 January 2018).
- SparkFun Electronics. (Model:MQ-7). Available online: https://cdn.sparkfun.com/datasheets/Sensors/Biometric/MQ-7%20Ver1.3%20-%20Manual.pdf (accessed on 29 January 2018).
- Pololu Robotics and Electronics. Available online: https://www.pololu.com/file/0J309/MQ2.pdf (accessed on 29 January 2018).
- MQ-9 Semiconductor Sensor for CO/Combustible GAS. Available online: http://www.haoyuelectronics.com/Attachment/MQ-9/MQ9.pdf (accessed on 29 January 2018).
- Suematsu, K.; Ma, N.; Watanabe, K.; Yuasa, M.; Kida, T.; Shimanoe, K. Effect of Humid Aging on the Oxygen Adsorption in SnO2 Gas Sensors. Sensors 2018, 18, 254. [Google Scholar] [CrossRef] [PubMed]
- Yamazoe, N.; Fuchigami, J.; Kishikawa, M.; Seiyama, T. Interactions of tin oxide surface with O2, H2O and H2. Surf. Sci. Rep. 1979, 86, 335–344. [Google Scholar] [CrossRef]
- Tamaki, J.; Nagaishi, M.; Teraoka, Y.; Miura, N.; Yamazoe, N.; Moriya, K.; Nakamura, Y. Adsorption behavior of CO and interfering gases on SnO2. Surf. Sci. Rep. 1989, 221, 183–196. [Google Scholar] [CrossRef]
- Wei, C.H.; Fahn, C.S. The multisynapse neural network and its application to fuzzy clustering. IEEE Trans. Neural Netw. 2002, 13, 600–618. [Google Scholar] [PubMed]
- Brezmes, J.; Cabre, P.; Rojo, S.; Llobet, E.; Vilanova, X.; Correig, X. Discrimination between different samples of olive oil using variable selection techniques and modified fuzzy artmap neural networks. IEEE Sens. J. 2005, 5, 463–470. [Google Scholar] [CrossRef]
- Zhang, L.; Tian, F. Performance study of multilayer perceptrons in a low-cost electronic nose. IEEE Trans. Instrum. Meas. 2014, 63, 1670–1679. [Google Scholar] [CrossRef]
- Pardo, M.; Sberveglieri, G. Remarks on the use of multilayer perceptrons for the analysis of chemical sensor array data. IEEE Sens. J. 2004, 4, 355–363. [Google Scholar] [CrossRef]
- Aguilera, T.; Lozano, J.; Paredes, J.A.; Alvarez, F.J.; Suarez, J.I. Electronic nose based on independent component analysis combined with partial least squares and artificial neural networks for wine prediction. Sensors 2012, 12, 8055–8072. [Google Scholar] [CrossRef] [PubMed]
- Buratti, S.; Benedetti, S.; Scampicchio, M.; Pangerod, E.C. Characterization and classification of Italian Barbera wines by using an electronic nose and an amperometric electronic tongue. Anal. Chim. Acta 2004, 525, 133–139. [Google Scholar] [CrossRef]
- Cheng, H.; Qin, Z.H.; Guo, X.F.; Hu, X.S.; Wu, J.H. Geographical origin identification of propolis using GC–MS and electronic nose combined with principal component analysis. Food Res. Int. 2013, 51, 813–822. [Google Scholar] [CrossRef]
- Pardo, M.; Sberveglieri, G. Classification of electronic nose data with support vector machines. Sens. Actuators B Chem. 2005, 107, 730–737. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Peng, S.; Xu, Q.; Ling, X.B.; Peng, X.; Du, W.; Chen, L. Molecular classification of cancer types from microarray data using the combination of genetic algorithms and support vector machines. FEBS Lett. 2003, 555, 358–362. [Google Scholar] [CrossRef]
- Machado, R.F.; Laskowski, D.; Deffenderfer, O.; Burch, T.; Zheng, S.; Mazzone, P.J.; Mekhail, T.; Jennings, C.; Stoller, J.K.; Pyle, J.; et al. Detection of lung cancer by sensor array analyses of exhaled breath. Am. J. Respir. Crit. Care Med. 2005, 171, 1286–1291. [Google Scholar] [CrossRef] [PubMed]
- Ojha, V.K.; Dutta, P.; Chaudhuri, A.; Saha, H. Study of various conjugate gradient based ann training methods for designing intelligent manhole gas detection system. In Proceedings of the IEEE 2013 International Symposium on Computational and Business Intelligence (ISCBI), New Delhi, India, 24–26 August 2013; pp. 83–87. [Google Scholar]
- Srivastava, A.K.; Srivastava, S.K.; Shukla, K.K. On the design issue of intelligent electronic nose system. In Proceedings of the IEEE International Conference on Industrial Technology 2000, Goa, India, 19–22 January 2000; pp. 243–248. [Google Scholar]
- Srivastava, A.K. Detection of Volatile Organic Compounds (VOCs) Using SnO2 Gas-Sensor Array and Artificial Neural Network. Sens. Actuators B Chem. 2003, 96, 24–37. [Google Scholar] [CrossRef]
- Osowski, S.; Siwek, K.; Grzywacz, T.; Brudzewski, K. Differential electronic nose in on-line dynamic measurements. Metrol. Meas. Syst. 2014, 21, 649–662. [Google Scholar] [CrossRef]
- Kotarski, M.; Smulko, J. Noise measurement set-ups for fluctuations-enhanced gas sensing. Metrol. Meas. Syst. 2009, 16, 457–464. [Google Scholar]
- Korotcenkov, G.; Cho, B.K. Engineering approaches for the improvement of conductometric gas sensor parameters. Part 1. Improvement of sensor sensitivity and selectivity (short survey). Sens. Actuators B Chem. 2013, 188, 709–728. [Google Scholar] [CrossRef]
- Kalinowski, P.; Wozniak, L.; Strzelczyk, A.; Jasinski, P.; Jasinski, G. Efficiency of linear and nonlinear classifiers for gas identification from electrocatalytic gas sensor. Metrol. Meas. Syst. 2013, 20, 501–512. [Google Scholar] [CrossRef][Green Version]
- Micropik. Available online: http://www.micropik.com/PDF/dht11.pdf (accessed on 12 March 2018).
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design; PWS Publishing Co: Boston, MA, USA, 1996; Volume 20, ISBN 0534943322. [Google Scholar]
- Kim, E.; Lee, S.; Kim, J.H.; Kim, C.; Byun, Y.T.; Kim, H.S.; Lee, T. Pattern recognition for selective odor detection with gas sensor arrays. Sensors 2012, 12, 16262–16273. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Quinonez, J.C.; Sergiyenko, O.; Gonzalez-Navarro, F.F.; Basaca-Preciado, L.; Tyrsa, V. Surface recognition improvement in 3D medical laser scanner using Levenberg–Marquardt method. Signal Process. 2013, 93, 378–386. [Google Scholar] [CrossRef]
- Çelik, O.; Teke, A.; Yildirim, H.B. The optimized artificial neural network model with Levenberg–Marquardt algorithm for global solar radiation estimation in Eastern Mediterranean Region of Turkey. J. Clean Prod. 2016, 116, 1–12. [Google Scholar] [CrossRef]
- Mukherjee, I.; Routroy, S. Comparing the performance of neural networks developed by using Levenberg–Marquardt and Quasi-Newton with the gradient descent algorithm for modelling a multiple response grinding process. Expert Syst. Appl. 2012, 39, 2397–2407. [Google Scholar] [CrossRef]
- Arduino. Available online: https://www.arduino.cc/en/Main/ArduinoBoardMega2560?setlang=en (accessed on 29 January 2018).
| Sensor | Sensor Model | Detecting Materials 1 | Range |
|---|---|---|---|
| CH4 | MQ-4 | CH4, LPG, H2, CO, Alcohol, smoke | 300–10,000 ppm CH4 |
| CO | MQ-7 | CO, H2, LPG, CH4, Alcohol | 10–500 ppm CO |
| Temperature and Humidity | DHT11 | Temperature, Humidity | 20–90% RH 0–50 °C |
| Training Parameter | Assigned Value |
|---|---|
| Epochs | 1000 |
| Performance (MSE) | 0.00 |
| Gradient | 1.00 × 10−7 |
| Mu | 1.00 × 1010 |
| Validation Checks | 20 |
| CH4 | CO | ||||
|---|---|---|---|---|---|
| Injected (ppm) | LSR Estimate (ppm) | Accuracy (%) | Injected (ppm) | LSR Estimate (ppm) | Accuracy (%) |
| 50 | 51.3 | 97.3 | 10 | 10.4 | 95.8 |
| 100 | 102.0 | 97.9 | 20 | 21.1 | 94.7 |
| 150 | 156.0 | 95.9 | 30 | 28.9 | 96.6 |
| 200 | 193.0 | 96.5 | 40 | 37.7 | 94.4 |
| 250 | 241.9 | 96.7 | 50 | 47.9 | 95.9 |
| 300 | 313.3 | 95.5 | 60 | 61.9 | 96.6 |
| 350 | 358.1 | 97.7 | 70 | 68.0 | 97.1 |
| 400 | 409.5 | 97.6 | 80 | 81.3 | 98.3 |
| 450 | 455.9 | 98.7 | 90 | 91.9 | 97.7 |
| 500 | 490.9 | 98.2 | 100 | 102.0 | 98.0 |
| 550 | 555.1 | 99.1 | 110 | 108.3 | 98.4 |
| 600 | 611.0 | 98.1 | 120 | 118.9 | 99.1 |
| 650 | 650.0 | 100.0 | 130 | 131.9 | 98.4 |
| 700 | 699.7 | 99.9 | 140 | 137.9 | 98.5 |
| 750 | 750.1 | 99.9 | 150 | 151.7 | 98.8 |
| 800 | 795.9 | 99.4 | 160 | 162.8 | 98.1 |
| 850 | 850.1 | 99.9 | 170 | 167.8 | 98.7 |
| 900 | 899.9 | 99.9 | 180 | 185.5 | 96.9 |
| 950 | 946.9 | 99.6 | 190 | 193.8 | 97.9 |
| 1000 | 1002.9 | 99.7 | 200 | 197.8 | 98.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahid, A.; Choi, J.-H.; Rana, A.U.H.S.; Kim, H.-S. Least Squares Neural Network-Based Wireless E-Nose System Using an SnO2 Sensor Array. Sensors 2018, 18, 1446. https://doi.org/10.3390/s18051446
Shahid A, Choi J-H, Rana AUHS, Kim H-S. Least Squares Neural Network-Based Wireless E-Nose System Using an SnO2 Sensor Array. Sensors. 2018; 18(5):1446. https://doi.org/10.3390/s18051446
Chicago/Turabian StyleShahid, Areej, Jong-Hyeok Choi, Abu Ul Hassan Sarwar Rana, and Hyun-Seok Kim. 2018. "Least Squares Neural Network-Based Wireless E-Nose System Using an SnO2 Sensor Array" Sensors 18, no. 5: 1446. https://doi.org/10.3390/s18051446
APA StyleShahid, A., Choi, J.-H., Rana, A. U. H. S., & Kim, H.-S. (2018). Least Squares Neural Network-Based Wireless E-Nose System Using an SnO2 Sensor Array. Sensors, 18(5), 1446. https://doi.org/10.3390/s18051446






