1. Introduction
Arrhythmias are prevalent in humans, and globally 2.5% of the population suffers from this disease [
1,
2,
3,
4]. This pathology produces a variation in the heart rate, and it can be mostly due to three causes, namely, automatism alteration, triggered activity, and reentry [
5,
6,
7]. The most widely used arrhythmia treatment is cardiac ablation, which consists of determining the diseased area of the heart that originates the arrhythmia, and then canceling the mechanism by using low temperatures or radio frequency [
8,
9]. The diagnosis and treatment are made in an electrophysiological study, which is an intervention on the patient consisting of the insertion of electrocatheters through the neck or legs veins, and then recording the electrical activity of the heart. This procedure allows the clinician to identify the arrhythmia mechanism and to supply an adequate therapy [
10,
11]. Systems LocaLisa and Carto
3 are widely used examples of this type of equipment, and they basically consist of a positioning subsystem, a set of advanced catheters, and data storage and processing equipment [
12,
13].
These intracardiac navigation systems are constantly evolving today, and the use of catheters incorporating force sensors is one of the most recent developments. This innovation improves the recording of the heart electrical activity by verifying that the catheter is in contact with the heart surface. In [
14], a system of contact force measurements was presented using optical fiber detection technology, which improved the precision of force measurement, and it was benchmarked in terms of the catheter angle and catheter deflection, the fluid irrigation, and the use of a sheath, among other conditions. Another recent study delivered a contact-force control system using a portable catheter controller that can be coupled to any combination of ablation catheters with adjustable sheath and force detection [
15]. Neither of the studies reported the use of those systems when applied for clinical data. Other recent works use real patient data, for instance, a comparison was presented in [
16] among contact force ablation, manual ablation, and Remote Magnetic Navigation (RMN) ablation, analyzing their safety and efficiency in acute and long-term outcomes. They demonstrated that RMN was superior with regard to acute success, reduction of major complications, and recurrence rate using an intention-to-treat analysis. Another study compared the procedural profiles and outcomes of persistent atrial fibrillation ablation with and without using contact-force sensing catheters. The use of contact-force sensing catheters in this setting was associated with shorter procedures, shorter fluoroscopy time, and reduction in arrhythmia recurrences [
17]. Therefore, this has recently been a field in intense technological evolution with respect to the hardware acquisition system and its use.
Studies to date in this setting are based on the use of force thresholds, in such a way that if force sensor registers a reading greater than 5 gr, then the catheter is considered to be well positioned and yielding correct voltage readings [
13]. The justification to use this threshold is based on the catheter being surrounded by blood, which usually produces a force lower than 5 gr when interacting with the sensor. However, no study has clearly established that this value can be considered as a consistent and suitable threshold. Moreover, the dynamic nature of the heart functioning presents several challenges when we want to ensure the application of this type of examinations, and one of them is the determination and identification of the time intervals when the catheter is in stable contact with the heart surface to be examined. In a previous study, electroanatomical maps of the electrophysiological examinations were analyzed in a group of patients with arrythmias [
13]. These electroanatomical maps were performed with a cardiac navigation system that included a force-sensing catheter. Authors considered healthy tissue when a greater than 5 gr force signal was recorded at the time of the maximum EGM voltage, assumed that its peak-to-peak value was greater than 1.5 mV, and the area was identified as diseased tissue or a scar.
The vorticity produced by the blood and the systole and diastole movements can produce disturbances in the electrical activity measurements, making it difficult to determine diseased areas on the surface of the heart, especially if the criterion of a static threshold is considered as a reference for decision making. In the present work, data exploration was carried out with the purpose of constructing contact models based on the force signal, as a criterion to determine if the catheter is in contact with the tissue. We scrutinize patterns such as pulsatility or trends in the force signals recorded during the electrophysiological examination of a patient, by considering a time window around the EGM maximum peak used for the static force threshold. The Principal Component Analysis (PCA) techniques are used to provide us with a multivariate decomposition of the most characteristic force signal profiles, and linear classification is used to determine their relevance. The patient database used for this purpose consists of 1391 force signals and their corresponding EGM, which were recorded during 2 and 8 s, respectively, from 17 patients (82 ± 60 points per patient) at electrophysiological study.
The outline of the document maintains the following structure. In
Section 2, the characteristics of the patient base, the PCA fundamentals, and the used linear classifiers are summarized.
Section 3 describes the experimental methods carried out and the obtained results.
Section 4 deals with the discussion, future work, and conclusions of our findings.
2. Methods
2.1. Database and Patients
The patient data used in this work comes from a previous clinical study [
13], carried out at the Arrhythmia Unit in University Hospital Virgen de la Arrixaca (Murcia, Spain). That study was approved by the Ethics Committee of the hospital, and recorded in the
clinicaltrials.gov register of clinical trials under identification number NCT01639365. It involved the acquisition in each patient of a left ventricular voltage map, during sinus rhythm and using the Carto
3 navigation system and the Navistar Thermocool catheter (Biosense-Webster, Diamond Bar, CA, United States). The population consisted of 17 patients (8 men, mean age 62, range 38–80 years) with ventricular arrhythmias due to ischemic cardiomyopathy or dilated cardiomyopathy, who underwent ventricular tachycardia ablation by clinical indications, and their clinical description is included in
Table 1. For each patient, a voltage map was first generated without accounting for the force signal. Then, the map was corrected by discarding those points with force below threshold, which yielded more compact voltage maps allowing to better identify arrhythmia channels and ablation targets.
The same set of patients and signals was used in this work. The Carto
3 System records the electrophysiological examination data in plain text format. Extract, Transformation, and Load techniques were used on these files [
18,
19], allowing the construction of a database in which anonymized patient identification, case identification, EMG data, and force sensor data were stored. This database facilitated the processing of the acquired signals with a custom-developed computer tool, as well as a subsequent manual data classification, called labeling, where the doctor-issued criteria were followed. This labeling aimed to determine the presence or absence of catheter contact with the tissue not only in terms of the force at a single time instant (EGM peak), but rather taking into account the force signal evolution on a time window around this instant, as well as the simultaneously observed EGM signal. It was evident that sometimes it is complicated to establish the contact with high confidence, hence, the labels allowed two possible levels for the confidence on contact, as considered by the observer. Therefore, four labels were used for this classification. On the one hand, those cases in which the expert observer was confident that there was (not) tissue-catheter contact were given
label 0 (
label 3). On the other hand, those cases in which there was some reasonable doubt whether there was contact were assigned
label 1 (
label 2).
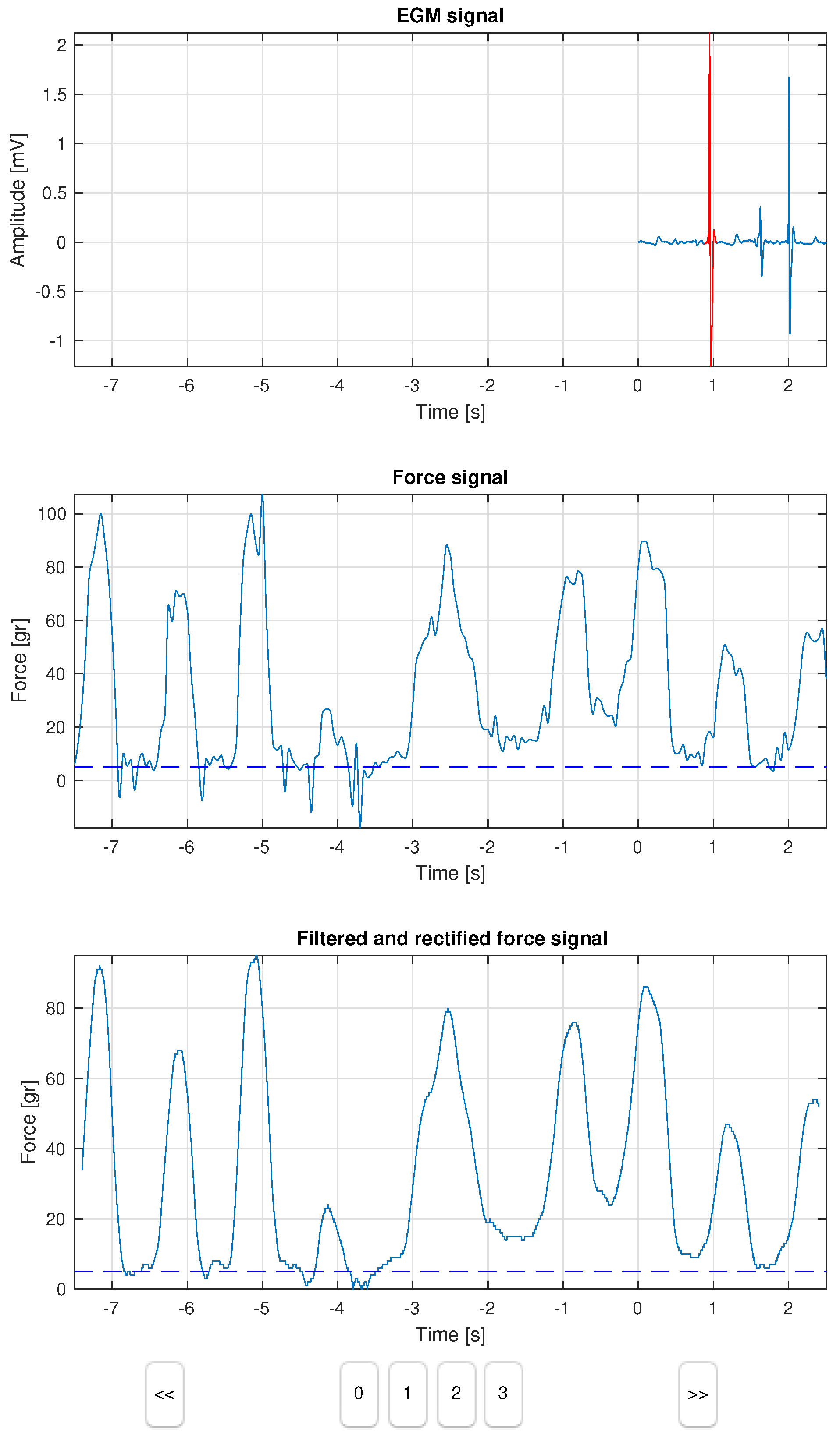
The developed computer tool consists of a dashboard with 3 panels, as shown in
Figure 1. The first panel plots two signals on a shared axis, namely, the 2 s of EGM signal (in blue), and the peak heartbeat selected within a window of ±80 ms (in red). The second panel represents the force sensor signal, which lasts 8 s, and it is synchronized with the EGM signal after 6 s, as seen in the figure. A dashed line represents the 5-gr threshold to be used as a reference by the observer. The third panel provides an additional view of the force signal after filtering and rectification, aiming to better support the labeling in some doubtful cases. Control buttons allowed the label selection, as well as the step forward (>>) and step back (<<) to review the cases. The result of this process was stored in a new label field in the database, which was specific to each case.
2.2. PCA Fundamentals
The catheter used for the electrophysiological examination acquires data within a dynamic environment, which exhibit a variety of patterns due to the heartbeat movement and to the blood vorticity. We want to group the different patterns present in a population of force measurements according to their contact labels and label confidence. For this reason, a multivariate technique is required in order to statistically extract the existing patterns and their relevance in that population. For this purpose, in this work we propose to use PCA, a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated vector observations into a set of linearly uncorrelated vector components. These new vectors and variables are characterized by their mutual uncorrelation. The amount of information conveyed in a component is measured by its variance, which can be used as an indicator to sort them in terms of their relevance, this is, the larger the variance associated to a component, the larger the amount of information in that component.
In statistics, PCA is often used to reduce the dimensionality of a data set, which makes it possible in our case to distinguish among the most relevant dynamic changes in the system, the redundant information, and the noise in the signal [
20]. This analysis defines a new coordinate space where the variance is maximized and the correlation among the variables is minimized. In our case, we measure a force signal during 8 s at a given anatomical location of the heart, which is represented by a signal vector
, where
M is the total number of signal samples in 8 s. Given a set of training data that contains
N observation vectors (corresponding to the aggregation of all the cases for every patient in the database), the array
is constructed with the observed vectors by rows, which represents the original data matrix. The covariance matrix
can be calculated from
in the following way,
. By decomposing this matrix in its eigenvalues and eigenvectors, the correlation structure of the variables is obtained,
where
is a diagonal matrix which contains the non-negative real eigenvalues of
, this is,
, and they are sorted in decreasing order; and matrix
conveys the sorted eigenvectors in columns. By holding only the
a eigenvectors (
) corresponding to the
a largest eigenvalues, we can build the so-called reduced principal component matrix
, which projects the observation vector
into a smaller space
, and it can be denoted by
.
Note that represents the optimal projection of onto the reduced dimensional subspace in terms of the variance. By applying this transformation to the entire data matrix, we obtain , where represents the new data matrix for the dimension-reduced observation vectors. To obtain an approximation to the original data from this matrix , we perform the following matrix product, , and then, we can calculate the residual matrix as the difference between the original and the estimated data matrices, as follows, . In many practical applications, a given observation vector is reconstructed with sufficient quality by using only a reduced number a of principal components, as seen later in our case.
2.3. Fisher and SVM Linear Classifiers
As shown in the experiments, the use of PCA provides us with a set of characteristic patterns on the force signals. Nevertheless, a criterion is further needed to establish the relevance of the reduced set of directions obtained from PCA. For this purpose, we used two linear classifiers, following a similar methodology to the one proposed in [
21]. The use of linear classifiers with the PCA projected signals allows us to determine the relevance of each projection direction by scrutinizing their weights. We selected the two linear classifier, namely, the Fisher Linear Discriminant (FLD), as it represents a classic and well-known method, and the linear support vector classifier, which has been successfully used in a number of applications during the last years [
22,
23].
On the one hand, the FLD is able to find a linear combination of features characterizing two or more sets with classification purposes. The method looks for the projection that maximizes the interclass variance and minimizes the intraclass variance [
24,
25]. In our case, we work with a set of multivariate observations
, with
, which in general can belong to two possible classes, with mean vectors
and
and covariance matrices
and
. The between-class (within-class) dispersion matrix is denoted as
(
), and they can be obtained by
A linear combination of features
has mean
and variance
, for
. Our objective is to maximize the between-class dispersion while minimizing the within-class dispersion, and for this purpose, the discrimination criterion is established as
It can be shown that the maximum separation is obtained when
where
c is a constant. In our case, the weights of Fisher projection vector
are indicators of the relevance of each of the considered eigenvectors.
On the other hand, the SVM is a supervised learning method that recognizes patterns for data analysis, and it can perform both pattern classification and regression. Vapnik proposed the SVM based on the Statistical Learning Theory, and it is considered one of the most effective classification algorithms [
26,
27]. In brief, this method uses optimization techniques to determine the classification function, and it consists of minimizing
subject to
with
, and where
is now the weight vector of the SVM;
is called the margin and it also accounts for the complexity of the model;
C is the trade-off parameter between margin and losses;
and
are the slack variables;
is a non-linear transformation that maps the input data to a high dimensional space; and
b is the interception. Lagrange multipliers
and
are introduced, and then the optimization problem described in the previous equations can be transformed into its dual optimization problem, which consists of maximizing:
where Mercer’s Theorem has been used to substitute
, and it is subject to
for
. The classification function of this SVM is obtained by solving the previous problem, and it can be shown to be
In our case, parameter
C can be calculated by using out-of-sample techniques, such as cross validation. In addition, several Mercer’s kernels can be used, but here we restrict ourselves to the linear kernel, as follows,
i.e., it is just the dot product between the two vectors. With this linear kernel, it is possible to calculate the weight vector of the SVM classifier, which is given by
Again, the weights of SVM classification vector are indicators of the relevance of each of the considered eigenvectors in our problem.
3. Experiments and Results
As previously described, our database consisted of 17 patients with a total of 1391 cases (82 ± 60 points per patient). The points in each case were tagged by the expert cardiologists. This database was randomly divided, in such a way that 80% (20%) of the data were in the training (test) set. The PCA was applied to the training group, and the projected vectors resulting from this analysis were used to train the Fisher and SVM classifiers. The trained classifiers were subsequently tested with the test group. Each process is specifically described below.
3.1. Results with the Conventional Force Threshold
With respect to the labels established by the experts on the catheter-tissue contact, a nomenclature was used to establish the vector groups according to the different confidence on the labels. On the one hand, cases with label 0 were included in the high-confidence contact group, whereas cases with label 3 were in the high-confidence non-contact group. On the other hand, cases with label either 0 or 1 were included in the likely contact group, whereas cases with labels 2 or 3 were in the likely non-contact group. Note that the first group accounts for those cases that were more clearly identified in terms of contact or not by the expert, whereas the second group also includes those doubtful cases in the analysis.
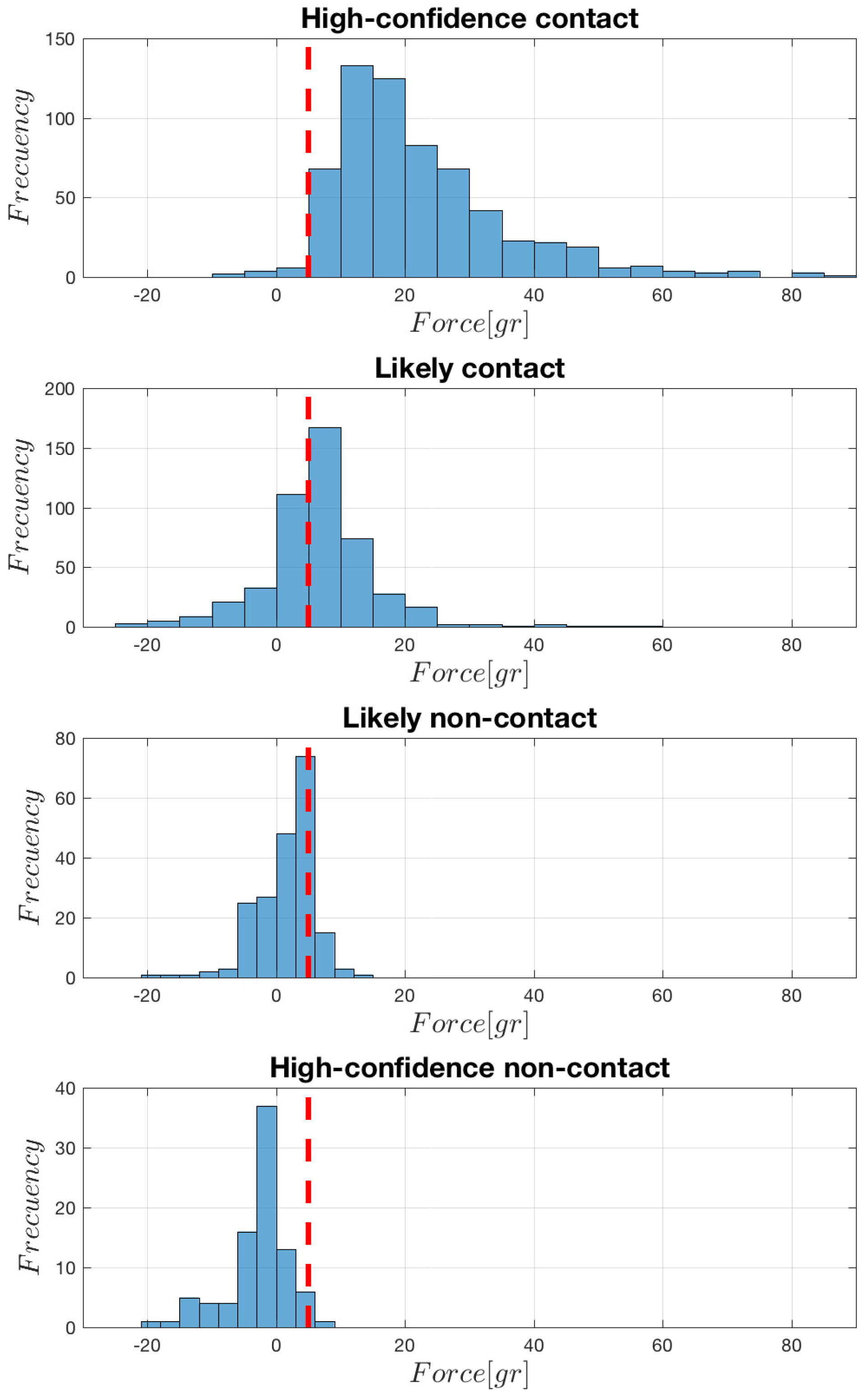
The histogram representation of the force signals as recorded at the peak time of each corresponding EGM is shown in
Figure 2. When analyzing each of the groups, it can be seen that the high-confidence contact group has a range about −10 gr to 80 gr of force applied to the sensor, in most cases above the 5-gr threshold. In the case of the likely contact group, it has a range between −25 gr to 60 gr, with the histogram bin around the threshold being about the distribution mode. In the case of the likely non-contact group, the force values present a range from −25 gr to 15 gr, and most of the signal samples are below the threshold. Finally, in the case of the contact high-confidence non-contact group, the force sample distributions are quite similar, though with a general amplitude decrease in the second one. Note the presence of negative tails in all the groups, specially (but not only) in the non-contact ones. Note also that discriminating between contact and non-contact by using the threshold can produce some number of misclassifications, as an overlap zone exists among groups, and the most likely error to happen is to establish that a point has no contact when it really represents a tissue-catheter position.
3.2. PCA on Force Signals
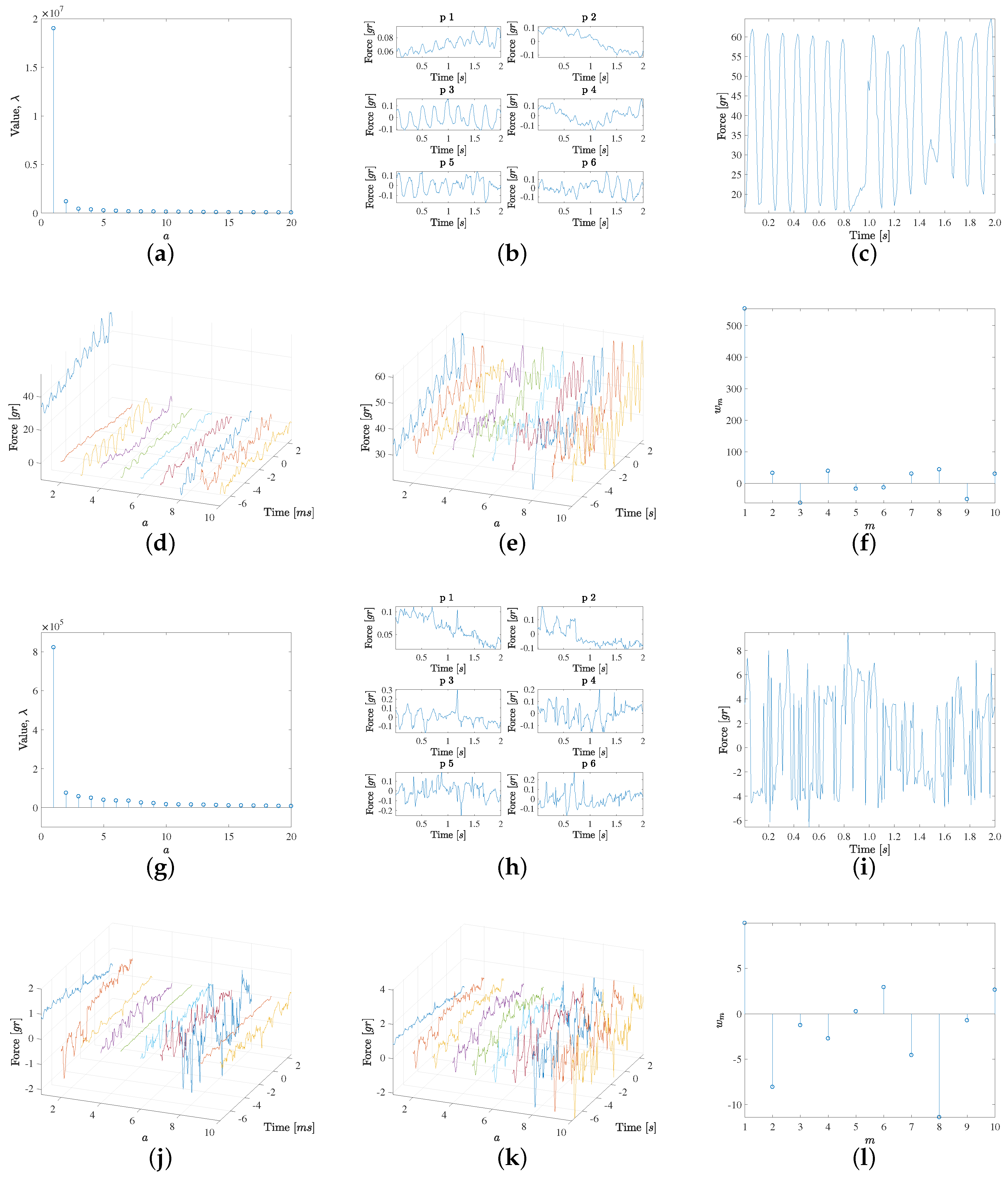
The PCA was used to scrutinize the data patterns of the force signals, first for each of the labels separately, and then in the two described sets of grouped labels. The following three figures that are next presented are related to the PCA of the different labels and label groups, and they follow the same structure and use six panels for each analysis, see
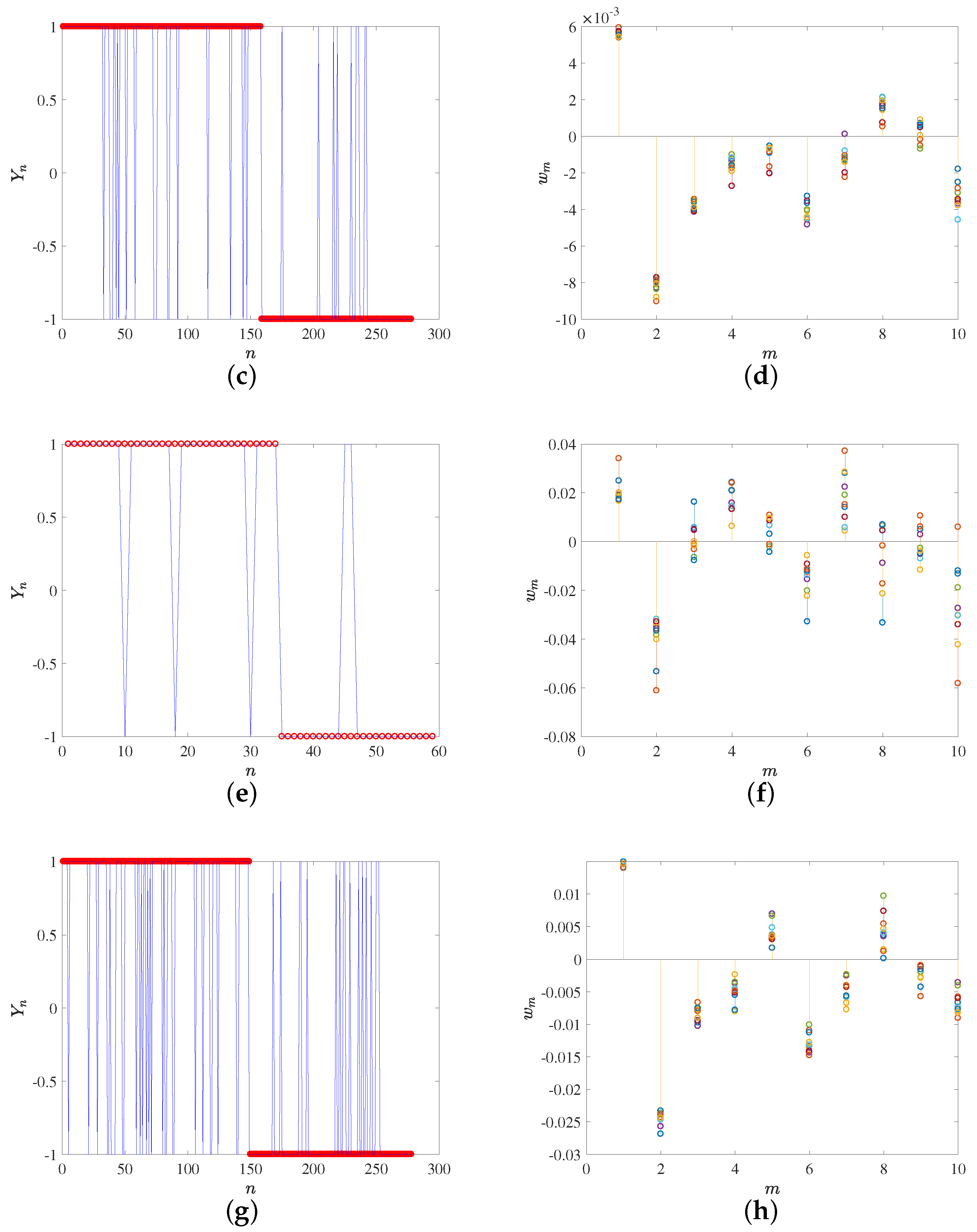
Figure 3. Panel (a) depicts the first 20 eigenvalues, hence yielding an idea of the relevance of their corresponding eigendirections, and Panel (b) represents the first six eigenvectors in order to be able to inspect their waveforms and to establish the characteristic signal patterns for the analyzed groups. Panel (c) shows a representative force signal example in each group, and then, the contributions of up to 10 eigendirections, as weighted by the projection of the example signal on them, are represented separately (Panel (d)) and accumulated (Panel (e)), in such a way that the convergence to a quality estimation (reduced residual) of the example signal can be readily scrutinized. Finally, Panel (f) shows the weights of the projected example signal on the first 10 eigenvectors, to give an idea of the relevance of each of the projected weights in that example.
Figure 3 shows the results obtained by analyzing the high-confidence contact (non-contact) groups from (a) to (f) (from (g) to (l)). The high-confidence contact group exhibits the following characteristics. On the one hand, the first eigenvalue is clearly the most relevant one and it is associated both to visible pulsatility as well as an increasing trend. This trend is consistent with the observed increased force values during the last two seconds when the EGM are recorded at each point. On the other hand, the second eigenvalue shows a decreasing trend, again consistent with those cases when the local average force is reduced at the end of the force recording period. Note that these patterns can be present either as plotted or with negative sign, according to the sign given by the projection of each specific force case. Additionally, the pulsatility is mostly related with the average cardiac rhythm cycle, but there are changes in the pulsatile force waveforms for each specific case, and these differences are provided by eigenvectors 3 and 5, which are associated to a moderately large eigenvector, but this is enough to contribute with the relevant waveform information in this set of cases. It can be seen too that eigenvector 4 provides an additional trend pattern (high, low, high again), whereas eigenvector 6 is a mixed one, given by noisy activity followed by a pulsatile pattern in the end of the signal, i.e., in the time interval where the EGM has been simultaneously recorded. Later, the following eigendirections seem to provide few relevant contributions to the signal patterns. In order to verify this, a signal example was chosen where the contact was clear and stable, in terms of pulsatility and average value, as seen in
Figure 3c. In this case, Panel (d) shows the eigendirections weighted by the example projection weights in Panel (f). While weights 7 to 10 in the weight vector obtained for
seem to be numerically relevant, it can be seen in Panel (e) that the accumulated signal reconstruction is very close to the original one with the first six components; hence, this group exhibits high signal-to-noise ratio.
Figure 3 also shows in Panels (g) to (l) the results for the high-confidence non-contact group, which has the following characteristics. The first eigenvalue is markedly smaller than in the case of the high-confidence contact group, but still it is markedly larger than the other eigenvalues in its group. In this case, this first eigendirection corresponds to a decreasing trend. It can be seen that the six first eigendirections have some moderate pattern of pulsatility, but there is no specific pulsatile direction, and instead it is at most mixed among random patterns. The example scrutinized in this group, at Panel (i), is again built with enough quality with about the first eight eigendirections. Note that in this case, the contribution of the first eigendirection is markedly smaller, as this example has a small average value.
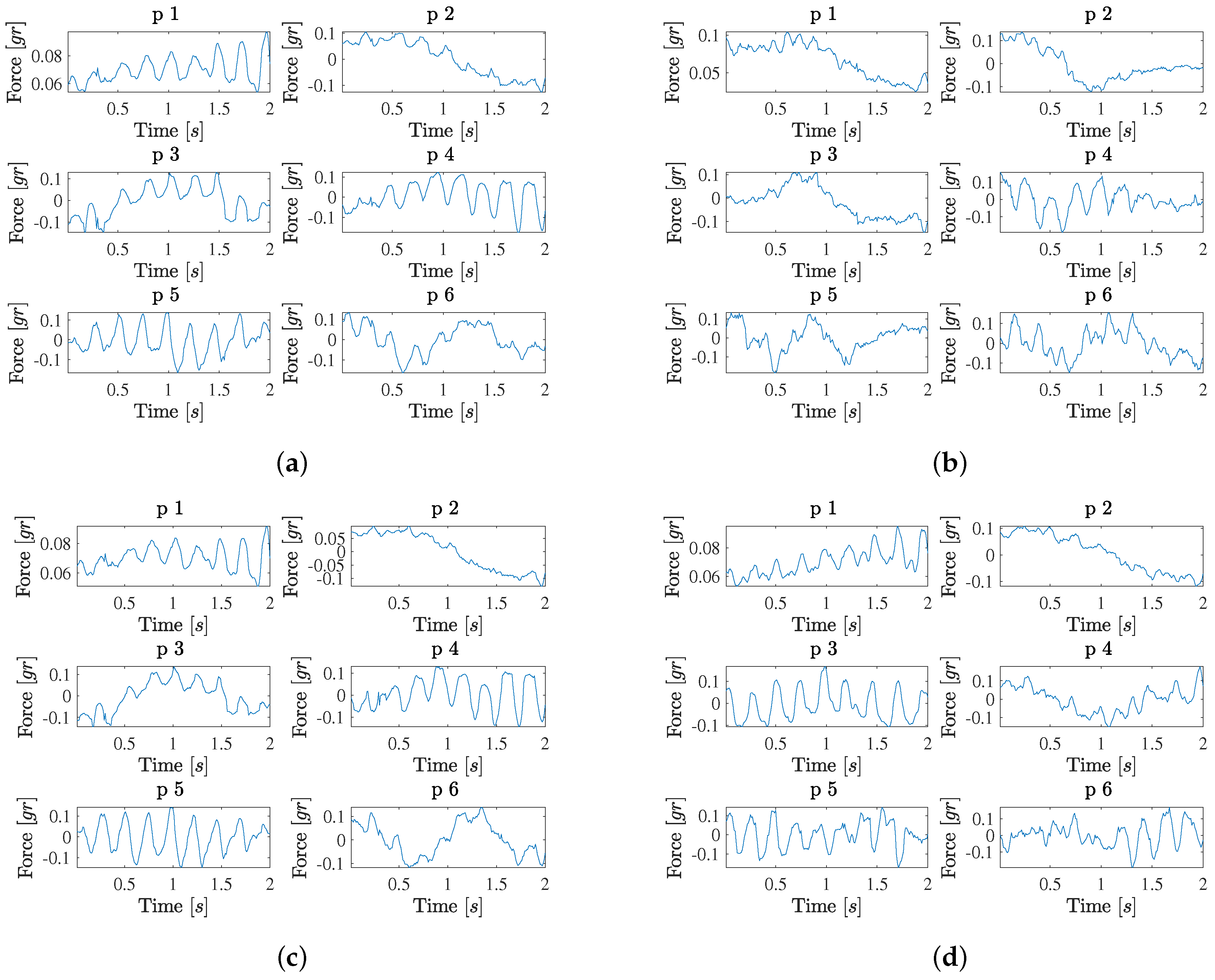
Figure 4 shows the results obtained when analyzing the likely-contact (likely non-contact) groups separately, in Panels (a) (Panel (b)). The eigenvalue profile in the contact group is similar to the high-confidence contact group, but now the most relevant profiles in Panel (b) often include mixed pulsatility and trends (eigendirections 1, 2, 3, 4, and 5). In addition, a new type of pattern can be seen, which consists of pulsatility that is modulated with its amplitude increasing to the end of the time interval (eigendirections 1 and 4). Again, the signal is estimated with acceptable quality by using 8 eigenvectors. A moderate signal-to-noise can be observed now in the force signals in this group. The eigenvalue profile in the likely non-contact group is also similar to the high-confidence non-contact group, though the first eigenvalue (corresponding to the group average) is in this case larger. Now, the first relevant eigendirections also include mixed patterns of trends with some presence of pulsatility (e.g., as in eigendirections 3 and 4).
After analyzing the patterns of the different contact and non-contact groups separately, we examined the patters of the complete database, as seen in
Figure 4. On the one hand, the likely-contact group (all cases together) shows an eigenvalue profile which is similar to the previous ones (and more similar to the contact subgroups). Current relevant patters in this complete set include a mixture of purely pulsatile waveforms (eigendirection 5), pulsatility with increasing amplitude (eigendirections 1 and 4), trends with some pulsatility (eigendirections 3 and 6), and just trends (eigendirection 2). On the other hand, in the high-confidence contact group (cases with
labels 0 and
3), eigendirections 1 and 2 are very similar to the ones in the complete dataset, and the patterns include purely pulsatile waveforms (eigendirections 3 and 5), pulsatility with increasing amplitude (eigendirection 1), trends with small pulsatility or pulsatility at the end of the signal (eigendirections 2, 4, and 6). Overall, we can check in all the examples that 8 to 10 components yield acceptable quality in the force signal reconstruction.
3.3. Classification Using PCA Weights
The weights from the projection of each force signal on the eigenvectors of different groups were shown for some examples in the previous section. These weights can be used to analyze which are the most relevant eigendirections and also their corresponding patterns, when analyzed in the complete data set.
This has been addressed in
Figure 5 (upper panel), where the projection weights
are represented for
and both in the high-confidence contact and non-contact (blue and red) data matrices. It can be seen that the weight of the first eigenvector is usually positive and notably larger in the contact than in the non-contact cases, nevertheless, the greatest amount of information is concentrated on it. The other weights (2 to 10) show a similar structure among them, given in the high-confidence contact cases by usually small weights together with a few greater weights, though the feature number of the prominent weights differ in each case. In addition, in general they are visibly smaller and distributed around zero in the high-confidence non-contact cases. With respect to the likely-contact cases (lower panel), the first weight is again prominent in the contact cases, but it is also noticeably higher than in the non-contact cases. The other weights (2 to 10) consist both on small values together with some larger positive and negative weights, but the number of larger weights seems to be higher in the contact cases. Accordingly, differences exist in the weights of contact and non-contact cases, but they cannot be immediately used quantitatively in order to discriminate if the catheter is in contact or not. Moreover, it is desirable to quantify how relevant each of the eigendirections are in the database.
For this purpose, we used the projected vectors of the signal force cases (again with ) to build several linear classifiers, which were trained and tested with 80% and 20% of the database cases, respectively. Note that only the training samples were used to perform the PCA projection matrices. This procedure was repeated 10 times, which allowed us to scrutinize the distribution of the estimations for each classifier weight.
The classification results for this experiment are shown in
Table 2, where the Area Under the Curve (AUC), is shown for the two classifiers applied to the different contact groups. Note the AUC can be seen as a merit figure for the classifiers, in such a way that the closer to one, the lower overlap between the two scrutinized classes. The likely-contact vs. likely non-contact classifiers exhibit greater overlap between classes, although 0.85 is a sufficient AUC value to indicate that the features given by the PCA projections in this case contain relevant information about the classification. The high-confidence contact vs. high-confidence non-contact classifiers yielded AUC average of 0.95, which represents a very good quality classifier and the features used for this classification can also be scrutinized to identify the most relevant patterns. As shown in the table, the AUC medians are similar to the means and the standard deviations are small in all the classifiers.
Further details on the classification performance can be seen in
Figure 6, where the left panels show the actual group and the estimated group for each classifier. Classification errors are more patent in the low-AUC classifiers, at the likely contact vs. non-contact groups, and these errors in general are similarly distributed between classes. However, in the high-AUC classifiers, the scarce errors only (SVM) and mostly (FLD) correspond to actual contact cases which have been misclassified as non-contact ones.
After checking that the classifiers provide enough performance in terms of the AUC, it is possible to study the relevance and significance of the weights in each classifier and to interpret the clinical meaning of the trained machines. Recall that each classification weight is associated to a given projection weight, so that by looking at its corresponding eigenvector it is possible to determine the patterns that are actually relevant to the classification. In
Figure 6 (right panels), the weights for the different classifiers are represented. In the likely contact vs. likely non-contact group classifiers, we can see that classifier weights 3 to 10 are in a rank which either overlaps zero or is very close to it, at least in one of the two classifiers. Therefore, it can be inferred that weights 1 and 2 are the most relevant to distinguish between these clearly differentiated classes, which corresponds to eigenvectors 1 and 2 in
Figure 4a,b, and hence to a pulsatile with increasing amplitude pattern and to a biphasic trend pattern. These patters convey enough information to distinguish between contact and non-contact groups. Note that classification weight 1 is always positive, which is consistent with the positive and larger mean in class
in the classifier (contact), and also, classification weight 2 is negative and multiplying a decreasing trend, which is consistent with an increased trend value in the end of the contact cases. In the high-confidence group classifiers, classifier weights 1 and 2 exhibit a similar trend to the previous case, and they are very similar, which is consistent with the similarity found in
Figure 4c,d on the two first eigendirections for both contact and non-contact groups. In this case, several other weights become relevant in both classifiers, namely, classifier weights 3, 4, 6, and 10. The patterns in these eigendirections allow a better description of the details required in the easier cases.
4. Discussion and Conclusions
In this work, the determination of the catheter-tissue contact in electrophysiological studies for arrhythmia therapy has been analyzed in terms of the force signals recorded in force sensors at the EGM recording catheter. The conventional criterion of using a single-sample threshold of 5-gr as measured at the EGM peak time has been shown to be limited for the clinical practice. A previous study from our group aimed to use simple statistical features, such as the correlation coefficient, in order to scrutinize the improvement of tissue-catheter contact, but these simple features were not enough to give an operative system [
28]. The use of PCA has allowed us to establish the relevant patterns that can be found in this type of signal, and the use of linear classifiers has further allowed the establishment of the suitability of these signals to identify the existence of contact or non-contact in an acceptable number of cases.
Several limitations to the presented study can be identified. The labeling of contact vs. non-contact was done by experts, but still it can sometimes be subjective. An objective index would undoubtedly improve the performance and quality of the proposed system. Nevertheless, the proposed methodology would be readily and similarly used in that case. The use of linear classifiers could be improved by nonlinear classifiers in terms of system accuracy; nevertheless, here we restricted ourselves to the first ones because they allow to scrutinize the relevant patterns for the classification, and hence to provide clinical understanding of the problem at hand and of the proposed solution. Nevertheless, both the signal processing procedures and the implementation of the tuned machine learning classifiers require a very moderate and acceptable computational burden.
We can conclude that the proposed system can be used to determine the presence of tissue-catheter contact during arrhythmia procedures, which would improve the quality of the maps elaborated by current intracardiac navigation systems, and in general the improvement of the functionality provided by current force sensors at EGM catheters. The proposed method could be used as a subsystem for current cardiac navigation systems supporting the clinical ablation procedures in two ways. On the one hand, it can be used on-line while recording the EGM and creating the maps, so that the clinician is advised of the likely good quality of the tissue-catheter contact, hence only those points which are clearly in contact are accepted. This represents a similar concept to the use of thresholds in current systems, but the use of signal processing profiles should improve this quality. On the other hand, they could be used off-line, after taking the patient measurements, in order to discard those points which were less-likely high-quality contact, and hence improving the final map. In both cases, force-signal profiles should be taken into account and would be advantageous to the clinical procedure.