Robust Pedestrian Dead Reckoning Based on MEMS-IMU for Smartphones
Abstract
1. Introduction
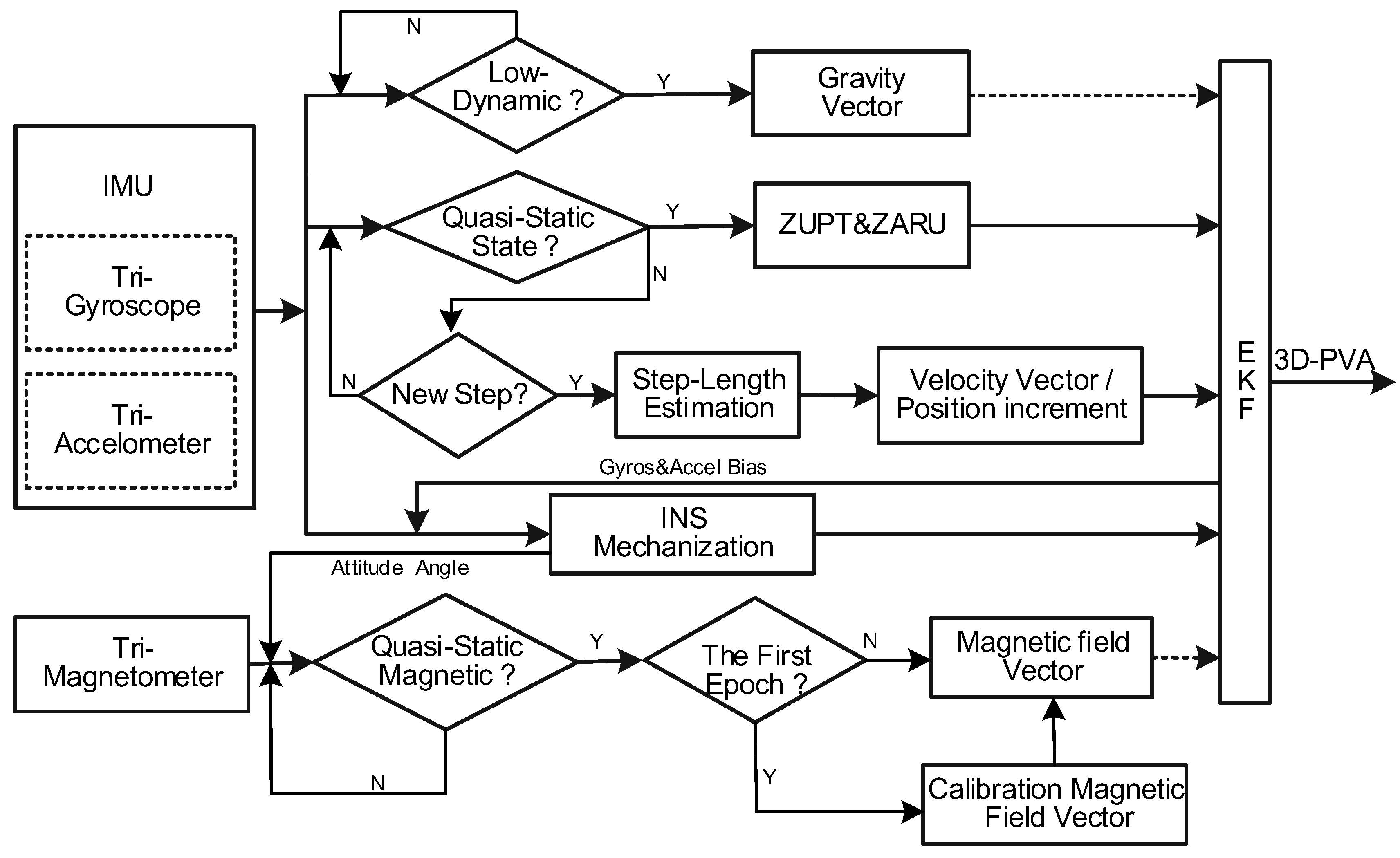
2. Materials and Methods
2.1. INS Mechanization
2.2. System Model
2.3. Multi-Level Measurements
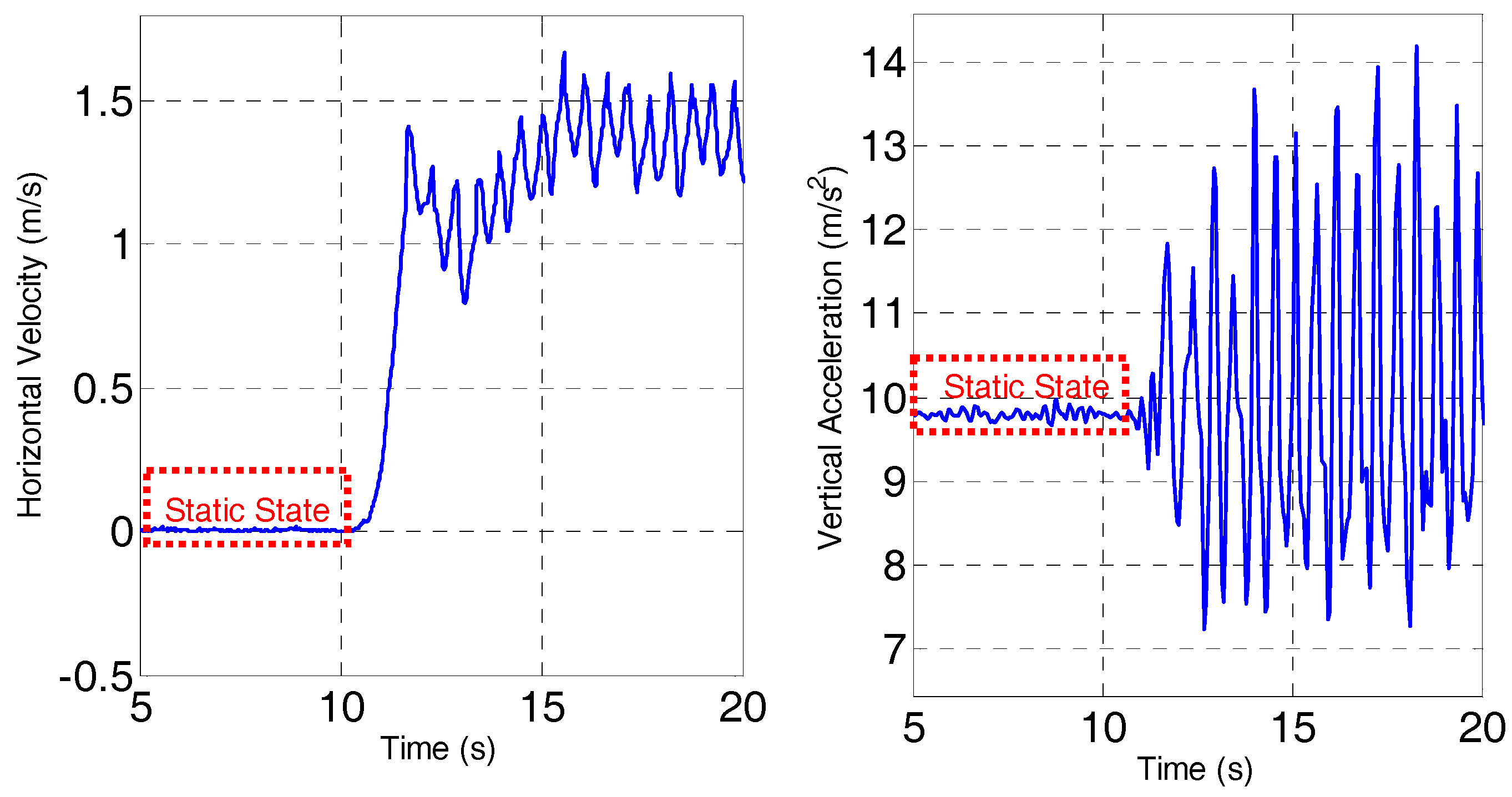
2.3.1. Quasi-State Update
2.3.2. Gait Model Update
2.3.3. Gravity Vector Update
2.3.4. Magnetic Field Vector Update
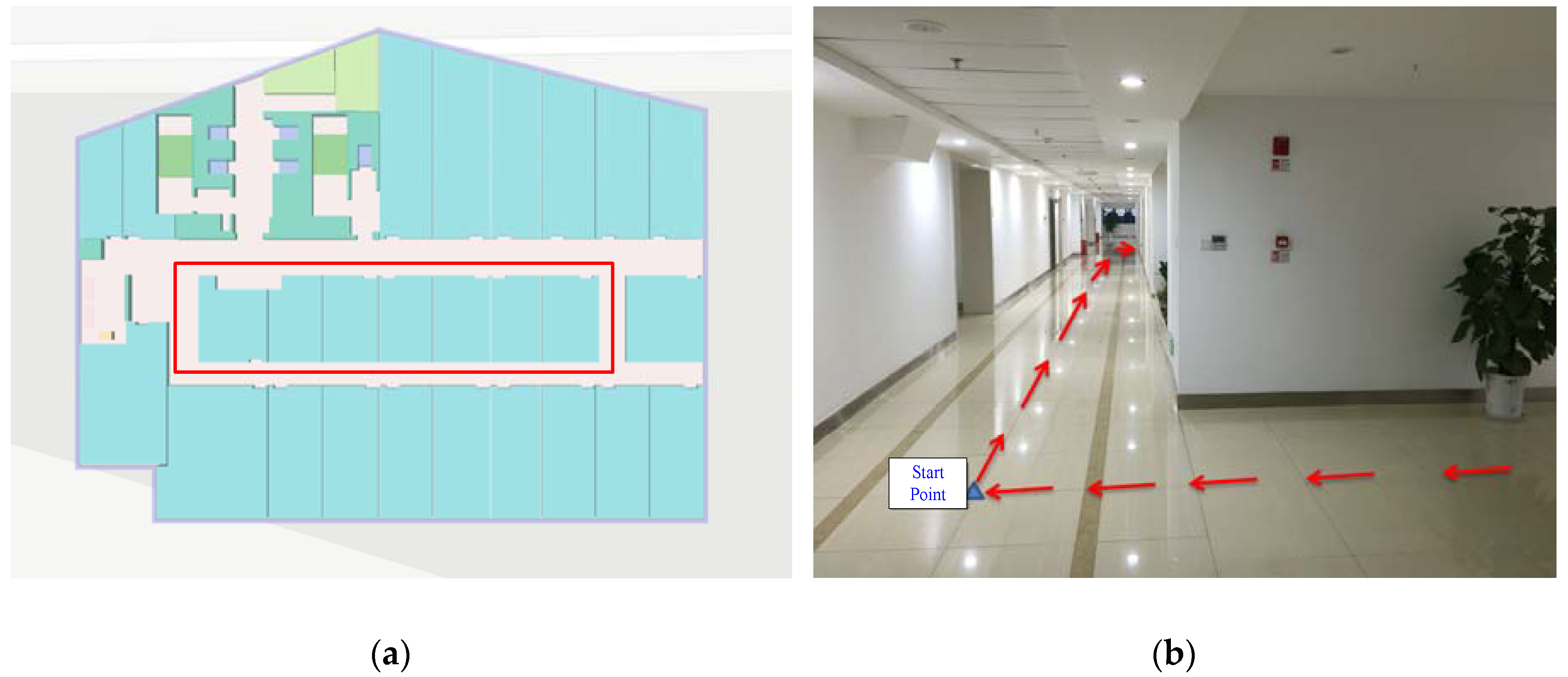
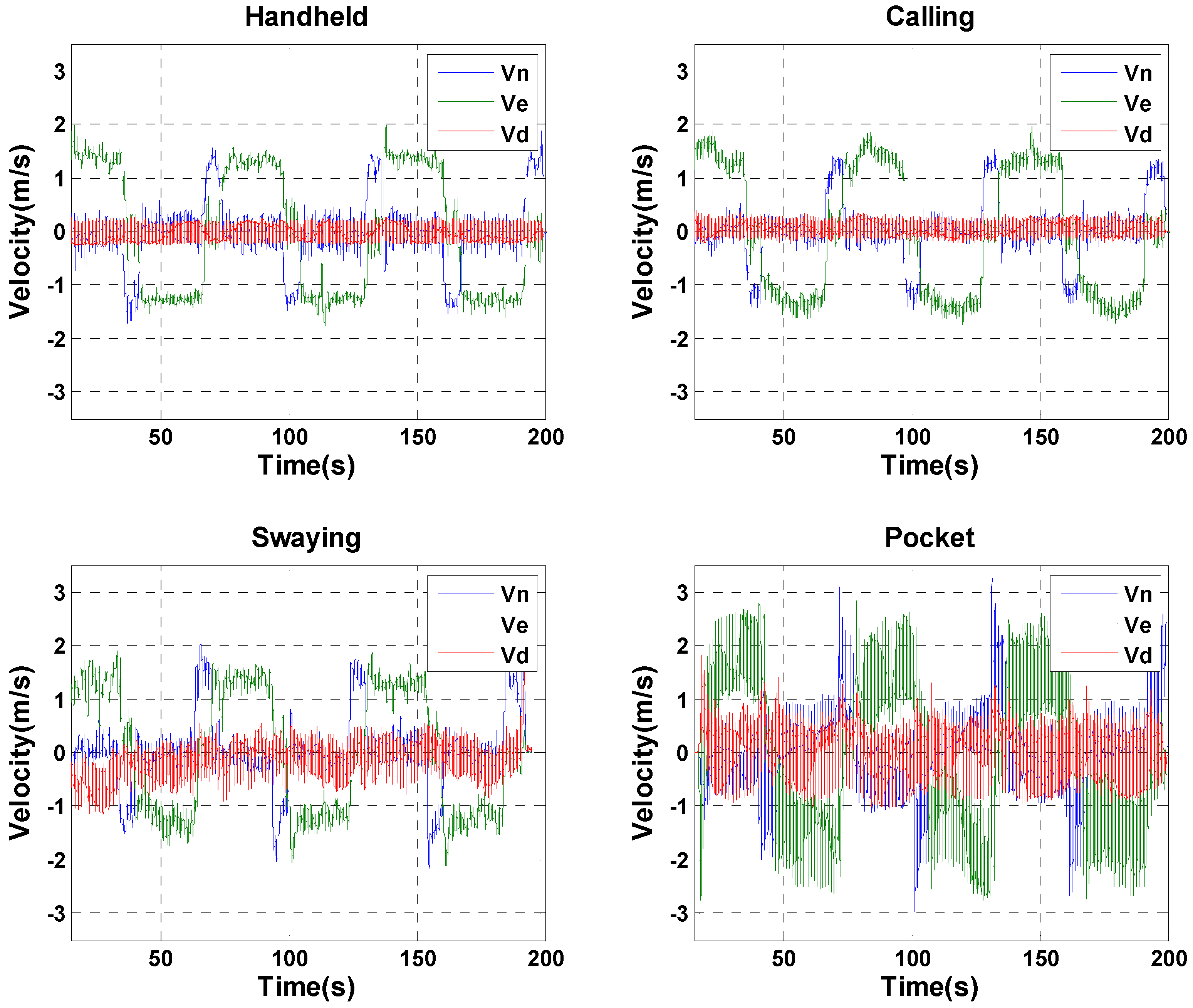
3. Results
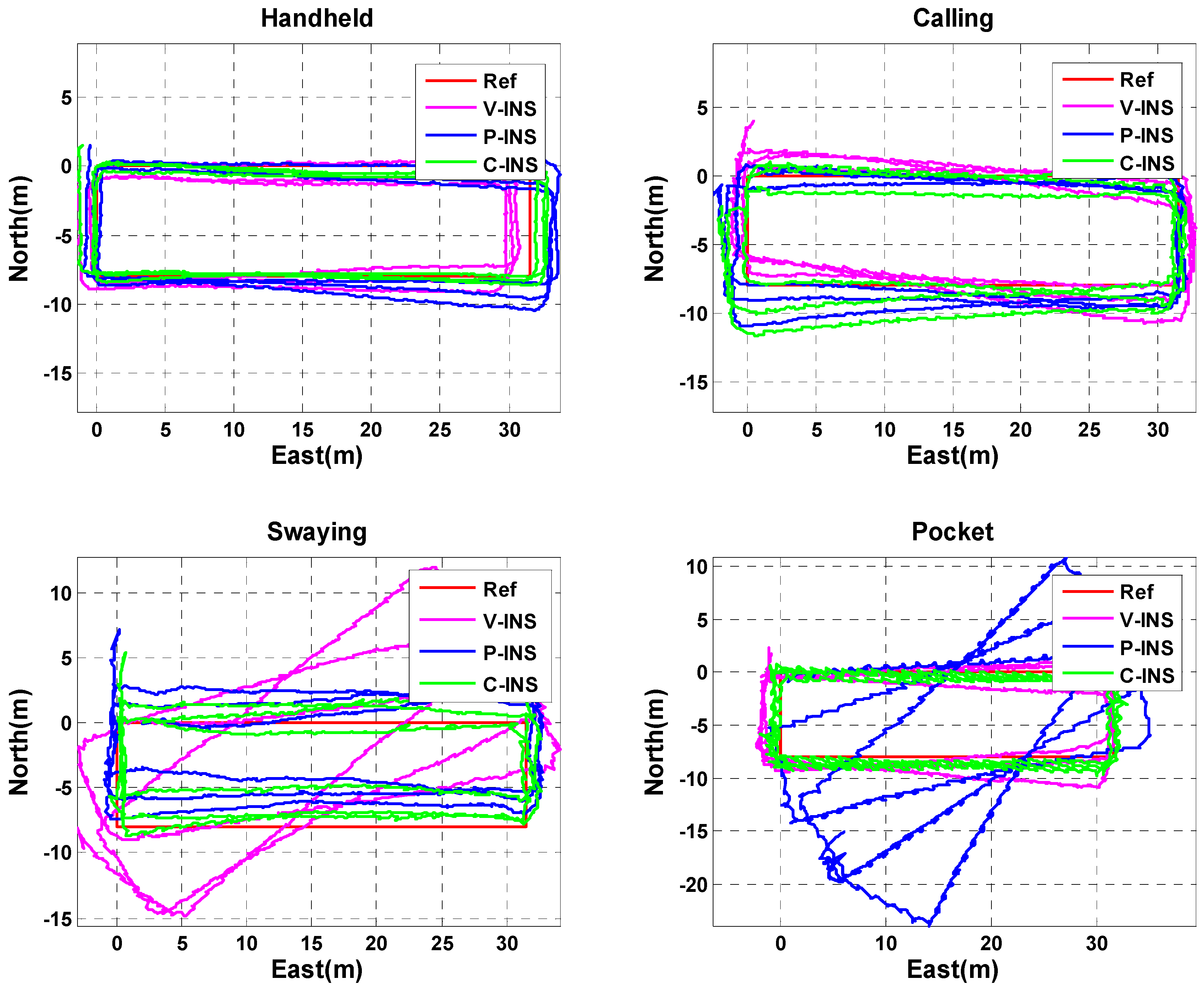
3.1. Position Estimation Performance Analysis for INS-Based Method
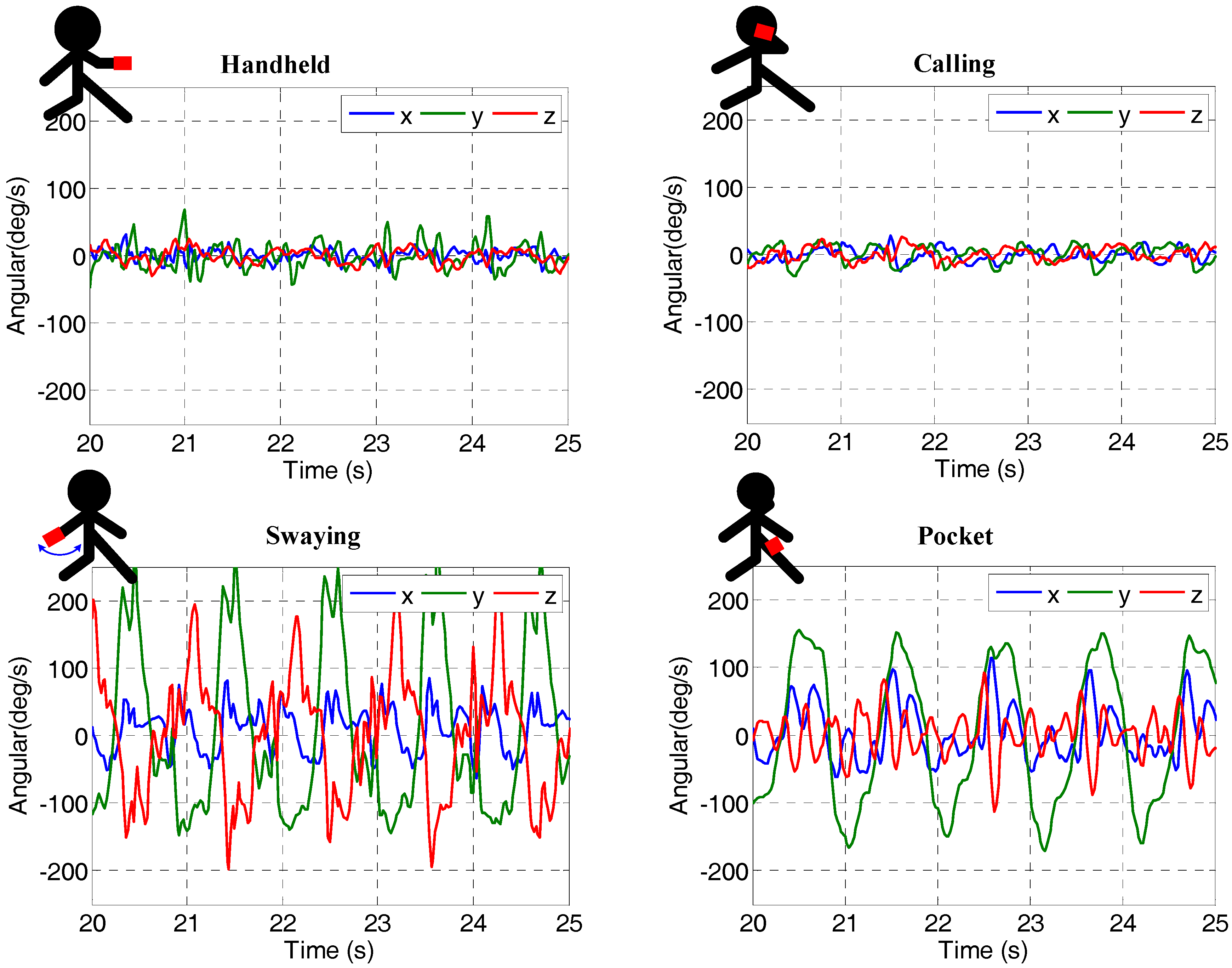
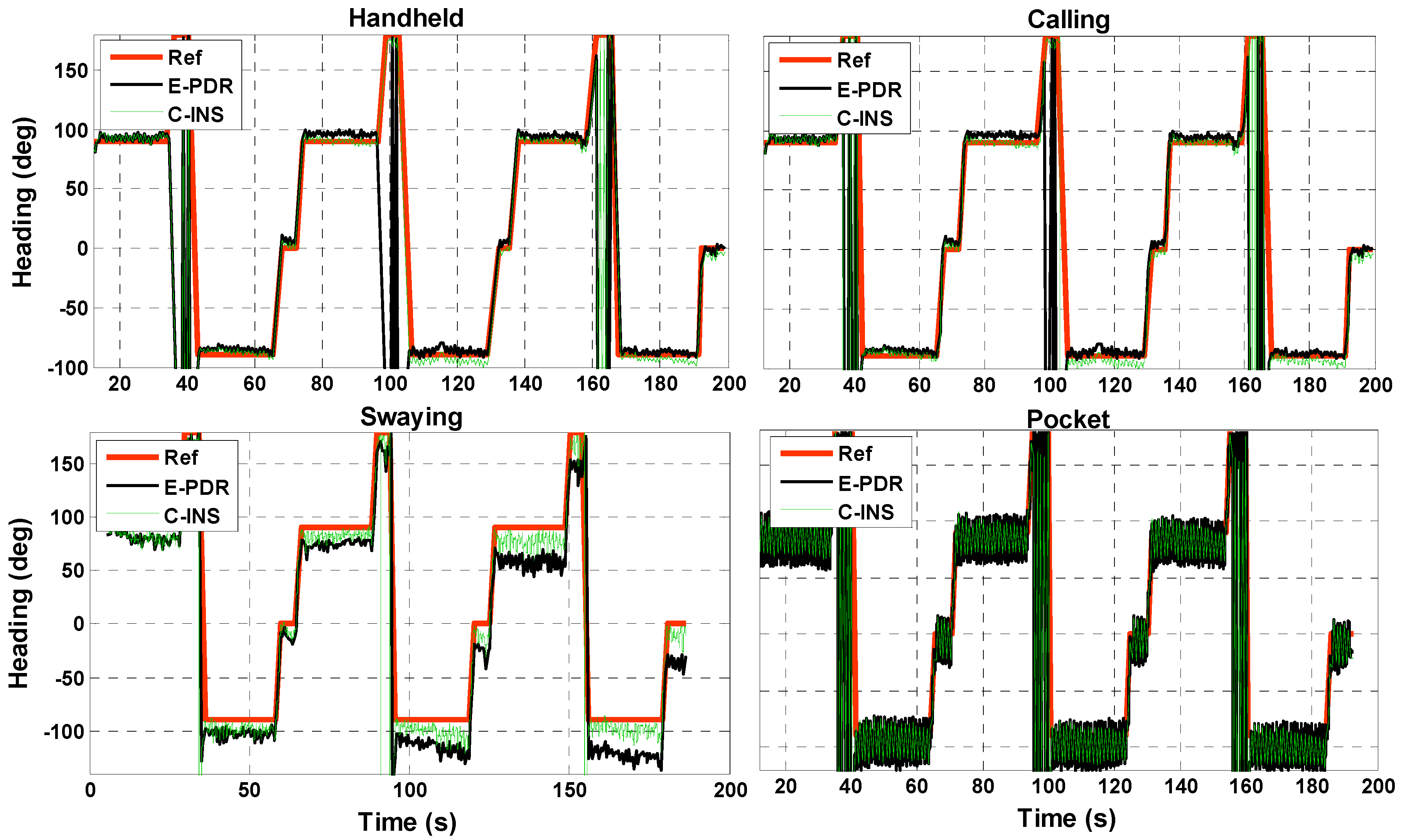
3.2. Heading Estimation between C-INS and E-PDR Methods
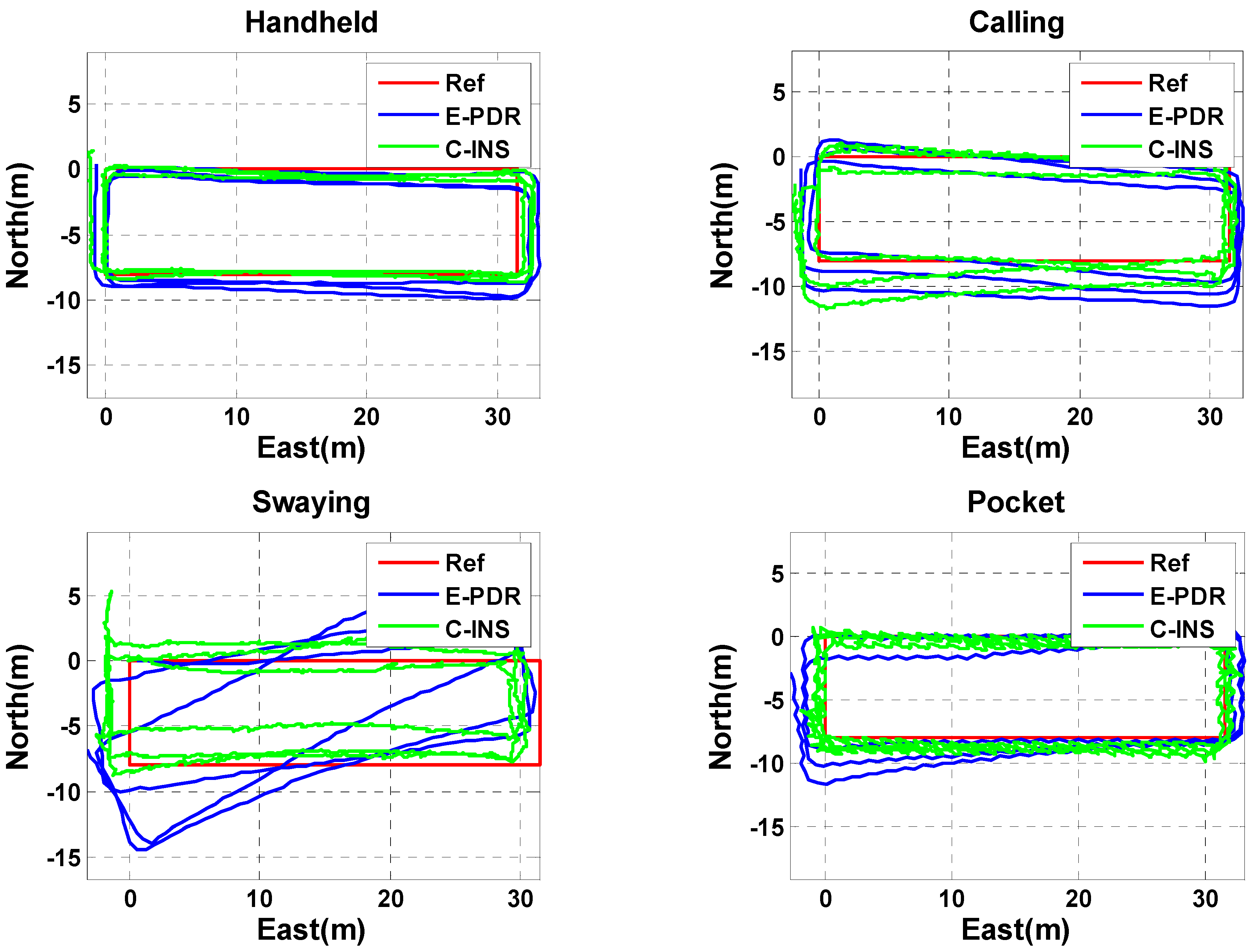
3.3. Position Estimation between C-INS and E-PDR Methods
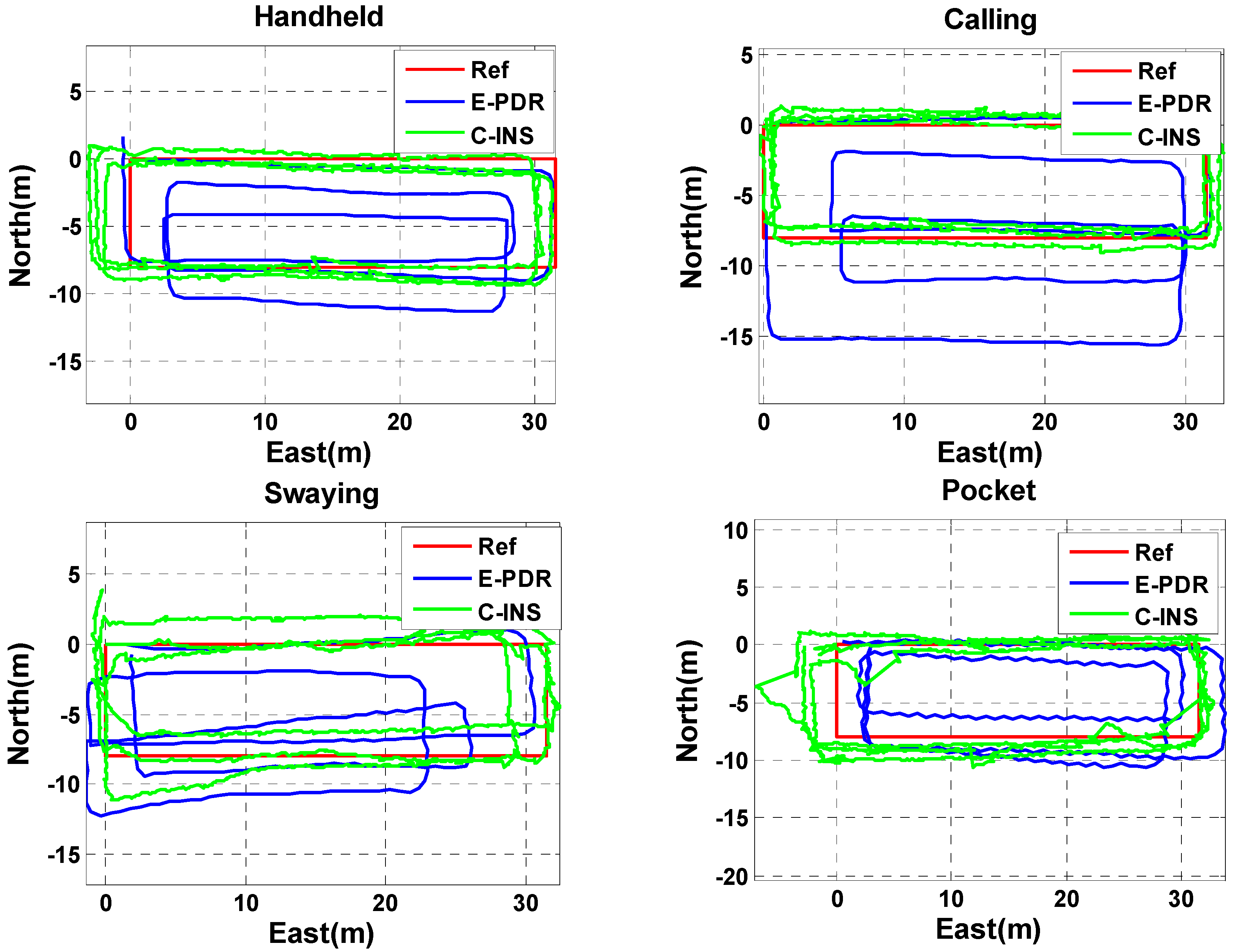
3.4. Step Detection Failure between C-INS and E-PDR Methods
4. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Alletto, S.; Cucchiara, R.; Del Fiore, G.; Mainetti, L.; Mighali, V.; Patrono, L.; Serra, G. An indoor location-aware system for an IoT-based smart museum. IEEE Internet Things J. 2016, 3, 244–253. [Google Scholar] [CrossRef]
- Li, Y.; Zhuang, Y.; Lan, H.; Zhang, P.; Niu, X.; El-Sheimy, N. WiFi-Aided Magnetic Matching for Indoor Navigation with Consumer Portable Devices. Micromachines 2015, 6, 747–764. [Google Scholar] [CrossRef]
- Chen, L.H.; Wu, E.H.K.; Jin, M.H.; Chen, G.H. Intelligent Fusion of Wi-Fi and Inertial Sensor-Based Positioning Systems for Indoor Pedestrian Navigation. IEEE Sens. J. 2014, 14, 4034–4042. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Z.; Zhang, X. An iBeacon-based indoor positioning systems for hospitals. Int. J. Smart Home 2015, 9, 161–168. [Google Scholar] [CrossRef]
- Lin, X.Y.; Ho, T.W.; Fang, C.C.; Yen, Z.S.; Yang, B.J.; Lai, F. A mobile indoor positioning system based on iBeacon technology. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society, Milan, Italy, 25–29 August 2015. [Google Scholar]
- Bekkali, A.; Sanson, H.; Matsumoto, M. RFID Indoor Positioning Based on Probabilistic RFID Map and Kalman Filtering. In Proceedings of the Third IEEE International Conference on Wireless and Mobile Computing, Networking and Communications (WiMOB 2007), White Plains, NY, USA, 8–10 October 2007. [Google Scholar]
- Ruiz, A.R.J.; Granja, F.S.; Honorato, J.C.P.; Rosas, J.I.G. Accurate Pedestrian Indoor Navigation by Tightly Coupling Foot-Mounted IMU and RFID Measurements. IEEE Trans. Instrum. Meas. 2011, 61, 178–189. [Google Scholar] [CrossRef]
- Ozdenizci, B.; Coskun, V.; Ok, K. NFC Internal: An Indoor Navigation System. Sensors 2015, 15, 7571–7595. [Google Scholar] [CrossRef] [PubMed]
- Yan, J. Algorithms for Indoor Positioning Systems Using Ultra-Wideband Signals. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- Angermann, M.; Frassl, M.; Doniec, M.; Julian, B.J.; Robertson, P. Characterization of the indoor magnetic field for applications in Localization and Mapping. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Sydney, NSW, Australia, 13–15 November 2012. [Google Scholar]
- Fan, X.; Wu, J.; Long, C.; Zhu, Y. Accurate and Low-cost Mobile Indoor Localization with 2-D Magnetic Fingerprints. In Proceedings of the First ACM Workshop on Mobile Crowdsensing Systems and Applications, Delft, The Netherlands, 6–8 November 2017. [Google Scholar]
- Pratama, A.R.; Widyawan; Hidayat, R. Smartphone-based Pedestrian Dead Reckoning as an indoor positioning system. In Proceedings of the International Conference on System Engineering and Technology, Bandung, Indonesia, 11–12 September 2012. [Google Scholar]
- Yang, Z.; Wu, C.; Zhou, Z.; Zhang, X.; Wang, X.; Liu, Y. Mobility Increases Localizability: A Survey on Wireless Indoor Localization using Inertial Sensors. ACM Comput. Surv. 2015, 47. [Google Scholar] [CrossRef]
- Mendoza-Silva, G.; Richter, P.; Torres-Sospedra, J.; Lohan, E.; Huerta, J. Long-Term WiFi Fingerprinting Dataset for Research on Robust Indoor Positioning. Date 2018, 3, 3. [Google Scholar] [CrossRef]
- Zhuang, Y.; El-Sheimy, N. Tightly-Coupled Integration of WiFi and MEMS Sensors on Handheld Devices for Indoor Pedestrian Navigation. IEEE Sens. J. 2015, 16, 224–234. [Google Scholar] [CrossRef]
- Jimenez, A.R.; Seco, F.; Prieto, C.; Guevara, J. A comparison of Pedestrian Dead-Reckoning algorithms using a low-cost MEMS IMU. In Proceedings of the IEEE International Symposium on Intelligent Signal Processing, Budapest, Hungary, 26–28 August 2009. [Google Scholar]
- Davidson, P.; Piche, R. A Survey of Selected Indoor Positioning Methods for Smartphones. IEEE Commun. Surv. Tutor. 2017, 19, 1347–1370. [Google Scholar] [CrossRef]
- Qian, J.; Ma, J.; Ying, R.; Liu, P.; Pei, L. An improved indoor localization method using smartphone inertial sensors. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Montbeliard-Belfort, France, 28–31 October 2013. [Google Scholar]
- Goyal, P.; Ribeiro, V.J.; Saran, H.; Kumar, A. Strap-down Pedestrian Dead-Reckoning system. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011. [Google Scholar]
- Rai, A.; Chintalapudi, K.K.; Padmanabhan, V.N.; Sen, R. Zee: Zero-effort crowdsourcing for indoor localization. In Proceedings of the 18th Annual International Conference on Mobile Computing and Networking, Istanbul, Turkey, 22–26 August 2012. [Google Scholar]
- Rong, L.; Zhiguo, D.; Jianzhong, Z.; Ming, L. Identification of Individual Walking Patterns Using Gait Acceleration. In Proceedings of the International Conference on Bioinformatics and Biomedical Engineering, Wuhan, China, 6–8 July 2007. [Google Scholar]
- Brajdic, A.; Harle, R. Walk detection and step counting on unconstrained smartphones. In Proceedings of the ACM International Joint Conference on Pervasive and Ubiquitous Computing, Zurich, Switzerland, 8–12 September 2013. [Google Scholar]
- Diaz, E.M.; Gonzalez, A.L.M.; Müller, F.D.P. Standalone inertial pocket navigation system. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium (PLANS 2014), Monterey, CA, USA, 5–8 May 2014. [Google Scholar]
- Zhuang, Y.; Lan, H.; Li, Y.; El-Sheimy, N. PDR/INS/WiFi Integration Based on Handheld Devices for Indoor Pedestrian Navigation. Micromachines 2015, 6, 793–812. [Google Scholar] [CrossRef]
- Rosario, M.B.D.; Lovell, N.H.; Redmond, S.J. Quaternion-Based Complementary Filter for Attitude Determination of a Smartphone. IEEE Sens. J. 2016, 16, 6008–6017. [Google Scholar] [CrossRef]
- Li, Y.; Lan, H.; Zhuang, Y.; Zhang, P.; Niu, X.; El-Sheimy, N. Real-time Attitude Tracking of Mobile Devices. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Banff, AB, Canada, 13–16 October 2015. [Google Scholar]
- Yadav, N.; Bleakley, C. Accurate orientation estimation using AHRS under conditions of magnetic distortion. Sensors 2014, 14, 20008–20024. [Google Scholar] [CrossRef] [PubMed]
- Afzal, M.H. Use of Earth’s Magnetic Field for Pedestrian Navigation. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2011. [Google Scholar]
- Renaudin, V.; Combettes, C. Magnetic, Acceleration Fields and Gyroscope Quaternion (MAGYQ)-based attitude estimation with smartphone sensors for indoor pedestrian navigation. Sensors 2014, 14, 22864–22890. [Google Scholar] [CrossRef] [PubMed]
- Renaudin, V.; Afzal, M.H.; Lachapelle, G. Magnetic perturbations detection and heading estimation using magnetometers. J. Locat. Based Serv. 2012, 6, 161–185. [Google Scholar] [CrossRef]
- Lee, J.K.; Park, E.J.; Robinovitch, S.N. Estimation of Attitude and External Acceleration Using Inertial Sensor Measurement during Various Dynamic Conditions. IEEE Trans. Instrum. Meas. 2012, 61, 2262–2273. [Google Scholar] [CrossRef] [PubMed]
- Afzal, M.H.; Renaudin, V.; Lachapelle, G. Use of Earth’s magnetic field for mitigating gyroscope errors regardless of magnetic perturbation. Sensors 2011, 11, 11390–11414. [Google Scholar] [CrossRef] [PubMed]
- Foxlin, E. Pedestrian tracking with shoe-mounted inertial sensors. IEEE Comput. Graph. Appl. 2005, 25, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Rajagopal, S. Personal Dead Reckoning System with Shoe Mounted Inertial Sensors. Master’s Thesis, Royal Institute of Technology, Stockholm, Sweden, 2008. [Google Scholar]
- Borenstein, J.; Ojeda, L.; Kwanmuang, S. Heuristic reduction of gyro drift in IMU-based personnel tracking systems. J. Navig. 2008, 62, 41–58. [Google Scholar] [CrossRef]
- Jimenez, A.R.; Seco, F.; Zampella, F.; Prieto, J.C.; Guevara, J. Improved Heuristic Drift Elimination (iHDE) for pedestrian navigation in complex buildings. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011. [Google Scholar]
- Zampella, F.; Khider, M.; Robertson, P.; Jiménez, A. Unscented Kalman filter and Magnetic Angular Rate Update (MARU) for an improved Pedestrian Dead-Reckoning. In Proceedings of the Position Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012. [Google Scholar]
- Gu, Y. Foot-mounted Pedestrian Navigation based on Particle Filter with an Adaptive Weight Updating Strategy. J. Navig. 2014, 68, 23–38. [Google Scholar] [CrossRef]
- Wahlström, J.; Skog, I.; Händel, P. Smartphone-Based Vehicle Telematics: A Ten-Year Anniversary. IEEE Trans. Intell. Transp. Syst. 2016, 18, 2802–2825. [Google Scholar] [CrossRef]
- Ladetto, Q.; Merminod, B. Digital magnetic compass and gyroscope integration for pedestrian navigation. In Proceedings of the 9th International Conference on Integrated Navigation Systems, Petersburg, Russia, 27–29 May 2002. [Google Scholar]
- Deng, Z.A. Heading Estimation for Indoor Pedestrian Navigation Using a Smartphone in the Pocket. Sensors 2015, 15, 21518–21536. [Google Scholar] [CrossRef] [PubMed]
- Combettes, C.; Renaudin, V. Comparison of misalignment estimation techniques between handheld device and walking directions. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Banff, AB, Canada, 13–16 October 2015. [Google Scholar]
- Kunze, K.; Lukowicz, P.; Partridge, K.; Begole, B. Which Way Am I Facing: Inferring Horizontal Device Orientation from an Accelerometer Signal. In Proceedings of the International Symposium on Wearable Computers, Linz, Austria, 4–7 September 2009. [Google Scholar]
- Yang, X.; Huang, B.; Miao, Q. A step-wise algorithm for heading estimation via a smartphone. In Proceedings of the Control and Decision Conference, Yinchuan, China, 28–30 May 2016. [Google Scholar]
- Liu, D.; Pei, L.; Qian, J.; Wang, L.; Liu, P.; Dong, Z.; Xie, S.; Wei, W. A novel heading estimation algorithm for pedestrian using a smartphone without attitude constraints. In Proceedings of the Fourth International Conference on Ubiquitous Positioning, Indoor Navigation and Location Based Services, Shanghai, China, 2–4 November 2016. [Google Scholar]
- Davidson, P.; Takala, J. Algorithm for pedestrian navigation combining IMU measurements and gait models. Gyroscopy Navig. 2013, 4, 79–84. [Google Scholar] [CrossRef]
- Lan, H. Multiple Systems Integration for Pedestrian Indoor Navigation. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2016. [Google Scholar]
- Lin, T.; Li, L.; Lachapelle, G. Multiple sensors integration for pedestrian indoor navigation. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Banff, AB, Canada, 13–16 October 2015. [Google Scholar]
- Shin, E.-H. Estimation Techniques for Low-Cost Inertial Navigation. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2005. [Google Scholar]
- Skog, I.; Handel, P.; Nilsson, J.-O.; Rantakokko, J. Zero-Velocity Detection—An Algorithm Evaluation. IEEE Trans. Biomed. Eng. 2010, 57, 2657–2666. [Google Scholar] [CrossRef] [PubMed]
- Abdul Rahim, K. Heading Drift Mitigation for Low-Cost Inertial Pedestrian Navigation. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2012. [Google Scholar]
- Li, Y.; Niu, X.; Zhang, Q.; Zhang, H.; Shi, C. An in situ hand calibration method using a pseudo-observation scheme for low-end inertial measurement units. Meas. Sci. Technol. 2012, 23, 105104. [Google Scholar] [CrossRef]
- Tabatabaei, S.; Gluhak, A.; Tafazolli, R. A Fast Calibration Method for Triaxial Magnetometers. IEEE Trans. Instrum. Meas. 2013, 62, 2929–2937. [Google Scholar] [CrossRef]


| Handled | Calling | Swaying | ||||||
|---|---|---|---|---|---|---|---|---|
| E-PDR | C-INS | E-PDR | C-INS | E-PDR | C-INS | E-PDR | C-INS | |
| Mean | 2.0 | 1.9 | 4.6 | 3.1 | 12.8 | 9.7 | 15.6 | 16.1 |
| RMS | 2.4 | 2.3 | 5.3 | 3.9 | 14.0 | 10.9 | 16.6 | 16.6 |
| Max | 6.4 | 5.8 | 10.8 | 11.1 | 36.8 | 29.1 | 27.4 | 27.4 |
| Handled | Calling | Swaying | ||||||
|---|---|---|---|---|---|---|---|---|
| E-PDR | C-INS | E-PDR | C-INS | E-PDR | C-INS | E-PDR | C-INS | |
| Mean | 1.09 | 0.81 | 1.00 | 1.16 | 2.28 | 2.08 | 0.90 | 0.77 |
| RMS | 1.22 | 0.92 | 1.20 | 1.33 | 2.54 | 2.23 | 1.11 | 0.90 |
| Max | 3.61 | 2.76 | 3.30 | 3.14 | 4.96 | 4.08 | 2.56 | 1.91 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuang, J.; Niu, X.; Chen, X. Robust Pedestrian Dead Reckoning Based on MEMS-IMU for Smartphones. Sensors 2018, 18, 1391. https://doi.org/10.3390/s18051391
Kuang J, Niu X, Chen X. Robust Pedestrian Dead Reckoning Based on MEMS-IMU for Smartphones. Sensors. 2018; 18(5):1391. https://doi.org/10.3390/s18051391
Chicago/Turabian StyleKuang, Jian, Xiaoji Niu, and Xingeng Chen. 2018. "Robust Pedestrian Dead Reckoning Based on MEMS-IMU for Smartphones" Sensors 18, no. 5: 1391. https://doi.org/10.3390/s18051391
APA StyleKuang, J., Niu, X., & Chen, X. (2018). Robust Pedestrian Dead Reckoning Based on MEMS-IMU for Smartphones. Sensors, 18(5), 1391. https://doi.org/10.3390/s18051391





