Analysis of Known Linear Distributed Average Consensus Algorithms on Cycles and Paths
Abstract
:1. Introduction
1.1. Deterministic Linear Distributed Averaging Algorithms
1.2. Randomized Linear Distributed Averaging Algorithms
1.3. Our Contribution
- a closed-form expression for the convergence time of the fastest LTI distributed averaging algorithm for symmetric weights on the considered topologies (see Section 2.1); moreover, we also compute a closed-form expression for the convergence time of this algorithm on a grid;
- a closed-form expression for the convergence time of the fastest constant edge weights algorithm on the considered topologies (see Section 2.2);
- a closed-form expression for the convergence time of the maximum-degree weights algorithm on the considered topologies (see Section 2.3);
- a closed-form expression for the convergence time of the Metropolis–Hastings algorithm on the considered topologies (see Section 2.3);
- closed-form lower and upper bounds for the convergence time of the pairwise gossip algorithm on the considered topologies (see Section 3.1);
- closed-form lower and upper bounds for the convergence time of the broadcast gossip algorithm on the considered topologies (see Section 3.2).
2. Convergence Time of Deterministic Linear Distributed Averaging Algorithms
2.1. Convergence Time of the Fastest LTI Distributed Averaging Algorithm for Symmetric Weights
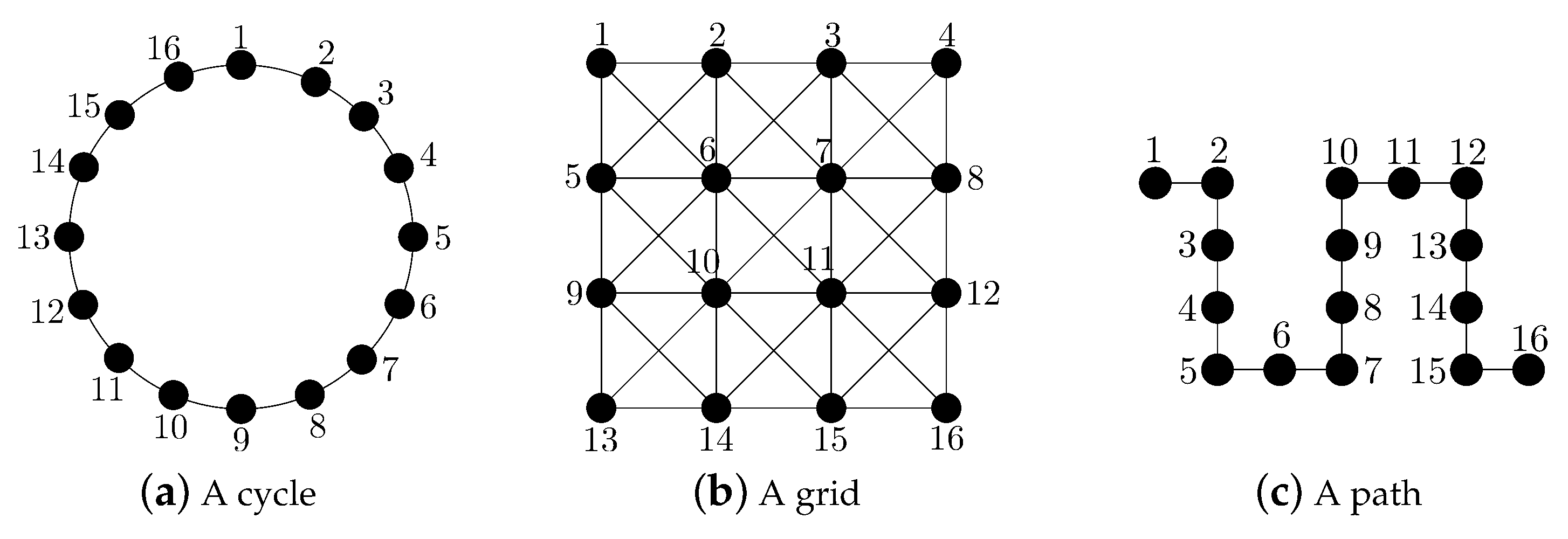
2.1.1. The Cycle
2.1.2. The Grid
2.1.3. The Path
2.2. Convergence Time of the Fastest Constant Edge Weights Algorithm
2.3. Convergence Time of the Maximum-Degree Weights Algorithm and of the Metropolis–Hastings Algorithm
2.3.1. The Cycle
2.3.2. The Path
3. Convergence Time of Randomized Linear Distributed Averaging Algorithms
3.1. Lower and Upper Bounds for the Convergence Time of the Pairwise Gossip Algorithm
3.1.1. The Cycle
3.1.2. The Path
3.2. Lower and Upper Bounds for the Convergence Time of the Broadcast Gossip Algorithm
3.2.1. The Cycle
3.2.2. The Path
4. Discussion
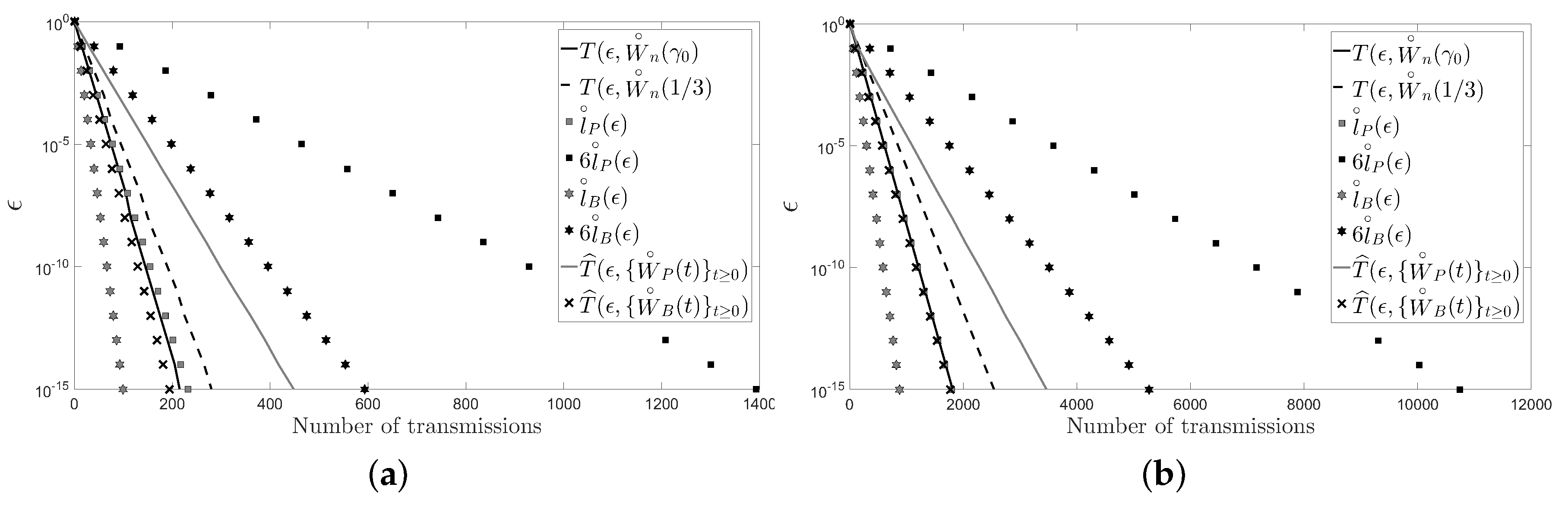
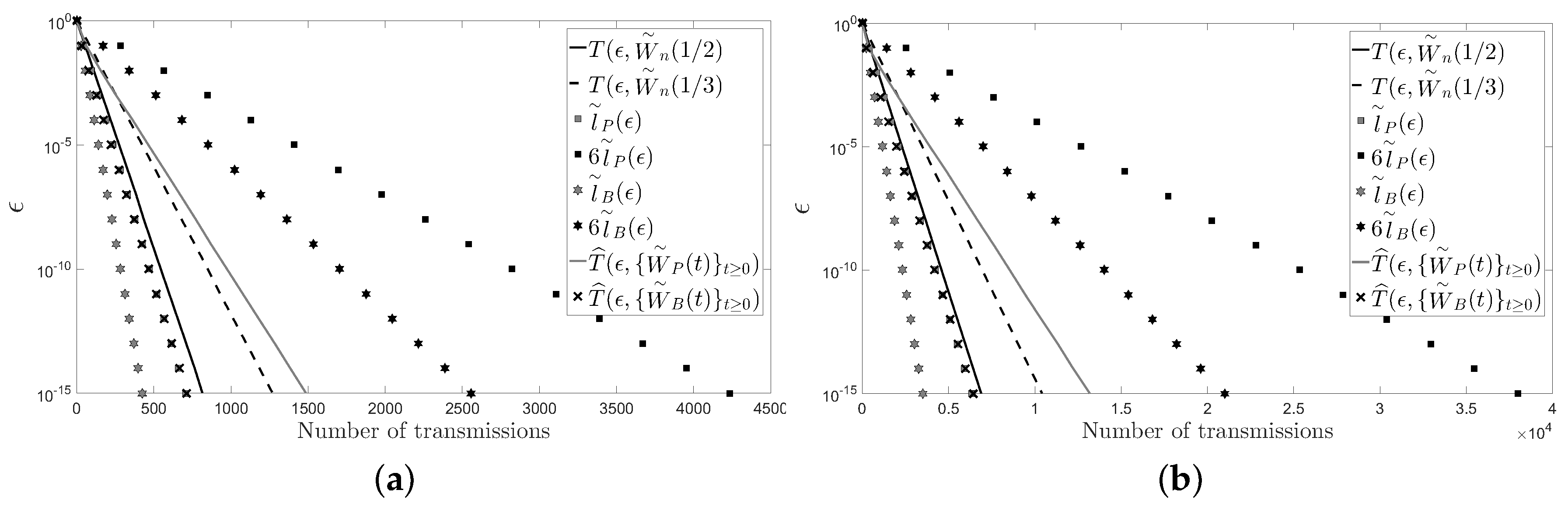
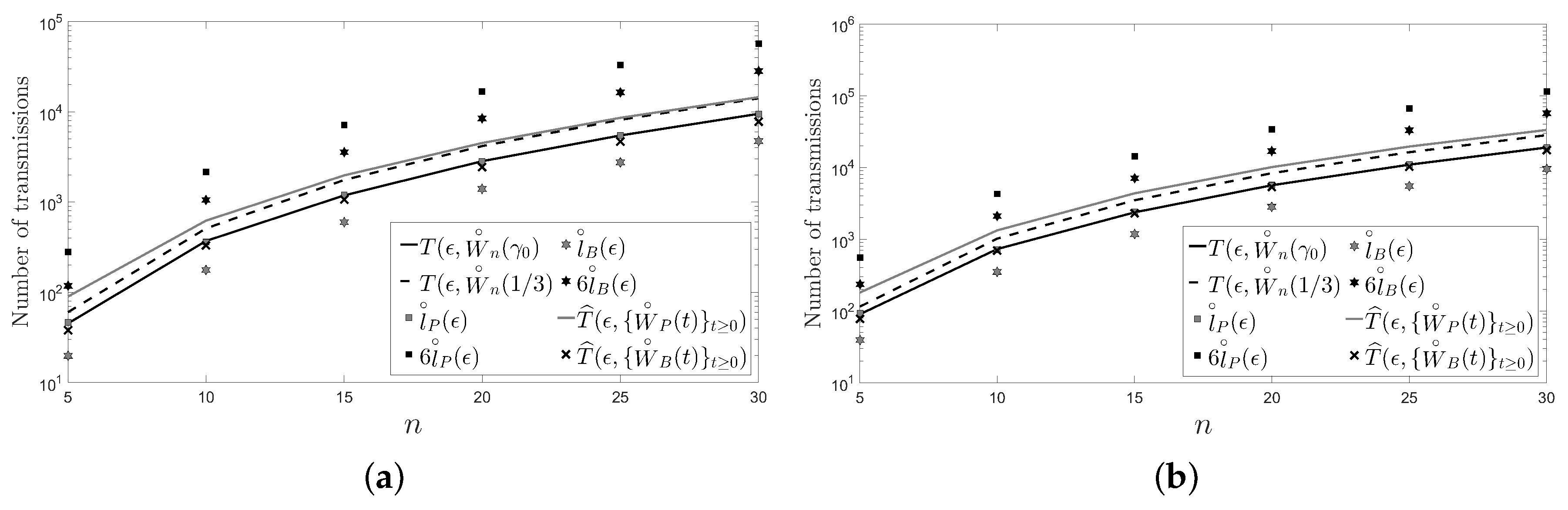
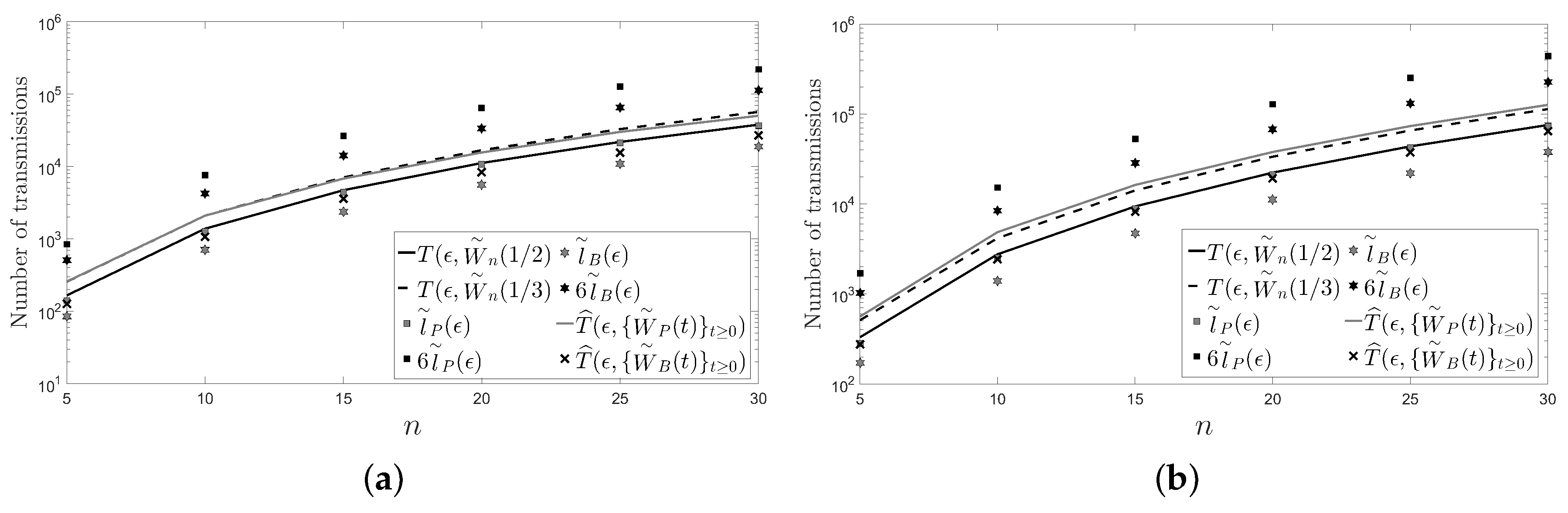
- The behavior of the considered deterministic linear distributed averaging algorithms is as good as the behavior of the considered randomized ones in terms of the number of transmissions required on a cycle and on a path with n sensors: .
- For a large enough number of sensors and regardless of the considered distributed averaging algorithm, the number of transmissions required on a path is four times larger than the number of transmissions required on a cycle.
5. Numerical Examples
6. Conclusions
- The best algorithm among the considered deterministic distributed averaging algorithms is not worse than the best algorithm among the considered randomized distributed averaging algorithms for cycles and paths.
- The weighting matrix of the fastest LTI distributed averaging algorithm for symmetric weights and the weighting matrix of the fastest constant edge weights algorithm are the same on cycles and on paths.
- The number of transmissions required on a path with n sensors is asymptotically four-times larger than the number of transmissions required on a cycle with the same number of sensors.
- The number of transmissions required grows as on cycles and on paths for the six algorithms considered.
- For the fastest LTI algorithm, the number of transmissions required grows as on a square grid of n sensors (i.e., ).
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Comparison of Several Definitions of Convergence Time
- for all .
- for all .
- for all .
- for all .
- for all .
Appendix B. Proof of Theorem 1
Appendix C. Proof of Theorem 2
Appendix D. Proof of Theorem 3
Appendix E. Proof of Theorem 9
Appendix F. Proof of Theorem 10
References
- Insausti, X.; Camaró, F.; Crespo, P.M.; Beferull-Lozano, B.; Gutiérrez-Gutiérrez, J. Distributed pseudo-gossip algorithm and finite-length computational codes for efficient in-network subspace projection. IEEE J. Sel. Top. Signal Process. 2013, 7, 163–174. [Google Scholar] [CrossRef]
- Xiao, L.; Boyd, S. Fast linear iterations for distributed averaging. Syst. Control Lett. 2004, 53, 65–78. [Google Scholar] [CrossRef]
- Xiao, L.; Boyd, S.; Kimb, S.J. Distributed average consensus with least-mean-square deviation. J. Parallel Distrib. Comput. 2007, 67, 33–46. [Google Scholar] [CrossRef]
- Insausti, X.; Gutiérrez-Gutiérrez, J.; Zárraga-Rodríguez, M.; Crespo, P.M. In-network computation of the optimal weighting matrix for distributed consensus on wireless sensor networks. Sensors 2017, 17, 1702. [Google Scholar] [CrossRef] [PubMed]
- Olshevsky, A.; Tsitsiklis, J. Convergence speed in distributed consensus and averaging. SIAM Rev. 2011, 53, 747–772. [Google Scholar] [CrossRef]
- Boyd, S.; Ghosh, A.; Prabhakar, B.; Shah, D. Randomized gossip algorithms. IEEE Trans. Inf. Theory 2006, 52, 2508–2530. [Google Scholar] [CrossRef]
- Aysal, T.C.; Yildiz, M.E.; Sarwate, A.D.; Scaglione, A. Broadcast gossip algorithms for consensus. IEEE Trans. Signal Process. 2009, 57, 2748–2761. [Google Scholar] [CrossRef]
- Wu, S.; Rabbat, M.G. Broadcast Gossip Algorithms for Consensus on Strongly Connected Digraphs. IEEE Trans. Signal Process. 2013, 61, 3959–3971. [Google Scholar] [CrossRef]
- Dimakis, A.D.G.; Kar, S.; Moura, J.M.F.; Rabbat, M.G.; Scaglione, A. Gossip algorithms for distributed signal processing. Proceed. IEEE 2010, 98, 1847–1864. [Google Scholar] [CrossRef]
- Olshevsky, A.; Tsitsiklis, J. Convergence speed in distributed consensus and averaging. SIAM J. Control Optim. 2009, 48, 33–55. [Google Scholar] [CrossRef] [Green Version]
- Olshevsky, A.; Tsitsiklis, J. A lower bound for distributed averaging algorithms on the line graph. IEEE Trans. Autom. Control 2011, 56, 2694–2698. [Google Scholar] [CrossRef]
- Apostol, T.M. Calculus; John Wiley & Sons: Hoboken, NJ, USA, 1967; Volume 1. [Google Scholar]
- Gutiérrez-Gutiérrez, J.; Crespo, P.M. Asymptotically equivalent sequences of matrices and Hermitian block Toeplitz matrices with continuous symbols: Applications to MIMO systems. IEEE Trans. Inf. Theory 2008, 54, 5671–5680. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.; Crespo, P.M. Asymptotically equivalent sequences of matrices and multivariate ARMA processes. IEEE Trans. Inf. Theory 2011, 57, 5444–5454. [Google Scholar] [CrossRef]
- Bernstein, D.S. Matrix Mathematics; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Gray, R.M. Toeplitz and circulant matrices: A review. Found. Trends Commun. Inf. Theory 2006, 2, 155–239. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.; Crespo, P.M. Block Toeplitz matrices: Asymptotic results and applications. Found. Trends Commun. Inf. Theory 2011, 8, 179–257. [Google Scholar] [CrossRef]
- Shor, N.Z. Minimization Methods for Non-Differentiable Functions; Springer: Berlin, Germany, 1985. [Google Scholar]
- Apostol, T.M. Mathematical Analysis; Addison-Wesley: Boston, MA, USA, 1974. [Google Scholar]
- Yueh, W.C.; Cheng, S.S. Explicit Eigenvalues and inverses of tridiagonal Toeplitz matrices with four perturbed corners. ANZIAM J. 2008, 49, 361–387. [Google Scholar] [CrossRef]
- Gray, R.M. On the asymptotic eigenvalue distribution of Toeplitz matrices. IEEE Trans. Inf. Theory 1972, 18, 725–730. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez-Gutiérrez, J.; Zárraga-Rodríguez, M.; Insausti, X. Analysis of Known Linear Distributed Average Consensus Algorithms on Cycles and Paths. Sensors 2018, 18, 968. https://doi.org/10.3390/s18040968
Gutiérrez-Gutiérrez J, Zárraga-Rodríguez M, Insausti X. Analysis of Known Linear Distributed Average Consensus Algorithms on Cycles and Paths. Sensors. 2018; 18(4):968. https://doi.org/10.3390/s18040968
Chicago/Turabian StyleGutiérrez-Gutiérrez, Jesús, Marta Zárraga-Rodríguez, and Xabier Insausti. 2018. "Analysis of Known Linear Distributed Average Consensus Algorithms on Cycles and Paths" Sensors 18, no. 4: 968. https://doi.org/10.3390/s18040968
APA StyleGutiérrez-Gutiérrez, J., Zárraga-Rodríguez, M., & Insausti, X. (2018). Analysis of Known Linear Distributed Average Consensus Algorithms on Cycles and Paths. Sensors, 18(4), 968. https://doi.org/10.3390/s18040968




