Bearing Fault Diagnosis by a Robust Higher-Order Super-Twisting Sliding Mode Observer
Abstract
:1. Introduction
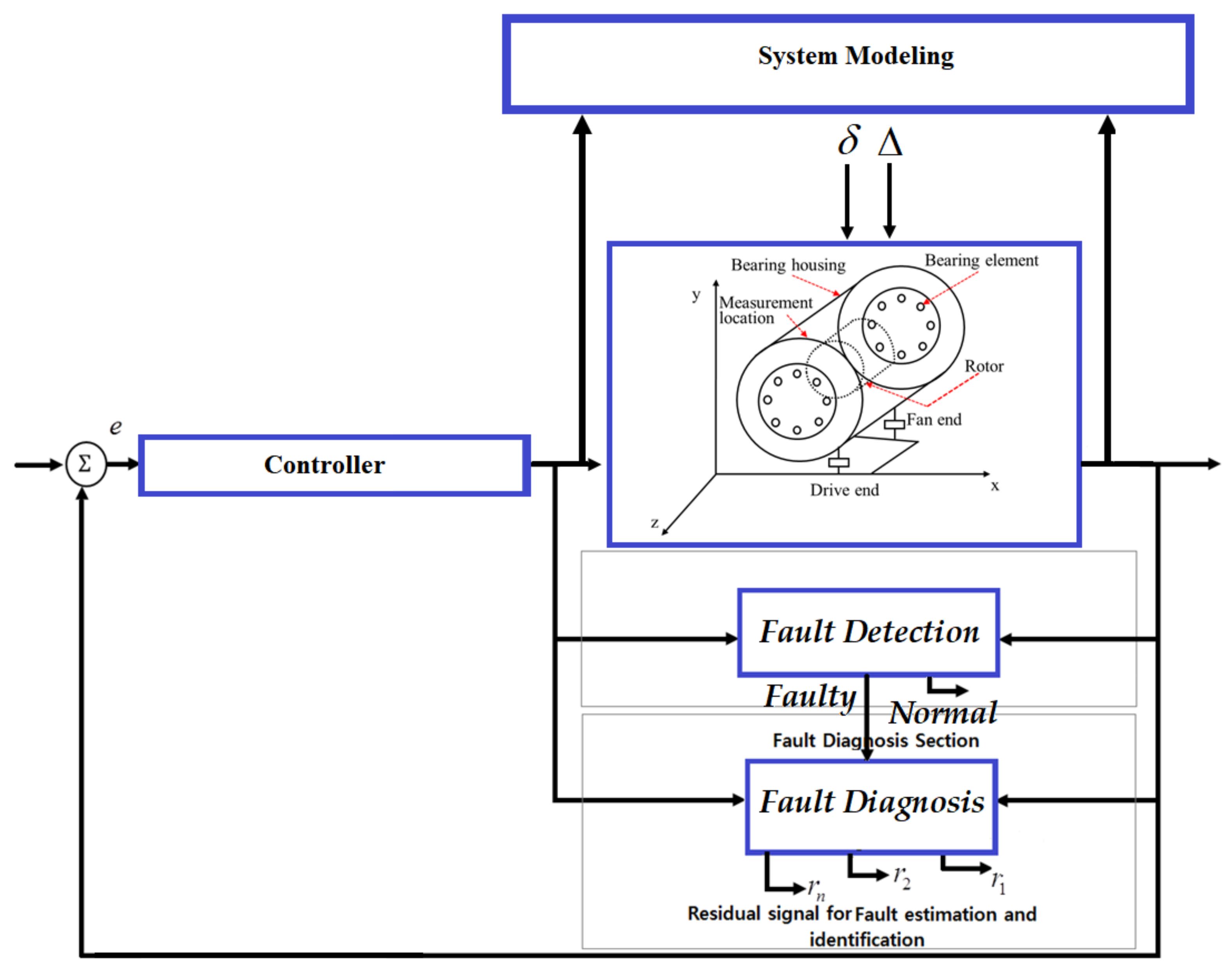
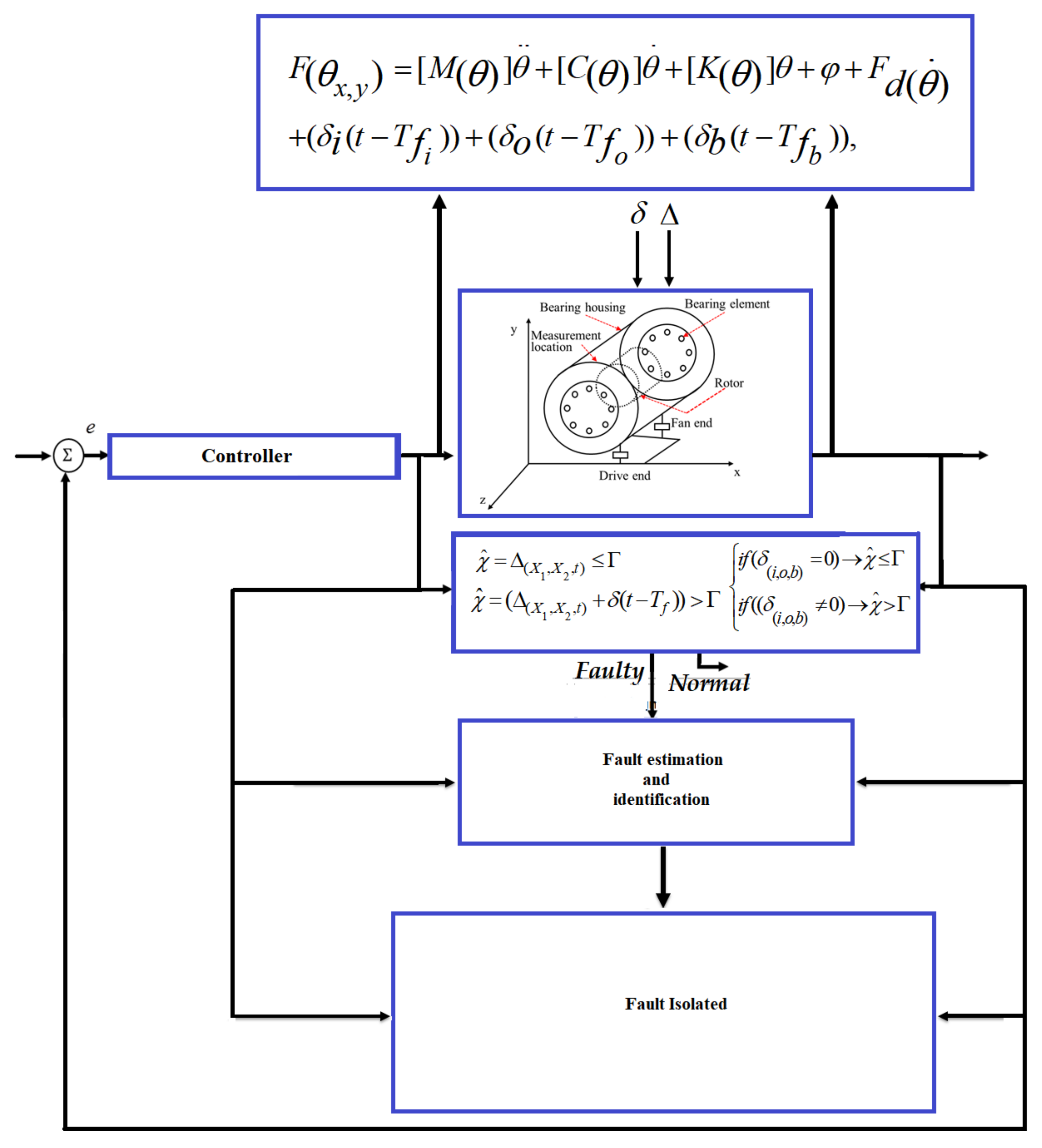
2. Problem Statements and Fault Diagnosis Objectives
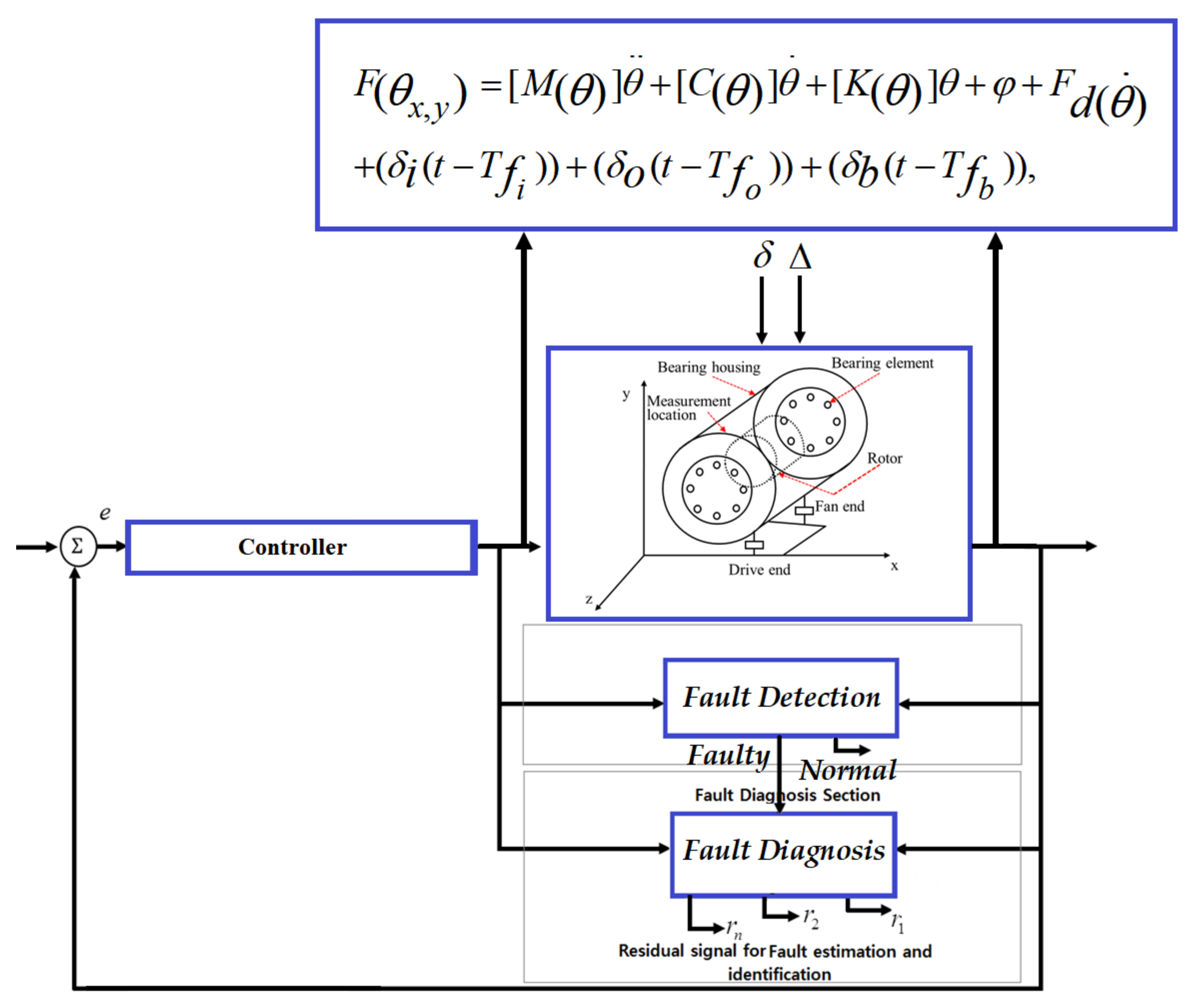
3. Mathematical Modeling of REBs
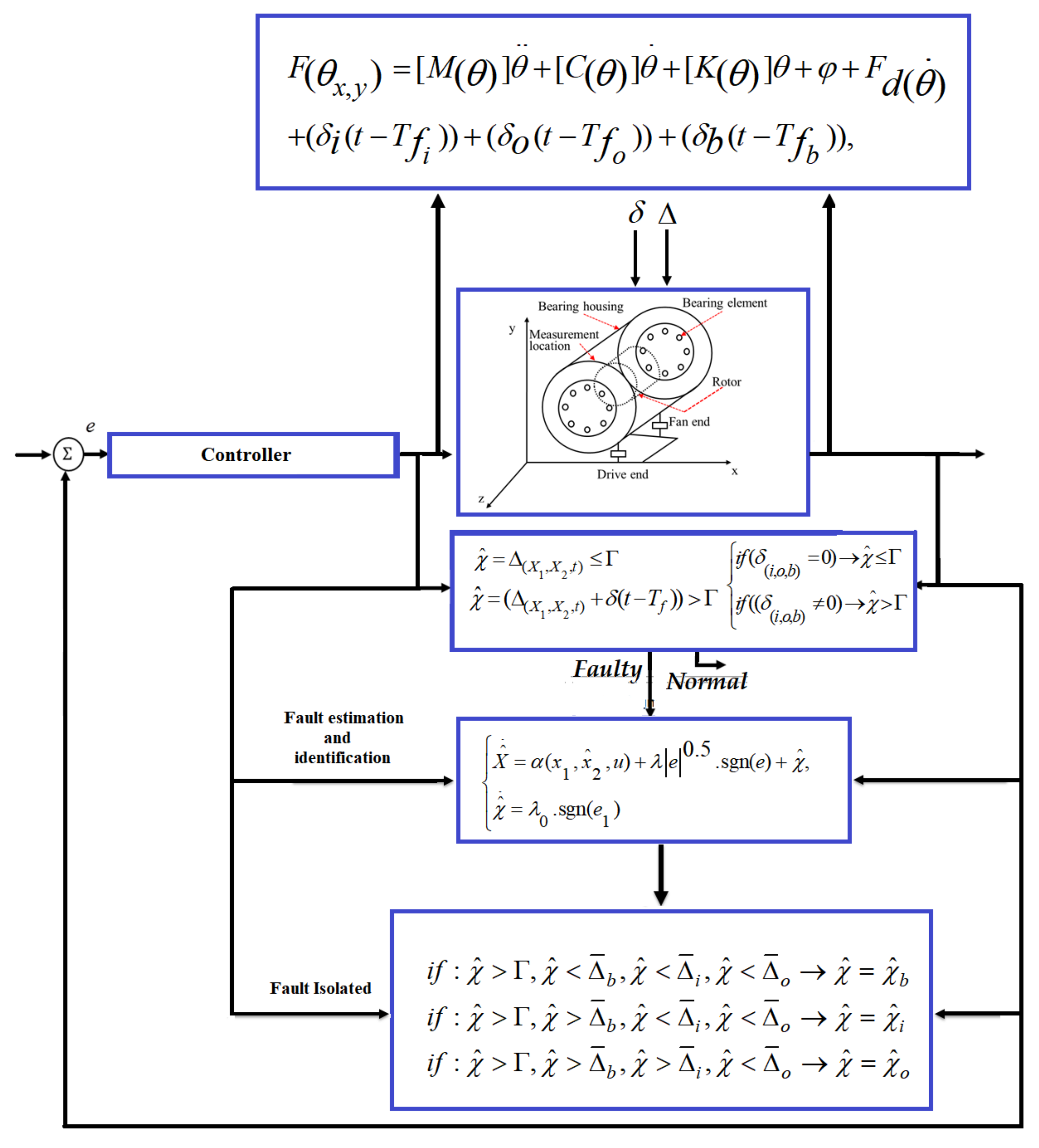
4. Proposed Method
4.1. ARX-Laguerre Proportional-Integral Observer (APIO)
4.2. Proposed Higher-Order Super-Twisting Sliding Mode Observer (HOSTSMO)
5. Datasets, Results, and Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Adams, M.L. Analysis of Rolling Element Bearing Faults in Rotating Machinery: Experiments, Modeling, Fault Detection and Diagnosis. Ph.D. Thesis, Case Western Reserve University, Cleveland, OH, USA, 2001. [Google Scholar]
- Agrawal, S.; Mohanty, S.R.; Agarwal, V. Bearing fault detection using Hilbert and high frequency resolution techniques. IETE J. Res. 2015, 61, 99–108. [Google Scholar] [CrossRef]
- Chen, H.; Lu, S. Fault diagnosis digital method for power transistors in power converters of switched reluctance motors. IEEE Trans. Ind. Electron. 2013, 60, 749–763. [Google Scholar] [CrossRef]
- Freire, N.M.A.; Estima, J.O.; Cardoso, A.J.M. Open-circuit fault diagnosis in PMSG drives for wind turbine applications. IEEE Trans. Ind. Electron. 2013, 60, 3957–3967. [Google Scholar] [CrossRef]
- Joksimović, G.M.; Riger, J.; Wolbank, T.M.; Perić, N.; Vasak, M. Stator-current spectrum signature of healthy cage rotor induction machines. IEEE Trans. Ind. Electron. 2013, 60, 4025–4033. [Google Scholar] [CrossRef]
- Gong, X.; Qiao, W. Bearing fault diagnosis for direct-drive wind turbines via current-demodulated signals. IEEE Trans. Ind. Electron. 2013, 60, 3419–3428. [Google Scholar] [CrossRef]
- Climente-Alarcon, V.; Antonino-Daviu, J.A.; Riera-Guasp, M.; Vlcek, M. Induction motor diagnosis by advanced notch FIR filters and the Wigner-Ville distribution. IEEE Trans. Ind. Electron. 2014, 61, 4217–4227. [Google Scholar] [CrossRef]
- Xiang, L.; Yan, X. A self-adaptive time-frequency analysis method based on local mean decomposition and its application in defect diagnosis. J. Vib. Control 2016, 22, 1049–1061. [Google Scholar] [CrossRef]
- Lafont, F.; Balmat, J.-F.; Pessel, N.; Fliess, M. A model-free control strategy for an experimental greenhouse with an application to fault accommodation. Comput. Electron. Agric. 2015, 110, 139–149. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Hong, H. Fault-tolerant cooperative control in an offshore wind farm using model-free and model-based fault detection and diagnosis approaches. Appl. Energy 2017, 201, 284–307. [Google Scholar] [CrossRef]
- Stavrou, D.; Eliades, D.G.; Panayiotou, C.G.; Polycarpou, M.M. Fault detection for service mobile robots using model-based method. Auton. Robots 2016, 40, 383–394. [Google Scholar] [CrossRef]
- López-Estrada, F.R.; Ponsart, J.-C.; Theilliol, D.; Zhang, Y.; Astorga-Zaragoza, C.-M. LPV model-based tracking control and robust sensor fault diagnosis for a quadrotor UAV. J. Intell. Robot. Syst. 2016, 84, 163–177. [Google Scholar] [CrossRef]
- Van, M.; Franciosa, P.; Ceglarek, D. Fault diagnosis and fault-tolerant control of uncertain robot manipulators using high-order sliding mode. Math. Probl. Eng. 2016, 2016, 7926280. [Google Scholar] [CrossRef]
- Ebrahimi, B.M.; Roshtkhari, M.J.; Faiz, J.; Khatami, S.V. Advanced eccentricity fault recognition in permanent magnet synchronous motors using stator current signature analysis. IEEE Trans. Ind. Electron. 2014, 61, 2041–2052. [Google Scholar] [CrossRef]
- Khalastchi, E.; Kalech, M.; Rokach, L. A hybrid approach for improving unsupervised fault detection for robotic systems. Expert Syst. Appl. 2017, 81, 372–383. [Google Scholar] [CrossRef]
- Cecati, C. A survey of fault diagnosis and fault-tolerant techniques—Part II: Fault diagnosis with knowledge-based and hybrid/active approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar]
- Mehrjou, M.R.; Marium, N.; Hamiruce, M.; Misron, N. Rotor fault condition monitoring techniques for squirrel-cage induction machine—A review. Mech. Syst. Signal Process. 2011, 25, 2827–2848. [Google Scholar] [CrossRef]
- Yau, H.-T.; Wu, S.-Y.; Chen, C.-L.; Li, Y.-C. Fractional-order chaotic self-synchronization-based tracking faults diagnosis of ball bearing systems. IEEE Trans. Ind. Electron. 2016, 63, 3824–3833. [Google Scholar] [CrossRef]
- Dai, X.; Gao, Z.; Breikin, T.; Wangm, H. Disturbance attenuation in fault detection of gas turbine engines: A discrete robust observer design. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2009, 39, 234–239. [Google Scholar]
- Forrai, A. System Identification and Fault Diagnosis of an Electromagnetic Actuator. IEEE Trans. Control Syst. Technol. 2017, 25, 1028–1035. [Google Scholar] [CrossRef]
- Gao, Z. Discrete-time proportional and integral observer and observer-based controller for systems with both unknown input and output disturbances. Opt. Control Appl. Methods 2008, 29, 171–189. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Cocquempot, V.; Zhang, H. A framework of robust fault estimation observer design for continuous-time/discrete-time systems. Opt. Control Appl. Methods 2013, 34, 442–457. [Google Scholar] [CrossRef]
- Gao, Z.; Ho, D. Proportional multiple-integral observer design for descriptor systems with measurement output disturbances. IEE Proc. Control Theory Appl. 2004, 151, 279–288. [Google Scholar] [CrossRef]
- Koenig, D. Unknown input proportional multiple-integral observer design for linear descriptor systems: Application to state and fault estimation. IEEE Trans. Autom. Control 2005, 50, 212–217. [Google Scholar] [CrossRef]
- Gao, Z.; Ding, S.; Ma, Y. Robust fault estimation approach and its application in vehicle lateral dynamic systems. Opt. Control Appl. Methods 2007, 28, 143–156. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, H. Descriptor observer approaches for multivariable systems with measurement noises and application in fault detection and diagnosis. Syst. Control Lett. 2006, 55, 304–313. [Google Scholar] [CrossRef]
- Gao, Z.; Shi, X.; Ding, S. Fuzzy state/disturbance observer design for T–S fuzzy systems with application to sensor fault estimation. IEEE Trans. Syst. Man Cybern. 2008, 38, 875–880. [Google Scholar]
- Zhang, Q.; Besancon, G. An adaptive observer for sensor fault estimation in a class of uniformly observable nonlinear systems. Int. J. Model. Identif. Control 2008, 4, 37–43. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Cocquempot, V. Adaptive observer-based fast fault estimation. Int. J. Control Autom. Syst. 2008, 6, 320–326. [Google Scholar]
- Gholizadeh, M.; Salmasi, F. Estimation of state of charge, unknown nonlinearities, and state of health of a lithium-ion battery based on a comprehensive unobservable model. IEEE Trans. Ind. Electron. 2014, 61, 1335–1344. [Google Scholar] [CrossRef]
- Cruz-Zavala, E.; Moreno, J.A.; Fridman, L. Uniform second-order sliding mode observer for mechanical systems. In Proceedings of the 2011 11th International Workshop on Variable Structure Systems (VSS), Mexico City, Mexico, 26–28 June 2010. [Google Scholar]
- Van, M.; Kang, H.-J.; Suh, Y.-S. A novel neural second-order sliding mode observer for robust fault diagnosis in robot manipulators. Int. J. Precis. Eng. Manuf. 2013, 14, 397–406. [Google Scholar] [CrossRef]
- Alwi, H.; Edwards, C. Robust fault reconstruction for linear parameter varying systems using sliding mode observers. Int. J. Robust Nonlinear Control 2014, 24, 1947–1968. [Google Scholar] [CrossRef]
- Han, X.; Emilia, F.; Sarah, S. Sampled-data sliding mode observer for robust fault reconstruction: A time-delay approach. Frankl. Inst. 2014, 351, 2125–2142. [Google Scholar] [CrossRef]
- Fridman, L.; Levant, A.; Davila, J. Observation of linear systems with unknown inputs via high-order sliding-modes. Int. J. Syst. Sci. 2007, 38, 773–791. [Google Scholar] [CrossRef]
- Fraguela, L.; Fridman, L.; Vladimir, V. Alexandrov. Position stabilization of a Stewart platform: High-order sliding mode observers based approach. J. Frankl. Inst. 2012, 349, 441–455. [Google Scholar] [CrossRef]
- Van, M.; Kang, H.-J.; Suh, Y.-S.; Shin, K.-S. Output feedback tracking control of uncertain robot manipulators via higher-order sliding-mode observer and fuzzy compensator. J. Mech. Sci. Technol. 2013, 27, 2487–2496. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwaeds, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Birkhauser: New York, NY, USA, 2014; Volume 10. [Google Scholar]
- Shtessel, Y.B.; Baev, S.; Edwaeds, C.; Spurgeon, S. HOSM observer for a class of non-minimum phase causal nonlinear MIMO systems. IEEE Trans. Autom. Control 2010, 55, 543–548. [Google Scholar] [CrossRef]
- Ferreira, A.; Bejarano, F.J.; Fridman, L.M. Robust control with exact uncertainties compensation: With or without chattering? IEEE Trans. Control Syst. Technol. 2011, 19, 969–975. [Google Scholar] [CrossRef]
- Davila, J.; Fridman, L.; Pisano, A.; Usai, E. Finite-time state observation for nonlinear systems with application to compressor surge detection: A high order sliding-mode approach. In Proceedings of the 2008 International Workshop on Variable Structure Systems, VSS’08, Antalya, Turkey, 8–10 June 2008. [Google Scholar]
- Davila, J.; Ríos, H.; Fridman, L. State Observation for Nonlinear Switched Systems Using Nonhomogeneous High-Order Sliding Mode Observers. Asian J. Control 2012, 14, 911–923. [Google Scholar] [CrossRef]
- Fridman, L.; Shtessel, Y.; Edwards, C.; Yan, X.-G. Higher-order sliding-mode observer for state estimation and input reconstruction in nonlinear systems. Int. J. Robust Nonlinear Control 2008, 18, 399–412. [Google Scholar] [CrossRef]
- Fridman, L.; Davila, J.; Levant, A. High-order sliding-mode observation for linear systems with unknown inputs. Nonlinear Anal. Hybrid Syst. 2011, 5, 189–205. [Google Scholar] [CrossRef]
- Ferrara, A.; Rubagotti, M. A sub-optimal second order sliding mode controller for systems with saturating actuators. IEEE Trans. Autom. Control 2009, 54, 1082–1087. [Google Scholar] [CrossRef]
- Van, M.; Kang, H.-J.; Shin, K.-S. Backstepping quasi-continuous high-order sliding mode control for a Takagi–Sugeno fuzzy system with an application for a two-link robot control. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 1488–1500. [Google Scholar] [CrossRef]
- Bartolini, G.; Pisano, A.; Punta, E.; Usai, E. A survey of applications of second-order sliding mode control to mechanical systems. Int. J. Control 2003, 76, 875–892. [Google Scholar] [CrossRef]
- Van, M.; Kang, H.-J.; Suh, Y.-S. A novel fuzzy second-order sliding mode observer-controller for a TS fuzzy system with an application for robot control. Int. J. Precis. Eng. Manuf. 2013, 14, 1703–1711. [Google Scholar] [CrossRef]
- Capisani, L.M.; Ferrara, A.; de Loza, A.F.; Fridman, L.M. Manipulator fault diagnosis via higher order sliding-mode observers. IEEE Trans. Ind. Electron. 2012, 59, 3979–3986. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B. Simulating gear and bearing interactions in the presence of faults: Part I. The combined gear bearing dynamic model and the simulation of localised bearing faults. Mech. Syst. Signal Process. 2008, 22, 1924–1951. [Google Scholar] [CrossRef]
- Harris, T.A.; Kotzalas, M.N. Essential Concepts of Bearing Technology; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Mishra, C.; Samantaray, A.K.; Chakraborty, G. Ball bearing defect models: A study of simulated and experimental fault signatures. J. Sound Vib. 2017, 400, 86–112. [Google Scholar] [CrossRef]
- Case Western Reserve University. Seeded Fault Test Data. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 22 March 2017).
- Simatrang, S. Fault Detection for Rolling Element Bearings Using Model-Based Technique. Master’s Thesis, Case Western Reserve University, Cleveland, OH, USA, 2015. [Google Scholar]
- Boudiaf, A.; Moussaoui, A.; Dahane, A.; Atoui, I. A comparative study of various methods of bearing faults diagnosis using the case Western Reserve University data. J. Fail. Anal. Prev. 2016, 16, 271–284. [Google Scholar] [CrossRef]
- Najeh, T.; Njima, C.B.; Garna, T.; Ragot, J. Input fault detection and estimation using PI observer based on the ARX-Laguerre model. Int. J. Adv. Manuf. Technol. 2017, 90, 1317–1336. [Google Scholar] [CrossRef]





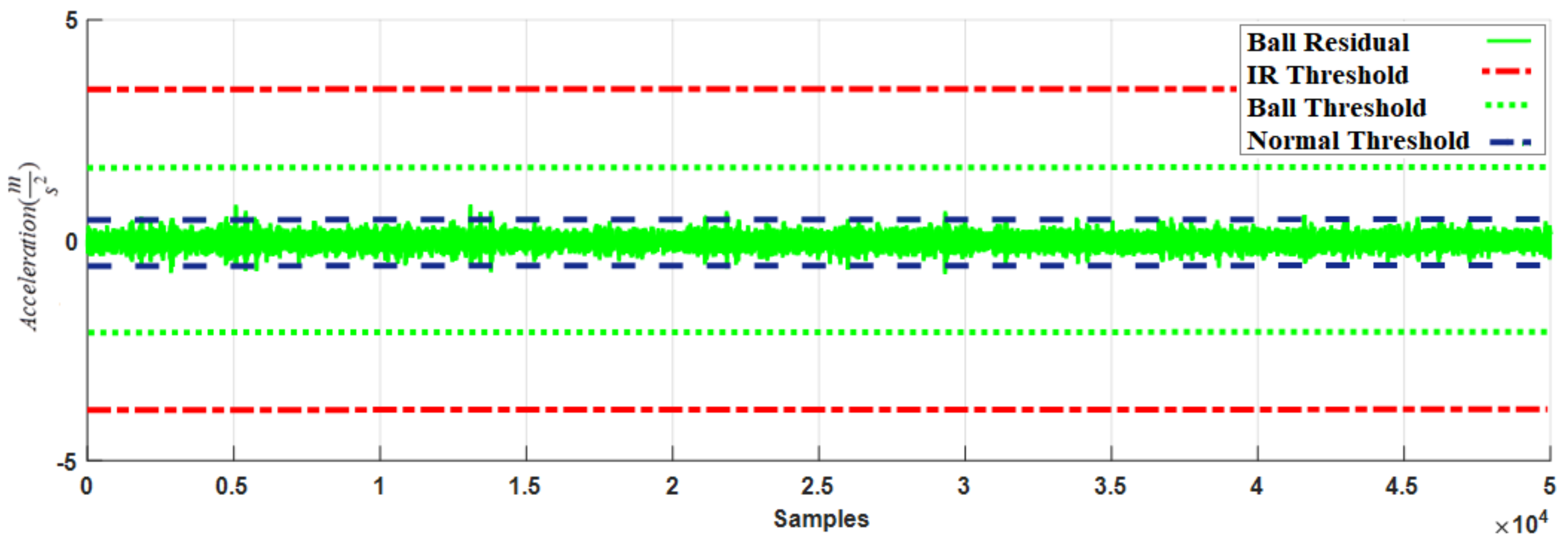
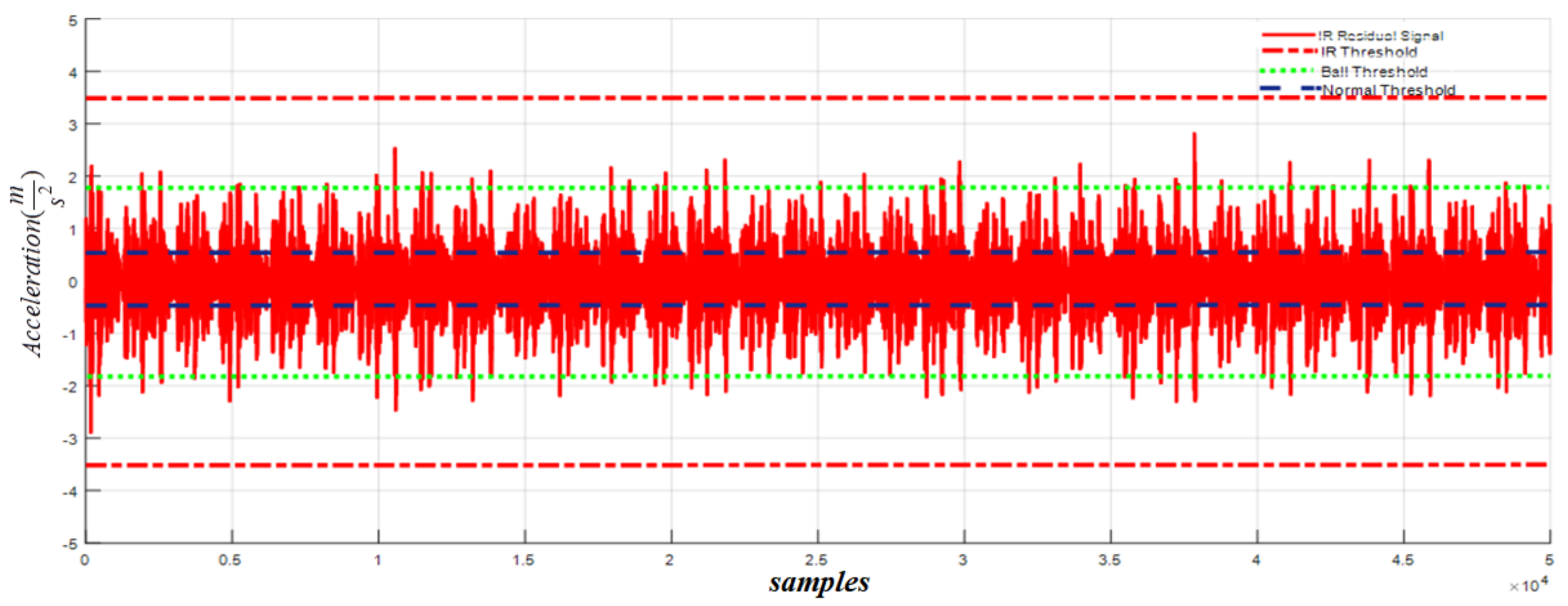
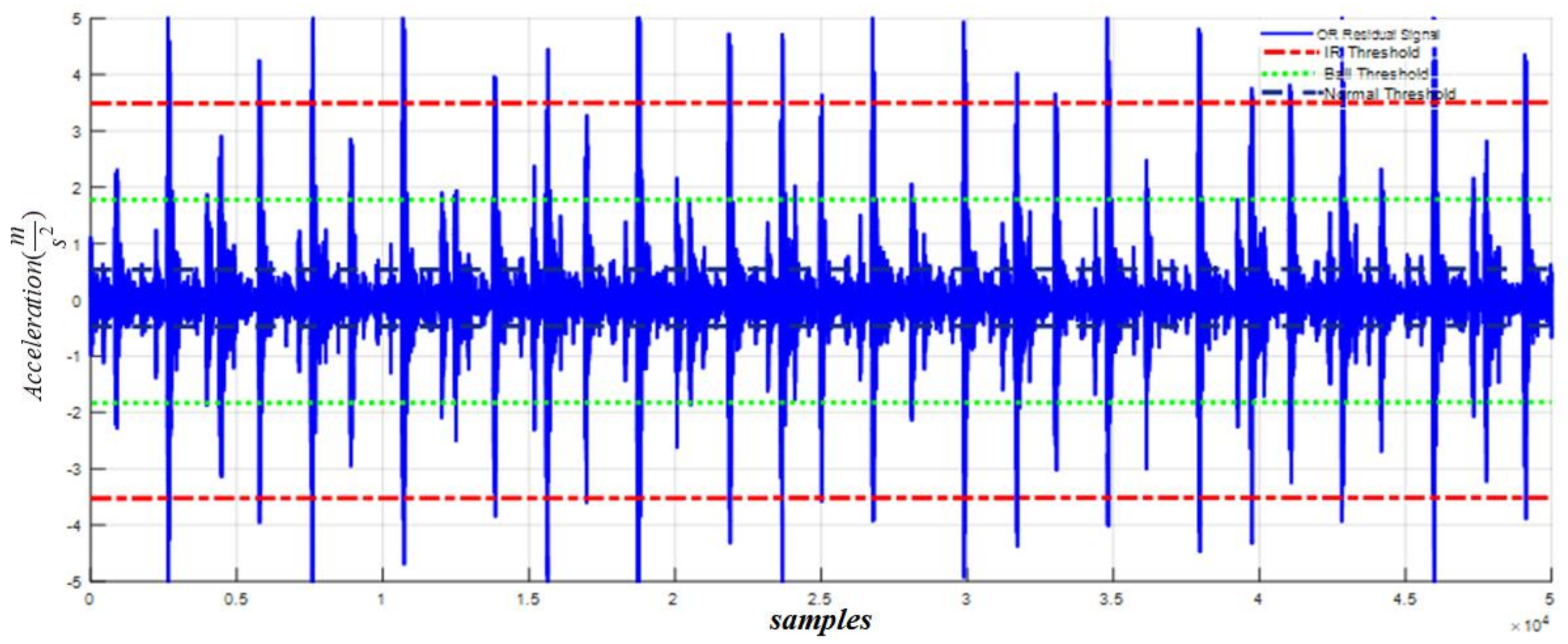
| Parameters | Value |
|---|---|
| Number of balls | 9 |
| Stiffness of ball | 5.96 × 107 () |
| Mass of outer (Kg) | 2.7 (Kg) |
| Stiffness of outer | 1.31 × 105 () |
| Mass of shaft (Kg) | 1.36 (Kg) |
| Stiffness of Shaft | 23.3 × 106 () |
| Damping | 654 () |
| Ball diameter | |
| Pitch diameter | |
| Defect size | |
| Defect depth |
| Dataset | Fault Types | Load (hp) | Fault Crack Sizes (in) |
|---|---|---|---|
| Dataset 1 | Normal state | 0 | 0.007, 0.014, and 0.021 |
| IR fault states | 0 | ||
| OR fault states | 0 | ||
| Ball fault states | 0 | ||
| Dataset 2 | Normal state | 1 | 0.007, 0.014, and 0.021 |
| IR fault states | 1 | ||
| OR fault states | 1 | ||
| Ball fault states | 1 | ||
| Dataset 3 | Normal state | 2 | 0.007, 0.014, and 0.021 |
| IR fault states | 2 | ||
| OR fault states | 2 | ||
| Ball fault states | 2 | ||
| Dataset 4 | Normal state | 3 | 0.007, 0.014, and 0.021 |
| IR fault states | 3 | ||
| OR fault states | 3 | ||
| Ball fault states | 3 |
| Algorithms | Proposed Method | ALPIO | ||||
|---|---|---|---|---|---|---|
| Crack Diameters (in) | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 |
| Normal State | 100% | 100% | 100% | 89% | 89% | 89% |
| IR Faults | 96% | 93% | 96% | 66% | 70% | 70% |
| OR Fault | 100% | 100% | 100% | 75% | 80% | 78% |
| Ball Fault | 100% | 100% | 100% | 81% | 81% | 84% |
| Average | 99% | 98.3% | 99% | 78% | 80% | 80.3% |
| Algorithms | Proposed Method | ALPIO | ||||
|---|---|---|---|---|---|---|
| Crack Diameters (in) | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 |
| Normal State | 100% | 100% | 100% | 89% | 89% | 89% |
| IR Faults | 100% | 100% | 100% | 66% | 70% | 70% |
| OR Fault | 95% | 93% | 95% | 75% | 80% | 78% |
| Ball Fault | 98% | 90% | 98% | 81% | 81% | 84% |
| Average | 98.3% | 95.7% | 98.3% | 78% | 80% | 80.3% |
| Algorithms | Proposed Method | ALPIO | ||||
|---|---|---|---|---|---|---|
| Crack Diameters (in) | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 |
| Normal State | 100% | 100% | 100% | 85% | 85% | 85% |
| IR Faults | 100% | 100% | 100% | 73% | 70% | 75% |
| OR Fault | 92% | 85% | 95% | 75% | 75% | 75% |
| Ball Fault | 93% | 90% | 90% | 78% | 81% | 81% |
| Average | 96.3% | 93.8% | 96.3% | 77.8% | 77.8% | 79% |
| Algorithms | Proposed Method | ALPIO | ||||
|---|---|---|---|---|---|---|
| Crack Diameters (in) | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 |
| Normal State | 100% | 100% | 100% | 90% | 90% | 90% |
| IR Faults | 94% | 100% | 100% | 75% | 75% | 75% |
| OR Fault | 90% | 90% | 90% | 75% | 75% | 78% |
| Ball Fault | 92% | 86% | 90% | 78% | 75% | 81% |
| Average | 94% | 94% | 95% | 79.5% | 78.75% | 81% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piltan, F.; Kim, J.-M. Bearing Fault Diagnosis by a Robust Higher-Order Super-Twisting Sliding Mode Observer. Sensors 2018, 18, 1128. https://doi.org/10.3390/s18041128
Piltan F, Kim J-M. Bearing Fault Diagnosis by a Robust Higher-Order Super-Twisting Sliding Mode Observer. Sensors. 2018; 18(4):1128. https://doi.org/10.3390/s18041128
Chicago/Turabian StylePiltan, Farzin, and Jong-Myon Kim. 2018. "Bearing Fault Diagnosis by a Robust Higher-Order Super-Twisting Sliding Mode Observer" Sensors 18, no. 4: 1128. https://doi.org/10.3390/s18041128
APA StylePiltan, F., & Kim, J.-M. (2018). Bearing Fault Diagnosis by a Robust Higher-Order Super-Twisting Sliding Mode Observer. Sensors, 18(4), 1128. https://doi.org/10.3390/s18041128






