Signal Quality Improvement Algorithms for MEMS Gyroscope-Based Human Motion Analysis Systems: A Systematic Review
Abstract
1. Introduction
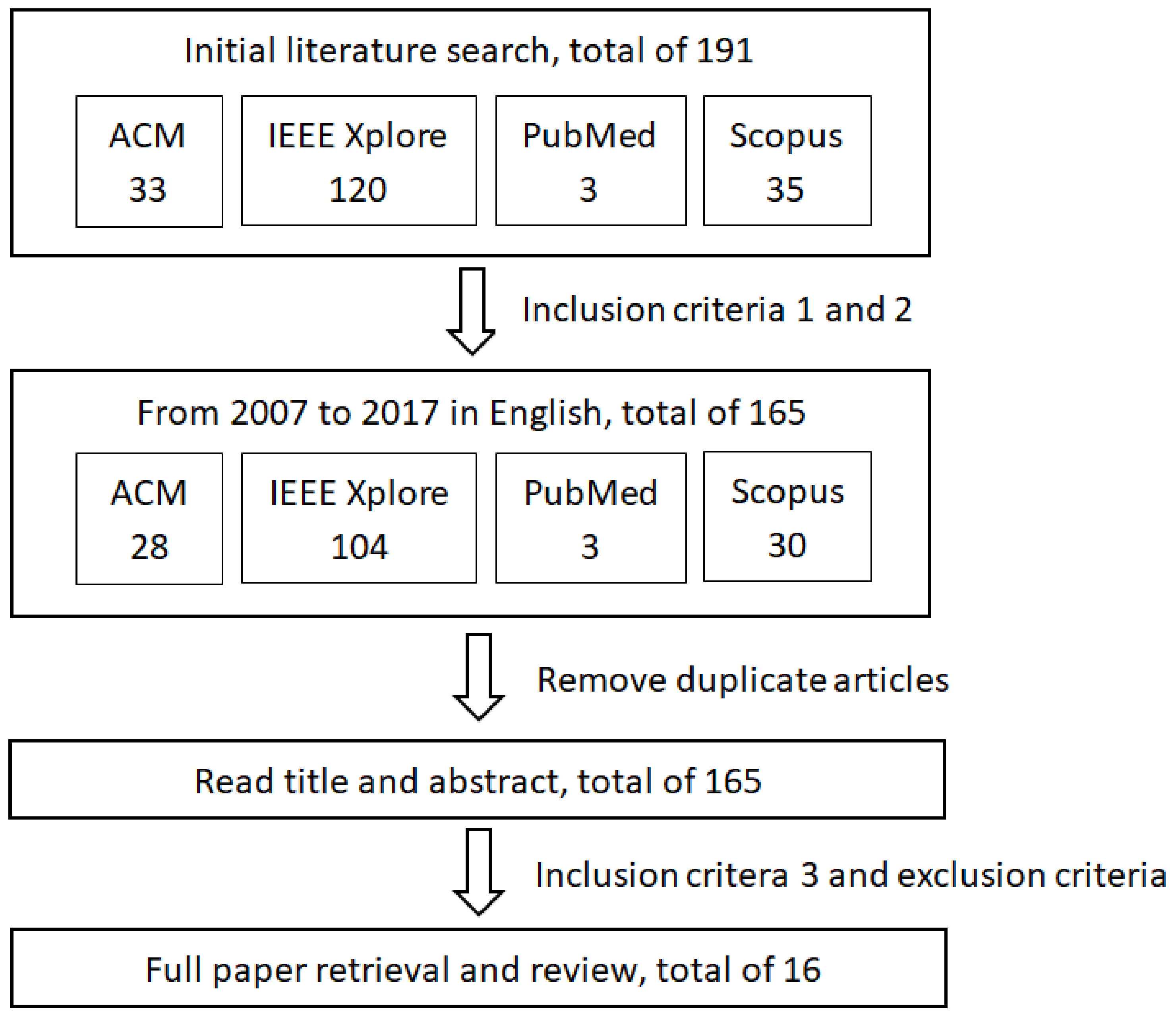
2. Methodology/Methods
2.1. Inclusion and Exclusion Criteria
- The article was published as a journal article or a conference paper in English.
- The article was published in the past 10 years (between 2007 and 2017).
- The primary subject of the study was signal error reduction methods/algorithms for MEMS gyroscope-based motion analysis systems that are intended for human motion analysis or have the potential to be used in this area.
2.2. Searching Strategy and Analysis
3. Results
3.1. Kalman Filter (KF)-Based Algorithms
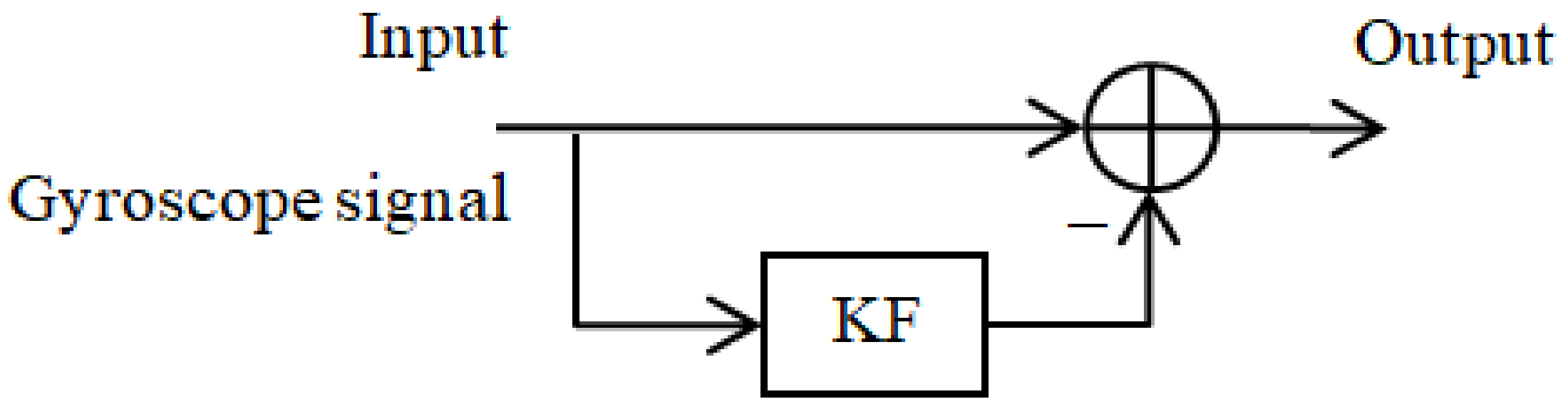
3.1.1. Kalman Filter
- First, initial estimates for and are obtained.
- Then, the two-step loop is entered, as shown below:
3.1.2. Discrete KF in an Optimal Approach
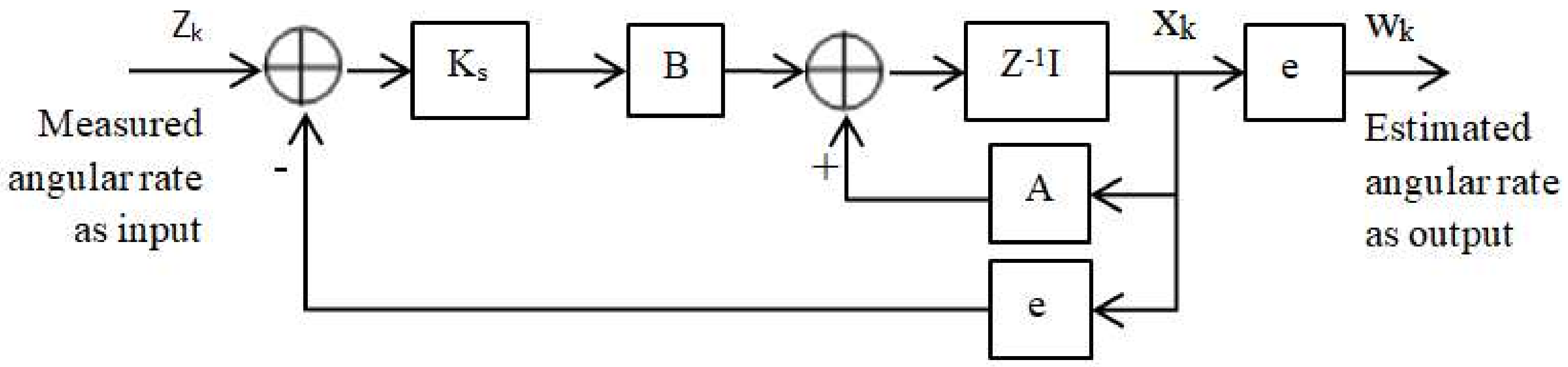
3.1.3. Simplified Basic KALMAN Filter
3.1.4. Kalman-Filter-Based Position Estimation Algorithm
3.2. Adaptive-Based Algorithms
3.2.1. Least Mean Square (LMS) Algorithm
3.2.2. Adaptive Sliding Mode Controller
3.2.3. Adaptive Bandpass Filter (ABPF)
3.2.4. Weighted-Frequency Fourier Linear Combiner (WFLC) Algorithm
3.2.5. Bandlimited Multiple Fourier Linear Combiner (BMFLC) Algorithm
3.2.6. Sensor Fusion
3.3. Simple Filter Algorithms
3.3.1. Low-Pass Filter
3.3.2. High-Pass Filter
3.3.3. Threshold with Delay Method (TWD)
3.4. Compensation-Based Algorithms
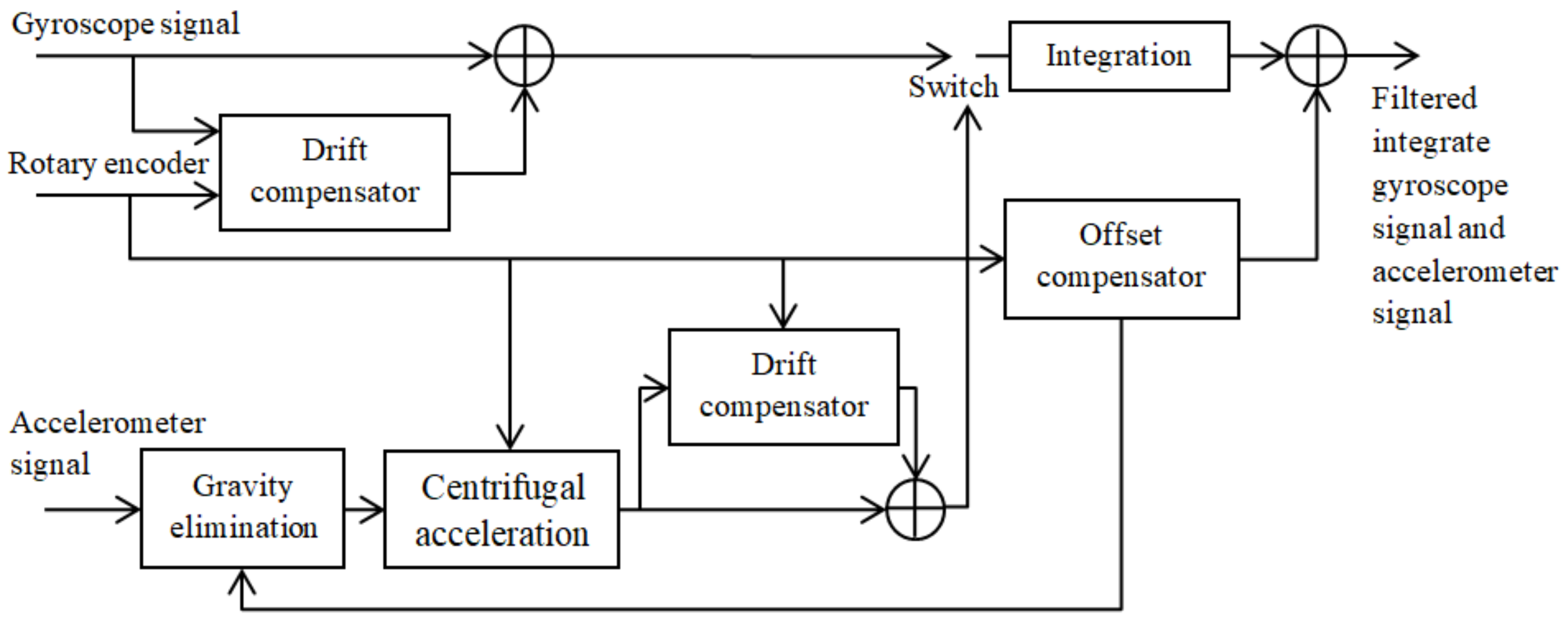
3.4.1. Drift and Offset Compensator (DOC)
3.4.2. Compensation Method with Temperature
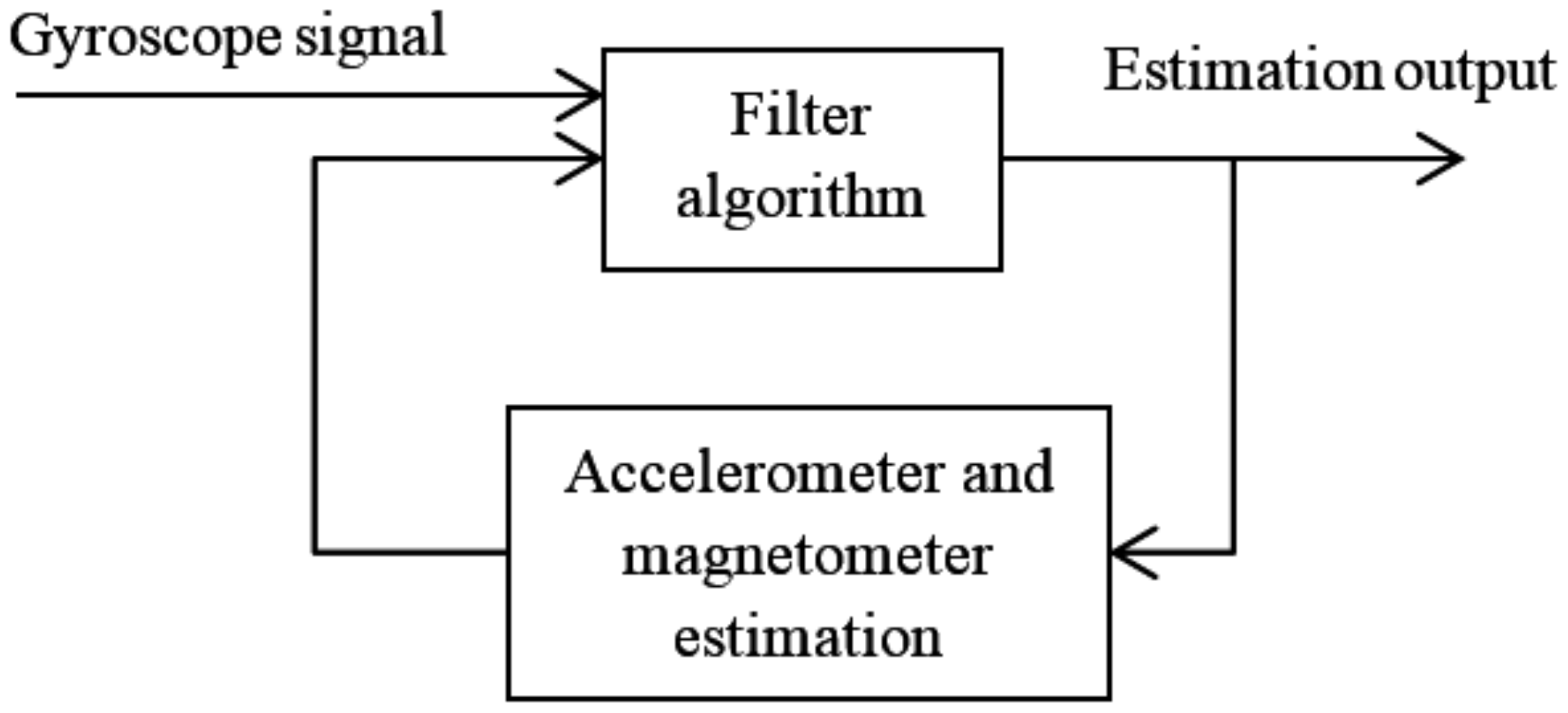
3.4.3. Compensation Method with Accelerometer and Magnetometer Data
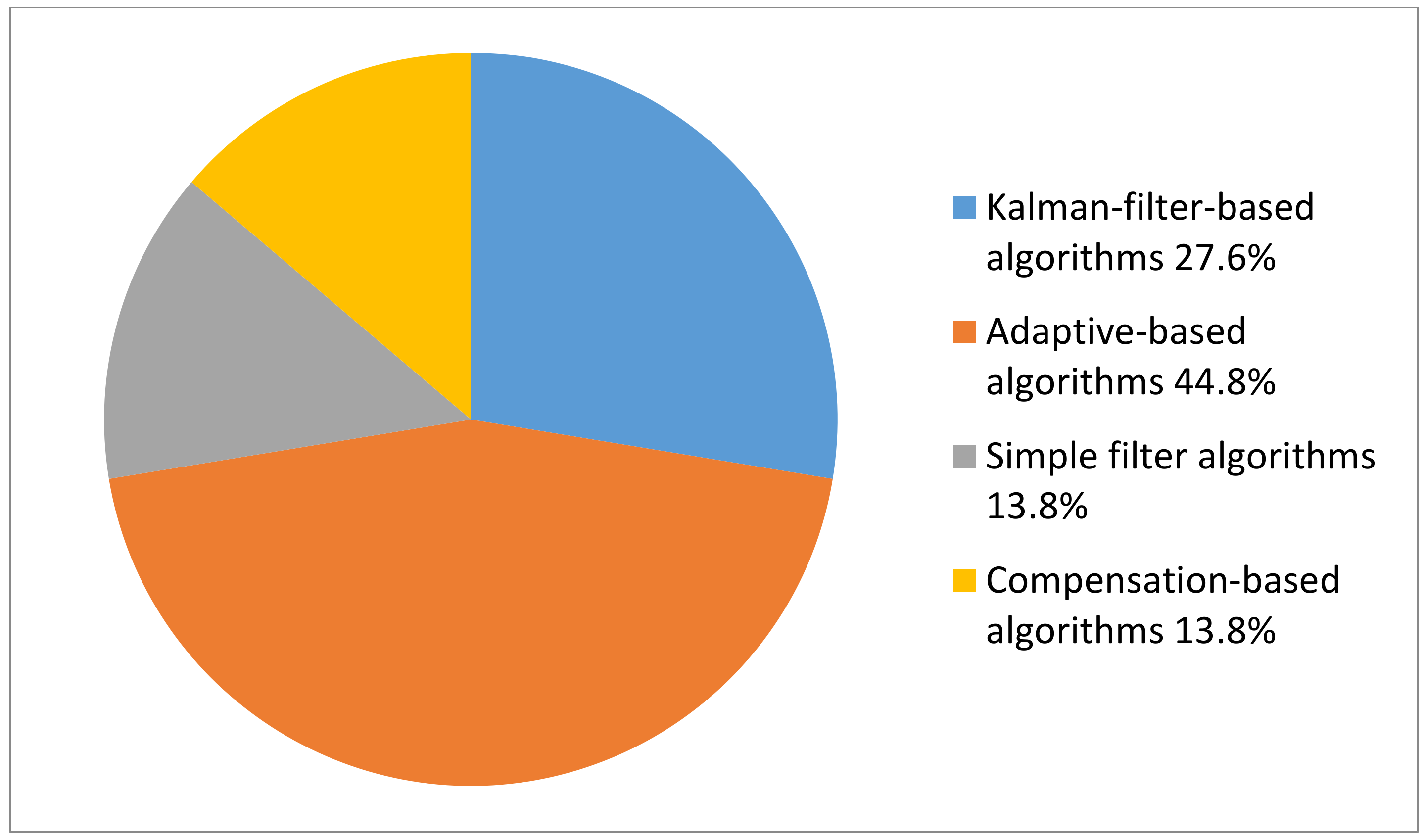
3.5. Category of the Algorithms
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- World Report on Ageing and Health, World Health Organisation. 2015. Available online: http://apps.who.int/iris/bitstream/10665/186463/1/9789240694811_eng.pdf?ua=1 (accessed on 31 March 2018).
- Aggarwal, J.K.; Cai, Q. Human motion analysis: A review. Comput. Vis. Image Underst. 1999, 73, 428–440. [Google Scholar] [CrossRef]
- Pantelopoulos, A.; Bourbakis, N.G. A survey on wearable sensor-based systems for health monitoring and prognosis. IEEE Trans. Syst. Man Cybern. 2010, 40, 1–12. [Google Scholar] [CrossRef]
- Patel, S.; Park, H.; Bonato, P.; Chan, L.; Rodgers, M. A review of wearable sensors and systems with application in rehabilitation. J. Neuro Eng. Rehabil. 2012, 9, 21. [Google Scholar] [CrossRef] [PubMed]
- Favre, J.; Aissaoui, R.; Jolles, B.M.; Siegrist, O.; de Guise, J.A.; Aminian, K. 3D joint rotation measurement using mems inertial sensors: Application to the knee joint. In Proceedings of the Ninth International Symposium on the 3-D Analysis of Human Movement, Valenciennes, France, 28–30 June 2006; pp. 28–30. [Google Scholar]
- Favre, J.; Jolles, B.M.; Aissaoui, R.; Aminian, K. Ambulatory measurement of 3D knee joint angle. J. Biomech. 2008, 41, 1029–1035. [Google Scholar] [CrossRef] [PubMed]
- Cooper, G.; Sheret, I.; McMillian, L.; Siliverdis, K.; Sha, N.; Hodgins, D.; Kenney, L.; Howard, D. Inertial sensor-based knee flexion/extension angle estimation. J. Biomech. 2009, 42, 2678–2685. [Google Scholar] [CrossRef] [PubMed]
- Saito, H.; Watanabe, T.; Arifin, A.; Dössel, O.; Schlegel, W.C. Ankle and knee joint angle measurements during gait with wearable sensor system for rehabilitation. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Munich, Germany, 7–12 September 2009; pp. 506–509. [Google Scholar]
- Takeda, R.; Tadano, S.; Todoh, M.; Morikawa, M.; Nakayasu, M.; Yoshinari, S. Gait analysis using gravitational acceleration measured by wearable sensors. J. Biomech. 2009, 42, 223–233. [Google Scholar] [CrossRef] [PubMed]
- Doheny, E.P.; Foran, T.G.; Greene, B.R. A single gyroscope method for spatial gait analysis. In Proceedings of the Engineering in Medicine and Biology Society (EMBS), Buenos Aires, Argentina, 31 August–4 September 2010; pp. 1300–1303. [Google Scholar]
- Liu, K.; Liu, T.; Shibata, K.; Inoue, Y. Ambulatory measurement and analysis of the lower limb 3D posture using wearable sensor system. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Changchun, China, 9–12 August 2009; pp. 3065–3069. [Google Scholar]
- Dejnabadi, H.; Jolles, B.M.; Casanova, E.; Fua, P.; Aminian, K. Estimation and visualization of sagittal kinematics of lower limbs orientation using body-fixed sensors. IEEE Trans. Biomed. Eng. 2006, 53, 1385–1393. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, J.H.; Mayagoitia, R.E.; Smith, I.C. A portable system for collecting anatomical joint angles during stair ascent: A comparison with an optical tracking device. Dyn. Med. 2009, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Zhou, S.; Li, W.J. MEMS accelerometer based nonspecific-user hand gesture recognition. IEEE Sens. J. 2012, 12, 1166–1173. [Google Scholar] [CrossRef]
- Linsie, A.A.; Mangaiyarkarasi, J. Hand gesture recognition using mems for specially challenged people. Int. J. VLSI Embed. Syst. 2013, 4, 238–241. [Google Scholar]
- Meenaakumari, M.; Muthulakshmi, M. Mems accelerometer based hand gesture recognition. Int. J. Adv. Res. Comput. Eng. Technol. 2013, 2, 1886–1892. [Google Scholar]
- Shetty, V.J.; Laxman, M.; Magdum, M.S.; Sidnal, S.B.; Paraddi, S. Head motion controlled wheel chair using mems. Int. Adv. Res. J. Sci. Eng. Technol. 2015, 2, 84–86. [Google Scholar]
- Anbarasu, V.; Ravi, T. Head mounted input device using mems sensors. Indian J. Comput. Sci. Eng. 2012, 3, 1886–1892. [Google Scholar]
- Gerdtman, C.; Bäcklund, Y.; Lindén, M. A gyro sensor based computer mouse with a USB interface: A technical aid for motor-disabled people. Technol. Disabil. 2012, 24, 117–127. [Google Scholar]
- Oarde, D.E.; Libatique, N.C.; Tangonan, G.L.; Sotto, D.M.; Pacaldo, A.T. Digital motion analysis system for rehabilitation using wearable sensors. In Proceedings of the 7th IEEE International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management (HNICEM), Palawan, Philippines, 12–16 November 2014; pp. 1–7. [Google Scholar]
- Gerdtman, C.; Folke, M.; Bexander, C.; Brodd, A.; Lindén, M. Portable sensor system for rehabilitation of wad patients. In Proceedings of the Wearable Micro and Nano Technologies for Personalized Health (pHealth), Oslo, Norway, 24–26 June 2009; pp. 65–68. [Google Scholar]
- MECH 466 Microelectromechanical Systems, University of Victoria, Department of Mechanical Engineering. 2015. Available online: http://www.engr.uvic.ca/~mech466/MECH466-Lecture-1.pdf (accessed on 16 February 2018).
- Maenaka, K. MEMS inertial sensors and their applications. In Proceedings of the 5th International Conference on Network Sensing Systems (INSS), Kanazawa, Japan, 17–19 June 2008; pp. 71–73. [Google Scholar]
- Li, J.; Mattila, T.; Vuorinen, V. MEMS Reliability. In Handbook of Silicon Based MEMS Materials and Technologies, 2nd ed.; Tilli, M., Motooka, T., VAiraksinen, M., Franssila, S., Paulasto-Krockel, M., Lindroos, V., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 751–752. ISBN 9780323299657. [Google Scholar]
- Du, J.; Gerdtman, C.; Lindén, M. Noise reduction for a MEMS-gyroscope-based head mouse. In Proceedings of the 12th International Conference on Wearable Micro and Nano Technologies for Personalized Health (pHealth2015), Västerås, Sweden, 2–4 June 2015; pp. 36–39. [Google Scholar]
- Du, J.; Gerdtman, C.; Lindén, M. Signal processing algorithms for temperature drift in a MEMS-gyro-based head mouse. In Proceedings of the 21st International Conference on Systems, Signals and Image Processing (IWSSIP2014), Dubrovnik, Croatia, 12–15 May 2014; pp. 123–126. [Google Scholar]
- Du, J.; Gerdtman, C.; Gharehbaghi, A.; Lindén, M. A signal processing algorithm for improving the performance of a gyroscopic head-borne computer mouse. J. Biomed. Signal Process. Control 2017, 35, 30–37. [Google Scholar] [CrossRef]
- Kempe, V. Inertial MEMS: Principle and Practice; Cambridge University Press: Cambridge, UK, 2011; ISBN 13 978-0521766586. [Google Scholar]
- ACM Digital Library. Available online: https://www.acm.org/publications/digital-library (accessed on 16 February 2018).
- IEEE Xplore Digital Library. Available online: http://ieeexplore.ieee.org.ep.bib.mdh.se/Xplore/home.jsp (accessed on 16 February 2018).
- PubMed US National Library of Medicine National Institutes of Health. Available online: https://www.ncbi.nlm.nih.gov/pubmed/ (accessed on 16 February 2018).
- Scopus. Available online: https://www.scopus.com (accessed on 16 February 2018).
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter, TR 95-041. 2006. Available online: https://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf (accessed on 16 February 2018).
- Lee, H.J.; Jung, S. Gyro sensor drift compensation by Kalman filter to control a mobile inverted pendulum robot system. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Gippsland, VIC, Australia, 10–13 February 2009; pp. 1–6. [Google Scholar]
- Gallego, A.; Rocon, E.; Roa, J.O.; Moreno, J.C.; Pons, J.L. Real-time estimation of pathological tremor parameters from gyroscope data. Sensors 2010, 10, 2129–2149. [Google Scholar] [CrossRef] [PubMed]
- Naik, N.S.; Rube, P.R. Physiological tremor estimation methods: An overview. Int. J. Innov. Sci. Eng. Technol. 2014, 1, 556–559. [Google Scholar]
- Xue, L.; Jiang, C.; Wang, L.; Liu, J.; Yuan, W. Noise reduction of MEMS gyroscope based on direct modeling for an angular rate signal. Micromachines 2015, 6, 266–280. [Google Scholar] [CrossRef]
- Neto, P.; Pires, J.N.; Moreira, A.P. 3-D position estimation from inertial sensing: Minimizing the error from the process of double integration of accelerations. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society (IECON 2013), Vienna, Austria, 10–13 November 2013; pp. 4026–4031. [Google Scholar]
- Fei, J.; Batur, C. Robust adaptive control for a MEMS vibratory gyroscope. Int. J. Adv. Manuf. Technol. 2009, 42, 293–300. [Google Scholar] [CrossRef]
- Popovic, L.Z.; Sekara, T.B.; Popovic, M.B. Adaptive band-pass filter for tremor extraction from inertial sensor data. Comput. Methods Programs Biomed. 2010, 99, 298–305. [Google Scholar] [CrossRef] [PubMed]
- Yean, S.; Lee, B.S.; Yeo, C.K.; Vun, C.H. Algorithm for 3D orientation estimation based on Kalman filter and gradient descent. In Proceedings of the 7th IEEE Annual Conference on Information Technology, Electronics and Mobile Communication (IEMCON), Vancouver, BC, Canada, 13–15 October 2016; pp. 1–6. [Google Scholar]
- Bergamini, E.; Ligorio, G.; Summa, A.; Vannozzi, G.; Cappozzo, A.; Sabatini, A.M. Estimating orientation using magnetic and inertial sensors and different sensor fusion approaches: Accuracy assessment in manual and locomotion tasks. Sensors 2014, 14, 18625–18649. [Google Scholar] [CrossRef] [PubMed]
- Pasciuto, I.; Ligorio, G.; Bergamini, E.; Vannozzi, G.; Sabatini, A.M.; Cappozzo, A. How angular velocity features and different gyroscope noise types interact and determine orientation estimation accuracy. Sensors 2015, 15, 23983–24001. [Google Scholar] [CrossRef] [PubMed]
- Krishna, S.M. Digital Implementation of RC Low Pass Filter, MathWorks, 2008. Available online: https://se.mathworks.com/matlabcentral/fileexchange/19407-digital-implementation-of-rc-low-pass-filter (accessed on 16 February 2018).
- Kubus, D.; Wahl, F.M. A sensor fusion approach to angle and angular rate estimation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September 2011; pp. 2481–2488. [Google Scholar]
- Jaiswal, R.; Nair, R.C.; Yarlagadda, N.K.; Senapati, A.A.K.; Mulage, P. Adaptive Gyroscope drift compensation based on Temporal Noise Modelling. In Proceedings of the International Conference on Microelectronics, Computing and Communications (MicroCom), Durgapur, India, 23–25 January 2016. [Google Scholar]
- Abbasi-Kesbi, R.; Nikfarjam, A. A mini wearable wireless sensor for rehabilitation applications. In Proceedings of the 3rd RSI International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 7–9 October 2015; pp. 618–622. [Google Scholar]
- Tedaldi, D.; Pretto, A.; Menegatti, E. A Robust and Easy to Implement Method for IMU Calibration without External Equipments. In Proceedings of the IEEE International Conference on Robotics & Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 3042–3049. [Google Scholar]


| Algorithm Group | Algorithms | Characteristics/Functions with References | Number of Papers | Supplements/Requirements | Applications | |||
|---|---|---|---|---|---|---|---|---|
| Limited Calculation Time | Real Time/on- or off-Line | Working Environment | Need for Combination | |||||
| Kalman-filter-based algorithm | Kalman filter (KF) | Noise reduction; signal prediction and estimation: human tremor estimation and modeling [35]; physiological tremor estimation [36]; drift compensation together with a compensation method [47] | 3 | - 1 | Real-time estimation of tremor parameters | MATLAB | Together with the WFLC algorithm to estimate the instantaneous tremor frequency; together with a compensation method to compensate for the drift | Tremor motion extraction from voluntary movement (hand motion/wrist rotation) estimation with MEMS gyroscope; Drift compensation for MEMS gyroscope in mobile devices for human motion analysis |
| Discrete KF in an optimal way | Optimal estimation of the bias drift and noise from MEMS gyroscopes signals [37] | 1 | Simplification of KF implementation | Real-time processing | Digital signal processor (DSP) | Without needing other sensor’s information | MEMS gyroscope (not human motion in the article, but with potential to be used in human motion analysis) | |
| Simplified basic Kalman filter | Noise reduction [25]; temperature drift estimation [26,27] | 3 | Within limited calculation time | Real time | MATLAB and DSPs | Can be used alone | Gyroscopic head-borne computer mouse | |
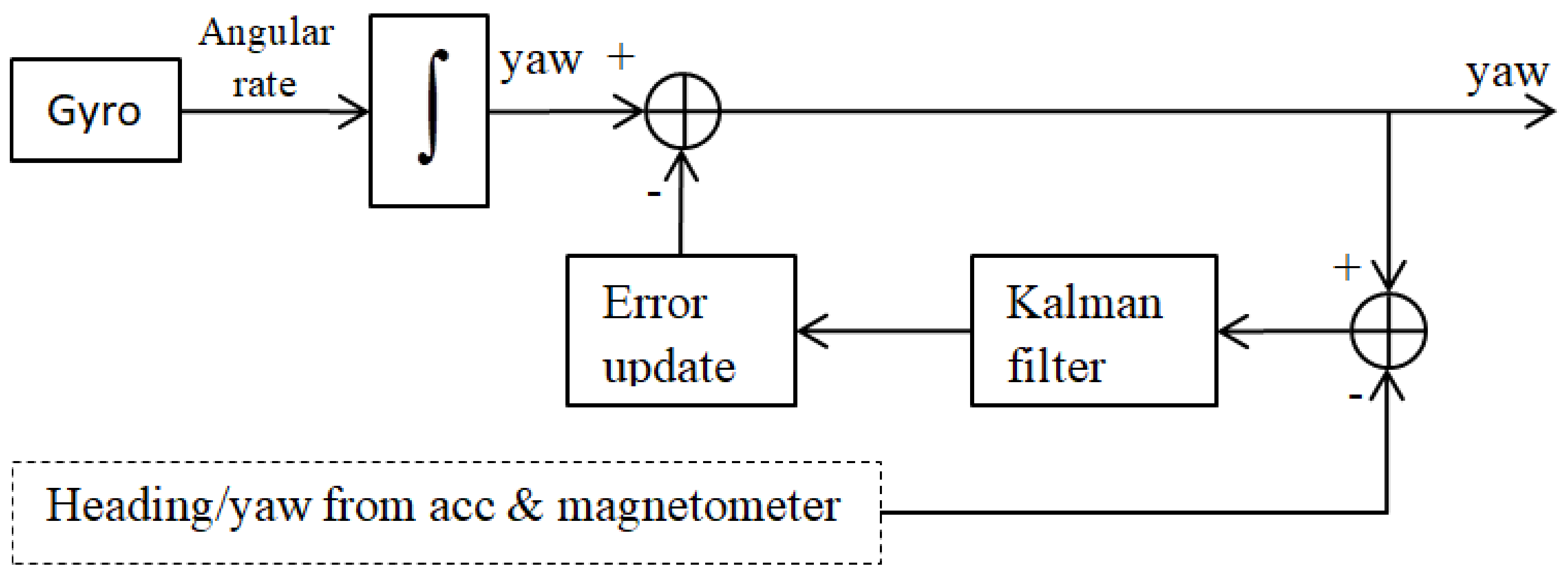
| KF based position estimation algorithm | Yaw correction during position estimation [38] | 1 | - 1 | Real time | MATLAB | Need additional accelerometer and magnetometer/compass data | Hand motion and hand position estimation | |
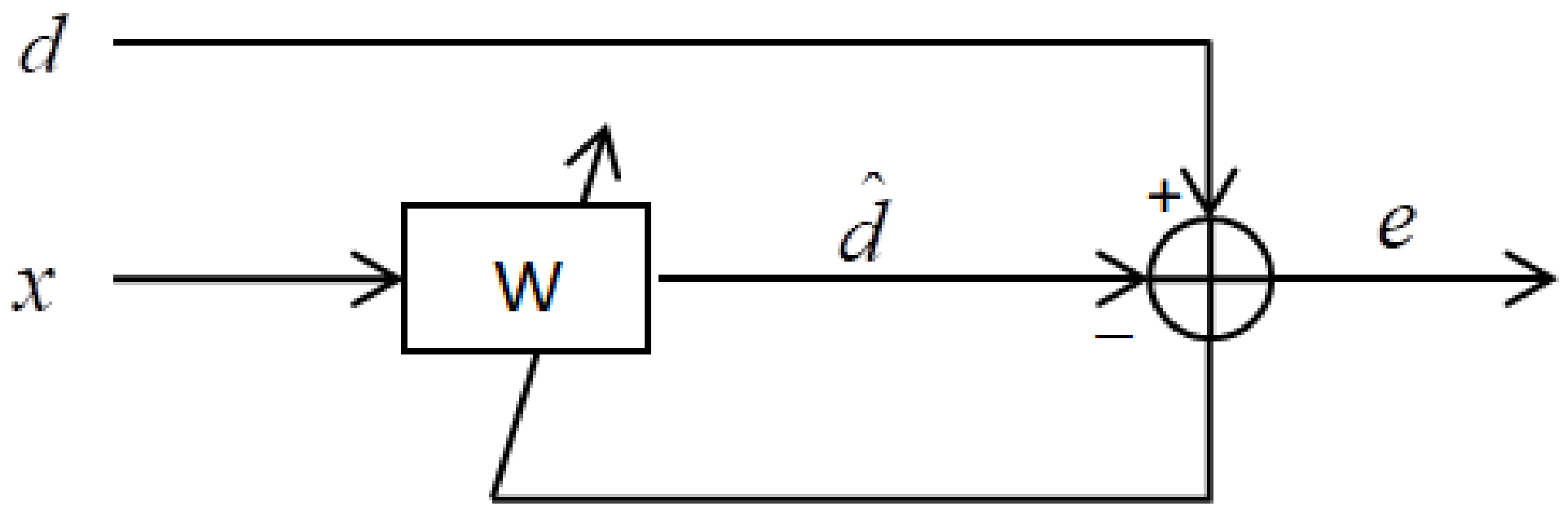
| Adaptive-based algorithm | Least Mean Square (LMS) | Noise reduction [25]; tremor modeling [35] | 2 | Within limited calculation | Real time | MATLAB and DSPs | Can be used alone | Gyroscopic head-borne computer mouse |
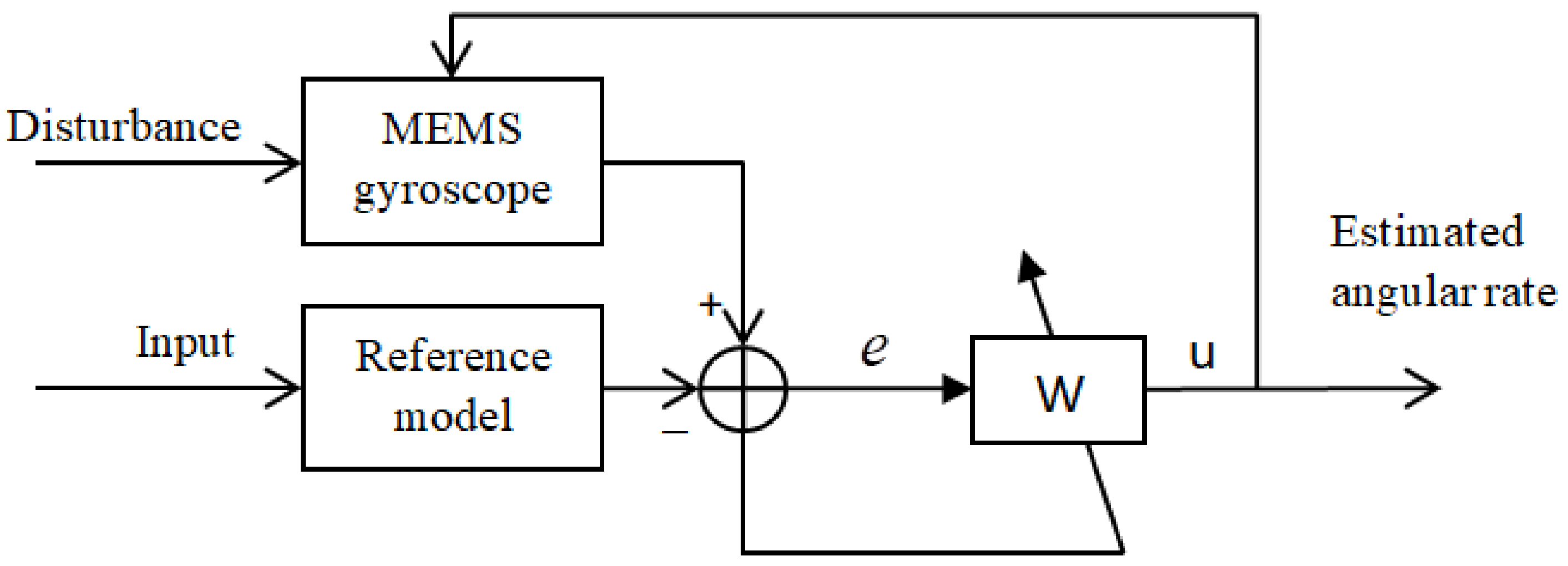
| Adaptive slide mode controller | Fabrication imperfection compensation, external disturbances reduction [39] | 1 | - 1 | Real time | MATLAB/Simulink | Need a reference model (ideal oscillator) | Oscillatory motion by MEMS z-axis vibrating gyroscope system (with potential to be used in human motion analysis) | |
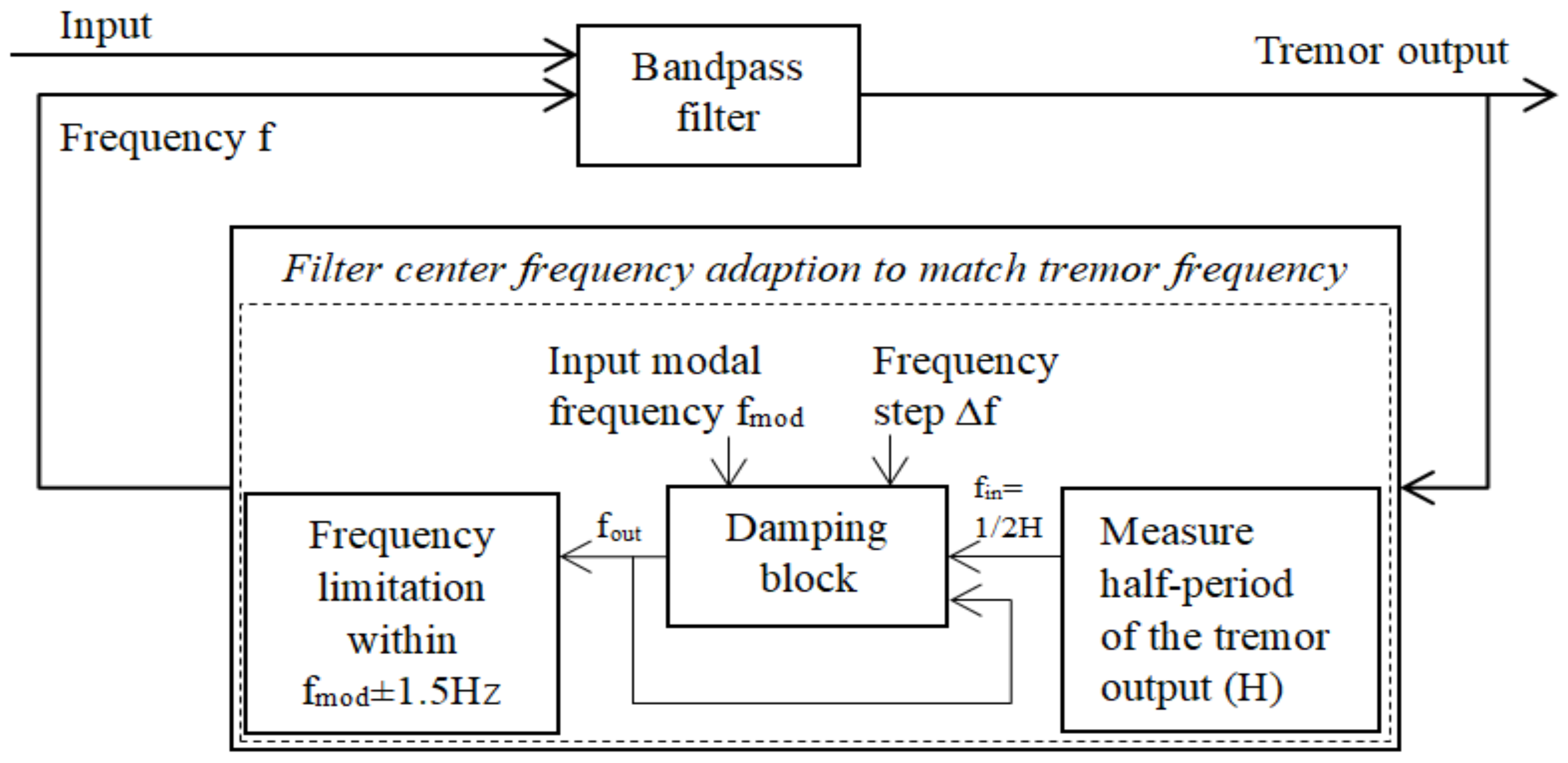
| Adaptive bandpass filter | Typical noise/pathological tremor reduction [40] | 1 | Simple and easy to implement | Real time | MATLAB Simulink | Both gyroscope and accelerometer | Volitional hand movement | |
| WFLC | Noise reduction [25,27]; human tremor frequency tracking [35]; physiological tremor estimation [36] | 4 | Within limited calculation time | Real time | MATLAB and DSPs | Can be used alone | Gyroscopic head-borne computer mouse | |
| BMFLC | Human tremor frequency tracking [35]; physiological tremor estimation [36] | 2 | - 1 | Real time | MATLAB | Can be used alone | Tremor motion extraction from voluntary movement (hand motion/wrist rotation) estimation with MEMS gyroscope | |
| Sensor fusion | Integration drift error reduction and error propagation reduction during orientation/position estimation [42,43]; drift compensation [41];, etc. | 3 | Developed with shorter computation time (than rotation matrix) | Real time [42] | MATLAB; Mobile phone API, IoT | Need to exploit accelerometer and magnetometer aiding sensors, and need reference data | 3D human movement analysis; rehabilitation application, monitoring dynamic changes of movement for clinical prognosis | |
| Simple filter algorithm | Low-pass filter | Noise reduction [25] | 1 | Within limited calculation time | Real time | MATLAB and DSPs | Can be used alone | Gyroscopic head-borne computer mouse |
| High-pass filter | Drift/offset reduction [26]; bias reduction [45] | 2 | Within limited calculation time | Real time | MATLAB and DSPs | Can be used alone | Gyroscopic head-borne computer mouse | |
| TWD | Noise reduction around zero within the threshold [27] | 1 | Within limited calculation time | Real time | MATLAB and DSPs | Followed with other algorithms to obtain better results | Gyroscopic head-borne computer mouse | |
| Compensation-based algorithm | Drift and offset compensator (DOC) | Drift/offset compensation [45] | 1 | Low computational demands | Real time | DSPs and FPGAs | Based on encoder measurement. Combination of encoder and even MEMS accelerometer | Demanding robotic and mechatronic systems; parallel or serial kinematic machines such as industrial manipulators (with the potential to be used in human motion analysis) |
| Compensation method with temperature | Noise reduction and drift compensation (including bias due to temperature) [46] | 1 | - 1 | Real time | Android | Combination of Median filter, Kalman filter | Drift compensation for MEMS gyroscope in mobile devices that are in motion, static, or with temperature variance. This method optimally filters drift to be usable in MARG, IMU, indoor navigation and human activity classification | |
| Compensation method with accelerometer and magnetometer | Noise reduction and angle estimation [47] | 1 | Required less computation | Real time | Microprocessor | Need to combine with MEMS accelerometer and magnetometer data | Capture real time body movement with a mini wearable wireless sensor system for rehabilitation | |
| IMU calibration method | Absolute error reduction; calibration parameter estimation [48] | 1 | Robust and easy to implement | Real time | MATLAB | An IMU consists of a tri-axial MEMS gyroscope, an accelerometer and often a magnetometer. Does not require other external equipment | Low-cost IMU sensors equipped on smartphones and similar devices for motion analysis of robotics. It is possible to use it for human motion analysis | |
| Main/Common Functions | Advantages | Disadvantages | Number of Studies | |
|---|---|---|---|---|
| Kalman-filter-based algorithm |
|
|
| 8 |
| Adaptive-based algorithm |
|
|
| 13 |
| Simple filter algorithm |
|
|
| 4 |
| Compensation-based algorithm |
|
|
| 4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J.; Gerdtman, C.; Lindén, M. Signal Quality Improvement Algorithms for MEMS Gyroscope-Based Human Motion Analysis Systems: A Systematic Review. Sensors 2018, 18, 1123. https://doi.org/10.3390/s18041123
Du J, Gerdtman C, Lindén M. Signal Quality Improvement Algorithms for MEMS Gyroscope-Based Human Motion Analysis Systems: A Systematic Review. Sensors. 2018; 18(4):1123. https://doi.org/10.3390/s18041123
Chicago/Turabian StyleDu, Jiaying, Christer Gerdtman, and Maria Lindén. 2018. "Signal Quality Improvement Algorithms for MEMS Gyroscope-Based Human Motion Analysis Systems: A Systematic Review" Sensors 18, no. 4: 1123. https://doi.org/10.3390/s18041123
APA StyleDu, J., Gerdtman, C., & Lindén, M. (2018). Signal Quality Improvement Algorithms for MEMS Gyroscope-Based Human Motion Analysis Systems: A Systematic Review. Sensors, 18(4), 1123. https://doi.org/10.3390/s18041123






