An Azimuth Antenna Pattern Estimation Method Based on Doppler Spectrum in SAR Ocean Images
Abstract
1. Introduction
2. Azimuth Antenna Pattern Estimation Method Based on Doppler Spectrum
2.1. The Principle of the Proposed Method
2.1.1. Analysis of Doppler Spectrum Composition
2.1.2. Methods and Solutions to Estimate the Antenna Pattern from the Doppler Spectrum
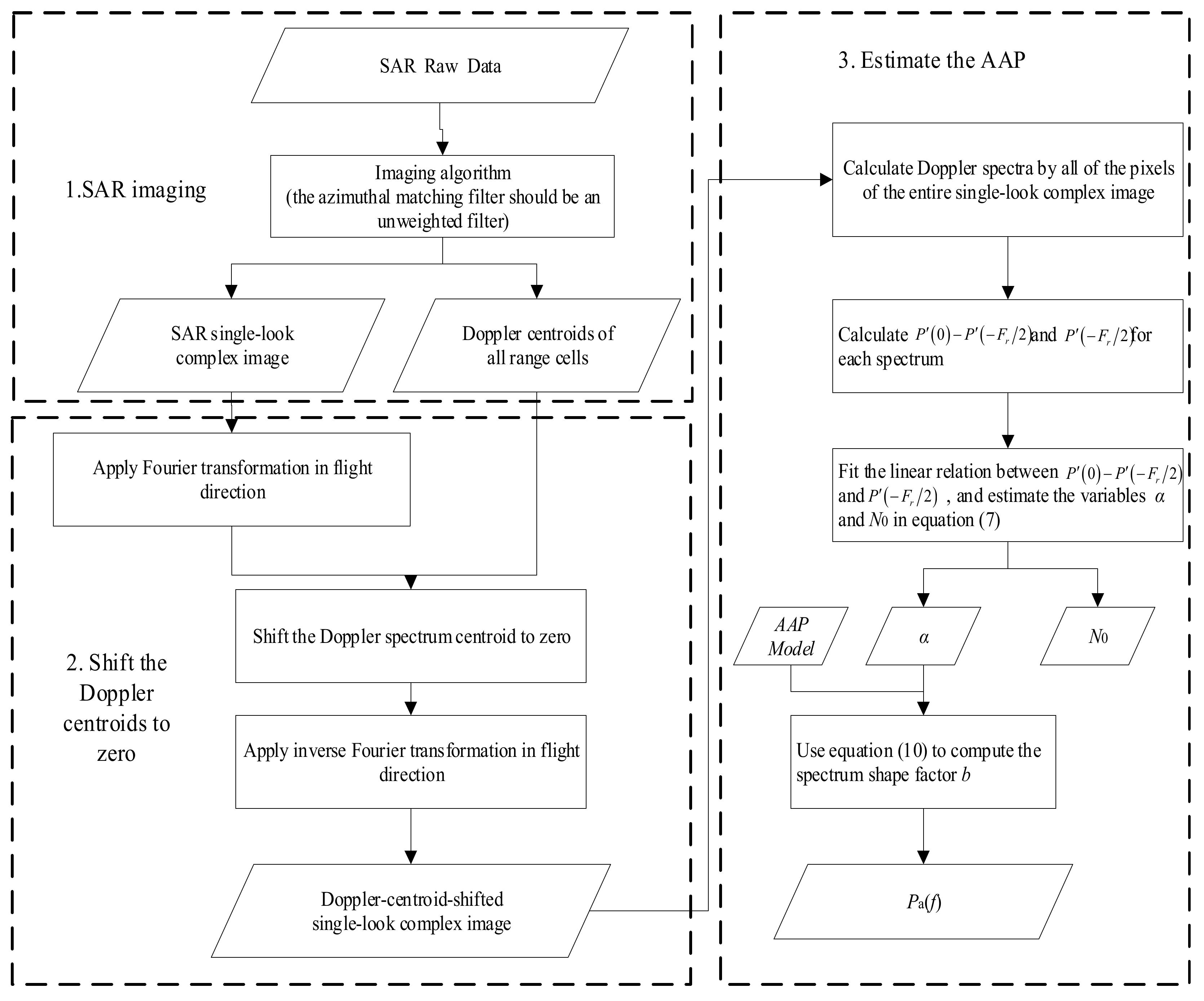
2.2. Method Flow Chart and Summary
3. Simulation Analysis of the Applicability of the Proposed Method
3.1. Parameters Settings of the Simulation
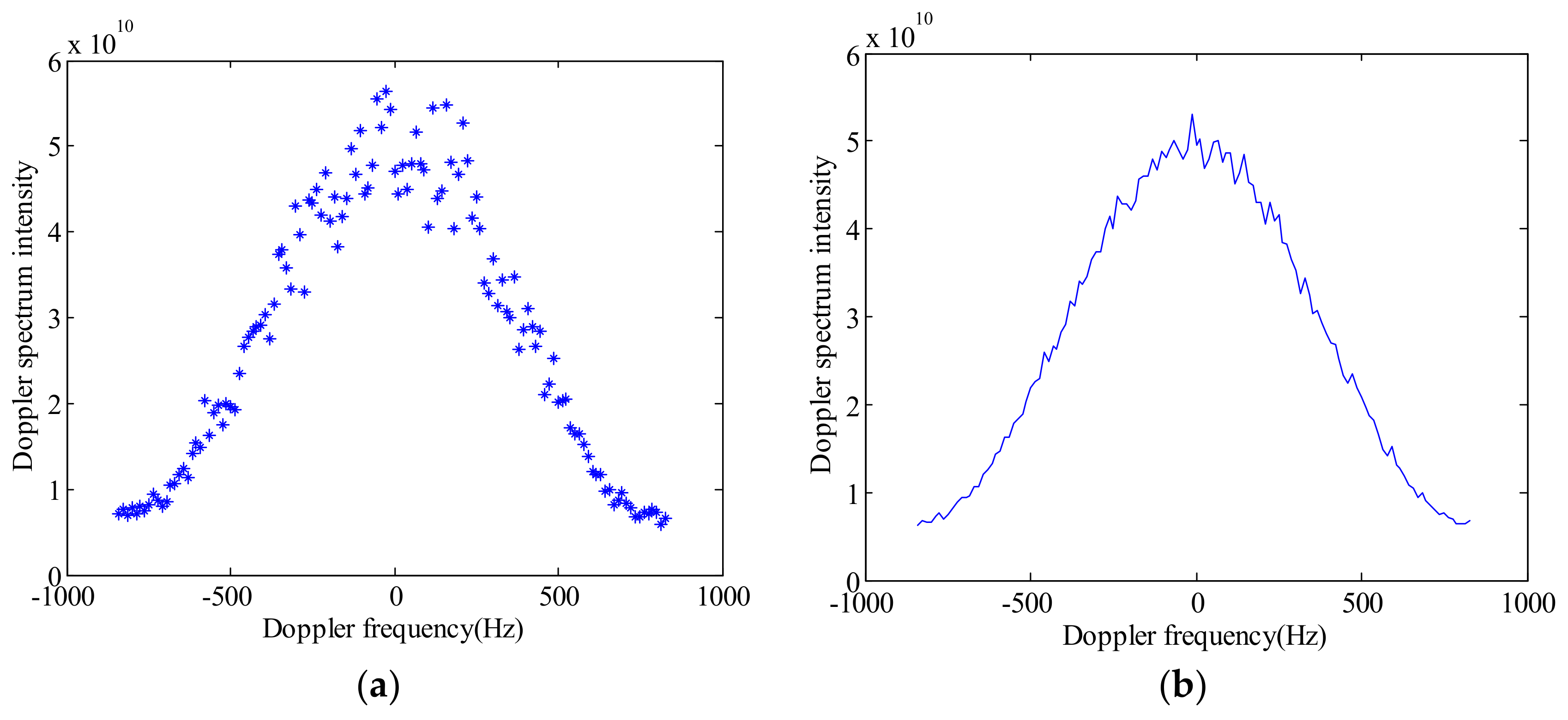
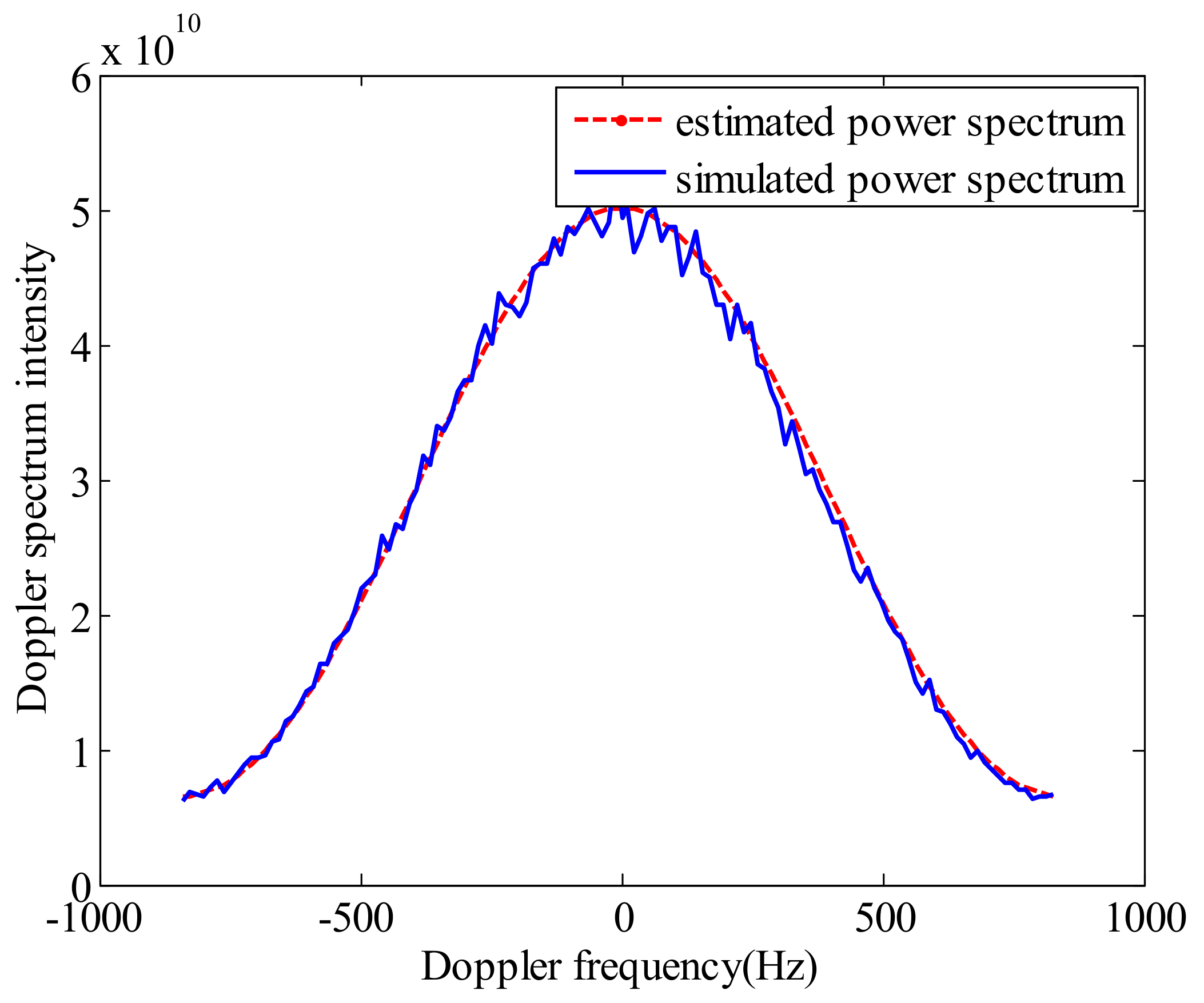
3.2. Simulation Results
3.3. Performance Analysis
3.4. Applicability Analysis of the Proposed Method
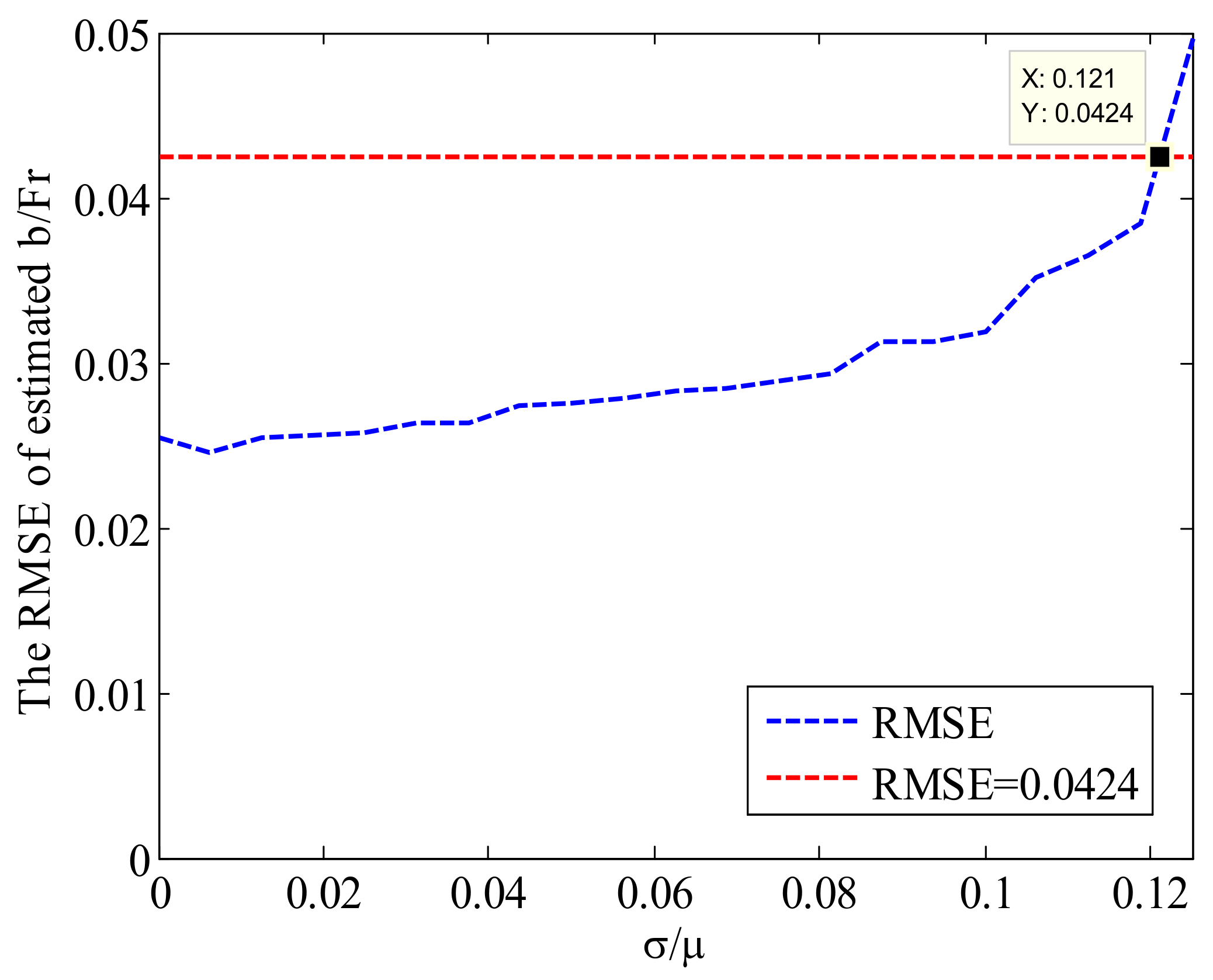
3.4.1. The Influence of SAR Image Uniformity on Estimation results
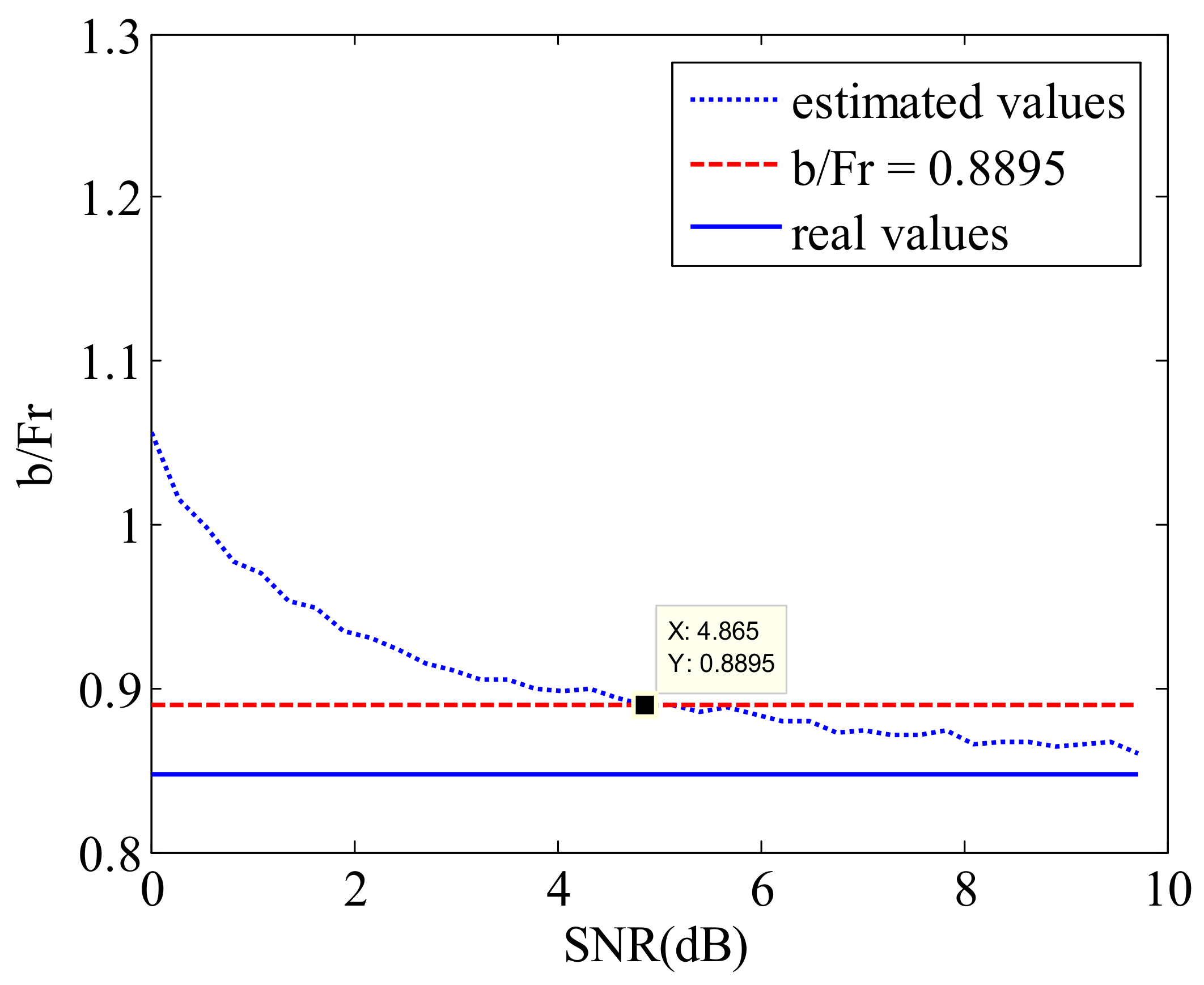
3.4.2. The Influence of the SNR of SAR Image on Estimation Results
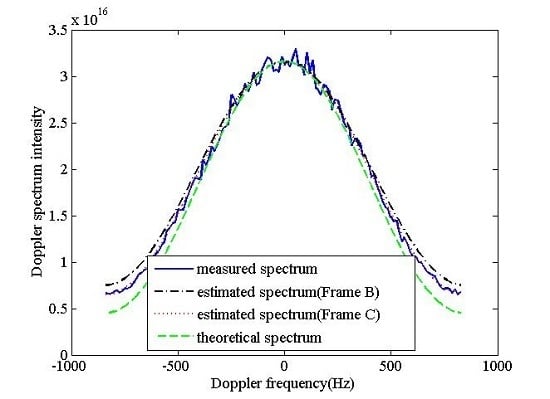
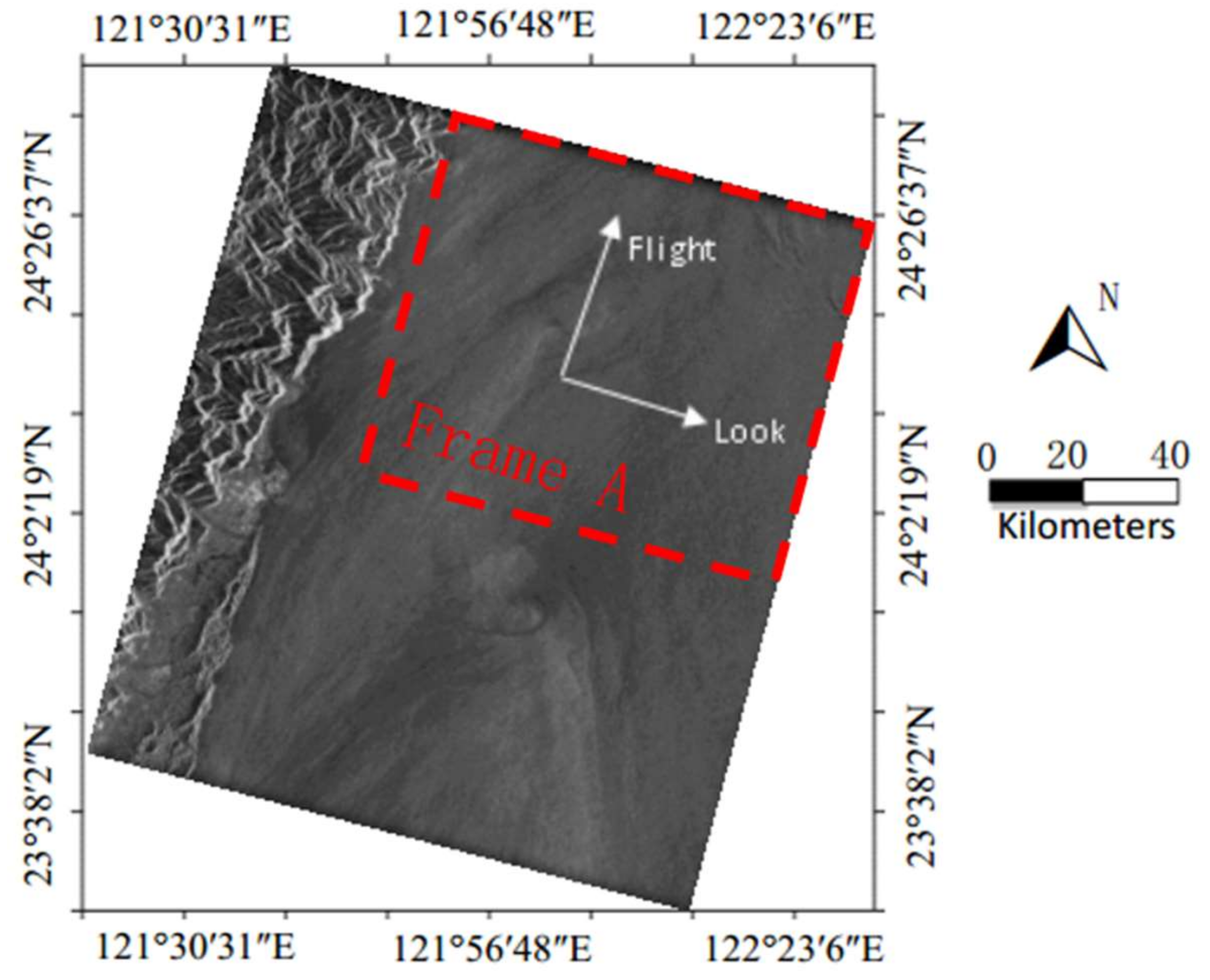
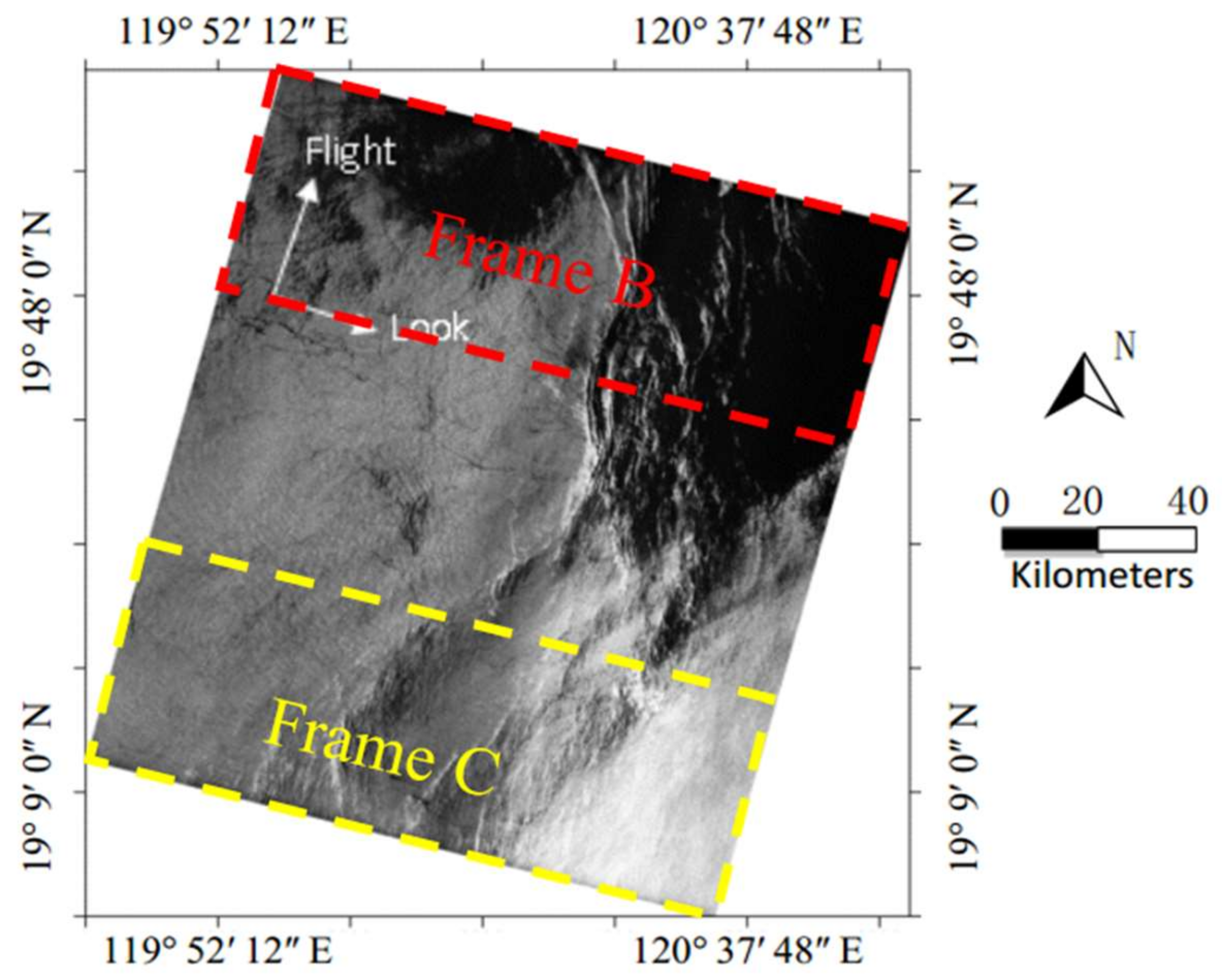
4. Validation of the Proposed Method Based on Spaceborne SAR Data
4.1. The SAR Ocean Images Preprocessing for Experimental Validation
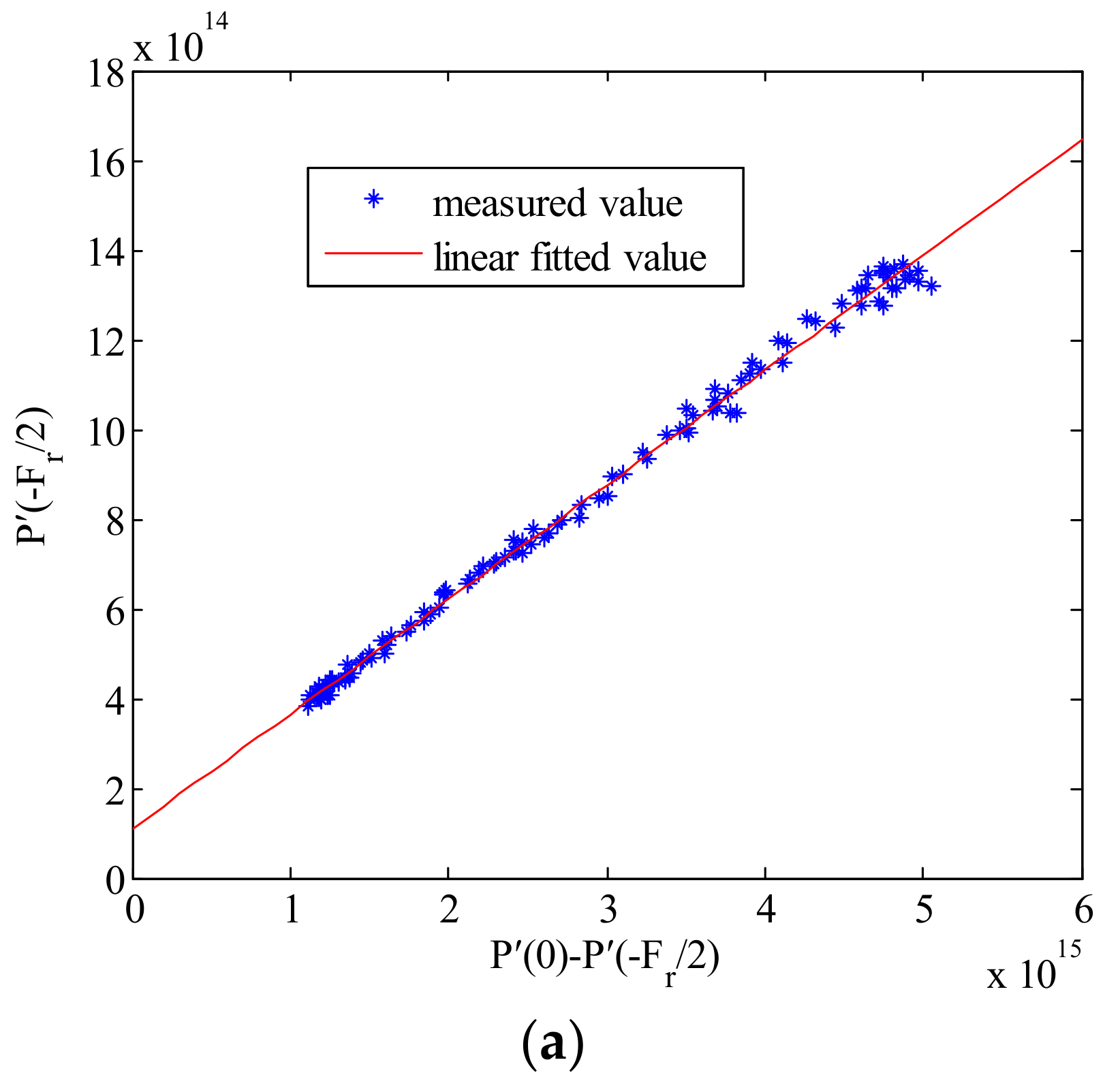
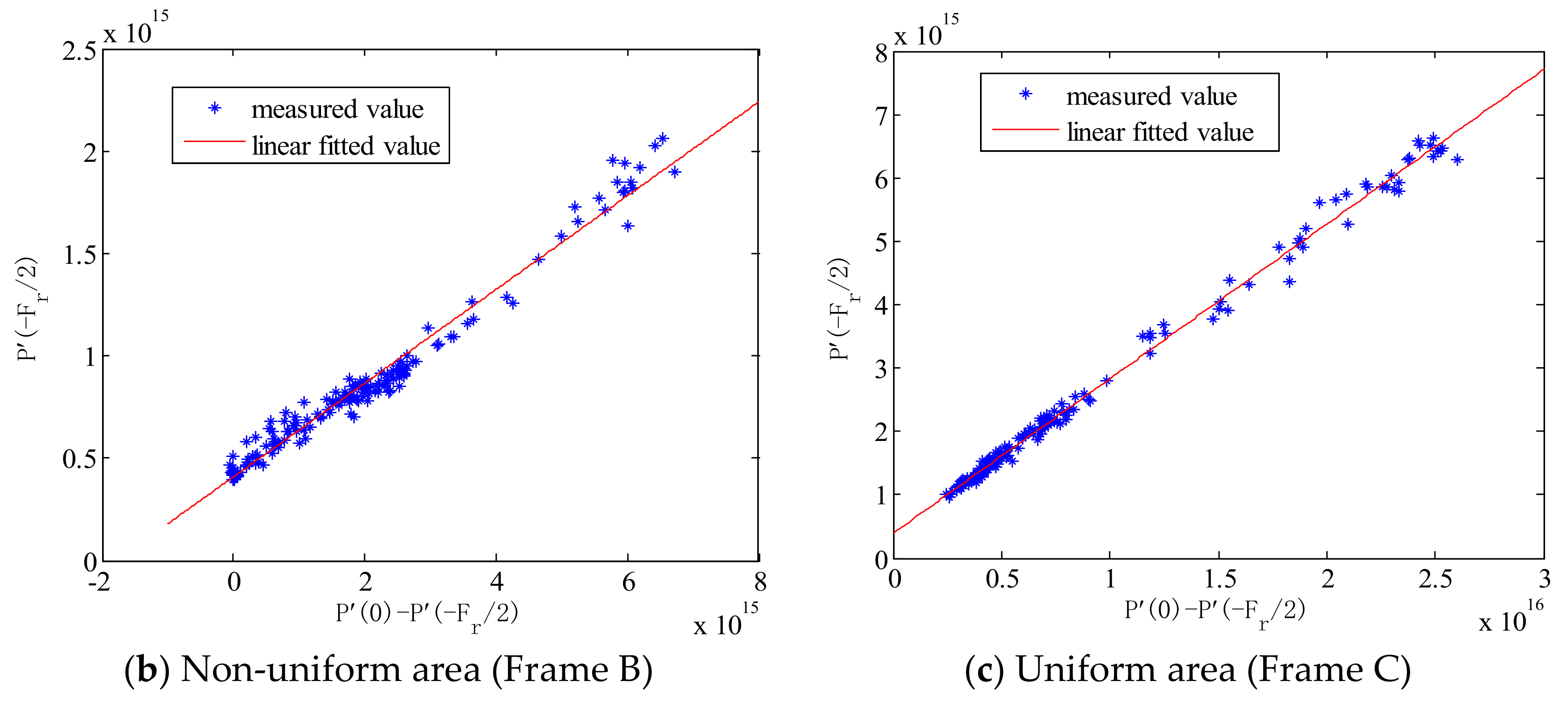
4.2. The Experimental Verification Results
5. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Multi-Parameter AAP Estimation Method
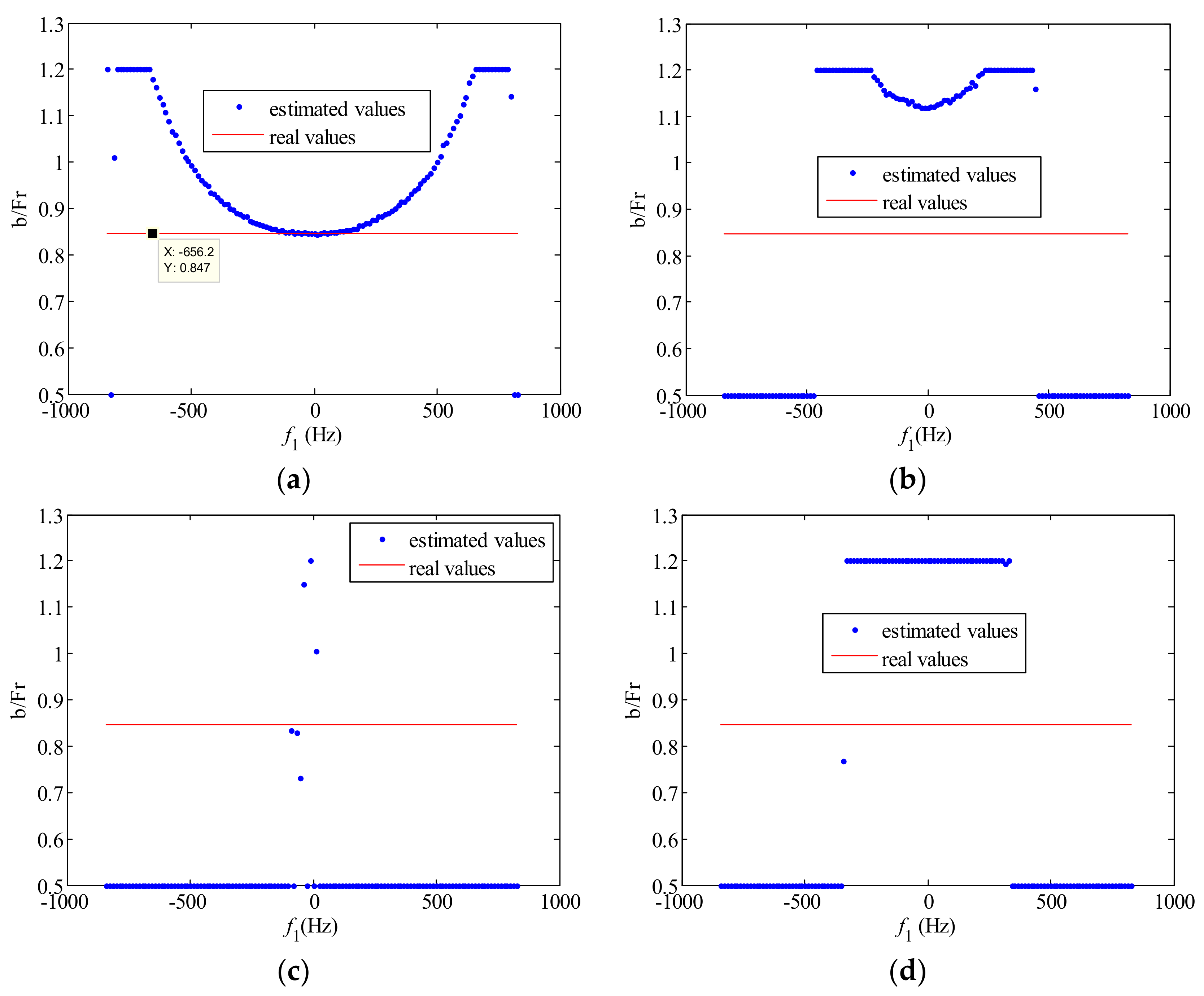
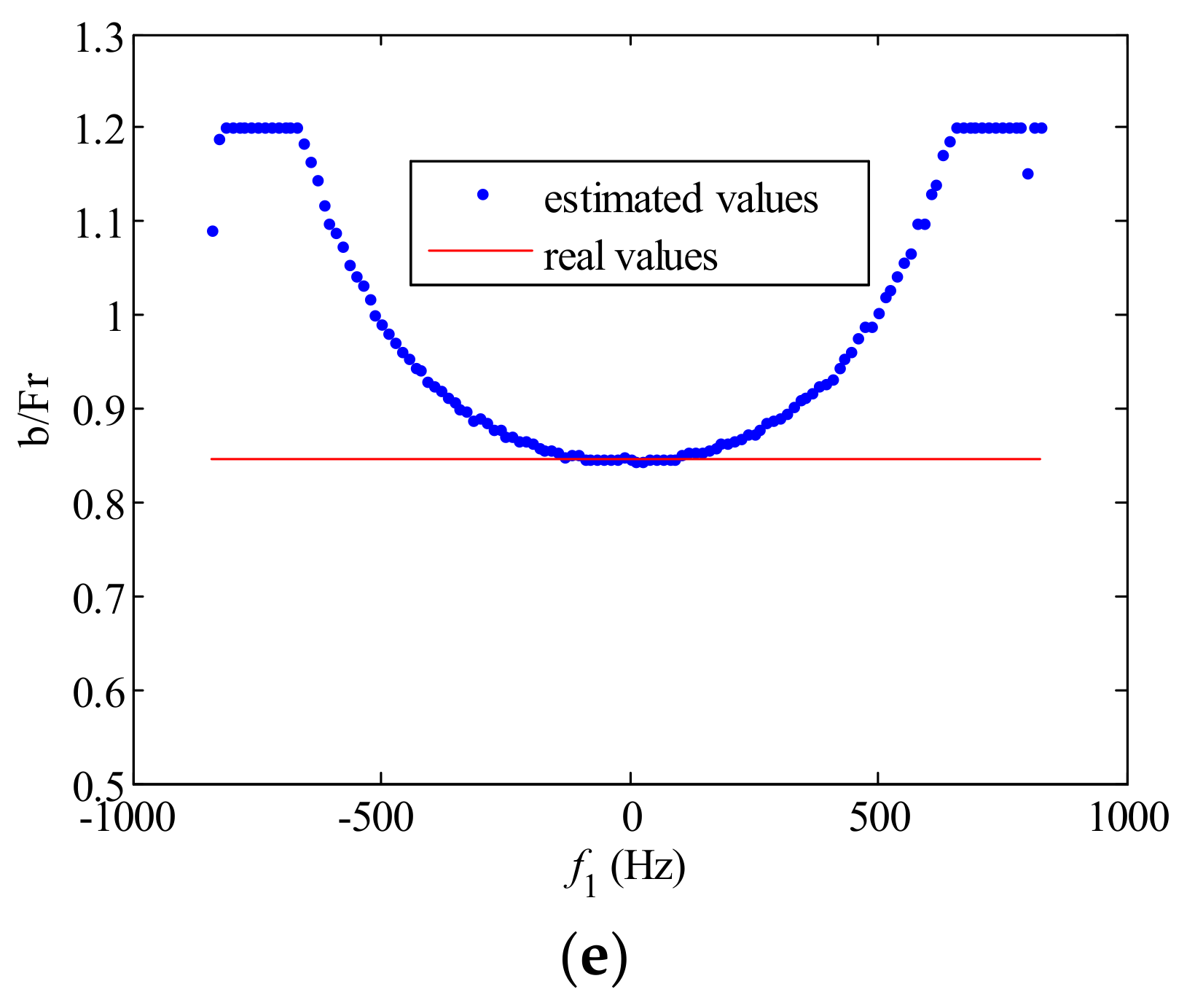
Appendix B. The Influence of Doppler Frequency Point Setting on AAP Estimation Accuracy
References
- Laycock, J.; Laur, H. ERS-1 SAR Antenna Pattern Estimation; ESA/ESRIN, ES-TN-DPE-OM-JL01; European Space Agency (ESA): Paris, France, 1994. [Google Scholar]
- Jackson, H.; Sinclair, I.; Tam, S. Envisat/asar precision transponders. In Proceedings of the SAR Workshop: CEOS Committee on Earth Observation Satellites, Toulouse, France, 26–29 October 1999; European Space Agency-Publications-ESA SP: Paris, France, 2000; Volume 450, pp. 311–316. [Google Scholar]
- Guarnieri, A.M.; D’Aria, D. Wide-angle azimuth antenna pattern estimation in SAR images. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IGARSS’03), Toulouse, France, 21–25 July 2003; pp. 3105–3107. [Google Scholar]
- Guarnieri, A.M.; Giudici, D. Accurate Estimate of the Azimuth Antenna Pattern from SAR Images. In Proceedings of the 6th European Conference on Synthetic Aperture Radar (EUSAR 2006), Dresden, Germany, 16–18 May 2006. [Google Scholar]
- Tan, H.; Zhang, R.; Hong, J. In SAR azimuth antenna pattern estimation using a strong point target. In Proceedings of the 1st Asian and Pacific Conference on Synthetic Aperture Radar (APSAR 2007), Huangshan, China, 5–9 November 2007; pp. 567–570. [Google Scholar]
- Guccione, P.; Monti Guarnieri, A. ML antenna pattern shape and pointing estimation in synthetic aperture radar. In Proceedings of the 31st EARSeL Symposium, Prague, Czech Republic, 30 May–2 June 2011. [Google Scholar]
- Guccione, P.; Guarnieri, A.M.; Zonno, M. Azimuth antenna maximum likelihood estimation by persistent point scatterers in SAR images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 947–955. [Google Scholar] [CrossRef]
- Castellanos Alfonzo, G.; Schwerdt, M.; Wollstadt, S.; Bachmann, M.; Döring, B.; Geudtner, D. First TerraSAR-X TOPS mode antenna pattern measurements using ground receivers. Int. J. Antennas Propag. 2013, 2013, 635069. [Google Scholar] [CrossRef]
- Meng, H.; Wang, X.; Chong, J.; Wei, X.; Kong, W. Doppler Spectrum-Based NRCS Estimation Method for Low-Scattering Areas in Ocean SAR Images. Remote Sens. 2017, 9, 219. [Google Scholar] [CrossRef]
- Leng, X.; Ji, K.; Zhou, S.; Zou, H. Azimuth Ambiguities Removal in Littoral Zones Based on Multi-Temporal SAR Images. Remote Sens. 2017, 9, 866. [Google Scholar] [CrossRef]
- Zuo, S.-S.; Xing, M.; Xia, X.-G.; Sun, G.-C. Improved Signal Reconstruction Algorithm for Multichannel SAR Based on the Doppler Spectrum Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1425–1442. [Google Scholar] [CrossRef]
- Bamler, R. Doppler frequency estimation and the Cramer-Rao bound. IEEE Trans. Geosci. Remote Sens. 1991, 29, 385–390. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X.; Chong, J.; Lu, Y. Optimal Parameter Estimation Method of Internal Solitary Waves in SAR Images and the Cramér–Rao Bound. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3143–3150. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital processing of synthetic aperture radar data. Artech House 2005, 1, 3. [Google Scholar]
- Madsen, S.N. Estimating the Doppler centroid of SAR data. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 134–140. [Google Scholar] [CrossRef]
- Bamler, R.; Runge, H. PRF-ambiguity resolving by wavelength diversity. IEEE Trans. Geosci. Remote Sens. 1991, 29, 997–1003. [Google Scholar] [CrossRef]
- Wong, F.; Cumming, I.G. A combined SAR Doppler centroid estimation scheme based upon signal phase. IEEE Trans. Geosci. Remote Sens. 1996, 34, 696–707. [Google Scholar] [CrossRef]
- Chang, C.-Y.; Curlander, J.C. Application of the multiple PRF technique to resolve Doppler centroid estimation ambiguity for spaceborne SAR. IEEE Trans. Geosci. Remote Sens. 1992, 30, 941–949. [Google Scholar] [CrossRef]
- Chapron, B.; Collard, F.; Ardhuin, F. Direct measurements of ocean surface velocity from space: Interpretation and validation. J. Geophys. Res. Oceans 2005, 110. [Google Scholar] [CrossRef]
- Hansen, M.W.; Collard, F.; Dagestad, K.; Johannessen, J.A.; Fabry, P.; Chapron, B. Retrieval of sea surface range velocities from Envisat ASAR Doppler centroid measurements. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3582–3592. [Google Scholar] [CrossRef]
- Johannessen, J.A.; Chapron, B.; Collard, F.; Kudryavtsev, V.; Mouche, A.; Akimov, D.; Dagestad, K.F. Direct ocean surface velocity measurements from space: Improved quantitative interpretation of Envisat ASAR observations. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Hawkins, R.K.; Teany, L.D.; Srivastava, S.; Tam, S.Y.K. RADARSAT precision transponder. Adv. Space Res. 1997, 19, 1455–1465. [Google Scholar] [CrossRef]


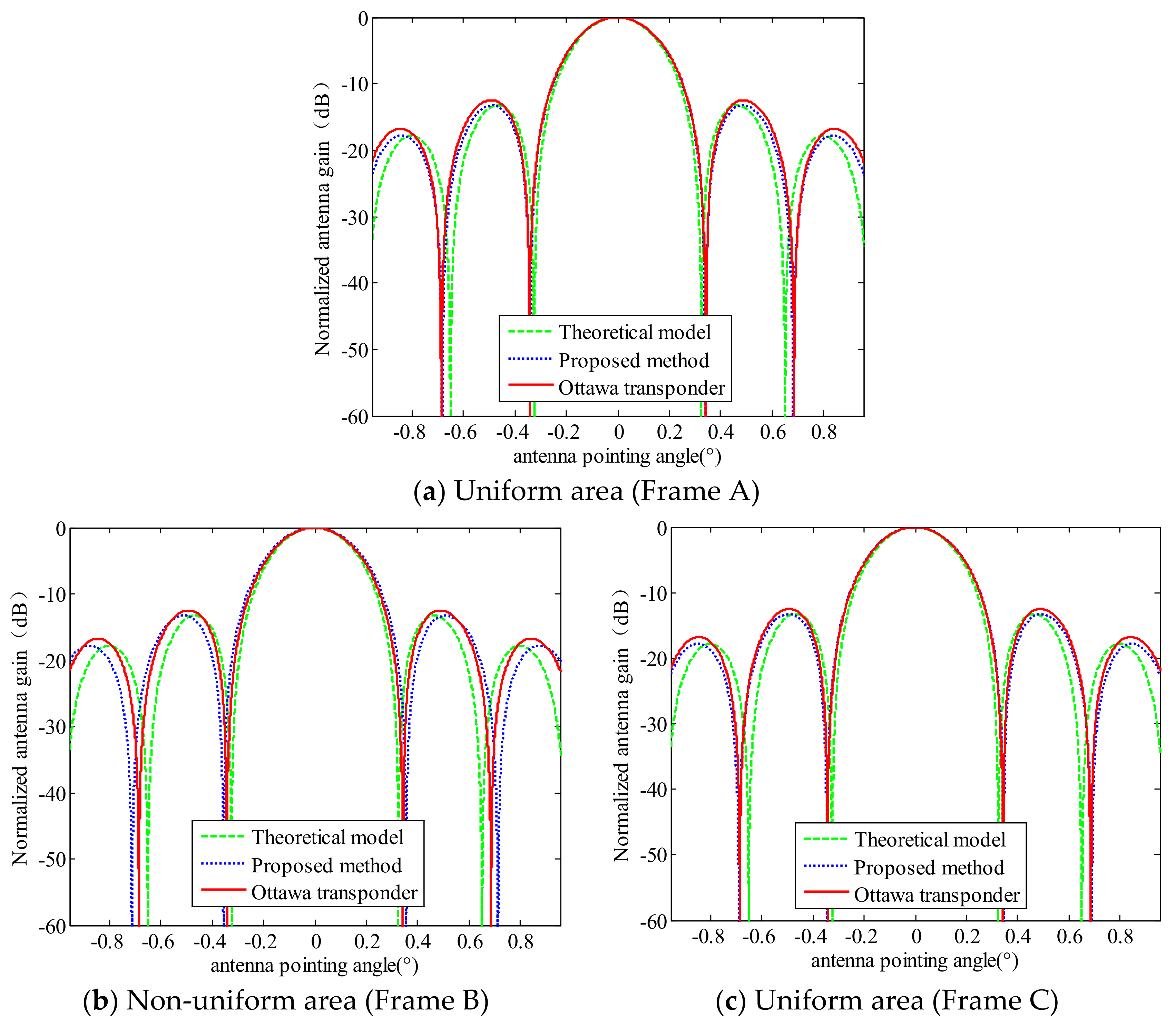
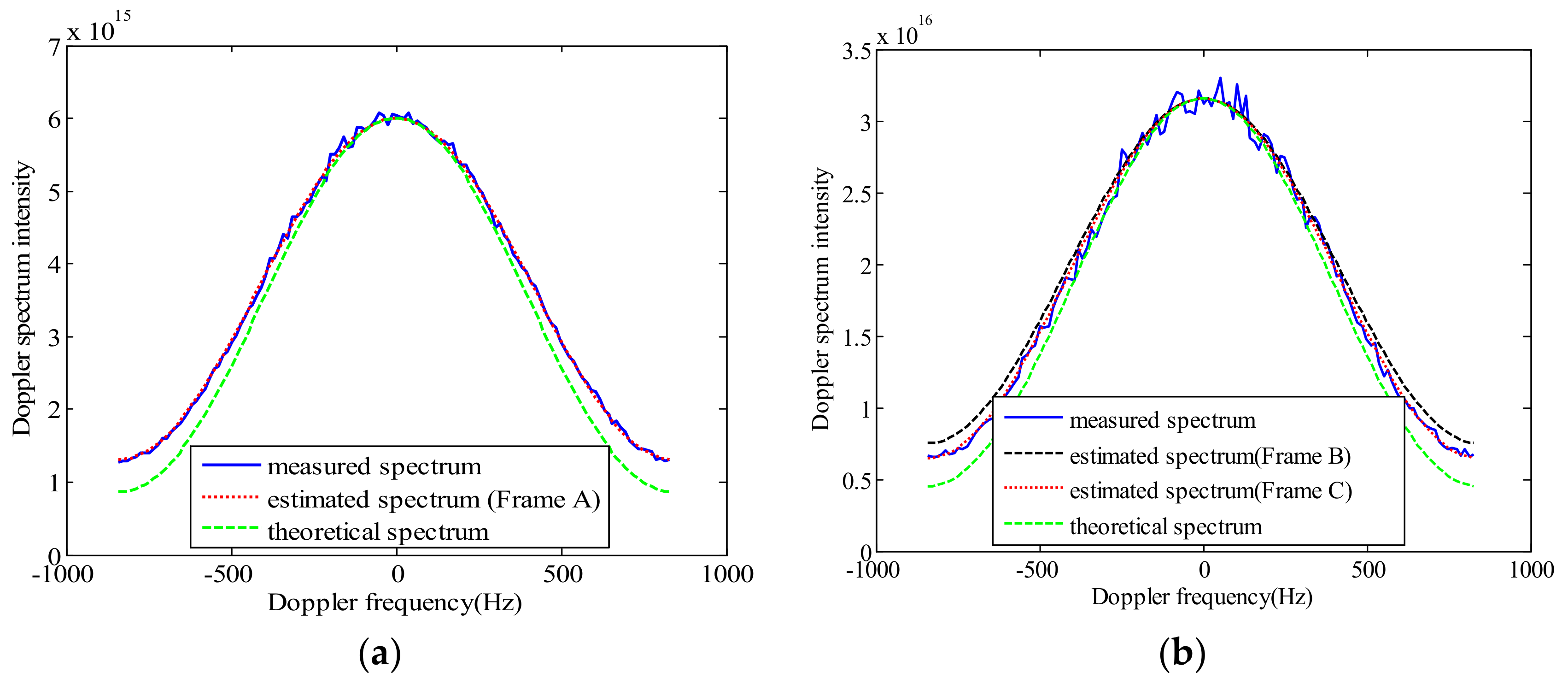
| Parametric Name | Parametric Symbol | Parametric Value |
|---|---|---|
| Pulse repetition frequency | 1679.902 (Hz) | |
| Number of Doppler spectrum pixels | 128 | |
| Simulation repeat number | 800 | |
| Look number of SAR image | 10 | |
| Signal-to-Noise Ratio | 5 dB | |
| AAP scale factor | ||
| Ratio of the scattering values of the blurred signal and the real target position | 0.9 |
| AAP Parameters | Mean | RMSE | |
|---|---|---|---|
| Real Value | Estimated Value | ||
| b/Fr | 0.849 | 0.843 | 0.025 |
| Values | |
|---|---|
| The average of the scattering coefficient () | |
| The standard deviation of the scattering coefficient () | |
| Simulation repeat number | 800 |
| Values | |
|---|---|
| 0–10 dB | |
| Simulation repeat number | 800 |
| Pixel number used for calculating one Doppler spectrum | 80 |
| Pulse Repetition Frequency () | Platform Velocity (V) (m/s) | Antenna Length (m) | Pulse Width () | Bandwidth (MHz) | Wavelength (m) |
|---|---|---|---|---|---|
| 1679.902 | 7131.7 | 10 | 37.12 | 15.5478 | 0.0566 |
| Frame A | Frame B | Frame C | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mainlobe Width (°) | PSLR(Peak Sidelobe Ratio) (dB) | ISLR (Integral Sidelobe Ratio) (dB) | Mainlobe Width (°) | PSLR (dB) | ISLR (dB) | Mainlobe Width (°) | PSLR (dB) | ISLR (dB) | |
| Transponder values | 0.3030 | −12.48 | −10.27 | 0.3030 | −12.48 | −10.27 | 0.3030 | −12.48 | −10.27 |
| Estimated values | 0.3014 | −13.26 | −10.27 | 0.3150 | −13.26 | −10.28 | 0.3048 | −13.26 | −10.27 |
| Theoretical values | 0.2874 | −13.26 | −10.28 | 0.2874 | −13.26 | −10.28 | 0.2874 | −13.26 | −10.28 |
| Number of Pixels Used to Calculate the Doppler Spectrum | 32 | 64 | 128 |
|---|---|---|---|
| Frame B (Non-uniform area) | 0.951 | 0.942 | 0.930 |
| Frame C (Uniform area) | 0.924 | 0.905 | 0.901 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, H.; Wang, X.; Chong, J. An Azimuth Antenna Pattern Estimation Method Based on Doppler Spectrum in SAR Ocean Images. Sensors 2018, 18, 1081. https://doi.org/10.3390/s18041081
Meng H, Wang X, Chong J. An Azimuth Antenna Pattern Estimation Method Based on Doppler Spectrum in SAR Ocean Images. Sensors. 2018; 18(4):1081. https://doi.org/10.3390/s18041081
Chicago/Turabian StyleMeng, Hui, Xiaoqing Wang, and Jinsong Chong. 2018. "An Azimuth Antenna Pattern Estimation Method Based on Doppler Spectrum in SAR Ocean Images" Sensors 18, no. 4: 1081. https://doi.org/10.3390/s18041081
APA StyleMeng, H., Wang, X., & Chong, J. (2018). An Azimuth Antenna Pattern Estimation Method Based on Doppler Spectrum in SAR Ocean Images. Sensors, 18(4), 1081. https://doi.org/10.3390/s18041081