Algorithms for Designing Unimodular Sequences with High Doppler Tolerance for Simultaneous Fully Polarimetric Radar
Abstract
1. Introduction
2. Simultaneous Polarimetric Measurement and Doppler Analysis
3. CAGI and CAGII
3.1. Cyclic Algorithm for Designing Sequences under One Motion State
3.2. Cyclic Algorithm for Designing Sequences under a Set of Motion States
4. Simulation Results and Discussion
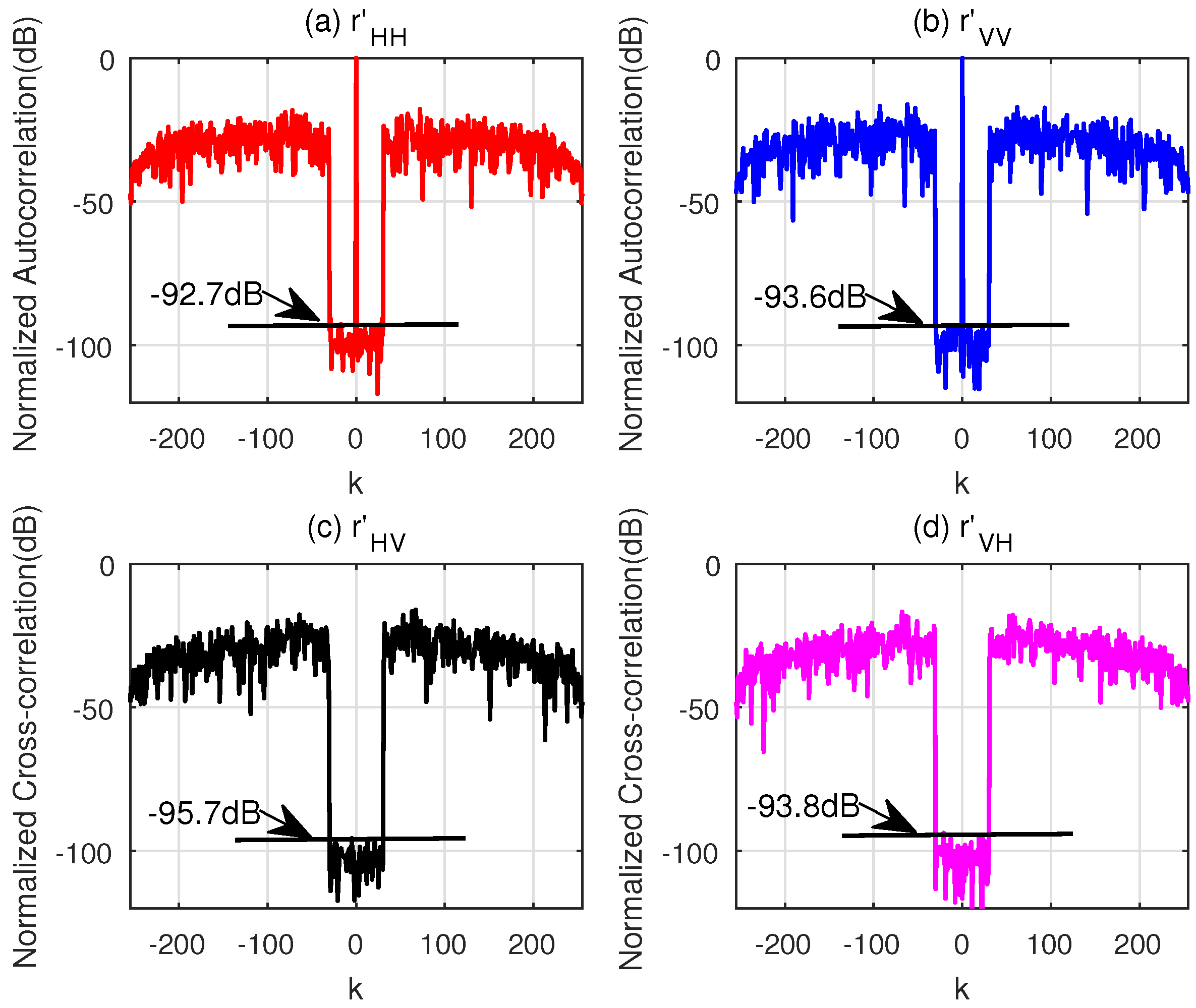
4.1. Suppressing Specified Parts of the Correlation Functions without Doppler Shift
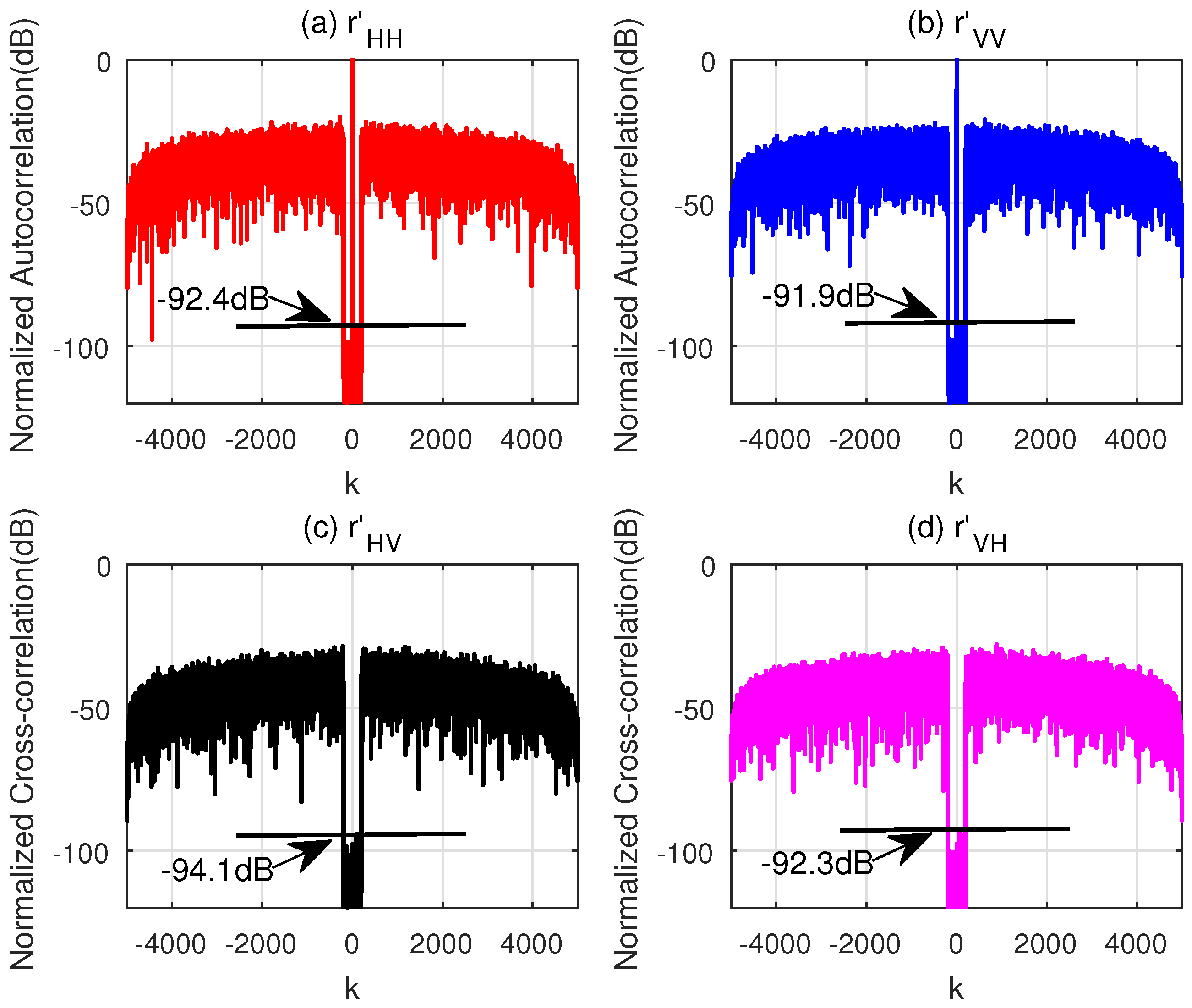
4.2. Suppressing Specified Parts of the Correlation Functions for One Motion State
4.3. Suppressing Specified Parts of the Correlation Functions for a Set of Motion States
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Details of Gradient Calculation
References
- Martorella, M.; Giusti, E.; Demi, L.; Zhou, Z.; Cacciamano, A.; Berizzi, F.; Bates, B. Target recognition by means of polarimetric ISAR images. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 225–239. [Google Scholar] [CrossRef]
- Lardeux, C.; Frison, P.L.; Tison, C.; Souyris, J.; Stoll, B.; Fruneau, B. Classification of tropical vegetation using multifrequency partial SAR polarimetry. IEEE Geosci. Remote Sens. Lett. 2011, 8, 133–137. [Google Scholar] [CrossRef]
- Sharma, J.J.; Hajnsek, I.; Papathanassiou, K.P.; Moreira, A. Polarimetric decomposition over glacier ice using long-wavelength airborne PolSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 519–535. [Google Scholar] [CrossRef]
- Sinclair, G. The Transmission and Reception of Elliptically Polarized Waves. IEEE Proc. IRE 1950, 38, 148–151. [Google Scholar] [CrossRef]
- Nashashibi, A.Y.; Sarabandi, K.; Frantzis, P.; de Roo, R.D.; Ulaby, F.T. An ultrafast wide-band millimeter-wave (MMW) polarimetric radar for remote sensing applications. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1777–1786. [Google Scholar] [CrossRef]
- Yanovsky, F.J.; Russchenberg, H.W.J.; Unal, C.M.H. Retrieval of information about turbulence in rain by using Doppler-polarimetric radar. IEEE Trans. Microw. Theory Tech. 2005, 53, 444–450. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.Z.; Wang, X.S. Instantaneous measurement for radar target polarization scattering matrix. IEEE J. Syst. Eng. Electron. 2010, 21, 968–974. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Li, Y.; Wang, X. Frequency Calibration for the Scattering Matrix of the Simultaneous Polarimetric Radar. IEEE Geosci. Remote Sens. Lett. 2018, 15, 429–433. [Google Scholar] [CrossRef]
- Giuli, D.; Fossi, M.; Facheris, L. Radar target scattering matrix measurement through orthogonal signals. IEE Proc. F Radar Signal Process. 1993, 140, 233–242. [Google Scholar] [CrossRef]
- Babur, G.; Krasnov, O.A.; Yarovoy, A.; Aubry, P. Nearly Orthogonal Waveforms for MIMO FMCW Radar. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1426–1437. [Google Scholar] [CrossRef]
- Liu, B. Orthogonal Discrete Frequency-Coding Waveform Set Design with Minimized Autocorrelation Sidelobes. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1650–1657. [Google Scholar] [CrossRef]
- Deng, H. Polyphase code design for orthogonal netted radar systems. IEEE Trans. Signal Process. 2004, 52, 3126–3135. [Google Scholar] [CrossRef]
- Song, J.; Babu, P.; Palomar, D.P. Sequence design to minimize the weighted integrated and peak sidelobe levels. IEEE Trans. Signal Process. 2016, 64, 2051–2064. [Google Scholar] [CrossRef]
- Esmaeili-Najafabadi, H.; Ataei, M.; Sabahi, M.F. Designing Sequence with Minimum PSL Using Chebyshev Distance and its Application for Chaotic MIMO Radar Waveform Design. IEEE Trans. Signal Process. 2017, 65, 690–704. [Google Scholar] [CrossRef]
- Stoica, P.; He, H.; Li, J. New Algorithm for designing unimodular sequences with good correlation properties. IEEE Trans. Signal Process. 2009, 57, 1415–1425. [Google Scholar] [CrossRef]
- He, H.; Stoica, P.; Li, J. Designing unimodular sequences sets with good correlations—Including an application to MIMO radar. IEEE Trans. Signal Process. 2009, 57, 4391–4405. [Google Scholar] [CrossRef]
- Khan, H.A.; Edwards, D.J. Doppler problems in orthogonal MIMO radar. In Proceedings of the 2006 IEEE Conference on Radar, New York, NY, USA, 24–27 April 2006; pp. 244–247. [Google Scholar]
- Kretschmer, F.F.; Lewis, B.L. Doppler properties of poly-phase coded pulse compression waveforms. IEEE Trans. Aerosp. Electron. Syst. 1983, 19, 521–531. [Google Scholar] [CrossRef]
- Arlery, F.; Kassab, R.; Tan, U. Efficient gradient method for locally optimizing the periodic/aperiodic ambiguity function. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2017; pp. 1–6. [Google Scholar]
- Cui, G.; Fu, Y.; Yu, X.; Li, J. Local Ambiguity Function Shaping via Unimodular Sequence Design. IEEE Signal Process. Lett. 2017, 24, 977–981. [Google Scholar] [CrossRef]
- Chi, Y.; Calderbank, R.; Pezeshki, A. Golay complementary waveforms for sparse delay-Doppler radar imaging. In Proceedings of the IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Dutch Antilles, The Netherlands, 13–16 December 2009; pp. 177–180. [Google Scholar]
- Pezeshki, A.; Calderbank, R.; Howard, S.D.; Moran, W. Doppler Resilient Golay Complementary Pairs for Radar. In Proceedings of the IEEE/SP Workshop on Statistical Signal Processing, Madison, WI, USA, 26–29 August 2007; Volume 54, pp. 483–487. [Google Scholar]
- Khan, H.A.; Zhang, Y.; Ji, C.; Stevens, C.J.; Edwards, D.J.; O’Brien, D. Optimizing polyphase sequences for orthogonal netted radar. IEEE Signal Process. Lett. 2006, 13, 589–592. [Google Scholar] [CrossRef]
- Xiao, J.J.; Nehorai, A. Joint Transmitter and Receiver Polarization Optimization for Scattering Estimation in Clutter. IEEE Trans. Signal Process. 2009, 57, 4142–4147. [Google Scholar] [CrossRef]
- Levanon, N.; Mozeson, E. Radar Signals; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2004; pp. 100–102. ISBN 0-471-47378-2. [Google Scholar]
- Kretschmer, F., Jr.; Gerlach, K. Low sidelobe radar waveform derived from orthogonal matrices. IEEE Trans. Aerosp. Electron. Syst. 1991, 27, 92–102. [Google Scholar] [CrossRef]
- Grippo, L.; Lampariello, F.; Lucidi, S. A nonmonotone line search technique for Newton’s method. SIAM J. Numercial Anal. 1986, 23, 707–716. [Google Scholar] [CrossRef]
- Pang, C.; Hoogeboom, P.; le Chevalier, F.; Russchenberg, H.W.J.; Dong, J.; Wang, T.; Wang, A.S. A Pulse Compression Waveform for Weather Radars with Solid-State Transmitters. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2026–2030. [Google Scholar] [CrossRef]







| : | the complex conjugate of a scalar a |
| : | the real part of a scalar a |
| : | the imaginary part of a scalar a |
| : | the reverse of a vector |
| : | the complex conjugate of a matrix |
| : | the transpose of a matrix |
| : | the conjugate transpose of a matrix |
| : | the Hadamard product of two matrices and with the same dimension |
| : | the modulus of a complex number a |
| ⊗: | the convolution operation between two signals |
|
|
| N | P | a | |||
|---|---|---|---|---|---|
| 256 | 30 | 0.03 m | 5 × 10−9 s | 3 km/s | 100 m/s2 |
| PCL | I | Iteration Number | Total Execution Time | Execution Time per Iteration | |
|---|---|---|---|---|---|
| CAGI | −93.15 dB | −94.75 dB | 6546 | 1093.3 s | 0.168 s |
| WeCAN | −25.73 dB | −24.15 dB | 123,521 | 23,047.5 s | 0.187 s |
| N | P | a | |||
|---|---|---|---|---|---|
| 5000 | 200 | 0.03 m | 5 × 10−9 s | 1 km/s | 100 m/s2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Pang, C.; Li, Y.; Wang, X. Algorithms for Designing Unimodular Sequences with High Doppler Tolerance for Simultaneous Fully Polarimetric Radar. Sensors 2018, 18, 905. https://doi.org/10.3390/s18030905
Wang F, Pang C, Li Y, Wang X. Algorithms for Designing Unimodular Sequences with High Doppler Tolerance for Simultaneous Fully Polarimetric Radar. Sensors. 2018; 18(3):905. https://doi.org/10.3390/s18030905
Chicago/Turabian StyleWang, Fulai, Chen Pang, Yongzhen Li, and Xuesong Wang. 2018. "Algorithms for Designing Unimodular Sequences with High Doppler Tolerance for Simultaneous Fully Polarimetric Radar" Sensors 18, no. 3: 905. https://doi.org/10.3390/s18030905
APA StyleWang, F., Pang, C., Li, Y., & Wang, X. (2018). Algorithms for Designing Unimodular Sequences with High Doppler Tolerance for Simultaneous Fully Polarimetric Radar. Sensors, 18(3), 905. https://doi.org/10.3390/s18030905





