Medium and Short Wave RF Energy Harvester for Powering Wireless Sensor Networks
Abstract
1. Introduction
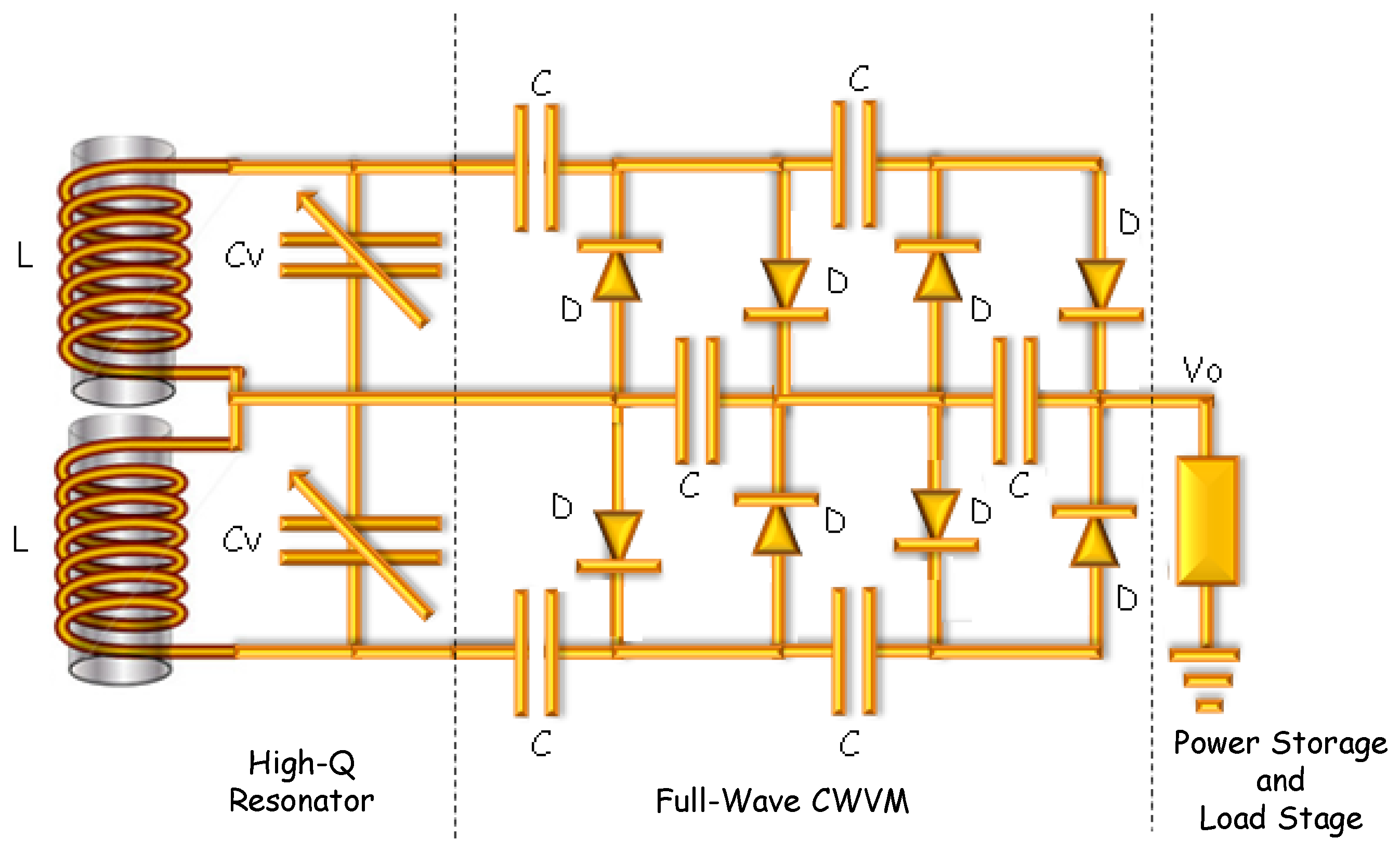
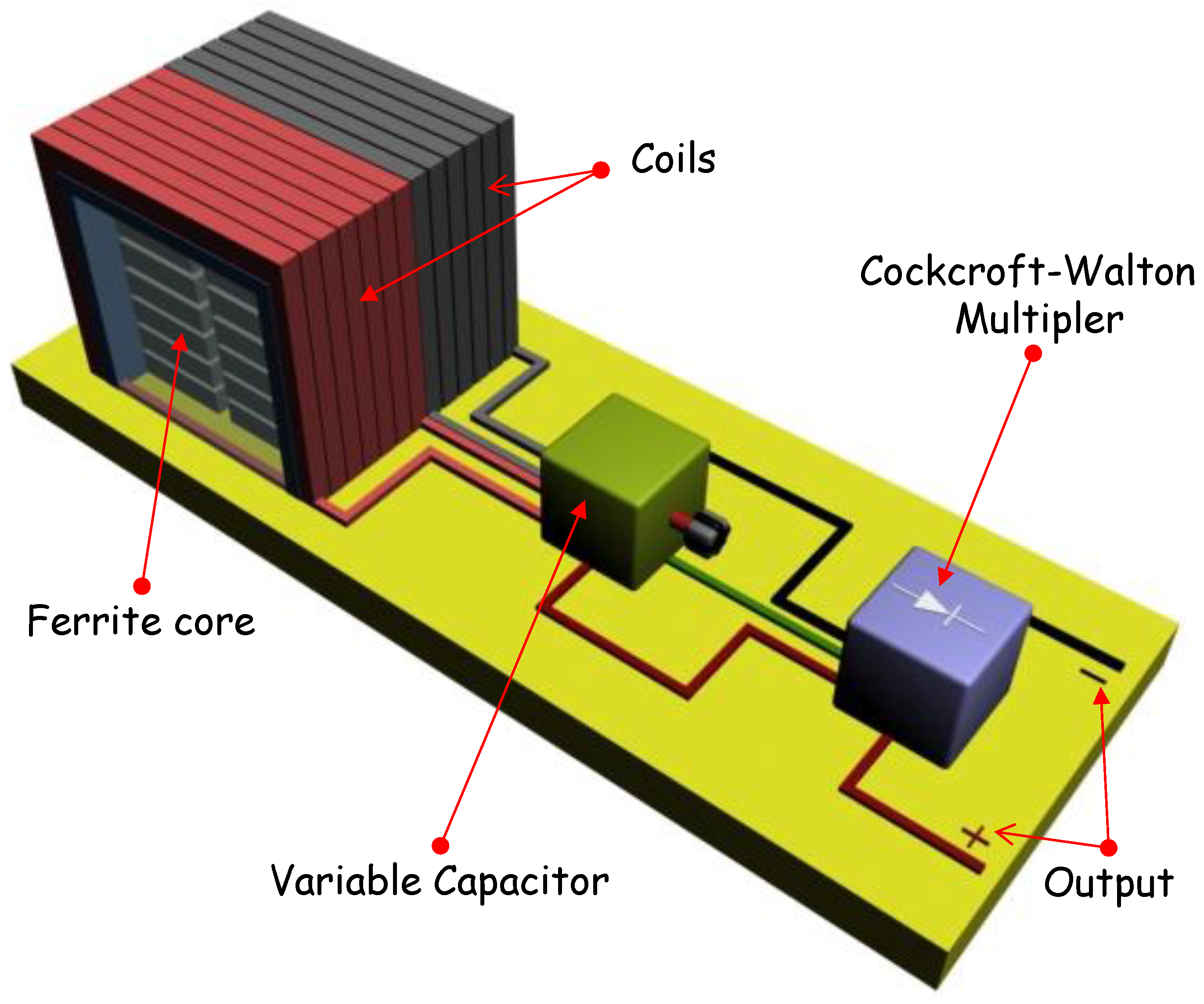
2. Portable Medium and Short Wave RF Energy Harvester Design
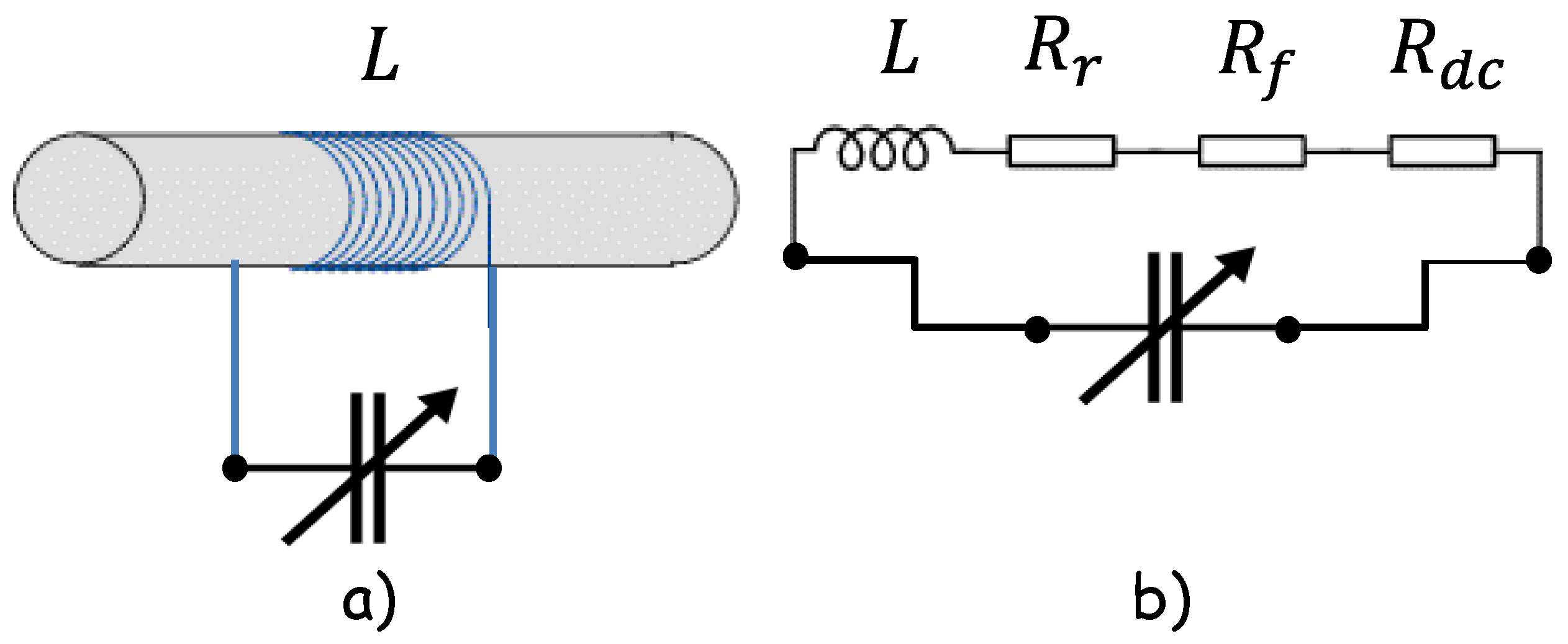
2.1. AM Resonator
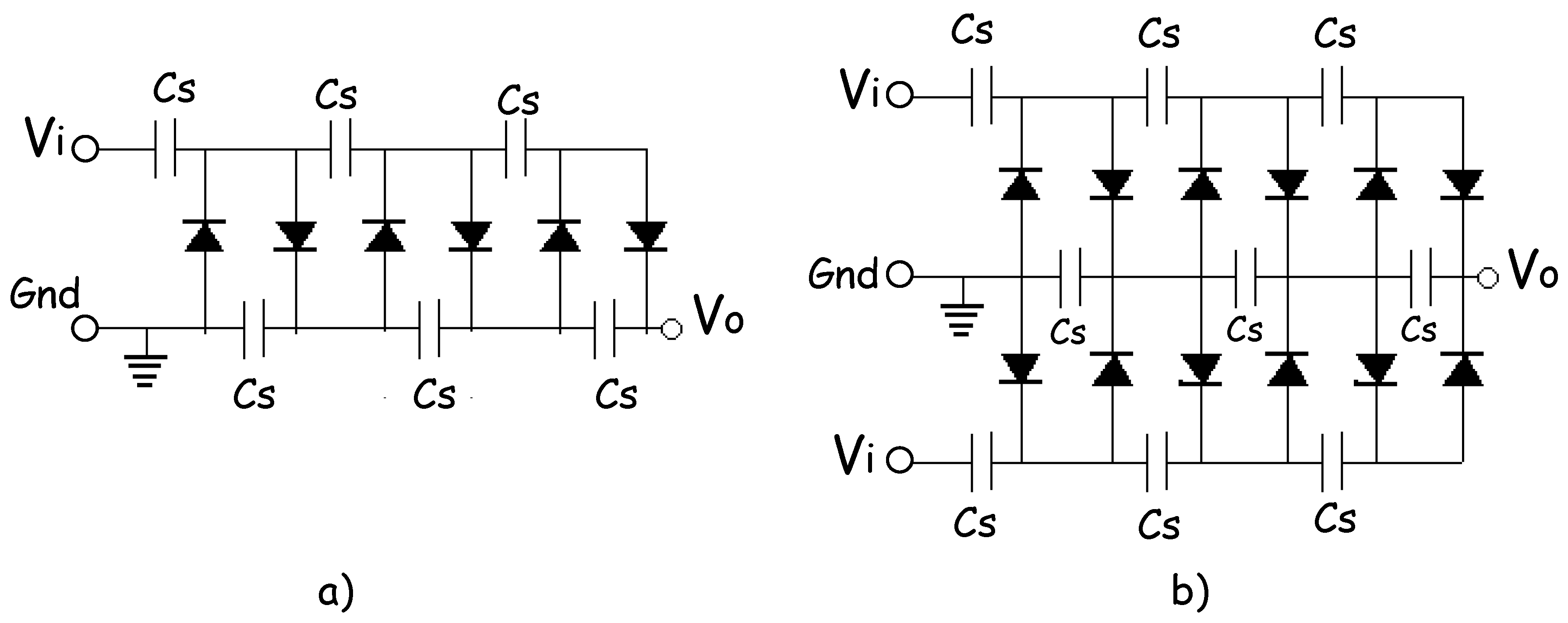
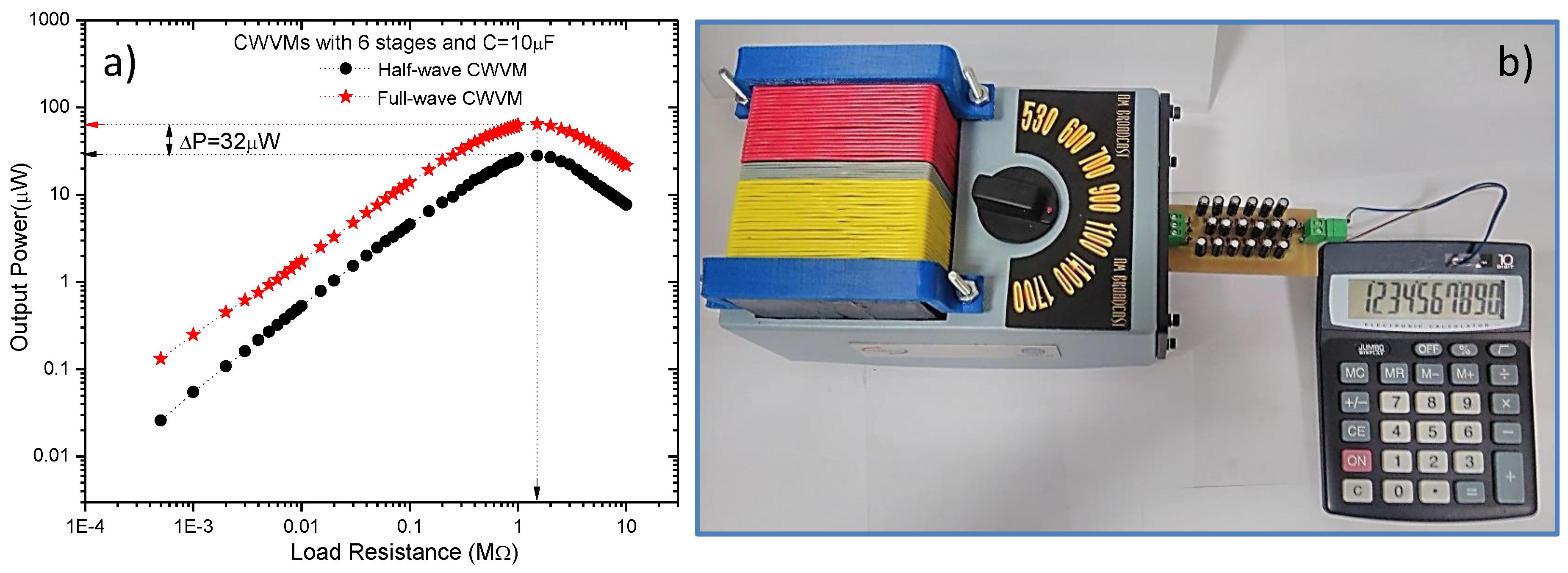
2.2. AC-DC Converter: Cockcroft-Walton Voltage Multiplier
2.3. Power Storage and Load Stage
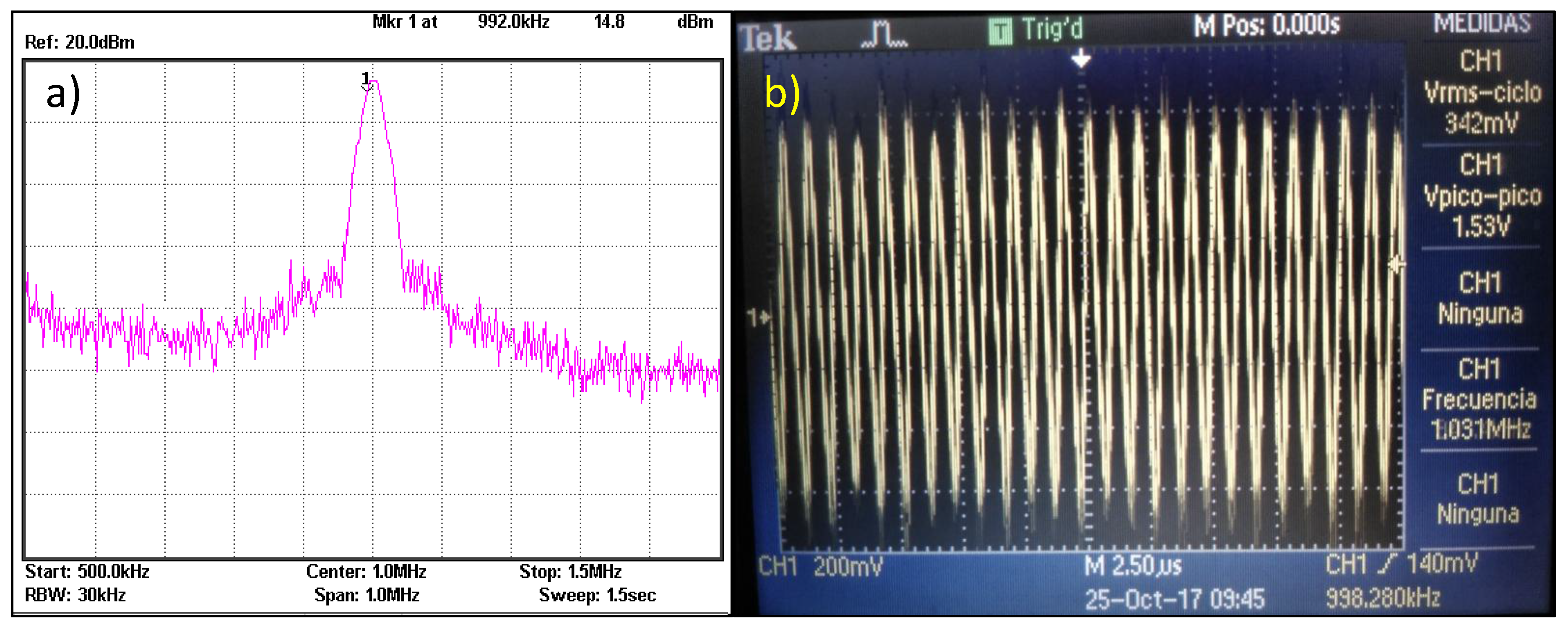
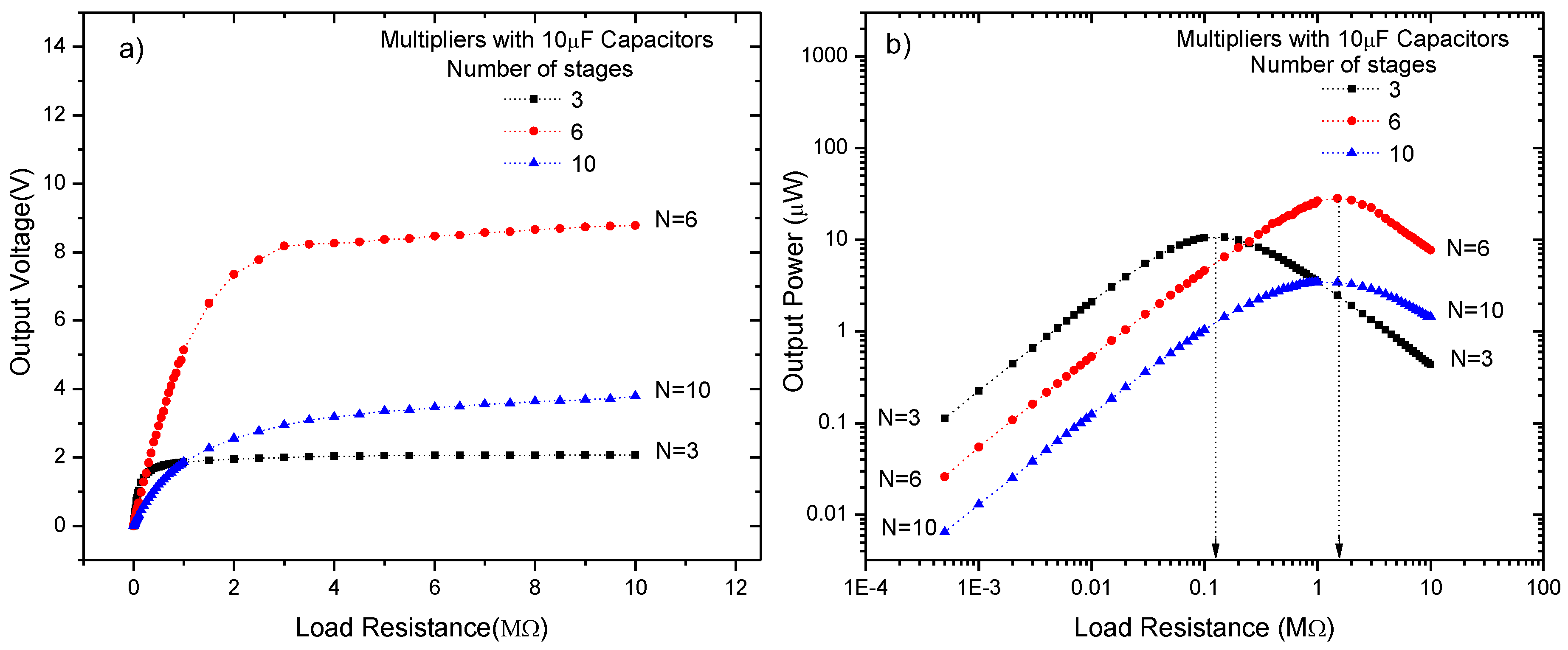
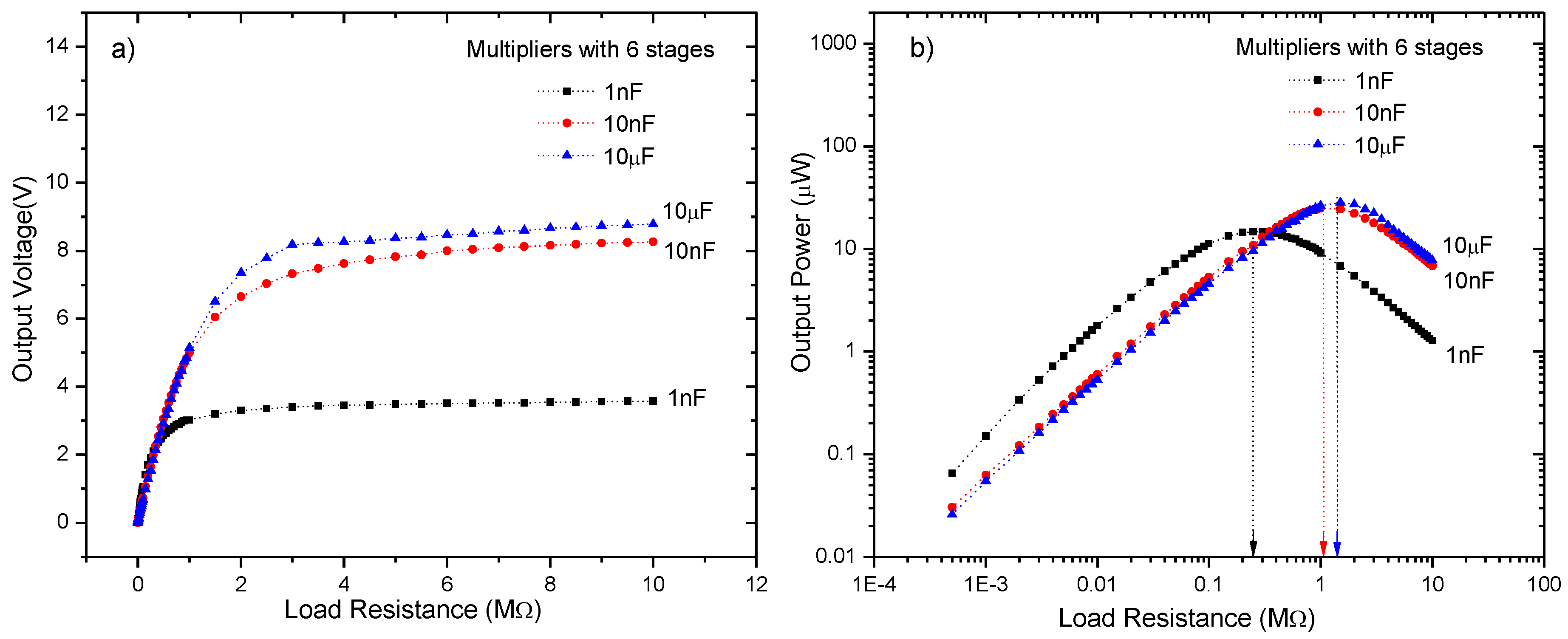
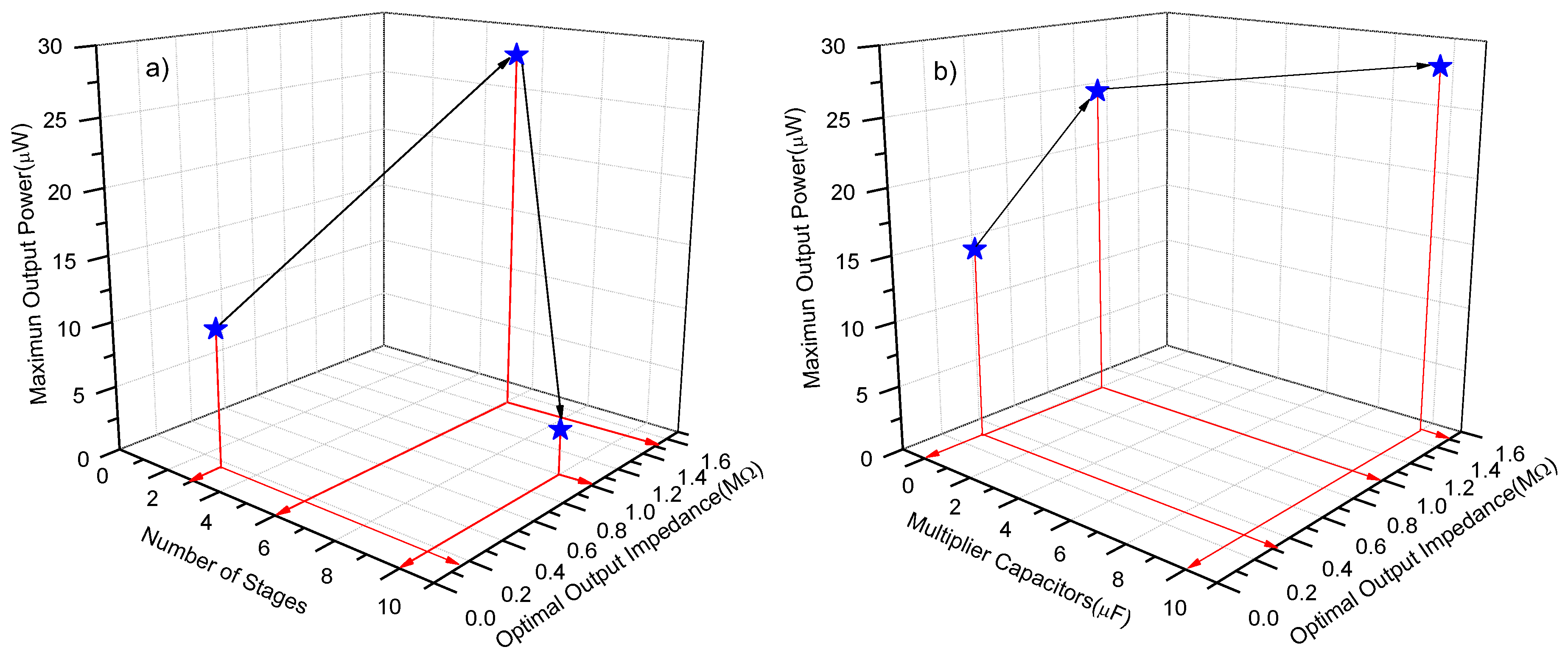
3. Performance of the RF Energy Harvesting System for AM Broadcasting
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vullers, R.J.M.; Van Schaijk, R.; Doms, I.; Van Hoof, C.; Mertens, R. Micropower energy harvesting. Solid State Electron. 2009, 53, 684–693. [Google Scholar] [CrossRef]
- Harb, A. Energy harvesting: State-of-the-art. Renew. Energy 2011, 36, 2641–2654. [Google Scholar] [CrossRef]
- Le, T.; Mayaram, K.; Fiez, T. Efficient far-field radio frequency energy harvesting for passively powered sensor networks. IEEE J. Solid State Circuits 2008, 43, 1287–1302. [Google Scholar] [CrossRef]
- Paing, T.; Shin, J.; Zane, R.; Popovic, Z. Resistor emulation approach to low-power RF energy harvesting. IEEE Trans. Power Electron. 2008, 23, 1494–1501. [Google Scholar] [CrossRef]
- Devi, K.K.; Din, N.M.D.; Chakrabarty, C.K. Optimization of the voltage doubler stages in an RF-DC convertor module for energy harvesting. Circuits Syst. 2012, 3, 216–222. [Google Scholar] [CrossRef]
- Volakis, J.L.; Olgun, U.; Chen, C.-C. Design of an efficient ambient WiFi energy harvesting system. IET Microw. Antennas Propag. 2012, 6, 1200–1206. [Google Scholar]
- Hagerty, J.; Helmbrecht, F.; McCalpin, W.; Zane, R.; Popovic, Z. Recycling ambient microwave energy with broad-band rectenna arrays. IEEE Trans. Microw. Theory Tech. 2004, 52, 1014–1024. [Google Scholar] [CrossRef]
- Monti, G.; Congedo, F.; De Donno, D.; Tarricone, L. Monopole-based rectenna for microwave energy harvesting of UHF RFID systems. Prog. Electromagn. Res. C 2012, 31, 109–121. [Google Scholar] [CrossRef]
- Russo, M.; Šolić, P.; Stella, M. Probabilistic modeling of harvested GSM energy and its application in extending UHF RFID tags reading range. J. Electromagn. Waves Appl. 2013, 27, 473–484. [Google Scholar] [CrossRef]
- Jeong, T. Energy-harvesting system design through Bluetooth environment for smart phone. IET Sci. Meas. Technol. 2013, 7, 201–205. [Google Scholar] [CrossRef]
- Piñuela, M.; Mitcheson, P.D.; Lucyszyn, S. Ambient RF energy harvesting in urban and semi-urban environments. IEEE Trans. Microw. Theory Tech. 2013, 61, 2715–2726. [Google Scholar] [CrossRef]
- Leon-Gil, J.A.; Perales-Cruz, J.C.; Licea-Jiménez, L.; Perez-Garcia, S.A.; Alvarez-Quintana, J. RF energy scavenging system for DC power from FM broadcasting based on an optimized Cockcroft-Walton voltaje multiplier. J. Electromagn. Waves Appl. 2015, 29, 1440–1453. [Google Scholar] [CrossRef]
- Mikami, S.; Matsuno, T.; Miyama, M.; Kawaguchi, H.; Yoshimoto, M.; Ono, H. An energy harvesting wireless-interface SoC for short-range data communication. IEEJ Trans. Electron. Inf. Syst. 2006, 126, 565–570. [Google Scholar] [CrossRef][Green Version]
- Halabe, U.B.; Maser, K.; Kausel, E. Propagation Characteristics of Electromagnetic Waves in Concrete; Technical Report AD-A207387; Cambridge Department Civil Engineering MIT: Cambridge, MA, USA, 1989. [Google Scholar]
- Cockcroft, J.D.; Walton, E.T. Experiments with high velocity positive ions. (I) Further developments in the method of obtaining high velocity positive ions. Proc. R. Soc. A Math. Phys. Eng. Sci. 1932, 136, 619–630. [Google Scholar] [CrossRef]
- Balanis, C. Antenna Theory: Analysis and Design, 2nd ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Sazonov, E.; Li, H.; Curry, D.; Pillay, P. Self-powered sensors for monitoring of highway bridges. IEEE Sens. J. 2009, 9, 1422–1429. [Google Scholar] [CrossRef]
- Marian, V.; Allard, B.; Vollaire, C.; Verdier, J. Strategy for Microwave Energy Harvesting from Ambient Field or a Feeding Source. IEEE Trans. Power Electron. 2012, 27, 4481–4491. [Google Scholar] [CrossRef]
- Maksimovic, D.; Cuk, S. Switching converters with wide DC conversion range. IEEE Trans. Power Electron. 1991, 6, 151–157. [Google Scholar] [CrossRef]
- Luo, F.L.; Ye, H. Positive output super-lift converters. IEEE Trans. Power Electron. 2003, 18, 105–113. [Google Scholar]
- Tseng, K.C.; Liang, T.J. Novel high-efficiency step-up converter. IEE Proc. Electr. Power Appl. 2004, 151, 182–190. [Google Scholar] [CrossRef]
- Inaba, C.Y.; Konishi, Y.; Nakaoka, M. High-frequency flyback-type soft-switching PWM DC–DC power converter with energy recovery transformer and auxiliary passive lossless snubbers. IEE Proc. Electr. Power Appl. 2004, 151, 32–37. [Google Scholar] [CrossRef]
- Hwang, F.; Shen, Y.; Jayaram, S.H. Low-ripple compact high-voltage DC power supply. IEEE Trans. Ind. Appl. 2006, 42, 1139–1145. [Google Scholar] [CrossRef]
- Shenkman, A.; Berkovich, Y.; Axelrod, B. Novel AC–DC and DC–DC converters with a diode-capacitor multiplier. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1286–1293. [Google Scholar] [CrossRef]
- Wang, X.; Mortazawi, A. Medium wave energy scavenging for Wireless structural health monitoring sensors. IEEE Trans. Microw. Theory Tech. 2014, 62, 1067–1073. [Google Scholar] [CrossRef]
- Wang, X.; Mortazawi, A. High sensitivity RF energy harvesting from AM broadcasting stations for civilian infrastructure degradation monitoring. In Proceedings of the IEEE International Wireless Symposium (IWS), Beijing, China, 14–18 April 2013; pp. 1–3. [Google Scholar]
- Kwan, J.C.; Fapojuwo, A.O. Radio Frequency Energy Harvesting and Data Rate Optimization in Wireless Information and Power Transfer Sensor Networks. IEEE Sens. J. 2017, 17, 4862–4874. [Google Scholar] [CrossRef]
- Stoopman, M.; Keyrouz, S.; Visser, H.J.; Philips, K.; Serdijn, W.A. A self-calibrating RF energy harvester generating 1 V at −26.3 dBm. In Proceedings of the IEEE Synposium on VLSI Circuits, Kyoto, Japan, 2013; pp. 226–227. [Google Scholar]
- Powercast Documentation. Available online: http://Powercastco.com/ (accessed on 31 January 2018).
- Sample, A.P.; Parks, A.N.; Southwood, S.; Smith, J.R. Wireless Ambient Radio Power. In Wirelessly Powered Sensor Networks and Computational RFDI; Springer: New York, NY, USA, 2013; pp. 223–234. [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leon-Gil, J.A.; Cortes-Loredo, A.; Fabian-Mijangos, A.; Martinez-Flores, J.J.; Tovar-Padilla, M.; Cardona-Castro, M.A.; Morales-Sánchez, A.; Alvarez-Quintana, J. Medium and Short Wave RF Energy Harvester for Powering Wireless Sensor Networks. Sensors 2018, 18, 768. https://doi.org/10.3390/s18030768
Leon-Gil JA, Cortes-Loredo A, Fabian-Mijangos A, Martinez-Flores JJ, Tovar-Padilla M, Cardona-Castro MA, Morales-Sánchez A, Alvarez-Quintana J. Medium and Short Wave RF Energy Harvester for Powering Wireless Sensor Networks. Sensors. 2018; 18(3):768. https://doi.org/10.3390/s18030768
Chicago/Turabian StyleLeon-Gil, Jesus A., Agustin Cortes-Loredo, Angel Fabian-Mijangos, Javier J. Martinez-Flores, Marco Tovar-Padilla, M. Antonia Cardona-Castro, Alfredo Morales-Sánchez, and Jaime Alvarez-Quintana. 2018. "Medium and Short Wave RF Energy Harvester for Powering Wireless Sensor Networks" Sensors 18, no. 3: 768. https://doi.org/10.3390/s18030768
APA StyleLeon-Gil, J. A., Cortes-Loredo, A., Fabian-Mijangos, A., Martinez-Flores, J. J., Tovar-Padilla, M., Cardona-Castro, M. A., Morales-Sánchez, A., & Alvarez-Quintana, J. (2018). Medium and Short Wave RF Energy Harvester for Powering Wireless Sensor Networks. Sensors, 18(3), 768. https://doi.org/10.3390/s18030768





