1. Introduction
Over the past decades, conductive polymer materials have attracted a great deal of attention due to their potential applications, especially in the field of intelligent artificial skin, tactile sensing and intelligent sensing gloves [
1,
2,
3,
4,
5]; Conductive silicone is a conductive polymer composite material that is the core material of flexible pressure sensors. There are lots of reasons to demonstrate that conductive silicone is suitable for flexible pressure sensors, which include: (1) the elasticity and softness of silicone rubber are similar to that of human skin and muscle and it has good biocompatibility, chemical stability and no toxicity, so it can be used to make wearable sensors [
6,
7,
8]; (2) it has larger deformation, so it can be used in the area of flexible sensing and so on [
9,
10]; (3) high sensitivity and resolution in detection [
11]; (4) low cost [
12]; (5) the chemical properties of silicon compounds are very stable so its sensor products have longer life than those made from other materials [
13,
14]; (6) it has good processing performance, shaping easily, and other advantages, so it can be used to produce sensor devices of various shapes through hot air vulcanization molding extrusion, mold processing, calendar molding, and other methods [
15,
16,
17,
18].
Conductive silicone rubber is usually prepared by adding conductive fillers to the silicone rubber [
19]. The commonly used conductive fillers are metal series conductive fillers or carbon series conductive fillers. Metal series materials are important fillers of conductive silicone rubber because of their excellent conductivity, the stable chemical properties of the filled polymer and the persistent conductive properties of the material [
20]. In recent years, the silver plating technology has overcome the shortcomings of high density and easy oxidation of metal series conductive fillers. However, it is also accompanied by defects of the filler coating that easily falls off [
21]. The carbon series conductive filler resources are abundant and they are not easily oxidized when being used, so the physical and mechanical properties of the polymer materials are ensured. Carbon black, which is cheap, can be made from a wide range of raw materials, and has small unit density, is easy to process and shape, gives good dispersions, good effects on the rubber compound, and chemical stability, is generally selected as the carbon-based conductive filler [
22].
The second area of research is the mechanical and electrical mechanism of conductive silicone rubber. The study of the conductive properties of conductive silica gel shows that the essence of the conductive process in conductive silicone is the directional movement of carriers in an electric field. The conductive channels formed by macromolecule inter-chains and sufficient numbers of carriers are two important factors in conducting polymer conductivity [
23]. The conductivity of conductive silica can be explained by the macro mechanism and the micro mechanism [
24]. When the content of conductive particles is low, the conductive particles occupy less volume in the basic body of the silica gel polymer, the resistivity of basic body is large and is basically acts as insulation, so the resistivity of conductive polymer filled with conductive powder is greater [
25]. As the number of conductive particles increases, the percentage in the main material increases, the distance between particles decreases, the motion of electrons in the particles increases and the transition probability increases, so the conductive mechanism can be explained by the microscopic quantum effect [
26]. As the amount of conductive filler increases, the number of particle collisions increases, and can easily form a continuous conductive chain, which explains the macroscopic conductive channel theory. When a conductive network is formed in the compound, the conductivity is basically stable, and further addition of conductive particles has little effect on its conductivity [
27].
The third kind of research is the application of conductive silica in various functional sensing applications. In one-dimensional array tactile sensor research, pressure-sensitive conductive silicone has been widely used in many fields such as artificial muscle [
28,
29,
30], intelligent clothing [
31], active wings [
32] and so on. For example, the force sensitive characteristics of conductive silica gel are applied by some researchers. They weave together conductive rubber sheet and ordinary gloves to get a flexible tactile glove that can sense the action of the human hand [
33]. Conductive rubber has more research results in one-dimensional force flexible tactile sensors because of its excellent force sensitive performance. The conductive rubber is limited by its preparation process (such as rubber basic body, filler, additives, vulcanization, etc.). Its application in multidimensional tactile sensors is relatively limited, but it has begun to develop from one-dimensional force sensing to multidimensional force perception. In recent years, researchers have been trying to make use of force sensitive conductive rubber to make the flexible touch intelligent skins for intelligent robots [
34] and have obtained certain research breakthroughs. Arrays of parallel and stretchable electrodes and piezoresistive elastomeric composites have been commonly utilized to obtain the tactile information from large areas [
35]. However, multi-directional tactile information requires additional stretchable electrodes in a limited space, which increases the difficulties in the fabrication process.
In this paper, a method for inversion of the stress distribution in large deformation conductive silicone rubber is proposed, which provides a theoretical basis for the design of cheap three-dimensional force flexible large deformation sensors.
The key contribution of this work is to establish a three-dimensional electrical characteristic model of conductive silicon rubber under large deformation stress state and then to inverse the distribution of its stress field, which will apply the electrical characteristics of conductive silicone rubber from one dimension to three-dimensional. Firstly, the mathematical model of conductive rubber current field distribution under constant force is established by using effective medium theory and the current field distribution model of conductive rubber under various geometric shapes, abundance of metals, conductive rubber relaxation parameters is deduced. Secondly, the inversion method of the three-dimensional stress field of conductive rubber is established, and the influence of electrode shape, electrode number and electrode position on the three-dimensional stress inversion mechanism under different geometric shapes is studied, which provides a theoretical basis for the design of a new tactile sensor, three-dimensional stress field and space force based on force sensitive materials.
2. Theory
2.1. Conductivity Mechanism
There are three mechanisms in the conductive mechanism of conductive silicone, which include conductive channel [
36], tunnel effect [
37] and field emission mechanism [
38], but the contribution of each one differs under different conditions. When the content of conductive filler is high, the spacing of conductive particles is short, so it is easy to form conductive channel chains. At this time, the conduction mode is mainly via the conductive channel, and the seepage mechanism is obvious. When the content of conductive filler is less and the voltage is low, the distance between conductive particles is larger, it is not easy to form chains of conductive channels, and thermal vibration induces electronic transitions to form tunneling currents, so the tunnel effect theory plays a leading role. When the content of conductive filler is less, and the voltage is higher, the electric field of conductive particles is very strong and the field emission effect theory plays a major role.
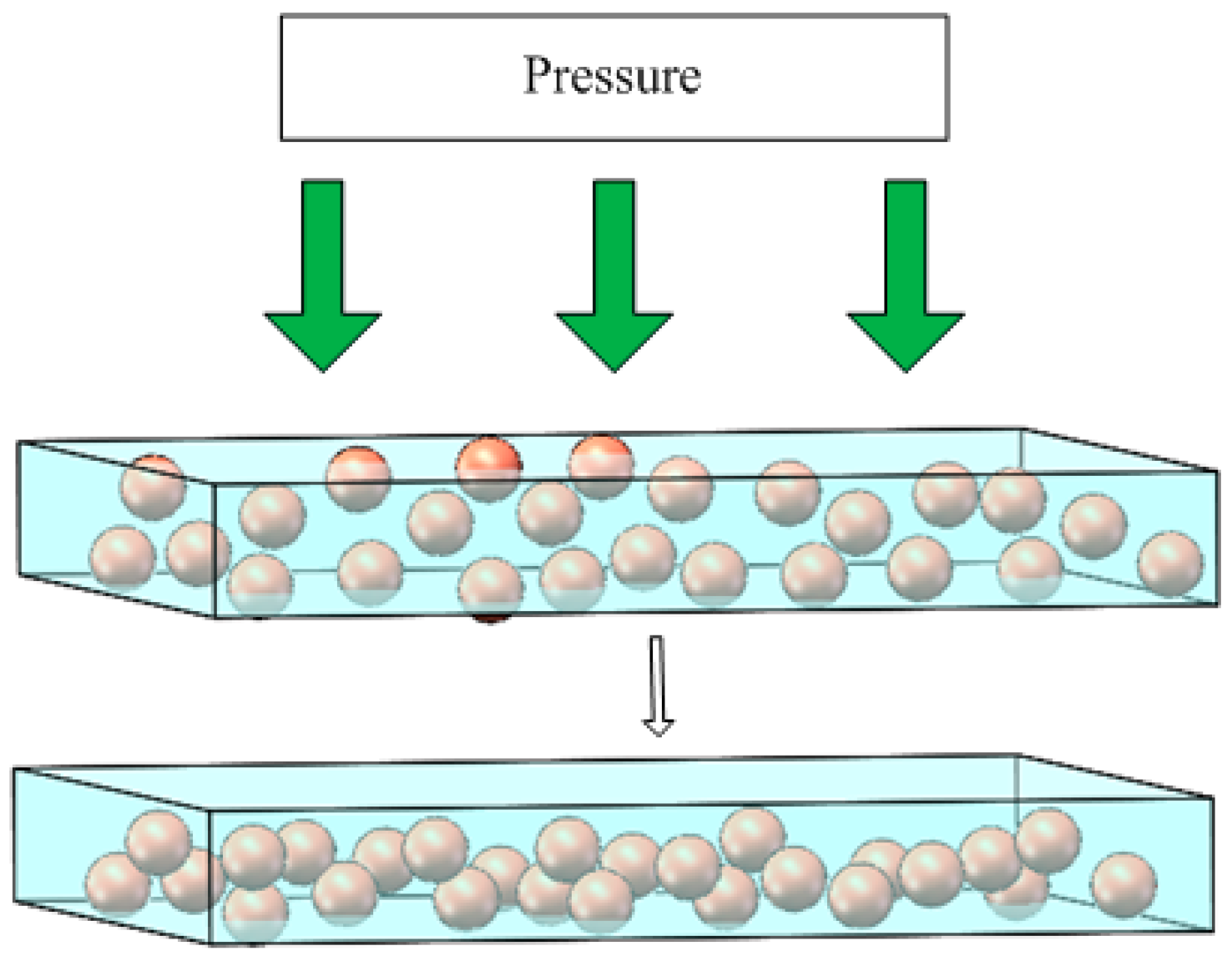
The conductive mechanism of conductive silica gel should be the result of the interaction of conduction channel theory and tunneling current theory. In short, the actual conductive mechanism of conductive silica is rather complex, and the final result will be the comprehensive effect of various conductive mechanisms. Conductive particles with different sizes and shapes are evenly distributed in the insulation matrix. When the volume fraction of the filler reaches a critical value, the conductive particles or aggregates contact each other, forming a large number of conductive network channels, and the resistivity drops sharply.
Figure 1 shows the contact of conductive particles with each other to form conductive channels.
McLachlan et al. proposed a general effective medium model [
39] to account for the conductive mechanism of composite polymeric materials with particle fillers. The general effective medium equation is:
In the formula: is the volume fraction of conductive filler; is the critical percolation threshold; is the conductivity of the substrate; is the conductivity of conductive filler; is the conductivity of the composite; is the percolation coefficient of composites.
Because the conductivity of the conductive particles is far greater than that of the rubber matrix,
, To
,
, and Equation (1) can be simplified to:
Obtained by Ohm’s law, the resistance
of the conductive composite material is:
where
,
is geometric coefficient of resistance;
is thickness of conductive composite,
is cross-sectional area,
is the resistivity of conductive silicon.
When the applied stress is between 0 and 2 MPa, the change of Poisson’s ratio
and Young’s modulus
is small.
is the pressure of the material. Conductive silicone rubber can be considered as ideal elastomer:
Integrating Equation (4):
where
is the geometric coefficient of resistance without load. The volume fraction of the conductive filler is
, where
is the volume of the conductive filler,
is the total volume of the silicone material, and its differential can be:
The metal filler can be seen as a rigid body, its volume change is approximately zero, that is
, then Equation (6) can be simplified to:
The conductive silicone rubber is ideal elastomer
, substituted into Equation (7):
Integrating gives Equation (8):
where,
is the volume fraction of metal under no external force, so substituting Equation (9) into Equation (2):
where
,
,
is the strain of conductive silicone rubber under stress. After further simplifying the formula we can get:
where
is volume strain. Equation (11) describes the relationship between the resistivity and volume strain of conductive silicone rubber.
2.2. Current Field Model
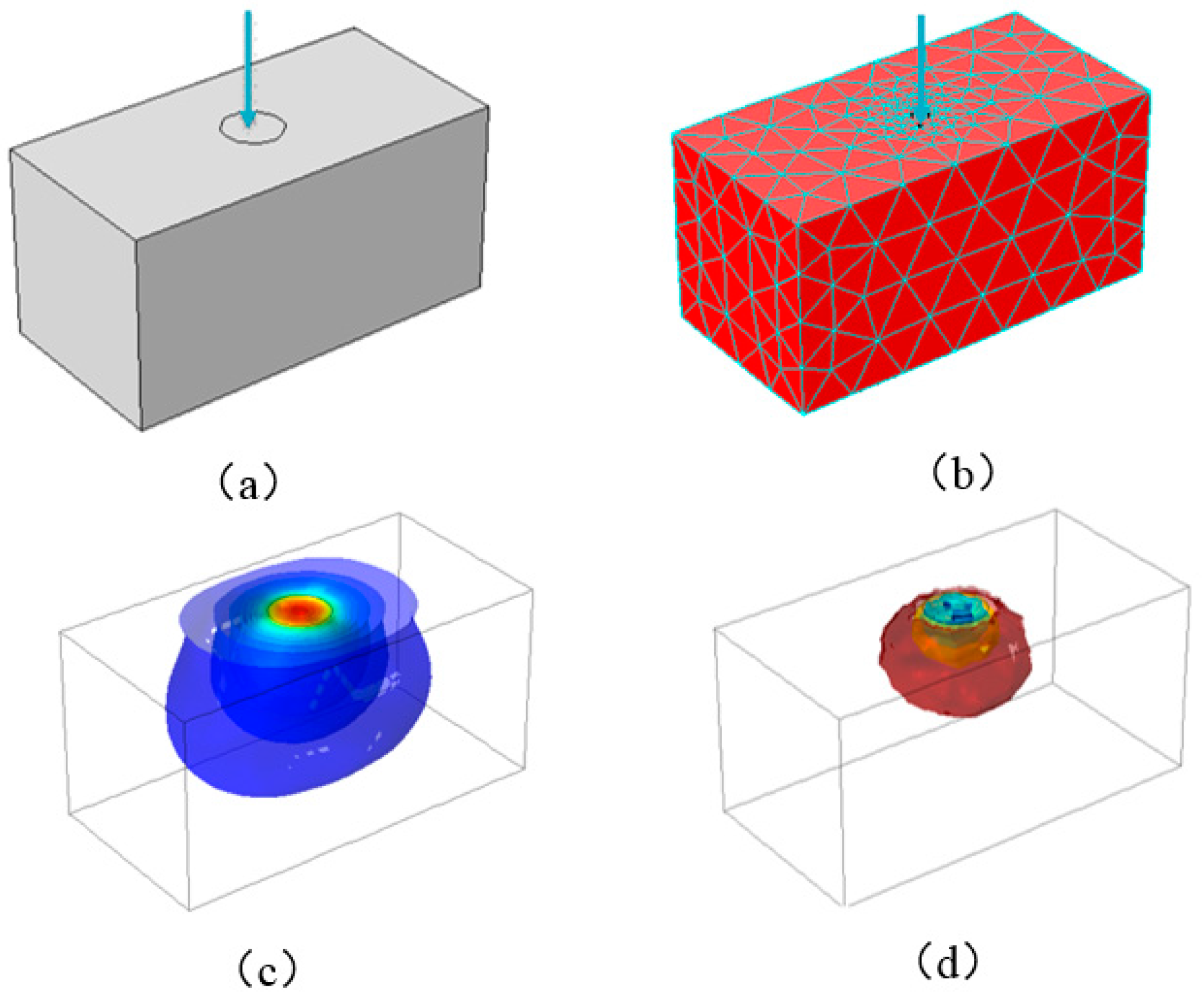
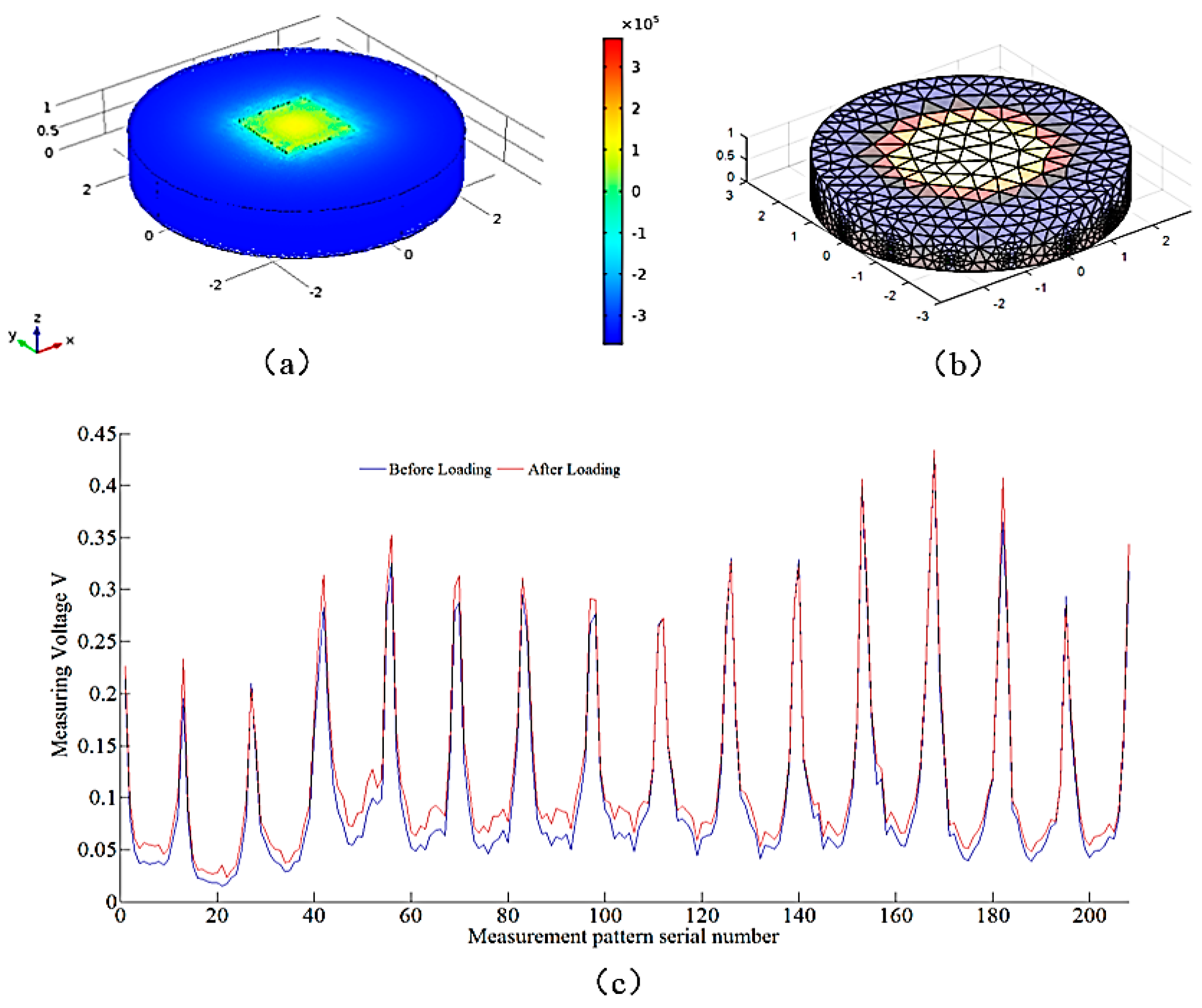
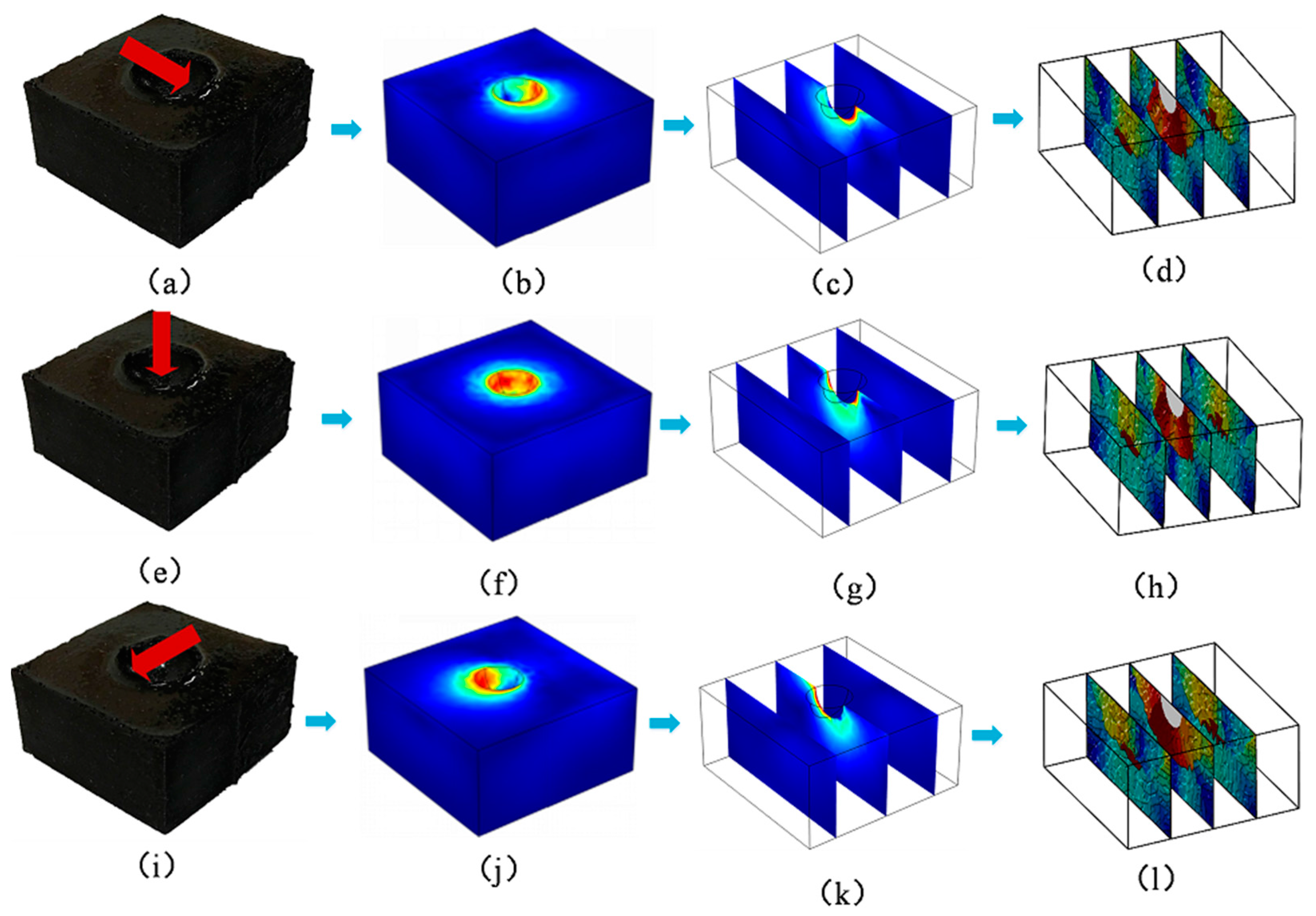
The resistivity of conductive silicone rubber is related to its volumetric strain. Suppose a piece of conductive rubber is subjected to the pressure shown in
Figure 2a.
Figure 2b–d are the three-dimensional stress distribution obtained by finite element analysis, It should be mentioned that the deformation of rubber usually be modeled by large deformation computational methods, such as nonlinear FEM and nonlinear discrete models [
40,
41].
Figure 2a is a schematic diagram of a conductive silicone rubber under the external force.
Figure 2b is a finite element model of conducting silicon rubber under the external force.
Figure 2c is the three-dimensional stress isometric surface of the conductive silicon rubber under the external force.
Figure 2d is the conductivity isometric surface.
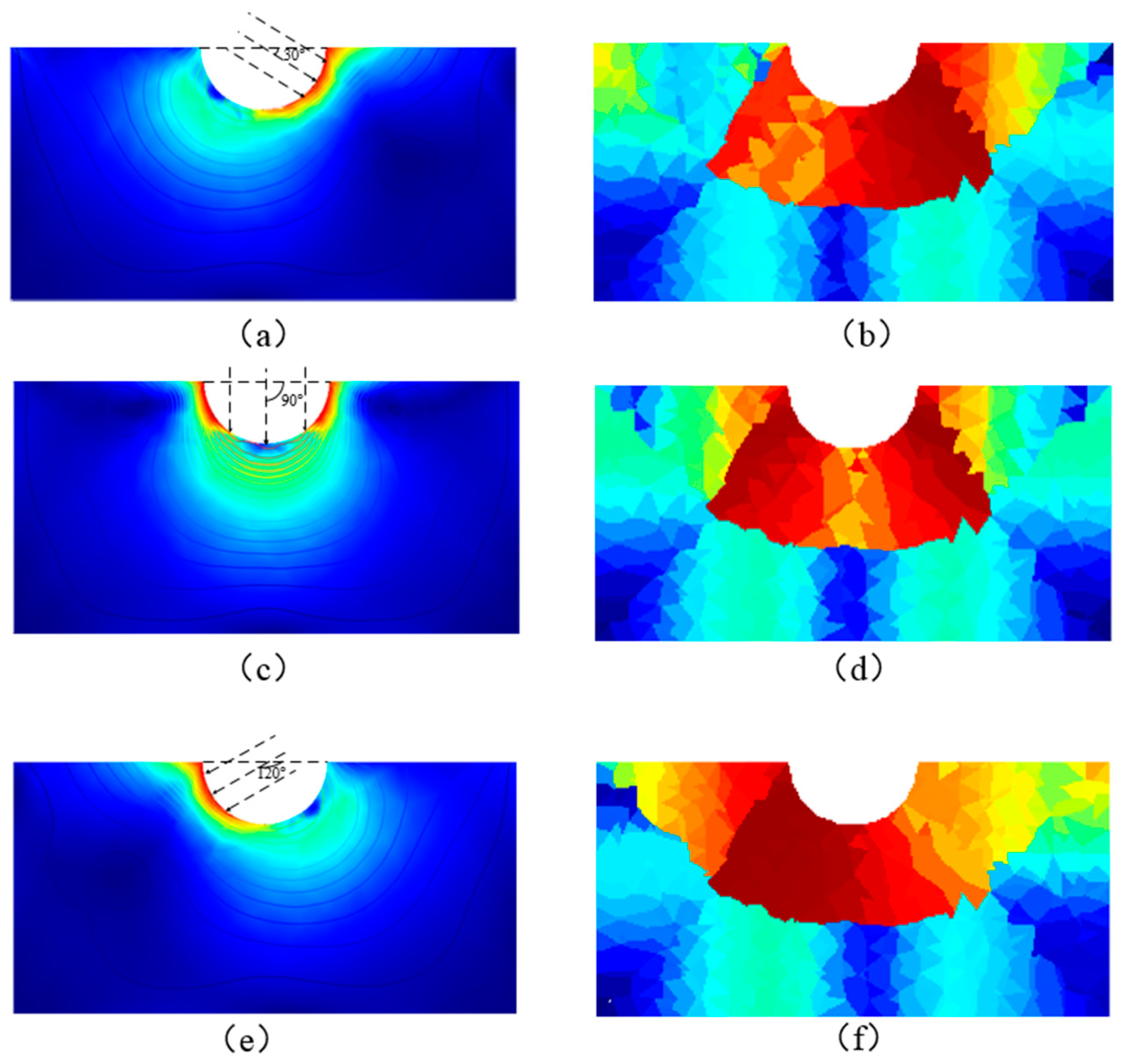
Therefore, if the resistivity distribution of the conductive silicone rubber can be obtained, the stress distribution can be reflected, and the direction and magnitude of the force can be analyzed. If a constant current source is applied to a variety of resistivity conductors, the voltage difference between any two points on the conductor surface can be measured. Through a series of potential differences, we should theoretically be able to reverse the distribution of internal resistivity. In order to achieve the above goal, we need to study the model of electric potential distribution in constant current excitation.
To solve the potential distribution of conductive silicon rubber under constant current excitation, which can be considered as the solution of steady field, one of the core implications of stable field is that the transmission time of current from one point to another can be ignored. Because there is no excitation source in conductive silicon rubber, the divergence of current in the solution domain is zero. Any point of the conductive silica satisfies the following formula:
where
is normal vector on the outer boundary,
is electric-field strength,
is electronic conductivity,
is potential distribution in the field,
is excitation current.
After establishing the field model under the excitation of constant current source of conductive silica, the analytic expression of the potential distribution in the field can be obtained by a theoretical method and the analytical result of the measured voltage in the boundary state can be obtained. The derivation of this method is complex, and it is suitable for the calculation of the potential distribution of conductive silica gel with simple two-dimensional shape or a simple non-homogeneous state. However, the analytical solution is difficult to obtain for the complex non homogeneous field with irregular shape and various 3-d fields. The finite element method is a general method to solve the above problems, which called grid method and discretizes the mesh in the field and boundaries. It converts the potential function in a continuous field into a set of discrete nodal potential functions. Through using the difference principle, the difference quotient of the potential function at discrete points is used instead of the partial derivative of this point, which transforms the boundary value problem into a set of algebraic equations. In the form of matrix, the finite element equations under constant current excitation of conductive silica gel are obtained:
where
is the number of total nodes of the field.
is the coefficient matrix of total electric field, which is a large, symmetric and positive definite sparse matrix.
is the voltage vector of all nodes in the field.
is consisted of unit load matrix
is zero for all quadrilateral elements that are not touched by all excitation sources. For the quadrilateral elements of the boundary and adjacent to the excitation element, the values of
are calculated by the following formula:
where
,
are the shape functions of node
respectively, and the expressions are:
2.3. Sensitive Field Analysis
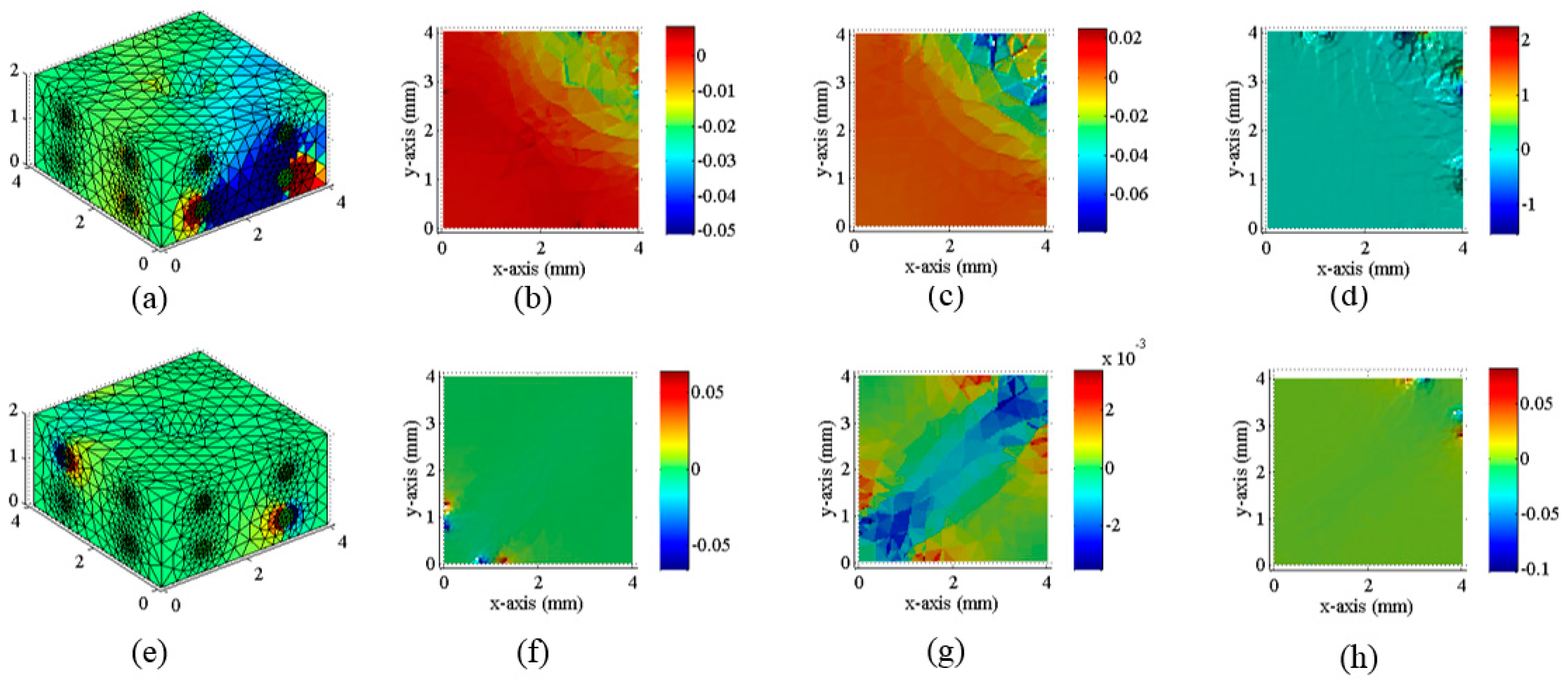
When the conductive silicone is loaded, the conductivity in the sensitive area will change, which will cause a change in the measured voltage of the boundary. Assume that the conductivity of conductive silica gel is uniform, its conductivity is . The excitation current is applied to the m-th pair of electrodes, the voltage measured on the nth pair of the electrodes is . When a slight change in conductivity in a certain micro domain is , the voltage value measured on the corresponding nth pair of electrodes is .
If
is small enough, the distribution of the potential equipotential surface in the sensitive field can be considered to be unchanged, then the change of measurement voltage is proportional to the conductivity. The ratio constant
is defined as the sensitivity coefficient of conductive silica gel:
where
is the sequence number of the excitation electrode,
is the sequence number of the measuring electrode, and
is the coordinate value of the sensitivity coefficient formula. The calculation of sensitivity coefficient can be converted into integral formula by compensation principle of Gese-Lowitz. Then the finite element method is used to calculate the following formula:
where subscript
represents the
i-th independent measurement.
represents the
j-th element
,
are the nodal potential distribution in the uniform conductivity distribution field. When excited current,
,
are applied to the
m-th and
n-th pair electrode, respectively.
is the volume of the
j-th elements.
,
is the potential of
nodes of the element
.
is the finite element coefficient matrix of element
.
2.4. Stress Field Inversion
The distribution of resistivity of conductive silica gel can be obtained by the load state of conductive silicone. If we can obtain the conductive silica gel conductivity distribution, the conductive silica loaded state can naturally be reversed. Therefore, the problem of stress field inversion is converted into solving the distribution of conductivity of conductive silica gel under the condition of the electrode potential difference of the known boundary measurement.
In the ideal noise-free conditions, the voltage of the measured electrode under the excitation of the constant current source can be expressed as a uniform operator equation. As shown in the following equation:
where
is the potential difference of the electrode pair,
is forward operator, and
is the conductivity distribution in the conductive silica gel. After Equation (18) is linearized, the relationship between the voltage difference
and the conductivity difference
can be obtained by the Taylor expansion method:
If
is very small, the higher order term in Equation (19) can be ignored, then Equation (19) can be reduced to:
where
S is called the sensitivity matrix, assuming that the sensitive field is divided into
m elements, a total of
n alone measured data. After the Equation (20) is discretized and normalized, the following equation can be obtained:
where
is the measured voltage vector after dimension normalization,
is the sensitivity matrix after
dimension normalization, and
is the conductivity distribution vector after
dimension normalization. The problem of conductivity reconstruction is the key to the reversal of stress field of conductive silica gel. The problem can be classified mathematically in the process of reversing the problem Equation (18):
The approximate linear solution of the inverse problem can be expressed as:
According to the voltage value of the electrode pairs, the stress distribution of the conductive rubber is equivalent to the resistivity distribution of the reversal conductive rubber, which is equivalent to solving the normalized gray value (it is proportional to that conductivity distribution of the material)
. The gray value
can be obtain according to an inversion algorithm; Landweber is a common iterative algorithm with the following iterative formula:
where
represents the number of iterations,
represents the image gray value at the time of the
th iteration,
represents the gain factor and
;
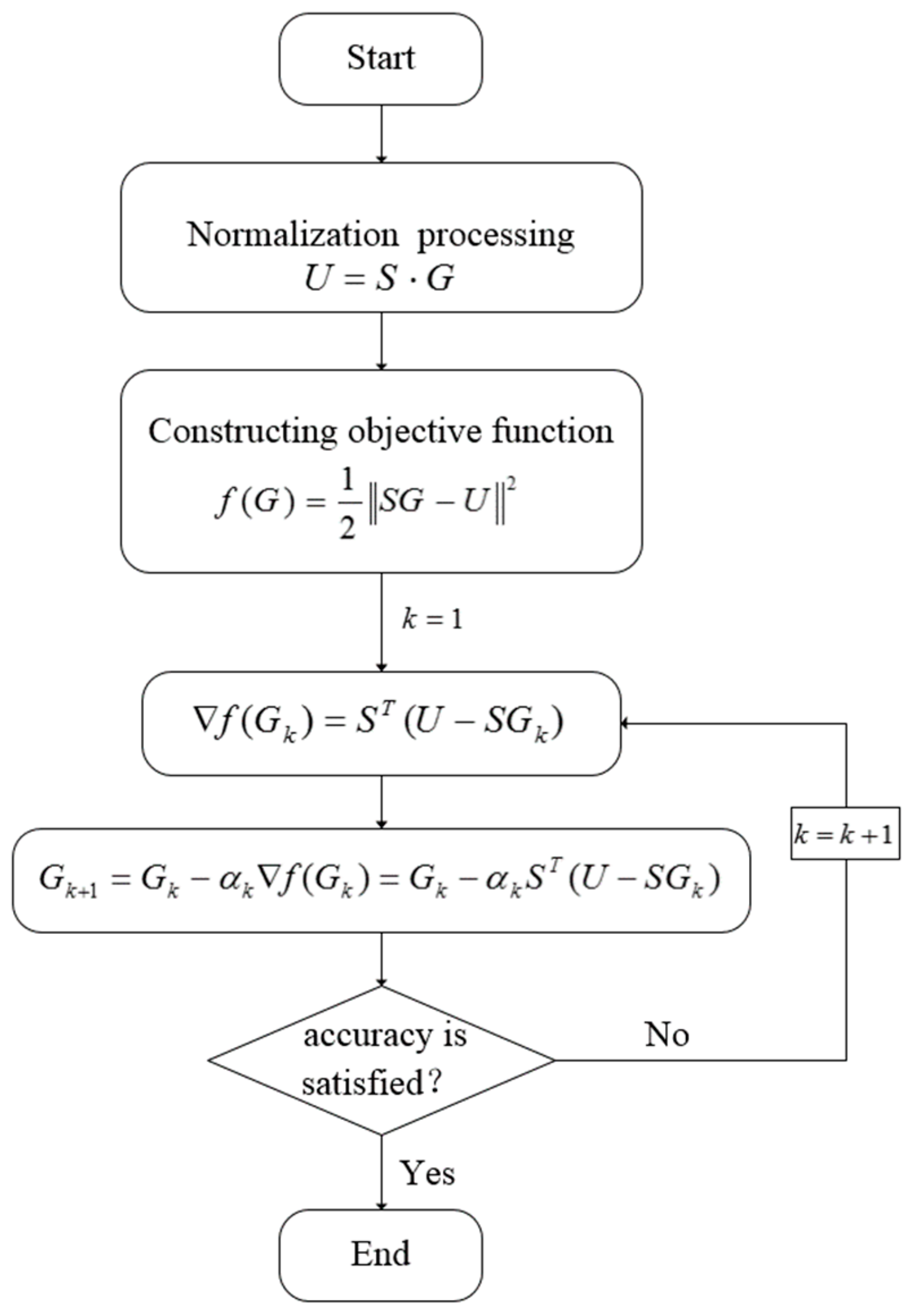
The Landweber inversion algorithm is shown in
Figure 3:
- (1)
The sensitive field is divided into a plurality of elements by finite element subdivision, and the sensitive field is normalized;
- (2)
Construct precision objective function. Image reconstruction according to the voltage value of the measurement electrode is equivalent to solving the normalized gray value . This problem can be evolved into an optimization problem, assuming that any given normalized gray value , according to , a theoretical calculated voltage value, then solve the gray value can be attributed to the optimization problem of the objective function;
- (3)
Set the iteration coefficient ; Update and calculating accord to an iteration formula;
- (4)
Judge whether reach a specified precision threshold value or not, and if so, taking as a final gray value; If the specified precision threshold is not reached, until the precision requirements are met.
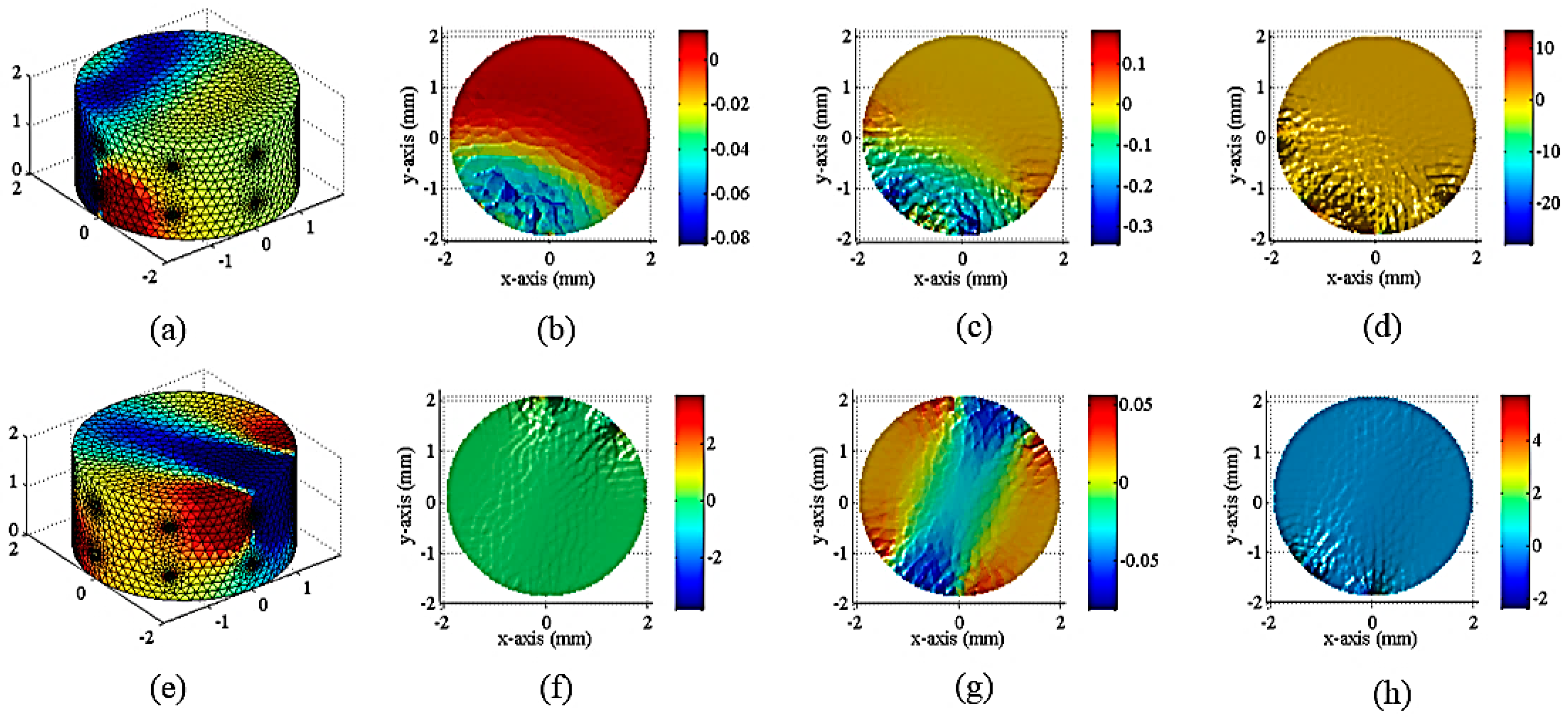
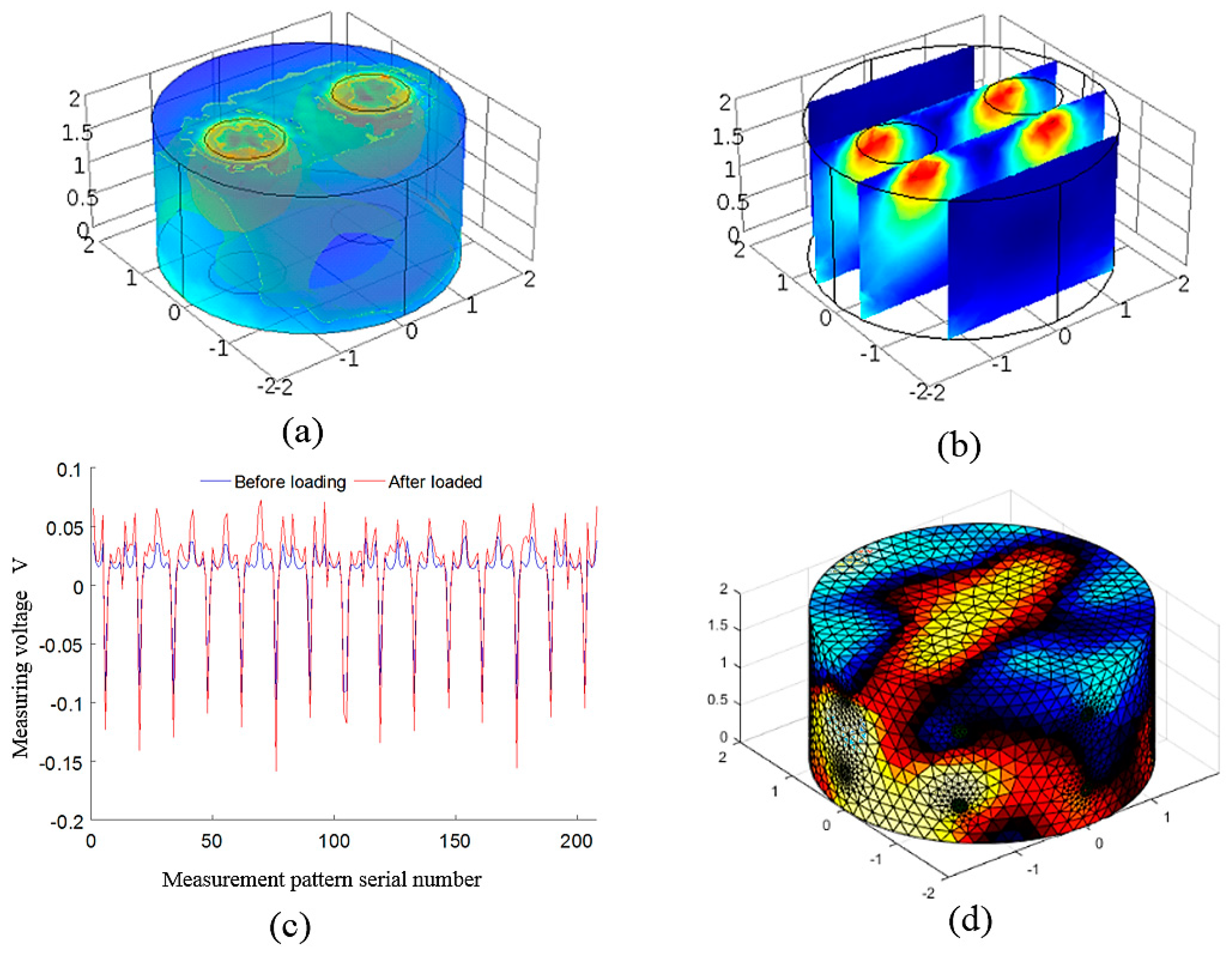
According to the relationship between conductivity and volume strain, the distribution of volume strain can be obtained. And then the stress distribution can be obtained.
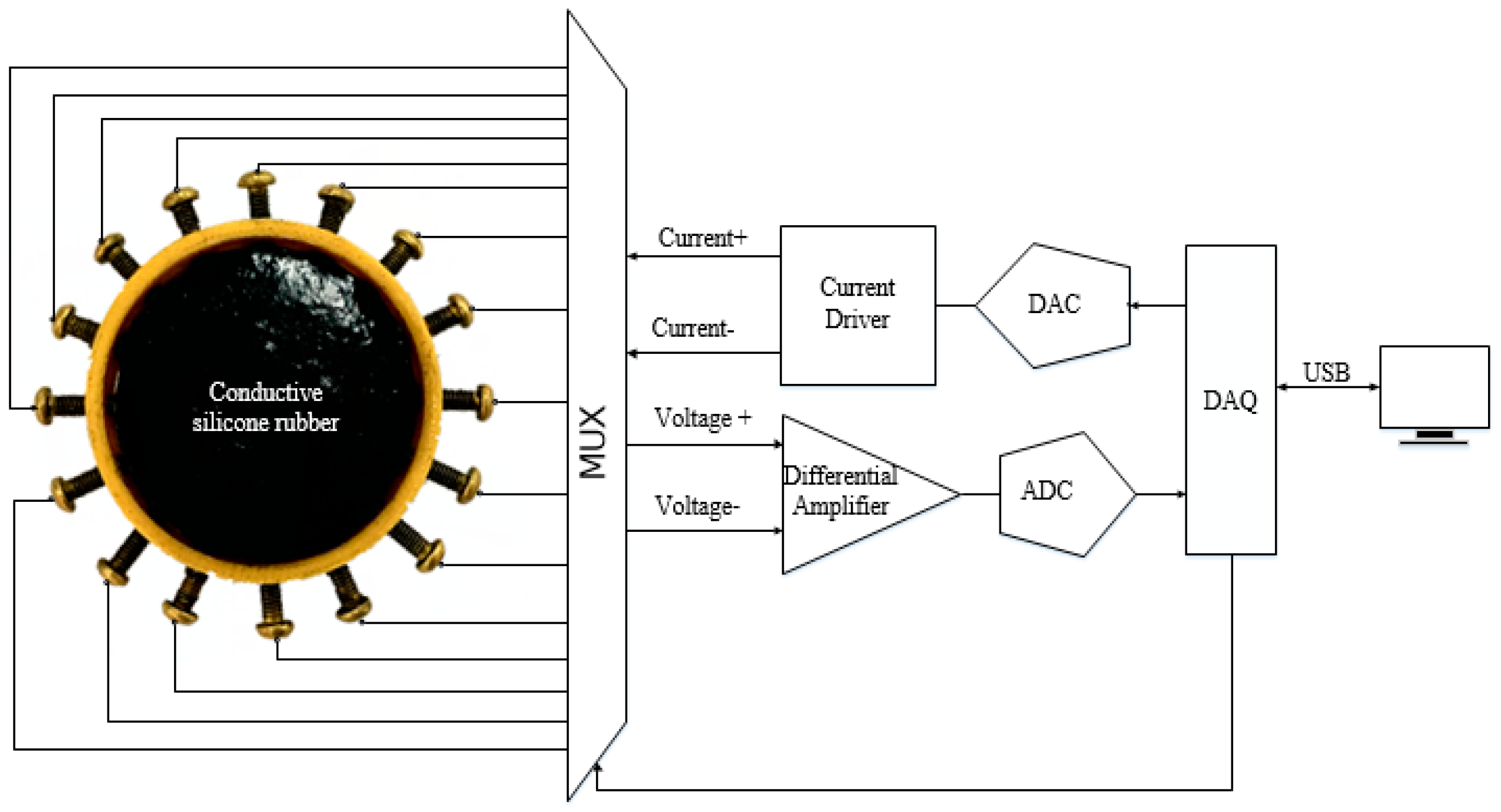
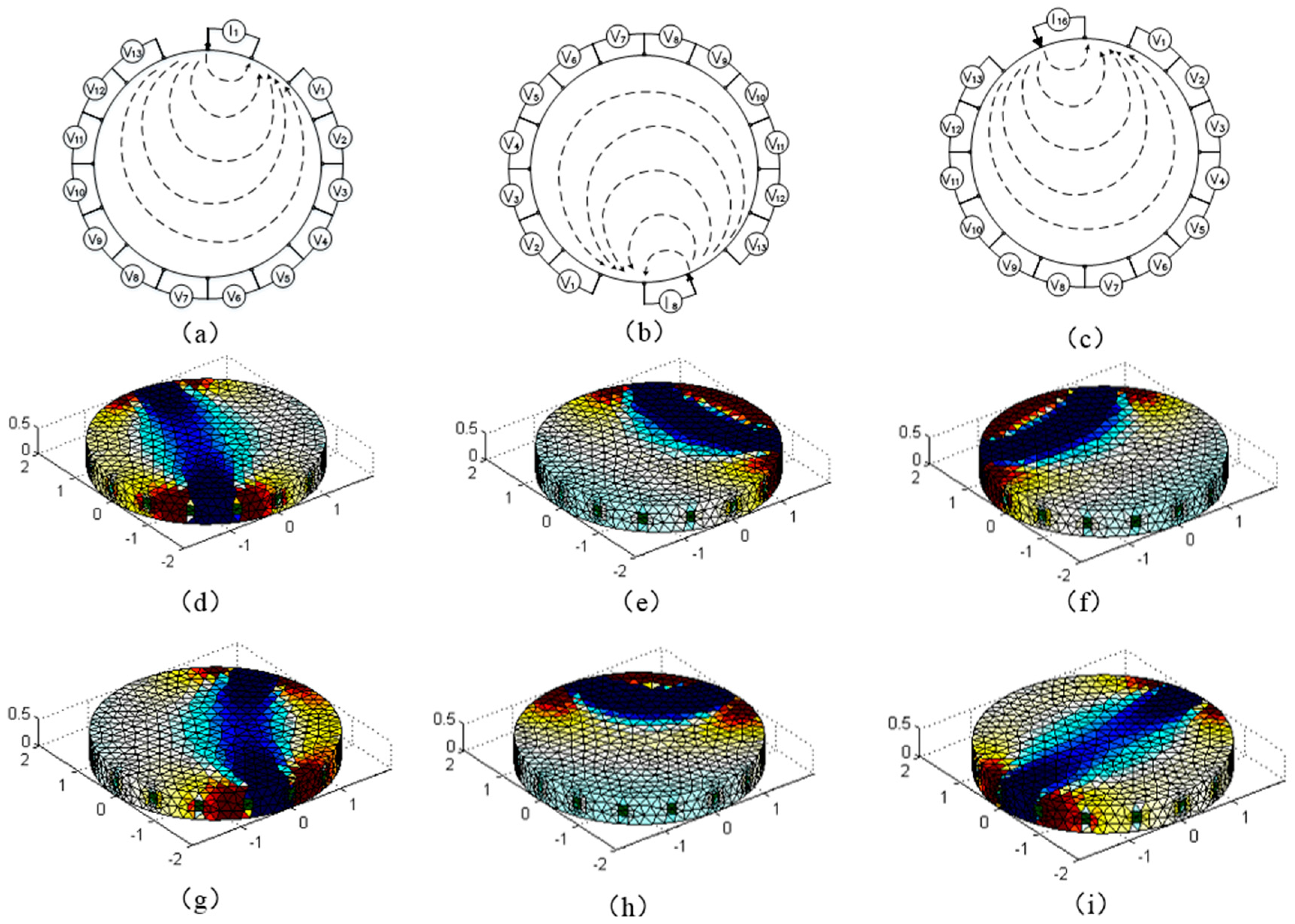
The measuring device of internal stress distribution of conductive silica gel is shown in
Figure 4. A series of conductive electrodes are arranged on the side of conductive silica gel. The conductive electrode is connected with a conductive adhesive for conductive rubber.
The conductive electrode is connected with a multiplex switch circuit which is controlled by a computer. A constant current source is injected into the conductive rubber through the electrode by a preset excitation sequence. The other electrode acts as the voltage collector to collect the voltage value of the adjacent electrodes. The voltage signal is input to the data acquisition card through the differential amplifier circuit, which will store the collected voltage signals to the computer according to certain rules .The rule refers to the order selection rules of constant current source excitation and measurement of the electrode affixed with conductive silica gel. Taking the circular silica disk in the illustration as an example, the sequence of excitation and measurement is: first, No.1 and No.2 electrodes on constant current I, measuring voltage of 2–3, 3–4, …, 15–16 on measurement circuit. The second, No.2 and No.3 electrodes connect constant current source I and measurement circuit to measure the voltage of 3–4, 4–5, …, 1–2, respectively.
By analogy, the excitation and measurement of all electrodes are completed. According to the measured voltage value, the gray distribution of representative resistivity can be obtained, and the stress field distribution can be obtained. The device can be used as a sensing device for plane stress, such as sensing the stress distribution of human body pressure [
42].
4. Materials and Methods
4.1. Preparation of Conductive Silicon Rubber
We use conductive silicone rubber as the pressure-sensitive sensing material, which be made by mixing conductive carbon black (BP2000, CABOT, Boston, MA, USA) and silicone rubber. The preparation process is as follows:
Step 1: The conductive carbon black (BP2000) was dispersed: The conductive carbon black was mixed with anhydrous ethanol and stirred for 10 min by electric mixer. It was dispersed for 30 min by ultrasonic dispersion machine, and dried for 3 h in vacuum drying oven (60 °C, 0.08 MPa), Finally, we obtain a dispersed uniformly conductive carbon black.
Figure 14 is the dispersion process of conductive carbon black.
Step 2: Petroleum ether (The quantity is 10 times that of the conductive carbon black) is mixed with Si-69 coupling agent (the mass is 5% of the silicone rubber). The conductive carbon black with 10% mass fraction was added, stirred for 10 min by electric mixer, and dispersed for 30 min by ultrasonic dispersion machine.
Step 3: The 107 silicone rubber was added to the mixture, and stirred for 5 min by electric mixer, and dispersed for 30 min by ultrasonic cleaning machine to distribute the conductive carbon black evenly in the silicone rubber. In order to accelerate the reaction, tetraethyl orthosilicate (7% mass fraction) and dibutyltin dilaurate (5% mass fraction) were added.
Step 4: Put the mixture into a vacuum drying oven and vacuum for 5 min at room temperature. The resulting viscous mixture is poured into a different mold to allow it to be completely cured for 24 h and made into circular, cylinder, rectangular conductive silicone rubber.
Figure 15 shows the preparation details of the conductive silicone rubber.
4.2. Measuring Device
In order to evaluate the effectiveness and accuracy of the proposed inversion method for the internal stress distribution of conductive silica gel, it needs to be tested by experiments. So far, however, no method has been found to measure the stress distribution of non-transparent non-metallic materials. Magnetic measurements are often used to measure the residual stress of metal. The principle of magnetic measurement is to determine the magnitude and direction of residual stress by measuring the change of permeability of ferromagnetic materials under the action of internal stress.
The material of force-sensitive sensing material used in this paper is conductive silica gel. It is not a ferromagnetic material, so it cannot be used to measure the three-dimensional stress distribution inside the material by magnetic measurements. In order to evaluate the correctness of the method described in this paper, the stress distribution of conductive silica gel can only be obtained by finite element analysis. The key of finite element analysis is to obtain the mechanical constitutive parameters of conductive silica gel, such as elastic modulus, young’s modulus, compression modulus, shear modulus and so on. Then we can get the three-dimensional stress distribution of conductive silica gel by finite element analysis.
4.2.1. Measurement of Physical Parameters
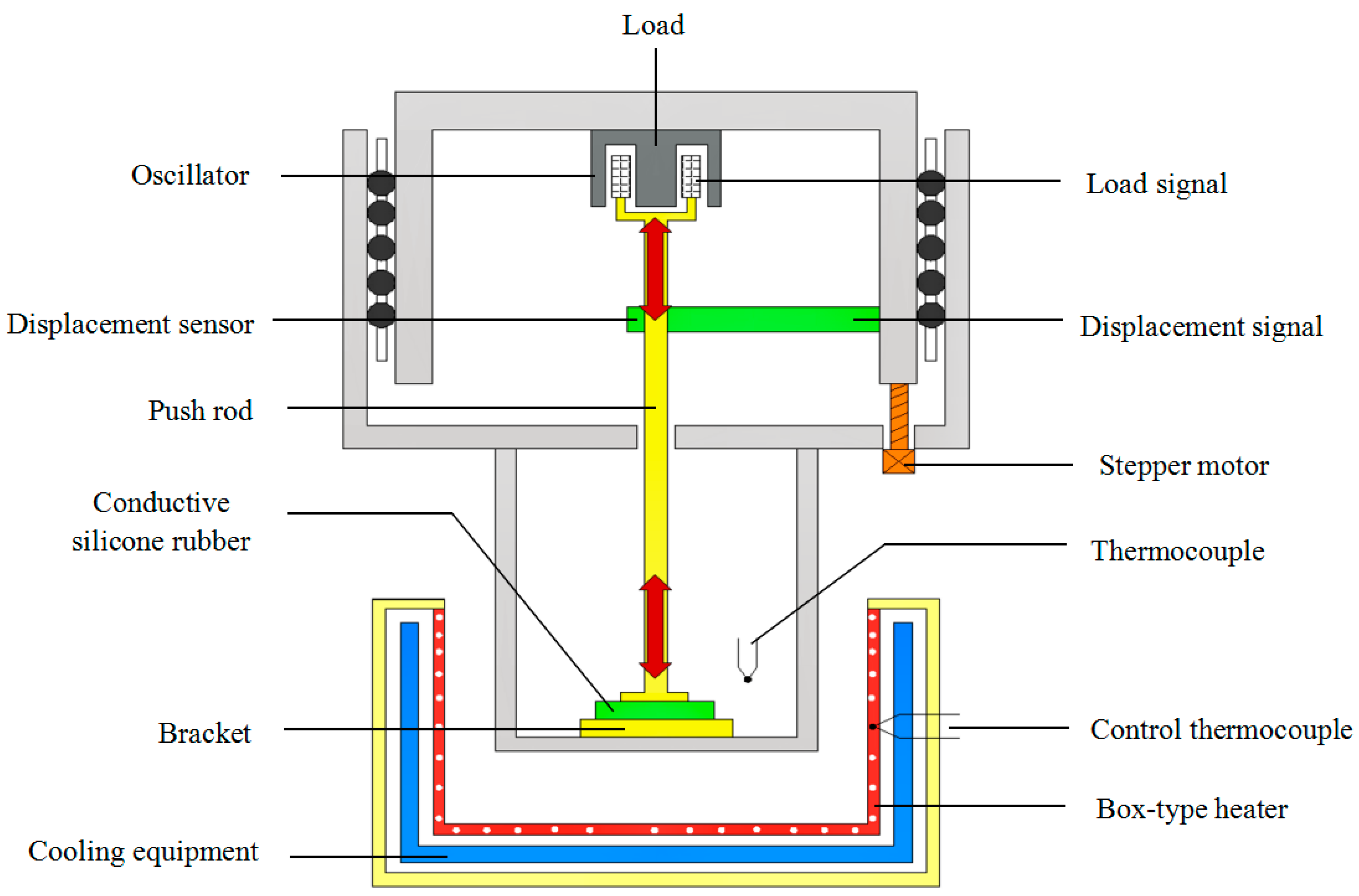
In order to observe and record the mechanical parameters of conductive silica gel, the conductive silicone rubber was cut into the sample of
3 specification. And the mechanical parameters of conductive silicone rubber were determined in the dynamic thermal analyzer (DMA 242, NETZSCH, Bavaria, Germany), which is a periodic oscillation force applied to the conductive silica gel sample under certain temperature control program. The corresponding deformation amplitude and hysteresis of conductive silica gel are measured to calculate and obtain the relevant characteristic parameters such as elastic modulus, loss factor and so on.
Figure 16 and
Figure 17 are respectively the measurement principle of DMA and a real live-action of the conductive silica gel mechanics test.
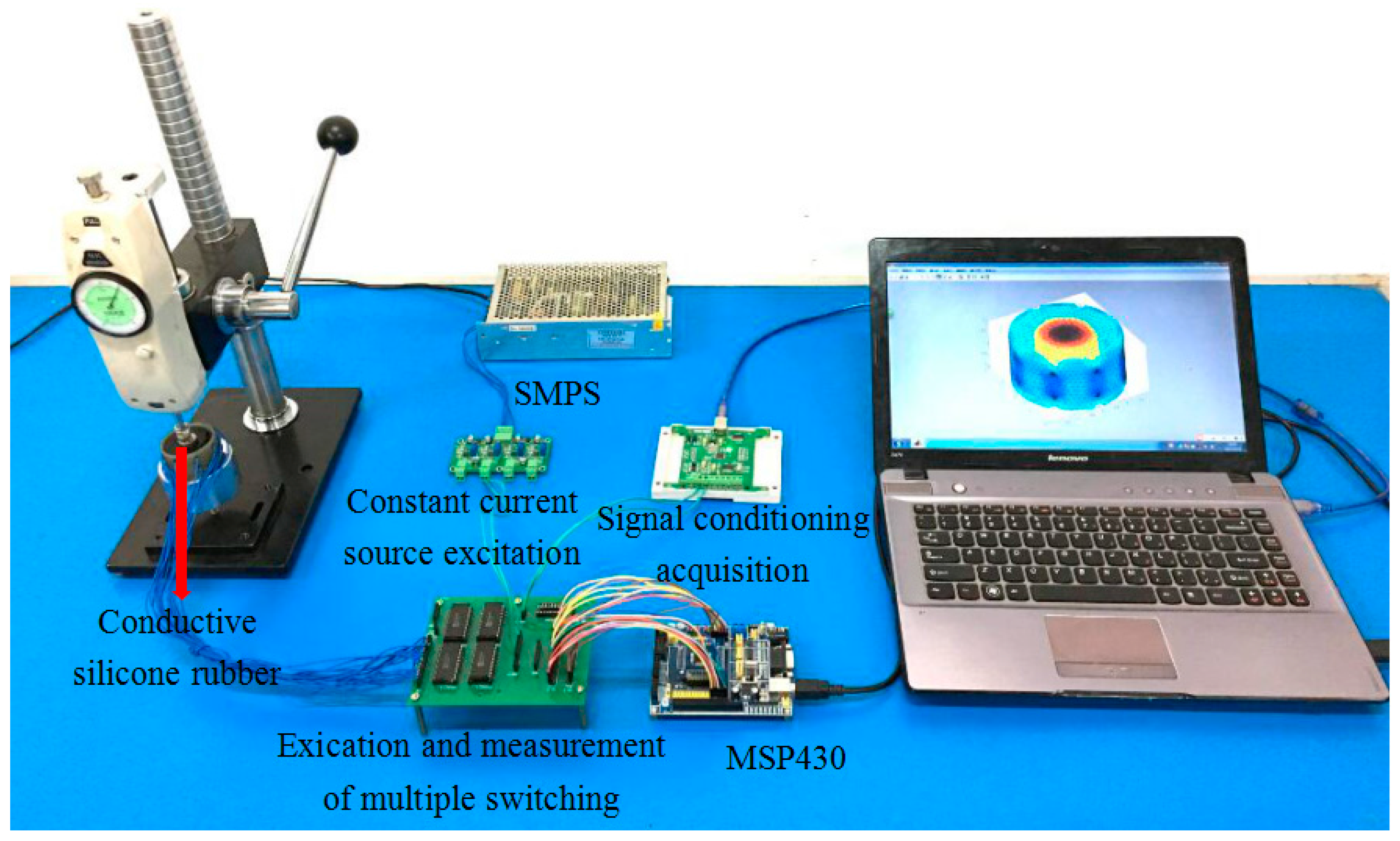
4.2.2. Voltage Measurement between Conductive Silica Electrodes
Sixteen electrodes that form a copper bolt with a diameter of 3 mm were evenly arranged around the conductive silicone rubber. In order to reduce the contact resistance at the measurement, we embed the electrodes inside the conductive rubber. The measurement of the voltage between the electrodes is as follows: the multi-channel selection module for excitation and measurement is connected to the conductive silicone rubber electrode. First, the microcontroller sends the control signal to the incentive multiple selection module. According to the preset excitation and measurement mode, the microcontroller unit takes turns to apply the excitation current of 8 mA to a pair of electrodes, and the sensitive field is established within the conductive silicone rubber. Then the microcontroller unit sends out the signal to the signal acquisition module. According to the given method, the voltage between the electrodes is measured, and the sampling frequency is 1 kHz.
Figure 18 is an electrode voltage measurement device around the conductive silicone rubber.
5. Conclusions
In this paper, a three-dimensional visualization method of silica gel stress field based on three-dimensional resistance tomography is proposed by using the piezoresistive effect of silica gel with conductive particles. The benefits of this approach are that the three-dimensional visualization of the internal stress of the silica can be carried out by the limited electrode on the surface of the silica gel, and the stress evolution of the conductive silica can be observed dynamically, which overcomes the shortcomings of the traditional dot matrix silica gel stress sensing device that cannot obtain the three-dimensional distribution of the stress in silica gel. Critical components of this work are the fabrication of conductive silicone composites with induced strain and a 3D resistance tomography inversion algorithm based on constant current excitation. The 3D stress distributions are computed from the voltage potentials measured at the electrodes on the boundary of the conductive silicone. This approach could be used to realize multi-directional strain distribution sensors with large coverage area and three dimensional contoured shapes. A remaining technical challenge is the enhancement of the 3D stress distribution of conductive silicone and calculation accuracy in the 3D resistance tomography inversion algorithm. The experimental results show that the proposed method can reflect the three-dimensional distribution of stress in conductive silica gel. This also implies that the method has a strong potential in the application of flexible three-dimensional force sensing.
Compared with the traditional mechanical tactile sensor, the sensor studied in this paper has the following advantages: (1) compared with the existing force sensor, the new three-dimensional stress sensor proposed in this paper has the characteristics of needing less measuring electrodes, simple structure and so on; (2) the sensor can be made into any desired shape according to the application situation, and the application scene of the sensor is thus widened; (3) the three-dimensional stress field sensing method based on electrical resistance tomography can invert the stress distribution of piezoresistive sensitive materials, and has higher time resolution and dynamic measurement of stress distribution state although the spatial resolution is low; (4) it not only can obtain that stress distribution on the surface of the sensing material, but also can obtain the stress distribution state inside the sensing material. The technique can be applied to real-time stress detection of seal rings to avoid tragedies similar to the one caused by failure of the seal of the Challenger Space Shuttle. In addition it can also be used for the perception of intelligent robots’ flexible joint three dimensional force.