Structured Kernel Subspace Learning for Autonomous Robot Navigation †
Abstract
1. Introduction
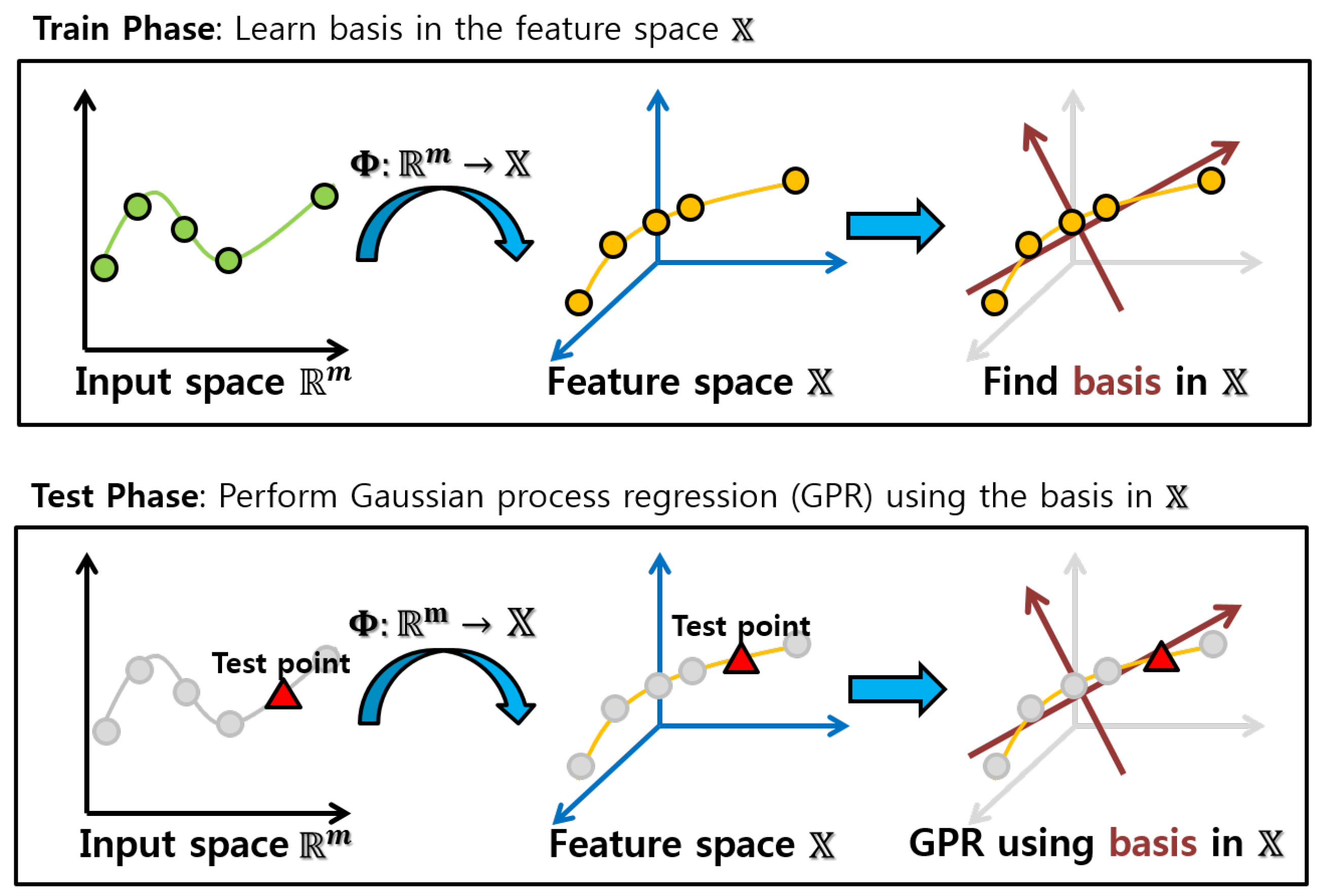
2. Kernel Subspace Learning
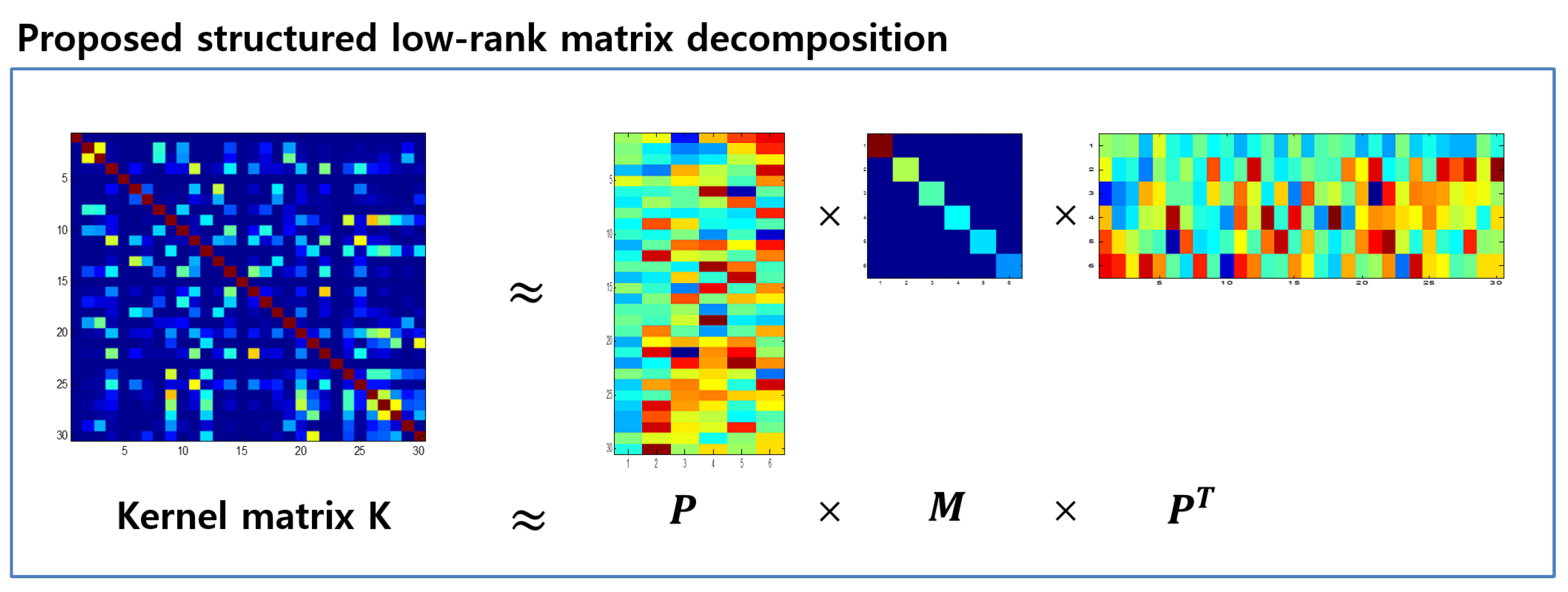
3. Proposed Method: FactGP
3.1. Formulation
3.2. Algorithm
| Algorithm 1 FactSPSD () | |
| 1: | Input: , rank r, , , and |
| 2: | Output: and |
| 3: | Initialization: and |
| 4: | while not converged do |
| 5: | while not converged do |
| 6: | Update M by Equation (12) |
| 7: | Update where |
| 8: | Update by Equation (17) |
| 9: | Update D by Equation (14) |
| 10: | end while |
| 11: | Update the Lagrange multipliers and by Equation (18) |
| 12: | Update |
| 13: | Check the convergence condition |
| 14: | end while |
| Algorithm 2 FactGP | |
| 1: | Input: , rank r, and |
| 2: | Output: |
| 3: | // Training |
| 4: | Compute |
| 5: | Perform kernel subspace learning: |
| 6: | = FactSPSD() |
| 7: | |
| 8: | Compute R and by performing PCA to L |
| 9: | // Testing |
| 10: | Compute |
| 11: | Compute by Equation (5) |
4. Proposed Method: FactGP
4.1. Gaussian Process Motion Controller
4.2. FactGP
| Algorithm 3 FactGP | |
| 1: | Input: , , , rank r, and |
| 2: | Output: |
| 3: | // Training |
| 4: | Compute |
| 5: | = FactSPSD() |
| 6: | |
| 7: | Compute and by performing PCA to |
| 8: | using Equation (2) |
| 9: | |
| 10: | // Testing |
| 11: | Compute |
| 12: | Compute |
5. Experimental Results
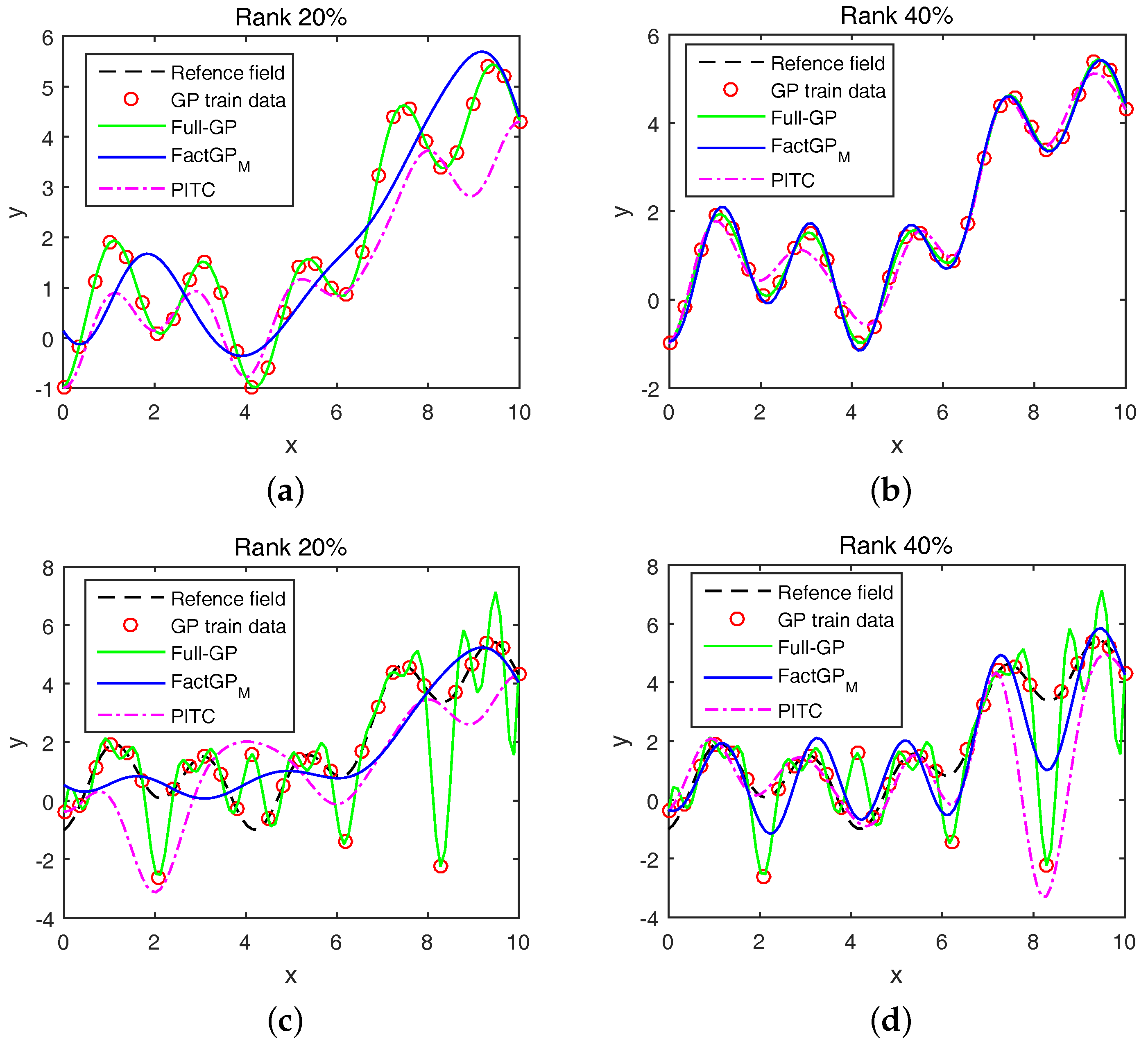
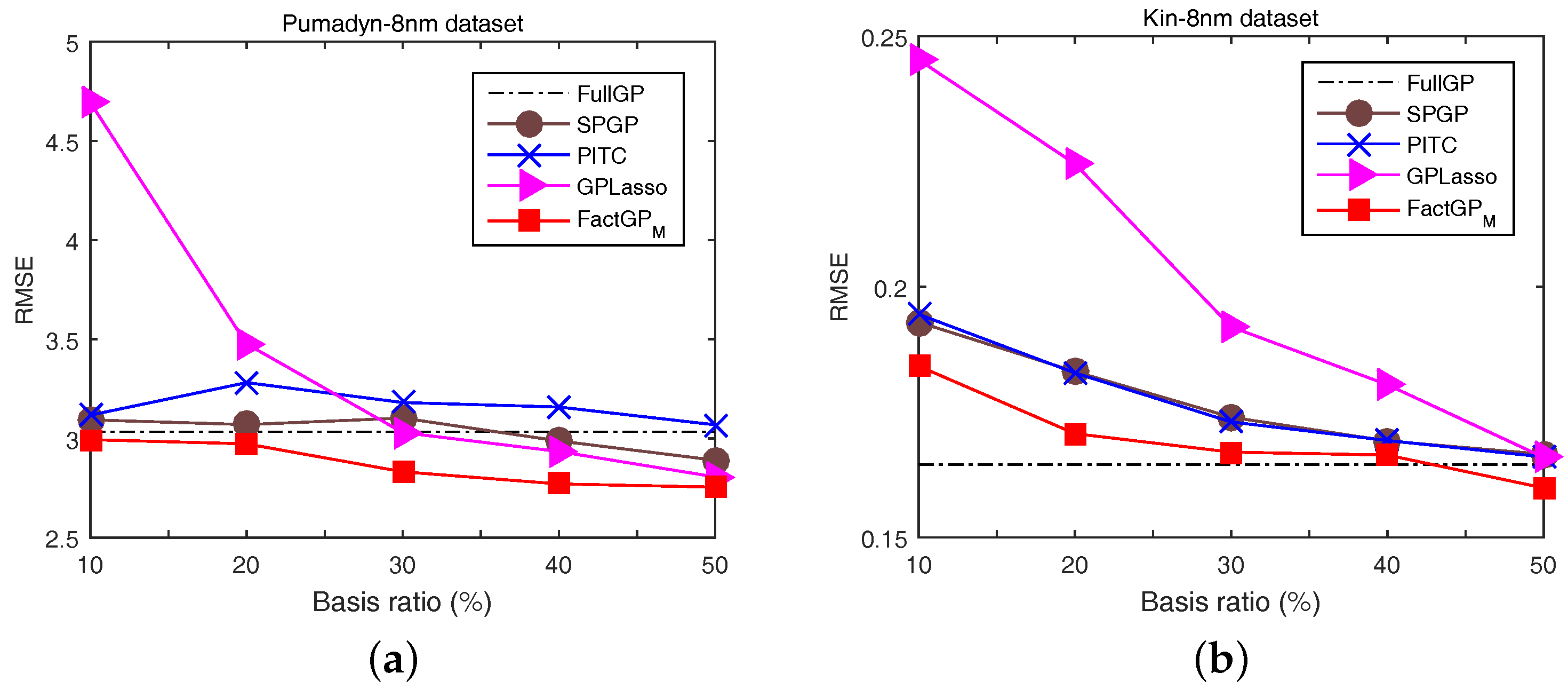
5.1. Regression Problems
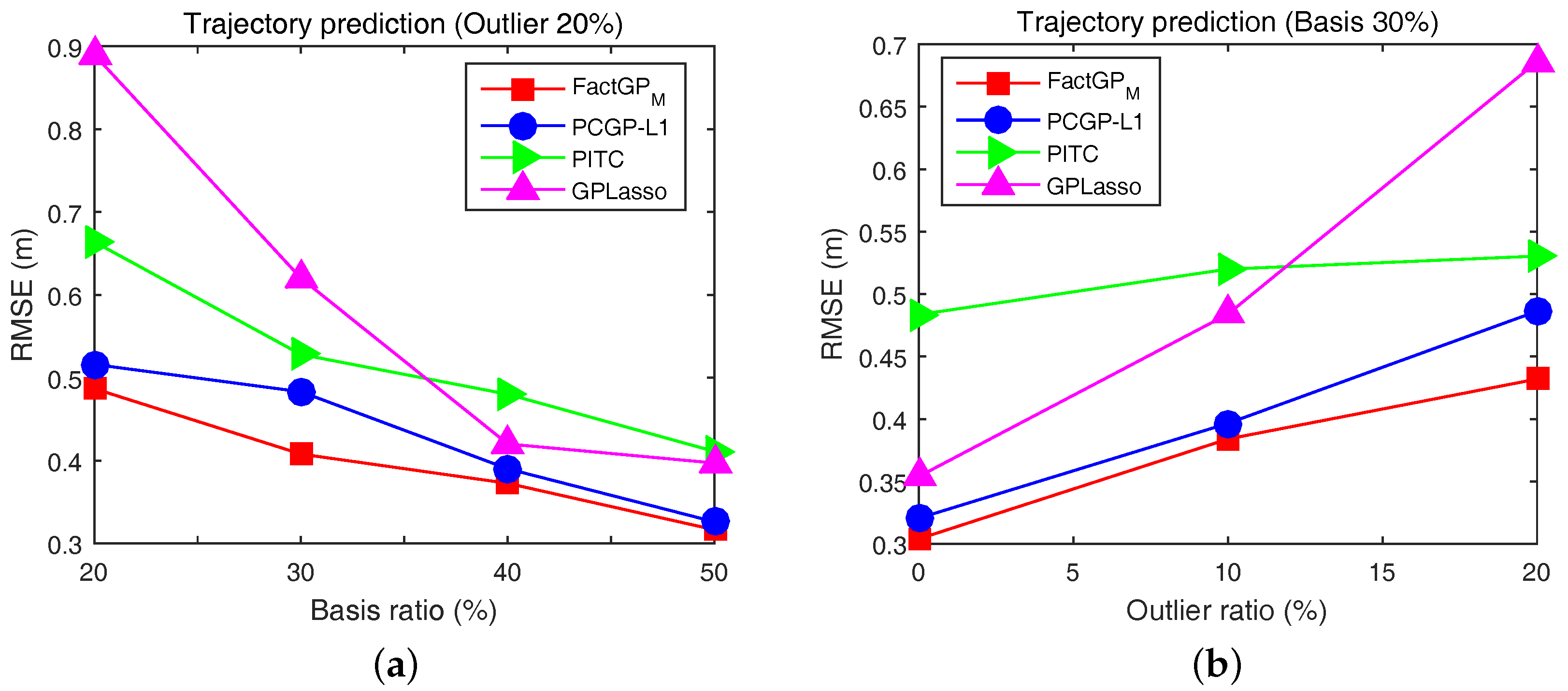
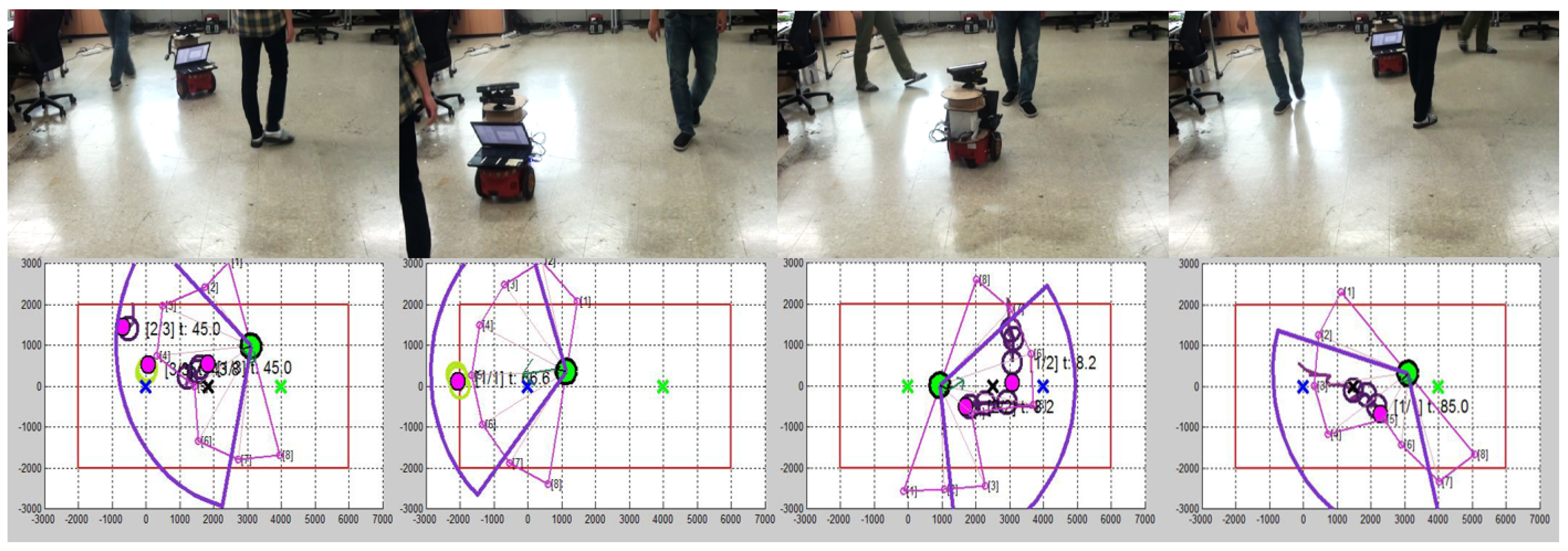
5.2. Motion Prediction of Human Trajectories
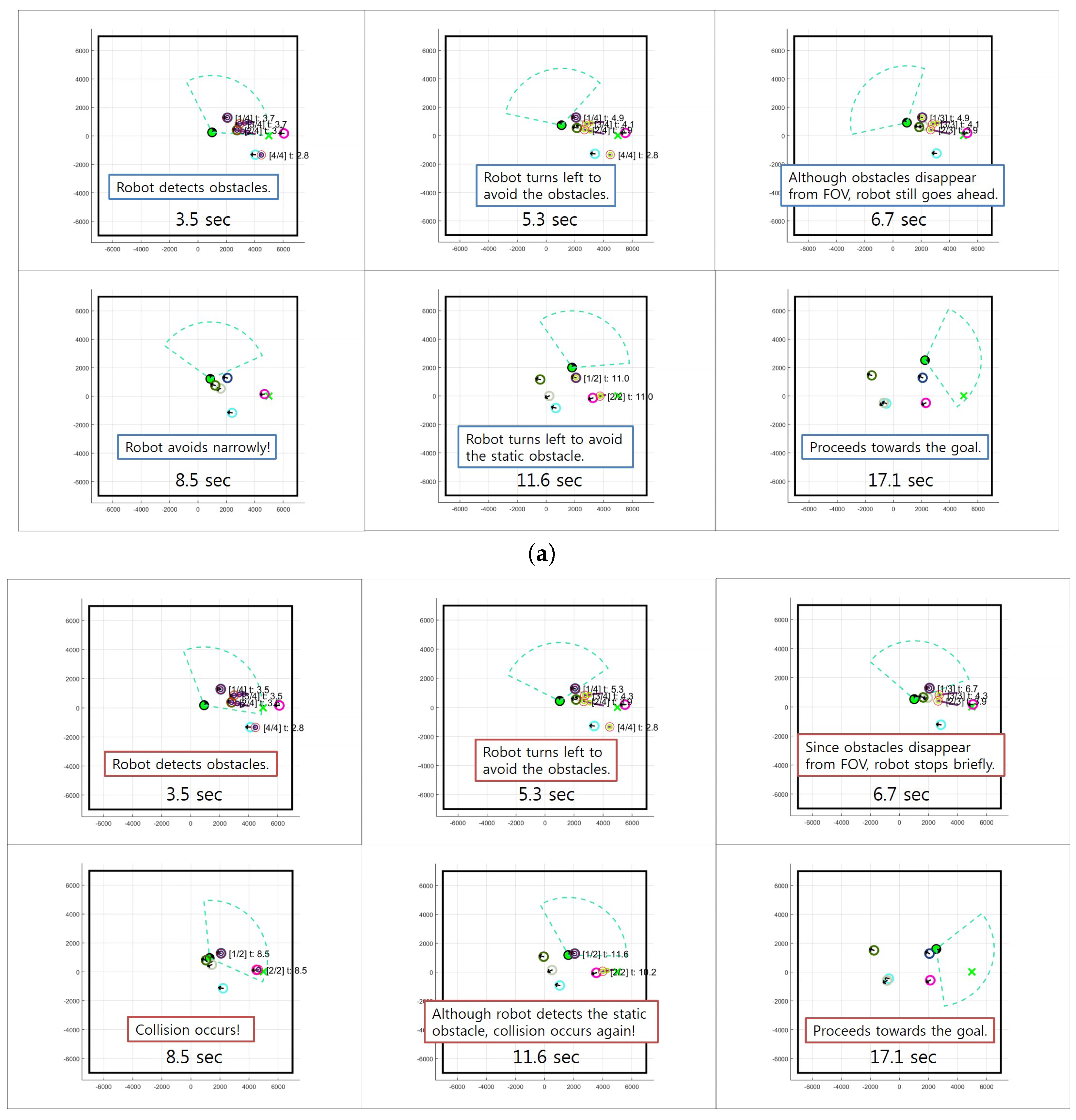
5.3. Motion Control
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Weng, Y.-H.; Chen, C.-H.; Sun, S.-T. Toward the human-robot coexistence society: On safety intelligence for next generation robots. Int. J. Soc. Robot. 2009, 1, 267–282. [Google Scholar] [CrossRef]
- Foka, A.F.; Trahanias, P.E. Predictive autonomous robot navigation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Lausanne, Switzerland, 30 September–4 October 2002. [Google Scholar]
- Fulgenzi, C.; Tay, C.; Spalanzani, A.; Laugier, C. Probabilistic navigation in dynamic environment using rapidly-exploring random trees and Gaussian processes. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Nice, France, 22–26 September 2008. [Google Scholar]
- Henry, P.; Vollmer, C.; Ferris, B.; Fox, D. Learning to navigate through crowded environments. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–7 May 2010. [Google Scholar]
- Asaula, R.; Fontanelli, D.; Palopoli, L. Safety provisions for human/robot interactions using stochastic discrete abstractions. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010. [Google Scholar]
- Ferrer, G.; Sanfeliu, A. Multi-Objective Cost-to-Go Functions on Robot Navigation in Dynamic Environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015. [Google Scholar]
- Lam, C.-P.; Chou, C.-T.; Chiang, K.-H.; Fu, L.-C. Human-centered robot navigation towards a harmoniously human-robot coexisting environment. IEEE Trans. Robot. 2011, 27, 99–112. [Google Scholar] [CrossRef]
- Pradhan, N.; Burg, T.; Birchfield, S. Robot crowd navigation using predictive position fields in the potential function framework. In Proceedings of the American Control Conference (ACC), San Francisco, CA, USA, 29 June–1 July 2011. [Google Scholar]
- Park, J.J.; Johnson, C.; Kuipers, B. Robot navigation with model predictive equilibrium point control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012. [Google Scholar]
- Jetchev, N.; Toussaint, M. Fast motion planning from experience: Trajectory prediction for speeding up movement generation. Auton. Robot. 2013, 34, 111–127. [Google Scholar] [CrossRef]
- Trautman, P.; Ma, J.; Murray, R.M.; Krause, A. Robot navigation in dense human crowds: The case for cooperation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Aoude, G.S.; Luders, B.D.; Joseph, J.M.; Roy, N.; How, J.P. Probabilistically safe motion planning to avoid dynamic obstacles with uncertain motion patterns. Auton. Robot. 2013, 35, 51–76. [Google Scholar] [CrossRef]
- Choi, S.; Kim, E.; Oh, S. Real-time navigation in crowded dynamic environments using Gaussian process motion control. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar]
- Godoy, J.E.; Karamouzas, I.; Guy, S.J.; Gini, M.L. Implicit coordination in crowded multi-agent navigation. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (AAAI), Phoenix, AZ, USA, 12–17 February 2016; pp. 2487–2493. [Google Scholar]
- Long, P.; Liu, W.; Pan, J. Deep-learned collision avoidance policy for distributed multiagent navigation. IEEE Robot. Autom. Lett. 2017, 2, 656–663. [Google Scholar] [CrossRef]
- Choi, S.; Kim, E.; Lee, K.; Oh, S. Real-time nonparametric reactive navigation of mobile robots in dynamic environments. Robot. Auton. Syst. 2017, 91, 11–24. [Google Scholar] [CrossRef]
- Rasmussen, C.; Williams, C. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Ulrich, I.; Borenstein, J. VFH*: Local obstacle avoidance with look-ahead verification. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), San Francisco, CA, USA, 24–28 April 2000. [Google Scholar]
- Ke, Q.; Kanade, T. Robust l1 norm factorization in the presence of outliers and missing data by alternative convex programming. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Eriksson, A.; van den Hengel, A. Efficient computation of robust weighted low-rank matrix approximations using the l1 norm. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1681–1690. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.; Lee, M.; Choi, C.-H.; Kwak, N.; Oh, S. Efficient l1-norm-based low-rank matrix approximations for large-scale problems using alternating rectified gradient method. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 237–251. [Google Scholar] [PubMed]
- Candes, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 11. [Google Scholar] [CrossRef]
- Kim, E.; Choi, S.; Oh, S. A robust autoregressive Gaussian process motion model using l1-norm based low-rank kernel matrix approximation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Kim, E.; Choi, S.; Oh, S. Structured low-rank matrix approximation in Gaussian process regression for autonomous robot navigation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- Yan, F.; Qi, Y. Sparse Gaussian process regression via l1 penalization. In Proceedings of the International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Williams, C.; Seeger, M. Using the Nyström method to speed up kernel machines. In Advances in Neural Information Processing Systems (NIPS); NIPS Foundation: Granada, Spain, 2001. [Google Scholar]
- Scholkopf, B.; Smola, A.; Muller, K.-R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Ni, Y.; Sun, J.; Yuan, X.; Yan, S.; Cheong, L.-F. Robust low-rank subspace segmentation with semidefinite guarantees. In Proceedings of the IEEE International Conference on Data Mining Workshops, Sydney, Australia, 13 December 2010; pp. 1179–1188. [Google Scholar]
- Wen, Z.; Yin, W.; Zhang, Y. Solving a Low-Rank Factorization Model For Matrix Completion by a Non-Linear Successive Over-Relaxation Algorithm; Rice University CAAM Technical Report TR10-07; Rice University: Houston, TX, USA, 2010. [Google Scholar]
- Oh, S.; Russell, S.; Sastry, S. Markov chain monte carlo data association for multi-target tracking. IEEE Trans. Autom. Control 2009, 54, 481–497. [Google Scholar]
- Kulesza, A.; Taskar, B. k-DPPs: Fixed-size determinantal point process. In Proceedings of the IEEE International Conference on Machine Learning (ICML), Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Snelson, E.; Ghahramani, Z. Sparse Gaussian processes using pseudo-inputs. In Advances in Neural Information Processing Systems (NIPS); NIPS Foundation: Vancouver, BC, Canada, 2005. [Google Scholar]
- Quinonero-Candela, J.; Rasmussen, C.E.; Herbrich, R. A unifying view of sparse approximate Gaussian process regression. J. Mach. Learn. Res. 2005, 6, 1939–1959. [Google Scholar]

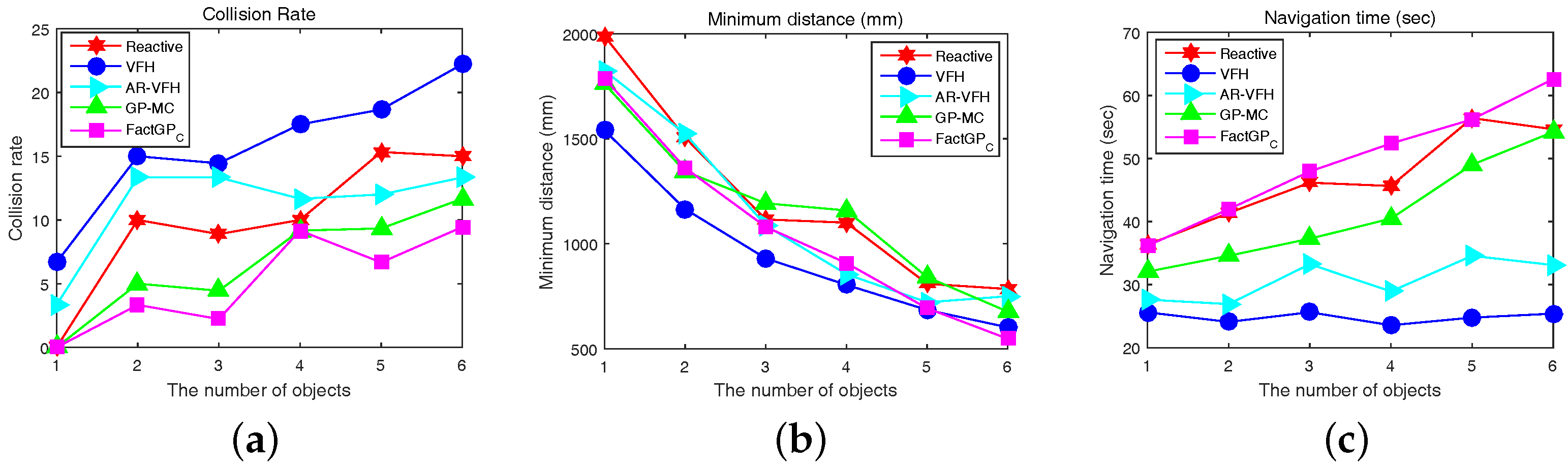



| Ours (10) | Ours (20) | Ours (40) | GP-MC | VFH | AR-VFH | Reactive | ||
|---|---|---|---|---|---|---|---|---|
| 1 object | ACR | 0 | 0 | 0 | 3.33 | 6.67 | 3.33 | 0 |
| MinD | 1969 | 1839 | 1708 | 1761 | 1539 | 1824 | 1988 | |
| 2 object | ACR | 6.67 | 3.33 | 3.33 | 5.0 | 15.0 | 13.33 | 10.0 |
| MinD | 1422 | 1400 | 1300 | 1344 | 1165 | 1523 | 1506 | |
| 3 object | ACR | 6.67 | 6.67 | 8.89 | 8.89 | 14.44 | 13.33 | 8.89 |
| MinD | 1062 | 1228 | 1254 | 1218 | 930.2 | 1087 | 1116 | |
| 4 object | ACR | 6.67 | 8.83 | 8.83 | 8.83 | 17.5 | 11.67 | 10.0 |
| MinD | 839.4 | 951.7 | 1083 | 1144 | 804 | 855 | 1100 | |
| 5 object | ACR | 11.33 | 8.67 | 12.0 | 8.0 | 18.67 | 12.0 | 15.33 |
| MinD | 836.2 | 785.9 | 1022 | 861 | 684.9 | 721.4 | 809.4 | |
| 5 object | ACR | 16.67 | 12.78 | 9.44 | 12.78 | 22.22 | 13.33 | 15.0 |
| MinD | 928.9 | 757.7 | 1008 | 783.8 | 602 | 749.9 | 784.5 | |
| Average | ACR | 8.01 | 6.63 | 7.00 | 7.72 | 15.75 | 11.16 | 9.87 |
| MinD | 1126.3 | 1160.4 | 1229.2 | 1185.3 | 954.2 | 1126.7 | 1217.3 |
| Algorithm | #obs 1 | #obs 2 | #obs 3 | #obs 4 | Average |
|---|---|---|---|---|---|
| FactGP | 0% | 0% | 20% | 20% | 10% |
| GP-MC | 0% | 20% | 30% | 50% | 25% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, E.; Choi, S.; Oh, S. Structured Kernel Subspace Learning for Autonomous Robot Navigation. Sensors 2018, 18, 582. https://doi.org/10.3390/s18020582
Kim E, Choi S, Oh S. Structured Kernel Subspace Learning for Autonomous Robot Navigation. Sensors. 2018; 18(2):582. https://doi.org/10.3390/s18020582
Chicago/Turabian StyleKim, Eunwoo, Sungjoon Choi, and Songhwai Oh. 2018. "Structured Kernel Subspace Learning for Autonomous Robot Navigation" Sensors 18, no. 2: 582. https://doi.org/10.3390/s18020582
APA StyleKim, E., Choi, S., & Oh, S. (2018). Structured Kernel Subspace Learning for Autonomous Robot Navigation. Sensors, 18(2), 582. https://doi.org/10.3390/s18020582





