Circular Array of Magnetic Sensors for Current Measurement: Analysis for Error Caused by Position of Conductor
Abstract
:1. Introduction
2. Mathematical Background
3. The Error Analysis
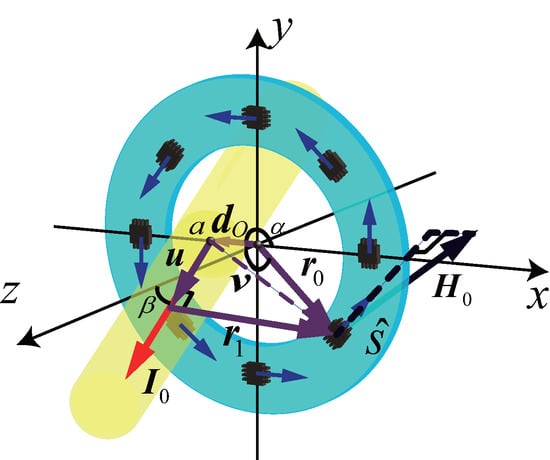
3.1. The Mathematical Model of the Errors from the Un-Centeredness and Un-Perpendicularity
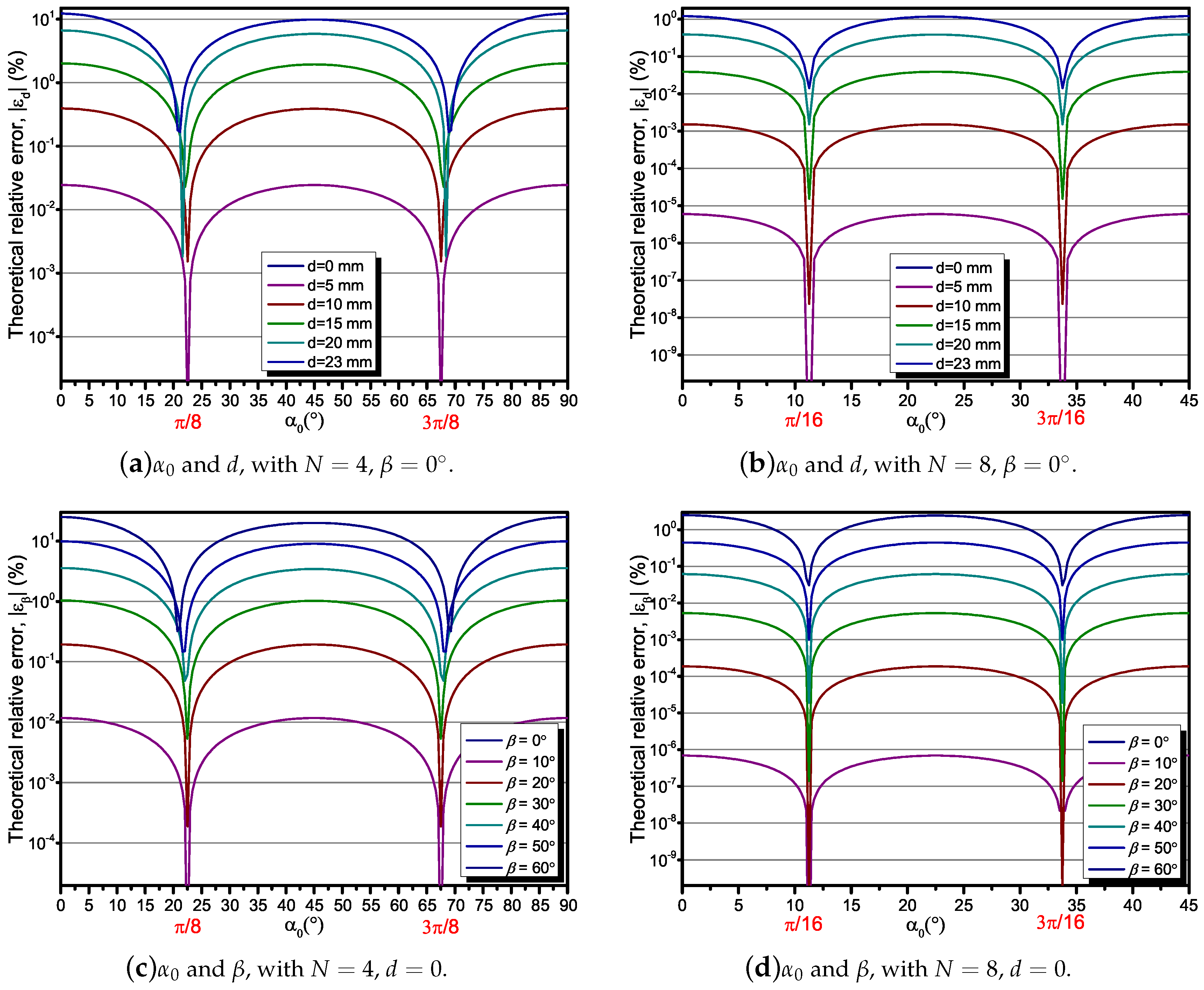
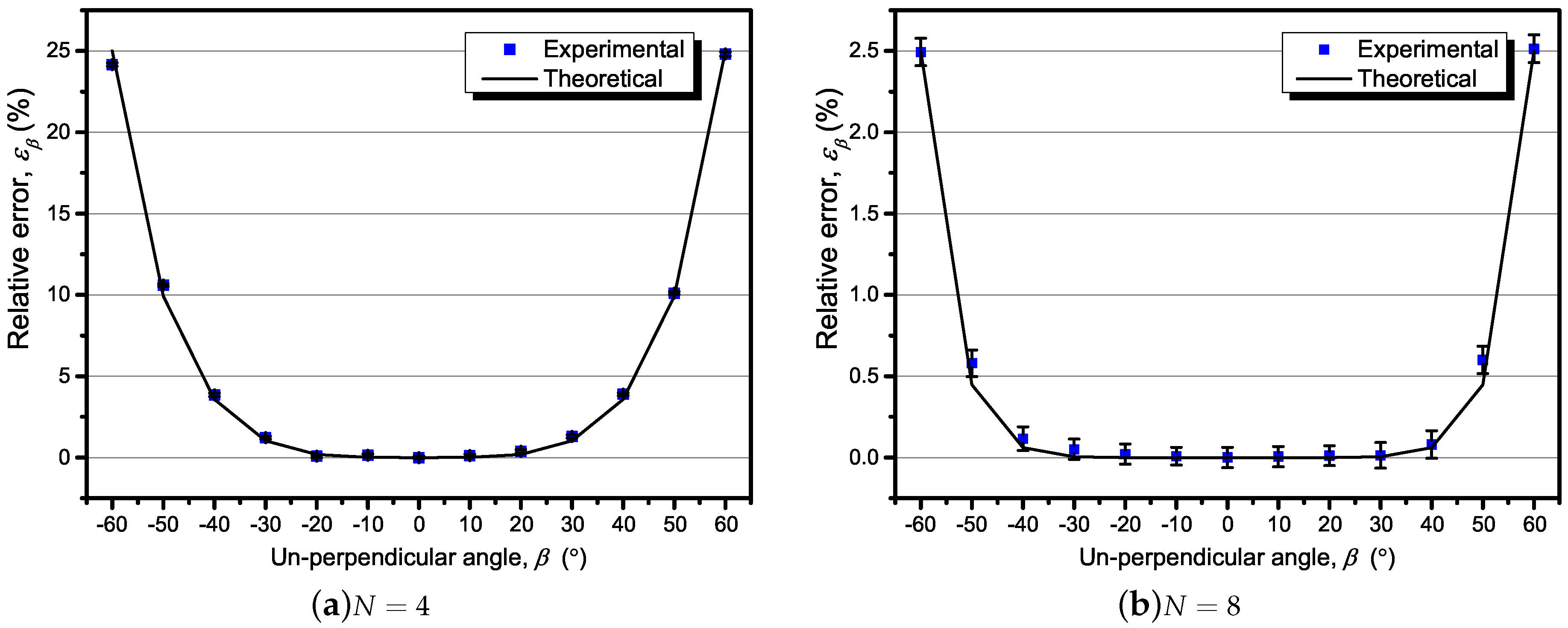
3.2. Analysis of the Effect of Displacement Angles of the Sensor Array
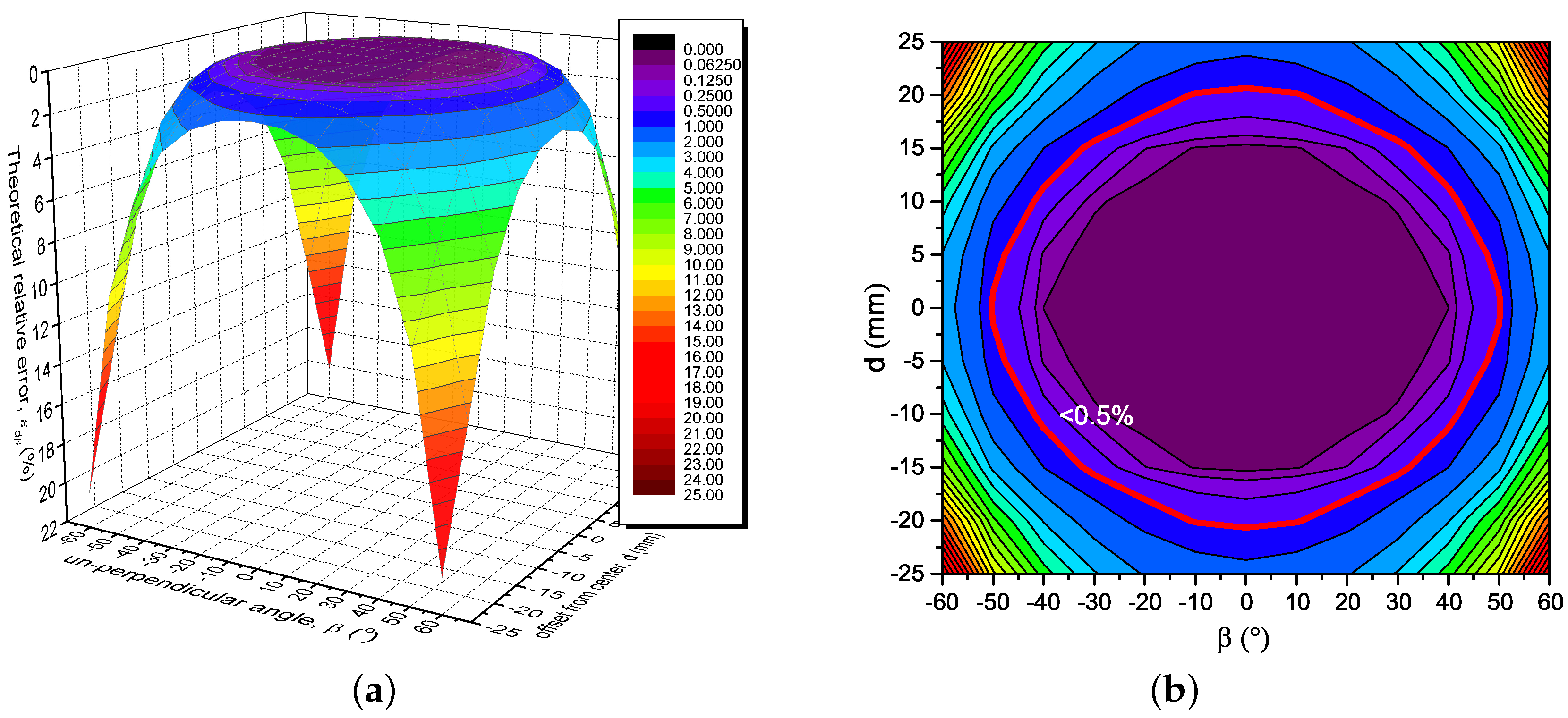
3.3. Analysis of the Effect of Un-Centeredness and Un-Perpendicularity
4. Experimental Procedure
5. Results
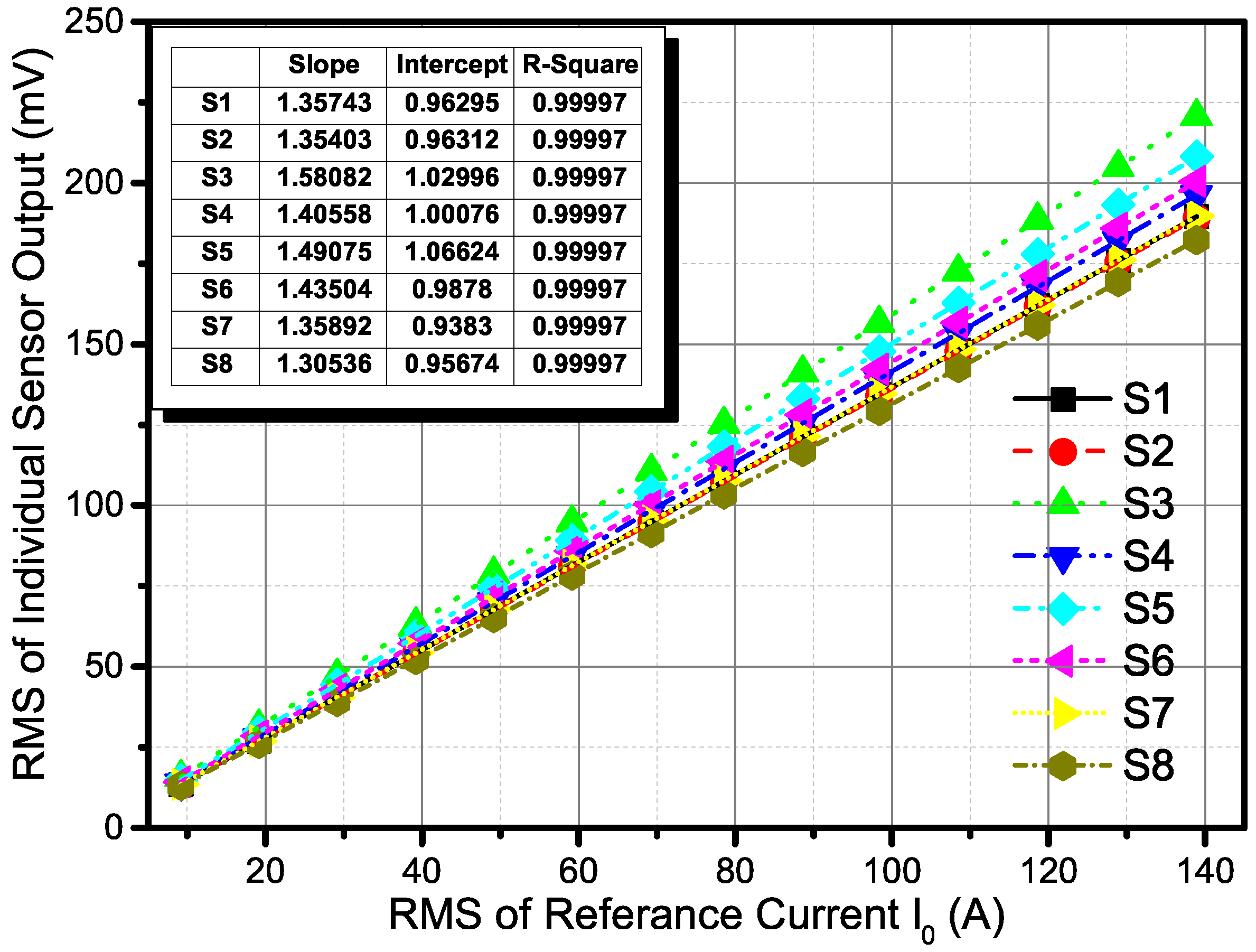
5.1. Calibration Results
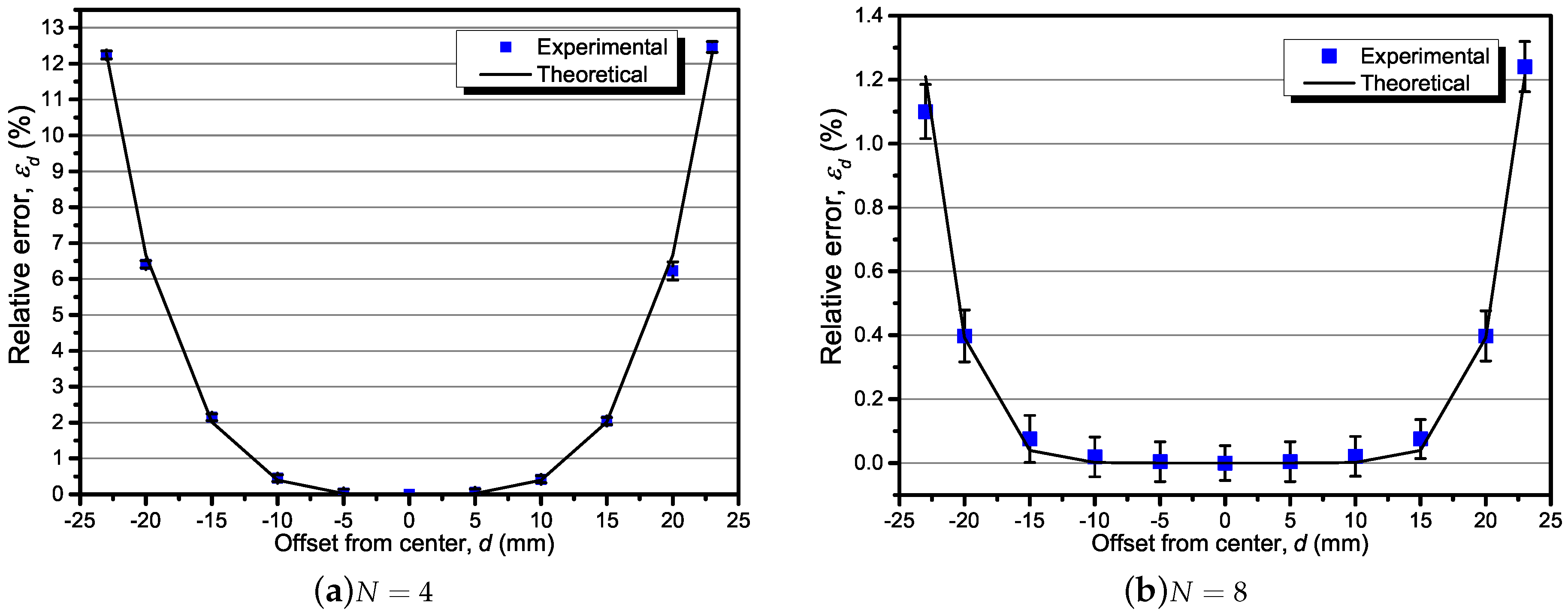
5.2. The Result of Un-Centeredness and Un-Perpendicularity
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AMR | Anisotropic Magnetoresistance |
| GMR | Giant Magnetoresistance |
| TMR | Tunnel Magnetoresistance |
| MTJ | Magnetic Tunnel Junction |
| AC | Alternation current |
| DC | Direct current |
| RMS | Root mean square |
References
- Ennen, I.; Kappe, D.; Rempel, T.; Glenske, C.; Hu¨tten, A. Giant Magnetoresistance: Basic Concepts, Microstructure, Magnetic Interactions and Applications. Sensors 2016, 16, 904. [Google Scholar] [CrossRef] [PubMed]
- Ripka, P. Electric current sensors: A review. Meas. Sci. Technol. 2010, 21, 112001. [Google Scholar] [CrossRef]
- Ripka, P.; Kejik, P.; Kaspar, P.; Draxler, K. Precise DC current sensors. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Brussels, Belgium, 4–6 June 1996; Volume 2, pp. 1479–1483. [Google Scholar]
- Bazzocchi, R.; Di Rienzo, L. Interference rejection algorithm for current measurement using magnetic sensor arrays. Sens. Actuators A Phys. 2000, 85, 38–41. [Google Scholar] [CrossRef]
- Di Rienzo, L.; Bazzocchi, R.; Manara, A. Circular arrays of magnetic sensors for current measurement. IEEE Trans. Instrum. Meas. 2001, 50, 1093–1096. [Google Scholar] [CrossRef]
- Mlejnek, P.; Vopa´lensky´, M.; Ripka, P. AMR current measurement device. Sens. Actuators A Phys. 2008, 141, 649–653. [Google Scholar] [CrossRef]
- Di Rienzo, L.; Zhang, Z. Spatial Harmonic Expansion for Use With Magnetic Sensor Arrays. IEEE Trans. Magn. 2010, 46, 53–58. [Google Scholar] [CrossRef]
- Weiss, R.; Makuch, R.; Itzke, A.; Weigel, R. Crosstalk in Circular Arrays of Magnetic Sensors for Current Measurement. IEEE Trans. Ind. Electron. 2017, 64, 4903–4909. [Google Scholar] [CrossRef]
- Weiss, R.; Itzke, A.; Weigel, R. Current measurement of flat conductors with a circular array of magnetic sensors. In Proceedings of the 2017 IEEE Second International Conference on DC Microgrids (ICDCM), Nuremburg, Germany, 27–29 June 2017; pp. 166–170. [Google Scholar]
- Guo, Q.; Fu, P.; Gao, G.; Jiang, L.; Wang, L.S.; Bai, Y.R. Rectangular Magnetic Sensor Array for Current Measurement by the Quadrature Method. IEEE Trans. Plasma Sci. 2017, PP, 1–7. [Google Scholar] [CrossRef]
- Ripka, P.; Chirtsov, A. Influence of External Current on Yokeless Electric Current Transducers. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Mlejnek, P.; Ripka, P. Off-Center Error Correction of AMR Yokeless Current Transducer. J. Sens. 2017, 2017, 1–7. [Google Scholar] [CrossRef]
- Ziegler, S.; Woodward, R.C.; Iu, H.H.C.; Borle, L.J. Current Sensing Techniques: A Review. IEEE Sens. J. 2009, 9, 354–376. [Google Scholar] [CrossRef]
- Wisniowski, P.; Wrona, J.; Stobiecki, T.; Cardoso, S.; Freitas, P.P. Magnetic Tunnel Junctions Based on Out-of-Plane Anisotropy Free and In-Plane Pinned Layer Structures for Magnetic Field Sensors. IEEE Trans. Magn. 2012, 48, 3840–3842. [Google Scholar] [CrossRef]
- Dabek, M.; Wisniowski, P. Dynamic response of tunneling magnetoresistance sensors to nanosecond current step. Sens. Actuators A Phys. 2015, 232, 148–150. [Google Scholar] [CrossRef]
- Dabek, M.; Wisniowski, P.; Stobiecki, T.; Wrona, J.; Cardoso, S.; Freitas, P.P. Sensitivity and 3 dB Bandwidth in Single and Series-Connected Tunneling Magnetoresistive Sensors. Sensors 2016, 16, 1821. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Xie, X.; Hu, Y.; Qian, Y.; Sheng, G.; Jiang, X. A Novel Transient Fault Current Sensor Based on the PCB Rogowski Coil for Overhead Transmission Lines. Sensors 2016, 16, 742. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.C. The Cambridge Handbook of Physics Formulas; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- MDT. TMR2103 Tunneling MagnetoResistance Sensor; MultiDimension Technology Co.: Zhangjiagang, China, 2015. [Google Scholar]
- Lenz, J.; Edelstein, A.S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Ouyang, Y.; He, J.; Hu, J.; Zhao, G.; Wang, Z.; Wang, S.X. Prediction and Optimization of Linearity of MTJ Magnetic Sensors Based on Single-Domain Model. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]
- Ouyang, Y.; Hu, J.; He, J.; Zhao, G.; Xue, F.; Wang, Z.; Wang, S.X.; Yuan, Z.; Ding, Z. Modeling the Frequency Dependence of Packaged Linear Magnetoresisitive Sensors Based on MTJ. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Xiaodong, Z.; Zheng, Q.; Yuan, T.; Jingyi, W.; Hao, Y. The error compensation for static hysteresis characteristics of Giant Magneto-Resistance sensor. In Proceedings of the 2016 IEEE Sensors Applications Symposium (SAS), Catania, Italy, 20–22 April 2016; pp. 1–5. [Google Scholar]
- Xiaodong, Z.; Zheng, Q.; Kaikai, P. The Analysis of Hysteresis in the Spin Valve Magneto-Resistance. In Proceedings of the 2013 Third International Conference on Instrumentation, Measurement, Computer, Communication and Control, Shenyang, China, 21–23 September 2013; pp. 736–739. [Google Scholar]
- Jedlicska, I.; Weiss, R.; Weigel, R. Linearizing the Output Characteristic of GMR Current Sensors through Hysteresis Modeling. IEEE Trans. Ind. Electron. 2010, 57, 1728–1734. [Google Scholar] [CrossRef]
- Xie, F.; Weiss, R.; Weigel, R. Hysteresis Compensation Based on Controlled Current Pulses for Magnetoresistive Sensors. IEEE Trans. Ind. Electron. 2015, 62, 7804–7809. [Google Scholar] [CrossRef]
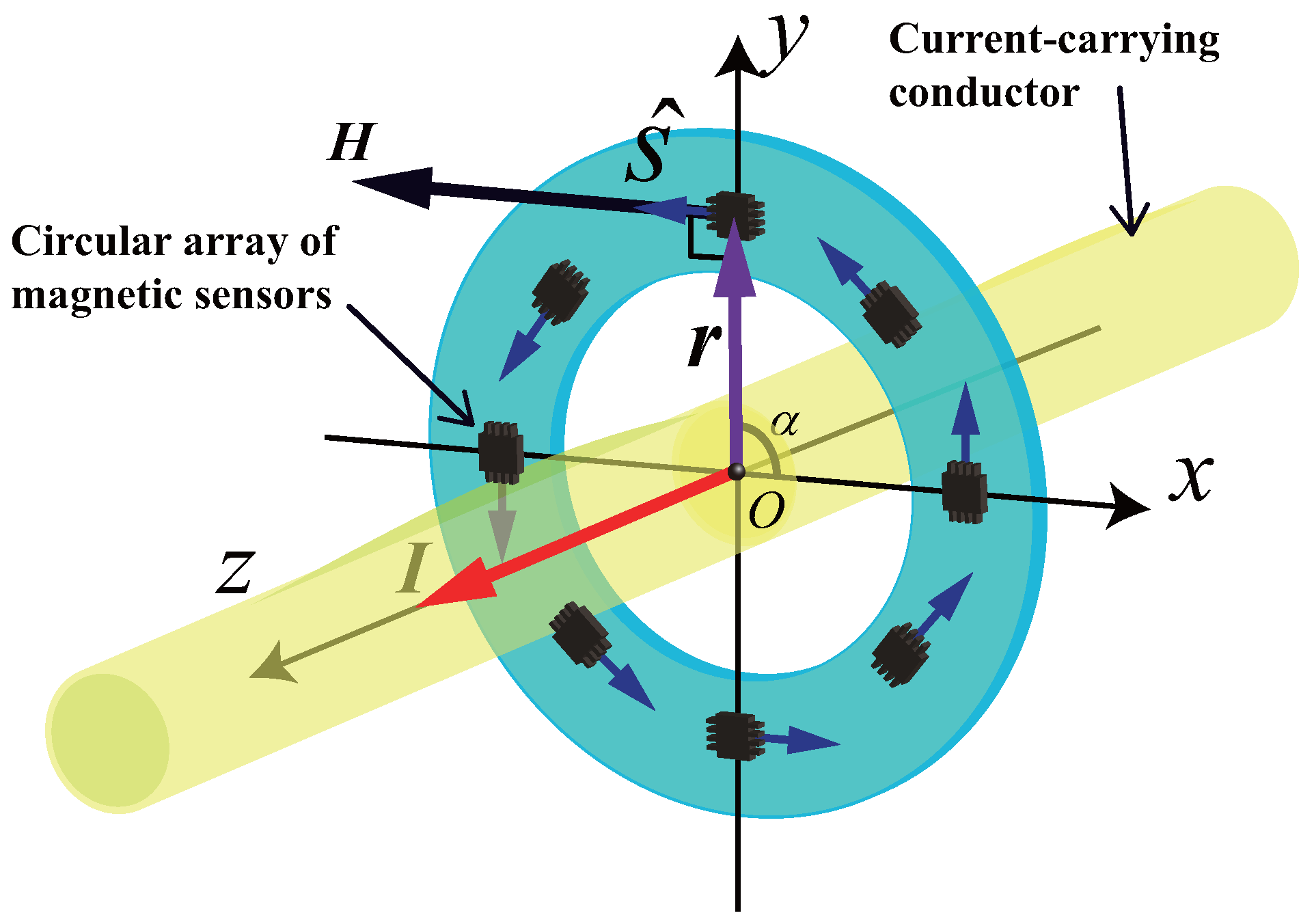
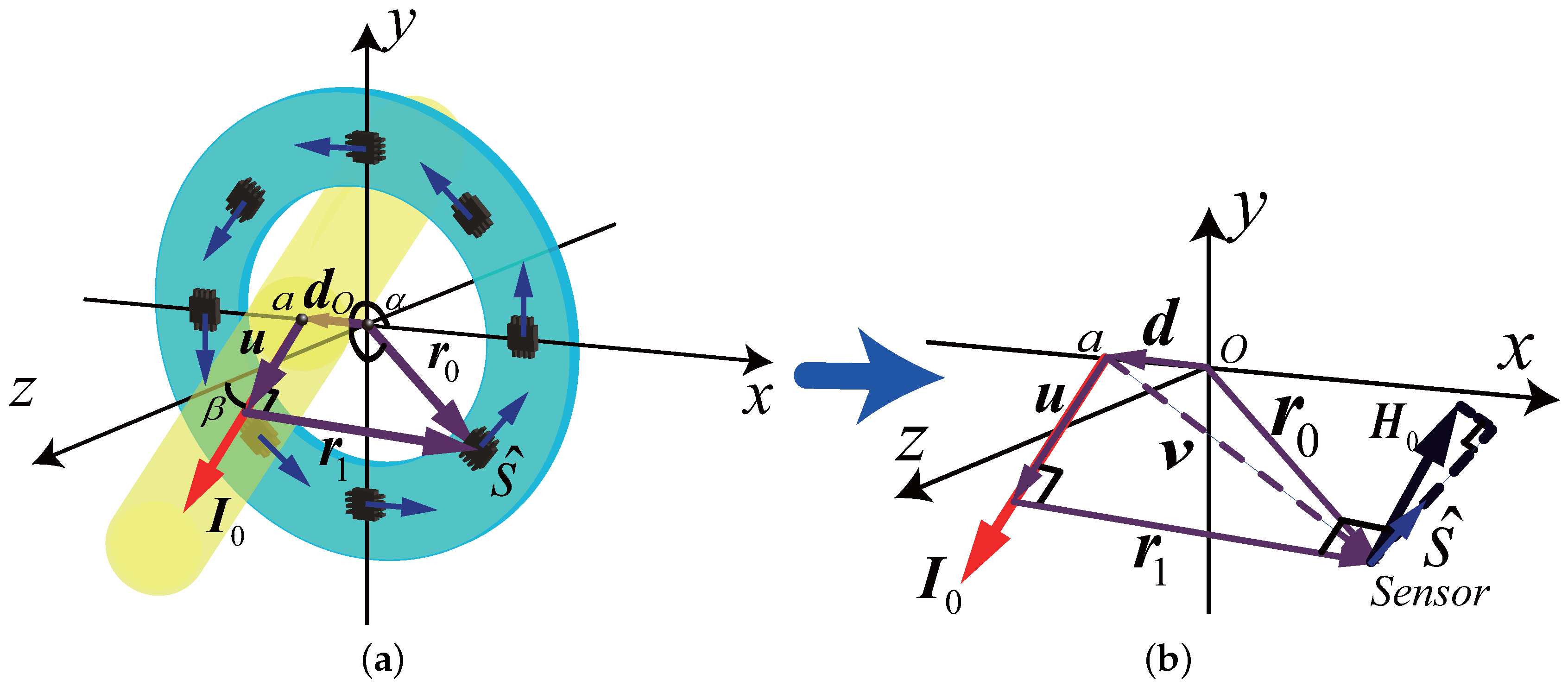

| Vector | Norm | Value | Definition |
|---|---|---|---|
| Under-measured current | |||
| d | Offset vector from the center | ||
| * | Position vector from O to sensor | ||
| v | Position vector from point a to sensor | ||
| Position vector from to sensor | |||
| u | see (5) | Position vector from O to | |
| ** | 1 | Sensitivity direction of sensor |
| N | (%) with | |
|---|---|---|
| , mm * | , mm | |
| 2 | 198.8 | 23.17 |
| 4 | 72.48 | 2.9464 |
| 6 | 36.05 | 0.4665 |
| 8 | 20.25 | 0.07696 |
| 10 | 12.04 | 0.01279 |
| 12 | 7.382 | 0.002129 |
| 14 | 4.601 | 0.0003544 |
| 16 | 2.896 | 0.000005899 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Qian, Z.; Liu, H.; Qu, J. Circular Array of Magnetic Sensors for Current Measurement: Analysis for Error Caused by Position of Conductor. Sensors 2018, 18, 578. https://doi.org/10.3390/s18020578
Yu H, Qian Z, Liu H, Qu J. Circular Array of Magnetic Sensors for Current Measurement: Analysis for Error Caused by Position of Conductor. Sensors. 2018; 18(2):578. https://doi.org/10.3390/s18020578
Chicago/Turabian StyleYu, Hao, Zheng Qian, Huayi Liu, and Jiaqi Qu. 2018. "Circular Array of Magnetic Sensors for Current Measurement: Analysis for Error Caused by Position of Conductor" Sensors 18, no. 2: 578. https://doi.org/10.3390/s18020578
APA StyleYu, H., Qian, Z., Liu, H., & Qu, J. (2018). Circular Array of Magnetic Sensors for Current Measurement: Analysis for Error Caused by Position of Conductor. Sensors, 18(2), 578. https://doi.org/10.3390/s18020578