Energy Efficient Data Transmission for Sensors with Wireless Charging
Abstract
:1. Introduction
- To the best of our knowledge, this is the first work to study data transmission in sensors taking into account the thermal effects in wireless charging and uses a periodical charging period to eliminate the thermal effect.
- This paper considers the problem where the wireless charging continues for a limited period of time. Algorithms are provided and the performance bounds of the algorithms are also analyzed.
- This paper also considers the problem where the wireless charging continues for a long enough time. Algorithms are provided and the performance bounds of the algorithms are also analyzed.
- The simulations are conducted to evaluate and confirm the performance of the provided algorithms.
2. Motivation and Problem Statement
2.1. Intermittent Wireless Charging
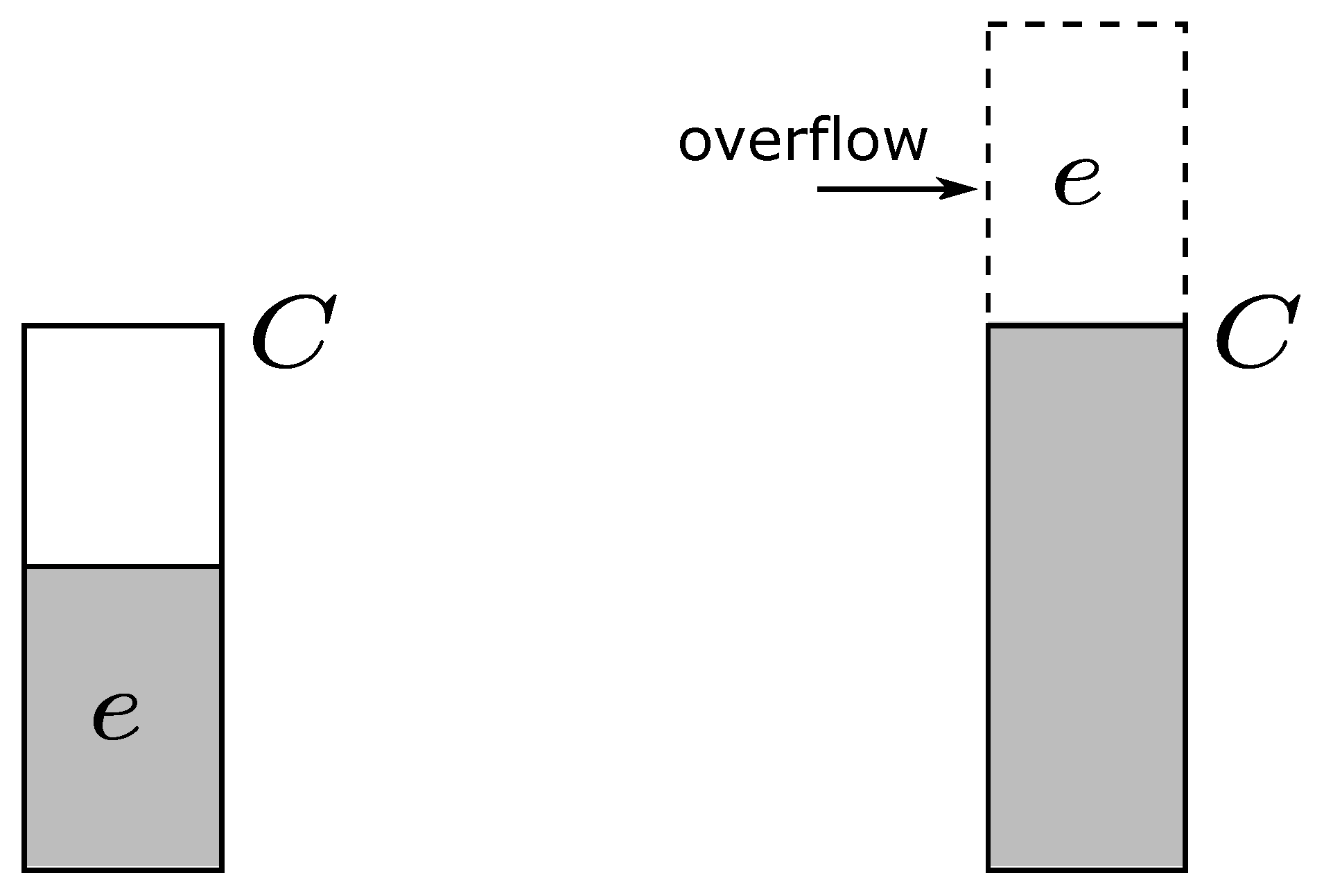
2.2. Energy Waste
2.3. Problem Statement
3. Transmission in Limited K Periods
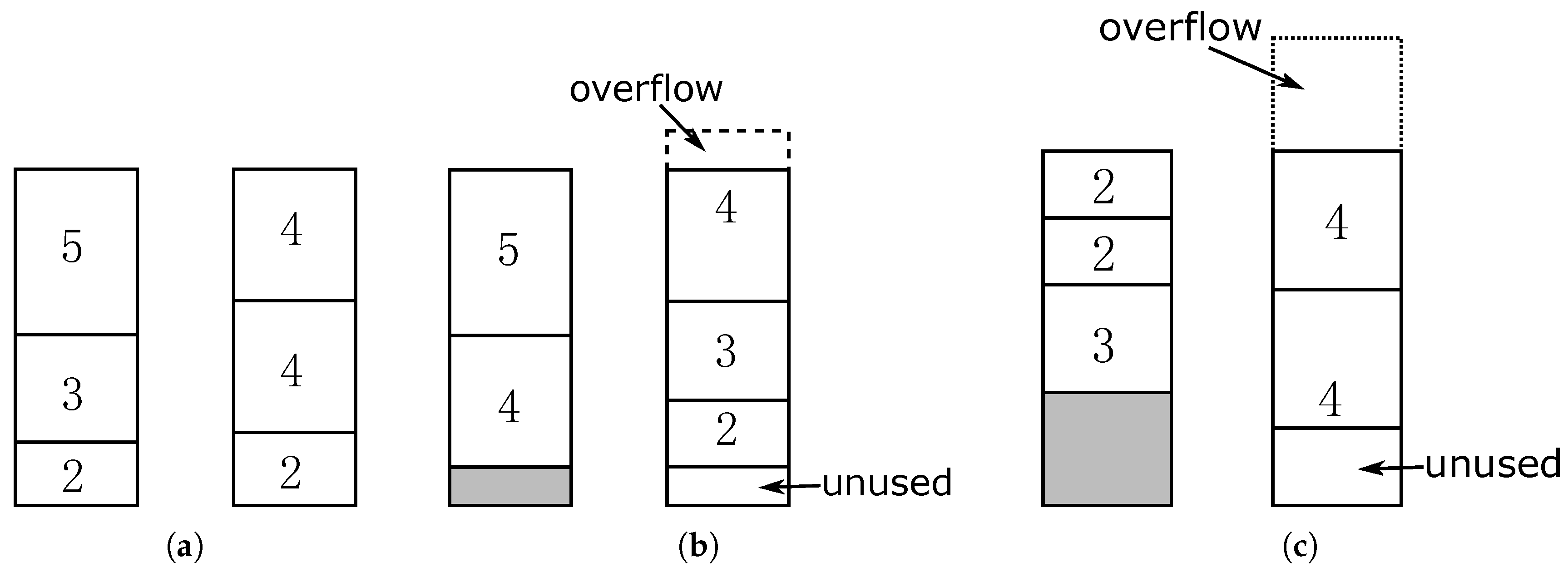
3.1. A Simple Problem with
| Algorithm 1: FillDecreasing (S) |
Input: and K, assuming Output: Transmit a subset of packets to maximize the total amount of data. 1: Sort S in non-increasing order. Let the ordered sequence be ; 2: for to K do 3: ; 4: for i = 1 to n do 5: if then 6: ; //Transmitting packet i in battery j 7: ; 8: end if 9: end for 10: end for |
3.2. Problem with
| Algorithm 2: LargerFirst (S) |
Input: , C, E and K, assuming Output: Transmit a subset of packets to maximize the total amount of data. 1: Sort S in non-increasing order, and let the ordered sequence be ; 2: ; 3: for i = 1 to n do 4: while and do 5: ; //Wireless charging 6: ; 7: end while 8: if then 9: ; //Energy overflows 10: end if 11: if then 12: exit; 13: end if 14: Transmit packet i; 15: ; 16: end for |
| Algorithm 3: LargerFirstImprove (S) |
Input: , C, E and K, assuming Output: Transmit a subset of packets to maximize the total amount of data. 1: Sort S in non-increasing order, and let the ordered sequence be ; 2: Append them into list L in non-increasing order; 3: ; 4: while L is not empty do 5: Get the first packet s in list L. 6: while and do 7: ; //Wireless charging 8: ; 9: end while 10: if then 11: ; //Energy overflows 12: end if 13: for do 14: Transmit packet ; // Transmit as more data as possible 15: ; 16: Remove from L; 17: end for 18: if then 19: exit; 20: end if 21: end while |
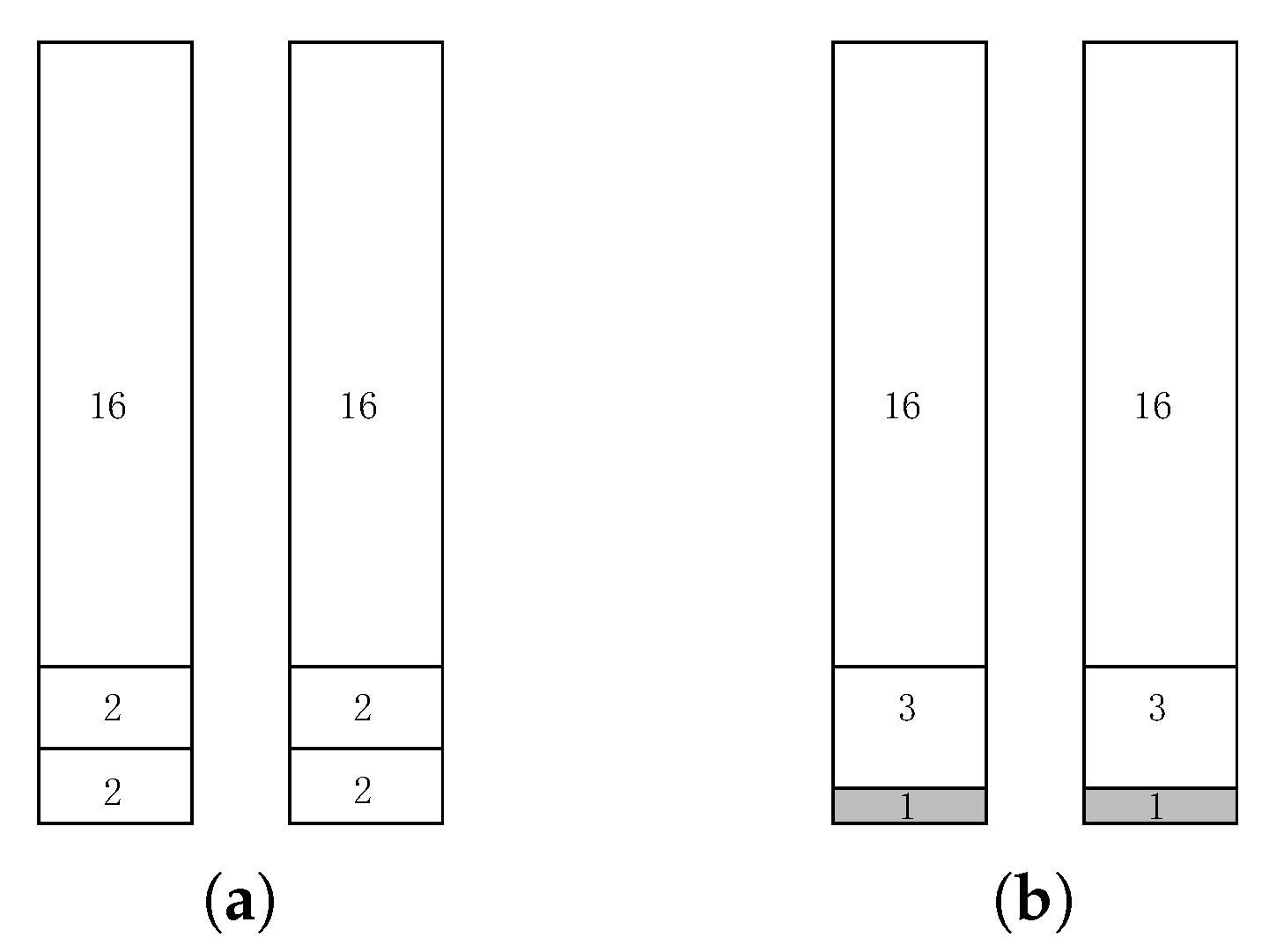
3.3. The General Problem with
4. Transmission in an Unlimited Number of Periods
4.1. A Simple Problem with
4.2. Problem with
| Algorithm 4: FirstFitDecreasing (S) |
Input: , assuming Output: The assignment of S and k 1: Sort S in non-increasing order, and let the ordered sequence be ; 2: ; 3: for i = 1 to n do 4: for to k do 5: if then 6: ; //assign item i to j, corresponding to transmit packet i in period j. 7: ; 8: end if 9: end for 10: if then 11: ; 12: ; 13: ; 14: ; 15: end if 16: end for |
4.3. The General Problem with
| Algorithm 5: LargerFirst2 (S) |
Input: , C, E and K, assuming Output: Transmit a subset of packets to maximize the total amount of data. 1: Sort S in non-increasing order, and let the ordered sequence be ; 2: ; 3: for i = 1 to n do 4: while do 5: ; //Wireless charging 6: end while 7: if then 8: ; //Energy overflows 9: end if 10: Transmit packet i; 11: ; 12: end for |
| Algorithm 6: LargerFirstImprove2 (S) |
Input: , C, E and K, assuming Output: Transmit a subset of packets to maximize the total amount of data. 1: Sort S in non-increasing order, and let the ordered sequence be ; 2: Append them into list L in non-increasing order; 3: ; 4: while L is not empty do 5: Get the first packet s in list L. 6: while do 7: ; //Wireless charging 8: end while 9: if then 10: ; //Energy overflows 11: end if 12: for do 13: Transmit packet ; // Transmit as much data as possible 14: ; 15: Remove from L; 16: end for 17: end while |
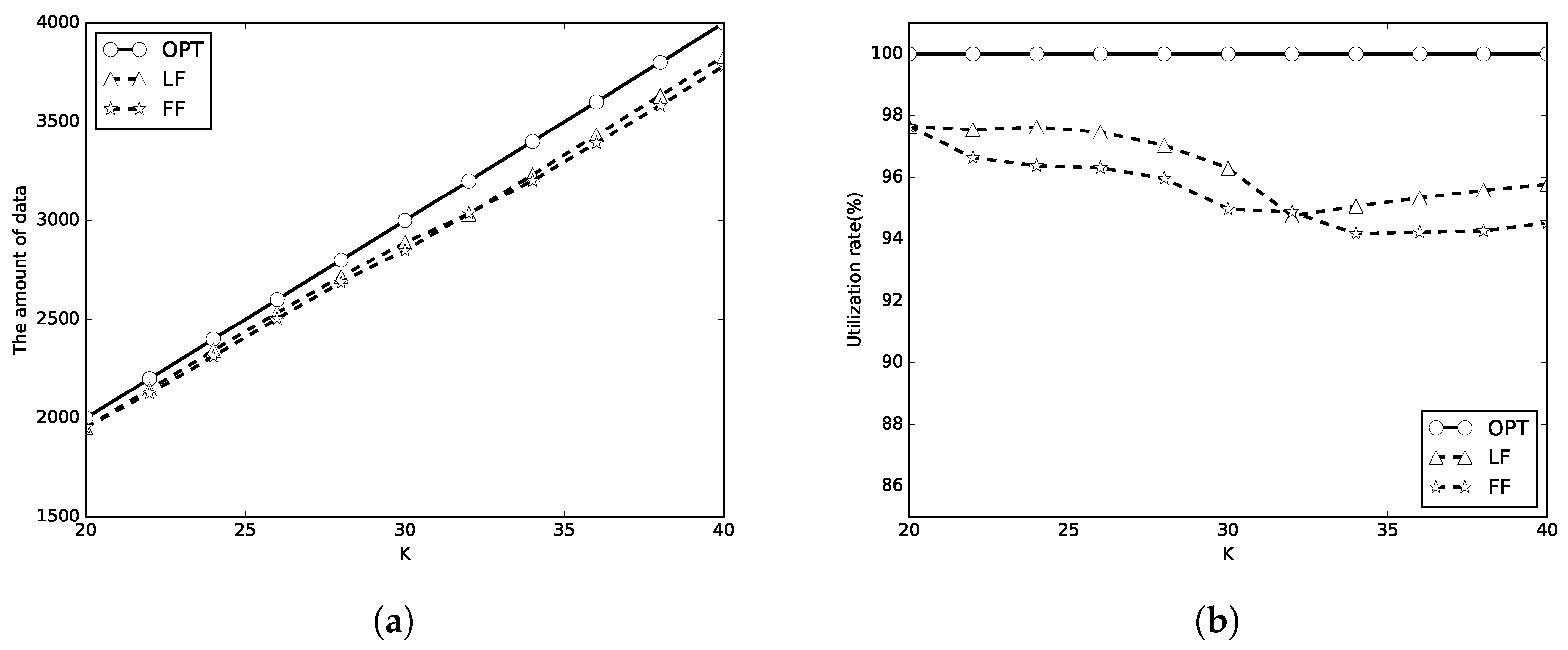
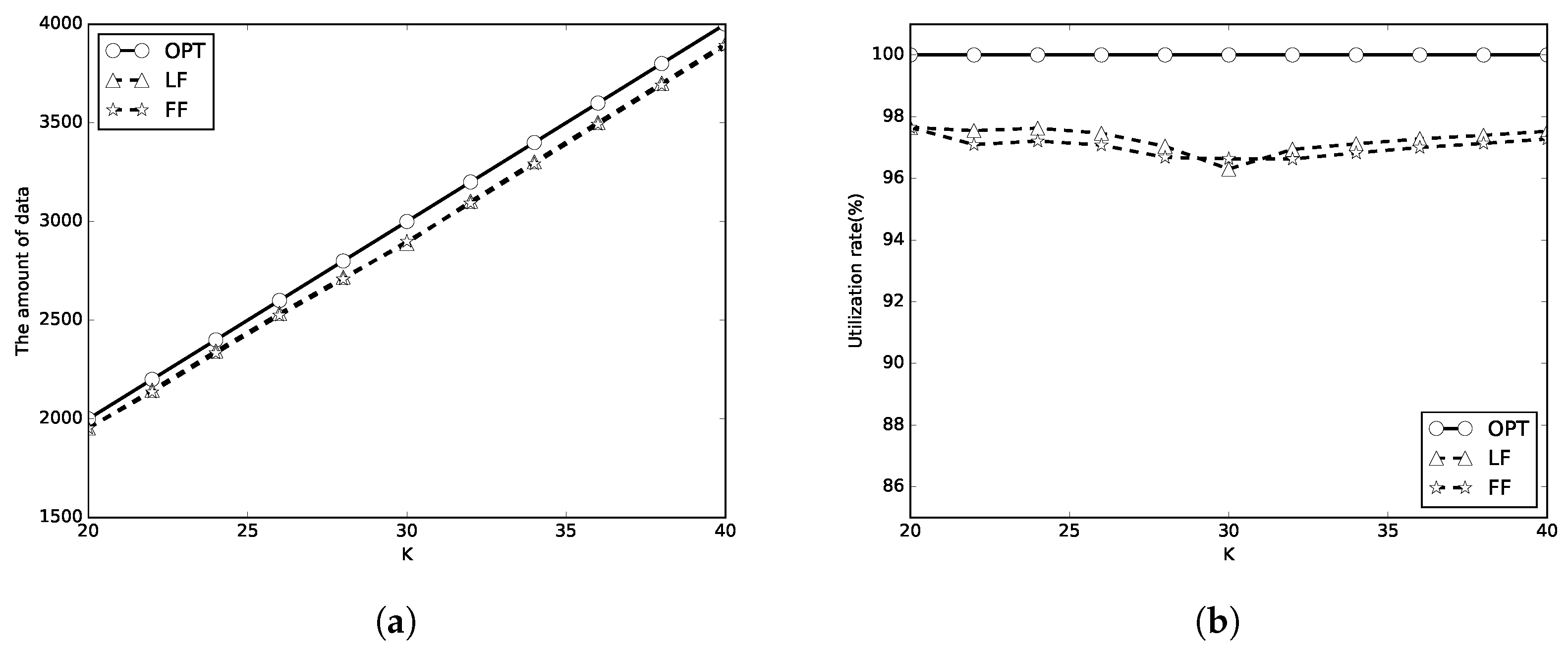
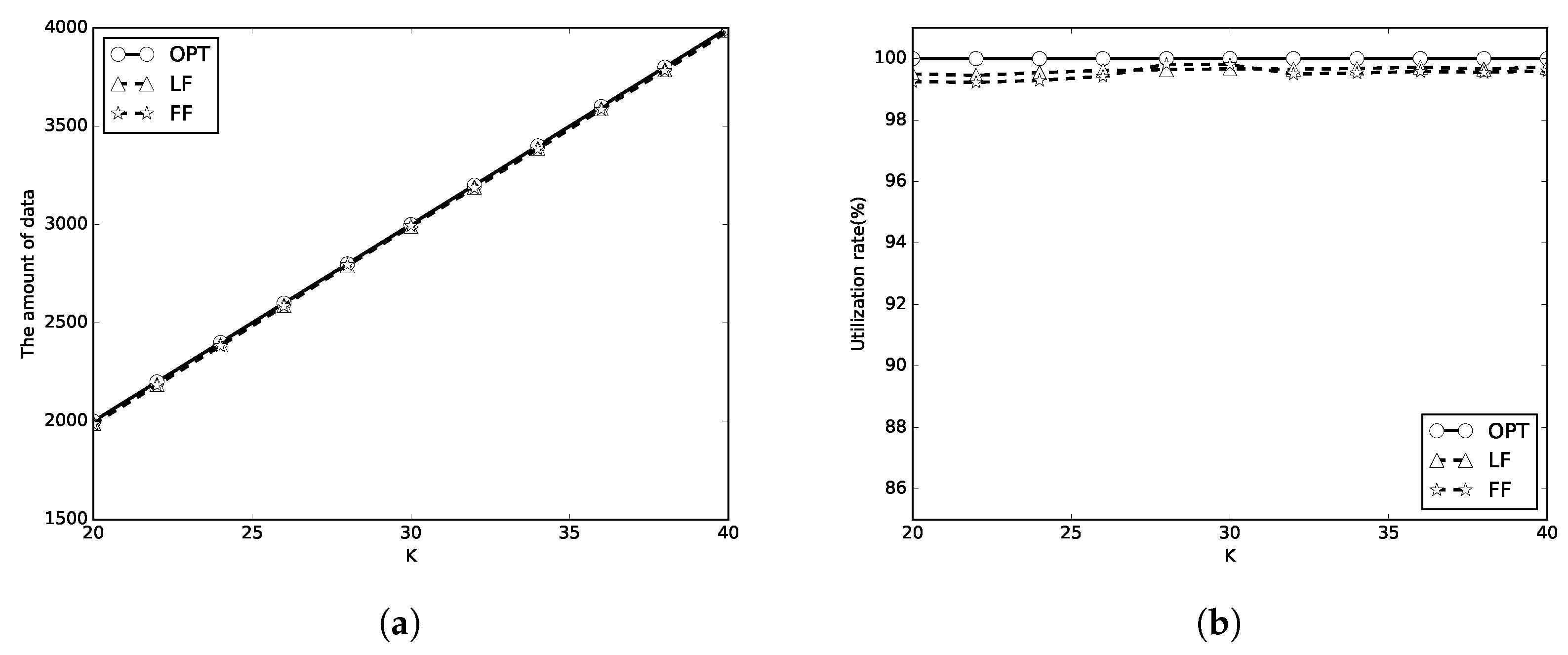
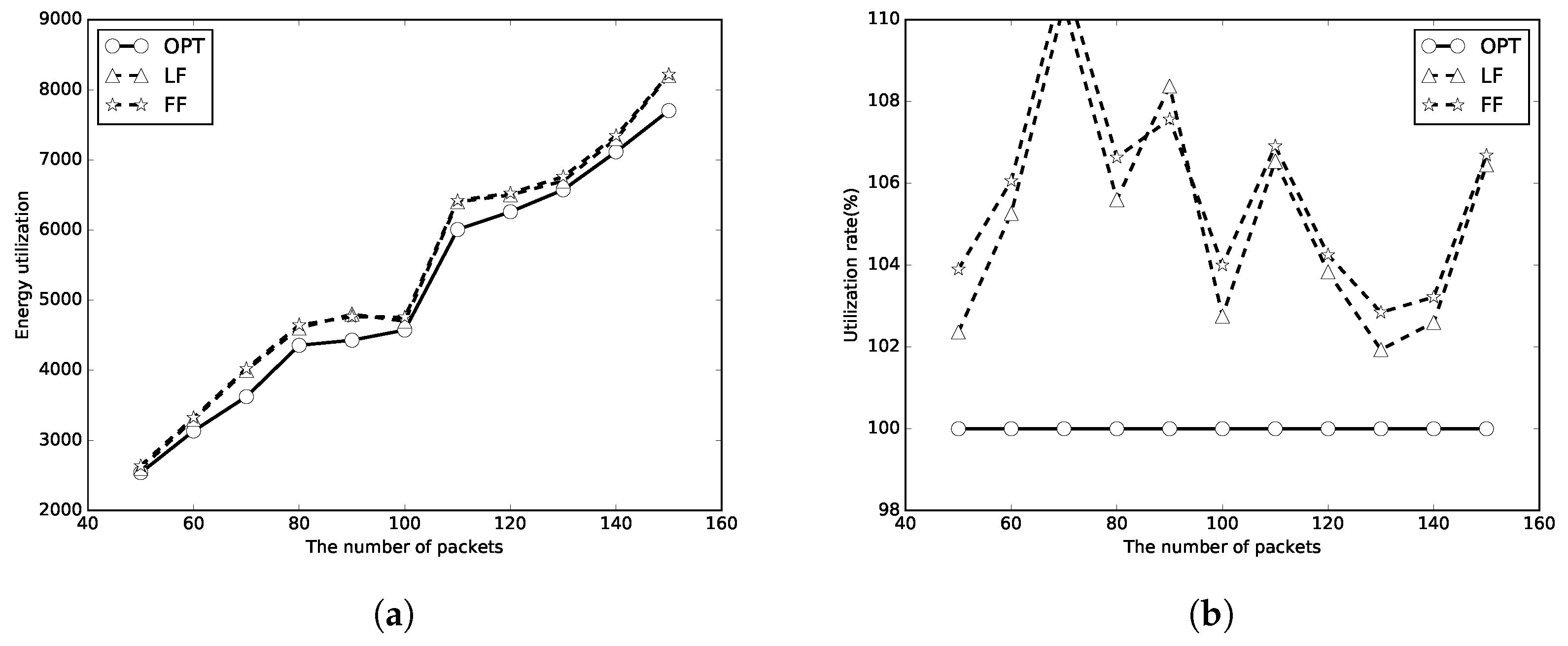
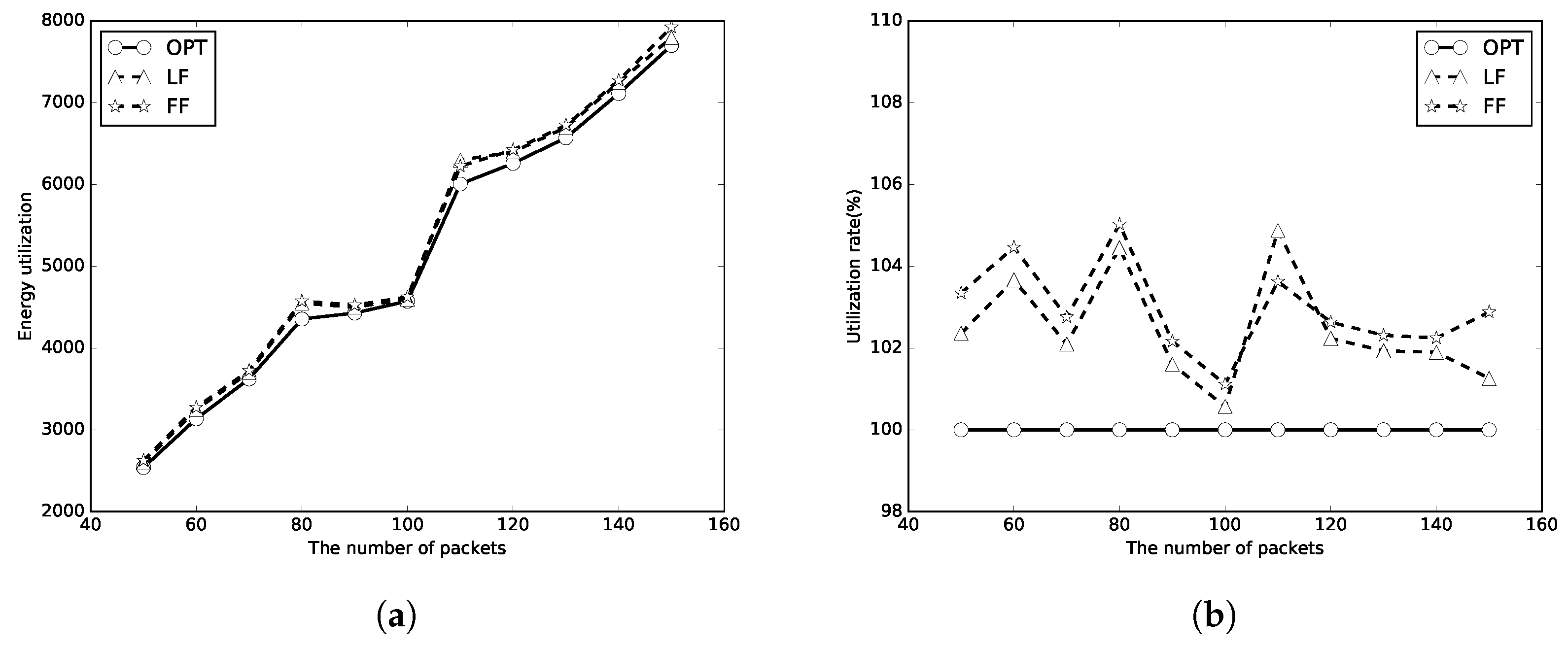
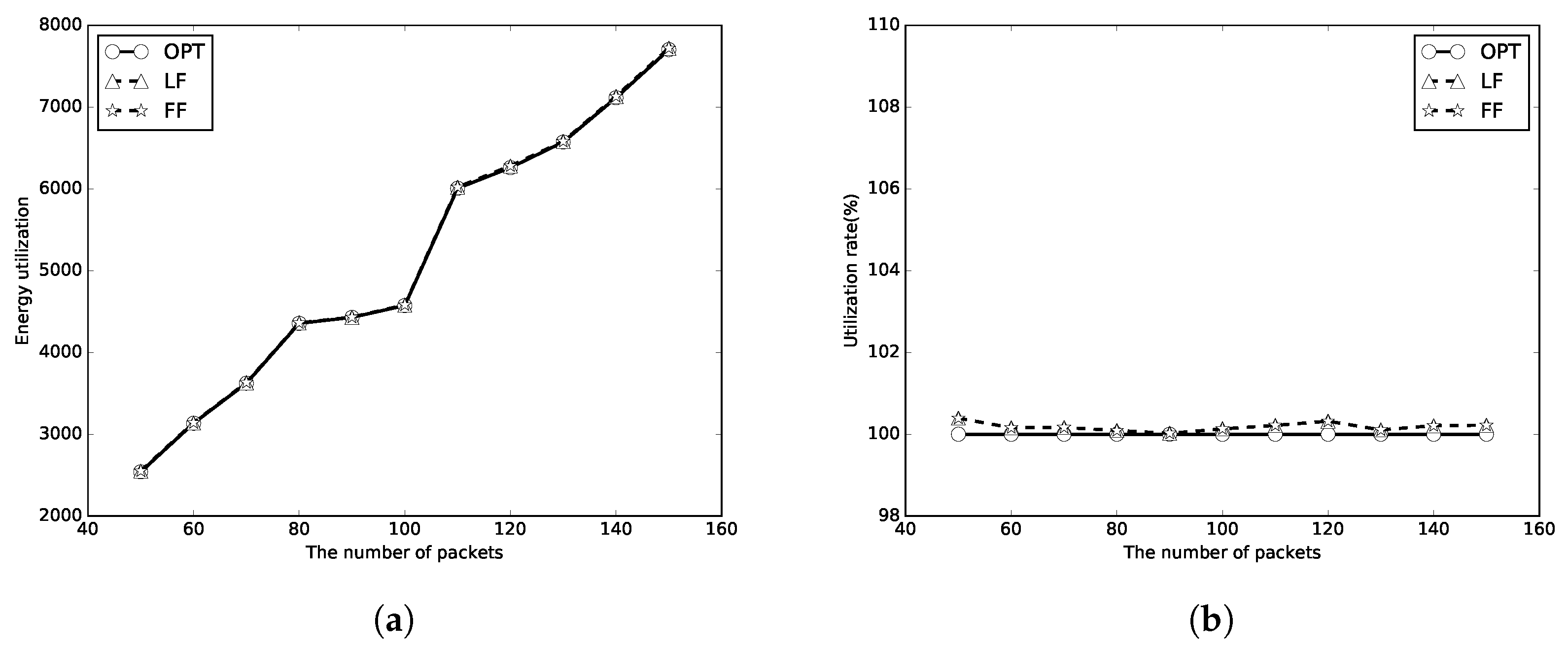
5. Simulations
6. Related Work
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tang, Q.; Tummala, N.; Gupta, S.; Schwiebert, L. TARA: Thermal-Aware Routing Algorithm for Implanted Sensor Networks. In Distributed Computing in Sensor Systems; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3560, pp. 206–217. [Google Scholar]
- Guo, T.; Zhang, L.; Liu, W.; Zhou, Z. A novel solution to power problems in implanted biosensor networks. In Proceedings of the 28th Annual International Conference of the IEEE on Engineering in Medicine and Biology Society, New York, NY, USA, 31 August–3 September 2006; pp. 5952–5955. [Google Scholar]
- Cheng, S.; Cai, Z.; Li, J. Curve Query Processing in Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2015, 64, 5198–5209. [Google Scholar] [CrossRef]
- Olivo, J.; Carrara, S.; De Micheli, G. Energy Harvesting and Remote Powering for Implantable Biosensors. IEEE Sens. J. 2011, 11, 1573–1586. [Google Scholar] [CrossRef]
- Schatz, D.; Hartford, J. Wireless Power for Medical Devices. Electronic Components. 2013. Available online: http://www.mddionline.com/article/wireless-power-medical-devices (accessed on 20 September 2013).
- Kim, A.; Maleki, T.; Ziaie, B. A novel electromechanical interrogation scheme for implant able passive transponders. In Proceedings of the IEEE 25th International Conference on Micro Electro Mechanical Systems, Paris, France, 29 January–2 February 2012; pp. 31–34. [Google Scholar]
- Katic, J. Efficient Energy Harvesting Interface for Implantable Biosensors; KTH Royal Institute of Technology Stockholm: Stockholm, Sweden, 2015. [Google Scholar]
- Antonacci, T. Cooling down Your Wireless Power Receiver. 2012. Available online: http://www.edn.com/design/power-management/4391074/Cooling-Down-your-Wireless-Power-Receiver (accessed on 25 July 2012).
- Gravina, R.; Alinia, P.; Ghasemzadeh, H.; Fortino, G. Multi-sensor fusion in body sensor networks: State-of-the-art and research challenges. Inf. Fusion 2017, 35, 68–80. [Google Scholar] [CrossRef]
- Ghamari, M.; Janko, B.; Sherratt, R.S.; Harwin, W.S.; Piechockic, R.; Soltanpur, C. A Survey on Wireless Body Area Networks for eHealthcare Systems in Residential Environments. Sensors 2016, 16, 831. [Google Scholar] [CrossRef] [PubMed]
- Tang, Q.; Tummala, N.; Gupta, S.; Schwiebert, L. Communication scheduling to minimize thermal effects of implanted biosensor networks in homogeneous tissue. IEEE Trans. Biomed. Eng. 2005, 52, 1285–1294. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Ushio, G.; Shiozawa, T. Calculation of Temperature Rises in the Human Eye Exposed to EM Waves in the ISM Frequency Bands. IEICE Trans. Commun. 2000, E83-B, 541–548. [Google Scholar]
- Schneider, J.; Lucke, L.; Wessels, D.; Schauer, T. Impacts of Wireless Power on Medical Device Design Safety. In Proceedings of the Design of Medical Devices Conference, Minneapolis, MN, USA, 14–16 April 2009. [Google Scholar]
- Frei, M.; Jauchem, J.; Padilla, J.; Merritt, J. Thermal and physiological responses of rats exposed to 2.45-GHz radiofrequency radiation: A comparison of E and H orientation. Radiat. Environ. Biophys. 1989, 28, 235–246. [Google Scholar] [CrossRef] [PubMed]
- Thiele, J.G.M.; Dössel, O. Thermal Heating of Human Tissue Induced by Electro-Magnetic Fields of Magnetic Resonance Imaging. Biomed. Tech. Biomed. Eng. 2009, 47, 743–746. [Google Scholar] [CrossRef]
- Psenakova, Z.; Psenak, V. Electromagnetic Heating of Human Tissue. Acta Mech. Slovaca 2005, 2-a, 1–6. [Google Scholar]
- Zheng, X.; Cai, Z.; Li, J.; Gao, H. A Study on Application-aware Scheduling in Wireless Networks. IEEE Trans. Mob. Comput. 2017, 16, 1787–1801. [Google Scholar] [CrossRef]
- Hyperphysics. Cooling of the Human Body. 2012. Available online: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/coobod.html (accessed on 18 May 2017).
- Nilsson, A.L. Blood Flow, Temperature, and Heat Loss of Skin Exposed to Local Radiative and Convective Cooling. J. Investig. Dermatol. 1987, 88, 586–593. [Google Scholar] [CrossRef] [PubMed]
- Korte, B.; Vygen, J. Chapter Bin-Packing. In Combinatorial Optimization: Theory and Algorithms; Springer: Berlin/Heidelberg, Germany, 2006; pp. 426–441. [Google Scholar]
- Movassaghi, S.; Abolhasan, M.; Lipman, J. A Review of Routing Protocols in Wireless Body Area Networks. J. Netw. 2013, 8, 559–575. [Google Scholar] [CrossRef]
- Bag, A.; Bassiouni, M.A. Energy Efficient Thermal Aware Routing Algorithms for Embedded Biomedical Sensor Networks. In Proceedings of the IEEE International Conference on Mobile Adhoc and Sensor Systems, Vancouver, BC, Canada, 9–12 October 2006; pp. 604–609. [Google Scholar]
- Takahashi, D.; Xiao, Y.; Hu, F.; Chen, J.; Sun, Y. Temperature-aware routing for telemedicine applications in embedded biomedical sensor networks. EURASIP J. Wirel. Commun. Netw. 2008, 2008, 26. [Google Scholar] [CrossRef]
- Bag, A.; Bassiouni, M.A. Hotspot Preventing Routing algorithm for delay-sensitive applications of in vivo biomedical sensor networks. Inf. Fusion 2008, 9, 389–398. [Google Scholar] [CrossRef]
- Bag, A.; Bassiouni, M.A. Routing algorithm for network of homogeneous and id-less biomedical sensor nodes (RAIN). In Proceedings of the Sensors Applications Symposium (SAS 2008), Atlanta, GA, USA, 12–14 February 2008; pp. 68–73. [Google Scholar]
- Xiao, L.; Ping, W.; Niyato, D.; Dong, I.K.; Zhu, H. Wireless Charging Technologies: Fundamentals, Standards, and Network Applications. IEEE Commun. Surv. Tutor. 2016, 18, 1413–1452. [Google Scholar]
- Dai, H.; Liu, Y.; Chen, G.; Wu, X.; He, T.; Liu, A.X.; Ma, H. Safe Charging for Wireless Power Transfer. IEEE/ACM Trans. Netw. 2014, 25, 3531–3544. [Google Scholar] [CrossRef]
- Olteanu, M.; Marincaş, C.; Rafiroiu, D. Dangerous Temperature Increase from EM Radiation around Metallic Implants. Acta Electroteh. 2012, 53, 175–180. [Google Scholar]
- Movassaghi, S.; Abolhasan, M.; Lipman, J.; Smith, D.; Jamalipour, A. Wireless Body Area Networks: A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 1658–1686. [Google Scholar] [CrossRef]
- Vazirani, V.V. Chapter Bin-Packing. In Approximation Algorithms; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Dósa, G.; Li, R.; Han, X.; Tuza, Z. Tight Absolute Bound for First Fit Decreasing Bin-packing: FFD(L)<=11/9OPT(L)+6/9. Theor. Comput. Sci. 2013, 510, 13–61. [Google Scholar]
- Dósa, G.; Sgall, J. First Fit bin packing: A tight analysis. In Proceedings of the International Symposium on Theoretical Aspects of Computer Science, Kiel, Germany, 27 February–2 March 2013. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Luo, J.; Wu, W.; Gao, H. Energy Efficient Data Transmission for Sensors with Wireless Charging. Sensors 2018, 18, 511. https://doi.org/10.3390/s18020511
Fang X, Luo J, Wu W, Gao H. Energy Efficient Data Transmission for Sensors with Wireless Charging. Sensors. 2018; 18(2):511. https://doi.org/10.3390/s18020511
Chicago/Turabian StyleFang, Xiaolin, Junzhou Luo, Weiwei Wu, and Hong Gao. 2018. "Energy Efficient Data Transmission for Sensors with Wireless Charging" Sensors 18, no. 2: 511. https://doi.org/10.3390/s18020511
APA StyleFang, X., Luo, J., Wu, W., & Gao, H. (2018). Energy Efficient Data Transmission for Sensors with Wireless Charging. Sensors, 18(2), 511. https://doi.org/10.3390/s18020511




