H∞ Robust Control of a Large-Piston MEMS Micromirror for Compact Fourier Transform Spectrometer Systems
Abstract
:1. Introduction
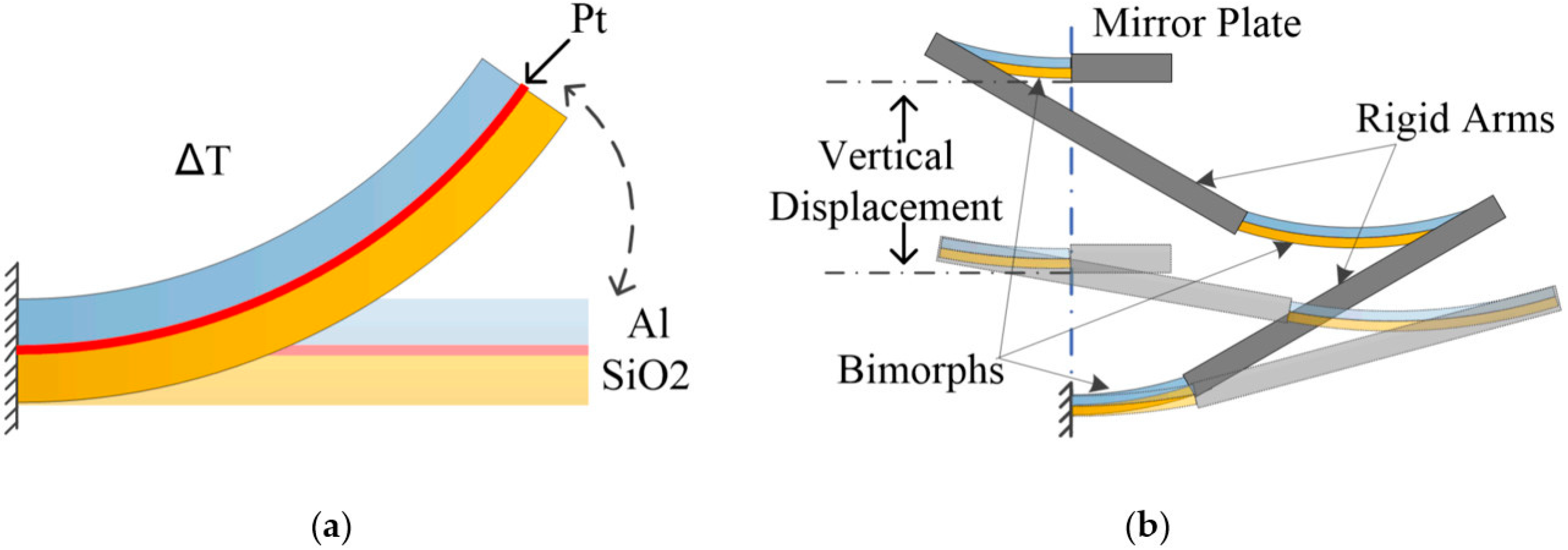
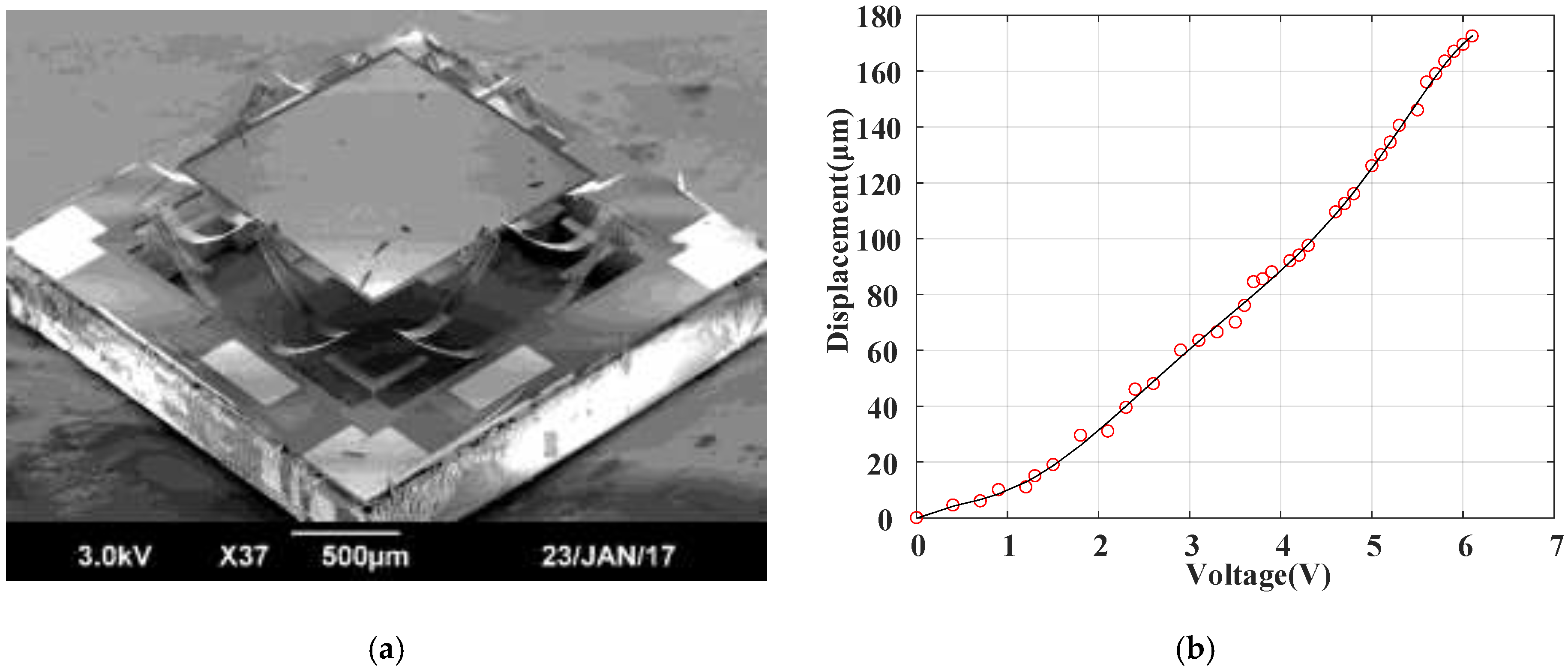
2. The Electrothermal Micromirror
2.1. Device Description
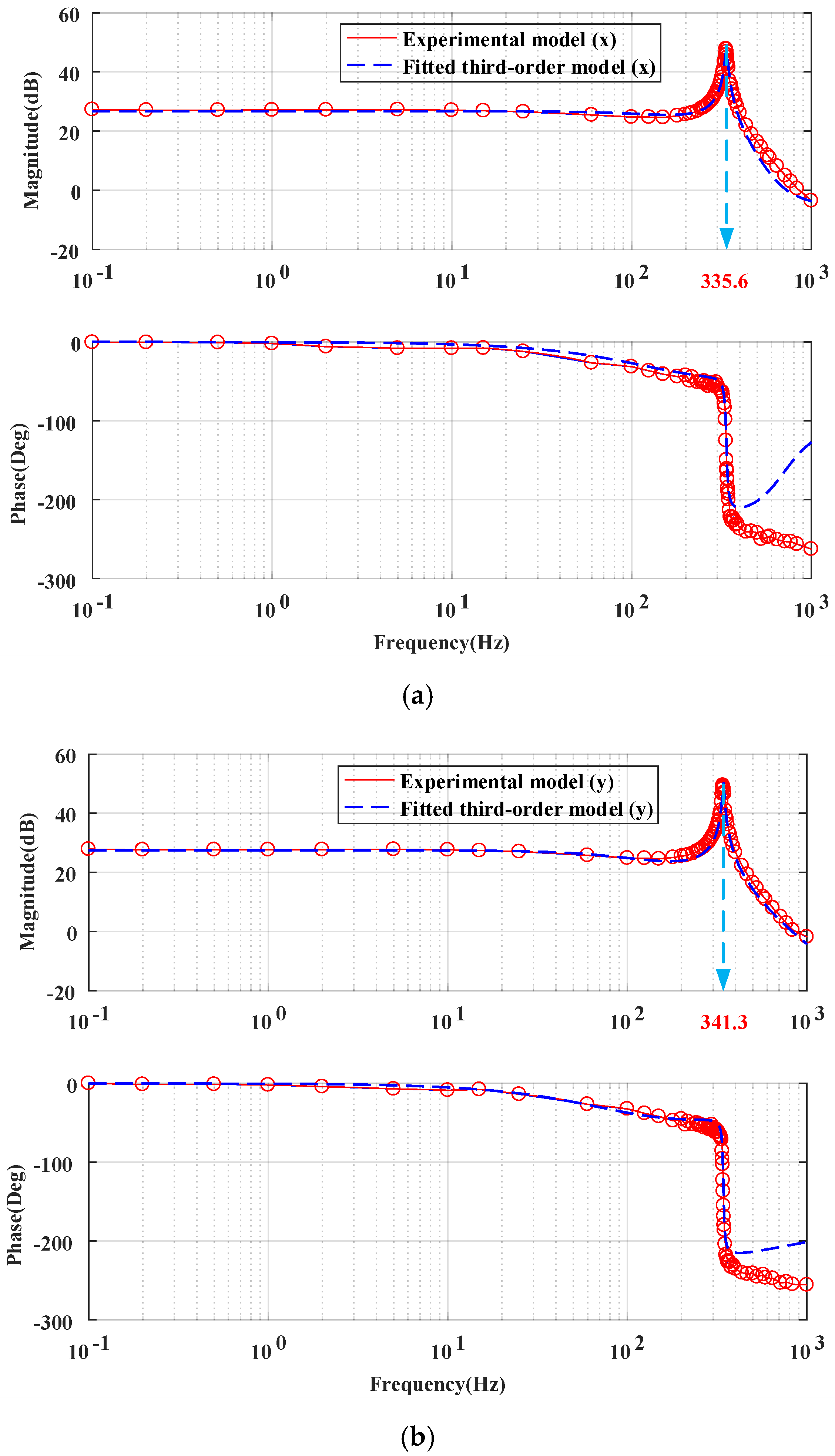
2.2. Dynamic Model of the Micromirror
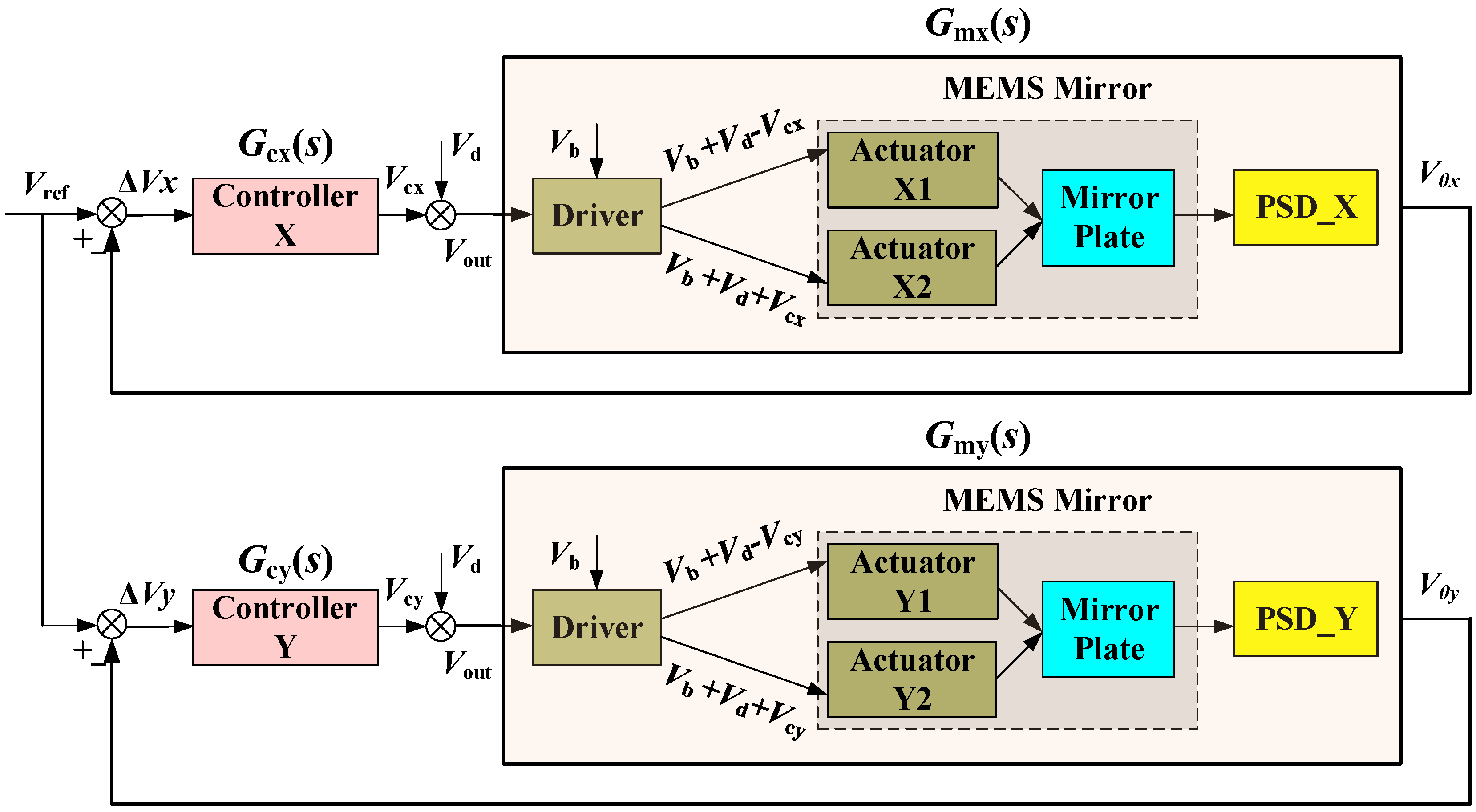
3. Design of Robust Controller
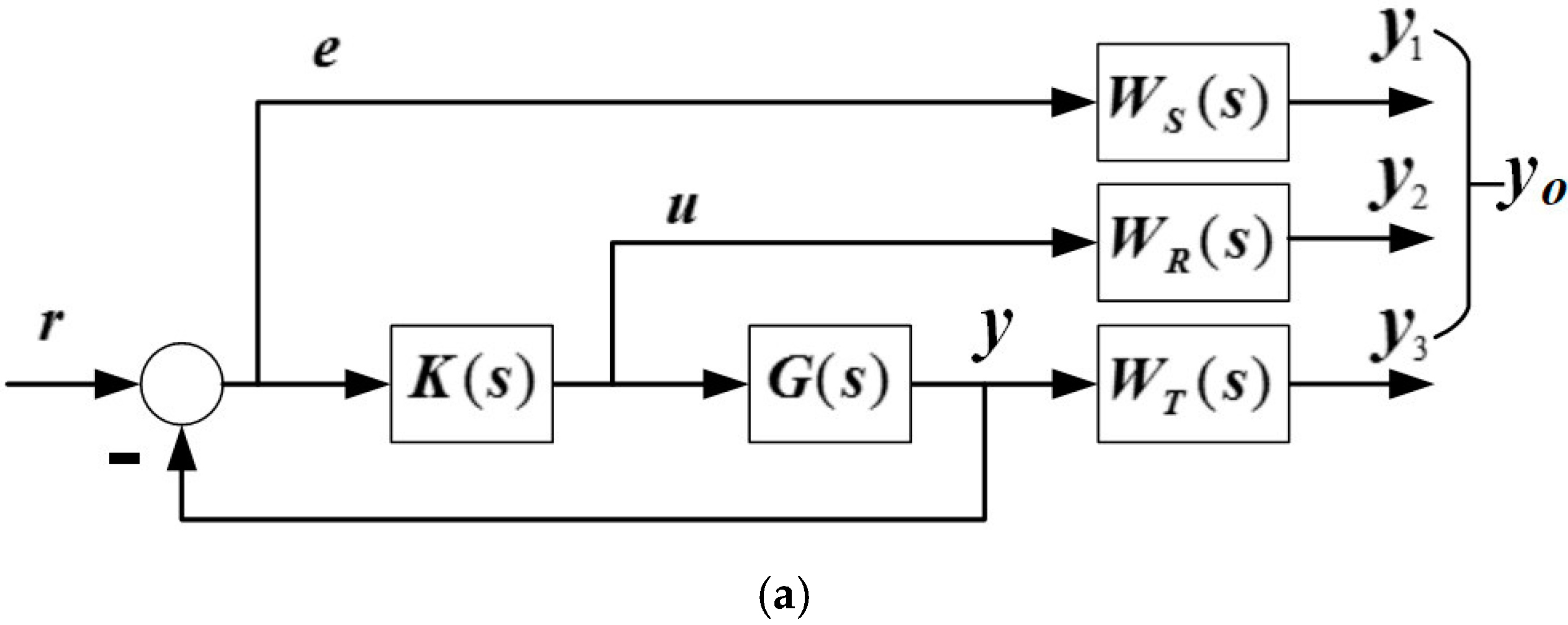
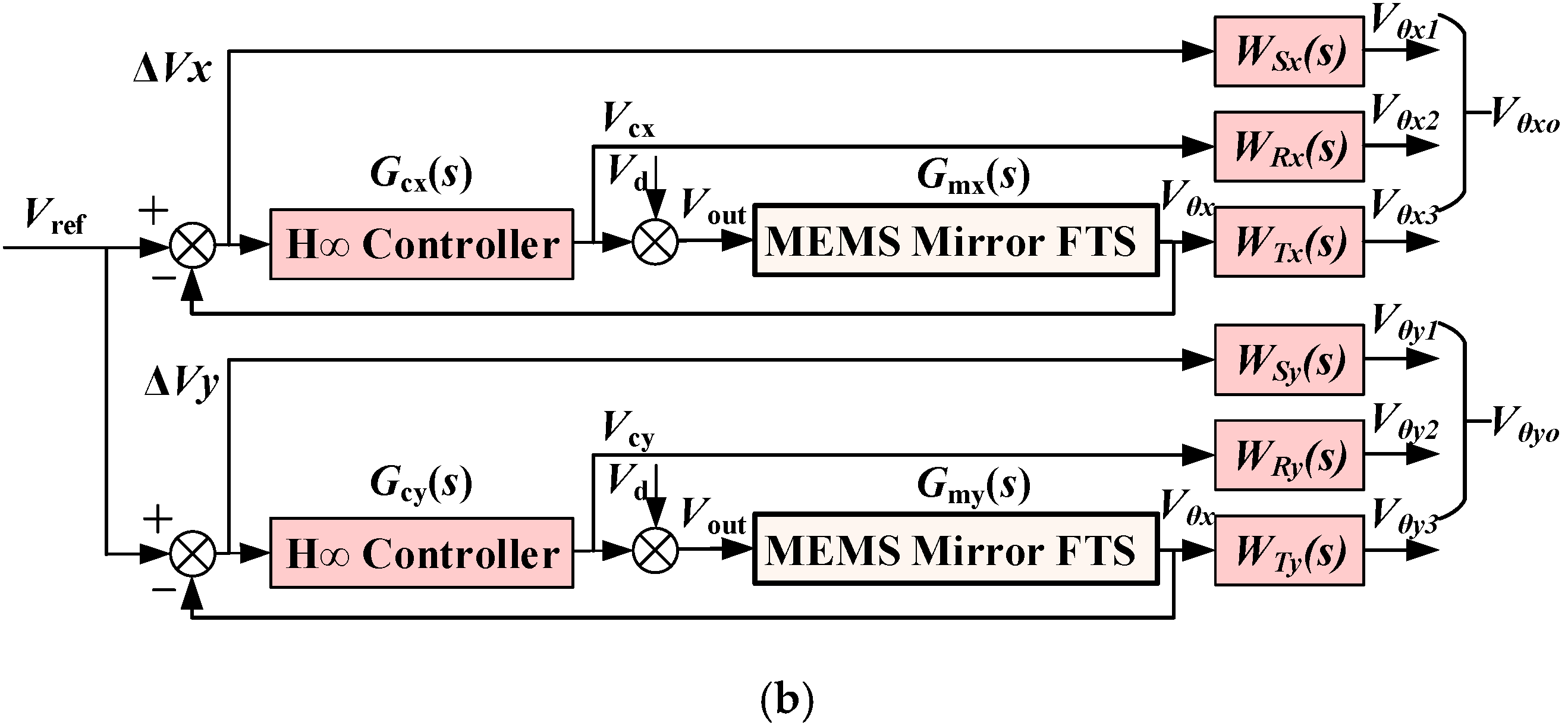
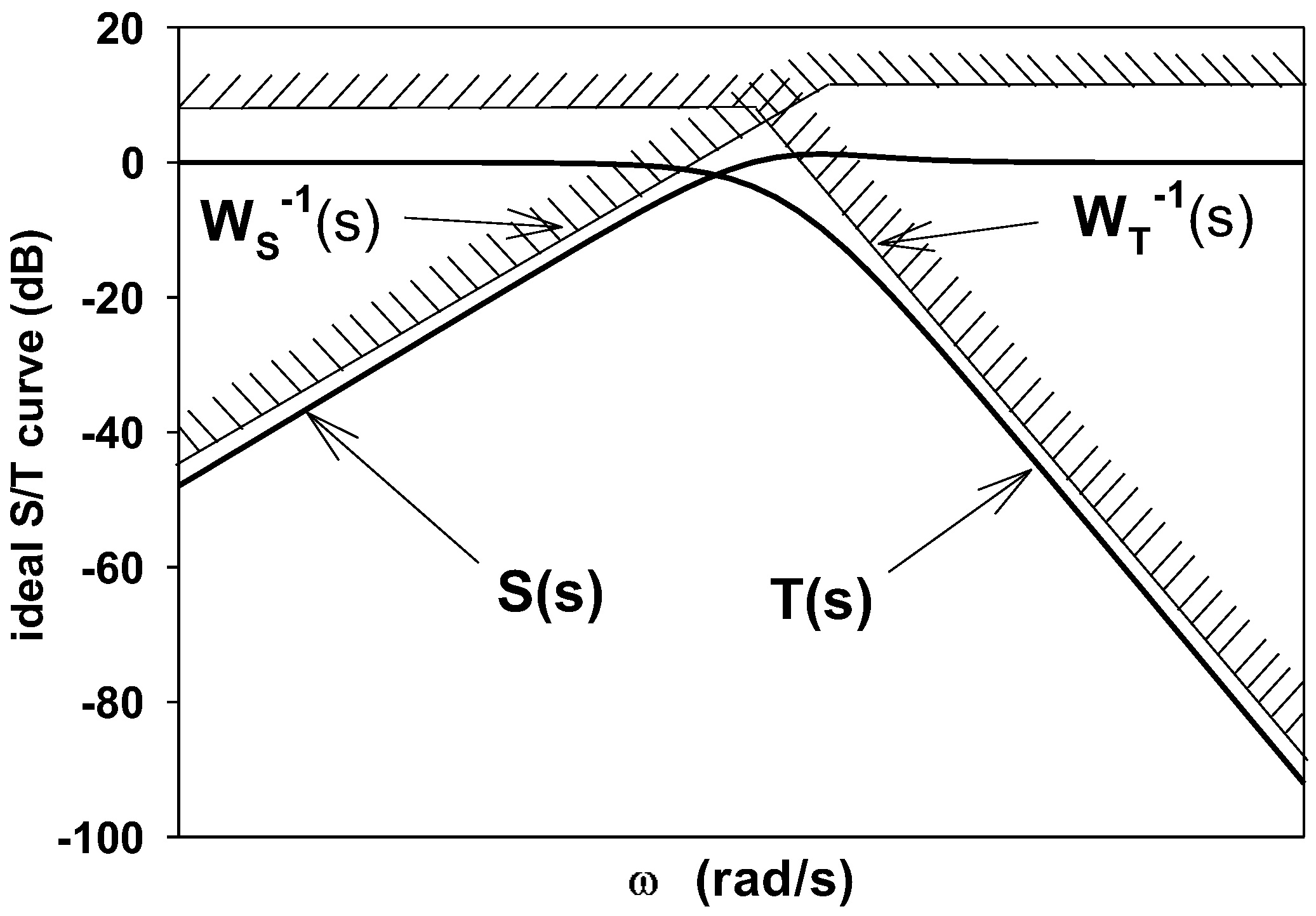
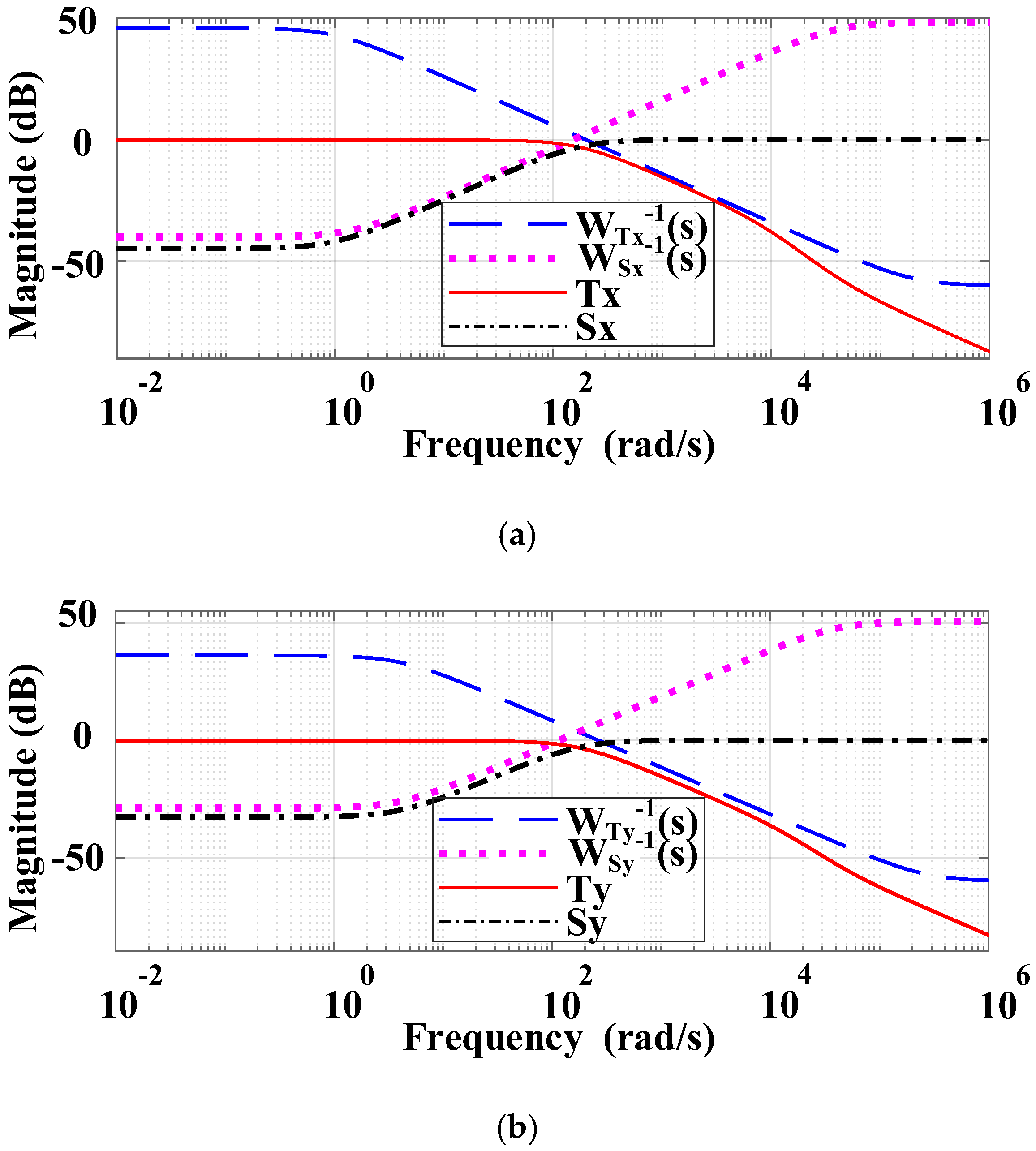
3.1. Design of H∞ Robust Controller
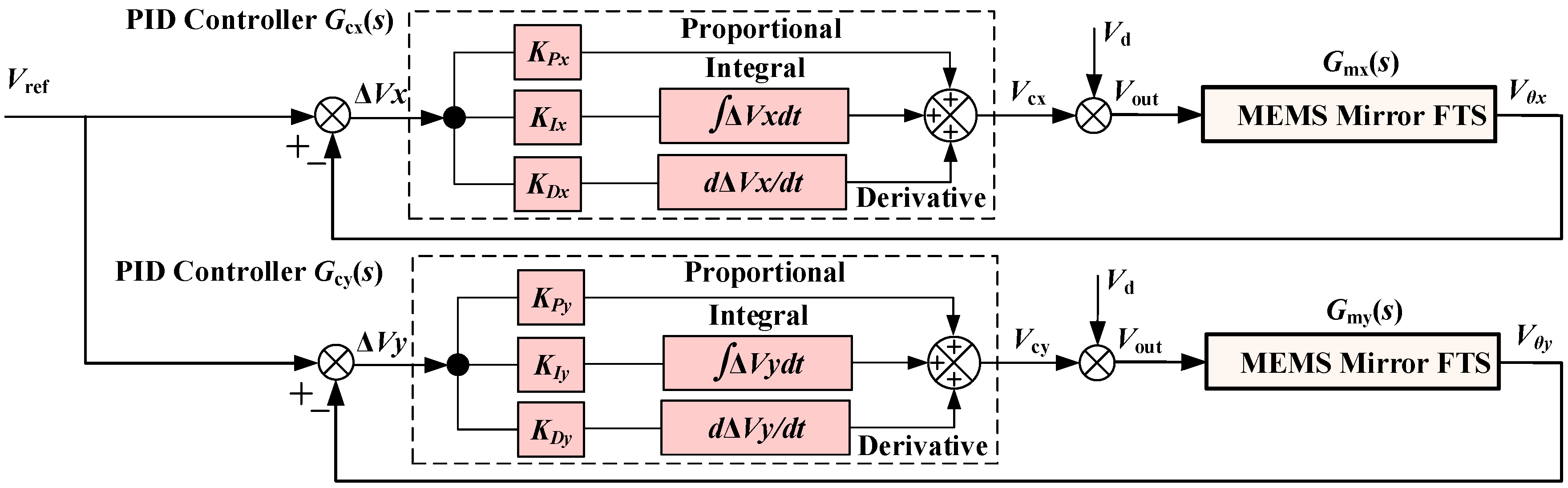
3.2. Design of the Proportional-Integral-Derivative (PID) Controller
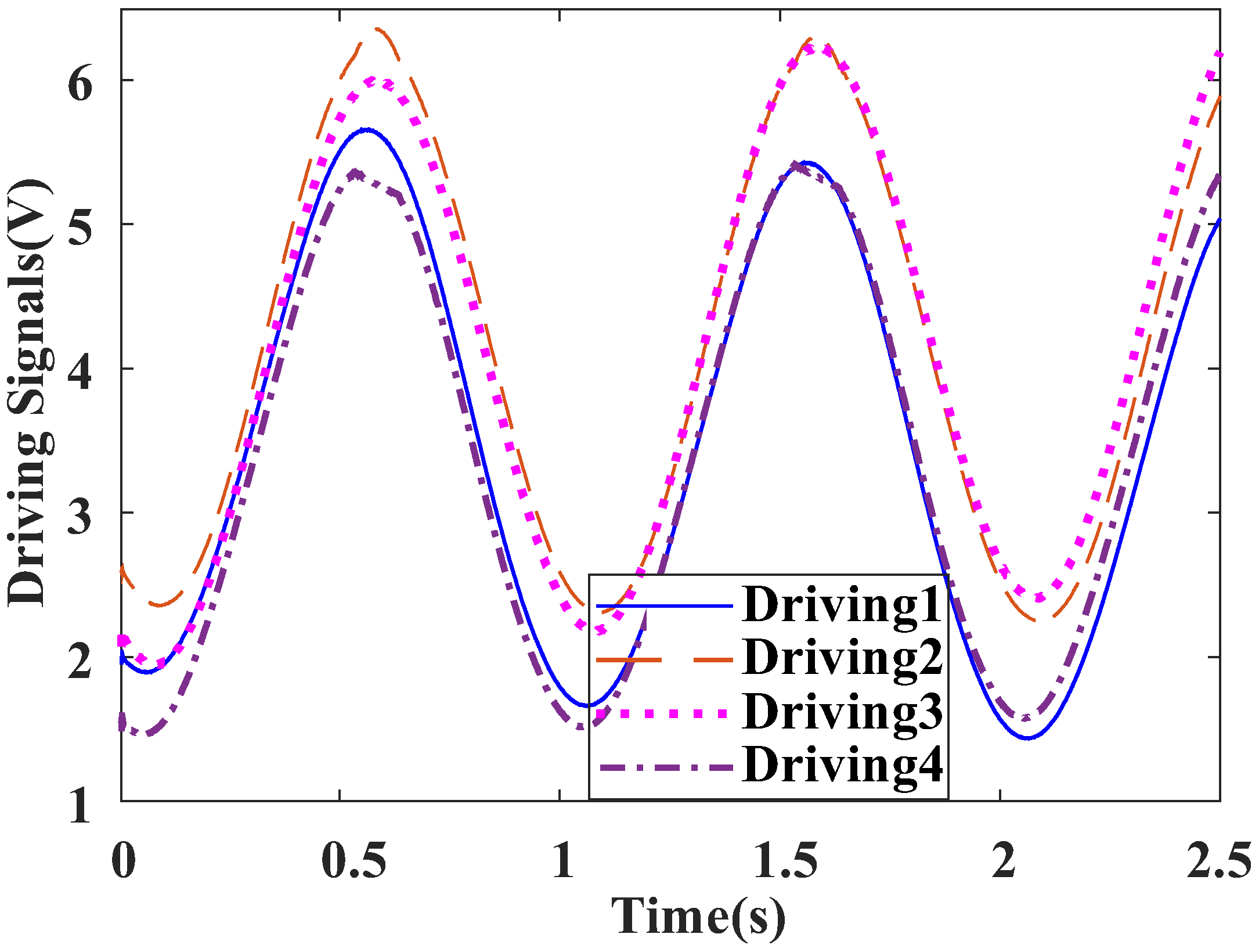
3.3. Design of Look up Table Controller
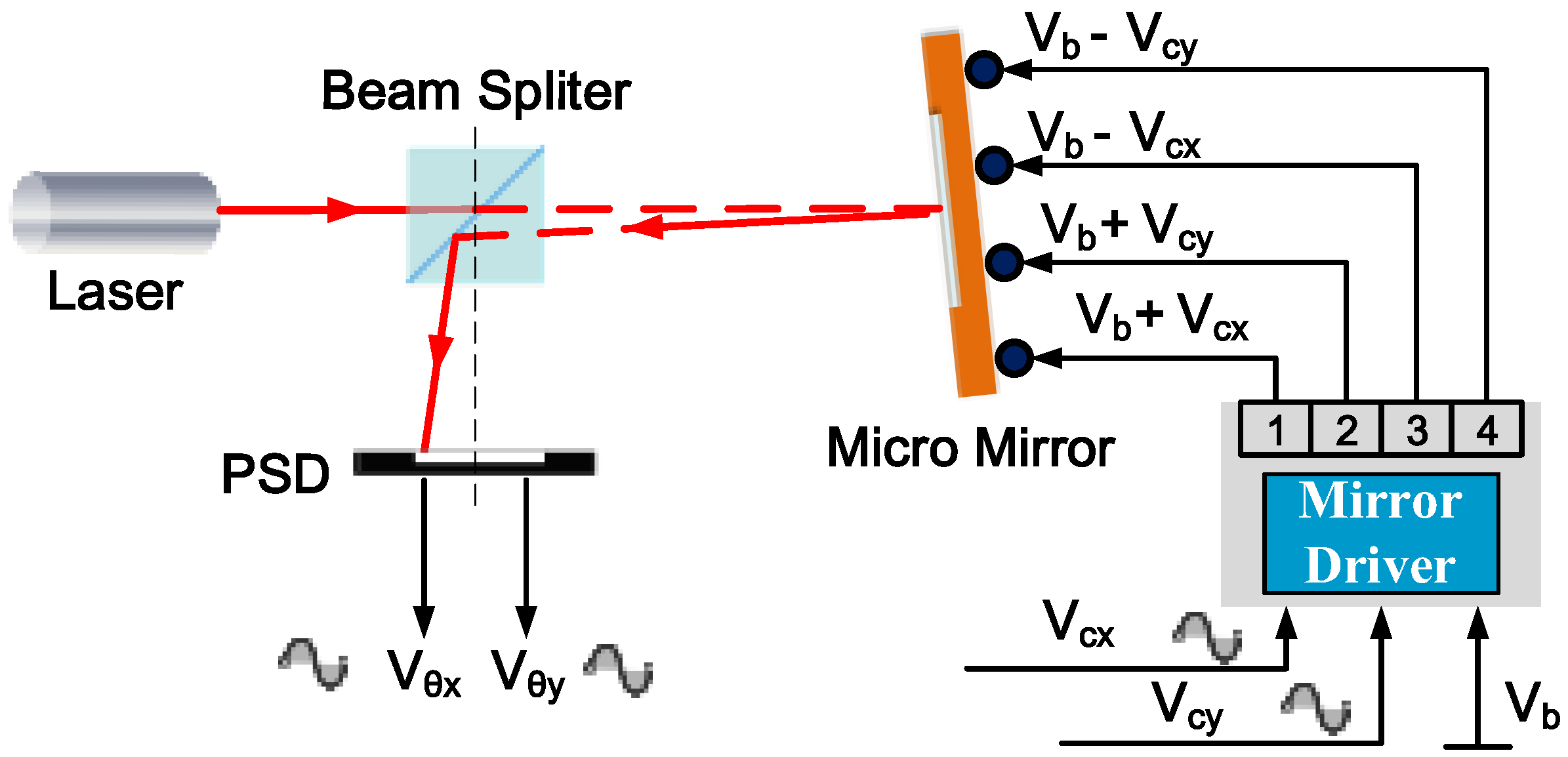
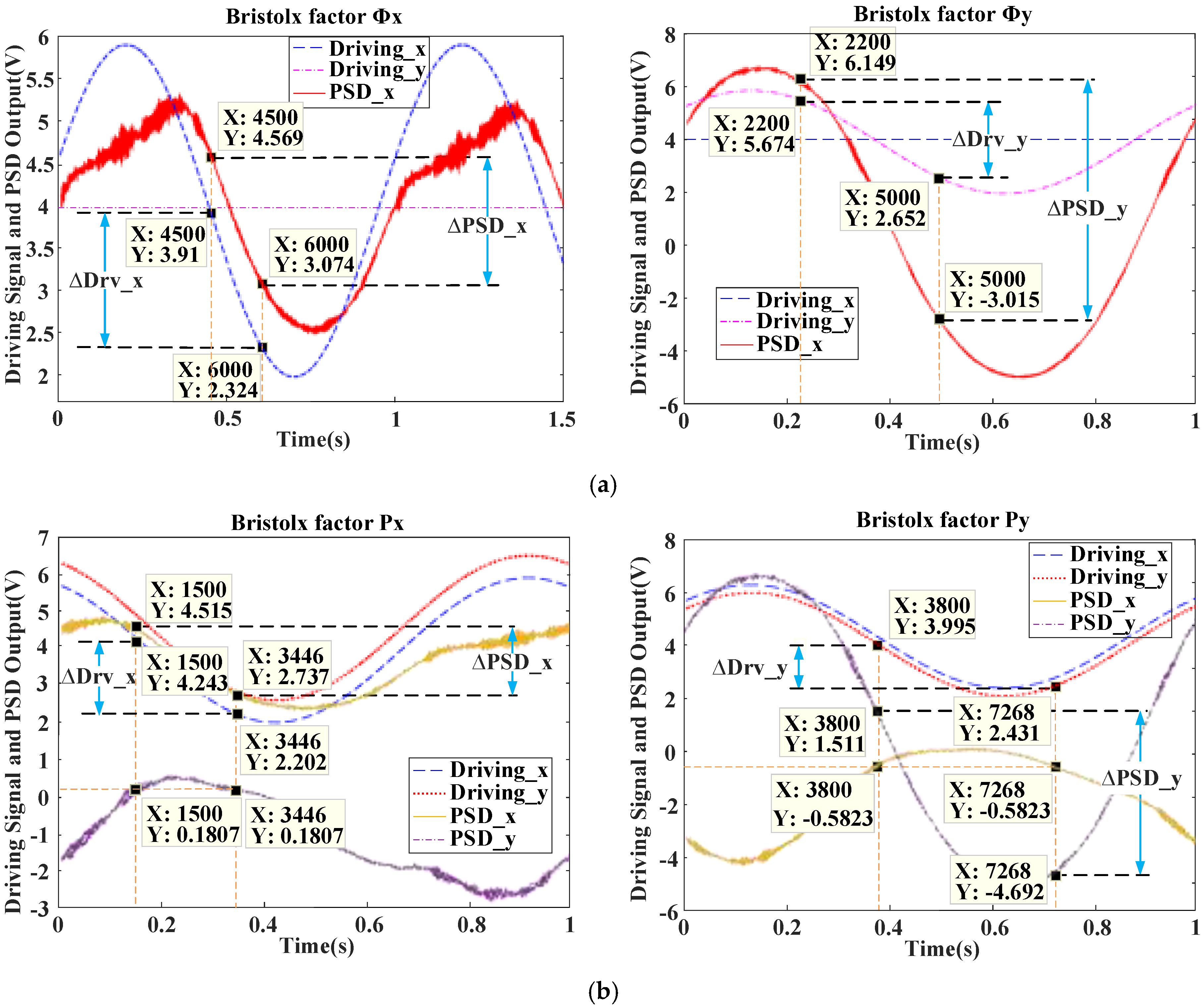
4. Experimental Results and Discussion
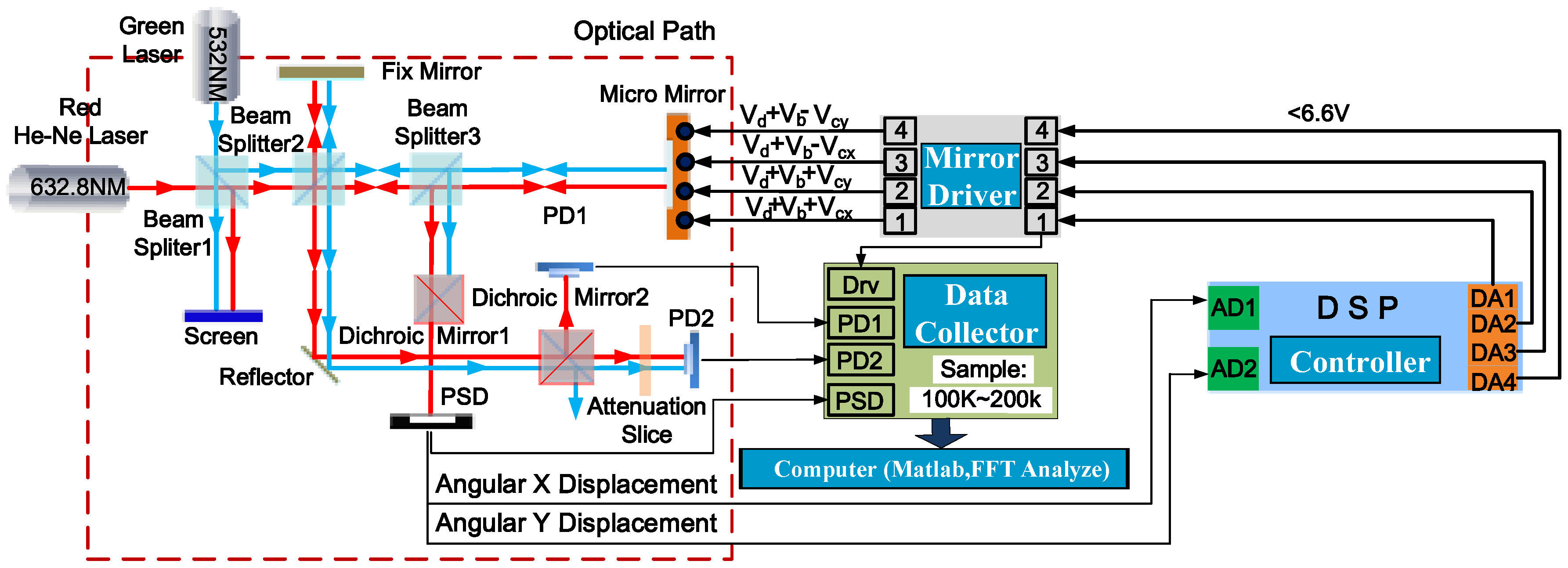
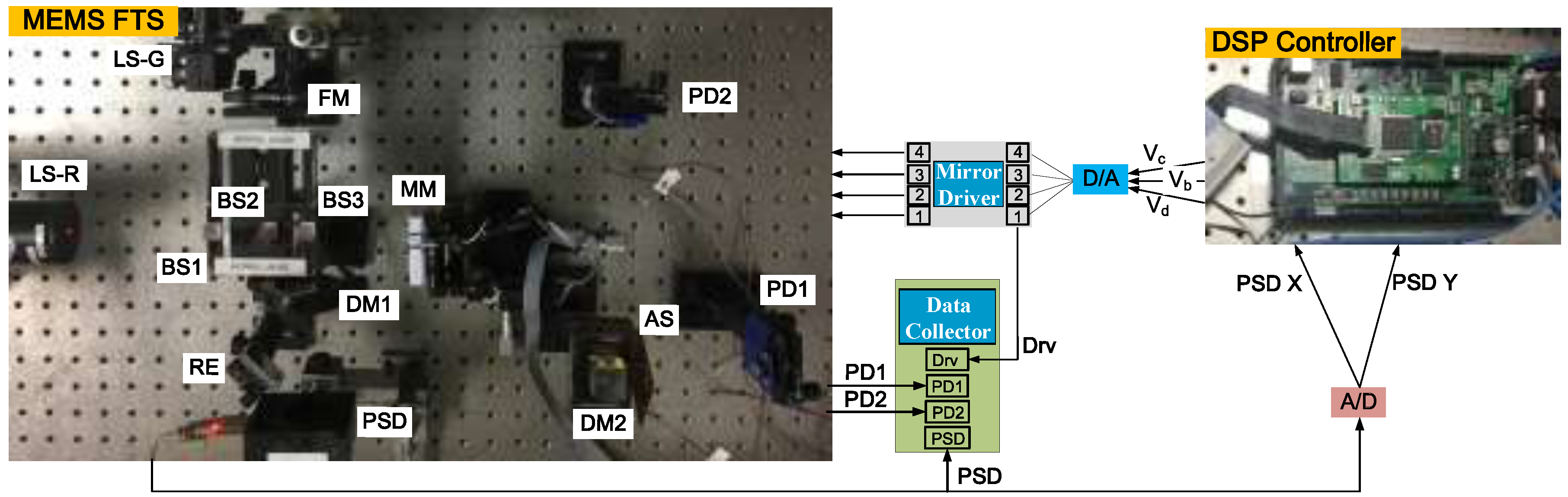
4.1. Experimental Setup
4.2. Tilting Control
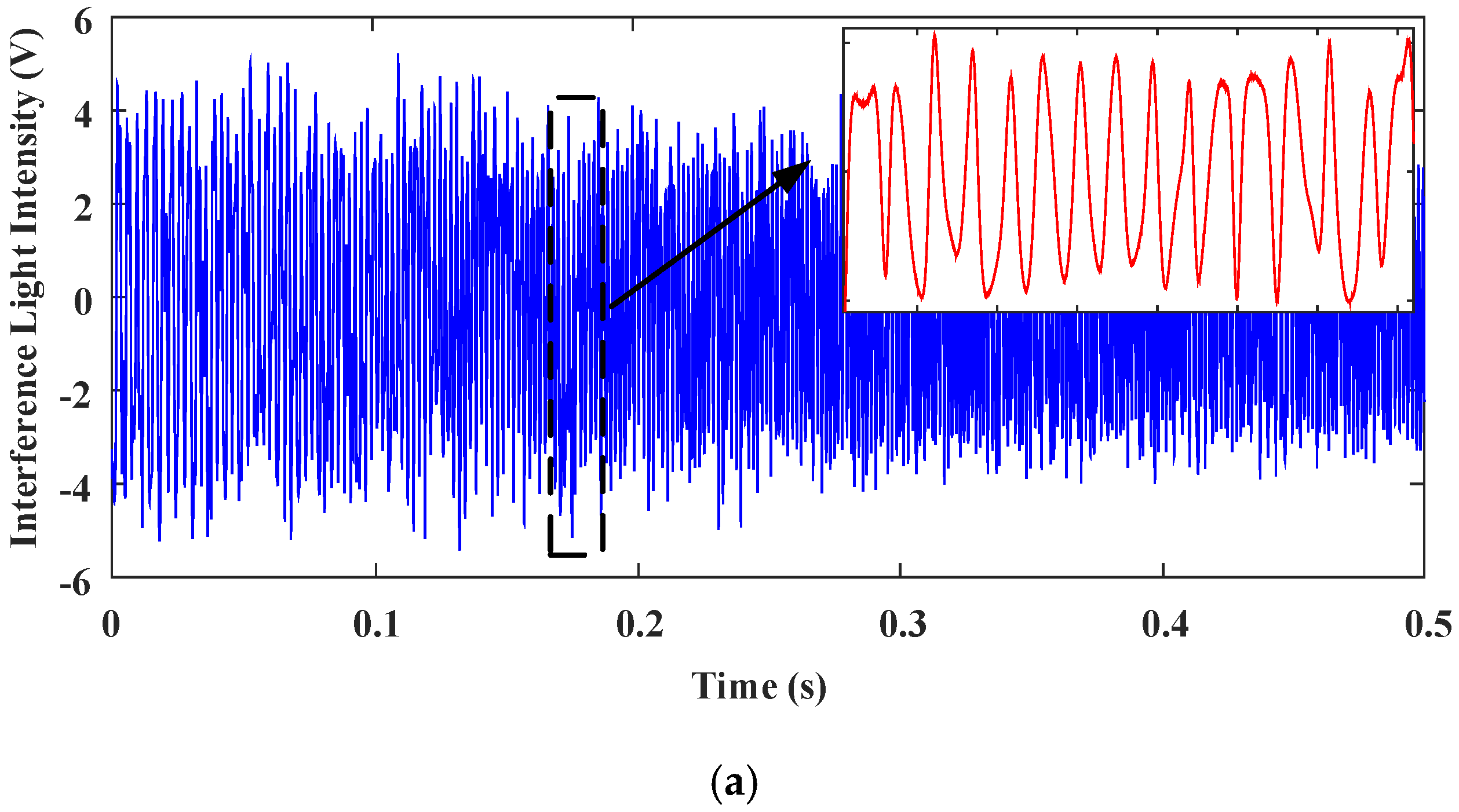
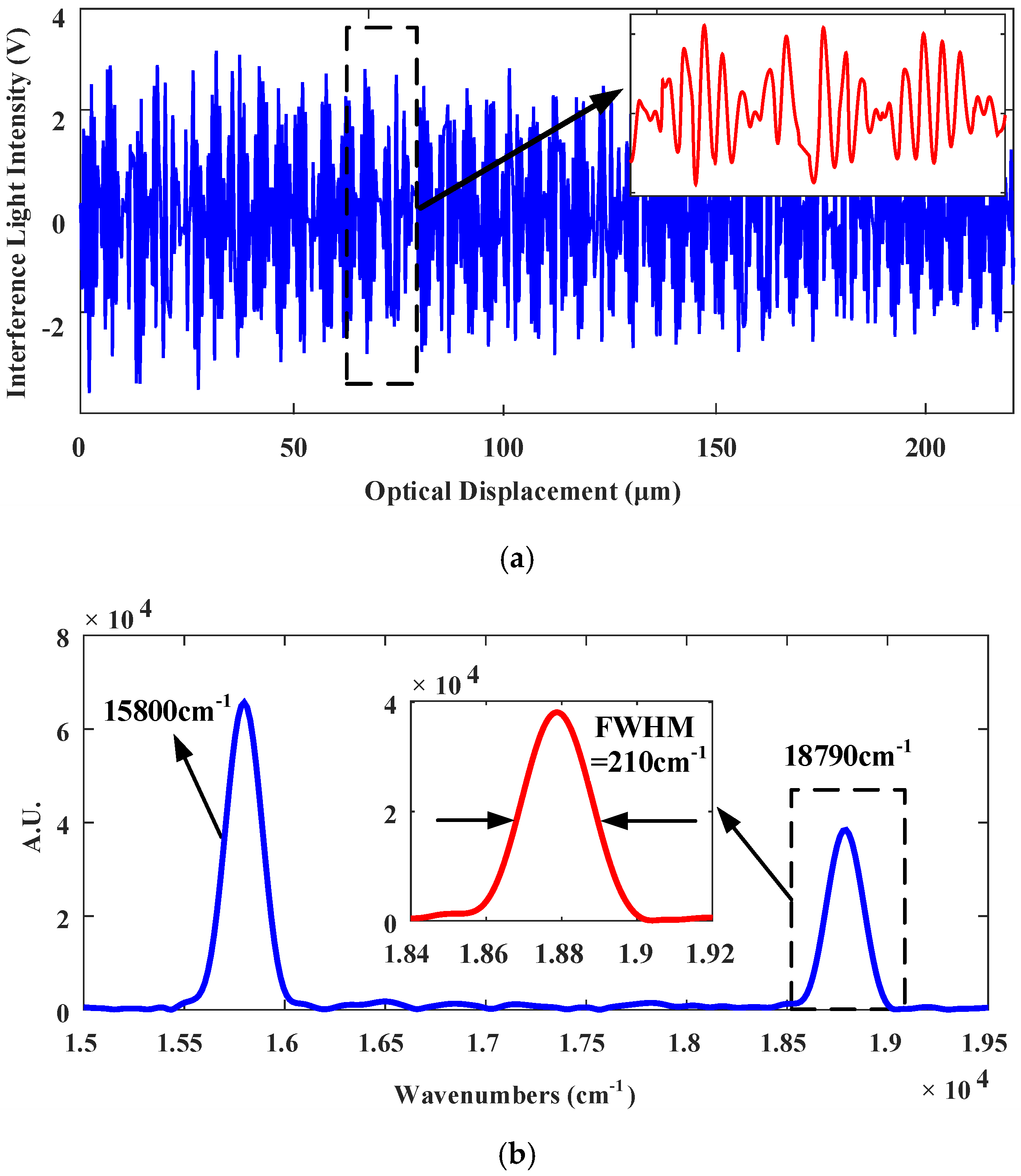
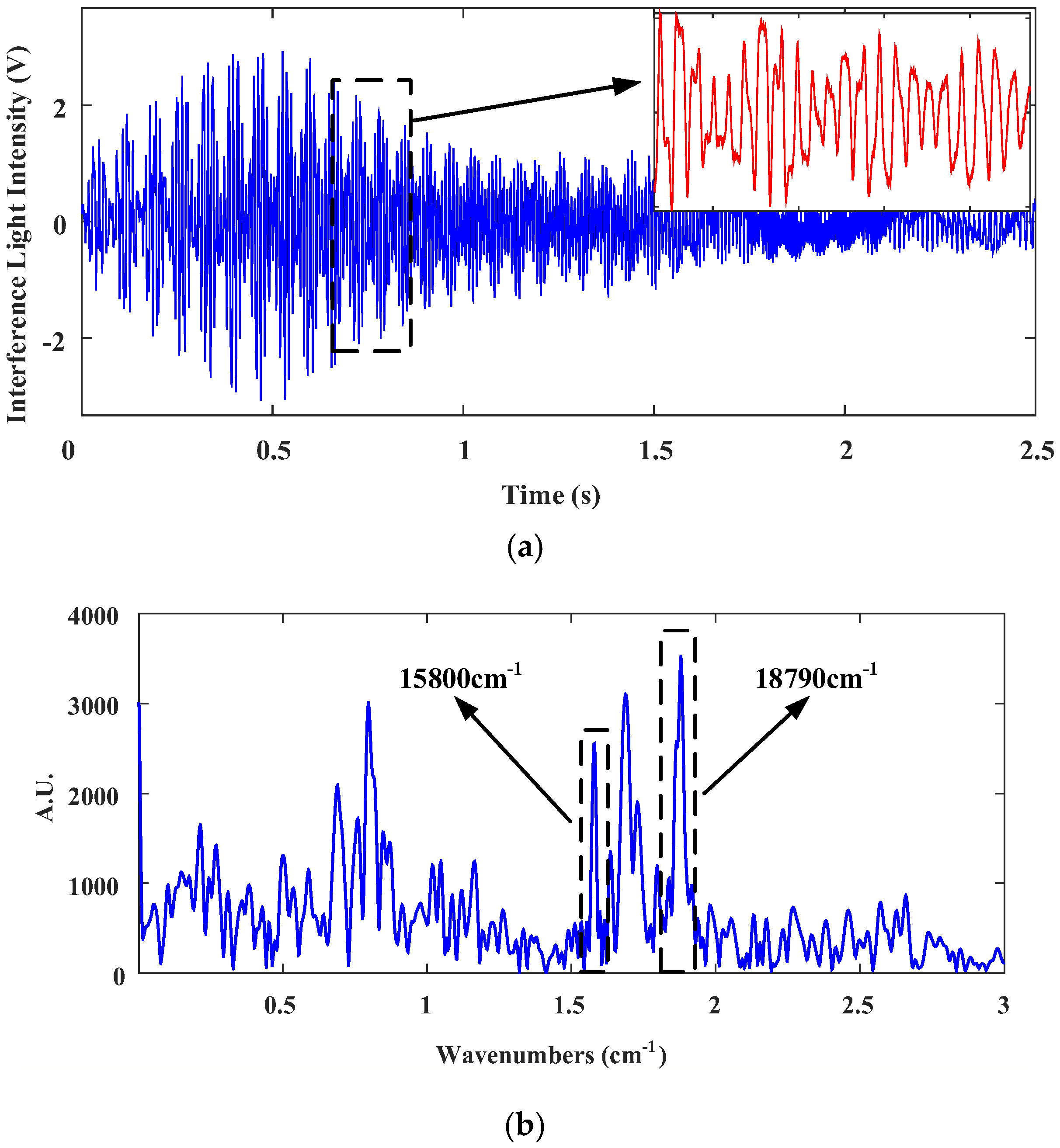
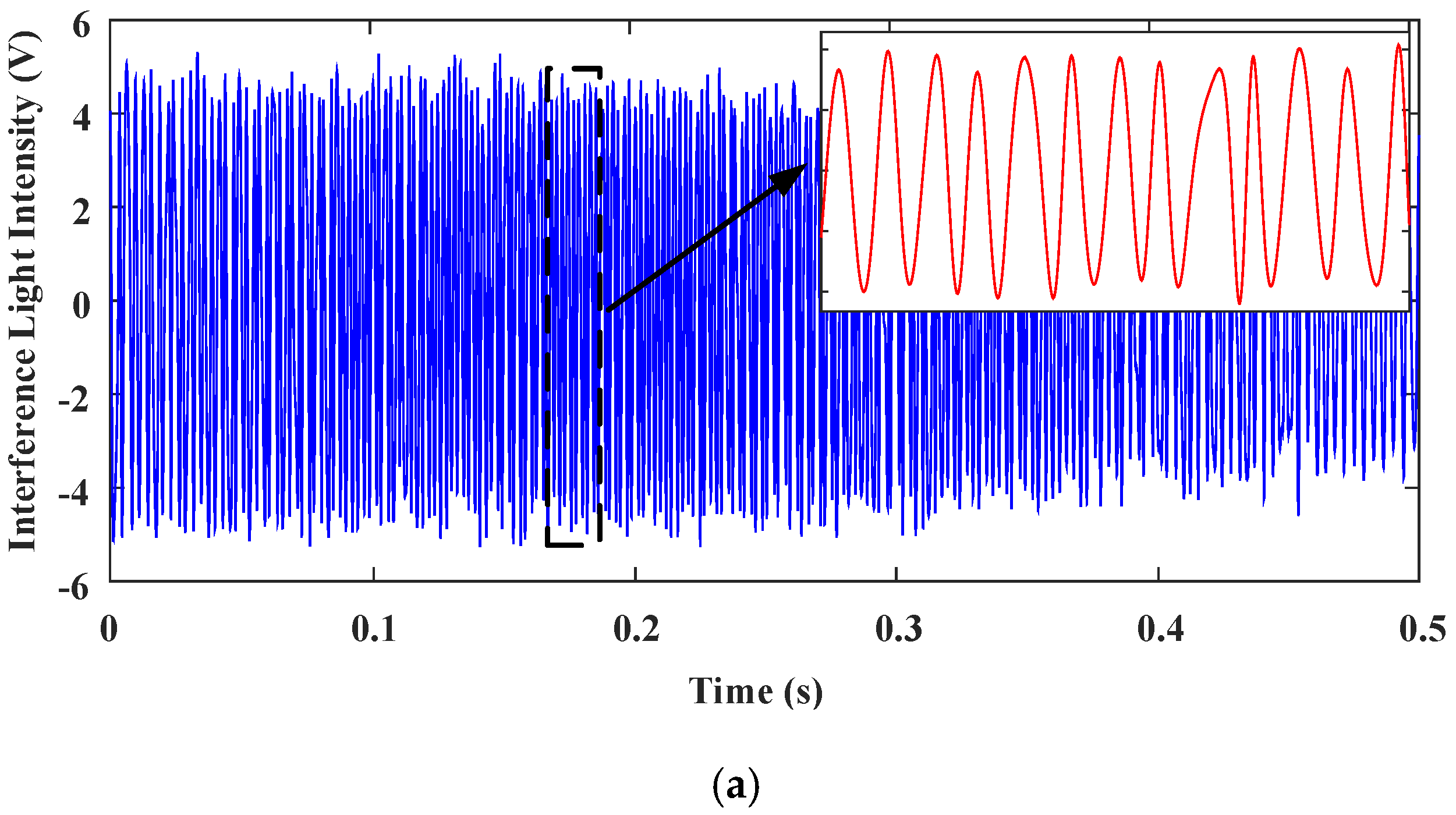
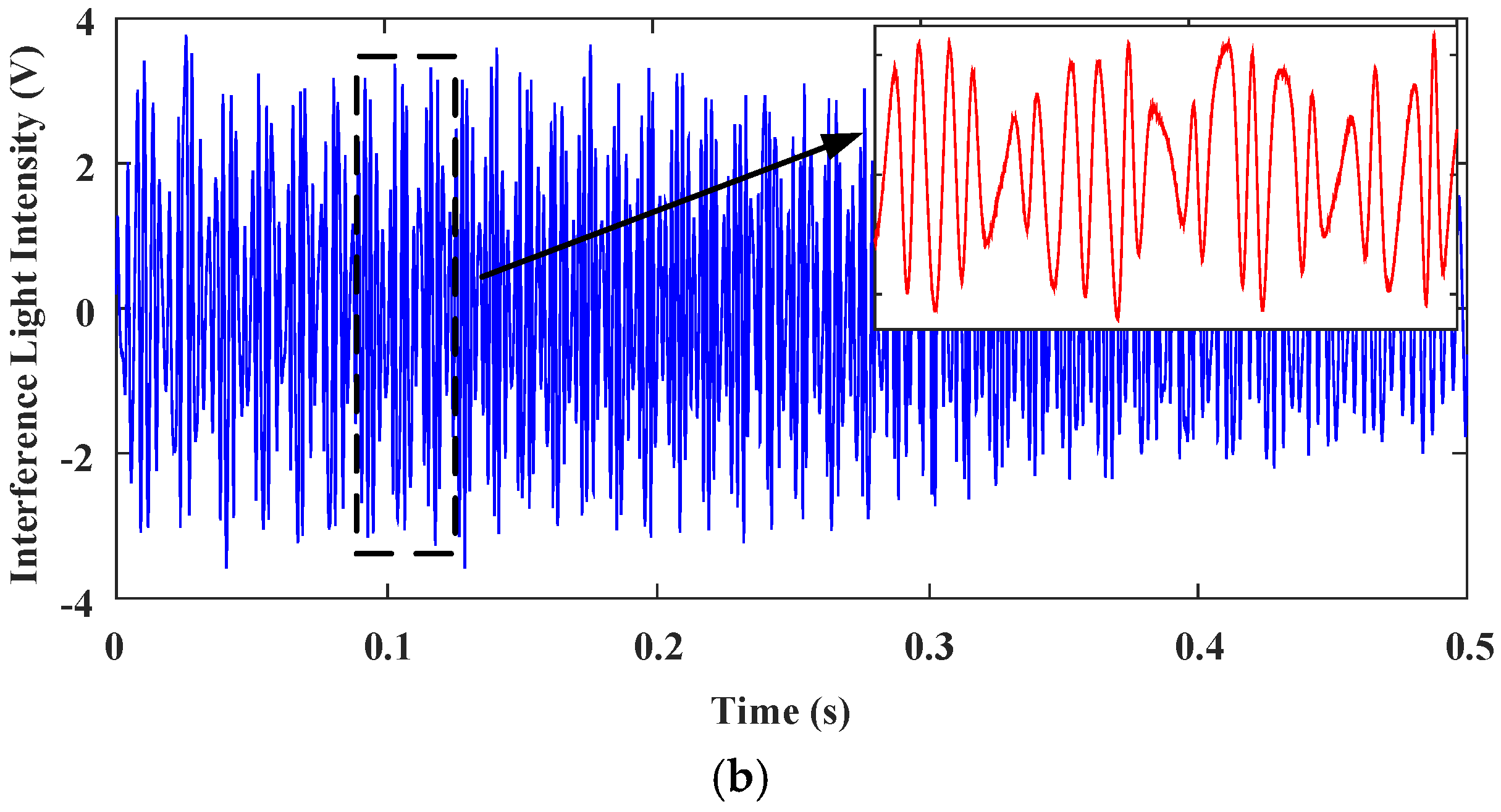
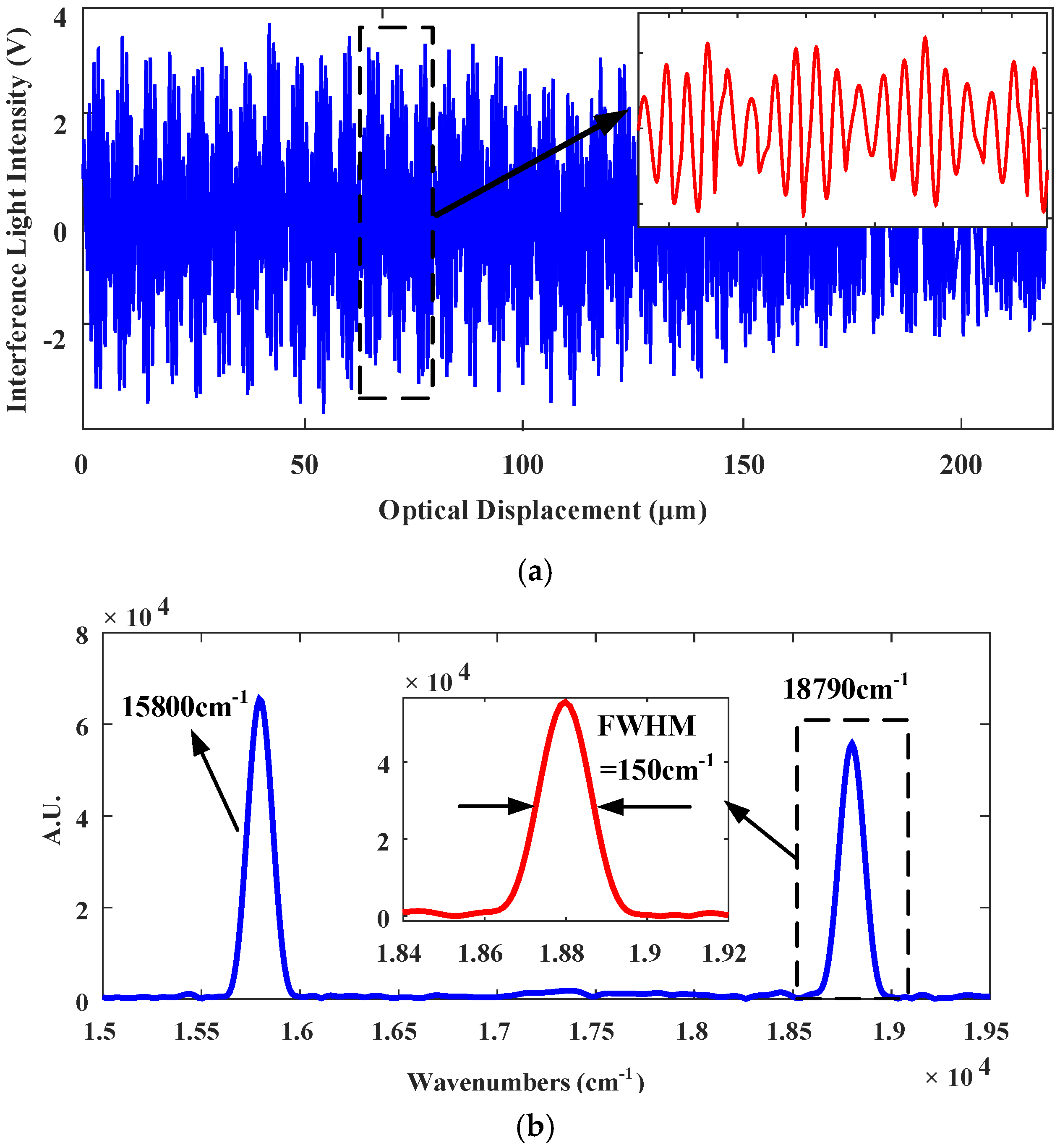
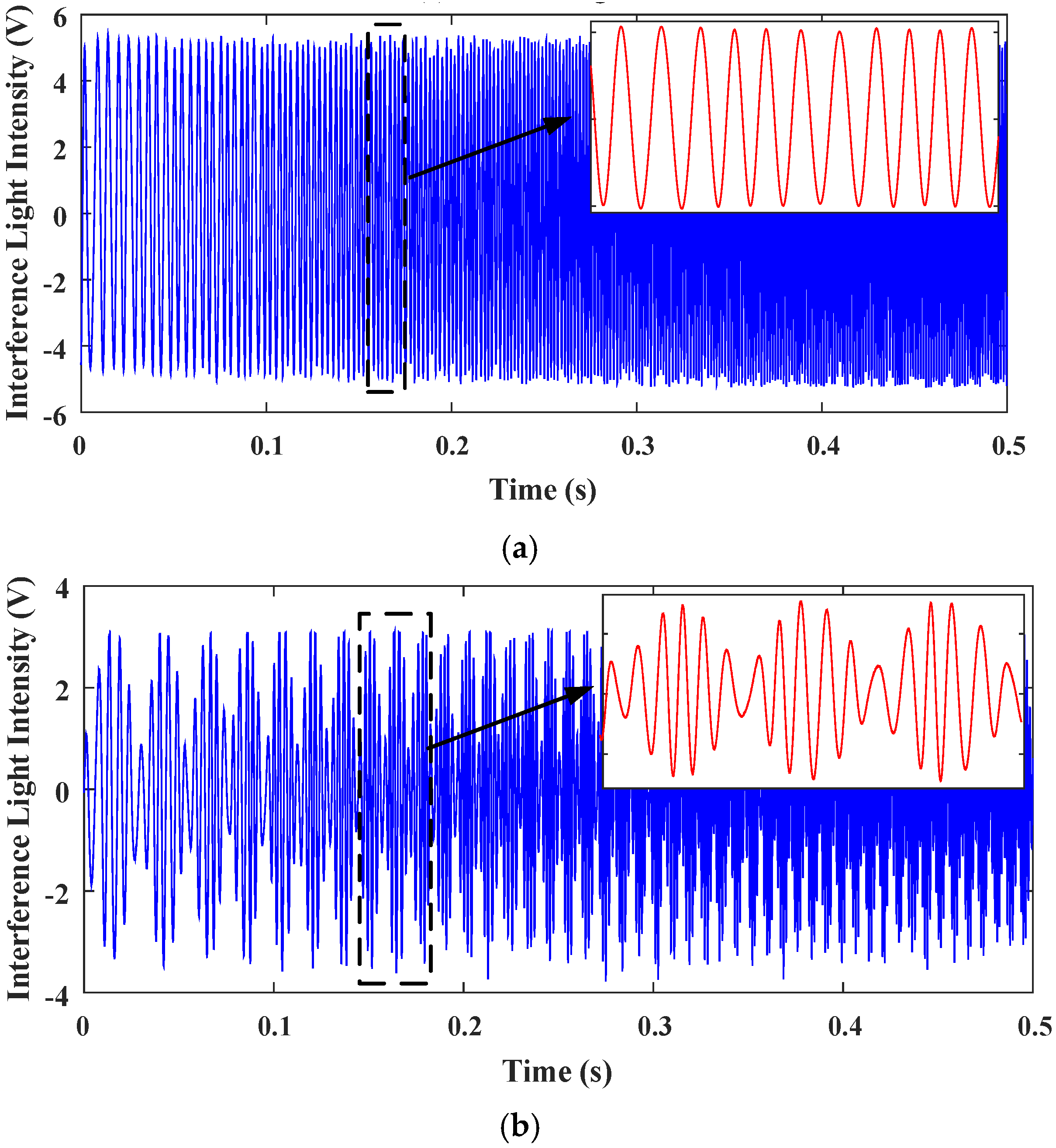
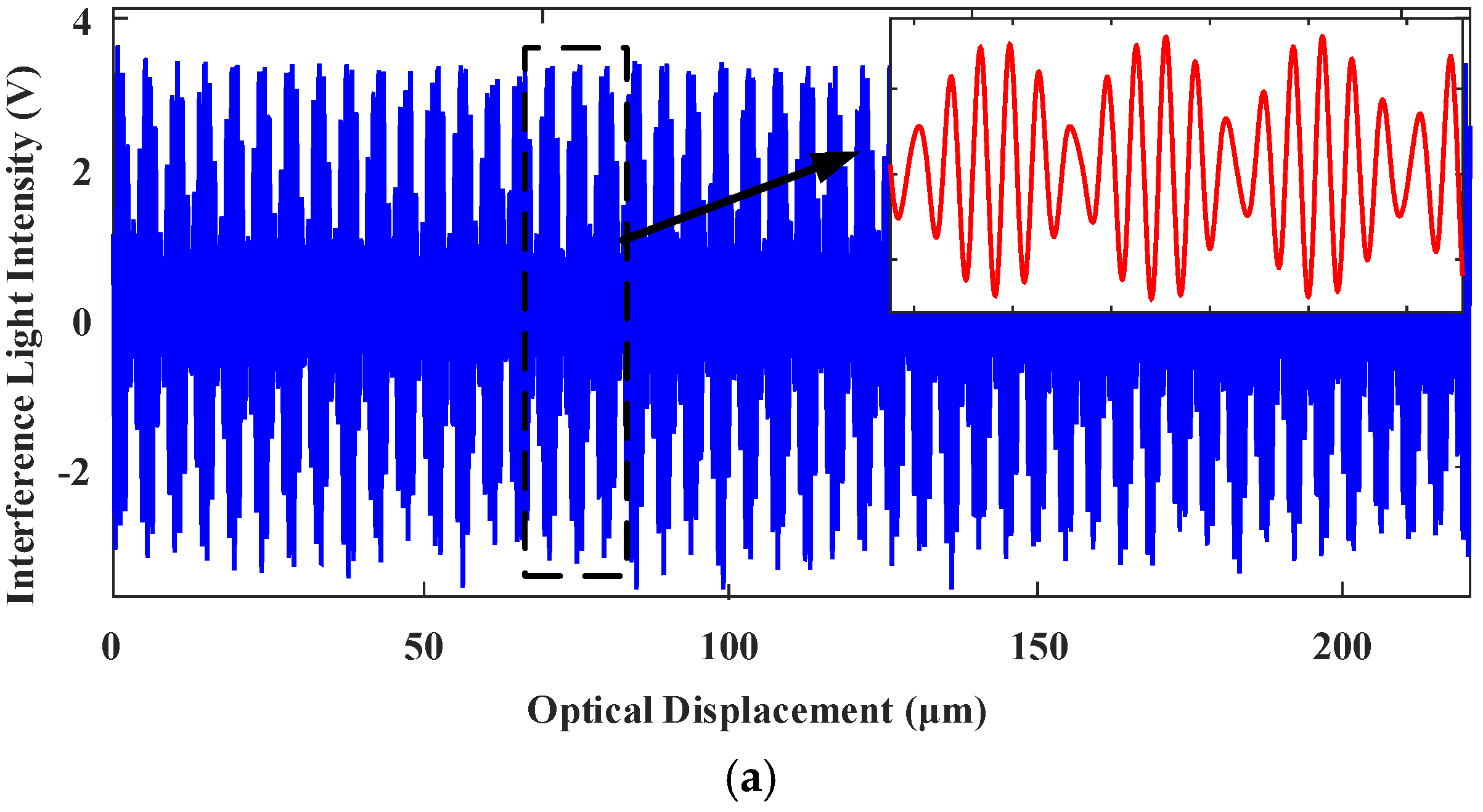
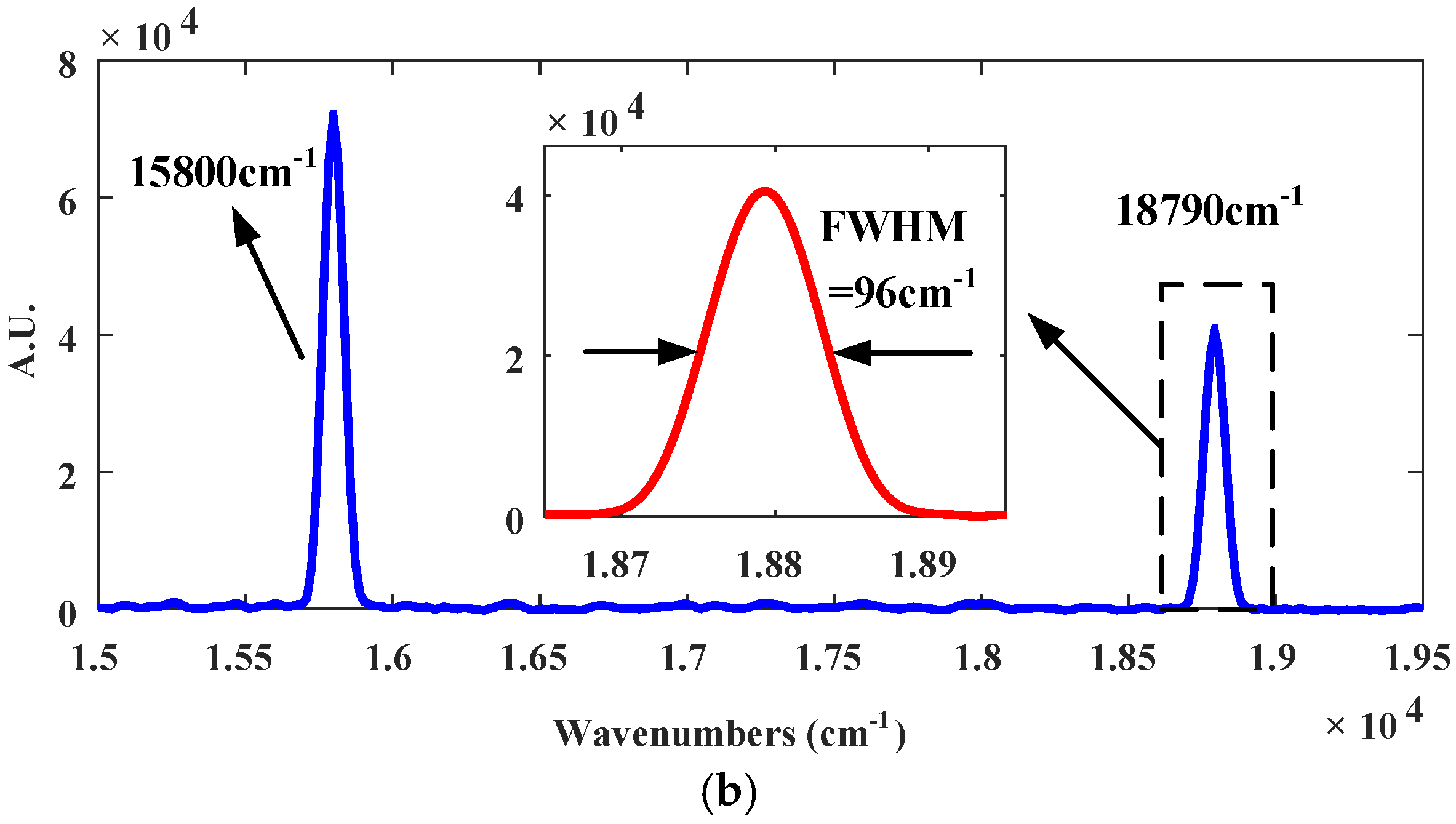
4.3. Spectral Measurement Experiments Using the H∞ controled Fourier-Transform Spectrometer
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Griffiths, P.R.; De Haseth, J.A. Theoretical background. In Fourier Transform Infrared Spectrometry, 2nd ed.; Wiley: Hoboken, NJ, USA, 2007; pp. 30–50, 110–112. ISBN 9780471194040. [Google Scholar]
- Xie, H.; Qi, Z.M. MEMS-based optical chemical sensors. In Semiconductor Device-Based Sensors for Gas, Chemical, and Biomedical Applications; Fan, R., Stephen, J.P., Eds.; CRC Press: Boca Raton, FL, USA, 2011; pp. 268–275. ISBN 9781439813874. [Google Scholar]
- Handheld and Portable FTIR Spectrometers for the Analysis of Materials: Taking the Lab to Sample. Available online: http://www.americanlaboratory.com (accessed on 30 September 2015).
- Wallrabe, U.; Solf, C.; Mohra, J.; Korvink, J.G. Miniaturized Fourier transform spectrometer for the near infrared wavelength regime incorporating an electromagnetic linear actuator. Sens. Actuators A Phys. 2005, 123–124, 459–467. [Google Scholar] [CrossRef]
- Sandner, T.; Grasshoff, T.; Gaumont, E.; Schenk, H.; Kenda, A. Translatory MOEMS actuator and system integration for miniaturized Fourier transform spectrometers. J. Micro/Nanolithogr. MEMS MOEMS 2012, 13, 011115. [Google Scholar] [CrossRef]
- Das, N.; Sin, J.; Popa, D.O.; Stephanou, H.E. Design and manufacturing of a Fourier transform microspectrometer. In Proceedings of the 8th IEEE Nanotechnology, Arlington, TX, USA, 18–21 August 2008; pp. 837–840. [Google Scholar]
- Jung, W.; Zhang, J.; Wang, L.; Wilder-Smith, P.; Chen, Z.; McCormick, D.T.; Tien, N.C. Three-dimensional optical coherence tomography employing a 2-axis microelectromechanical scanning mirror. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 806–810. [Google Scholar] [CrossRef]
- Duan, C.; Wang, W.; Zhang, X.; Ding, J.; Chen, Q.; Pozzi, A.; Xie, H. A 45°-tilted 2-axis scanning micromirror integrated on a silicon optical bench for 3D endoscopic optical imaging. In Proceedings of the 28th IEEE MEMS, Estoril, Portugal, 18–22 January 2015; pp. 948–951. [Google Scholar]
- Solgaard, O.; Godil, A.A.; Howe, R.T.; Lee, L.P.; Peter, Y.-A.; Zappe, H. Optical MEMS: From micromirrors to complex systems. J. Microelectromech. Syst. 2014, 23, 517–538. [Google Scholar] [CrossRef]
- Wu, L.; Xie, H. A millimeter-tunable-range microlens for endoscopic biomedical imaging applications. IEEE J. Quantum Electron. 2010, 46, 1237–1244. [Google Scholar] [CrossRef]
- Wang, W.; Chen, J.; Zivkovic, A.S.; Tanguy, Q.A.A.; Xie, H. A compact Fourier transform spectrometer on a silicon optical bench with an electrothermal MEMS mirror. J. Microelectromech. Syst. 2016, 25, 347–355. [Google Scholar] [CrossRef]
- Wu, L.; Pais, A.; Samuelson, S.R.; Guo, S.; Xie, H. A mirror tilt-insensitive Fourier transform spectrometer based on a large vertical displacement micromirror with dual reflective surface. In Proceedings of 15th TRANSDUCERS—International Solid-State Sensors, Actuators and Microsystems Conference, Denver, CO, USA, 21–25 June 2009; pp. 2090–2093. [Google Scholar]
- Samuelson, S.R.; Xie, H. A large piston displacement MEMS mirror with electrothermal ladder actuator arrays for ultra-low tilt applications. J. Microelectromech. Syst. 2014, 23, 39–49. [Google Scholar] [CrossRef]
- Wang, W.; Samuelson, S.R.; Chen, J.; Xie, H. Miniaturizing Fourier transform spectrometer with an electrothermal micromirror. IEEE Photonics Technol. Lett. 2015, 27, 1418–1421. [Google Scholar] [CrossRef]
- Ma, Y.; Islam, S.; Pan, Y.J. Electrostatic torsional micromirror with enhanced tilting angle using active control methods. IEEE/Asme Trans. Mechatron. 2011, 16, 994–1001. [Google Scholar] [CrossRef]
- Chen, H.; Sun, W.J.; Sun, Z.D.; Yeow, J.T.W. Second order sliding mode control of a 2D torsional MEMS micromirror with sidewall electrodes. J. Micromech. Microeng. 2013, 23, 015006. [Google Scholar] [CrossRef]
- Chen, H.; Pallapa, M.; Sun, W.J.; Sun, Z.D.; Yeow, J.T.W. Nonlinear control of an electromagnetic polymer MEMS hard-magnetic micromirror and its imaging application. J. Micromech. Microeng. 2012, 24, 57–63. [Google Scholar] [CrossRef]
- Wu, L.; Xie, H. A large vertical displacement electrothermal bimorph microactuator with very small lateral shift. Sens. Actuators A Phys. 2008, 145–146, 371–379. [Google Scholar] [CrossRef]
- Ferrara, A.; Lombardi, C. Interaction control of robotic manipulators via second-order sliding modes. Int. J. Adapt. Control Signal Process. 2007, 21, 708–730. [Google Scholar] [CrossRef]
- Yu, H.; Huang, S.; Chen, G.; Pan, Y.; Guo, Z. Human-Robot Interaction Control of Rehabilitation Robots with Series Elastic Actuators. IEEE Trans. Robot. 2015, 31, 1089–1100. [Google Scholar] [CrossRef]
- Li, X.; Pan, Y.; Chen, G.; Yu, H. Adaptive Human-Robot Interaction Control for Robots Driven by Series Elastic Actuators. IEEE Trans. Robot. 2017, 33, 169–182. [Google Scholar] [CrossRef]
- Sivaranjani, K.; Rakkiyappan, R.; Cao, J.; Alsaedi, A. Synchronization of nonlinear singularly perturbed complex networks with uncertain inner coupling via event triggered control. Appl. Math. Comput. 2017, 311, 283–299. [Google Scholar] [CrossRef]
- Vromant, P.; Weyns, D.; Malek, S.; Andersson, J. On interacting control loops in self-adaptive systems. In Proceedings of the 6th International Symposium on Software Engineering for Adaptive and Self-Managing Systems, Waikiki, HI, USA, 23–24 May 2011; pp. 202–207. [Google Scholar]
- Bristol, E.H. On a New Measure of Interaction for Multivariable Process Control. IEEE Trans. Autom. Control 1966, 11, 133–134. [Google Scholar] [CrossRef]
- Doyle, J.C.; Glover, K.; Khargonekar, P.P.; Francis, B.A. State-space solutions to standard H2 and H∞ control problems. IEEE Trans. Autom. Control 1989, 34, 831–847. [Google Scholar] [CrossRef]
- Glover, K.; Doyle, J.C. State-space formulae for all stabilizing controllers that satisfy an H∞ norm bound and relations to risk sensitivity. Syst. Control Lett. 1988, 11, 167–172. [Google Scholar] [CrossRef]
- Han, F.T.; Wang, W.; Zhang, X.; Xie, H. Modeling and control of a large-stroke electrothermal MEMS mirror for Fourier transform microspectrometers. J. Microelectromech. Syst. 2016, 25, 750–760. [Google Scholar] [CrossRef]
- Porter, C.D.; Tanner, D.B. Correction of phase errors in Fourier spectroscopy. Int. J. Infrared Millim. Waves 1983, 4, 273–298. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, L.; Xie, H. A fast, large-stroke electrothermal MEMS mirror based on Cu/W bimorph. Micromachines 2015, 6, 1876–1889. [Google Scholar] [CrossRef]
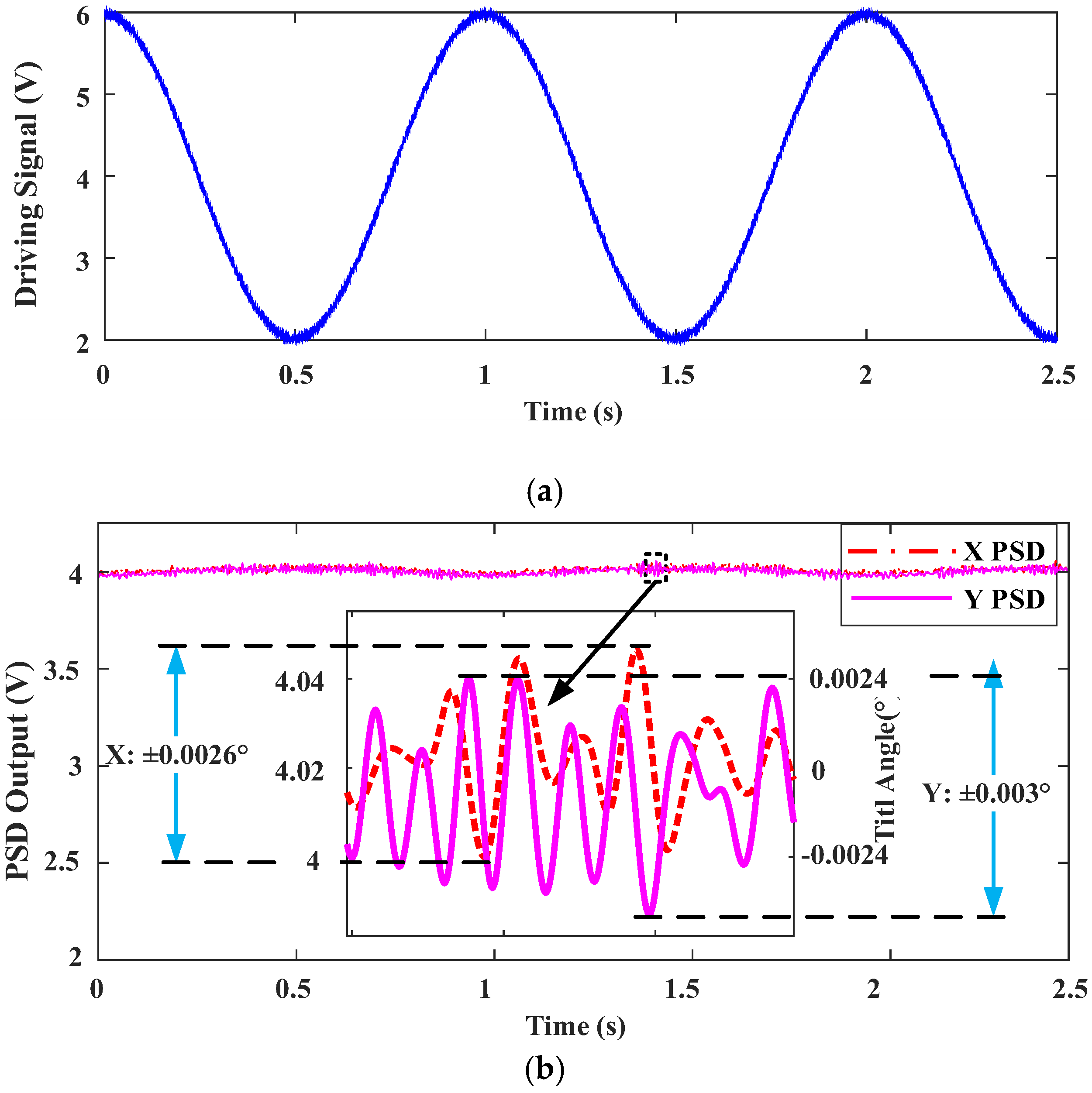
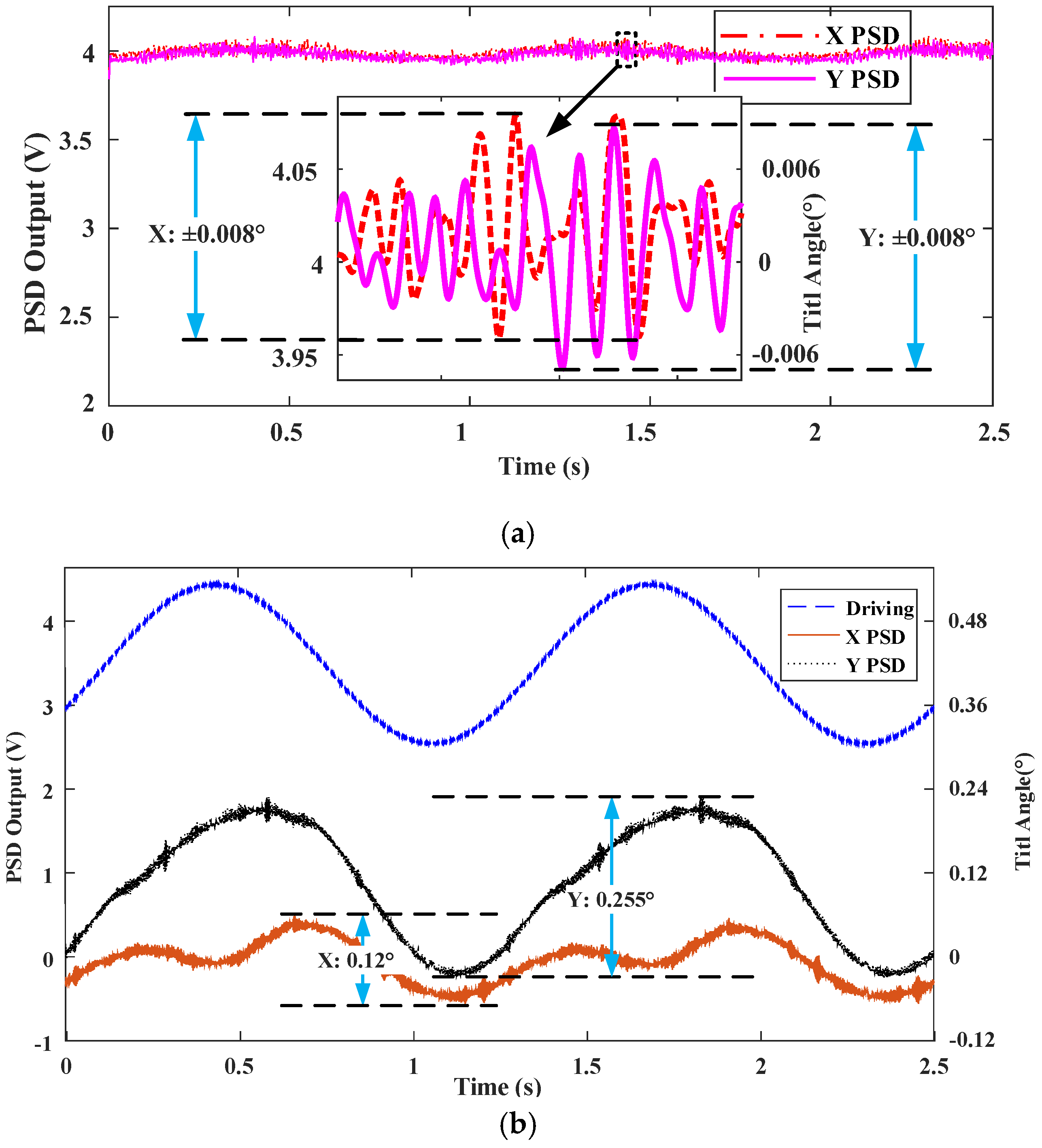


| Tilting Angle | Drive Signal Frequency (Hz) | |||
|---|---|---|---|---|
| 0.2 | 0.5 | 1 | 2 | |
| X direction | ±0.0028° | ±0.0029° | ±0.0026° | ±0.0029° |
| Y direction | ±0.0031° | ±0.0033° | ±0.003° | ±0.0035° |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Li, M.; Zhang, Y.; Xie, H.; Chen, C.; Peng, Z.; Su, S. H∞ Robust Control of a Large-Piston MEMS Micromirror for Compact Fourier Transform Spectrometer Systems. Sensors 2018, 18, 508. https://doi.org/10.3390/s18020508
Chen H, Li M, Zhang Y, Xie H, Chen C, Peng Z, Su S. H∞ Robust Control of a Large-Piston MEMS Micromirror for Compact Fourier Transform Spectrometer Systems. Sensors. 2018; 18(2):508. https://doi.org/10.3390/s18020508
Chicago/Turabian StyleChen, Huipeng, Mengyuan Li, Yi Zhang, Huikai Xie, Chang Chen, Zhangming Peng, and Shaohui Su. 2018. "H∞ Robust Control of a Large-Piston MEMS Micromirror for Compact Fourier Transform Spectrometer Systems" Sensors 18, no. 2: 508. https://doi.org/10.3390/s18020508
APA StyleChen, H., Li, M., Zhang, Y., Xie, H., Chen, C., Peng, Z., & Su, S. (2018). H∞ Robust Control of a Large-Piston MEMS Micromirror for Compact Fourier Transform Spectrometer Systems. Sensors, 18(2), 508. https://doi.org/10.3390/s18020508






