Analytic and Unambiguous Phase-Based Algorithm for 3-D Localization of a Single Source with Uniform Circular Array
Abstract
:1. Introduction
- The estimation algorithm sufficiently exploits the centro-symmetry and periodicity of a circular aperture by Fourier transforms and has established algebraic relations between 3-D localization parameters and phase samples on the circumference of a UCA.
- The phase-based HODI property of a UCA has been exploited, based on which a novel ambiguity resolution has been addressed without accuracy loss. Ambiguity resolution and parameter estimation have been merged into one process, resulting in a computationally efficient algorithm.
- It is first revealed that the minimum number of sensors for single source localization with a UCA is five.
- Estimation accuracy has been analyzed in the Fourier domain to provide mathematical insights into the parameter estimation using a UCA.
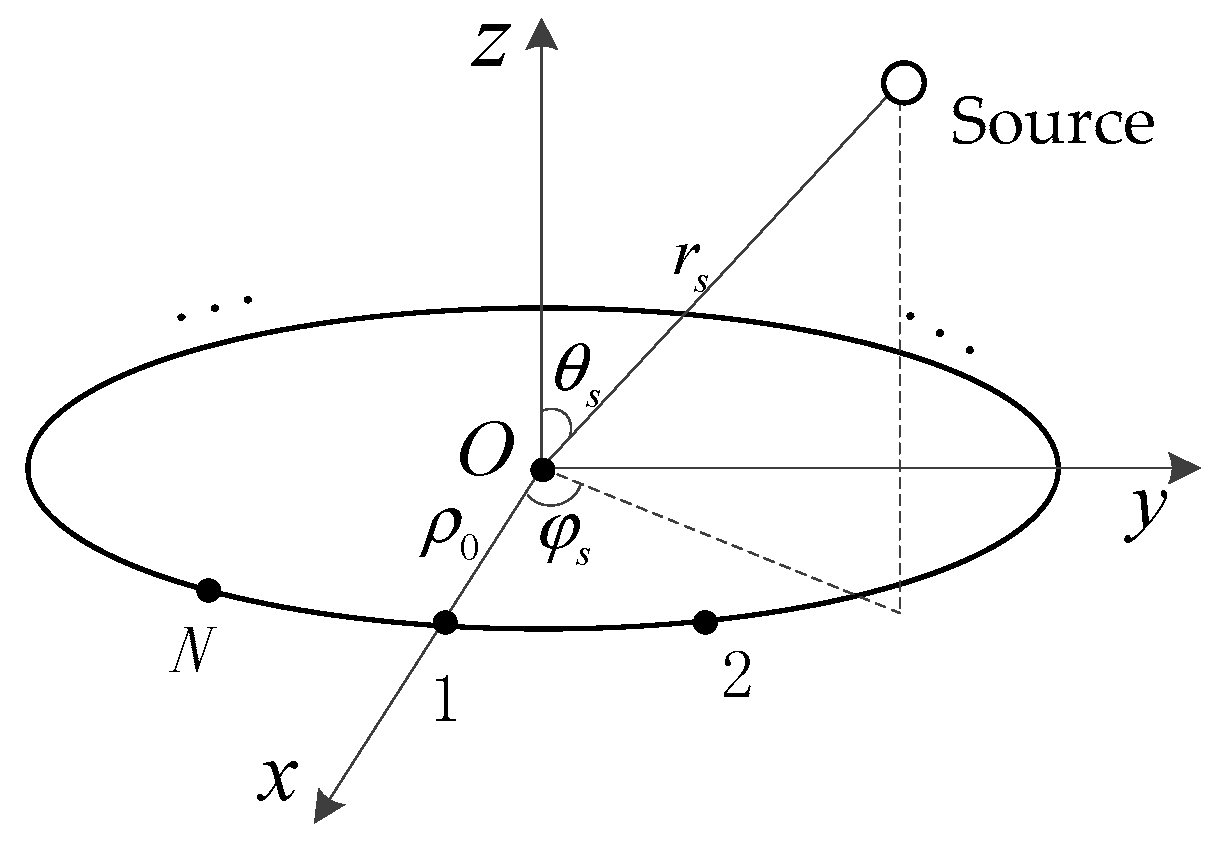
2. Signal Modeling
2.1. Phase Distribution
2.2. Phase Extraction
3. Proposed 3-D Localization Algorithm
3.1. Continuous Aperture Phase Distribution
3.2. Discrete Phase Samples
3.3. Equivalence to Previous Method
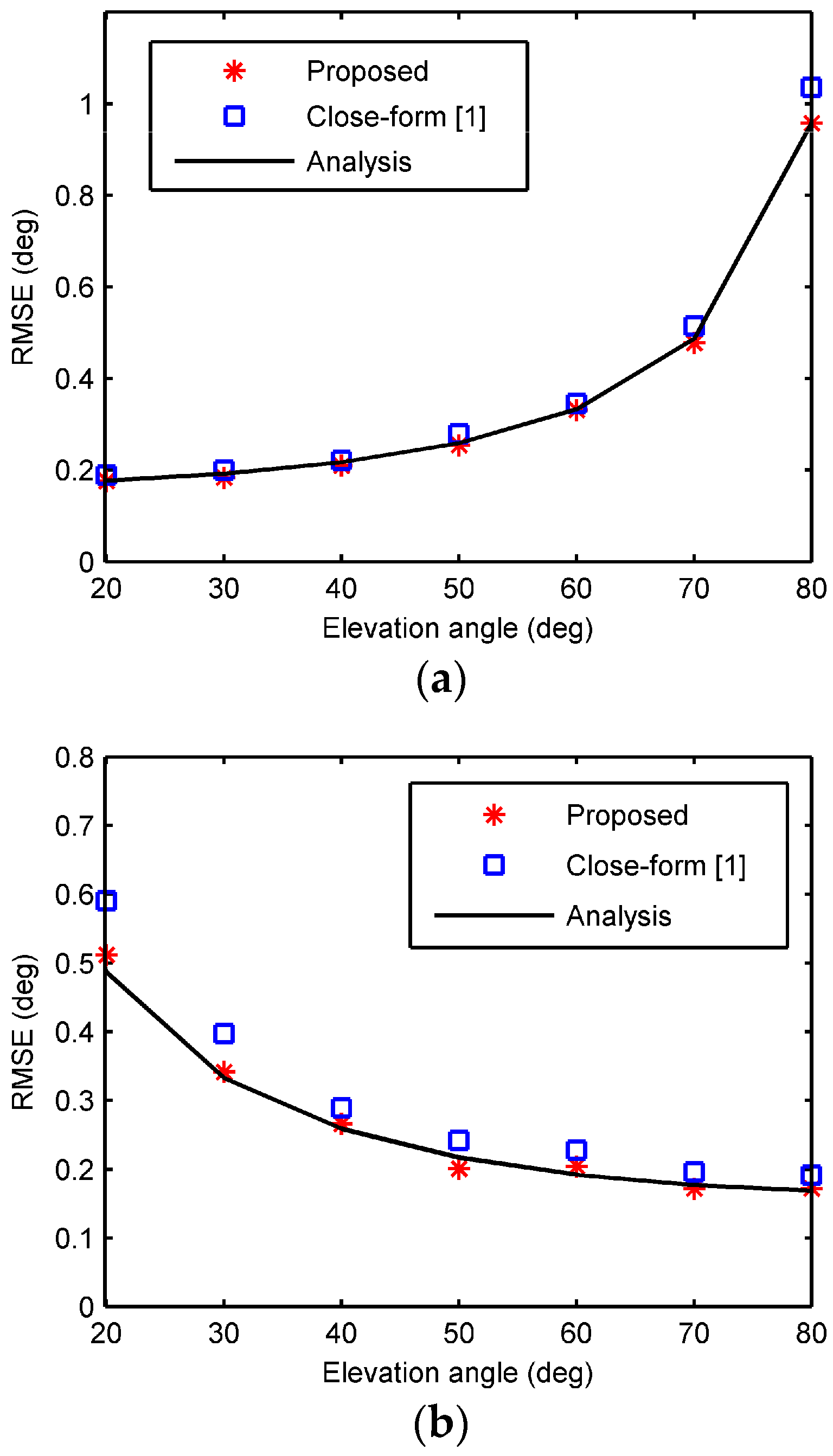
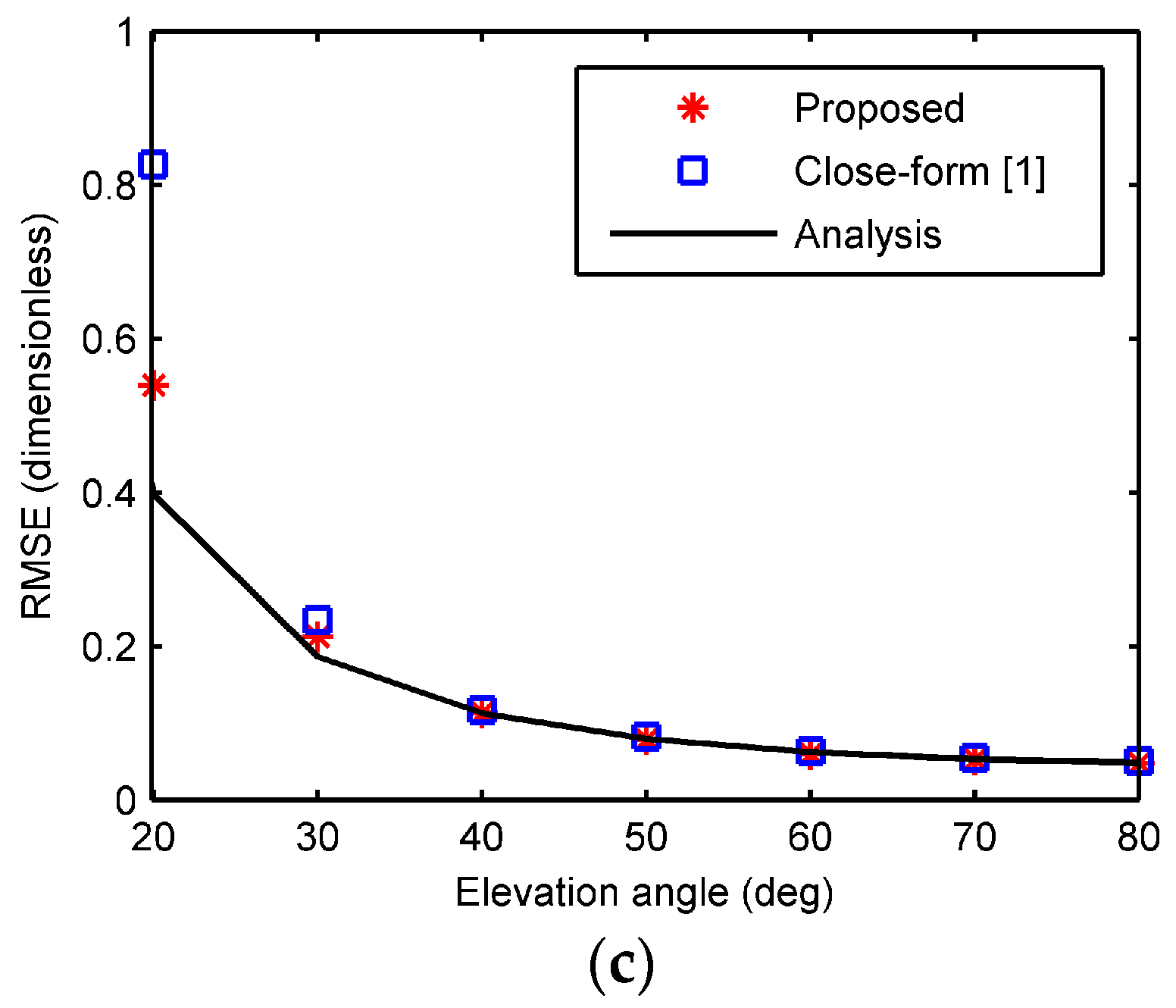
4. Accuracy Analysis
4.1. Accuracy of Fourier Spectrums
4.2. Accuracy of 3-D Localization Estimation
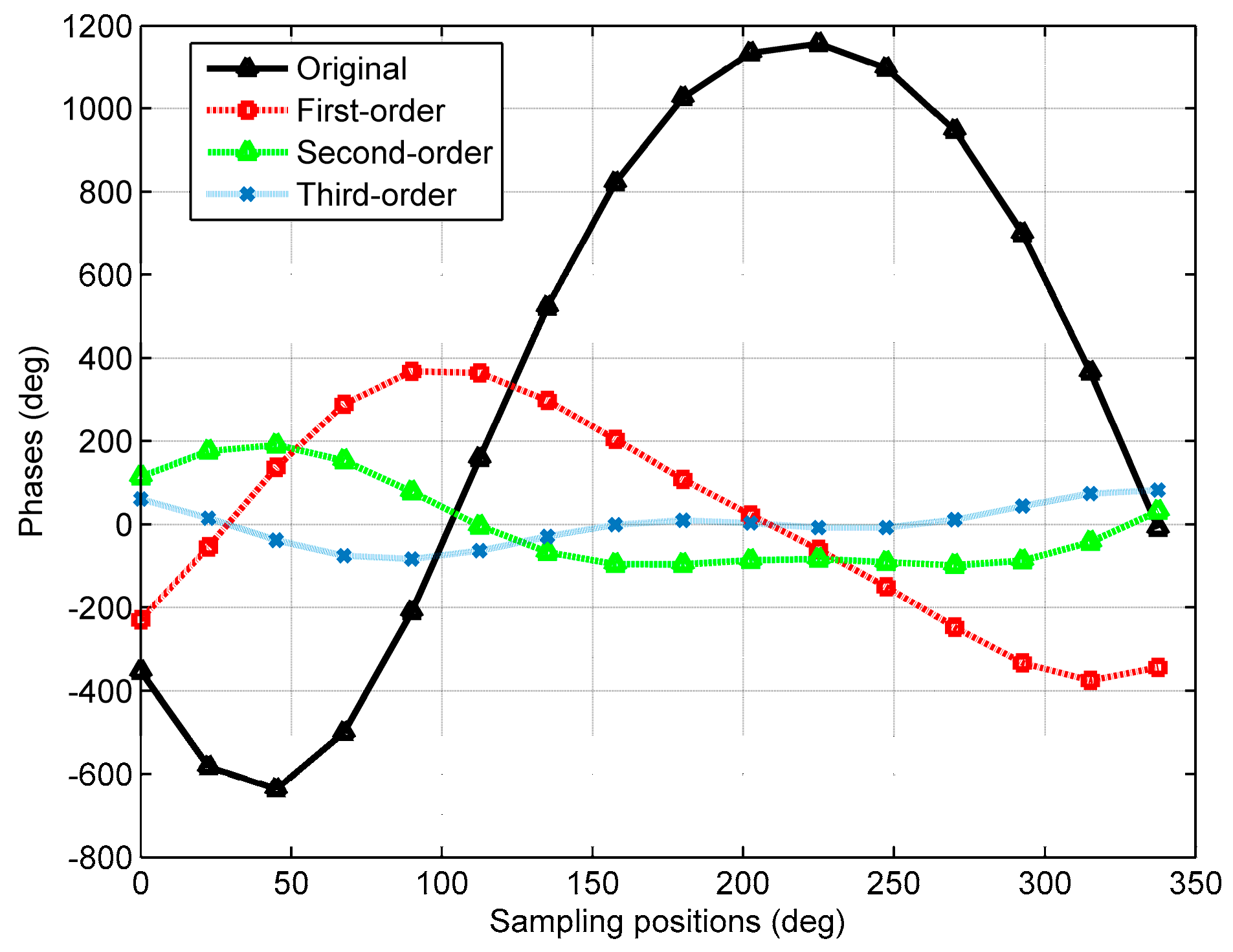
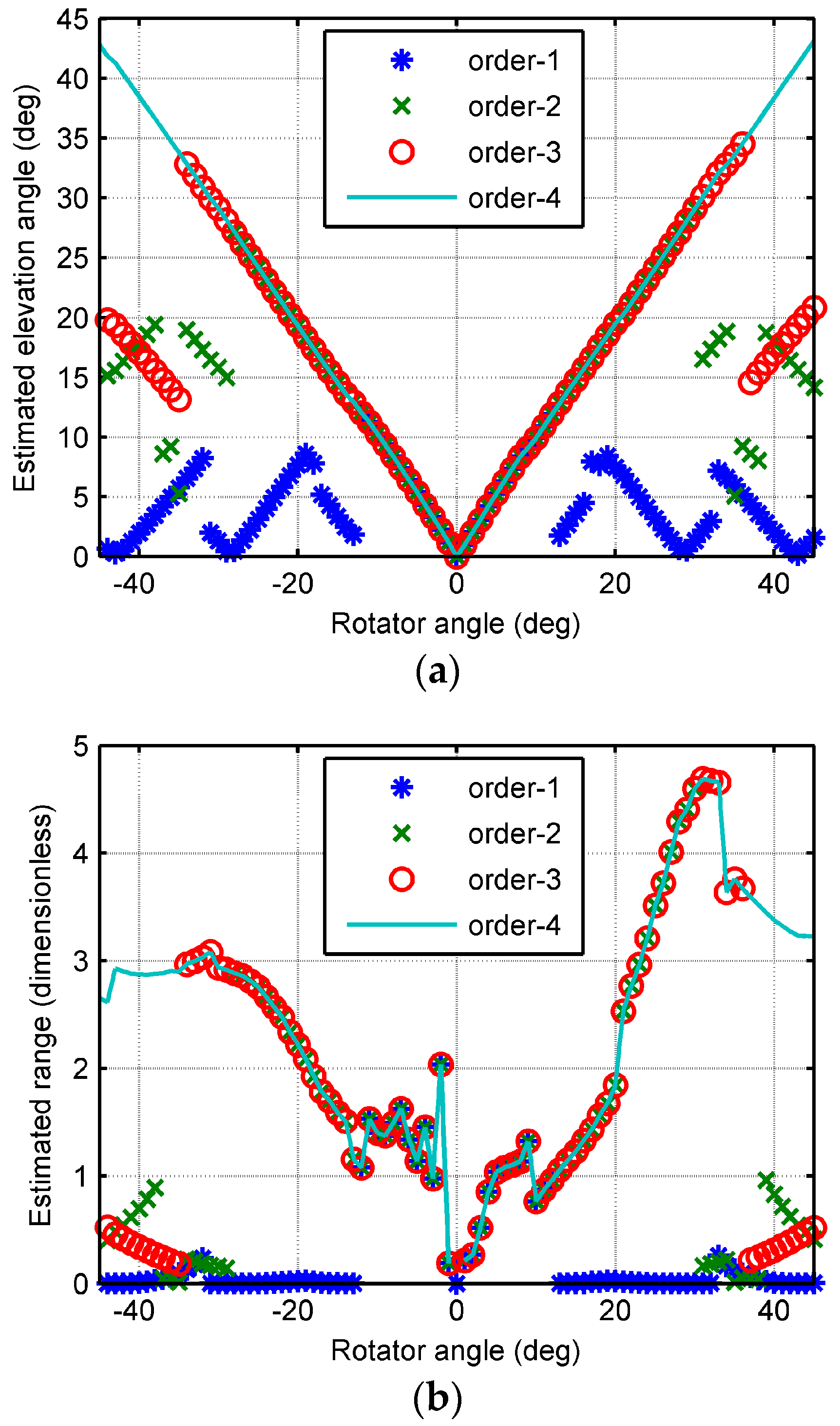
5. Unambiguous 3-D Localization Estimation
5.1. Phase Range Compression
5.2. HODI of UCA
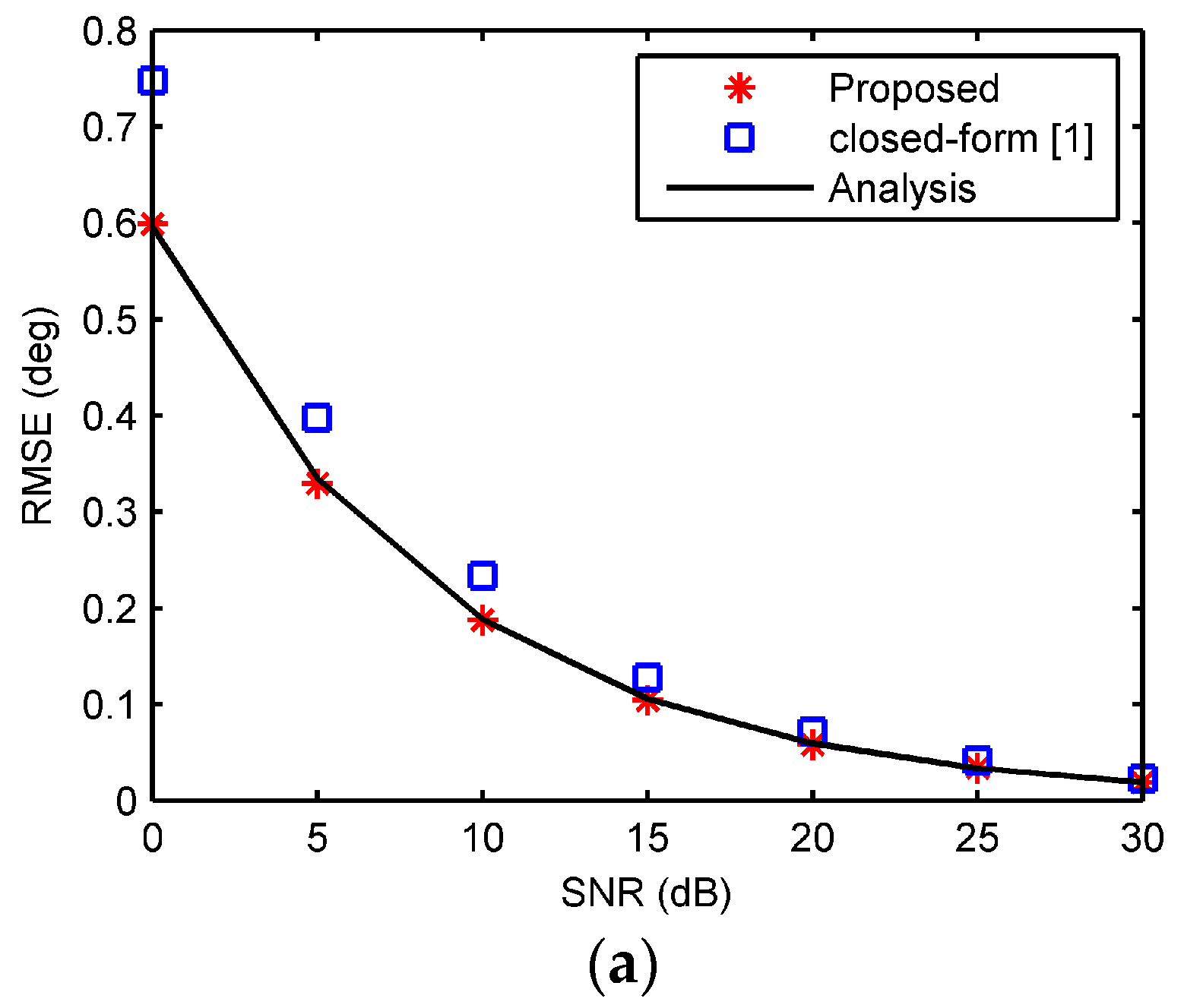
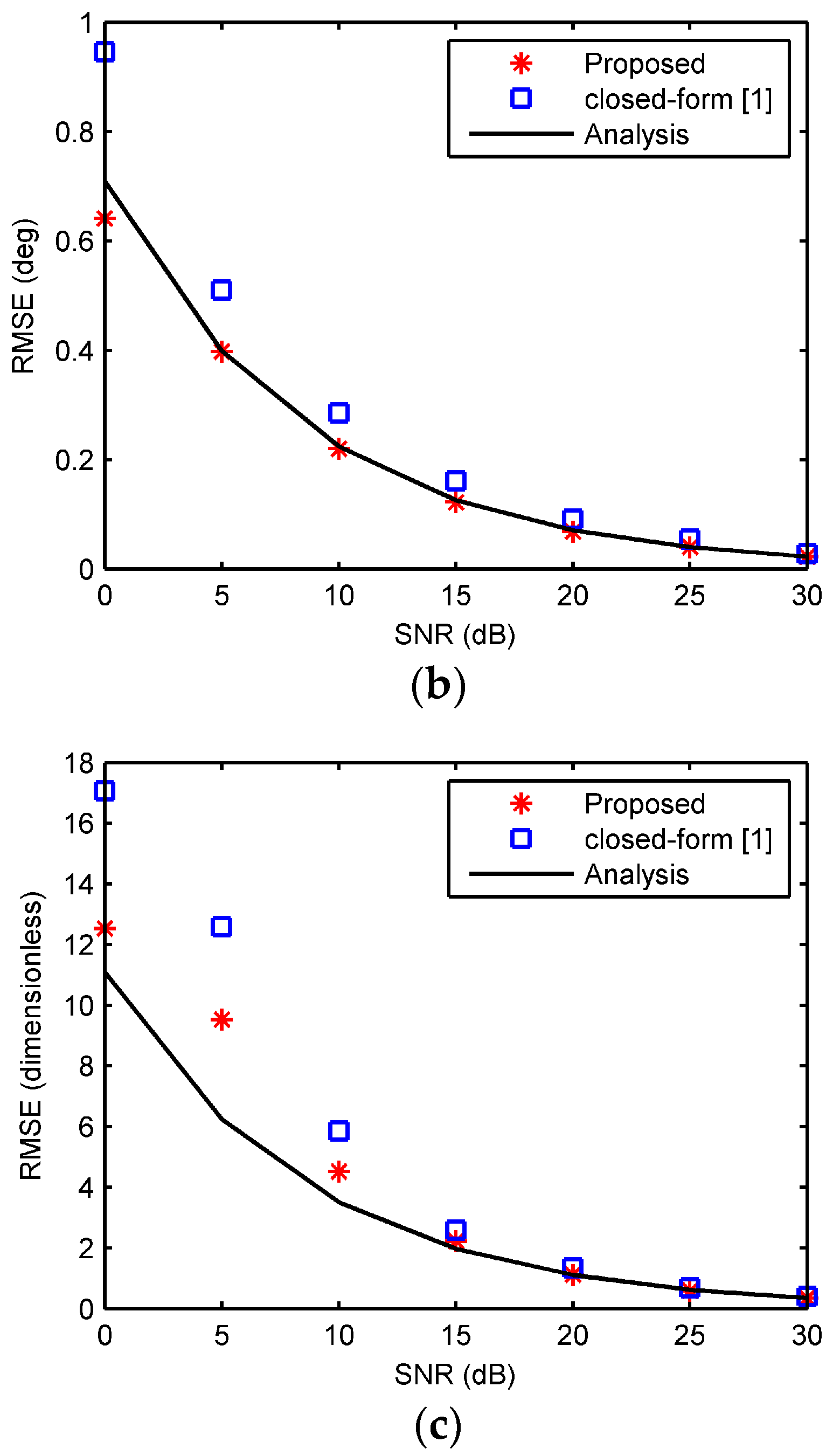
6. Simulation Results
7. Experimental Results
8. Conclusions
Author Contributions
Conflicts of Interest
References
- Jung, T.J.; Lee, K.K. Closed-Form Algorithm for 3-D single-source localization with uniform circular array. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1096–1099. [Google Scholar] [CrossRef]
- Lee, J.H.; Park, D.H.; Park, G.T. Algebraic path-following algorithm for localising 3-D near-field sources in uniform circular array. Electron. Lett. 2003, 39, 1283–1285. [Google Scholar] [CrossRef]
- Huang, Y.D.; Barkat, M. Near-field multiple source localization by passive sensor array. IEEE Trans. Antennas Propag. 1991, 39, 968–975. [Google Scholar] [CrossRef]
- Bae, E.H.; Lee, K.K. Closed-form 3-D localization for single source in uniform circular array with a center sensor. IEICE Trans. Commun. 2009, E92-B, 1053–1056. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Wei, X. Ambiguity resolution for phase-based 3-D source localization under fixed uniform circular array. Sensors 2017, 17, 1086. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, E.; Ralston, E.W. Ambiguity resolution in interferometry. IEEE Trans. Aerosp. Electron. Syst. 1981, 17, 66–78. [Google Scholar] [CrossRef]
- Ballal, T.; Bleakley, C.J. Phase-difference ambiguity resolution for a single-frequency signal. IEEE Signal Process. Lett. 2008, 15, 853–856. [Google Scholar] [CrossRef]
- Sundaram, K.R.; Mallik, R.K.; Murthy, U.M.S. Modulo conversion method for estimating the direction of arrival. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 1391–1396. [Google Scholar]
- Liu, Z.M.; Guo, F.C. Azimuth and elevation estimation with rotating long-baseline interferometers. IEEE Trans. Signal Process. 2015, 63, 2405–2419. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Wei, X.Z. Unambiguous parameter estimation of multiple near-field sources via rotating uniform circular array. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 872–875. [Google Scholar] [CrossRef]
- Lin, M.; Liu, P.; Liu, J. Rotary way to resolve ambiguity for planar array. In Proceedings of the IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Guilin, China, 5–8 August 2014; pp. 170–174. [Google Scholar]
- Kay, S. A fast and accurate single frequency estimator. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1987–1990. [Google Scholar] [CrossRef]
- Tretter, S.A. Estimating the frequency of a noisy sinusoid by linear regression. IEEE Trans. Inf. Theory 1985, 31, 832–835. [Google Scholar] [CrossRef]
- Rife, D.; Boorstyn, R. Single tone parameter estimation from discrete-time observations. IEEE Trans. Inf. Theory 1974, 20, 591–598. [Google Scholar] [CrossRef]
- Fu, H.; Kam, P.Y. Exact phase noise model for single-tone frequency estimation in noise. Electron. Lett. 2008, 44, 937–938. [Google Scholar] [CrossRef]
- Mcaulay, R. Interferometer design for elevation angle estimation. IEEE Trans. Aerosp. Electron. Syst. 1977, 13, 486–503. [Google Scholar] [CrossRef]
- Jackson, B.R.; Rajan, S.; Liao, B.J. Direction of arrival estimation using directive antennas in uniform circular arrays. IEEE Trans. Antennas Propag. 2015, 63, 736–747. [Google Scholar] [CrossRef]
- Jeruchim, M.C.; Balaban, P.; Shanmugan, K.S. Simulation of Communication Systems; Springer: Boston, MA, USA, 1992. [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, L.; Pan, J.; Ma, B. Analytic and Unambiguous Phase-Based Algorithm for 3-D Localization of a Single Source with Uniform Circular Array. Sensors 2018, 18, 484. https://doi.org/10.3390/s18020484
Zuo L, Pan J, Ma B. Analytic and Unambiguous Phase-Based Algorithm for 3-D Localization of a Single Source with Uniform Circular Array. Sensors. 2018; 18(2):484. https://doi.org/10.3390/s18020484
Chicago/Turabian StyleZuo, Le, Jin Pan, and Boyuan Ma. 2018. "Analytic and Unambiguous Phase-Based Algorithm for 3-D Localization of a Single Source with Uniform Circular Array" Sensors 18, no. 2: 484. https://doi.org/10.3390/s18020484
APA StyleZuo, L., Pan, J., & Ma, B. (2018). Analytic and Unambiguous Phase-Based Algorithm for 3-D Localization of a Single Source with Uniform Circular Array. Sensors, 18(2), 484. https://doi.org/10.3390/s18020484




