Development of a Kalman Filter in the Gauss-Helmert Model for Reliability Analysis in Orientation Determination with Smartphone Sensors
Abstract
:1. Introduction
2. Orientation Determination
2.1. Existing Approach
2.2. Problem Description
2.3. Kalman Filter in the Gauss-Helmert Model
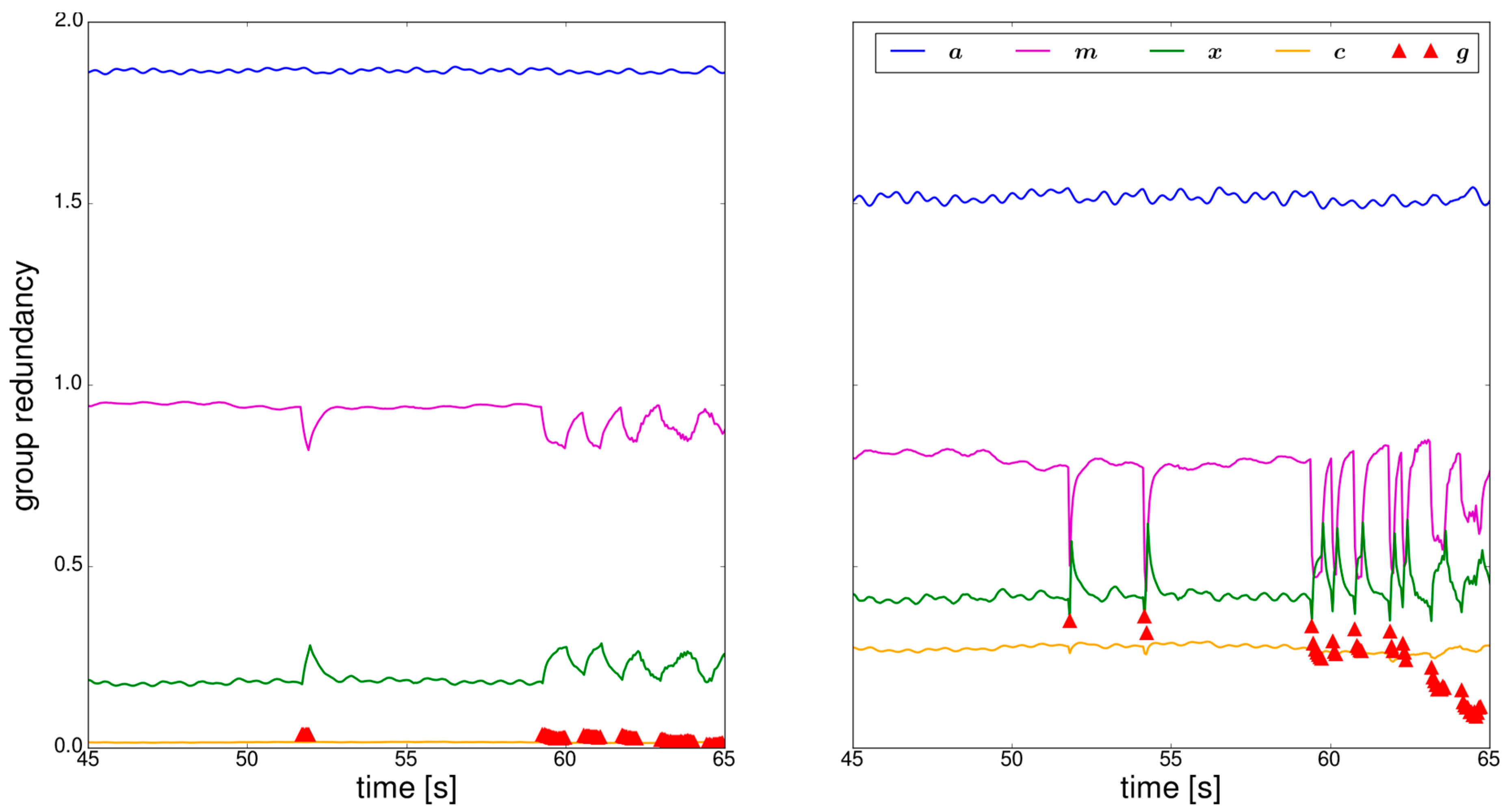
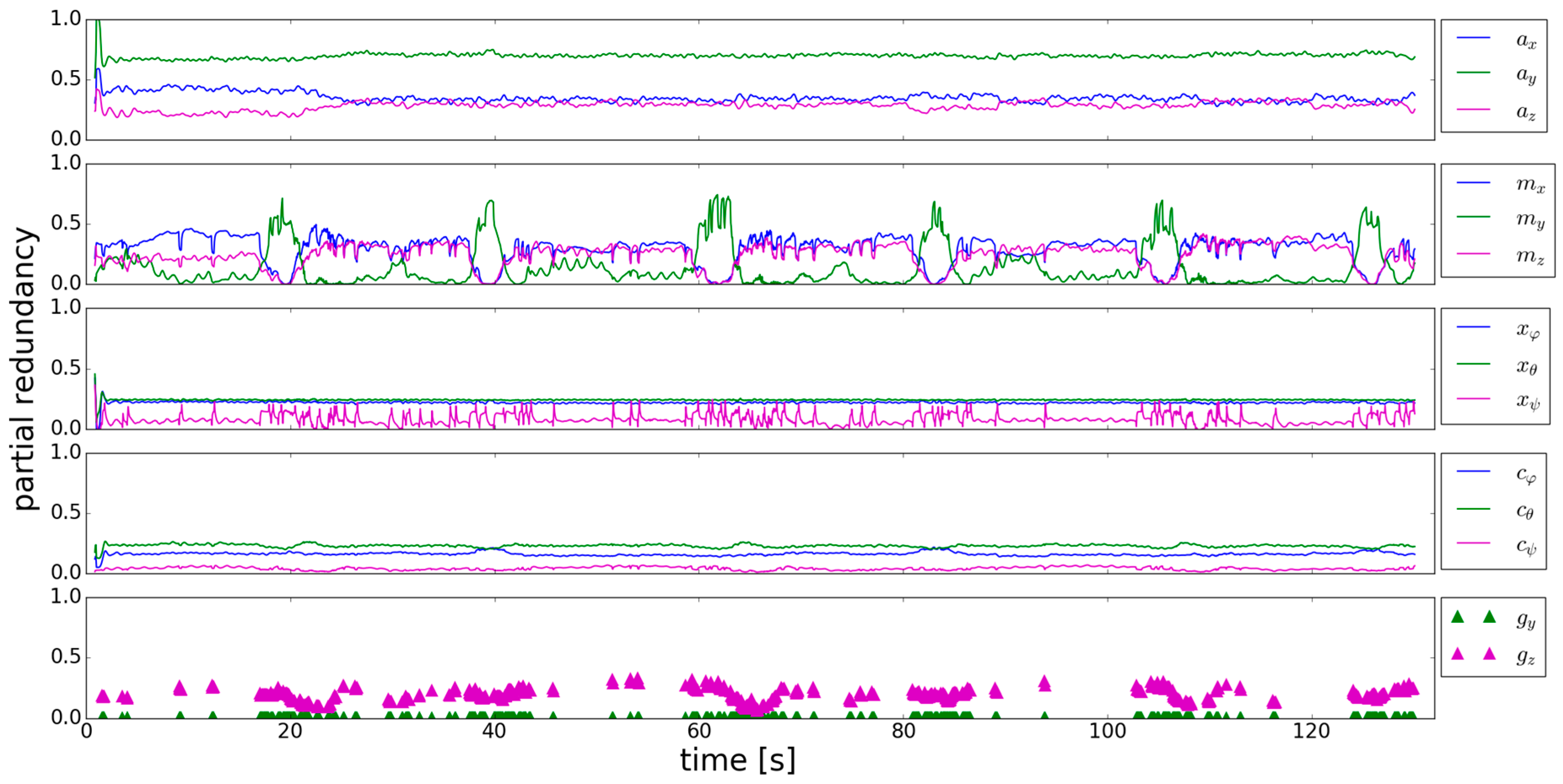
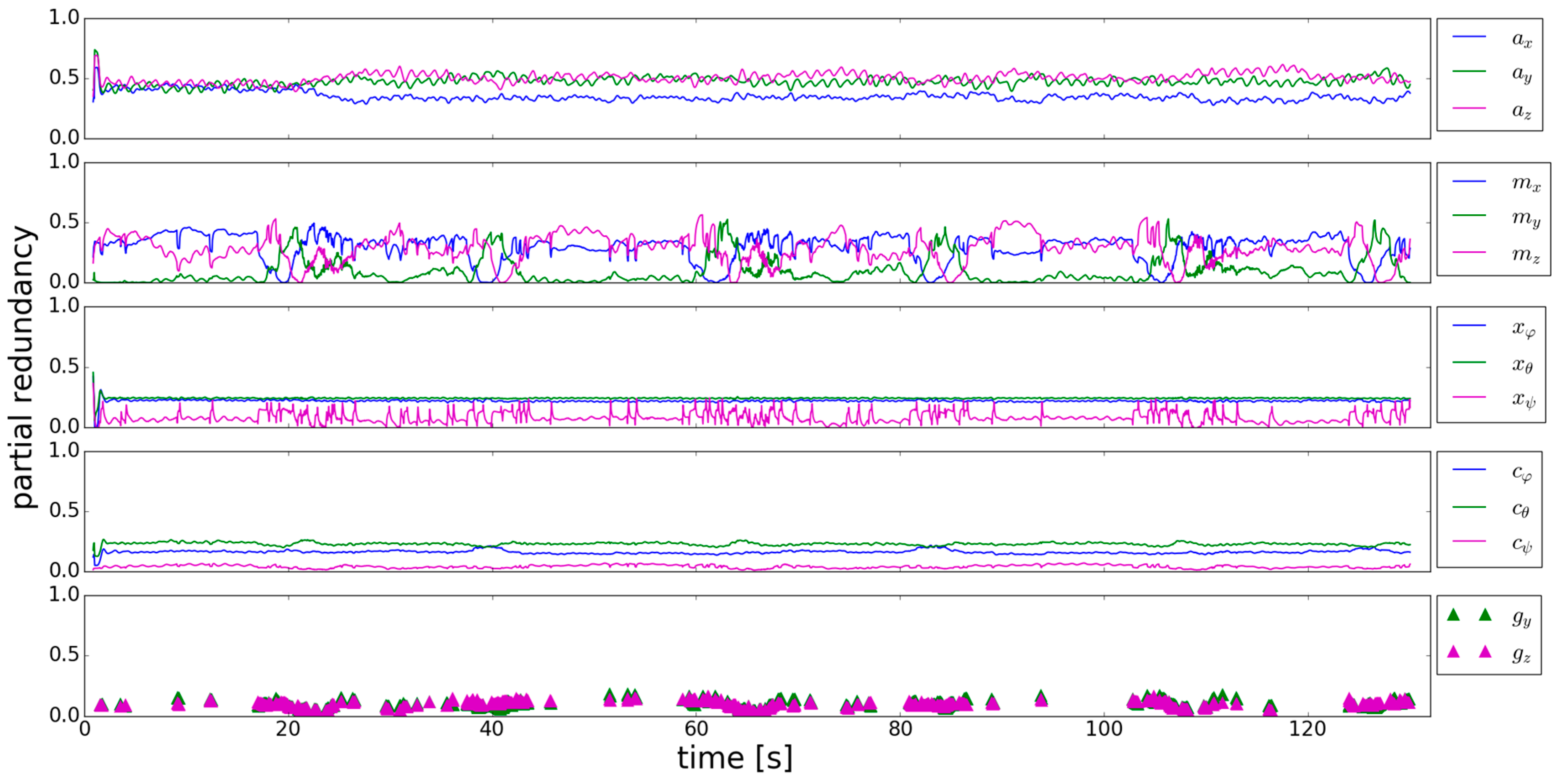
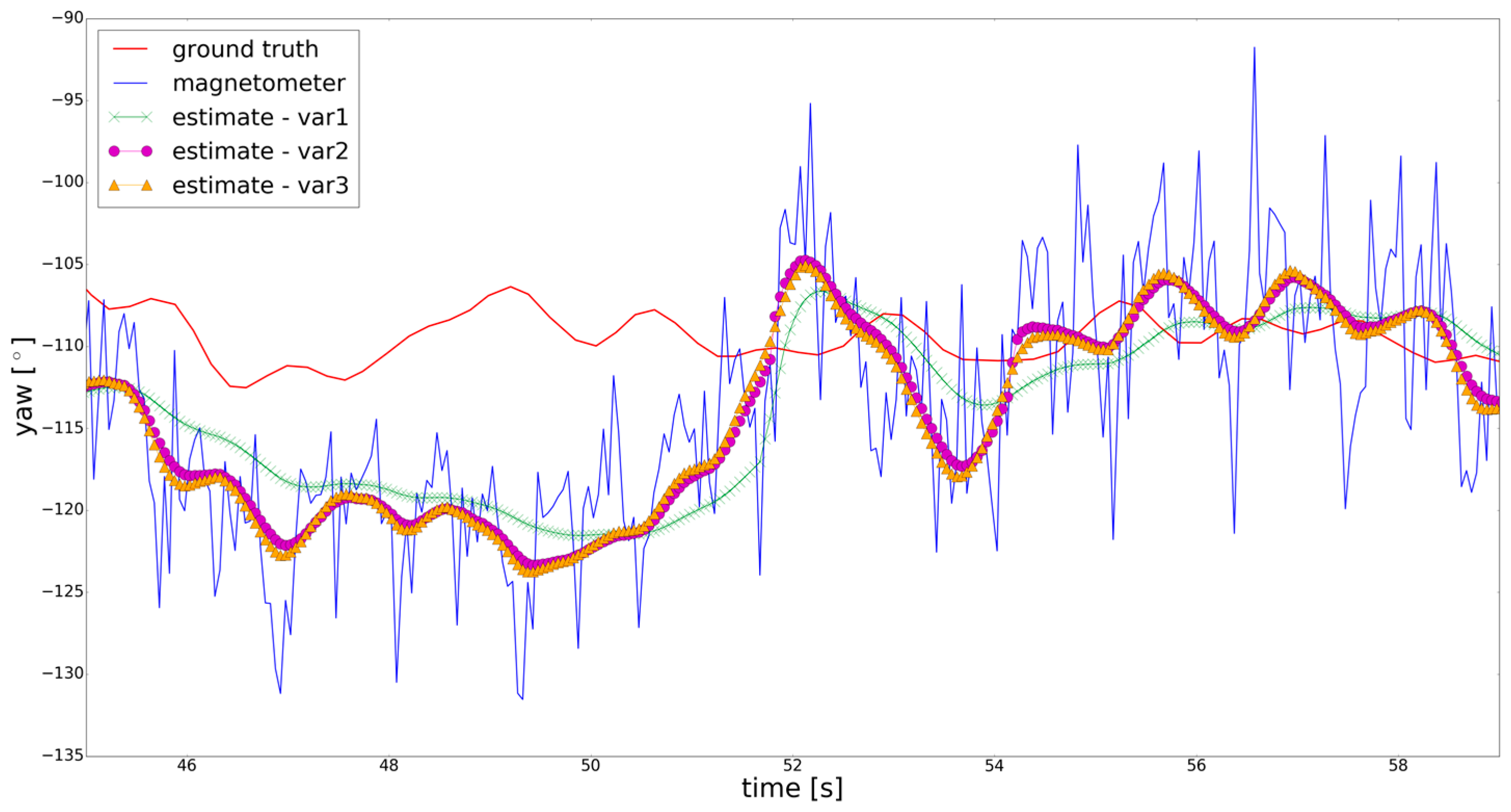
3. Results
3.1. Adaption of the Stochastic Model
3.2. Adaption of the Functional Model
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Titterton, D.; Weston, J. Strapdown Inertial Navigation Technology, 2nd ed.; Institution of Engineering and Technology: Stevenage, UK, 2004; ISBN 978-0-86341-358-2. [Google Scholar]
- Särkkä, S.; Tolvanen, V.; Kannala, J.; Rahtu, E. Adaptive Kalman filtering and smoothing for gravitation tracking in mobile systems. In Proceedings of the 2015 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Groves, P.D. Principles of GNSS, Inertial and Multisensor Integrated Navigation Systems, 2nd ed.; Artech House: London, UK, 2013; ISBN 179-1-60807-005-3. [Google Scholar]
- Kang, W.; Nam, S.; Han, Y.; Lee, S. Improved heading estimation for smartphone-based indoor positioning systems. In Proceedings of the 2012 IEEE 23rd International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC), Sidney, NSW, Australia, 9–12 September 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Crassidis, J.L.; Markley, F.L.; Cheng, Y. Survey of nonlinear attitude estimation methods. J. Guid. Control Dyn. 2007, 30, 12–28. [Google Scholar] [CrossRef]
- Sabatini, A.M. Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing. IEEE Trans. Biomed. Eng. 2006, 53, 1346–1356. [Google Scholar] [CrossRef] [PubMed]
- Tian, Z.; Zhang, Y.; Zhou, M.; Liu, Y. Pedestrian dead reckoning for MARG navigation using a smartphone. EURASIP J. Adv. Signal Process. 2014, 2014. [Google Scholar] [CrossRef]
- Renaudin, V.; Combettes, C. Magnetic, Acceleration Fields and Gyroscope Quaternion (MAGYQ)-Based Attitude Estimation with Smartphone Sensors for Indoor Pedestrian Navigation. Sensors 2014, 14, 22864–22890. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Li, Q.; Chen, G. APT: Accurate outdoor pedestrian tracking with smartphones. In Proceedings of the INFOCOM 2013, Turin, Italy, 14–19 April 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Borenstein, J.; Ojeda, L.; Kwanmuang, S. Heuristic reduction of gyro drift in IMU-based personnel tracking systems. J. Navig. 2009, 62, 41–58. [Google Scholar] [CrossRef]
- Jiménez, A.R.; Seco, F.; Prieto, J.C.; Guevara, J. Indoor pedestrian navigation using an INS/EKF framework for yaw drift reduction and a foot-mounted IMU. In Proceedings of the 7th Workshop on Positioning Navigation and Communication (WPNC), Dresden, Germany, 11–12 March 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Blankenbach, J.; Sternberg, H.; Tilch, S. Indoor-Positionierung. In Handbuch der Geodäsie; Freeden, W., Rummel, R., Eds.; Springer: Berlin, Germany, 2015; pp. 1–36. ISBN 978-3-662-46900-2. [Google Scholar]
- Sternberg, H.; Willemsen, T. Ein topologischer Ansatz zur Innenraumnavigation mit MEMS in Smartphones basierend auf dem Routing-Graph. In Internationale Geodätische Woche Obergurgl 2017; Hanke, K., Weinbold, T., Eds.; Wichmann: Berlin, Germany, 2017; pp. 51–60. [Google Scholar]
- Bahl, P.; Padmanabhan, V. RADAR: An In-building RF-based User Location and Tracking System. In Proceedings of the INFOCOM 2000 19th Annual Joint Conference of the IEEE Computer and Communications Societies, Tel Aviv, Israel, 26–30 March 2000; IEEE: Piscataway, NJ, USA, 2000. [Google Scholar]
- Honkavirta, V.; Perälä, T.; Ali-Löytty, S.; Piche, R. A Comparative Survey of WLAN Location Fingerprinting Methods. In Proceedings of the 6th Workshop on Positioning, Navigation and Communication (WPNC), Hannover, Germany, 19 March 2009; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar]
- Schmid, J.; Gädeke, T.; Curtis, D.; Ledlie, J. Improving sparse organic WiFi localization with inertial sensors. In Proceedings of the 9th Workshop on Positioning Navigation and Communication (WPNC), Dresden, Germany, 15–16 March 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Zhu, J.; Sen, S.; Mohapatra, P.; Kim, K.H. Navigating in Signal Space: A Crowd-Sourced Sensing Map Construction for Navigation. In Proceedings of the 11th International Conference on Mobile Ad Hoc and Sensor Systems, Philadelphia, PA, USA, 28–30 October 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Wang, Y.; Wong, A.K.S.; Cheng, R.S.K. Adaptive room-level localization system with crowd-sourced WiFi data. In Proceedings of the 2015 SAI Intelligent Systems Conference (IntelliSys), London, UK, 10–11 November 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Abadi, M.J.; Luceri, L.; Hassan, M.; Chou, C.T.; Nicoli, M. A Collaborative Approach to Heading Estimation for Smartphone-based PDR Indoor Localisation. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Korea, 27–30 October 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Dong, B.; Burgess, T. Adaptive Kalman Filter for Indoor Navigation. In Proceedings of the 2016 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Madrid, Spain, 4–7 October 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Guan, T.; Fang, L.; Dong, W.; Qiao, C. Robust Indoor Localization with Smartphones through Statistical Filtering. In Proceedings of the 2017 International Conference on Computing, Networking and Communications (ICNC), Santa Clara, CA, USA, 26–29 January 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Retscher, G.; Tatschl, T. Indoor positioning using Wi-Fi lateration—Comparison of two common range conversion models with two novel differential approaches. In Proceedings of the 2016 Fourth International Conference on Ubiquitous Positioning, Indoor Navigation and Location Based Services (UPINLBS), Shanghai, China, 2–4 November 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Kaemarungsi, K. Design of Indoor Positioning Systems Based on Location Fingerprinting Technique. Ph.D. Thesis, School of Information Science, University of Pittsburgh, Pittsburgh, PA, USA, 2005. [Google Scholar]
- Gikas, V.; Dimitratos, A.; Perakis, H.; Retscher, G.; Ettlinger, A. Full-scale testing and performance evaluation of an active RFID system for positioning and personal mobility. In Proceedings of the 2016 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Madrid, Spain, 4–7 October 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Hellmers, H.; Eichhorn, A.; Norrdine, A.; Blankenbach, J. IMU/magnetometer based 3D indoor positioning for wheeled platforms in NLoS scenarios. In Proceedings of the 2016 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Madrid, Spain, 4–7 October 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Niedermayr, S. Positionsbestimmung durch Kombination geometrie- und merkmalsbasierter Verfahren unter Einbeziehung der Qualität. Ph.D. Thesis, Fakultät für Mathematik und Geoinformation, TU Wien, Vienna, Austria, 2015. [Google Scholar]
- Gelb, A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 1974; ISBN 978-0-262-20027-1. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006; ISBN 978-0-471-70858-2. [Google Scholar]
- Heunecke, O.; Kuhlmann, H.; Welsch, W.; Eichhorn, A.; Neuner, H. Auswertung Geodätischer Überwachungsmessungen, 2nd ed.; Wichmann: Berlin, Germany, 2013; ISBN 978-3-87907-467-9. [Google Scholar]
- Petersen, A.; Koch, R. Statistical Analysis of Kalman Filters by Conversion to Gauss-Helmert Models with Applications to Process Noise Estimation. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Wang, J.G. Filtermethoden zur Fehlertoleranten Kinematischen Positionsbestimmung. Ph.D. Thesis, Universität der Bundeswehr München, Neubiberg, Germany, 1997. [Google Scholar]
- Ettlinger, A.; Neuner, H.; Burgess, T. Smartphone Sensor-Based Orientation Determination for Indoor-Navigation. In Progress in Location-Based Services 2016, 1st ed.; Gartner, G., Huang, H., Eds.; Springer: Berlin, Germany, 2017; pp. 49–68. ISBN 978-3-319-47288-1. [Google Scholar]
- Ozyagcilar, T. Implementing a Tilt-Compensated eCompass Using Accelerometer and Magnetometer Sensors; AN 2012, 4248; Freescale Semiconductor: Austin, TX, USA, 2015. [Google Scholar]
- Niemeier, W. Ausgleichungsrechnung: Statistische Auswertemethoden, 2nd ed.; Walter de Gruyter: Berlin, Germany, 2008; ISBN 978-3-11-019055-7. [Google Scholar]
- Wieser, A.; Petovello, M.G.; Lachapelle, G. Failure scenarios to be considered with kinematic high precision relative GNSS positioning. In Proceedings of the 17th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS), Long Beach, CA, USA, 21–24 September 2004; ION: Manassas, VA, USA, 2004. [Google Scholar]
- Yang, L.; Li, B.; Shen, Y.; Rizos, C. Extension of Internal Reliability Analysis regarding Seperability Analysis. J. Surv. Eng. 2017, 143, 1–10. [Google Scholar] [CrossRef]
- Wang, J.G. Reliability analysis in Kalman filtering. J. Glob. Position. Syst. 2009, 8, 101–111. [Google Scholar] [CrossRef]
- Wang, J.G. Test Statistics in Kalman Filtering. J. Glob. Position. Syst. 2008, 7, 81–90. [Google Scholar] [CrossRef]
- Koch, K.R. Outlier detection for the nonlinear Gauss Helmert model with variance components by the expectation maximization algorithm. J. Appl. Geod. 2014, 8, 185–194. [Google Scholar] [CrossRef]
- Koch, K.R. Robust estimations for the nonlinear Gauss Helmert model by the expectation maximization algorithm. J. Geod. 2014, 88, 263–271. [Google Scholar] [CrossRef]
- Jäger, R.; Müller, T.; Saler, H.; Schwäble, R. Klassische und Robuste Ausgleichungsverfahren; Wichmann: Berlin, Germany, 2005; ISBN 3-87907-370-8. [Google Scholar]
- Voigt, C.; Adamy, J. Formelsammlung der Matrizenrechnung, 1st ed.; Oldenbourg Wissenschaftsverlag GmbH: München, Germany, 2007; ISBN 978-3-486-58350-2. [Google Scholar]
- Kuusniemi, H.; Wieser, A.; Lachapelle, G.; Takala, J. User-level reliability monitoring in urban personal satellite-navigation. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1305–1318. [Google Scholar] [CrossRef]




| Gauss-Markov | Gauss-Helmert (Simplification) | Gauss-Helmert | |
|---|---|---|---|
| Standard Deviations | Gyroscope | System Noise | Accelerometer | Magnetometer |
|---|---|---|---|---|
| Original | 30°/s | 10°/s | 1 m/s2 | 5 μT |
| Adapted | 60°/s | 20°/s | 0.5 m/s2 | 2.5 μT |
| σg-y | σg-z | σc-ϕ | σc-θ | σc-ψ | σa-x | σa-y | σa-z | σm-x | σm-y | σm-z | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| rx-ϕ | −|− | −|+ | |||||||||
| rx-θ | −|− | −|+ | −|+ | ||||||||
| rx-ψ | +|− | +| | −|+ | −|+ | −|+ | ||||||
| rg-y | +| | ||||||||||
| rg-z | +|− | −|+ | −|+ | −|+ | |||||||
| rc-ϕ | +|− | −|+ | |+ | ||||||||
| rc-θ | +|− | −|+ | −|+ | |+ | |||||||
| rc-ψ | +|− | ||||||||||
| ra-x | −|+ | +|− | −|+ | ||||||||
| ra-y | −|+ | +|− | |||||||||
| ra-z | −|+ | −|+ | +|− | |+ | |||||||
| rm-x | −|+ | +|− | −|+ | −|+ | |||||||
| rm-y | −|+ | −|+ | +|− | −|+ | |||||||
| rm-z | −|+ | −|+ | −|+ | +|− |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ettlinger, A.; Neuner, H.; Burgess, T. Development of a Kalman Filter in the Gauss-Helmert Model for Reliability Analysis in Orientation Determination with Smartphone Sensors. Sensors 2018, 18, 414. https://doi.org/10.3390/s18020414
Ettlinger A, Neuner H, Burgess T. Development of a Kalman Filter in the Gauss-Helmert Model for Reliability Analysis in Orientation Determination with Smartphone Sensors. Sensors. 2018; 18(2):414. https://doi.org/10.3390/s18020414
Chicago/Turabian StyleEttlinger, Andreas, Hans Neuner, and Thomas Burgess. 2018. "Development of a Kalman Filter in the Gauss-Helmert Model for Reliability Analysis in Orientation Determination with Smartphone Sensors" Sensors 18, no. 2: 414. https://doi.org/10.3390/s18020414
APA StyleEttlinger, A., Neuner, H., & Burgess, T. (2018). Development of a Kalman Filter in the Gauss-Helmert Model for Reliability Analysis in Orientation Determination with Smartphone Sensors. Sensors, 18(2), 414. https://doi.org/10.3390/s18020414




