Classification of Partial Discharge Signals by Combining Adaptive Local Iterative Filtering and Entropy Features
Abstract
1. Introduction
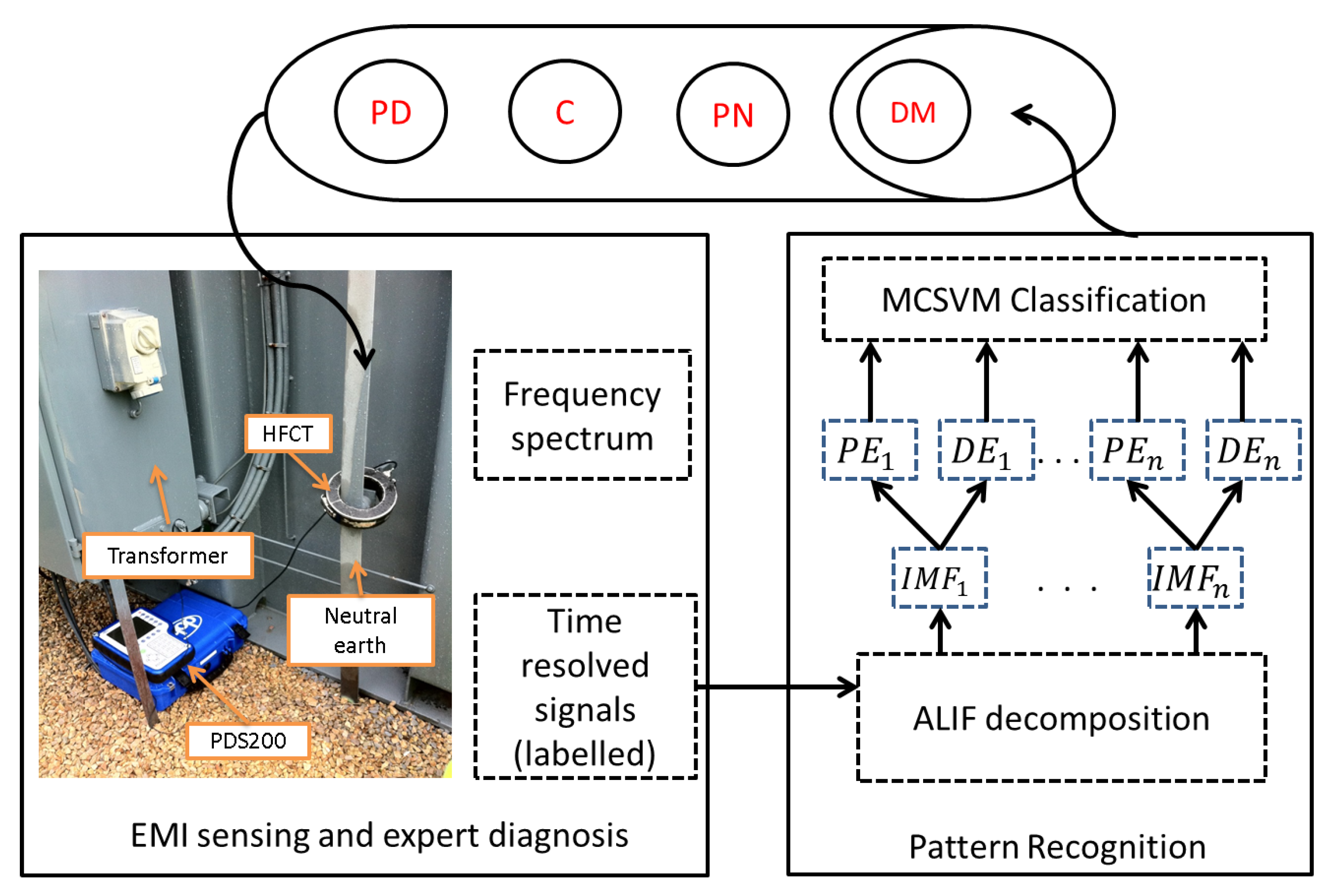
2. Proposed Solution
3. EMI Measurement Technique
4. Classification Theory
4.1. Adaptive Local Iterative Filtering
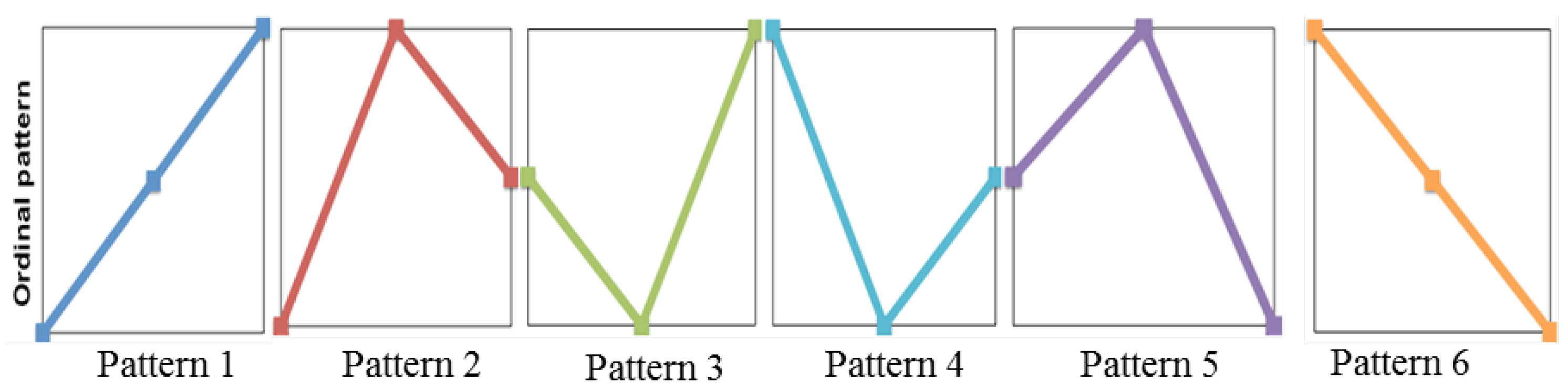
4.2. Permutation Entropy
4.3. Dispersion Entropy
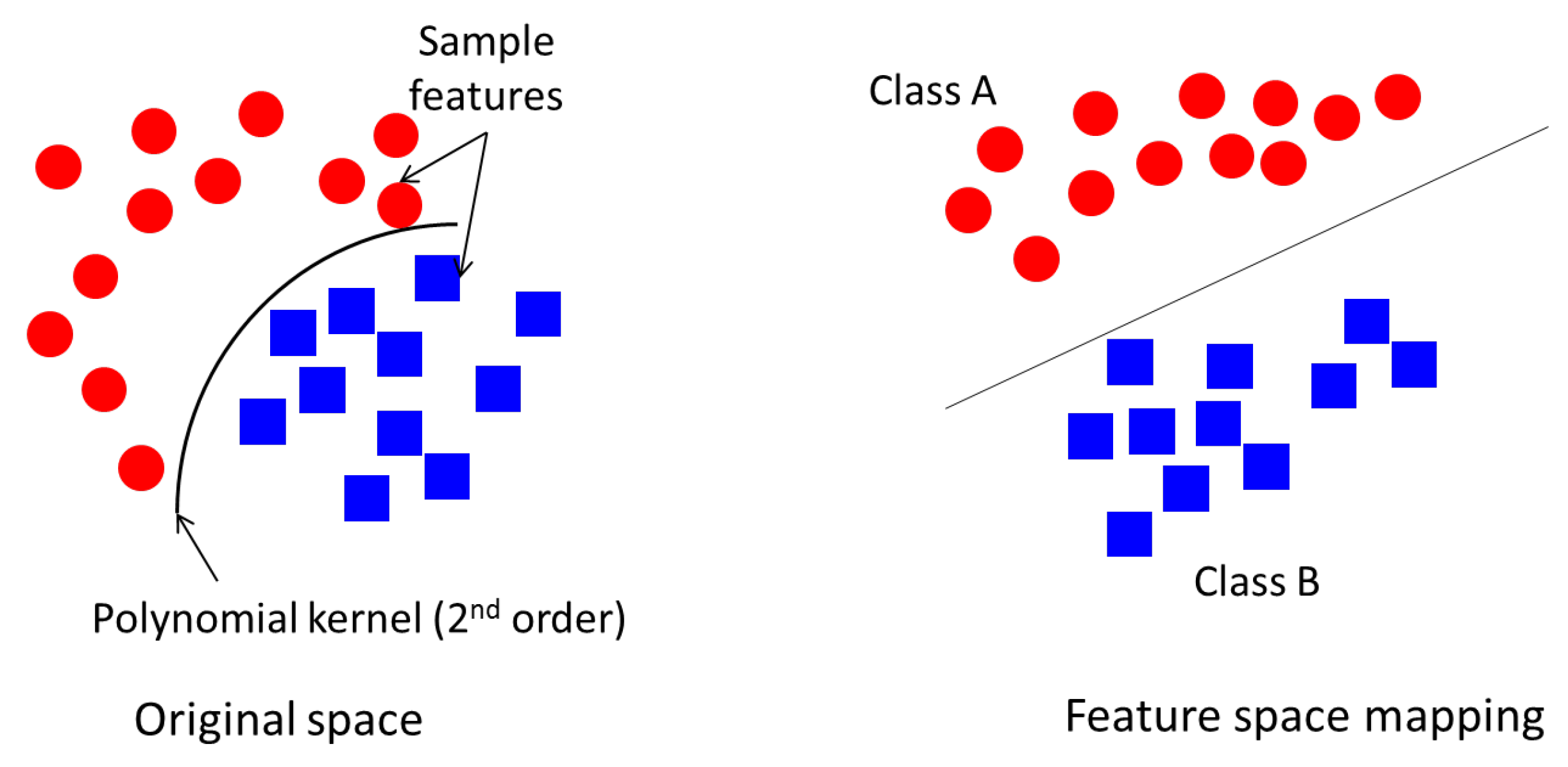
4.4. Support Vector Machine
- SVM generates an optimal line that separates the two different data features, such that feature clusters of one class are grouped on one side of the feature space and the remaining ones are grouped on the other side. This yields to the SVM model which is used in future data classification.
- SVM classifies the training data set based on the trained model in the previous step; this is known as the testing phase.
5. Application to EMI Data
- Site 1: The data was measured at the neutral earth cable of a 661 MVA hydrogen/water cooled synchronous generator operating at 23.5 kV, 19 kA, 3 phase, 50 Hz, 3000 RPM, 0.85 lag/0.95 lead power factor and 2 pole. A total of 13 signals were identified to contain E+mPD, C+E, C, N, PN and mPD.
- Site 2: similar to the previous site, the measurements were taken at the neutral earth of different assets including a General Step-Up (GSU) Transformer operating at 430/15.5 kV, 444/12329 A, 3 phase, 50 Hz, 331 MVA, IPB and Station Transformer (Sta XFMR). The events identified in the GSU transformer are mPD+mA, PD+mA, PD+A, PD and the events identified in the IPB are PD and PN. Finally, the DM event was identified in the Sta XFMR.
- Site 3: The data was measured at the neutral earth cable of an H2 cooled generator, operating at 294.25 MVA, 15 kV, 0.85 PF, 2 pole and 3000 RPM, from which seven signals were selected with an additional signal selected from an H2 cooled Steam Turbine Generator (STG) operating at 15 kV, 2 pole and 3000 RPM. The labelled events found at the neutral earth cable are PN, PD, NVFD, E and the ones found at the STG are: PD, E+mPD and E+PD.
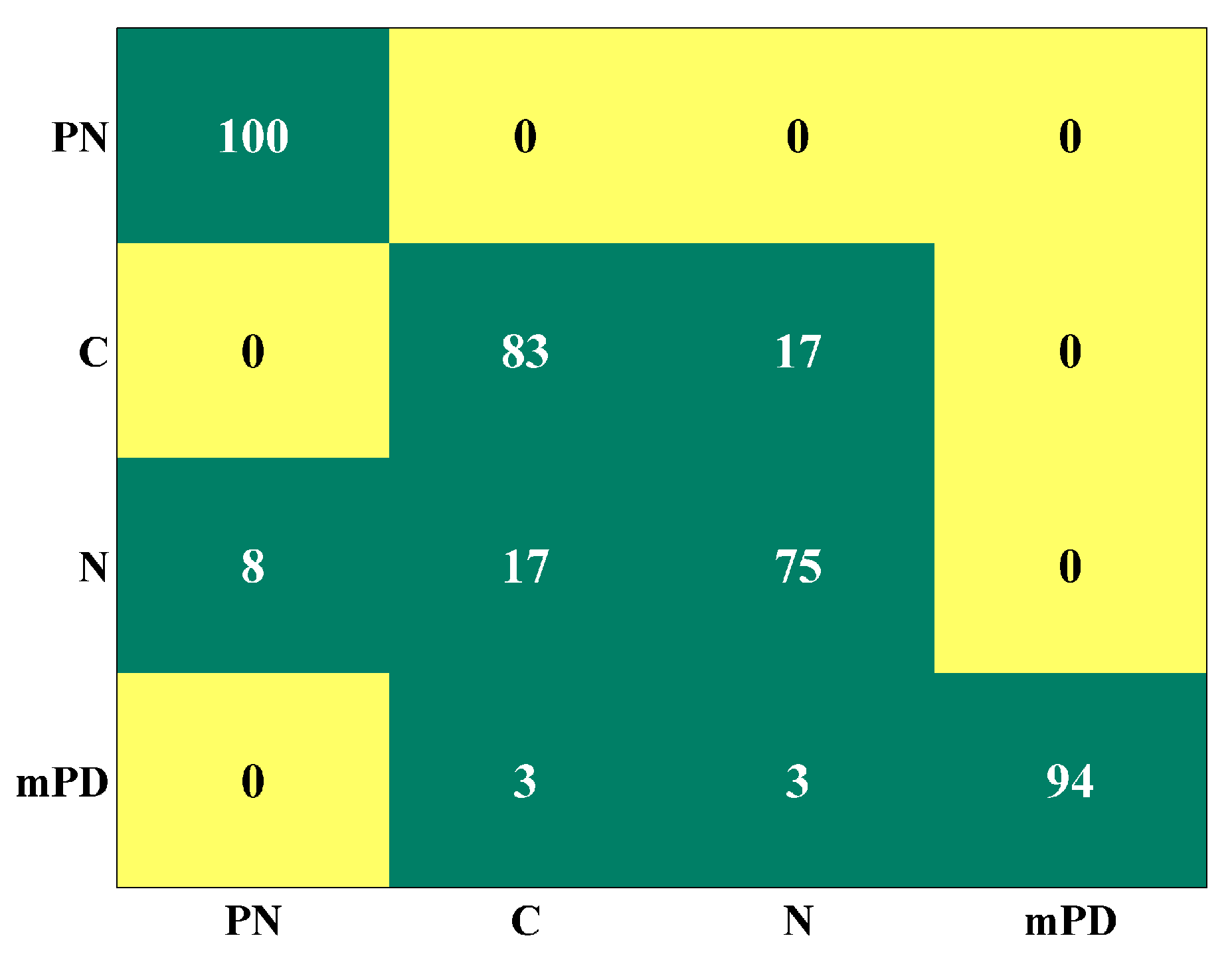
6. Results and Discussion
7. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| A | Arcing |
| ALIF | Adaptive Local Iterative Filtering |
| C | Corona |
| DE | Dispersion Entropy |
| DM | Data Modulation |
| E | Exciter |
| EMI | Electro-Magnetic Interference |
| GSU | General Step-Up |
| HFCT | High Frequency Current Transformer |
| HV | High Voltage |
| IMF | Intrinsic Mode Function |
| IPB | Isolated Phase Bus |
| MCSVM | Multi-Class SVM |
| NVFD | Non Variable Frequency Drive |
| PD | Partial Discharge |
| PDE | Partial Differential Equation |
| PDS200 | Partial Discharge Surveyor 200 |
| PE | Permutation Entropy |
| PN | Process Noise |
| PRPD | Phase Resolved PD |
| SD | Stopping Distance |
| STG | Step Up Generator |
| Sta XFMR | Station Transformer |
| SVM | Support Vector Machine |
| UHF | Ultra-High-Frequency |
References
- Timperley, J.E.; Vallejo, J.M. Condition Assessment of Electrical Apparatus With EMI Diagnostics. IEEE Trans. Ind. Appl. 2017, 53, 693–699. [Google Scholar] [CrossRef]
- Mitiche, I.; Morison, G.; Hughes-Narborough, M.; Nesbitt, A.; Boreham, P.; Stewart, B.G. Classification of Partial Discharge Signals by Combining Adaptive Local Iterative Filtering and Entropy Features. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena, FortWorth, TX, USA, 22–25 October 2017; pp. 335–338. [Google Scholar]
- Álvarez, F.; Garnacho, F.; Khamlichi, F.; Ortego, J. Classification of partial discharge sources by the characterization of the pulses waveform. In Proceedings of the IEEE International Conference on Dielectrics (ICD), Montpellier, France, 3–7 July 2016; pp. 514–519. [Google Scholar]
- Altenburger, R.; Heitz, C.; Timmer, J. Analysis of Phase-Resolved Partial Discharge Patterns of Voids Based on a Stochastic Process Approach. J. Phys. D Appl. Phys. 2002, 35, 1149–1163. [Google Scholar] [CrossRef]
- Badieu, L.V.; Koltunowicz, W.; Broniecki, U.; Batlle, B. Increased Operation Reliability Through PD Monitoring of Stator Winding. In Proceedings of the 13th INSUCON Conference, Birmingham, UK, 16–18 May 2017; pp. 1–6. [Google Scholar]
- Raymond, W.J.K.; Illias, H.A.; Abu Bakar, A.H. Classification of Partial Discharge Measured under Different Levels of Noise Contamination. PLoS ONE 2017, 12, 1–20. [Google Scholar] [CrossRef]
- Chatpattananan, V.; Pattanadech, N.; Vicetjindavat, K. PCA-LDA for Partial Discharge Classification on High Voltage Equipment. In Proceedings of the IEEE 8th International Conference on Properties applications of Dielectric Materials, Bali, Indonesia, 26–30 June 2006; pp. 479–481, ISBN 1-4244-0189-5. [Google Scholar]
- Pattanadech, N.; Nimsanong, P.; Potivejkul, S.; Yuthagowith, P.; Polmai, S. Partial discharge classification using probabilistic neural network model. In Proceedings of the 18th International Conference on Electrical Machines and Systems, Pattaya, Thailand, 25–28 October 2015; pp. 1176–1180, ISBN 978-1-4799-8805-1. [Google Scholar]
- Lalitha, E.M.; Satish, L. Wavelet analysis for classification of multi-source PD patterns. IEEE Trans. Dielectr. Electr. Insul. 2000, 7, 40–47. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.; Zhang, S.; Qiu, Y.; Liao, R. Time-frequency features extraction and classification of partial discharge UHF signals. In Proceedings of the International Conference on Information Science, Electronics and Electrical Engineering, Sapporo, Japan, 26–28 April 2014; pp. 1231–1235, ISBN 978-1-4799-3197-2. [Google Scholar]
- Hunter, J.A.; Hao, L.; Lewin, P.L.; Evagorou, D.; Kyprianou, A.; Georghiou, G.E. Comparison of two partial discharge classification methods. In Proceedings of the Conference Record of the 2010 IEEE International Symposium on Electrical Insulation, San Diego, CA, USA, 6–9 June 2010; pp. 1–5, ISBN 978-1-4244-6301-5. [Google Scholar]
- Albarracín, R.; Robles, G.; Martínez-Tarifa, J.M.; Ardila-Rey, J. Separation of Sources in Radiofrequency Measurements of Partial Discharges using Time-Power Ratios Maps. ISA Trans. 2015, 58, 389–397. [Google Scholar] [CrossRef] [PubMed]
- Moore, P.J.; Portugues, I.E.; Glover, I.A. Radiometric Location of Partial Discharge Sources on Energized High-Voltage Plant. IEEE Trans. Power Deliv. 2005, 20, 2264–2272. [Google Scholar] [CrossRef]
- Robles, G.; Fresno, J.M.; Martínez-Tarifa, J.M. Separation of Radio-Frequency Sources and Localization of Partial Discharges in Noisy Environments. Sensors 2015, 15, 9882–9898. [Google Scholar] [CrossRef] [PubMed]
- Albarracín, R.; Ardila-Rey, J.A.; Mas’ud, A.A. On the Use of Monopole Antennas for Determining the Effect of the Enclosure of a Power Transformer Tank in Partial Discharges Electromagnetic Propagation. Sensors 2016, 16, 148. [Google Scholar] [CrossRef] [PubMed]
- Cicone, A.; Liu, J.; Zhou, H. Adaptive local iterative filtering for signal decomposition and instantaneous frequency analysis. Appl. Comput. Harmon. Anal. 2016, 41, 384–411. [Google Scholar] [CrossRef]
- Xie, Y.; Tang, J.; Zhou, Q. Feature extraction and recognition of UHF partial discharge signals in GIS based on dual-tree complex wavelet transform. Eur. Trans. Electr. Power 2010, 20, 639–649. [Google Scholar] [CrossRef]
- Ravelo-García, A.G.; Navarro-Mesa, J.L.; Casanova-Blancas, U.; Martín-González, S.I.; Quintana-Morales, P.J.; Guerra Moreno, I.; Canino-Rodríguez, J.M.; Hernández-Pérez, E. Application of the Permutation Entropy over the Heart Rate Variability for the Improvement of Electrocardiogram-based Sleep Breathing Pause Detection. Entropy 2015, 17, 914–927. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Timperley, J.E.; Vallejo, J.M. Condition assessment of electrical apparatus with EMI diagnostics. In Proceedings of the IEEE Petroleum and Chemical Industry Committee Conference, Houston, TX, USA, 5–7 October 2015; pp. 1–8, ISBN 978-1-4799-8502-9. [Google Scholar]
- Specification for Radio Disturbance and Immunity Measurement Apparatus and Methods-Part 1: Radio Disturbance and Immunity Measuring Apparatus, IEC: 2015, CISPR 16-1-1, Part 1-1. Available online: http://www.iec.ch/emc/basic_emc/basic_cispr16.htm (accessed on 26 January 2018).
- Timperley, J.E.; Vallejo, J.M.; Nesbitt, A. Trending of EMI data over years and overnight. In Proceedings of the IEEE Electrical Insulation Conference, Philadelphia, PA, USA, 8–11 June 2014; pp. 176–179, ISBN 978-1-4799-2789-0. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and The Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Lin, L.; Wang, Y.; Zhou, H. Iterative Filtering as an Alternative Algorithm for Empirical Mode Decomposition. Adv. Adapt. Data Anal. 2009, 1, 543–560. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Rathie, P.; Da Silva, S. Shannon, Levy, and Tsallis. Appl. Math. Sci. 2008, 2, 1359–1363. [Google Scholar]
- Riedl, M.; Müller, A.; Wessel, N. Practical Considerations of Permutation Entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R.X. Permutation Entropy: A nonlinear Statistical Measure for Status Characterization of Rotary Machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Massimiliano, Z.; Luciano, Z.; Osvaldo, R.A.; Papo, D. Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1961. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Cambridge, UK, 2006. [Google Scholar]
- Lesniak, J.M.; Hupse, R.; Blanc, R.; Karssemeijer, N.; Székely, G. Comparative Evaluation of Support Vector Machine Classification for Computer Aided Detection of Breast Masses in Mammography. Phys. Med. Biol. 2012, 57, 2560–2574. [Google Scholar] [CrossRef] [PubMed]
- Boardman, M.; Trappenberg, T. A Heuristic for Free Parameter Optimization with Support Vector Machines. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, BC, Canada, 16–21 July 2006; pp. 1337–1344, ISBN 978-1-4799-2789-0. [Google Scholar]
- Widodo, A.; Yang, B.-S. Support Vector Machine in Machine Condition Monitoring and Fault Diagnosis. Mech. Syst. Signal Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Robles, R.; Albarracín, R.; Vázquez-Roy, J.L.; Rajo-Iglesias, E.; Martínez-Tarifa, J.M.; Rojas-Moreno, M.V.; Sánchez-Fernández, M.; Ardila-Rey, J. On the use of vivaldi antennas in the detection of partial discharges. In Proceedings of the IEEE International Conference on Solid Dielectrics, Bologna, Italy, 30 June–4 July 2013; pp. 302–305, ISBN 978-1-4799-2789-0. [Google Scholar]

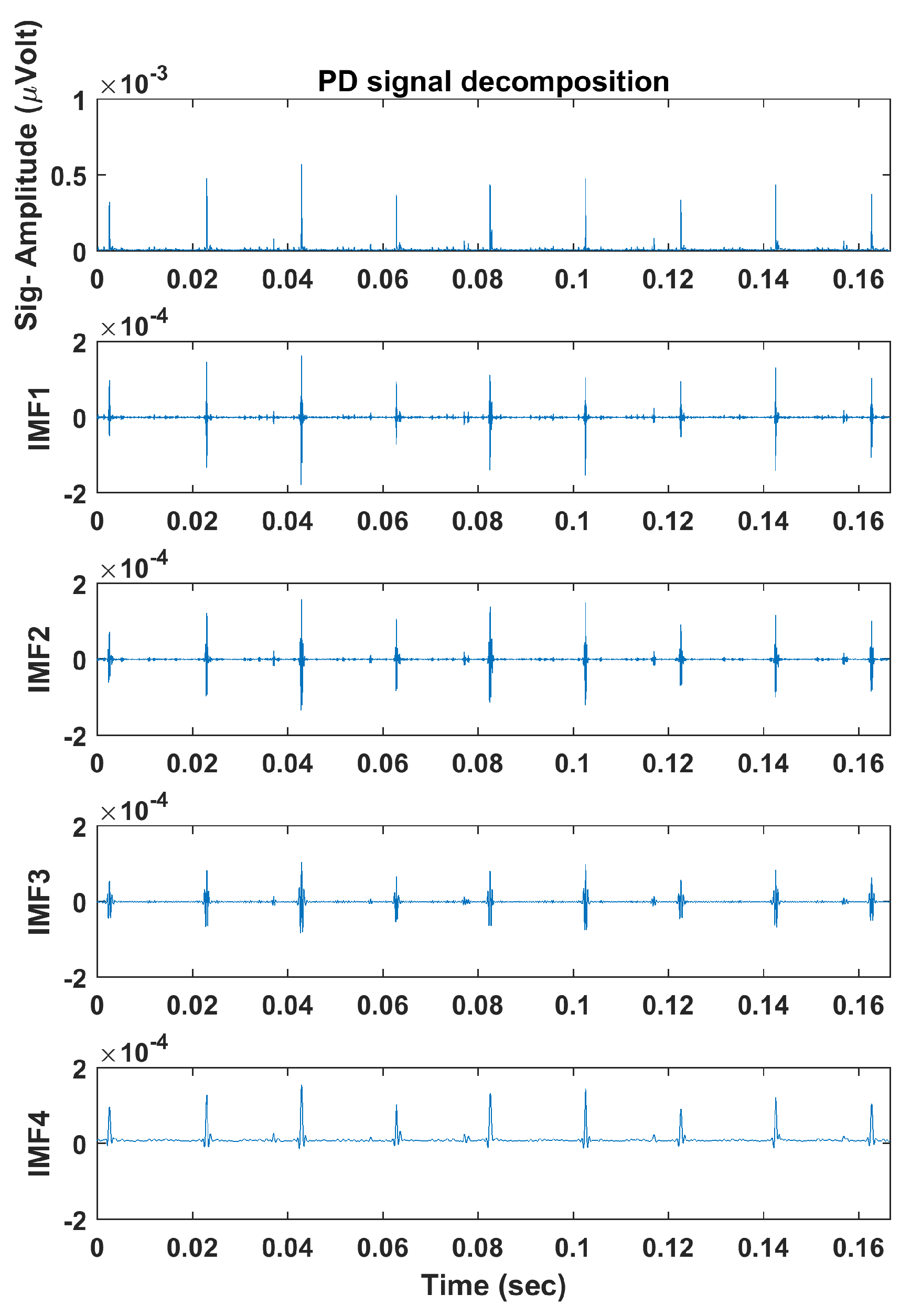

| Signal | Feature | IMF1 | IMF2 | IMF3 | IMF4 |
|---|---|---|---|---|---|
| PD | |||||
| PE | 1.75 | 1.45 | 1.24 | 1.06 | |
| DE | 1.13 | 1.42 | 1.50 | 1.34 | |
| PN | |||||
| PE | 1.79 | 1.39 | 1.14 | 0.95 | |
| DE | 2.01 | 1.82 | 1.64 | 1.39 |
| Case | Classification Accuracy % |
|---|---|
| Site 1 | 91 |
| Site 2 | 100 |
| Site 3 | 100 |
| Common data subset | 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitiche, I.; Morison, G.; Nesbitt, A.; Hughes-Narborough, M.; Stewart, B.G.; Boreham, P. Classification of Partial Discharge Signals by Combining Adaptive Local Iterative Filtering and Entropy Features. Sensors 2018, 18, 406. https://doi.org/10.3390/s18020406
Mitiche I, Morison G, Nesbitt A, Hughes-Narborough M, Stewart BG, Boreham P. Classification of Partial Discharge Signals by Combining Adaptive Local Iterative Filtering and Entropy Features. Sensors. 2018; 18(2):406. https://doi.org/10.3390/s18020406
Chicago/Turabian StyleMitiche, Imene, Gordon Morison, Alan Nesbitt, Michael Hughes-Narborough, Brian G. Stewart, and Philip Boreham. 2018. "Classification of Partial Discharge Signals by Combining Adaptive Local Iterative Filtering and Entropy Features" Sensors 18, no. 2: 406. https://doi.org/10.3390/s18020406
APA StyleMitiche, I., Morison, G., Nesbitt, A., Hughes-Narborough, M., Stewart, B. G., & Boreham, P. (2018). Classification of Partial Discharge Signals by Combining Adaptive Local Iterative Filtering and Entropy Features. Sensors, 18(2), 406. https://doi.org/10.3390/s18020406






