A Flexible Tactile Sensor with Irregular Planar Shape Based on Uniform Electric Field
Abstract
:1. Introduction
2. Principle of the Tactile Sensor
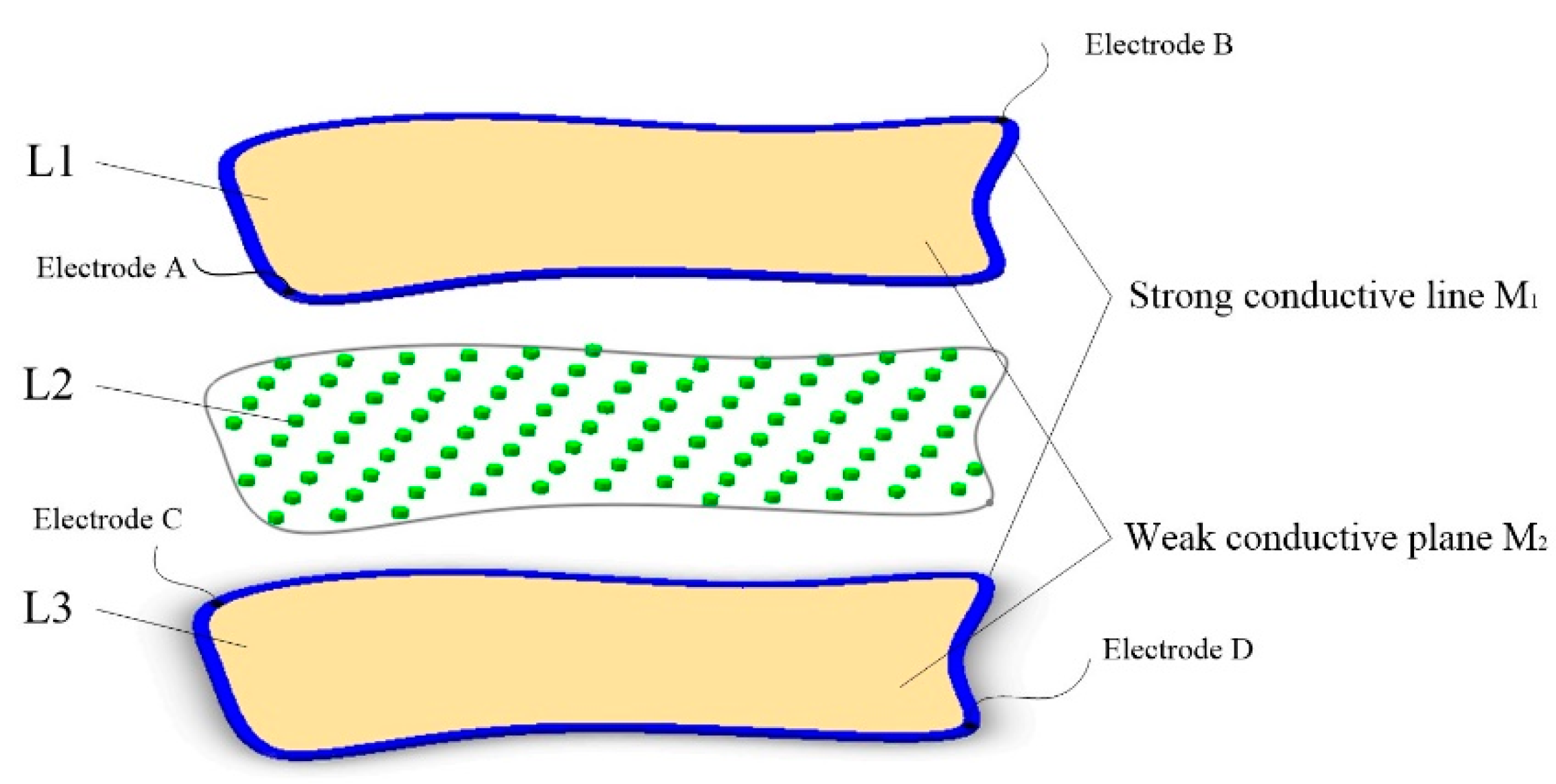
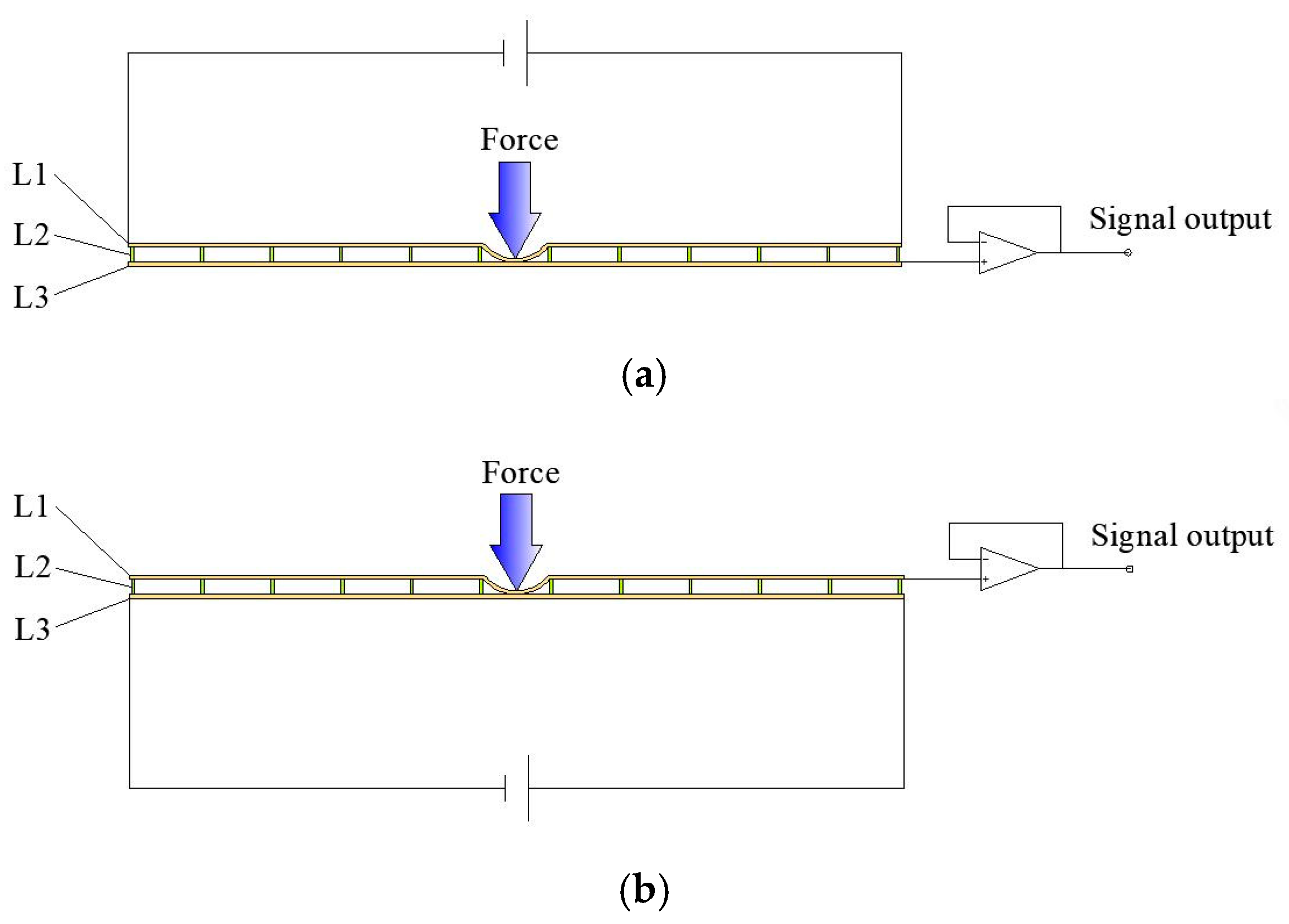
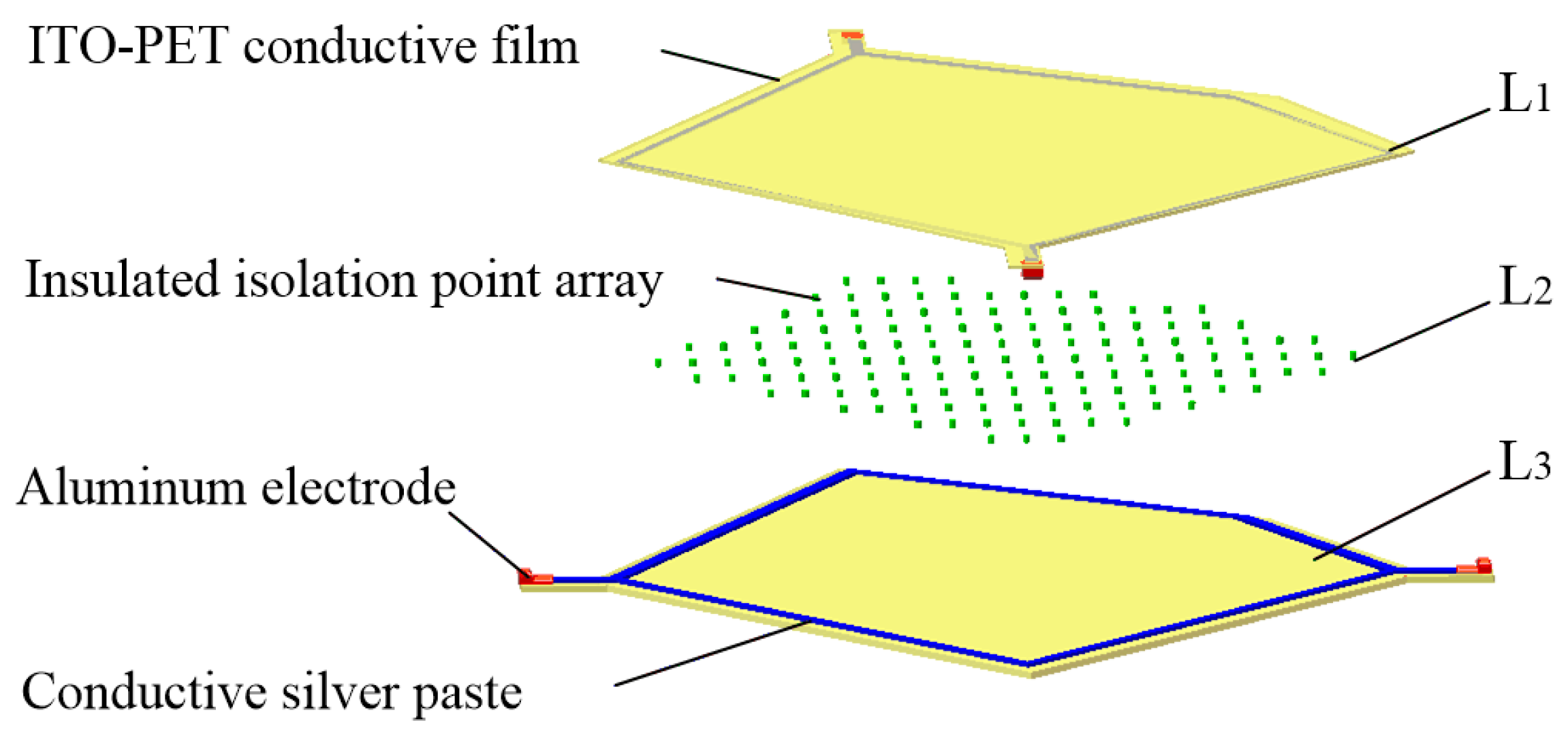
2.1. Structural Model of the Tactile Sensor
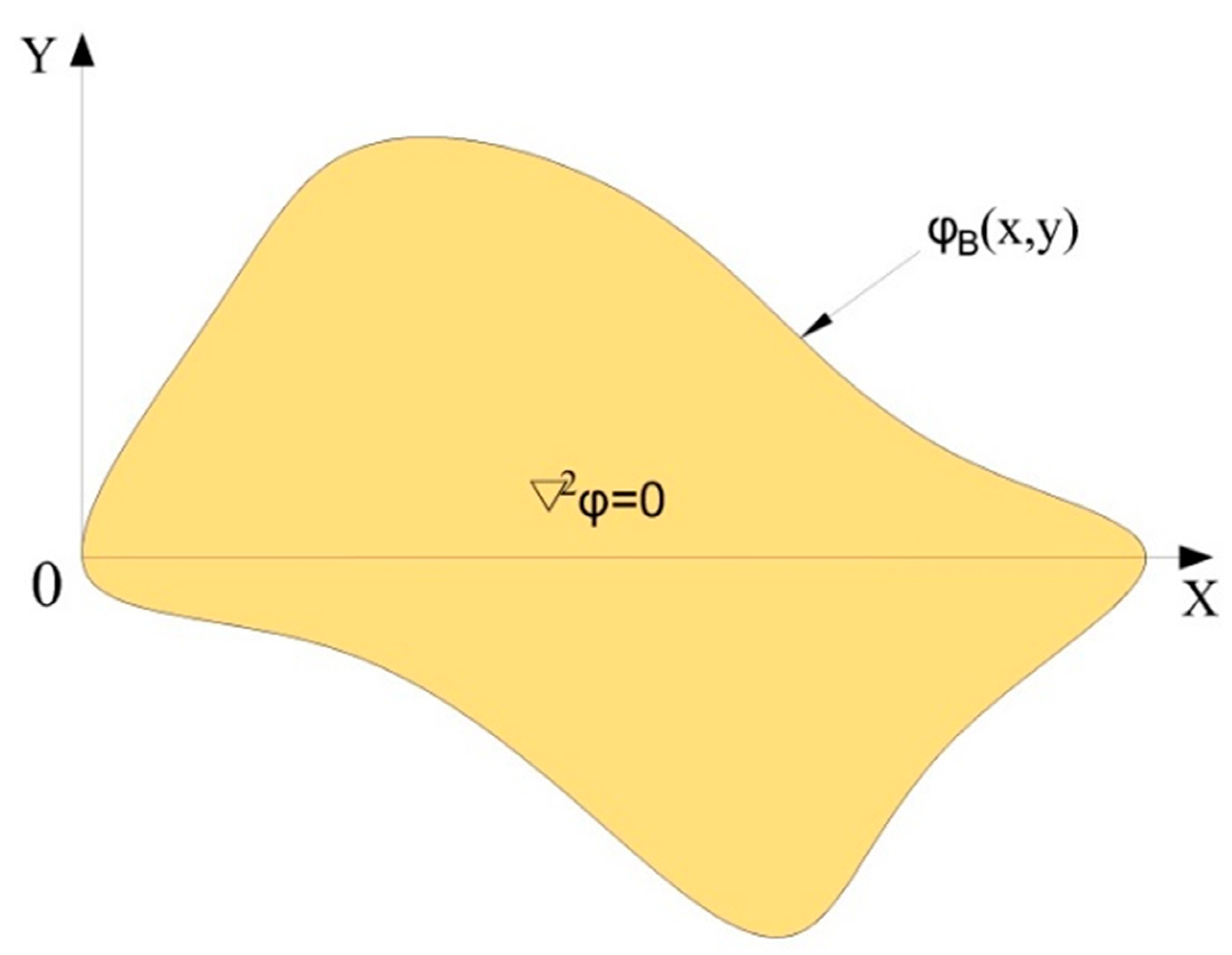
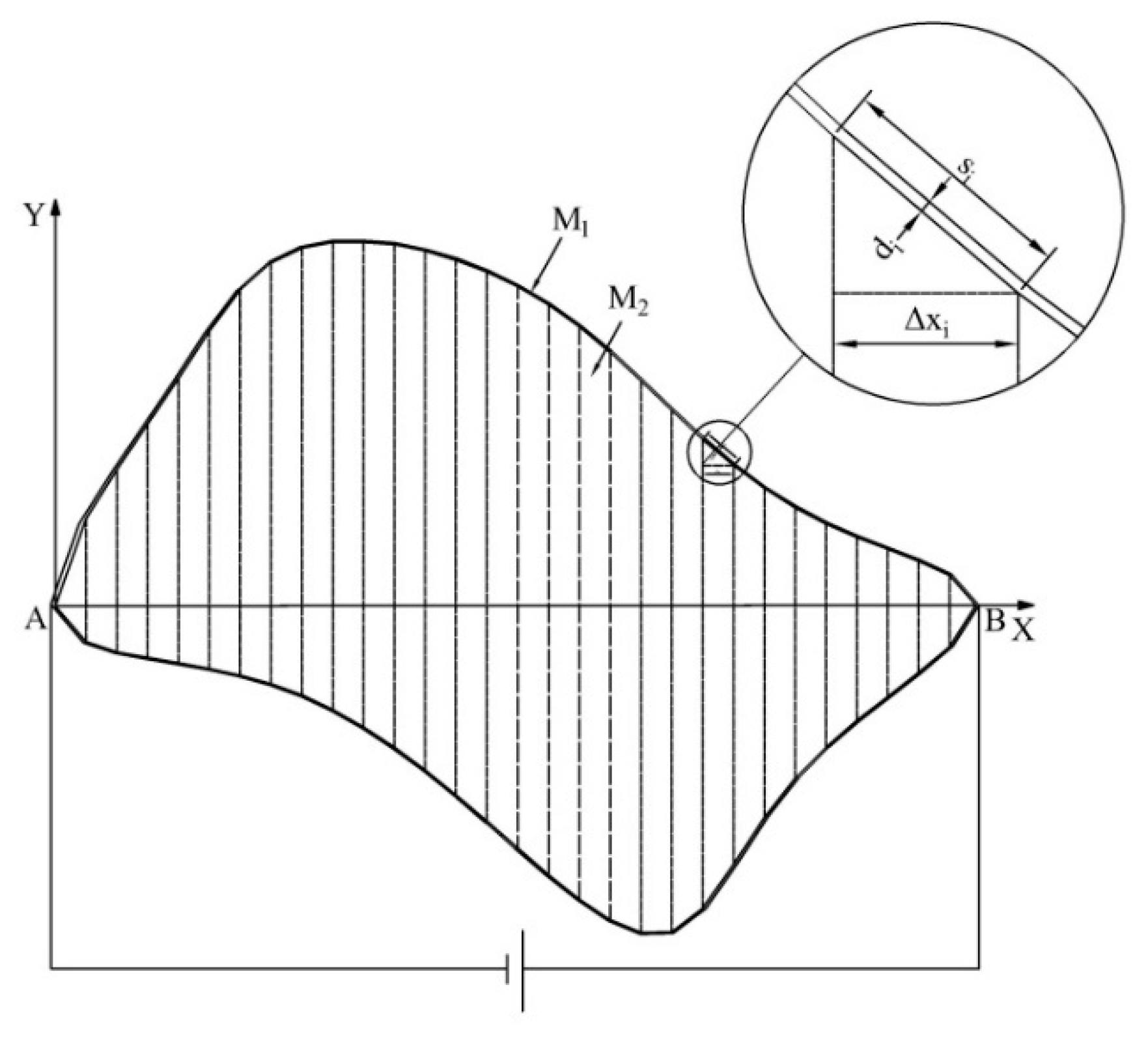
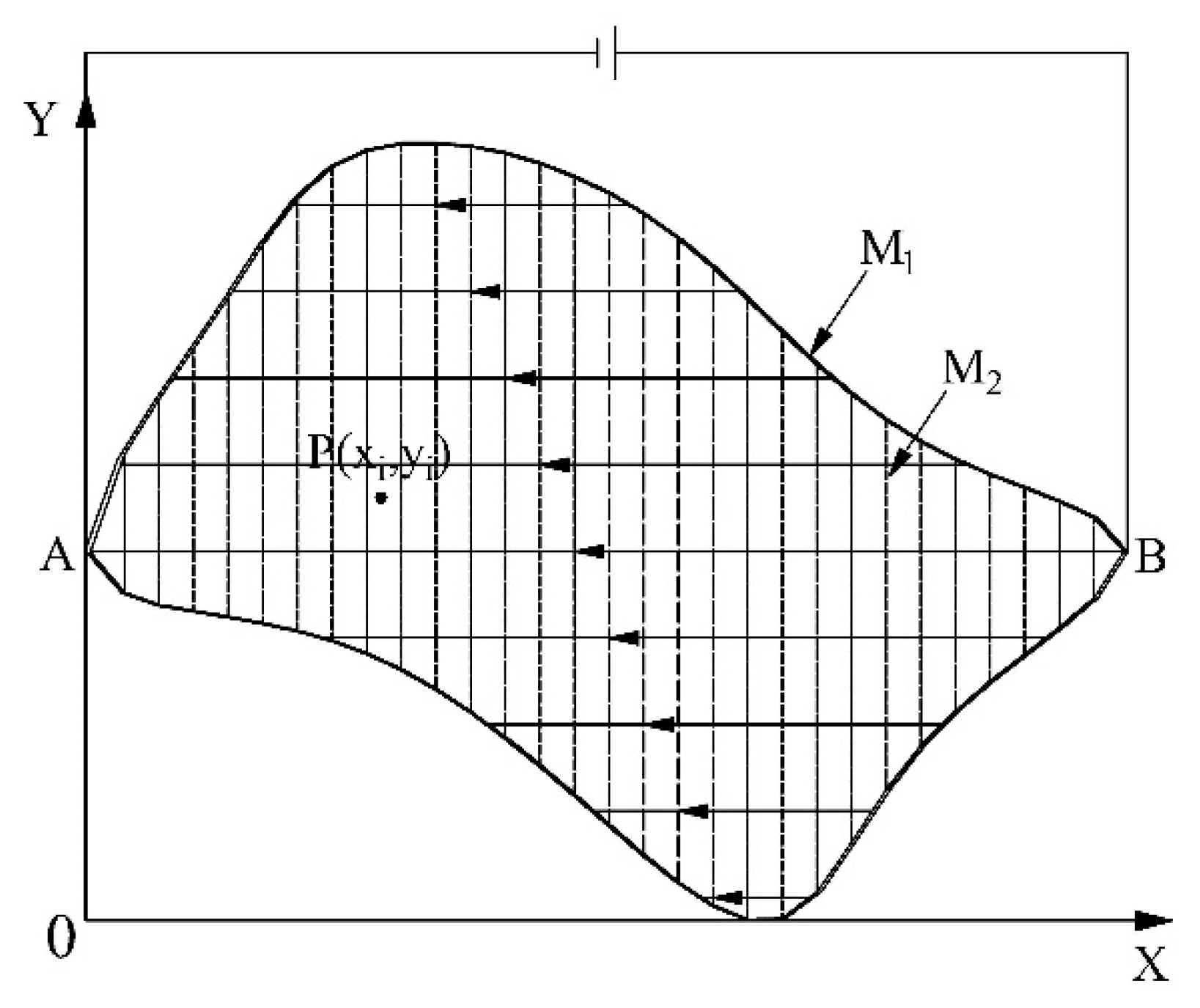
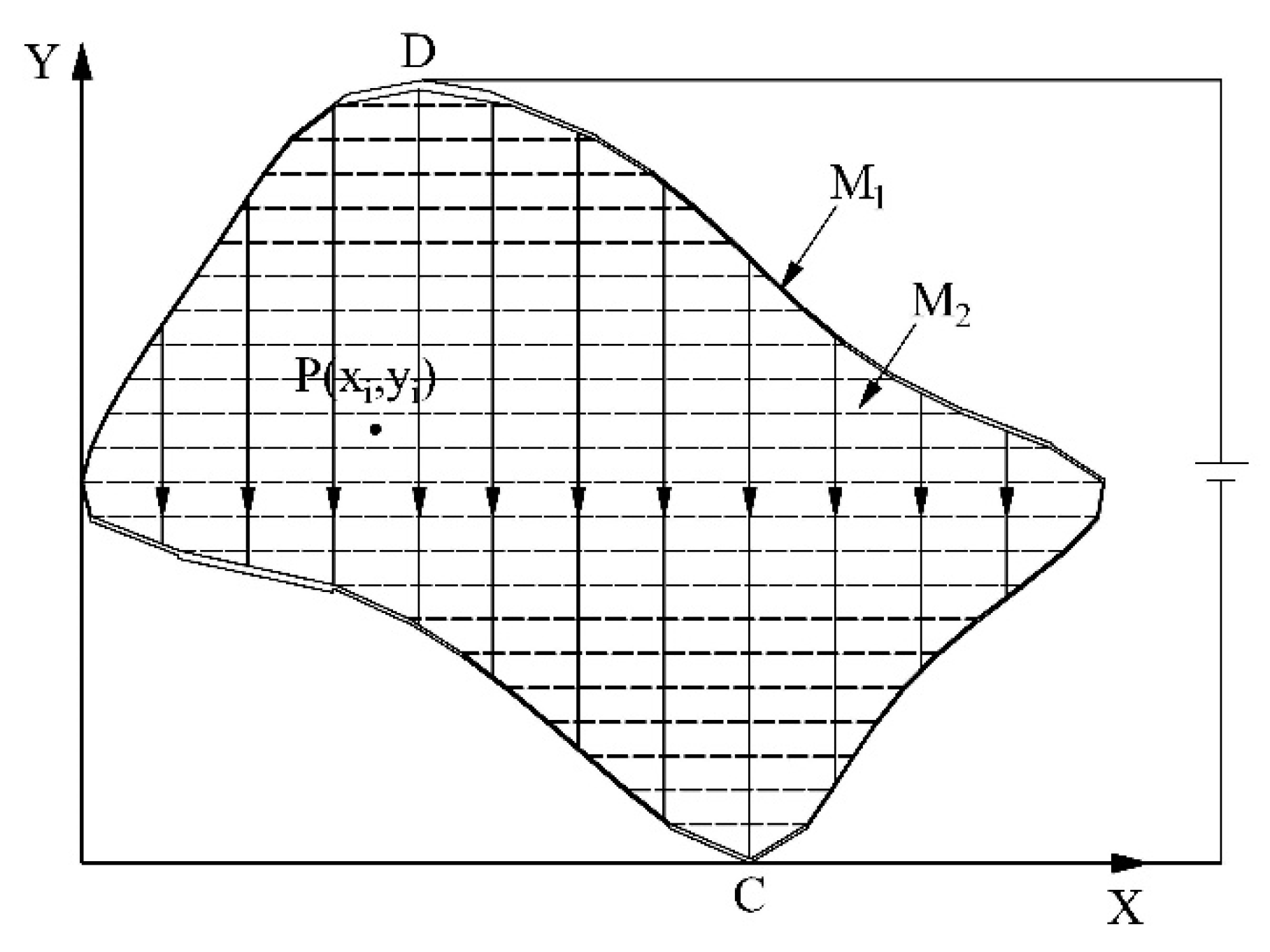
2.2. Construction of the Uniform Electric Field
2.3. Construction of the Boundary Potential Distribution Meeting
2.4. Contact Point Position Detection
3. Finite Element Analysis of Conductive Plane
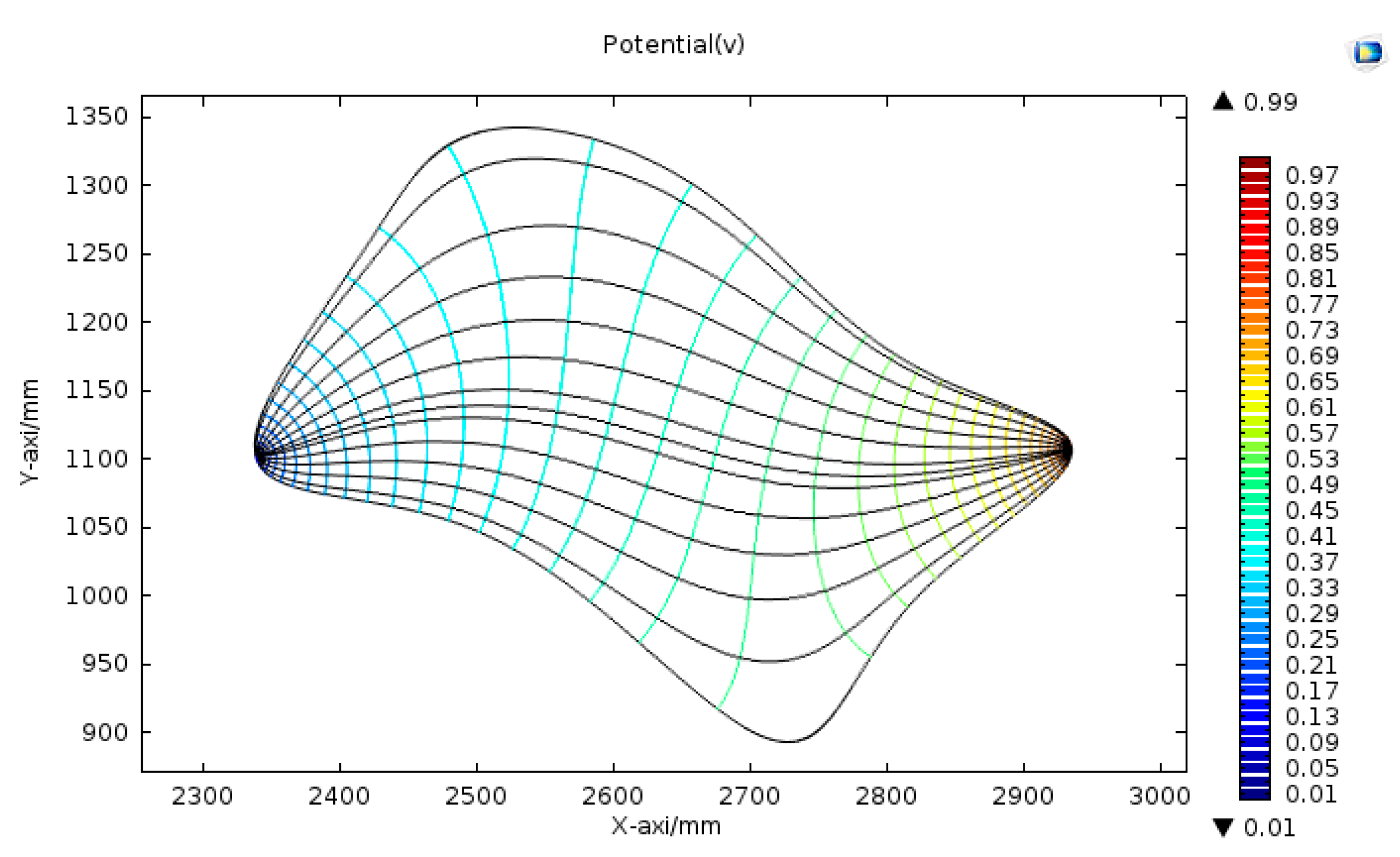
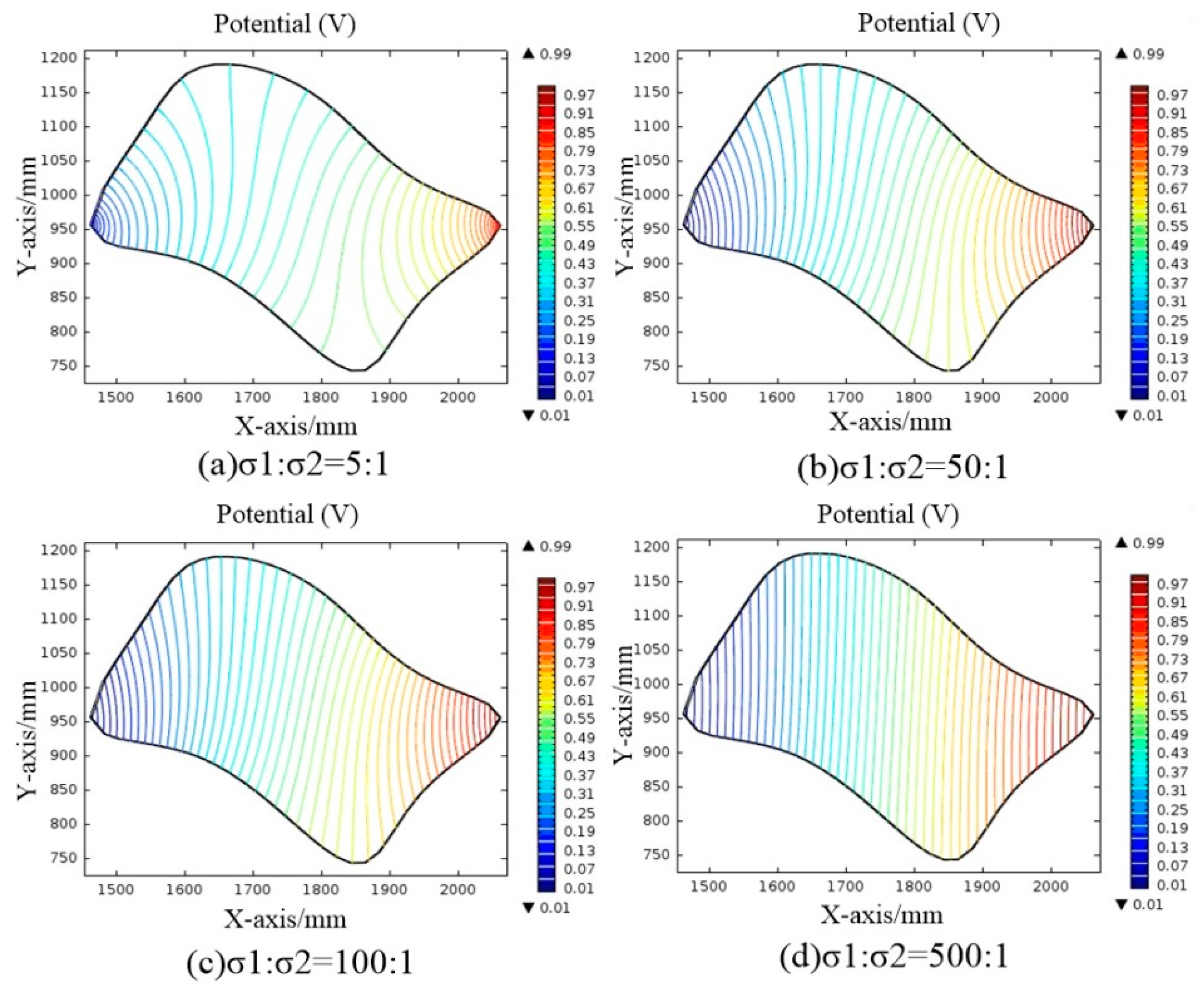
3.1. Influence of the Ratio of the Conductivity of M1 to M2
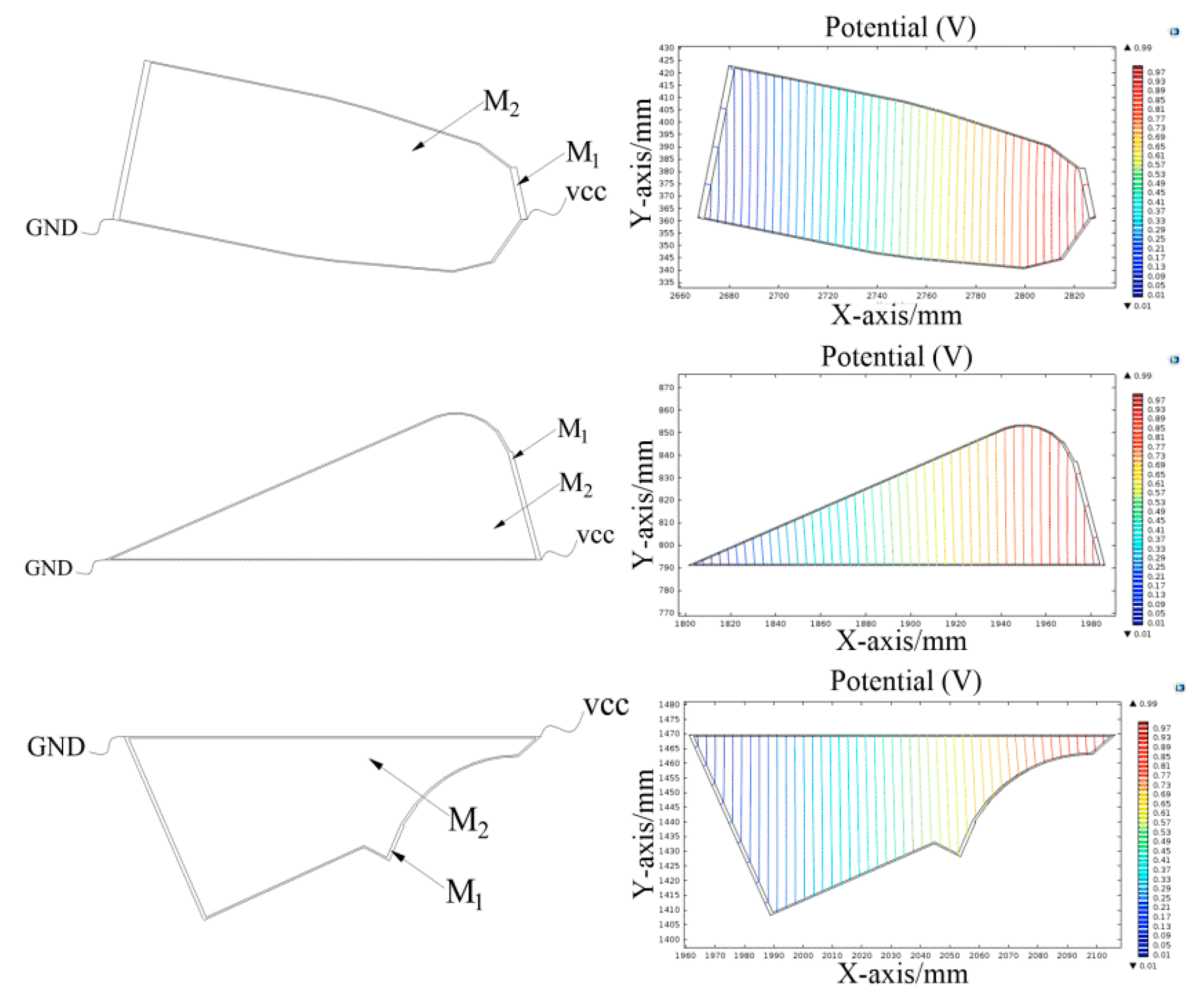
3.2. Simulation of Different Shaped Tactile Sensors
4. Experiments
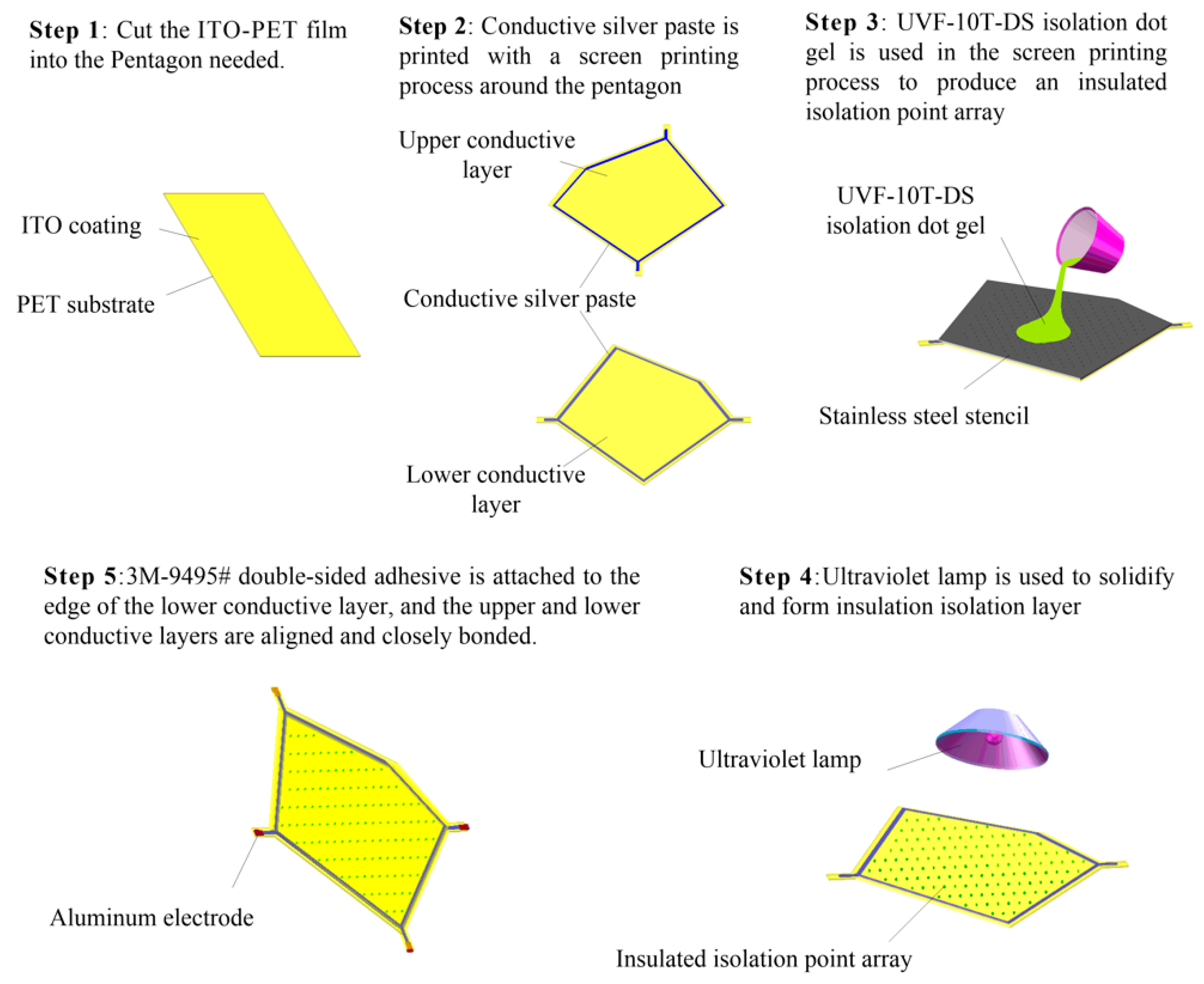
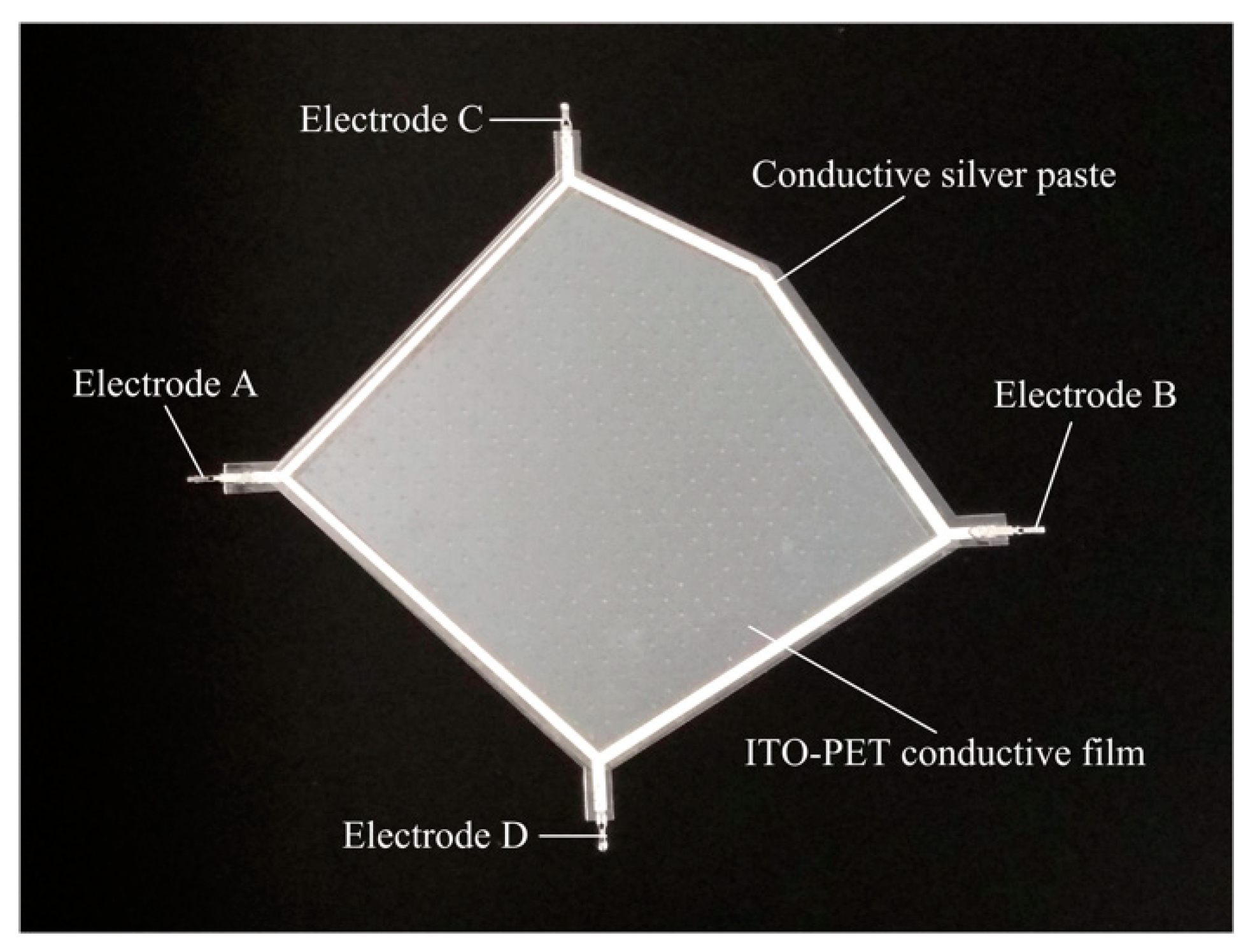
4.1. Sample Production
- (1)
- Upper layer L1: An ITO-PET conductive film with sheet resistance of 100 Ω/cm2 and a thickness of 0.175 mm (where the thickness of the ITO film was 70 nm) was cut into a pentagon. A conductive silver paste with a conductivity of about 2.4 × 107 S/m was printed using a screen printing process around the pentagon sides onto ITO-PET conductive film. A pair of aluminum electrodes were fitted at both corners of the pentagon.
- (2)
- Isolating layer L2: UVF-10T-DS isolation dot gel was used in the screen printing process to produce an insulated isolation point array with a diameter of 0.3 mm, a spacing of 4 × 4 mm, and a height 0.1 mm in the upper composite conductive layer. An ultraviolet lamp was used to solidify and form the insulation isolation layer.
- (3)
- Lower layer L3: This was similar to the upper layer L1 and was also composed of the ITO-PET conductive film and the conductive silver paste. However, the shape of the strong conductive line printed by the conductive silver paste was different to that of the upper layer L1.
- (4)
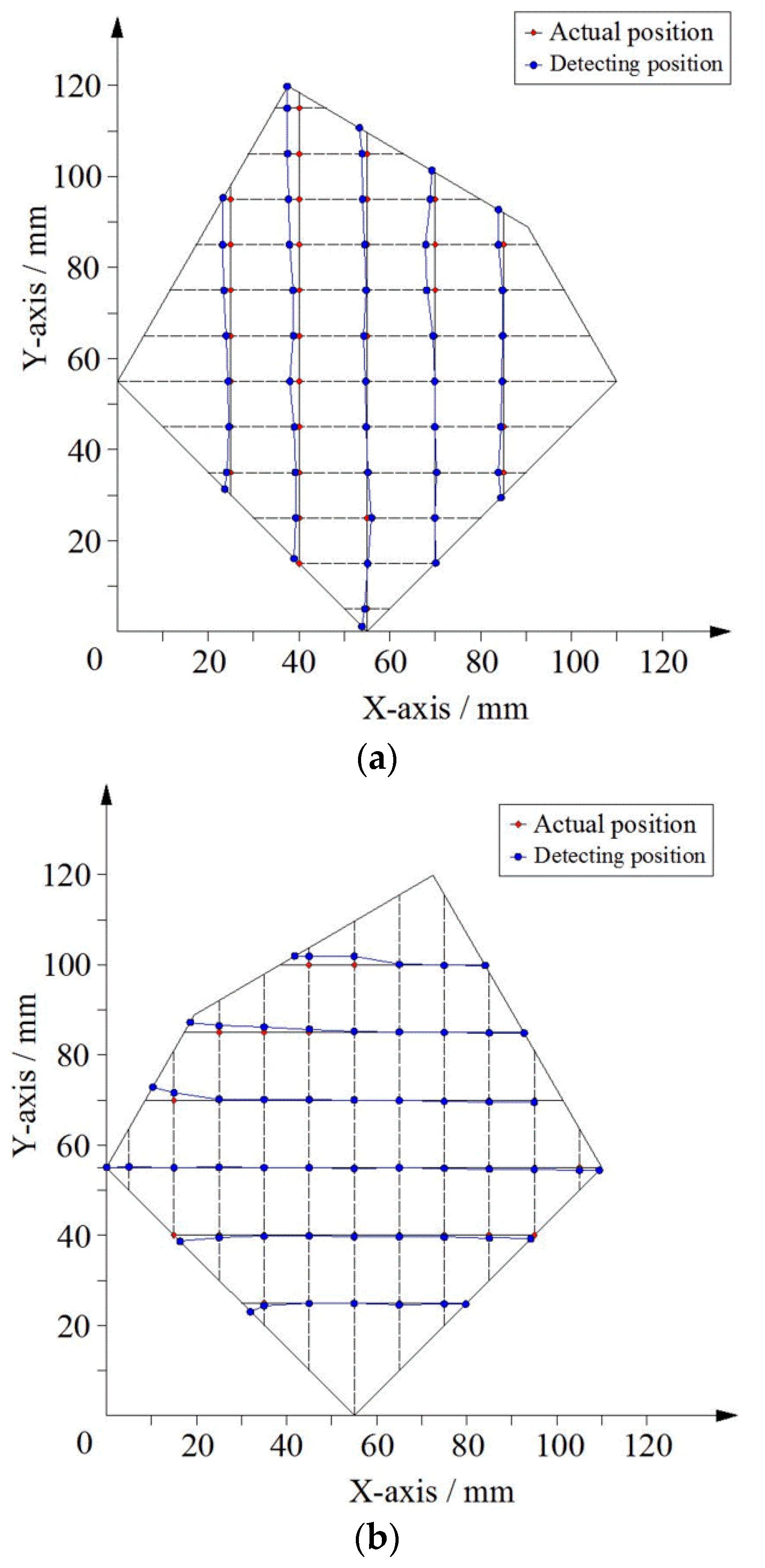
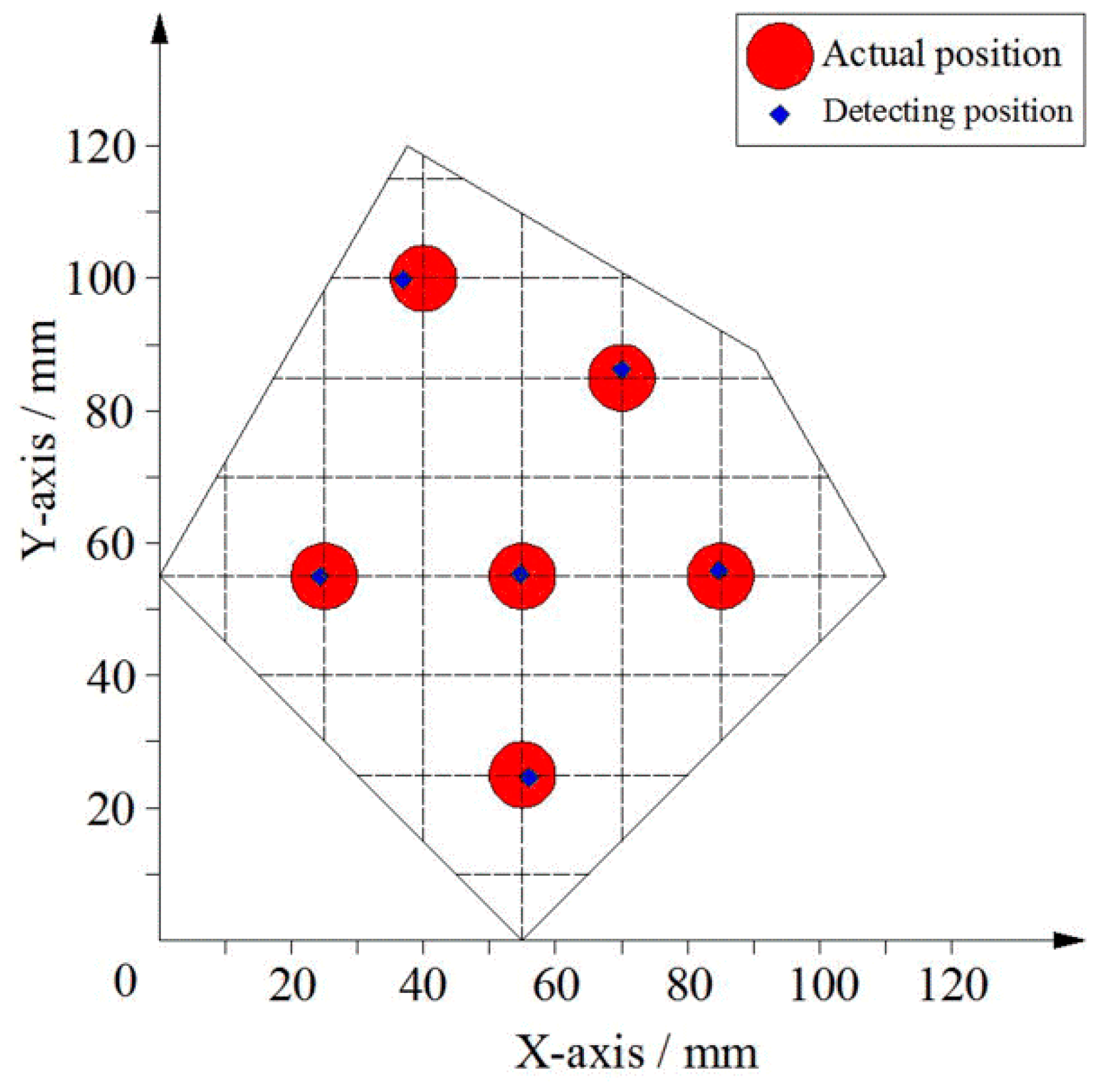
4.2. Contact Experiment of Tactile Sensor
4.3. Signal Processing of Tactile Sensor
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mallory, L.; Alex, C.; Benjamin, C.; Jeffrey, B.; Zhenan, B. 25th anniversary article: The evolution of electronic skin (E-Skin): A brief history, design considerations, and recent progress. Adv. Mater. 2013, 25, 5997–6038. [Google Scholar] [CrossRef]
- Alex, C.; Jia, L.; Zhenan, B. Pursuing prosthetic electronic skin. Nat. Mater. 2016, 15, 937–950. [Google Scholar] [CrossRef]
- Ravinder, S.; Philipp, M.; Maurizio, V.; Gordon, C.; Vladimir, J. Directions toward effective utilization of tactile skin: A review. IEEE Sens. J. 2013, 13, 4121–4138. [Google Scholar] [CrossRef]
- Rogers, J.; Someya, T.; Huang, Y. Materials and mechanics for stretchable electronics. Science 2010, 327, 1603–1607. [Google Scholar] [CrossRef]
- Cao, J.; Zhou, J.; Miao, C.; Yin, H.; Li, W.; Xia, F. Research progress and development strategy on tactile sensors for e-skin. J. Harbin Inst. Technol. 2017, 49, 1–13. [Google Scholar] [CrossRef]
- Morteza, V.; Erik, D.; Jae, W. Force and slip detection with direct-write compliant tactile sensor using multi-walled carbon nanotube/polymer composites. Sens. Actuators A Phys. 2013, 195, 90–97. [Google Scholar] [CrossRef]
- Morteza, V.; Erik, D.; Jae, W. Detection of the position, direction and speed of sliding contact with a multi-layer compliant tactile sensor fabricated using direct-print technology. Smart Mater. Struct. 2014, 23, 95008–95018. [Google Scholar] [CrossRef]
- Chen, M.; Lin, C.; Lai, Y.; Yang, Y. A polymer-based capacitive sensing array for normal and shear force measurement. Sensors 2010, 10, 10211–10225. [Google Scholar] [CrossRef]
- Aaron, P.; Hadrien, O.; Stephanie, P. Elastomeric electronic skin for prosthetic tactile sensation. Adv. Mater. 2015, 25, 2287–2295. [Google Scholar] [CrossRef]
- Song, A.; Han, Y.; Hu, H.; Li, J. A novel texture sensor for fabric texture measurement and classification. IEEE Trans. Instrum. Meas. 2014, 63, 1739–1747. [Google Scholar] [CrossRef]
- Saleem, K.; Sajina, T.; Leandro, L.; Ravinder, S. Flexible tactile sensors using screen-printed P(VDF-TrFE) and MWCNT/PDMS composites. IEEE Sens. J. 2015, 15, 3146–3155. [Google Scholar] [CrossRef]
- Ahmed, A.; Jurgen, K. Magnetic nanocomposite cilia tactile sensor. Adv. Mater. 2015, 27, 7888–7892. [Google Scholar] [CrossRef]
- Roozbeh, A.; Muthukumaran, P.; Javad, D.; Renzo, C. Discretely loaded beam-type optical fiber tactile sensor for tissue manipulation and palpation in minimally invasive robotic surgery. IEEE Sens. J. 2012, 12, 22–32. [Google Scholar] [CrossRef]
- Sung, H.; Sangyoon, J.; Seiho, C.; Kyoung, H.; Byeong, W.; Jihun, P.; Joohee, K.; Ju, Y.; Ki, S.; Soon, Y.; et al. Integrated arrays of air-dielectric graphene transistors as transparent active-matrix pressure sensors for wide pressure ranges. Nat. Commun. 2017, 8, 14950–14958. [Google Scholar] [CrossRef]
- Mohammad, A.; Saeed, S.; Javad, D.; Mojtaba, K. A micro-tactile sensor for in situ tissue characterization in minimally invasive surgery. Biomed. Microdevices 2008, 10, 823–837. [Google Scholar]
- Mohammad, A.; Saeed, S.; Javad, D.; Mojtaba, K. PVDF-based microfabricated tactile sensor for minimally invasive surgery. J. Microelectromec. Syst. 2009, 18, 195–207. [Google Scholar] [CrossRef]
- Dana, D.; Taylor, H.; Rolf, P.; Allison, M. Artificial tactile sensing of position and slip speed by exploiting geometrical features. IEEE/ASME Trans. Mechatron. 2015, 20, 263–274. [Google Scholar] [CrossRef]
- Pan, Z.; Cui, H.; Zhu, Z. Flexible full-body tactile sensor of low cost and minimal output connections for service robot. Ind. Robot 2005, 32, 485–491. [Google Scholar] [CrossRef]
- Wu, H.; Chen, J.; Su, Y.; Li, Z.; Ye, J. New tactile sensor for position detection based on distributed planar electric field. Sens. Actuators A Phys. 2016, 242, 146–161. [Google Scholar] [CrossRef]
- Vincent, D.; Nicolas, L.; Mathieu, B.; Marc, A.; Clement, G. A flexible robot skin for physical human robot interaction. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 12–17. [Google Scholar]
- Wu, H.; Wang, H.; Huang, J.; Zhang, Y.; Ye, J. A flexible annular sectorial sensor for detecting contact position based on constant electric field. Micromachines 2018, 9, 309. [Google Scholar] [CrossRef]
- Francesco, V.; Paolo, F.; Kenji, S. A deformable smart skin for continuous sensing based on electrical impedance tomography. Sensors 2016, 16, 1928. [Google Scholar] [CrossRef]
- Yang, Z.; Gierad, L.; Chris, H. Electrick: Low-cost touch sensing using electric field tomography. In Proceedings of the CHI Conference on Human Factors in Computing Systems, Denver, CO, USA, 6–11 May 2017; pp. 1–14. [Google Scholar]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Ye, J.; Wang, H.; Huang, S.; Wu, H. A Flexible Tactile Sensor with Irregular Planar Shape Based on Uniform Electric Field. Sensors 2018, 18, 4445. https://doi.org/10.3390/s18124445
Zhang Y, Ye J, Wang H, Huang S, Wu H. A Flexible Tactile Sensor with Irregular Planar Shape Based on Uniform Electric Field. Sensors. 2018; 18(12):4445. https://doi.org/10.3390/s18124445
Chicago/Turabian StyleZhang, Youzhi, Jinhua Ye, Haomiao Wang, Shuheng Huang, and Haibin Wu. 2018. "A Flexible Tactile Sensor with Irregular Planar Shape Based on Uniform Electric Field" Sensors 18, no. 12: 4445. https://doi.org/10.3390/s18124445
APA StyleZhang, Y., Ye, J., Wang, H., Huang, S., & Wu, H. (2018). A Flexible Tactile Sensor with Irregular Planar Shape Based on Uniform Electric Field. Sensors, 18(12), 4445. https://doi.org/10.3390/s18124445




