Security Cost Aware Data Communication in Low-Power IoT Sensors with Energy Harvesting
Abstract
1. Introduction
- We study the problem of energy utilization that resulted by data transmission in IoT devices that use capacitors to receive wireless energy. Different from existing studies, if the sensors use capacitors to receive wireless energy, the wireless energy receiving rate changes over time, and it gets slower and slower.
- If the IoT sensors do not have enough wireless energy receiving time, the minimum completion time problem, which transmits all the data, is studied. An online algorithm is provided and the competitive ratio is .
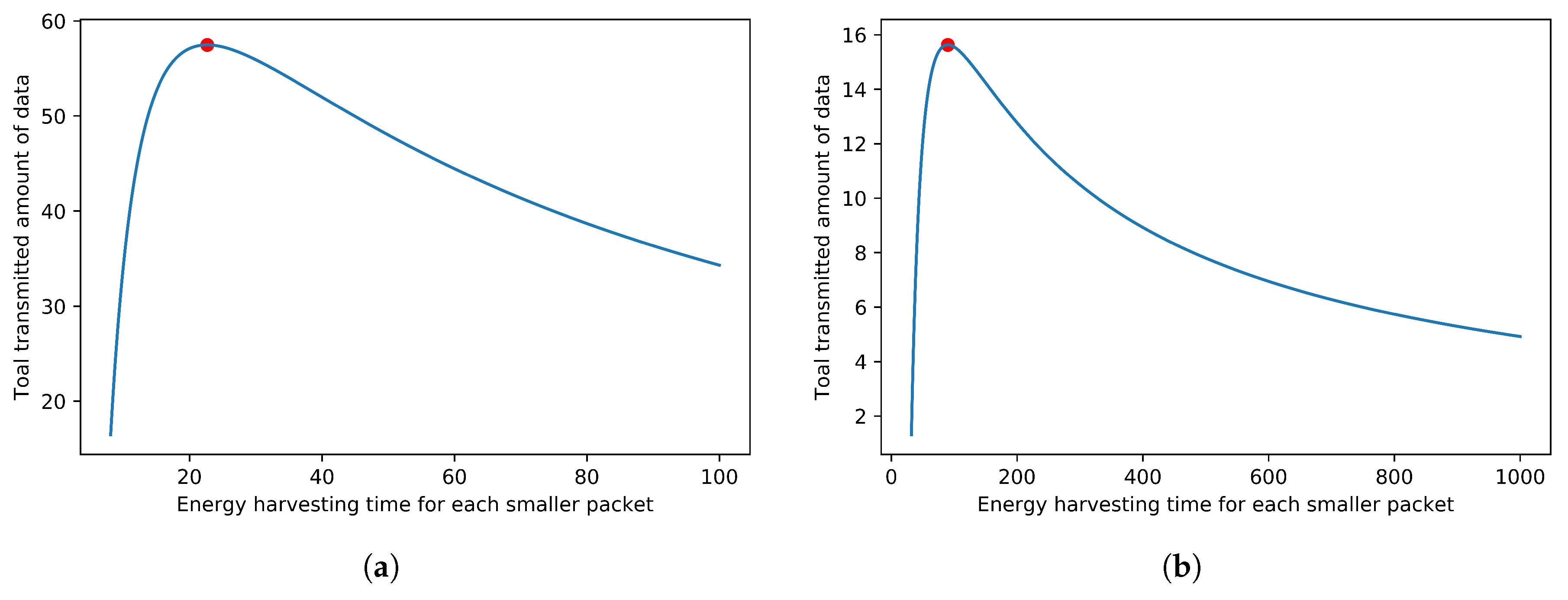
- If the IoT sensors have enough wireless energy receiving time, the problem of transmitting the max amount of data is studied. Two cases for this situation where there is only one energy receiving period and there are multiple energy receiving periods are studied. Two competitive ratio online algorithms for both of these two cases are provided in this paper.
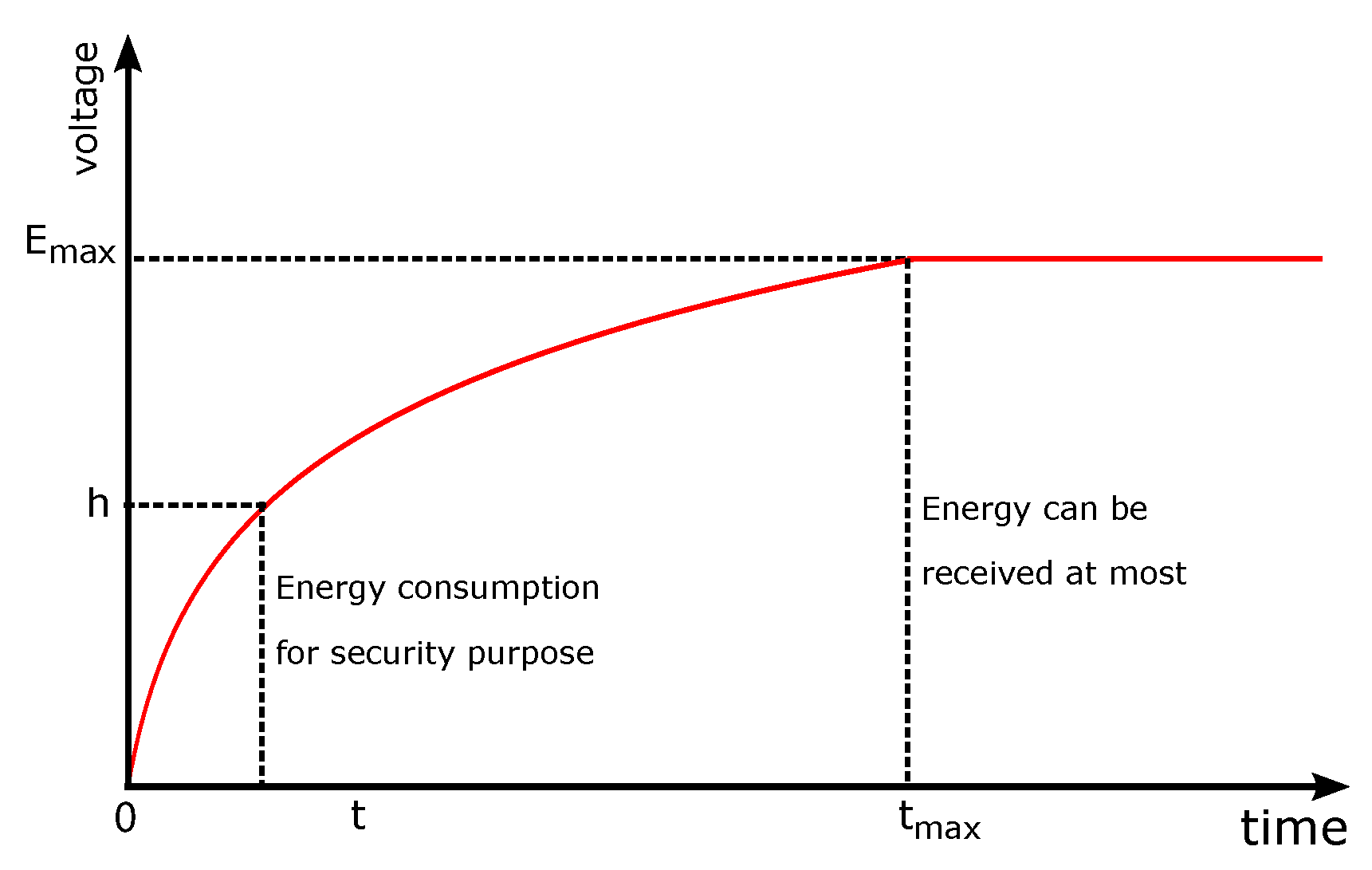
2. Preliminary and Problem Statement
3. The Sensor Can Receive Enough Wireless Energy
3.1. Only One Huge Block of Data
3.2. Data Arrives at Different Times
| Algorithm 1: Minimize the total completion time. |
| Input: One enough long wireless energy receiving period , and n data blocks , each denotes an online block of data with size arrives at time . Output: Find a solution to minimize the completion time of the data transmission.
|
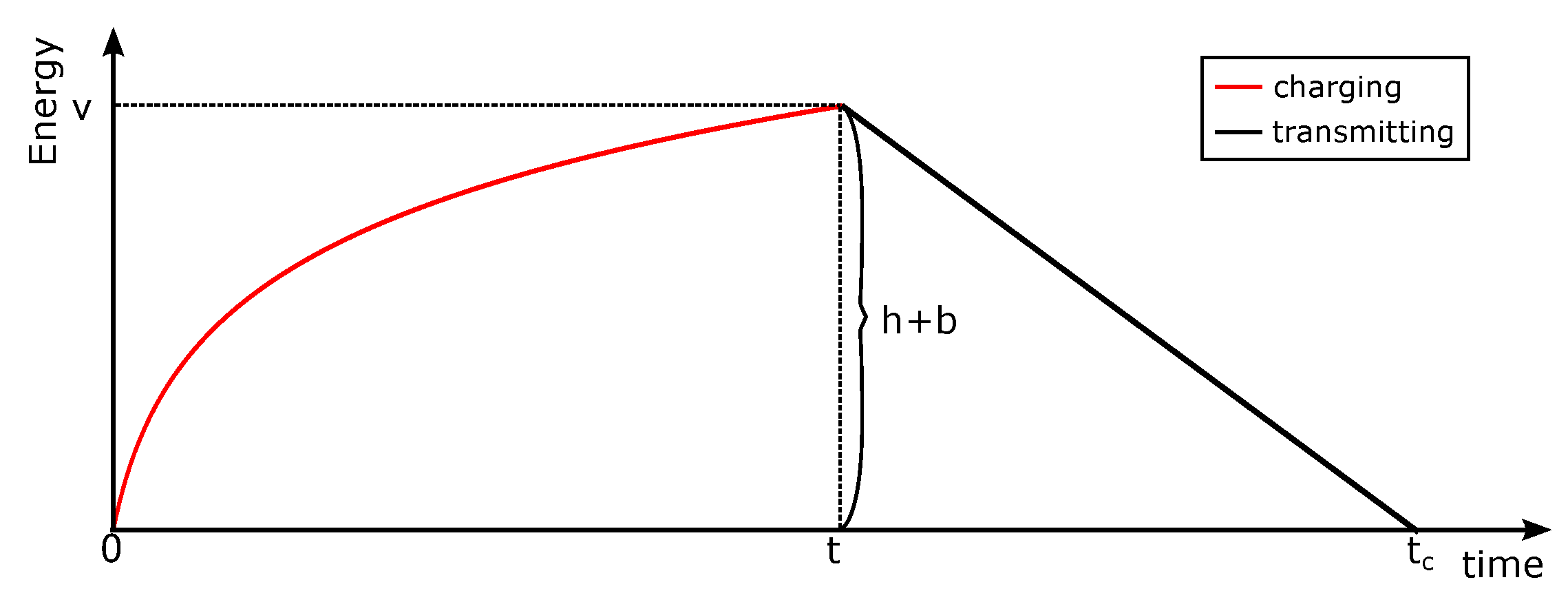
4. Not Enough Wireless Energy Receiving Time
4.1. Receiving Only One Period of Wireless Energy
4.1.1. Only One Block of Data with an Extremely Large Size
4.1.2. Multiple Data Blocks Arrivng at Different Times
| Algorithm 2: Transmission algorithm when data arrives over time. |
| Input: One wireless energy receiving period , and n data blocks , each denotes an online block of data with size arrives at time , . Output: Schedule the data transmission to maximize the amount of transmitted data.
——————————————————————————–
|
4.2. Receive Multiple Periods of Wireless Energy
| Algorithm 3: Transmission algorithm when data and energy receiving time arrive over time. |
| Input: m wireless energy receiving periods , and n blocks of data arriving over time, where represents the jth period of energy receiving period, and indicates an online block of data with size arrives at time . Output: Find a solution to maximize the amount of successfully transmitted data
——————————————————————————–
|
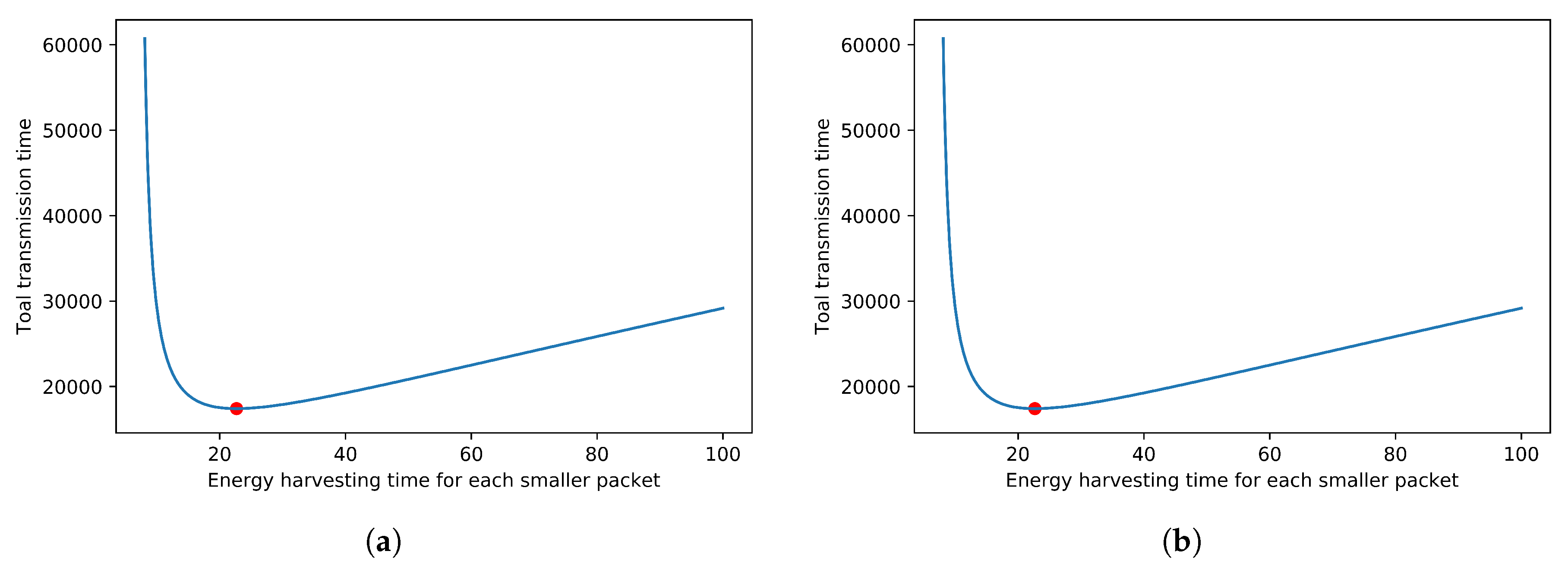
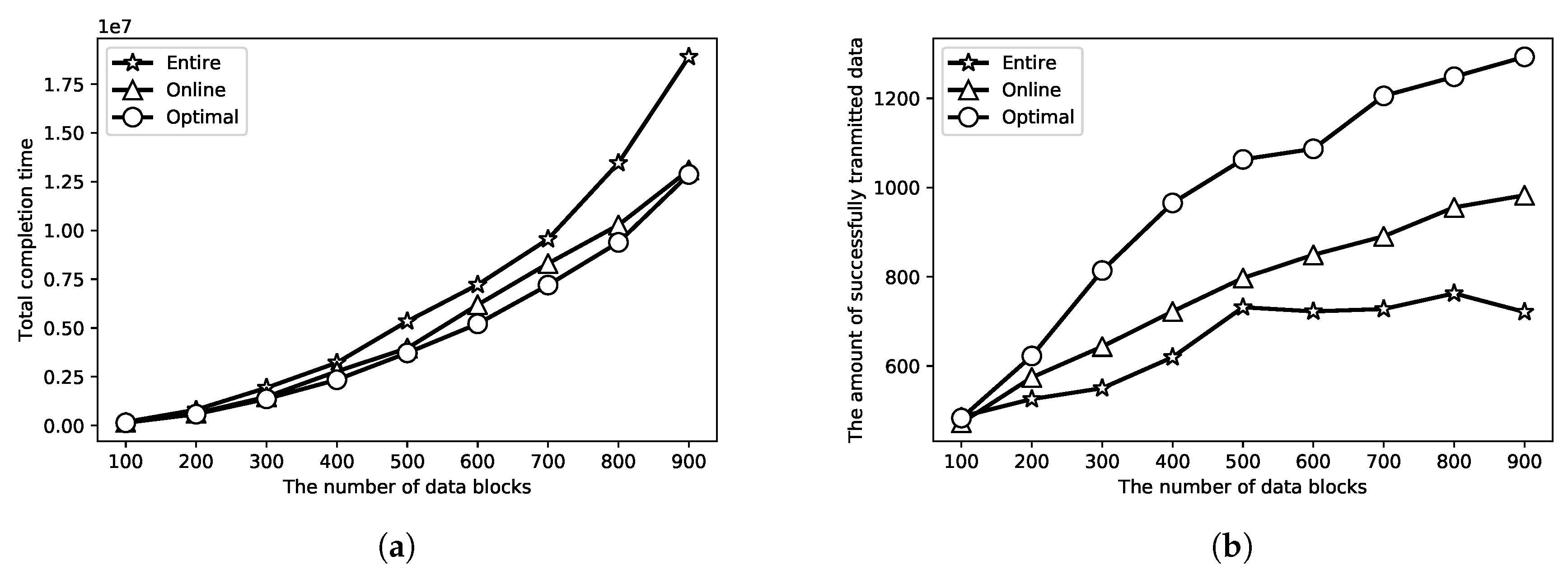
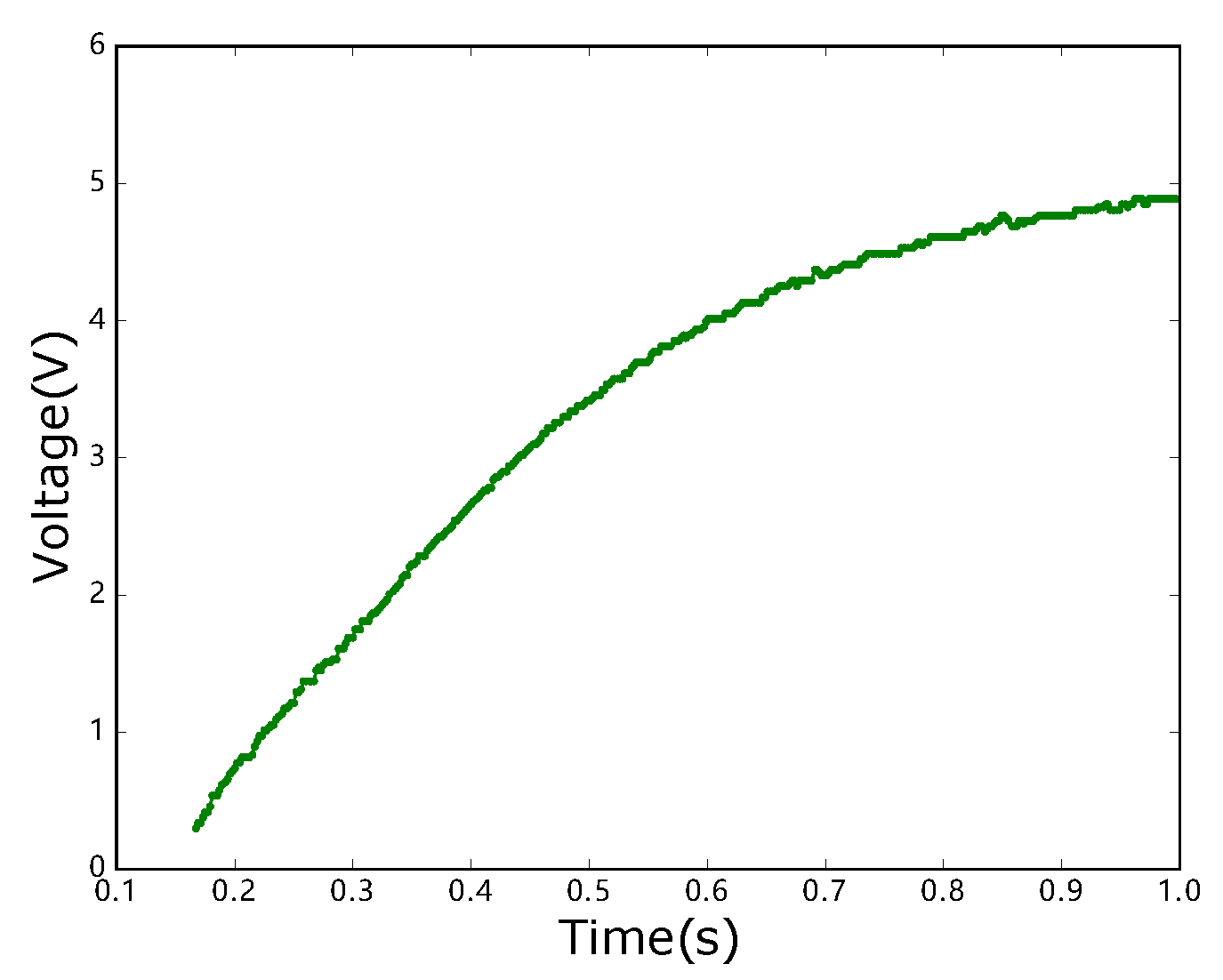
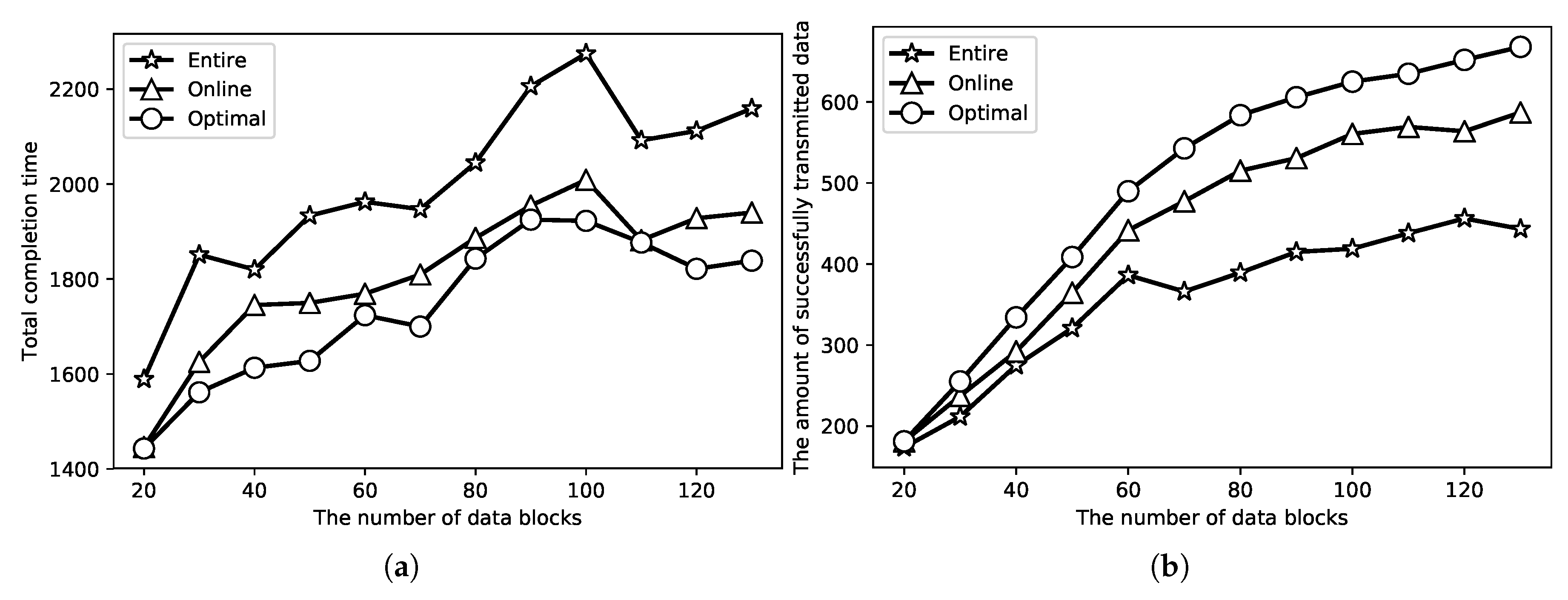
5. Evaluations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Castiglione, A.; Palmieri, F.; Fiore, U.; Castiglione, A.; Santis, A.D. Modeling energy-efficient secure communications in multi-mode wireless mobile devices. J. Comput. Syst. Sci. 2015, 81, 1464–1478. [Google Scholar] [CrossRef]
- Castiglione, A.; D’Arco, P.; Santis, A.D.; Russo, R. Secure group communication schemes for dynamic heterogeneous distributed computing. Future Gener. Comput. Syst. 2017, 74, 313–324. [Google Scholar] [CrossRef]
- Merlo, A.; Migliardi, M.; Caviglione, L. A survey on energy-aware security mechanisms. Pervasive Mobile Comput. 2015, 24, 77–90. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, G.; Liu, A.; Bhuiyan, M.Z.A.; Jin, Q. A Secure IoT Service Architecture with an Efficient Balance Dynamics Based on Cloud and Edge Computing. IEEE Internet Things J. 2018, in press. [Google Scholar] [CrossRef]
- Frustaci, M.; Pace, P.; Aloi, G.; Fortino, G. Evaluating Critical Security Issues of the IoT World: Present and Future Challenges. IEEE Internet Things J. 2018, 5, 2483–2495. [Google Scholar] [CrossRef]
- Siegel, J.E.; Kumar, S.; Sarma, S.E. The Future Internet of Things: Secure, Efficient, and Model-Based. IEEE Internet Things J. 2018, 5, 2386–2398. [Google Scholar] [CrossRef]
- Lin, J.; Yu, W.; Zhang, N.; Yang, X.; Zhang, H.; Zhao, W. A Survey on Internet of Things: Architecture, Enabling Technologies, Security and Privacy, and Applications. IEEE Internet Things J. 2017, 4, 1125–1142. [Google Scholar] [CrossRef]
- Dai, H.; Liu, Y.; Chen, G.; Wu, X.; He, T.; Liu, A.X.; Ma, H. Safe Charging for Wireless Power Transfer. IEEE/ACM Trans. Netw. 2017, 25, 3531–3544. [Google Scholar] [CrossRef]
- Teo, A.; Mishra, A.; Park, I.; Kim, Y.J.; Park, W.T.; Yong, J.Y. Polymeric Biomaterials for Medical Implants & Devices. Acs Biomater. Sci. Eng. 2016, 2, 454–472. [Google Scholar]
- Katic, J. Efficient Energy Harvesting Interface for Implantable Biosensors; KTH Royal Institute of Technology: Stockholm, Sweden, 2015. [Google Scholar]
- Olivo, J.; Carrara, S.; De Micheli, G. Energy Harvesting and Remote Powering for Implantable Biosensors. Sens. J. IEEE 2011, 11, 1573–1586. [Google Scholar] [CrossRef]
- Tran, H.V.; Kaddoum, G. RF Wireless Power Transfer: Regreening Future Networks. IEEE Potentials 2018, 37, 35–41. [Google Scholar] [CrossRef]
- Tran, H.; Kaddoum, G.; Truong, K.T. Resource Allocation in SWIPT Networks Under a Nonlinear Energy Harvesting Model: Power Efficiency, User Fairness, and Channel Nonreciprocity. IEEE Trans. Veh. Technol. 2018, 67, 8466–8480. [Google Scholar] [CrossRef]
- Ercan, A.O.; Sunay, O.; Akyildiz, I.F.; Ercan, A.O.; Sunay, O.; Akyildiz, I.F. RF Energy Harvesting and Transfer for Spectrum Sharing Cellular IoT Communications in 5G Systems. IEEE Trans. Mobile Comput. 2017, 17, 1680–1694. [Google Scholar] [CrossRef]
- Yu, H.; Neely, M.J. Learning Aided Optimization for Energy Harvesting Devices with Outdated State Information. In Proceedings of the IEEE International Conference on Computer Communications, Honolulu, HI, USA, 15–19 April 2018. [Google Scholar]
- Huang, L.; Neely, M.J. Utility Optimal Scheduling in Energy Harvesting Networks. IEEE/ACM Trans. Netw. 2013, 21, 1117–1130. [Google Scholar] [CrossRef]
- Le, T.D.; Kaddoum, G.; Shin, O.S. Joint Channel Resources Allocation and Beamforming in Energy Harvesting Systems. IEEE Wirel. Commun. Lett. 2018, 7, 884–887. [Google Scholar] [CrossRef]
- Arslan, S.; Shah, S.A.A.; Lee, J.J.; Kim, H.W. An Energy Efficient Charging Technique for Switched Capacitor Voltage Converters with Low Duty-Ratio. IEEE Trans. Circuits Syst. II Express Briefs 2017, 65, 779–783. [Google Scholar] [CrossRef]
- Xia, S.; Chen, L. Theoretical and experimental investigation of optimal capacitor charging process in RC circuit. Eur. Phys. J. Plus 2017, 132, 235. [Google Scholar] [CrossRef]
- Pardo, D.; Vaz, A.; Gil, S.; Gomez, J.; Ubarretxena, A.; Puente, D.; Morales-Ramos, R.; Garcia-Alonso, A.; Berenguer, R. Design Criteria for Full Passive Long Range UHF RFID Sensor for Human Body Temperature Monitoring. In Proceedings of the 2007 IEEE International Conference on RFID, Grapevine, TX, USA, 26–28 March 2007; pp. 141–148. [Google Scholar] [CrossRef]
- Cheng, S.; Cai, Z.; Li, J.; Fang, X. Drawing dominant dataset from big sensory data in wireless sensor networks. In Proceedings of the 2015 IEEE Conference on Computer Communications (INFOCOM), Kowloon, Hong Kong, 26 April–1 May 2015; pp. 531–539. [Google Scholar] [CrossRef]
- Ou, J.; Li, M.; Zheng, Y. Come and Be Served: Parallel Decoding for COTS RFID Tags. IEEE/ACM Trans. Netw. 2017, 25, 1569–1581. [Google Scholar] [CrossRef]
- Cheng, S.; Cai, Z.; Li, J.; Gao, H. Extracting Kernel Dataset from Big Sensory Data in Wireless Sensor Networks. IEEE Trans. Knowl. Data Eng. 2017, 29, 813–827. [Google Scholar] [CrossRef]
- Buettner, M.; Prasad, R.; Philipose, M.; Wetherall, D. Recognizing Daily Activities with RFID-based Sensors. In Proceedings of the 11th International Conference on Ubiquitous Computing, Orlando, FL, USA, 30 September–3 October 2009; ACM: New York, NY, USA, 2009; pp. 51–60. [Google Scholar] [CrossRef]
- Sample, A.P.; Yeager, D.J.; Powledge, P.S.; Mamishev, A.V.; Smith, J.R. Design of an RFID-Based Battery-Free Programmable Sensing Platform. IEEE Trans. Instrum. Measur. 2008, 57, 2608–2615. [Google Scholar] [CrossRef]
- Lundén, M.; Dunkels, A. The politecast communication primitive for low-power wireless. Acm Sigcomm Comput. Commun. Rev. 2016, 41, 31–37. [Google Scholar] [CrossRef]
- Dai, H.; Ma, H.; Liu, A.X. Radiation Constrained Scheduling of Wireless Charging Tasks. In Proceedings of the ACM International Symposium on Mobile Ad Hoc NETWORKING and Computing (Mobihoc), Chennai, India, 10–14 July 2017; p. 17. [Google Scholar]
- Pagán, J.; Zapater, M.; Ayala, J.L. Power transmission and workload balancing policies in eHealth mobile cloud computing scenarios. Future Gener. Comput. Syst. 2018, 78, 587–601. [Google Scholar] [CrossRef]
- Usman, M.; Ahmed, I.; Aslam, M.I.; Khan, S.; Shah, U.A. SIT: A Lightweight Encryption Algorithm for Secure Internet of Things. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 1–10. [Google Scholar] [CrossRef]
- Yao, X.; Chen, Z.; Tian, Y. A lightweight attribute-based encryption scheme for the Internet of Things. Future Gener. Comput. Syst. 2015, 49, 104–112. [Google Scholar] [CrossRef]
- Oualha, N.; Nguyen, K.T. Lightweight Attribute-Based Encryption for the Internet of Things. In Proceedings of the International Conference on Computer Communication and Networks, Waikoloa, HI, USA, 1–4 August 2016; pp. 1–6. [Google Scholar]
- Singh, J.; Pasquier, T.; Bacon, J.; Ko, H.; Eyers, D. Twenty Security Considerations for Cloud-Supported Internet of Things. IEEE Internet Things J. 2016, 3, 269–284. [Google Scholar] [CrossRef]
- Fang, X.; Luo, J.; Luo, G.; Wu, W.; Cai, Z.; Pan, Y. Big Data Transmission in Industrial IoT Systems with Small Capacitor Supplying Energy. IEEE Trans. Ind. Inf. 2018, in press. [Google Scholar] [CrossRef]
- Mashkani, O.; Moslehi, G. Minimising the total completion time in a single machine scheduling problem under bimodal flexible periodic availability constraints. Int. J. Comput. Integr. Manuf. 2016, 29, 323–341. [Google Scholar] [CrossRef]
- Beldar, P.; Costa, A. Single machine batch processing problem with release dates to minimize total completion time. Int. J. Ind. Eng. Comput. 2018, 9, 331–348. [Google Scholar] [CrossRef]
- Buettner, M.; Greenstein, B.; Wetherall, D. Dewdrop: An Energy-aware Runtime for Computational RFID. In Proceedings of the 8th USENIX Conference on Networked Systems Design and Implementation, Boston, MA, USA, 30 March–1 April 2011; USENIX Association: Berkeley, CA, USA, 2011; pp. 197–210. [Google Scholar]



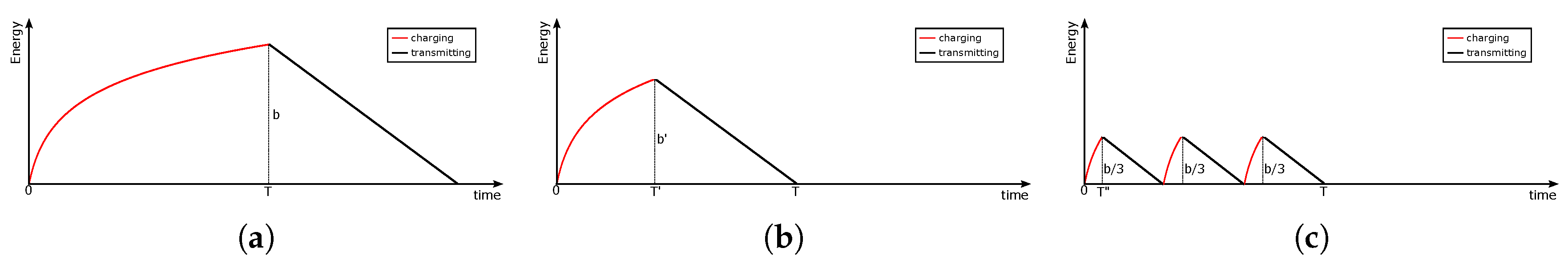
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Yang, M.; Wu, W. Security Cost Aware Data Communication in Low-Power IoT Sensors with Energy Harvesting. Sensors 2018, 18, 4400. https://doi.org/10.3390/s18124400
Fang X, Yang M, Wu W. Security Cost Aware Data Communication in Low-Power IoT Sensors with Energy Harvesting. Sensors. 2018; 18(12):4400. https://doi.org/10.3390/s18124400
Chicago/Turabian StyleFang, Xiaolin, Ming Yang, and Wenjia Wu. 2018. "Security Cost Aware Data Communication in Low-Power IoT Sensors with Energy Harvesting" Sensors 18, no. 12: 4400. https://doi.org/10.3390/s18124400
APA StyleFang, X., Yang, M., & Wu, W. (2018). Security Cost Aware Data Communication in Low-Power IoT Sensors with Energy Harvesting. Sensors, 18(12), 4400. https://doi.org/10.3390/s18124400



