Construction of an Omnidirectional Parametric Loudspeaker Consisting in a Spherical Distribution of Ultrasound Transducers
Abstract
1. Introduction
2. Foundations of the Parametric Acoustic Array
3. Construction of an Omnidirectional Parametric Loudspeaker
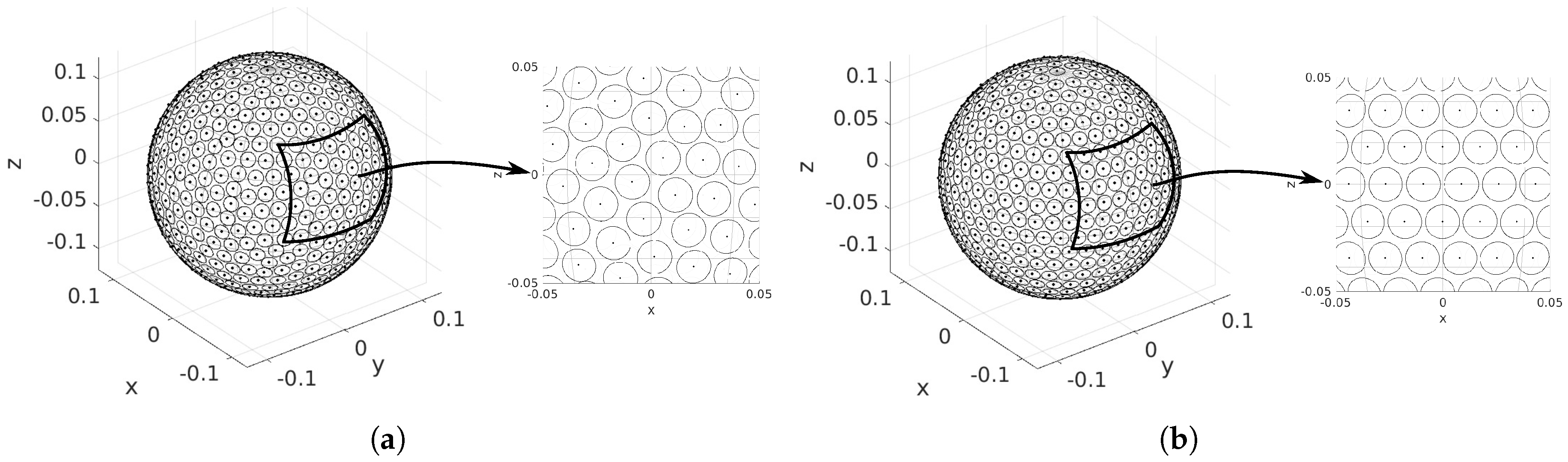
3.1. Design
3.2. Spherical Casing
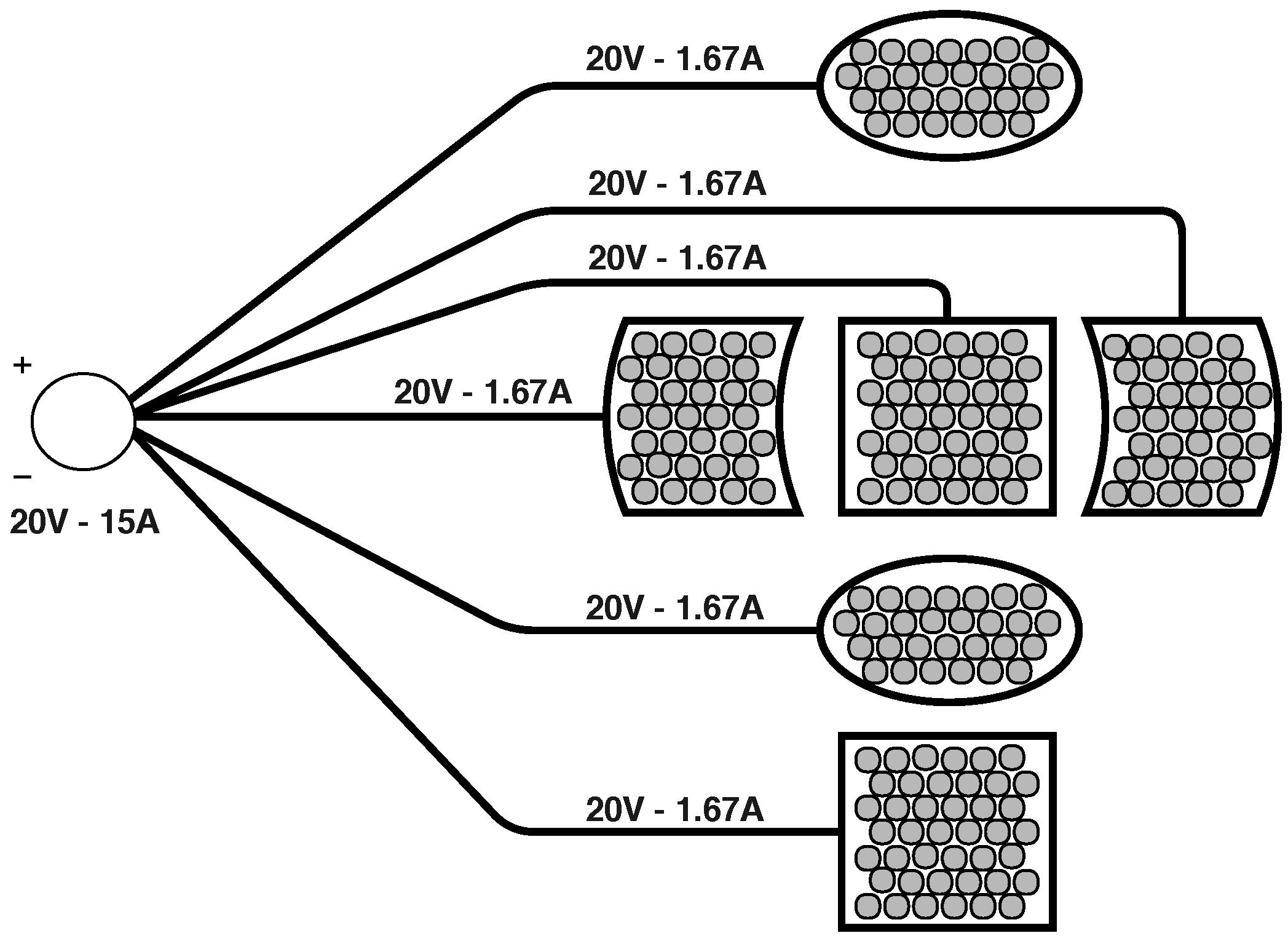
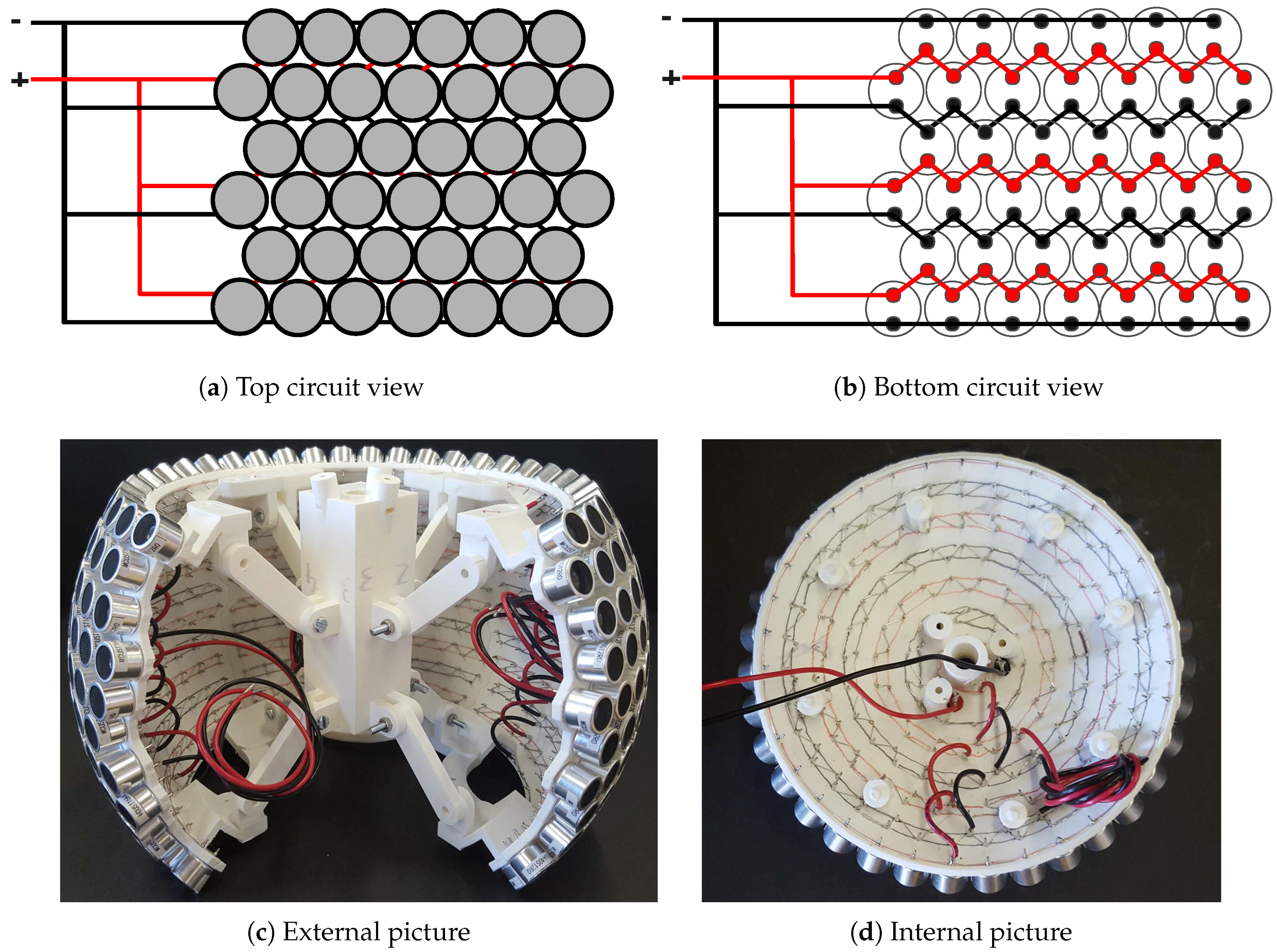
3.3. Circuitry
4. Experimental Testing in an Anechoic Chamber
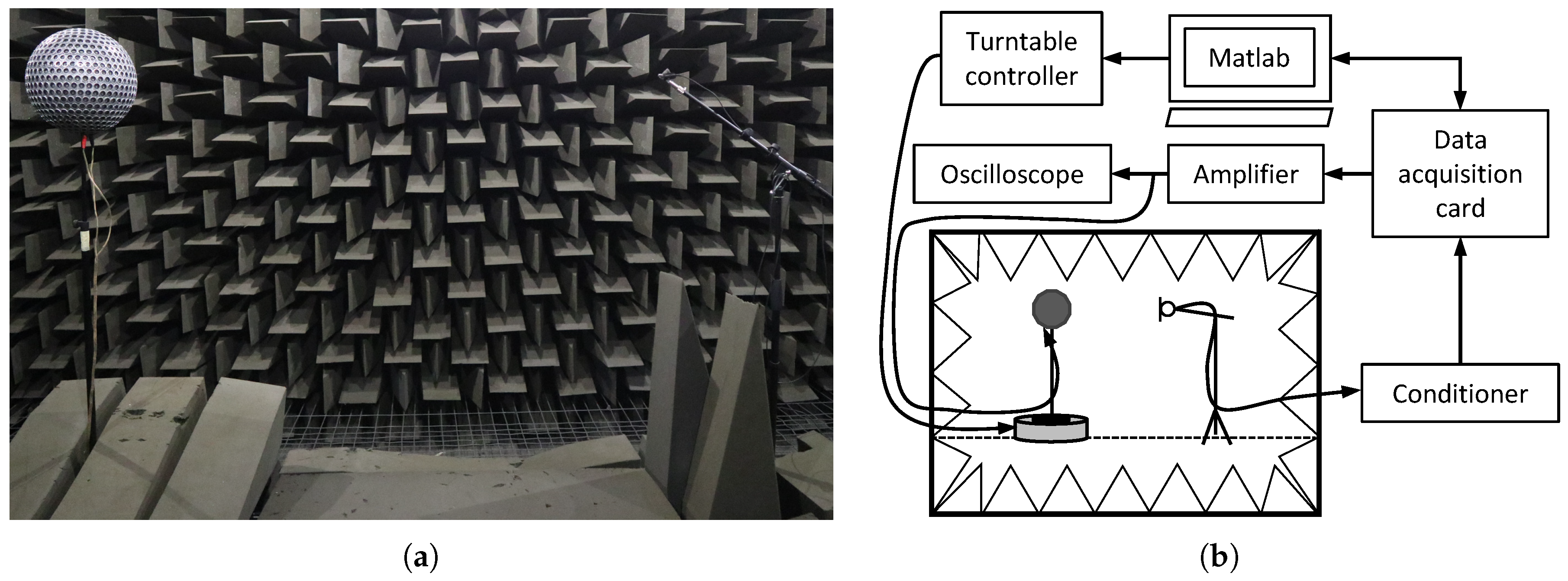
4.1. Experimental Setup
4.2. Results
5. Conclusions
6. Patents
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| DI | Directivity Index |
| OPL | Omnidirectional Parametric Loudspeaker |
| PAA | Parametric Acoustic Array |
| PZT | Piezoelectric Transducer |
| RPL | Regular Polyhedron Loudspeaker |
| SPL | Sound Pressure Level |
| USBAM | Upper Side Band Amplitude Modulation |
References
- ISO 3382-2:2008. Acoustics—Measurement of Room Acoustic Parameters—Part 2: Reverberation Time in Ordinary Rooms; International Organization for Standardization: Geneva, Switzerland, 2008. [Google Scholar]
- ISO 16283-1:2014. Acoustics—Field Measurement of Sound Insulation in Buildings and of Building Elements—Part 1: Airborne Sound Insulation; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- ISO 354:2003. Acoustics—Measurement of Sound Absorption in a Reverberation Room; International Organization for Standardization: Geneva, Switzerland, 2003. [Google Scholar]
- Leishman, T.W.; Rollins, S.; Smith, H.M. An experimental evaluation of regular polyhedron loudspeakers as omnidirectional sources of sound. J. Acoust. Soc. Am. 2006, 120, 1411–1422. [Google Scholar] [CrossRef]
- Quested, C.; Moorhouse, A.; Piper, B.; Hu, B. An analytical model for a dodecahedron loudspeaker applied to the design of omni-directional loudspeaker arrays. Appl. Acoust. 2014, 85, 161–171. [Google Scholar] [CrossRef]
- San Martín, R.; Arana, M.; Machín, J.; Arregui, A. Impulse source versus dodecahedral loudspeaker for measuring parameters derived from the impulse response in room acoustics. J. Acoust. Soc. Am. 2013, 134, 275–284. [Google Scholar] [CrossRef] [PubMed]
- ISO 3382-12:2009. Acoustics—Measurement of Room Acoustic Parameters—Part 1: Performance Spaces; International Organization for Standardization: Geneva, Switzerland, 2009. [Google Scholar]
- Knüttel, T.; Witew, I.B.; Vorländer, M. Influence of “omnidirectional” loudspeaker directivity on measured room impulse responses. J. Acoust. Soc. Am. 2013, 134, 3654–3662. [Google Scholar] [CrossRef] [PubMed]
- Martellotta, F. Optimizing stepwise rotation of dodecahedron sound source to improve the accuracy of room acoustic measures. J. Acoust. Soc. Am. 2013, 134, 2037–2048. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, N.; Stavroulakis, G. Low Cost Omnidirectional Sound Source Utilizing a Common Directional Loudspeaker for Impulse Response Measurements. Appl. Sci. 2018, 8, 1703. [Google Scholar] [CrossRef]
- Gómez Bolaños, J.; Pulkki, V.; Karppinen, P.; Hæggström, E. An optoacoustic point source for acoustic scale model measurements. J. Acoust. Soc. Am. 2013, 133, EL221–EL227. [Google Scholar] [CrossRef] [PubMed]
- Shibayama, H.; Fukunaga, K.; Kido, K. Directional characteristics of pulse sound source with spark discharge. J. Acoust. Soc. Jpn. E 1985, 6, 73–77. [Google Scholar] [CrossRef]
- Arana, M.; Vela, A.; San Martin, L. Calculating the impulse response in rooms using pseudo-impulsive acoustic sources. Acta Acust. United Acust. 2003, 89, 377–380. [Google Scholar]
- Sugimoto, T.; Ando, A.; Ono, K.; Morita, Y.; Hosoda, K.; Ishii, D.; Nakamura, K. A lightweight push-pull acoustic transducer composed of a pair of dielectric elastomer films. J. Acoust. Soc. Am. 2013, 134, EL432–EL437. [Google Scholar] [CrossRef]
- Hosoya, N.; Baba, S.; Maeda, S. Hemispherical breathing mode speaker using a dielectric elastomer actuator. J. Acoust. Soc. Am. 2015, 138, EL424–EL428. [Google Scholar] [CrossRef] [PubMed]
- Sugimoto, T.; Ono, K.; Ando, A.; Morita, Y.; Hosoda, K.; Ishii, D. Semicylindrical acoustic transducer from a dielectric elastomer film with compliant electrodes. J. Acoust. Soc. Am. 2011, 130, 744–752. [Google Scholar] [CrossRef] [PubMed]
- Polack, J.D.; Christensen, L.S.; Juhl, P.M. An innovative design for omnidirectional sound sources. Acta Acust. United Acust. 2001, 87, 505–512. [Google Scholar]
- Westervelt, P.J. Parametric Acoustic Arrays. J. Acoust. Soc. Am. 1963, 35, 535–537. [Google Scholar] [CrossRef]
- Hamilton, M.F. Sound beams. In Nonlinear Acoustics: Theory and Applications; Academic Press Inc.: Cambridge, MA, USA, 1997; pp. 233–261. [Google Scholar]
- Gan, W.; Yang, J.; Kamakura, T. A review of parametric acoustic array in air. Appl. Acoust. 2012, 73, 1211–1219. [Google Scholar] [CrossRef]
- Sayin, U.; Guasch, O. Directivity control and efficiency of parametric loudspeakers with horns. J. Acoust. Soc. Am. 2013, 134, EL153–EL157. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Lai, S.; Yan, J.; Li, C. Highly directional acoustic waves generated by a horned parametric acoustic array loudspeaker. J. Vib. Acoust. 2019, 141, 011012. [Google Scholar] [CrossRef]
- Tanaka, N.; Tanaka, M. Mathematically trivial control of sound using a parametric beam focusing source. J. Acoust. Soc. Am. 2011, 129, 165–172. [Google Scholar] [CrossRef]
- Tanaka, N.; Tanaka, M. Active noise control using a steerable parametric array loudspeaker. J. Acoust. Soc. Am. 2010, 127, 3526–3537. [Google Scholar] [CrossRef]
- Sayin, U.; Artís, P.; Guasch, O. Realization of an omnidirectional source of sound using parametric loudspeakers. J. Acoust. Soc. Am. 2013, 134, 1899–1907. [Google Scholar] [CrossRef]
- Guasch, O.; Sánchez-Martín, P. Far-field directivity of parametric loudspeaker arrays set on curved surfaces. Appl. Math. Model. 2018, 60, 721–738. [Google Scholar] [CrossRef]
- Arnela, M.; Sánchez-Martín, P.; Hervás, M.; Camps, J.; Guasch, O.; Martínez-Suquía, C.; Alsina-Pagès, R.M. Construction and characterization of an omnidirectional parametric loudspeaker consisting of ultrasound transducers set on a sphere. In Proceedings of the Noise and Vibration: Emerging Methods (NOVEM2018), Balearic Islands, Spain, 7–9 May 2018. [Google Scholar]
- Cervenka, M.; Bednarik, M. Non-paraxial model for a parametric acoustic array. J. Acoust. Soc. Am. 2013, 134, 933–938. [Google Scholar] [CrossRef] [PubMed]
- Yoneyama, M.; Kawamo, Y.; Fujimoto, J.; Sasabe, S. The audio spotlight: An application of nonlinear interaction of sound waves to a new type of loudspeaker design. J. Acoust. Soc. Am. 1983, 73, 1532–1536. [Google Scholar] [CrossRef]
- Pompei, F.J. The Use of Airborne Ultrasonics for Generating Audible Sound Beams. J. Audio Eng. Soc. 1999, 47, 726. [Google Scholar]
- Berktay, H.O.; Leahy, D.J. Far-field performance of parametric transmitters. J. Acoust. Soc. Am. 1974, 55, 539. [Google Scholar] [CrossRef]
- Shi, C.; Gan, W. Product directivity models for parametric loudspeakers. J. Acoust. Soc. Am. 2012, 131, 1938–1945. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.; Kajikawa, Y. A convolution model for computing the far-field directivity of a parametric loudspeaker array. J. Acoust. Soc. Am. 2015, 137, 777–784. [Google Scholar] [CrossRef]
- Multicomp. MCUST16A40S12RO Ultrasonic Sensor, Datasheet. Available online: http://www.farnell.com/datasheets/1759979.pdf?_ga=2.151429437.506299326.1540473700-312362127.1525941708 (accessed on 6 November 2018).
- Saff, E.B.; Kuijlaars, A.B. Distributing many points on a sphere. Math. Intell. 1997, 19, 5–11. [Google Scholar] [CrossRef]
- Katanforoush, A.; Shahshahani, M. Distributing points on the sphere, I. Exp. Math. 2003, 12, 199–209. [Google Scholar] [CrossRef]
- Persson, P.; Strang, G. A simple mesh generator in MATLAB. SIAM Rev. 2004, 46, 329–345. [Google Scholar] [CrossRef]
- pro POWER. Soft Tinned Copper Wire, Datasheet. Available online: http://www.farnell.com/datasheets/2363855.pdf?_ga=2.112218690.755014876.1531728225-398181845.1531728225 (accessed on 6 November 2018).
- International Electrotechnical Commission. International Standard: Low-Voltage Electrical Installations; IEC 60364-5-52; IEC: Geneva, Switzerland, 2012. [Google Scholar]
- Pro POWER. BS4808 1 mm2 (32/0.2 mm) PVC Equipment Wire, Datasheet. Available online: http://www.farnell.com/datasheets/1850522.pdf?_ga=2.112218690.755014876.1531728225-398181845.1531728225 (accessed on 6 November 2018).
- Farina, A. Simultaneous Measurement of Impulse Response and Distortion with a Swept-Sine Technique. In Proceedings of the 108th Audio Engineering Society Convention, Paris, France, 19–22 February 2000. [Google Scholar]
- ISO 3745:2012. Acoustics—Determination of Sound Power Levels and Sound Energy Levels of Noise Sources Using Sound Pressure—Precision Methods For Anechoic Rooms and Hemi-Anechoic Rooms; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]



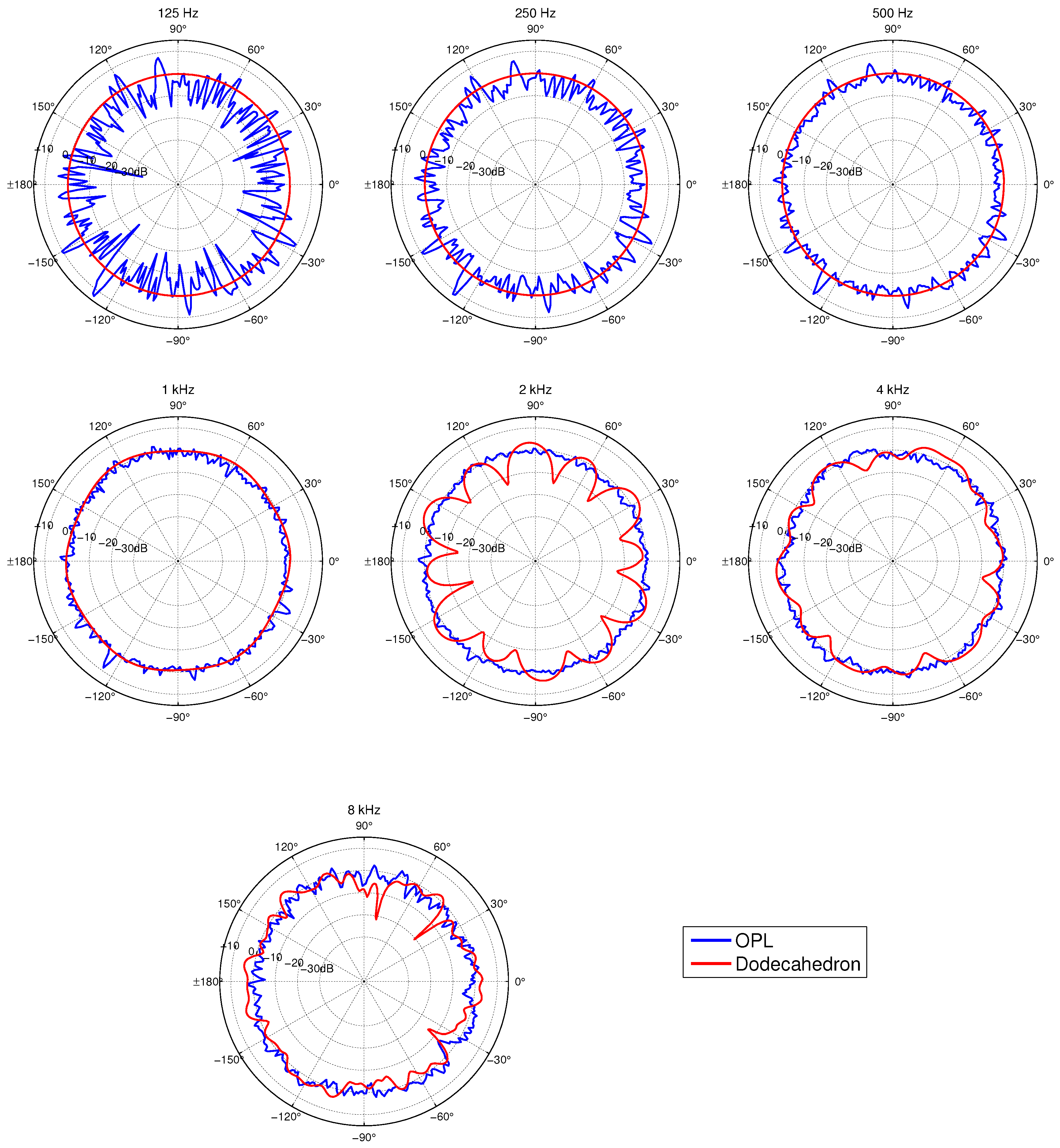
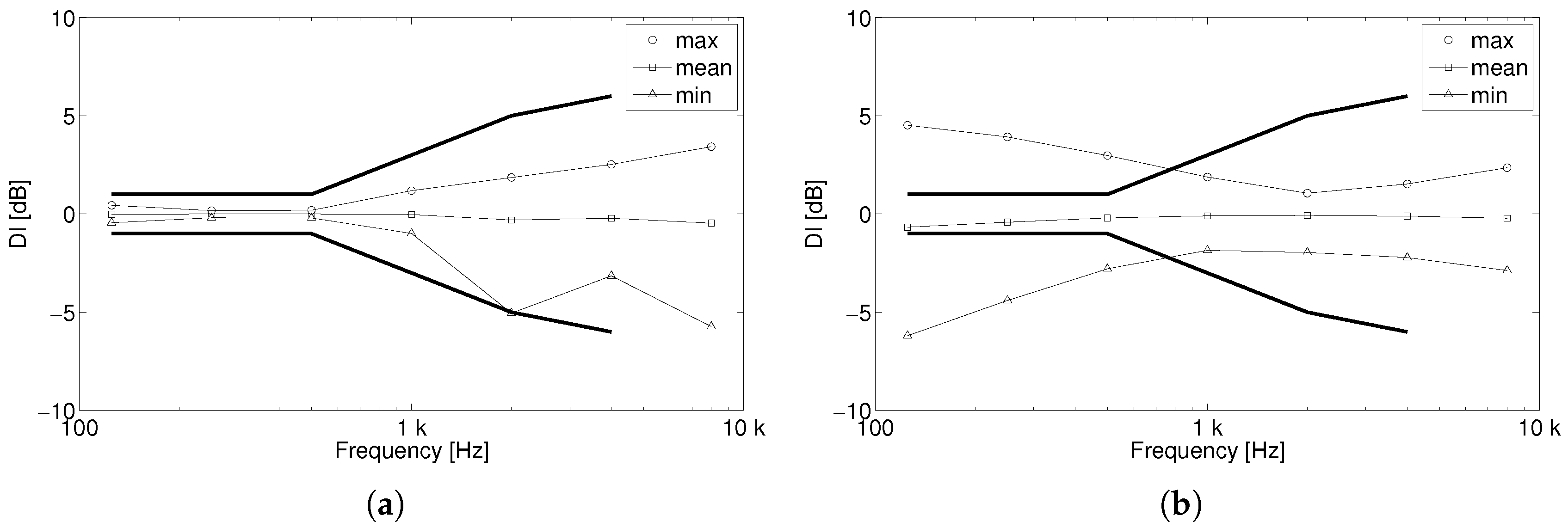
| Sound Source | Levels | 125 Hz | 250 Hz | 500 Hz | 1 kHz | 2 kHz | 4 kHz | 8 kHz |
|---|---|---|---|---|---|---|---|---|
| OPL | Q2 | 43.6 | 48.2 | 51.9 | 56.6 | 58.6 | 52.7 | 45.6 |
| Q1-Q2 | −5.2 | −3.4 | −1.3 | −0.9 | −0.8 | −1.2 | −1.8 | |
| Q3-Q2 | 4 | 2.5 | 2 | 1.2 | 0.8 | 0.9 | 1.7 | |
| Min-Q2 | −29.5 | −8 | −5.1 | −5.5 | −3.5 | −4.7 | −7.8 | |
| Max-Q2 | 17 | 14.2 | 12.5 | 9.4 | 4.2 | 4.4 | 5.6 | |
| 47.6 | 50.6 | 53.4 | 57.3 | 58.7 | 52.9 | 46.1 | ||
| 62.1 | 65.1 | 67.9 | 71.8 | 73.3 | 67.4 | 60.6 | ||
| Dodechaedron | Q2 | 94.9 | 100.5 | 94.8 | 90.1 | 88.1 | 83.8 | 77.1 |
| Q1-Q2 | −0.3 | −0.1 | −0.1 | −0.6 | −3.9 | −1.7 | −1.8 | |
| Q3-Q2 | 0.3 | 0.1 | 0.1 | 0.5 | 3.4 | 2 | 2.6 | |
| Min-Q2 | −0.5 | −0.2 | −0.2 | −1.3 | −19 | −8.3 | −20.4 | |
| Max-Q2 | 0.5 | 0.2 | 0.2 | 1.5 | 5.6 | 3.8 | 5.9 | |
| 97.2 | 103.2 | 98 | 94.2 | 93.7 | 88.3 | 83.9 | ||
| 111.7 | 117.7 | 112.5 | 108.7 | 108.2 | 102.8 | 98.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arnela, M.; Guasch, O.; Sánchez-Martín, P.; Camps, J.; Alsina-Pagès, R.M.; Martínez-Suquía, C. Construction of an Omnidirectional Parametric Loudspeaker Consisting in a Spherical Distribution of Ultrasound Transducers. Sensors 2018, 18, 4317. https://doi.org/10.3390/s18124317
Arnela M, Guasch O, Sánchez-Martín P, Camps J, Alsina-Pagès RM, Martínez-Suquía C. Construction of an Omnidirectional Parametric Loudspeaker Consisting in a Spherical Distribution of Ultrasound Transducers. Sensors. 2018; 18(12):4317. https://doi.org/10.3390/s18124317
Chicago/Turabian StyleArnela, Marc, Oriol Guasch, Patricia Sánchez-Martín, Joan Camps, Rosa Ma Alsina-Pagès, and Carme Martínez-Suquía. 2018. "Construction of an Omnidirectional Parametric Loudspeaker Consisting in a Spherical Distribution of Ultrasound Transducers" Sensors 18, no. 12: 4317. https://doi.org/10.3390/s18124317
APA StyleArnela, M., Guasch, O., Sánchez-Martín, P., Camps, J., Alsina-Pagès, R. M., & Martínez-Suquía, C. (2018). Construction of an Omnidirectional Parametric Loudspeaker Consisting in a Spherical Distribution of Ultrasound Transducers. Sensors, 18(12), 4317. https://doi.org/10.3390/s18124317







