Online Prediction of Ship Behavior with Automatic Identification System Sensor Data Using Bidirectional Long Short-Term Memory Recurrent Neural Network
Abstract
1. Introduction
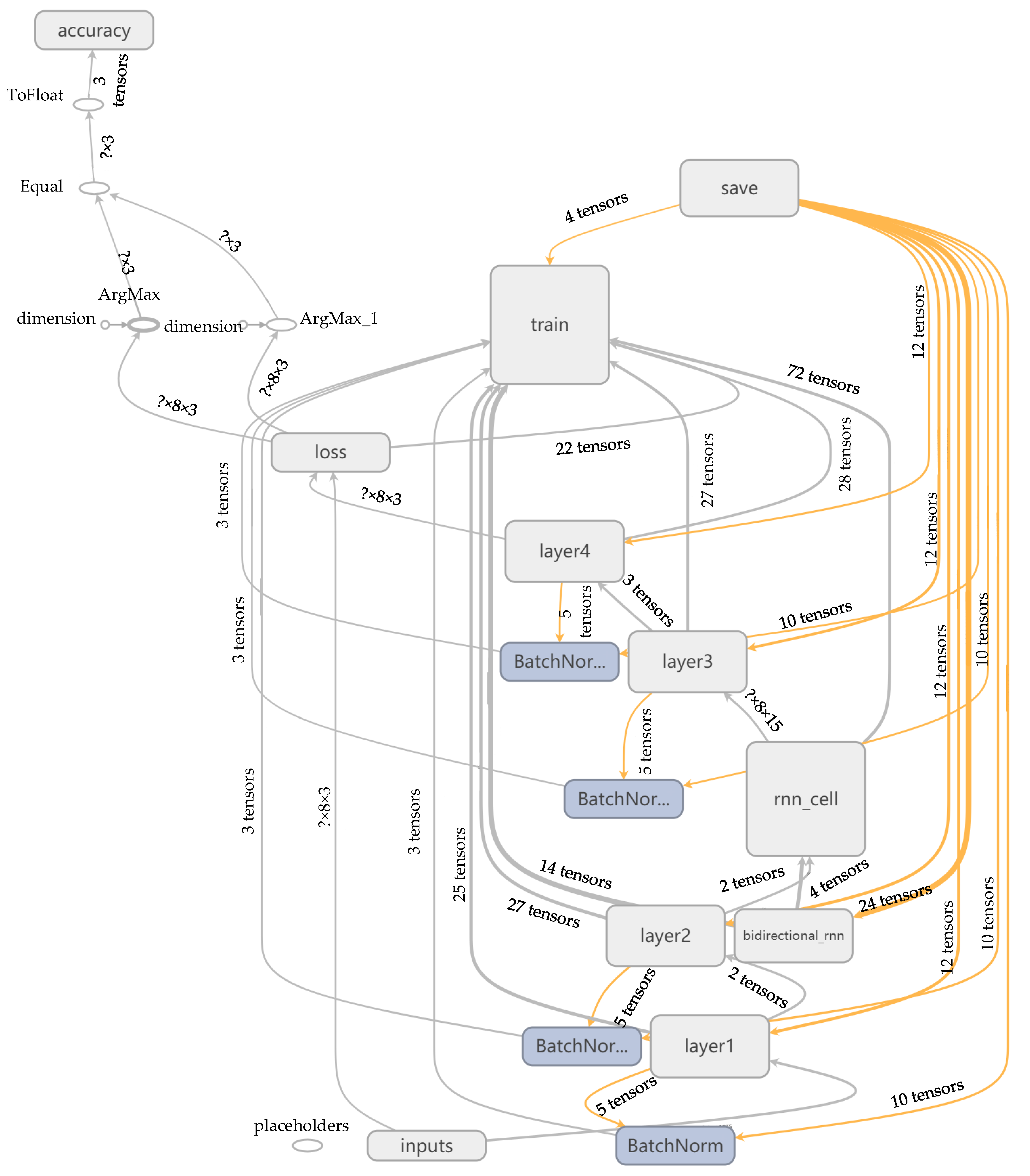
2. Navigation Behavior Learning Model
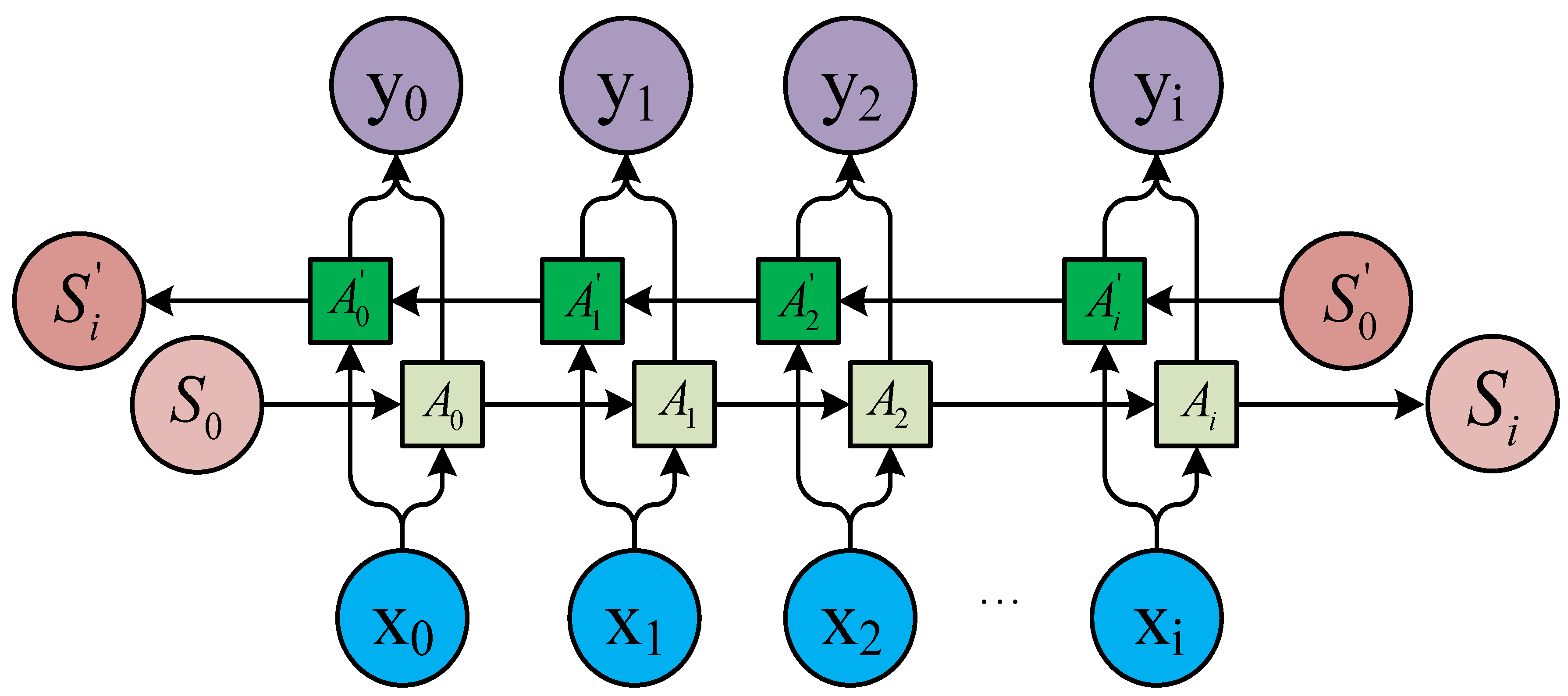
2.1. RNN Structure
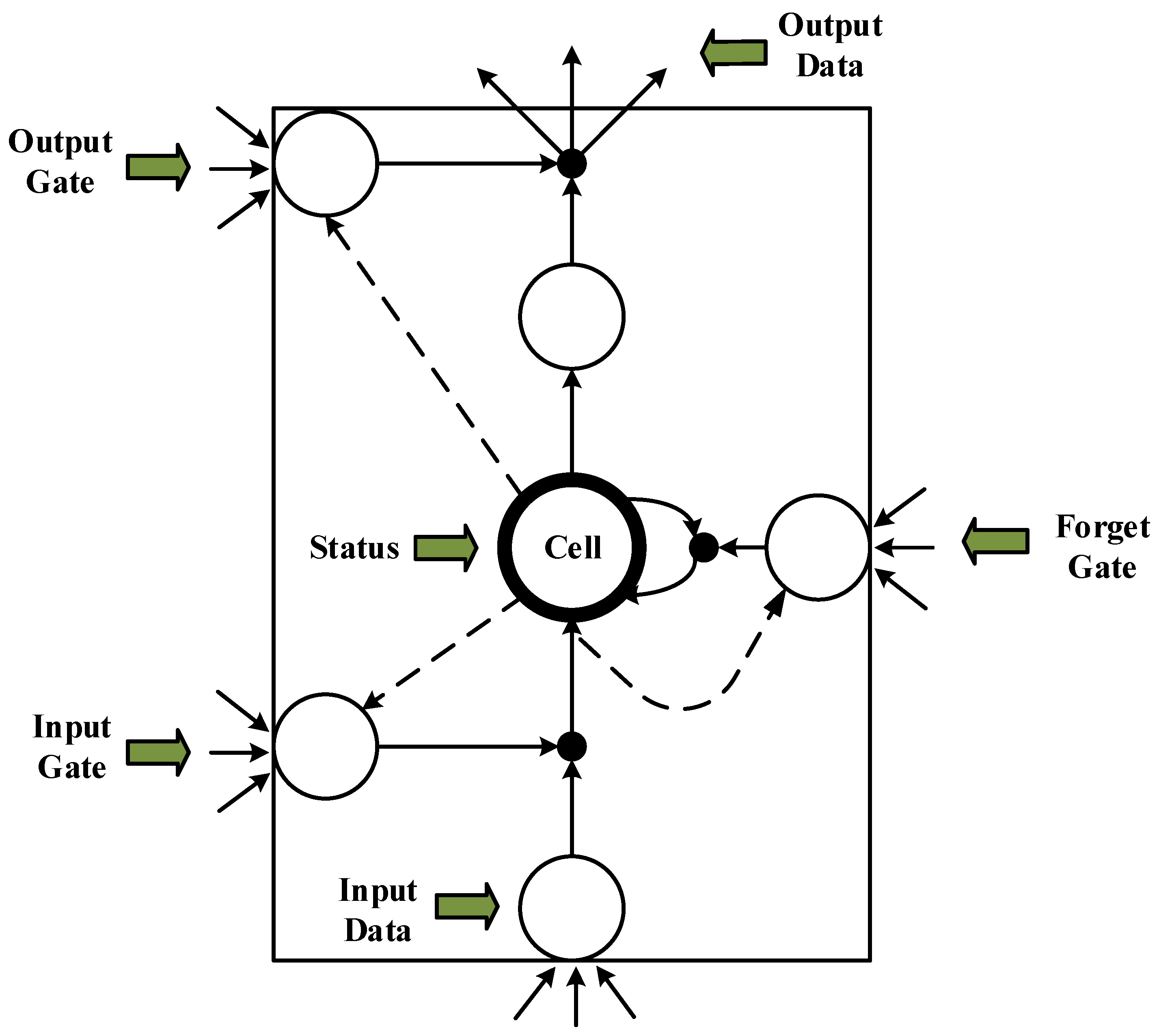
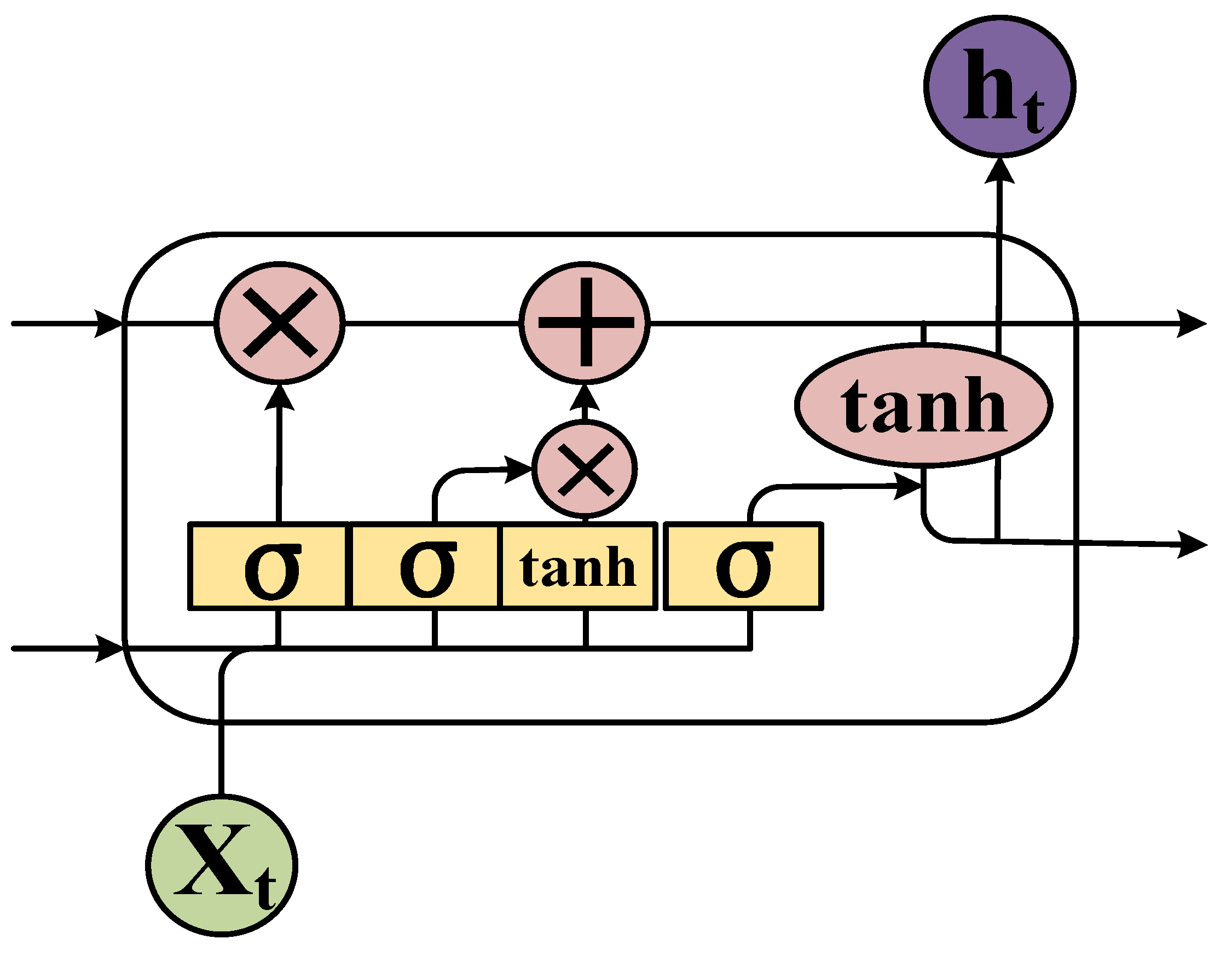
2.2. LSTM Cell Structure
- (1)
- State initialization: The number of neural nodes in the input layer, number of output nodes, and number of each cell unit (k) are determined. The initial state {S} of each cell unit is equal to 0, and the link weight () of each layer is equal to 0. The average value (±1) is a randomly generated range. The offset is initialized to 0.1. W represents the weight of the matrix.
- (2)
- The output data (H) are calculated from the input layer, according to and from Equation (1):
- (3)
- LSTM unit calculation: The output of the unit above the forget gate and the input of this unit are used as inputs for the sigmoid function (Figure 4), which adds to the degree of forgetting used to control the previous unit.
- (4)
- The input gate integrates the Ct−1 of the previous state with the Ct of the current state to update the cell unit state.
- (5)
- The output value () from the output gate is passed to the status value () of the next unit to complete the training procedure.
- (6)
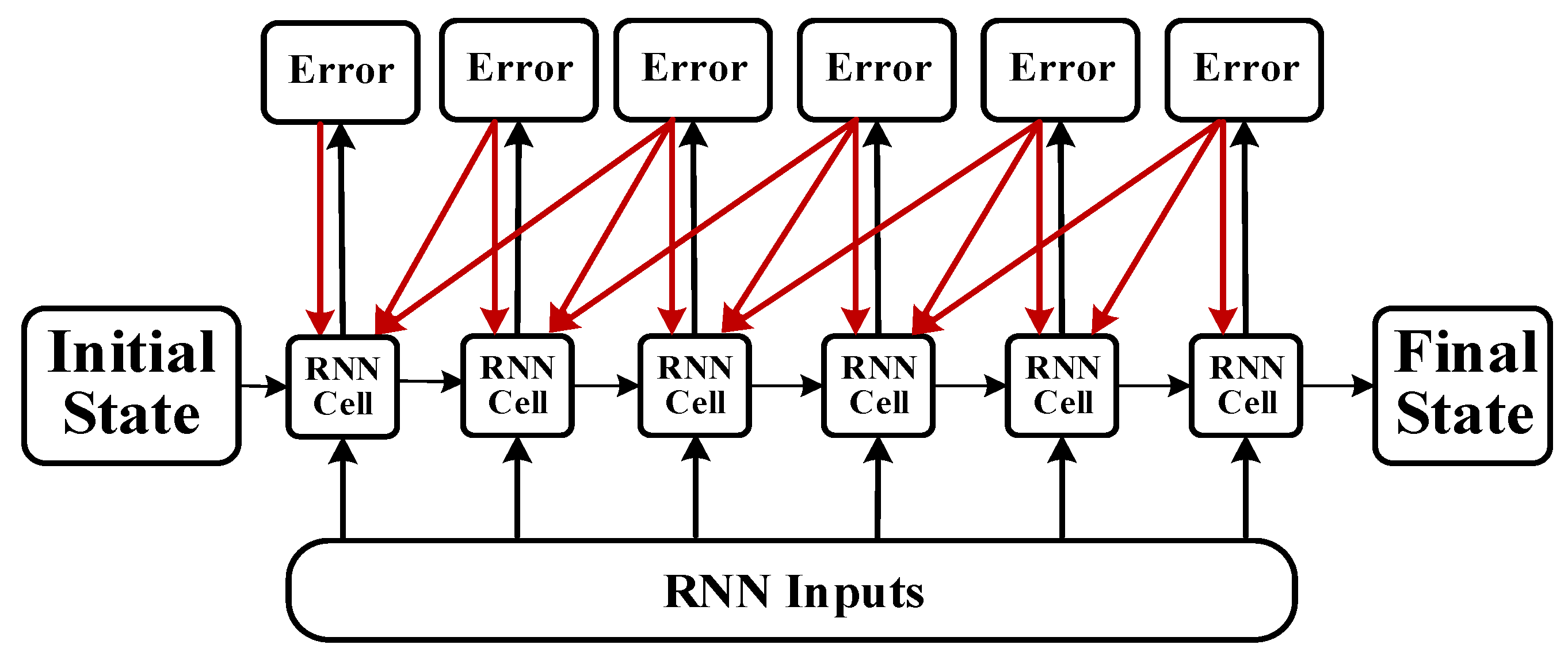
- Error calculation: The prediction error () is calculated according to O and the expected output () of the RNN prediction error, returning the error number of each batch.
- (7)
- Weight updating: The random gradient descent method is used to optimize the error depending on the value. For each update parameter, it is unnecessary to traverse all of the training sets; only one value is used to update a parameter. Such an algorithm is more suitable for big data and has fast searching capability.
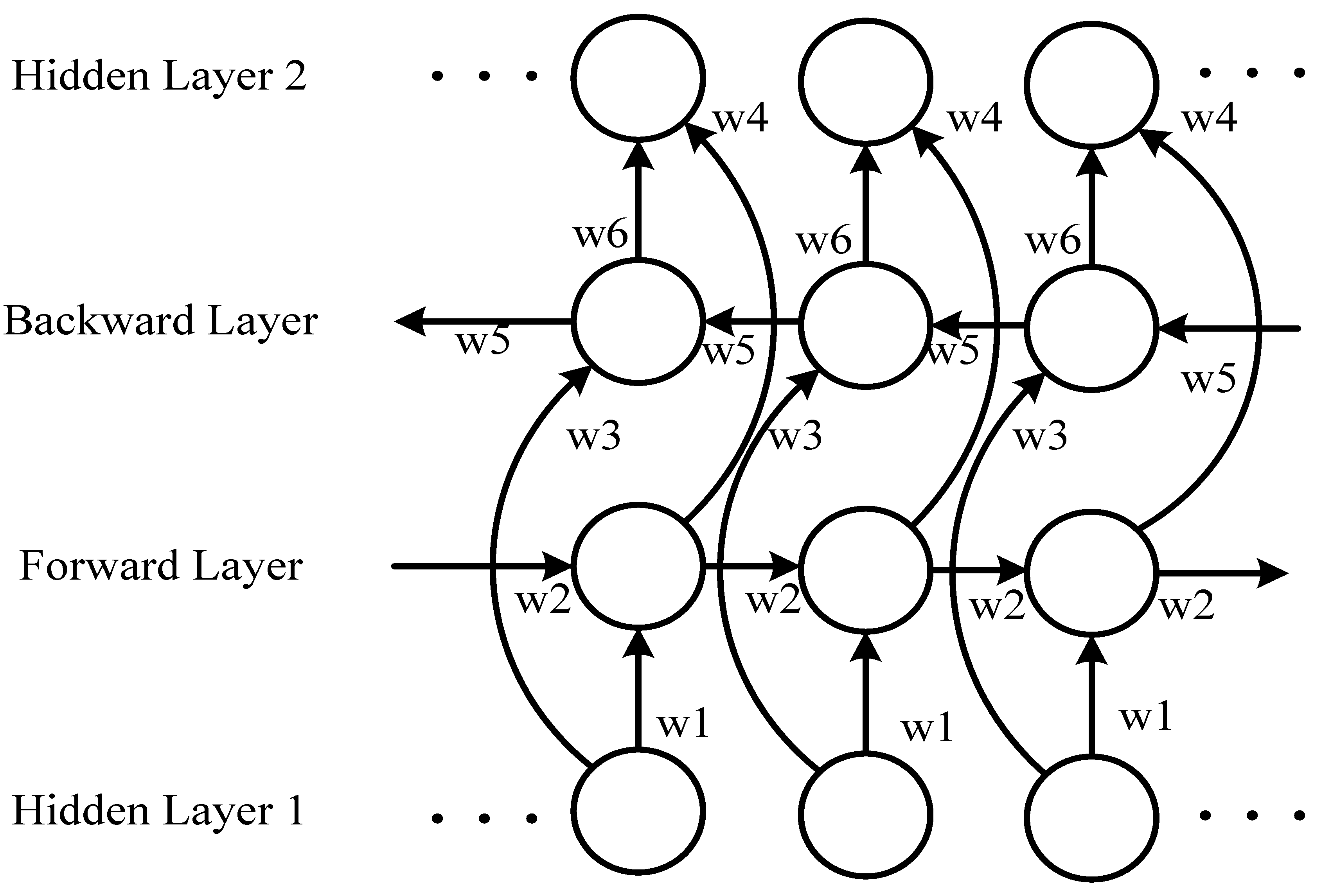
2.3. Bidirectional Structure
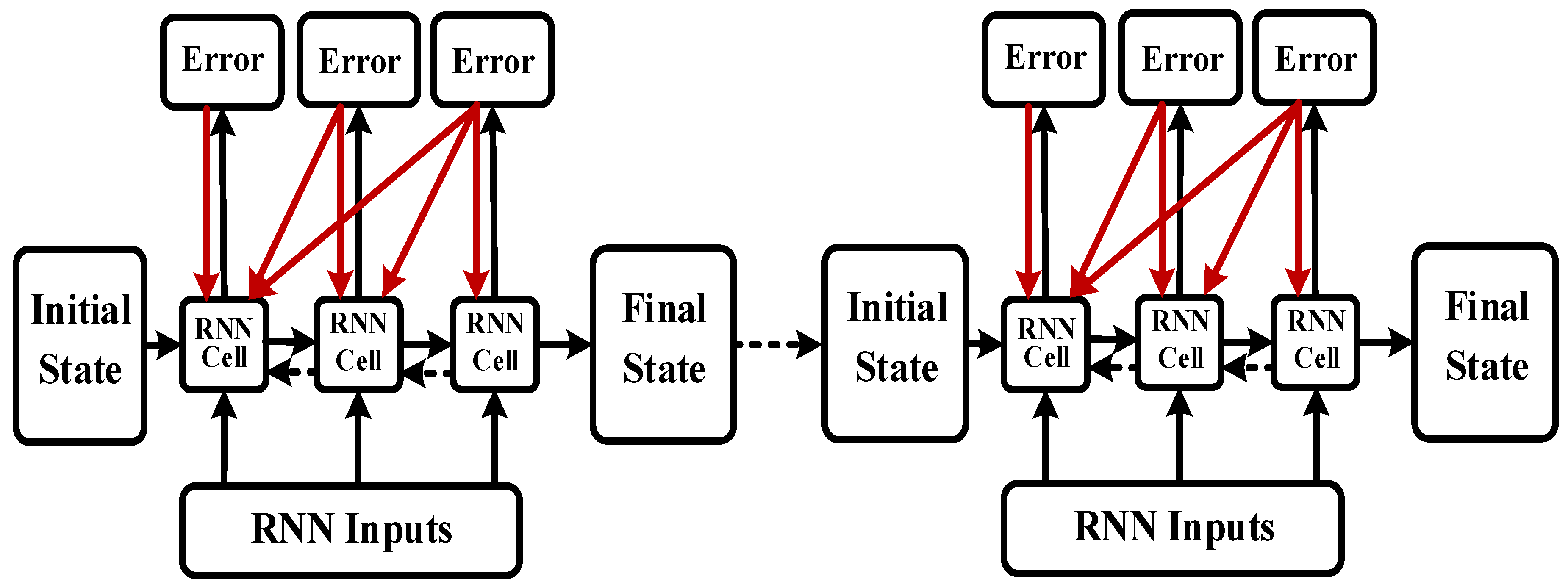
2.4. Batch Training Structure
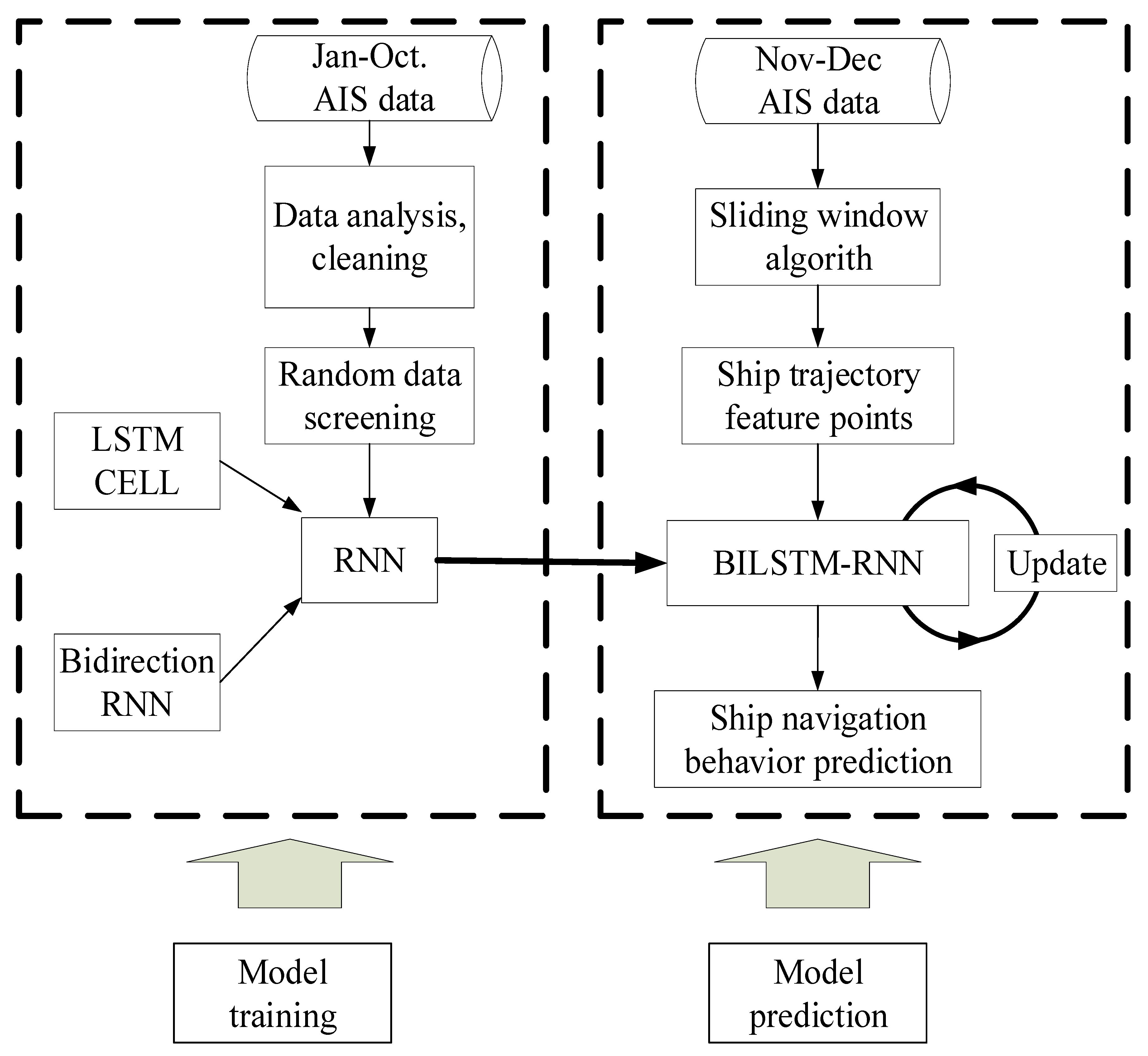
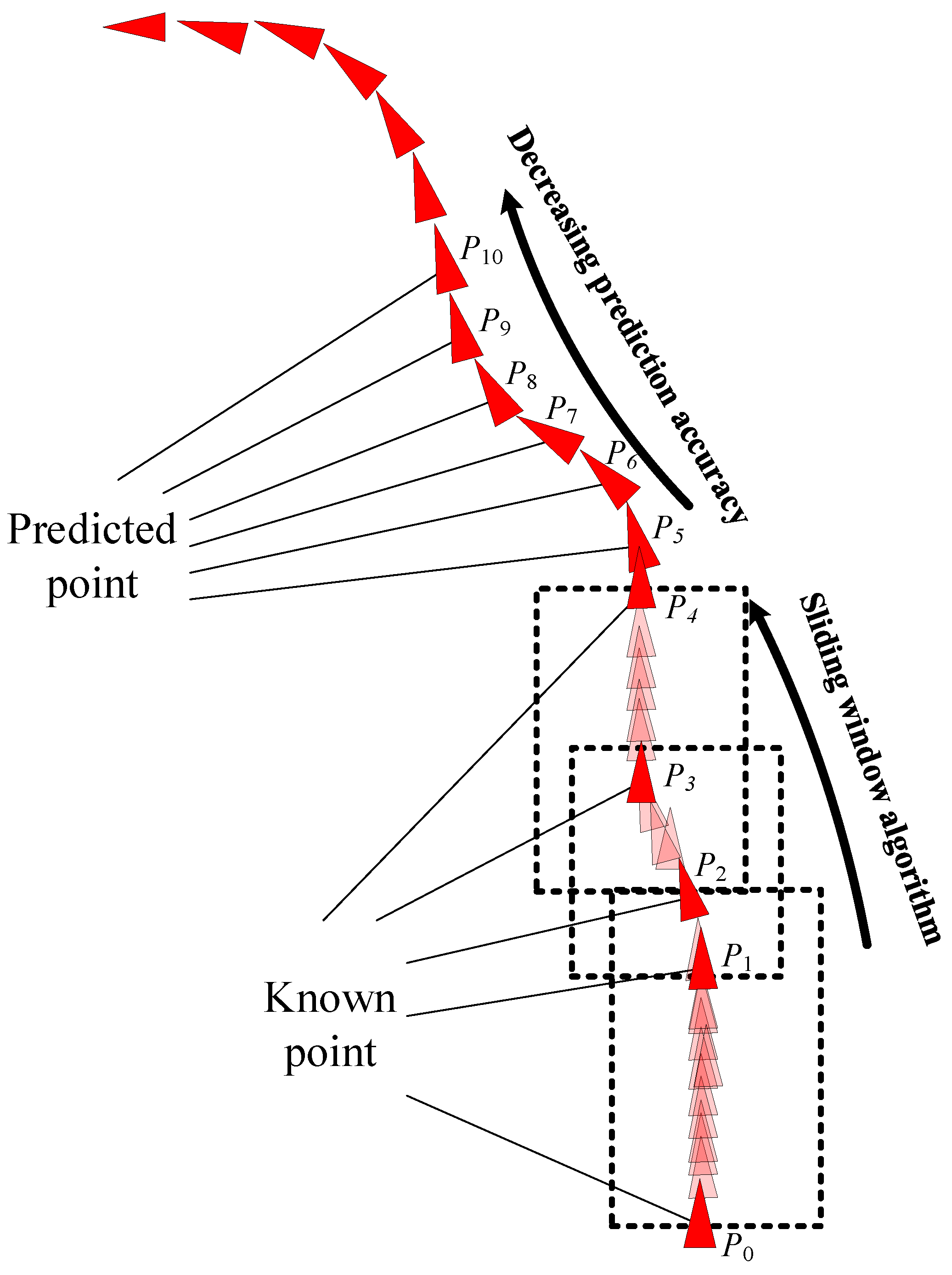
3. Navigation Behavior Prediction Model
3.1. Parameter Analysis
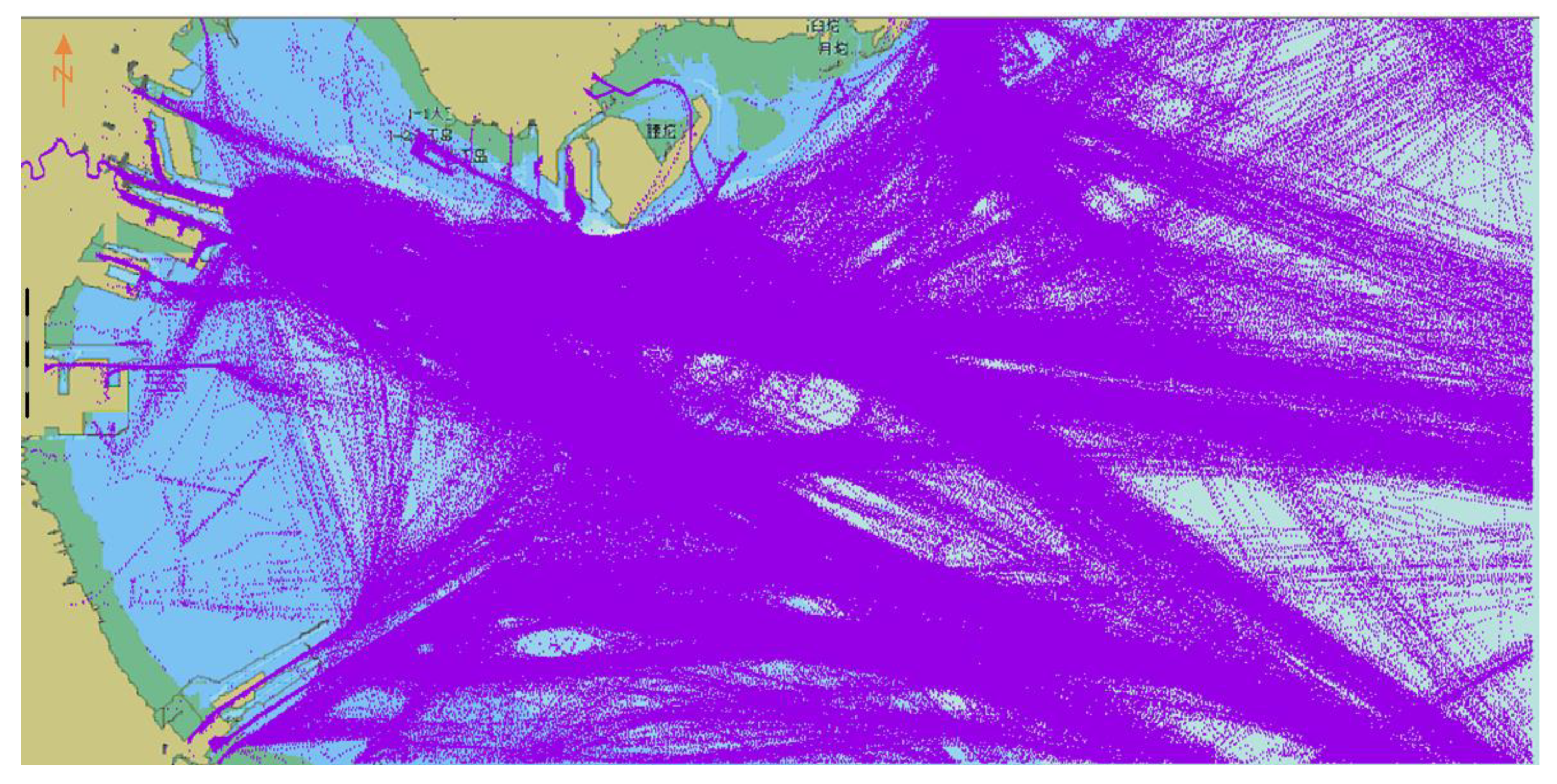
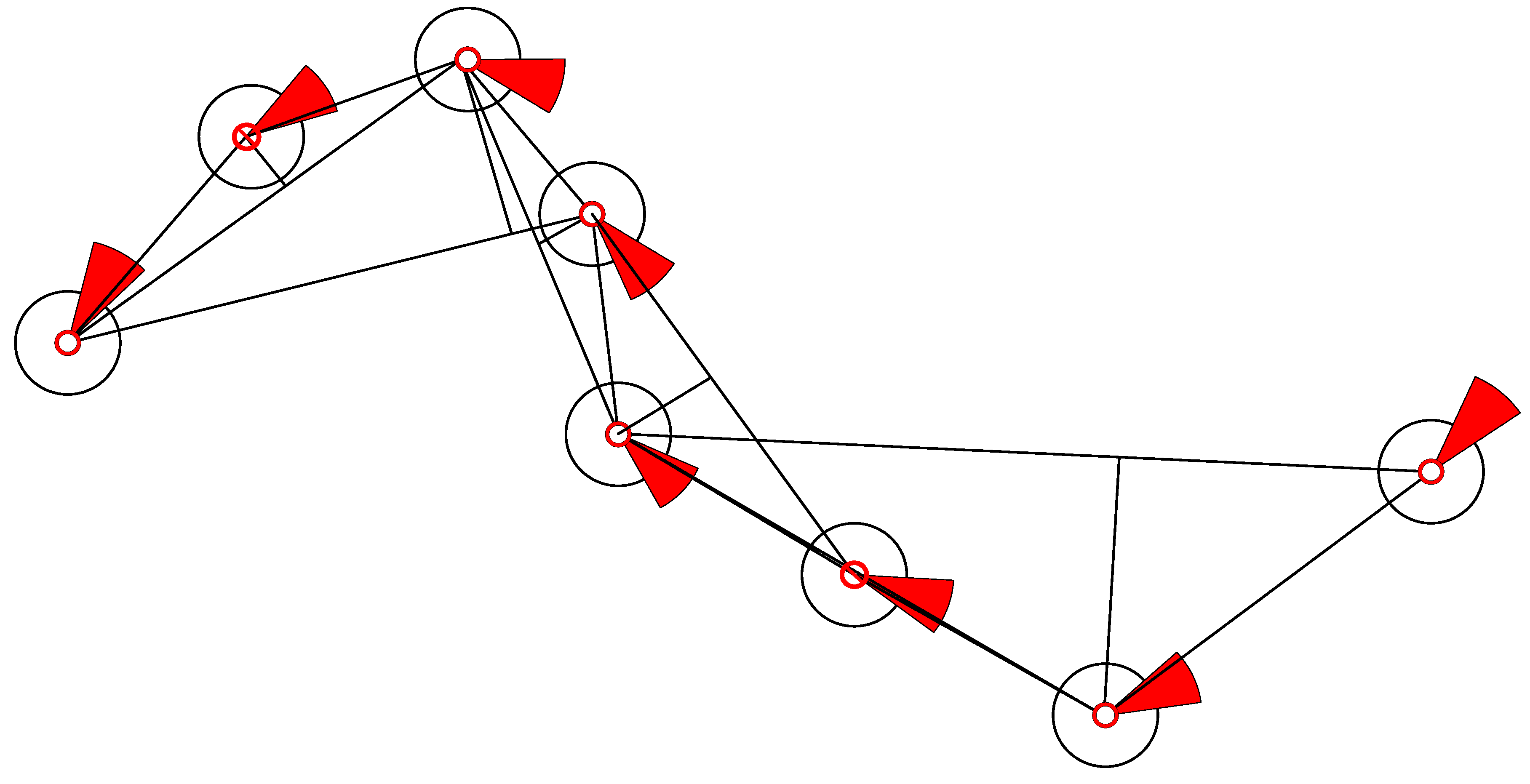
3.2. AIS Trajectory Data Value Filter
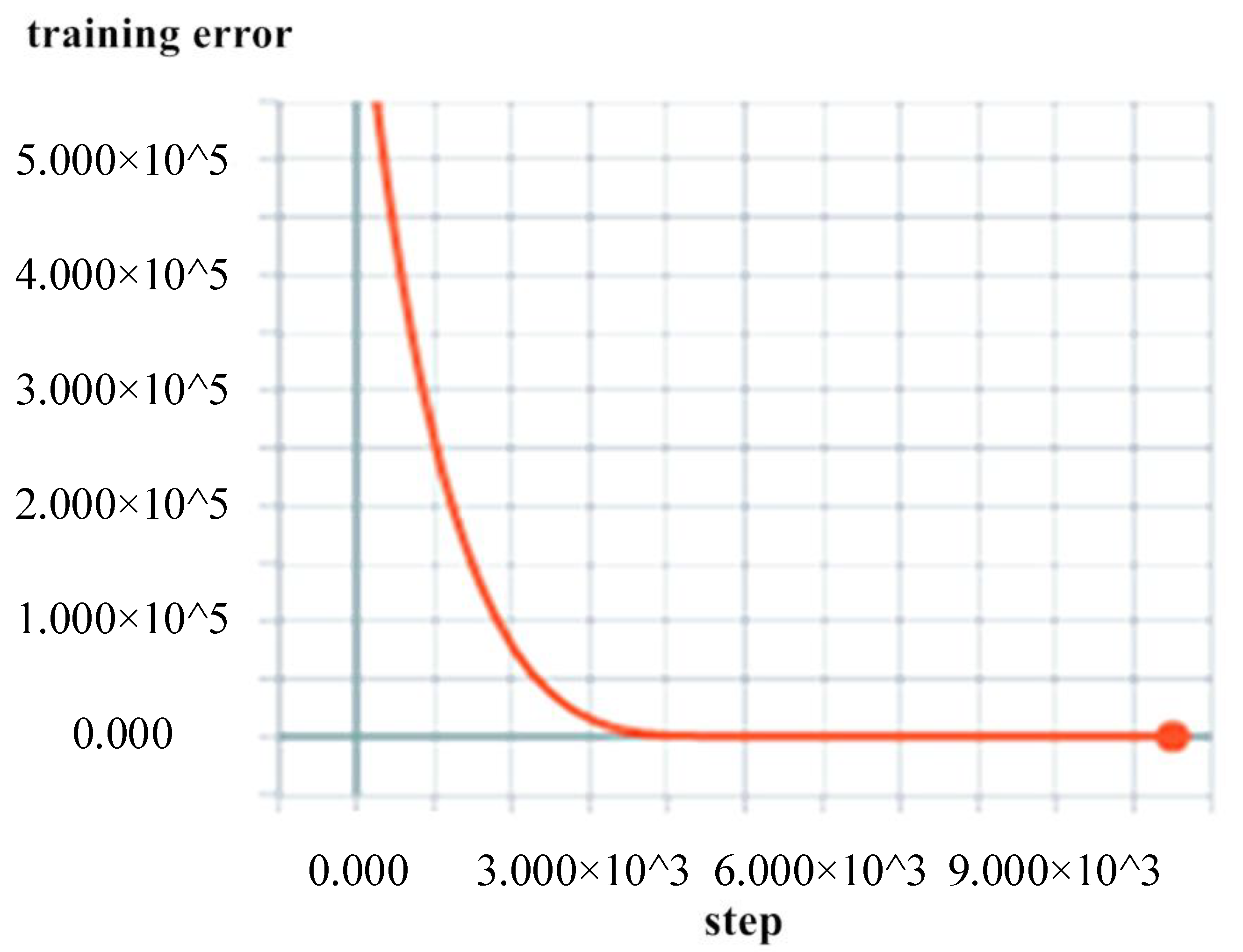
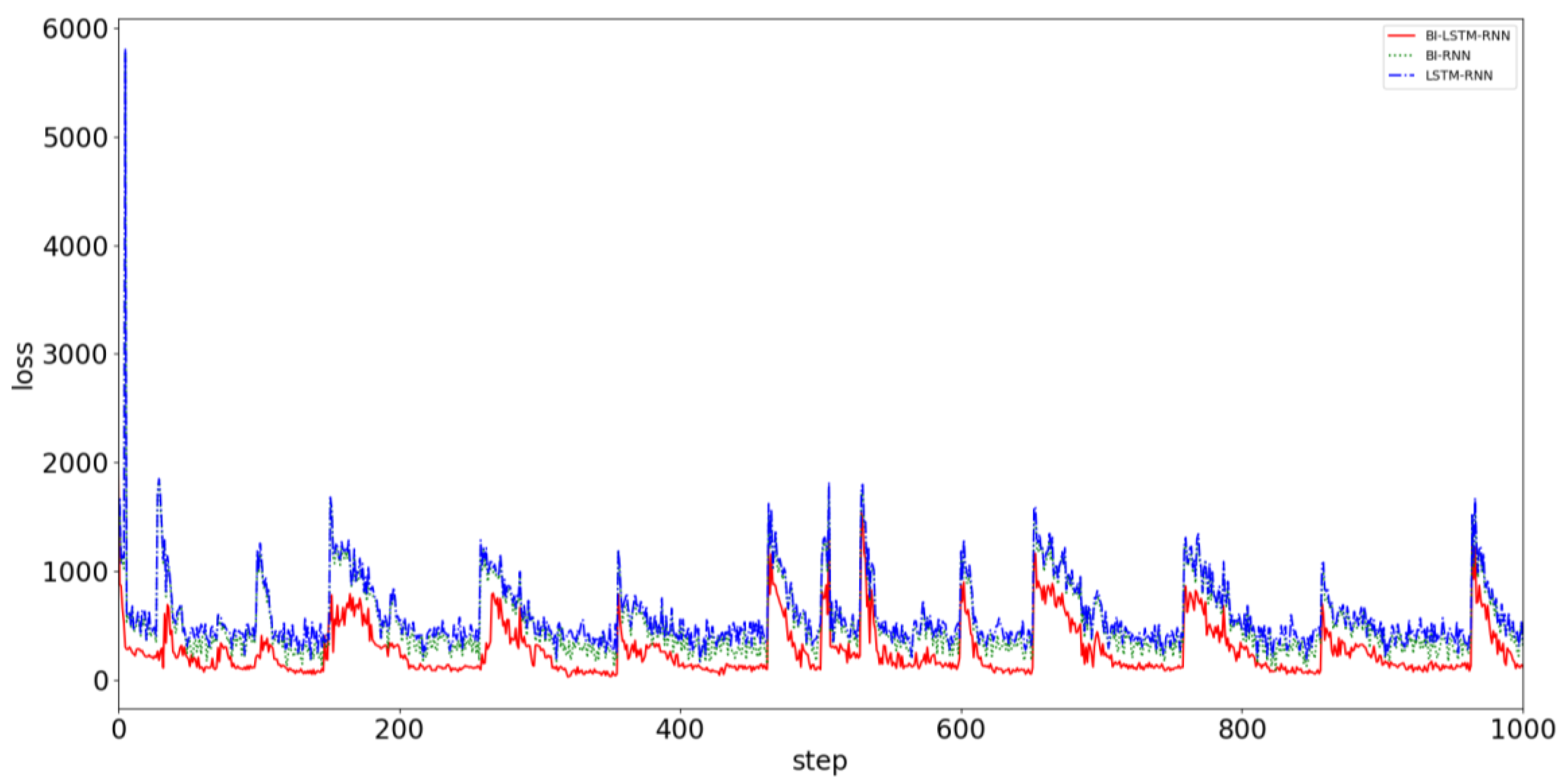
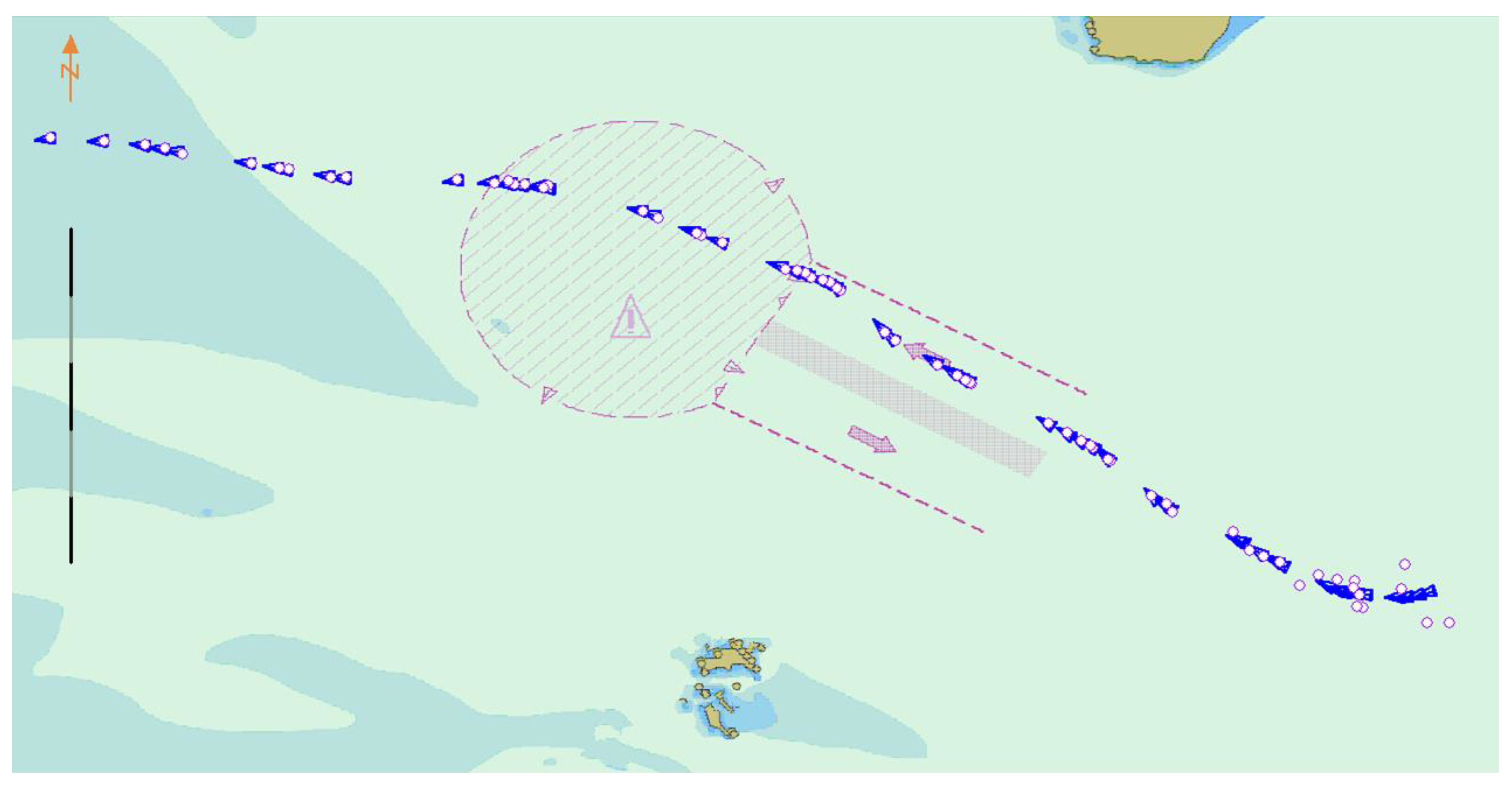
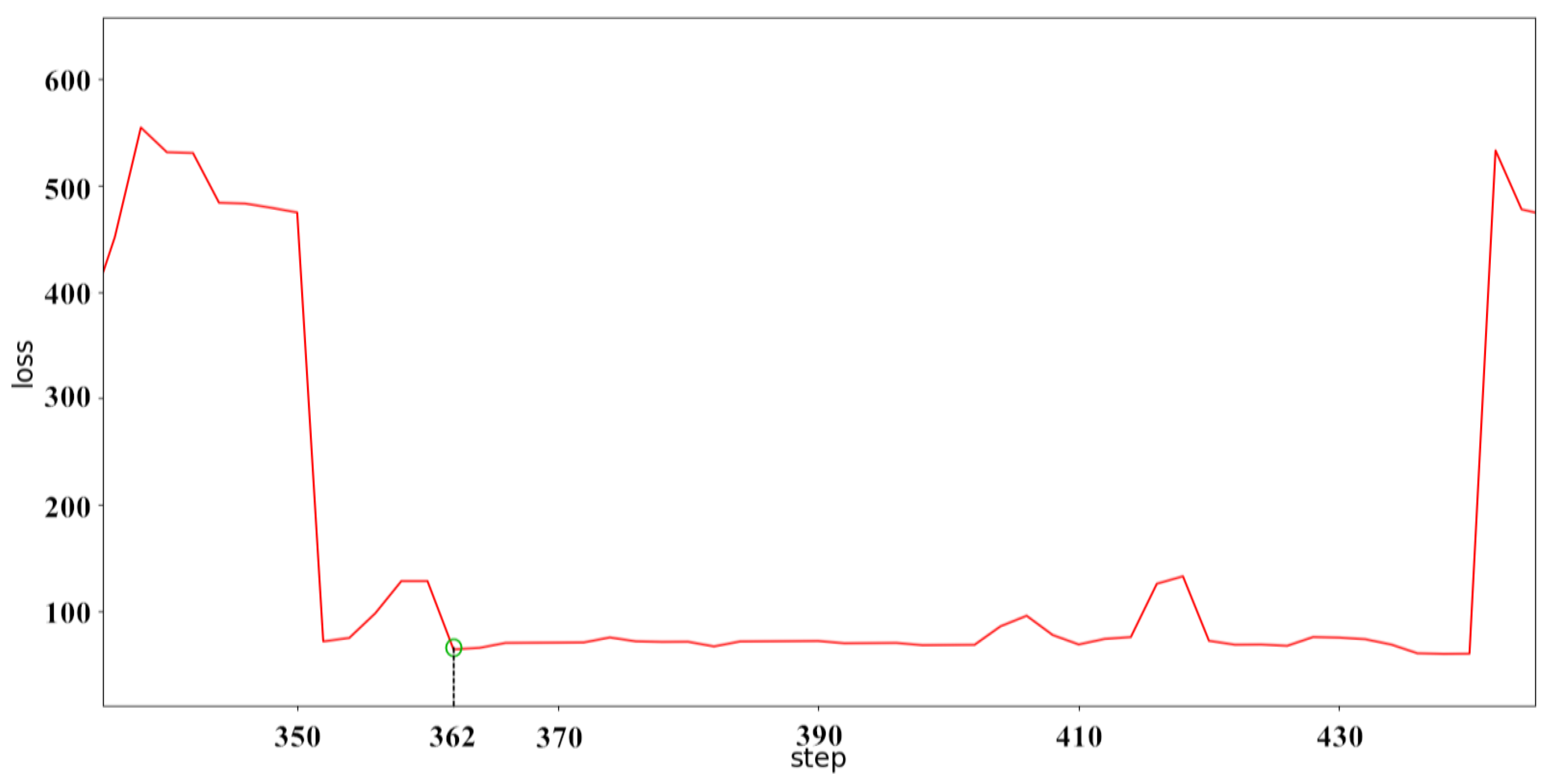
4. Results
5. Conclusions
- Selecting an RNN for the time-series data characteristics of AIS big data allows training regarding the general rules of ship maneuvering and motion characteristics.
- Adding the LSTM unit improves the gradient loss caused by infinite-sequence data in the loop training. An RNN can remember the common features of the AIS big data and forget personality differences. Thus, the RNN has an autonomous choice to remember or forget.
- By incorporating a two-way RNN structure, the network can learn the information provided by historical data and optimize the network by using future data. The current prediction can establish a strong correlation related to the context.
- The trained BI-LSTM-RNN can accurately predict future ship navigation behavior and adjust parameters in real time with existing data as input.
Author Contributions
Funding
Conflicts of Interest
References
- Han, Y.X.; Tang, X.M.; Han, S.C. Conflict-Free 4D Trajectory Prediction Based on Hybrid System Theory. J. Southwest Jiaotong Univ. 2012, 47, 1069–1074. [Google Scholar]
- Xu, T.; Liu, X.; Yang, X. Ship Trajectory Online Prediction Based on BP Neural Network Algorithm. In Proceedings of the International Conference on Information Technology, Computer Engineering and Management Sciences, Nanjing, China, 24–25 September 2011; Volume 1, pp. 103–106. [Google Scholar]
- Xu, T.; Cai, F.J.; Hu, Q.Y.; Chun, Y. Research on estimation of AIS vessel trajectory data based on Kalman filter algorithm. Mod. Electron. Tech. 2014, 5, 97–100. [Google Scholar]
- Liu, X.L.; Ruan, Q.S.; Gong, Z.Q. New Prediction Model of Ships GPS Navigation Positioning Trajectory. J. Jiangnan Univ. (Nat. Sci. Ed.) 2014, 13, 686–692. [Google Scholar]
- Zhen, R.; Jin, Y.X.; Hu, Q.Y.; Shi, C.J.; Wang, S.Z. Vessel Beavior Prediction Based on AIS Data and BP Neural Network. Navig. China 2017, 40, 6–10. [Google Scholar]
- Zhao, S.B.; Tang, C.; Liang, S.; Wang, D.J. Track prediction of vessel in controlled waterway based on improved Kalman filter. J. Comput. Appl. 2012, 32, 3247–3250. [Google Scholar] [CrossRef]
- Tong, X.; Chen, X.; Sang, L.; Mao, Z.; Wu, Q. Vessel trajectory prediction in curving channel of inland river. In Proceedings of the International Conference on Transportation Information and Safety (ICTIS), Wuhan, China, 25–28 June 2015; pp. 706–714. [Google Scholar]
- Kim, Y.S.; Hong, K.S. An imm algorithm for tracking maneuvering vehicles in an adaptive cruise control environment. Int. J. Control Autom. Syst. 2004, 2, 613–625. [Google Scholar]
- Mehrotra, K.; Mahapatra, P.R. A jerk model for tracking highly maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 1094–1105. [Google Scholar] [CrossRef]
- Vaidehi, V.; Chitra, N.; Chokkalingam, M.; Krishnan, C.N. Neural network aided kalman filtering for multitarget tracking applications. Comput. Electr. Eng. 2001, 27, 217–228. [Google Scholar] [CrossRef]
- Gan, S.; Liang, S.; Li, K.; Deng, J.; Cheng, T. Ship trajectory prediction for intelligent traffic management using clustering and ANN. In Proceedings of the 2016 UKACC International Conference on Control (CONTROL), Belfast, UK, 31 August–2 September 2016; pp. 1–6. [Google Scholar]
- Cai, X.; Zhang, N.; Venayagamoorthy, G.K. Time series prediction with recurrent neural networks trained by a hybrid PSO-EA algorithm. Neurocomputing 2007, 70, 2342–2353. [Google Scholar] [CrossRef]
- Mao, C.H.; Pan, C.; Yin, B.; Lu, Y.N.; Xu, X.Q. Ship navigation trajectory prediction based on Gaussian process regression. Technol. Innov. Appl. 2017, 4, 28–29. [Google Scholar]
- Perera, L.P.; Oliveira, P.; Soares, C.G. Maritime Traffic Monitoring Based on Vessel Detection, Tracking, State Estimation, and Trajectory Prediction. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1188–1200. [Google Scholar] [CrossRef]
- Becker, M.H.; Richard, K.; SaschaMacek, K.S.; Roland, J. 2D laser-based probabilistic motion tracking in urban-like environments. J. Braz. Soc. Mech. Sci. Eng. 2009, 31, 83–96. [Google Scholar] [CrossRef]
- Stubberud, S.C.; Kramer, K.A. Kinematic prediction for intercept using a neural kalman filter. IFAC Proc. Vol. 2005, 38, 144–149. [Google Scholar] [CrossRef]
- Sang, L.; Yan, X.; Wall, A. CPA Calculation Method based on AIS Position Prediction. J. Navig. 2016, 69, 1409–1426. [Google Scholar] [CrossRef]
- Nagai, T.; Watanabe, R. Applying position prediction model for path following of ship on curved path. In Proceedings of the 2016 IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016; pp. 3675–3678. [Google Scholar]
- Borkowski, P. The Ship Movement Trajectory Prediction Algorithm Using Navigational Data Fusion. Sensors 2017, 17, 1432. [Google Scholar] [CrossRef] [PubMed]
- Zissis, D.; Xidias, E.K.; Lekkas, D. Real-time vessel behavior prediction. Evol. Syst. 2016, 7, 29–40. [Google Scholar] [CrossRef]
- Yin, J.C.; Zou, Z.J.; Xu, F.; Wang, N.N. Online ship roll motion prediction based on grey sequential extreme learning machine. Neurocomputing 2014, 129, 168–174. [Google Scholar] [CrossRef]
- Zhang, W.; Zou, Z.J.; Deng, D.H. A study on prediction of ship maneuvering in regular waves. Ocean Eng. 2017, 137, 367–381. [Google Scholar] [CrossRef]
- Breda, V.L. Capability Prediction: An Effective, Way to Improve Navigational Performance. J. Navig. 2000, 53, 343–354. [Google Scholar] [CrossRef]
- Potter, C.; Venayagamoorthy, G.K.; Kosbar, K. RNN based MIMO channel prediction. Signal Process. 2010, 90, 440–450. [Google Scholar] [CrossRef]
- Williams, R.J.; Zipser, D.A. Learning algorithm for continually running fully recurrent neural networks. Neural Comput. 2014, 1, 270–280. [Google Scholar] [CrossRef]
- Han, M.; Xi, J.; Xu, S.; Yin, F.L. Prediction of chaotic time series based on the recurrent predictor neural network. IEEE Trans. Signal Process. 2004, 52, 3409–3416. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 2002, 45, 2673–2681. [Google Scholar] [CrossRef]
- Sak, H.; Senior, A.; Beaufays, F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. arXiv, 2014; arXiv:1402.1128. [Google Scholar]
- Yi, J.; Wen, Z.; Tao, J.; Ni, H.; Liu, B. CTC Regularized Model Adaptation for Improving LSTM RNN Based Multi-Accent Mandarin Speech Recognition. J. Signal Process. Syst. 2017, 90, 1–13. [Google Scholar]
- Gers, F.A.; Schmidhuber, E. LSTM recurrent networks learn simple context-free and context-sensitive languages. IEEE Trans. Neural Netw. 2001, 12, 1333–1340. [Google Scholar] [CrossRef] [PubMed]
- Blanco, A.; Delgado, M.; Pegalajar, M.C. A real-coded genetic algorithm for training recurrent neural networks. Neural Netw. 2001, 14, 93–105. [Google Scholar] [CrossRef]
- Pearlmutter, B.A. Learning state space trajectories in recurrent neural networks. Neural Comput. 1988, 1, 263–269. [Google Scholar] [CrossRef]
- Kumar, J.; Goomer, R.; Singh, A.K. Long Short Term Memory Recurrent Neural Network (LSTM-RNN) Based Workload Forecasting Model for Cloud Datacenters. Procedia Comput. Sci. 2018, 125, 676–682. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Kumar, K.; Gong, Y. Investigations on speaker adaptation of LSTM RNN models for speech recognition. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing, Shanghai, China, 20–25 March 2016; pp. 5020–5024. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Agarap, A.F.; Grafilon, P. Statistical analysis on e-commerce reviews, with sentiments classification using bidirectional recurrent neural network (RNN). arXiv, 2018; arXiv:1805.03687. [Google Scholar]
- Sundermeyer, M.; Alkhouli, T.; Wuebker, J.; Ney, H. Translation Modeling with Bidirectional Recurrent Neural Networks. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014. [Google Scholar]
- Gao, M.; Shi, G.Y.; Li, W.F. Online compression algorithm of AIS trajectory data based on improved sliding window. J. Traffic Transp. Eng. 2018, 18, 218–227. [Google Scholar]
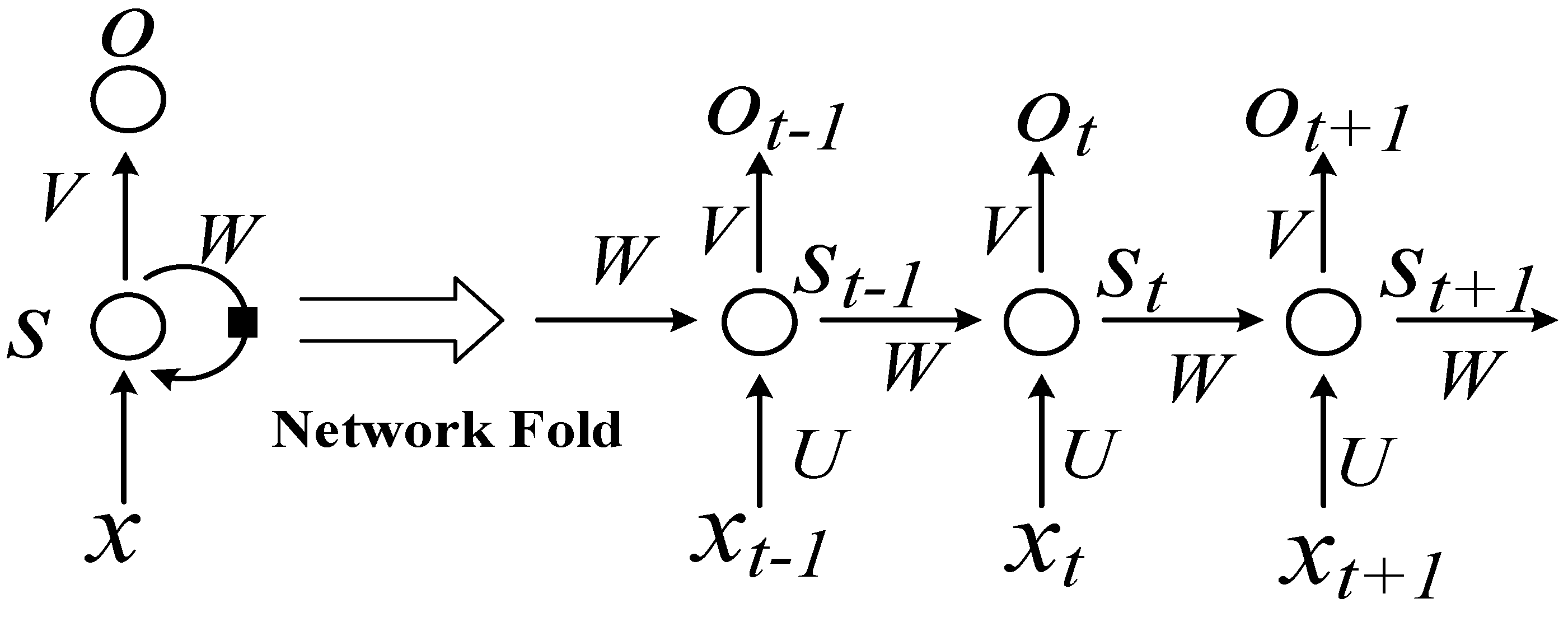
| MMSI | Heading (°) | Course (°) | Speed (Kn) | UnixTime (ms) | Lon_d (°) | Lat_d (°) |
|---|---|---|---|---|---|---|
| 100900000 | 5.0 | 5.6 | 2.4 | 1,422,721,505 | 117.997973 | 38.669028 |
| 100900000 | 2.0 | 2.5 | 2.4 | 1,422,721,943 | 117.998265 | 38.673763 |
| 100900000 | 208.0 | 208.1 | 2.9 | 1,422,723,323 | 117.999900 | 38.677282 |
| 100900000 | 177.0 | 177.3 | 2.7 | 1,422,728,073 | 118.000740 | 38.682742 |
| 100900000 | 183.0 | 183.8 | 2.7 | 1,422,753,718 | 118.011620 | 38.683072 |
| 100900000 | 185.0 | 185.4 | 2.6 | 1,422,814,193 | 117.996735 | 38.675307 |
| 100900000 | 216.0 | 216.4 | 2.9 | 1,422,820,375 | 118.000242 | 38.684793 |
| 100900000 | 184.0 | 241.5 | 3.4 | 1,422,845,041 | 117.993773 | 38.679000 |
| 100900000 | 187.0 | 184.6 | 2.5 | 1,422,851,329 | 117.991593 | 38.677032 |
| 100900000 | 180.0 | 187.7 | 2.8 | 1,422,925,499 | 117.991617 | 38.654512 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Shi, G.; Li, S. Online Prediction of Ship Behavior with Automatic Identification System Sensor Data Using Bidirectional Long Short-Term Memory Recurrent Neural Network. Sensors 2018, 18, 4211. https://doi.org/10.3390/s18124211
Gao M, Shi G, Li S. Online Prediction of Ship Behavior with Automatic Identification System Sensor Data Using Bidirectional Long Short-Term Memory Recurrent Neural Network. Sensors. 2018; 18(12):4211. https://doi.org/10.3390/s18124211
Chicago/Turabian StyleGao, Miao, Guoyou Shi, and Shuang Li. 2018. "Online Prediction of Ship Behavior with Automatic Identification System Sensor Data Using Bidirectional Long Short-Term Memory Recurrent Neural Network" Sensors 18, no. 12: 4211. https://doi.org/10.3390/s18124211
APA StyleGao, M., Shi, G., & Li, S. (2018). Online Prediction of Ship Behavior with Automatic Identification System Sensor Data Using Bidirectional Long Short-Term Memory Recurrent Neural Network. Sensors, 18(12), 4211. https://doi.org/10.3390/s18124211





