Model Order Identification for Cable Force Estimation Using a Markov Chain Monte Carlo-Based Bayesian Approach
Abstract
:1. Introduction
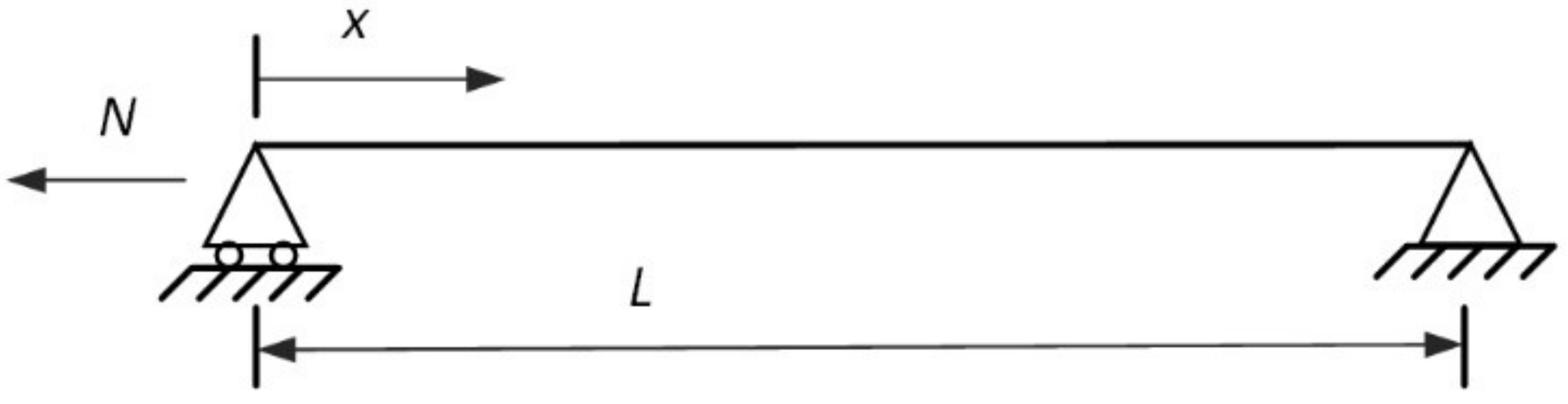
2. Dynamics of a Cable with the Flexural Rigidity
3. Model Order Identification
3.1. Frequency-Domain Analysis
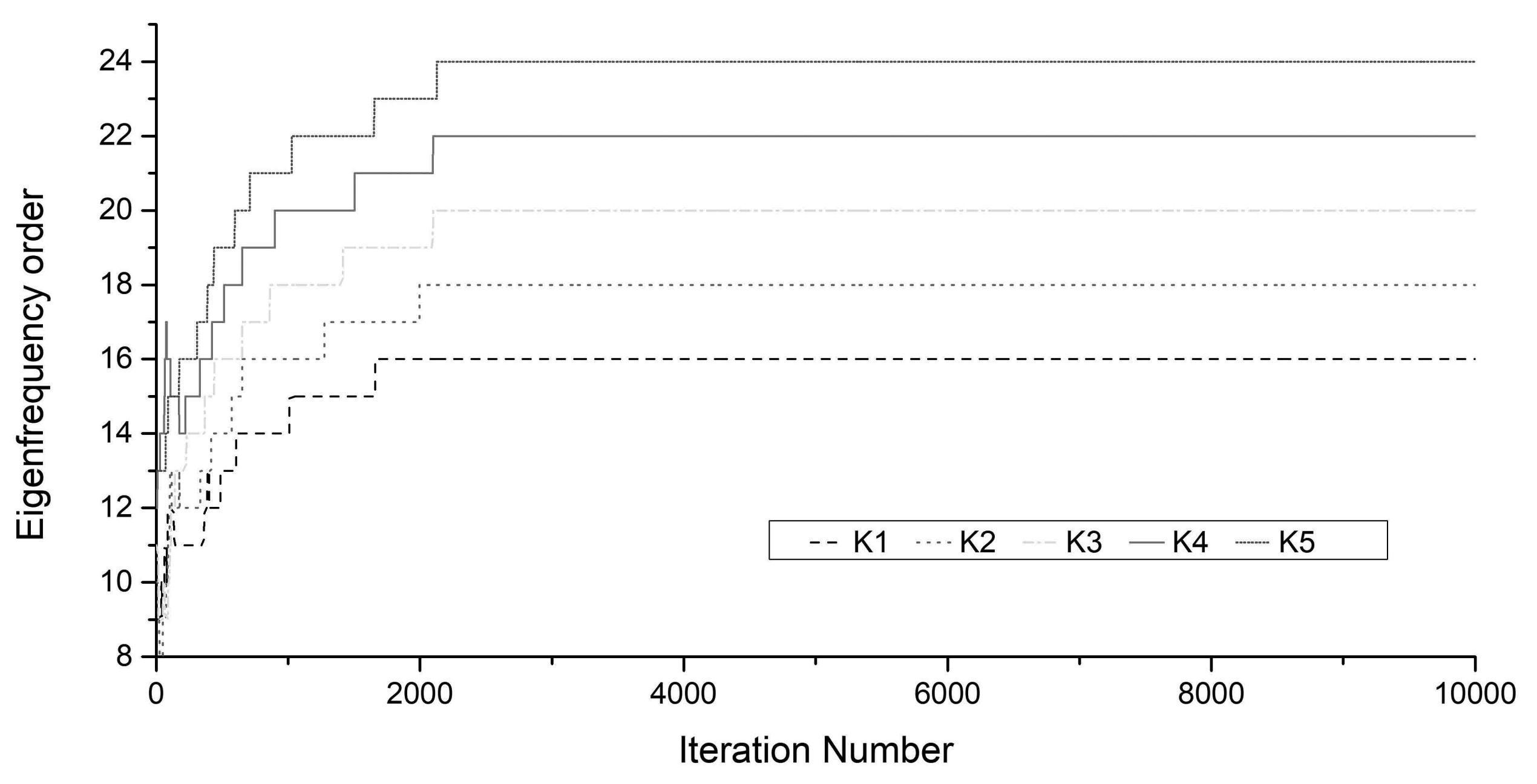
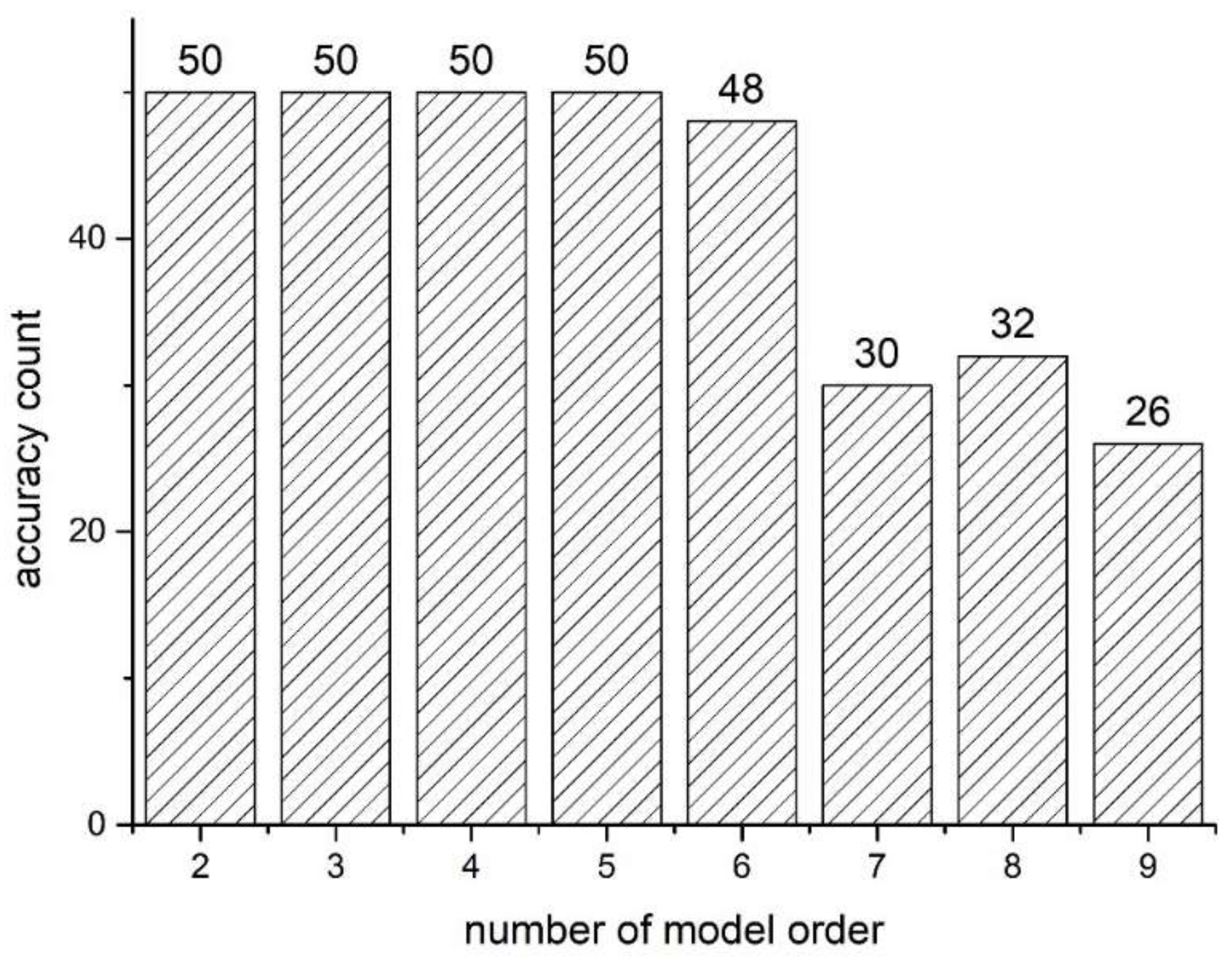
3.2. Model Order Range Limitation
3.3. Bayesian Parameter Estimation
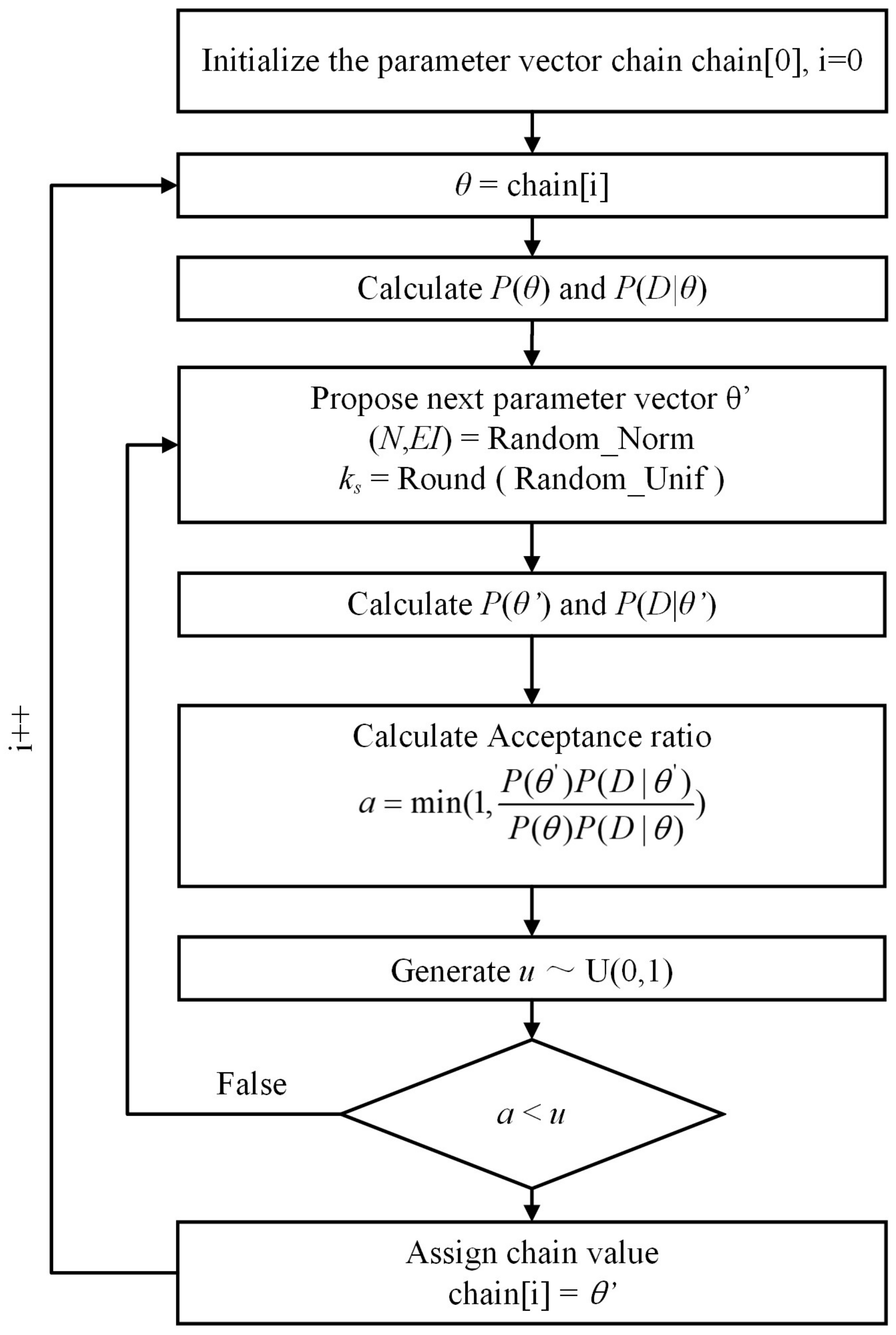
3.4. Markov Chain Monte Carlo (MCMC) Method
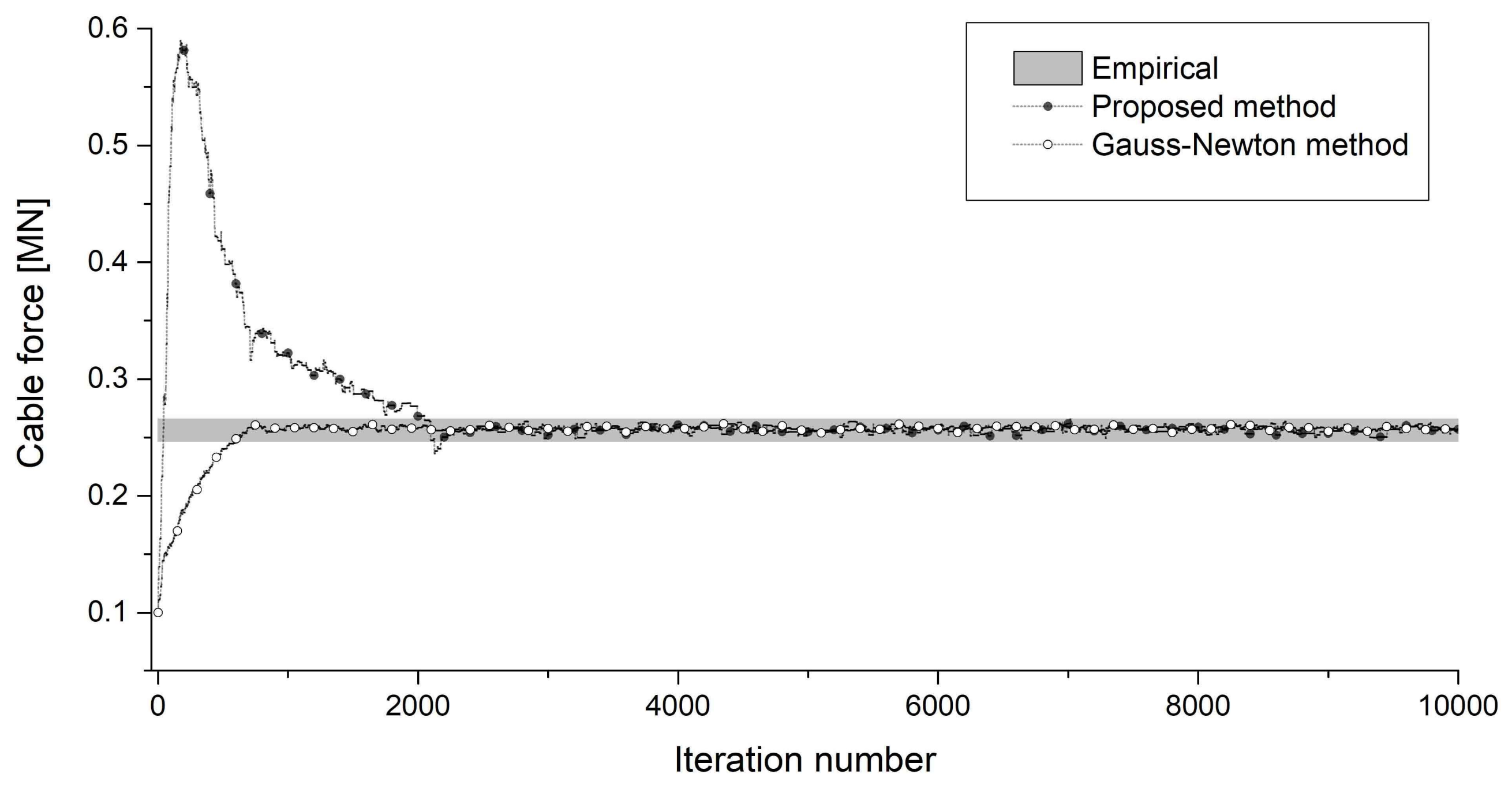
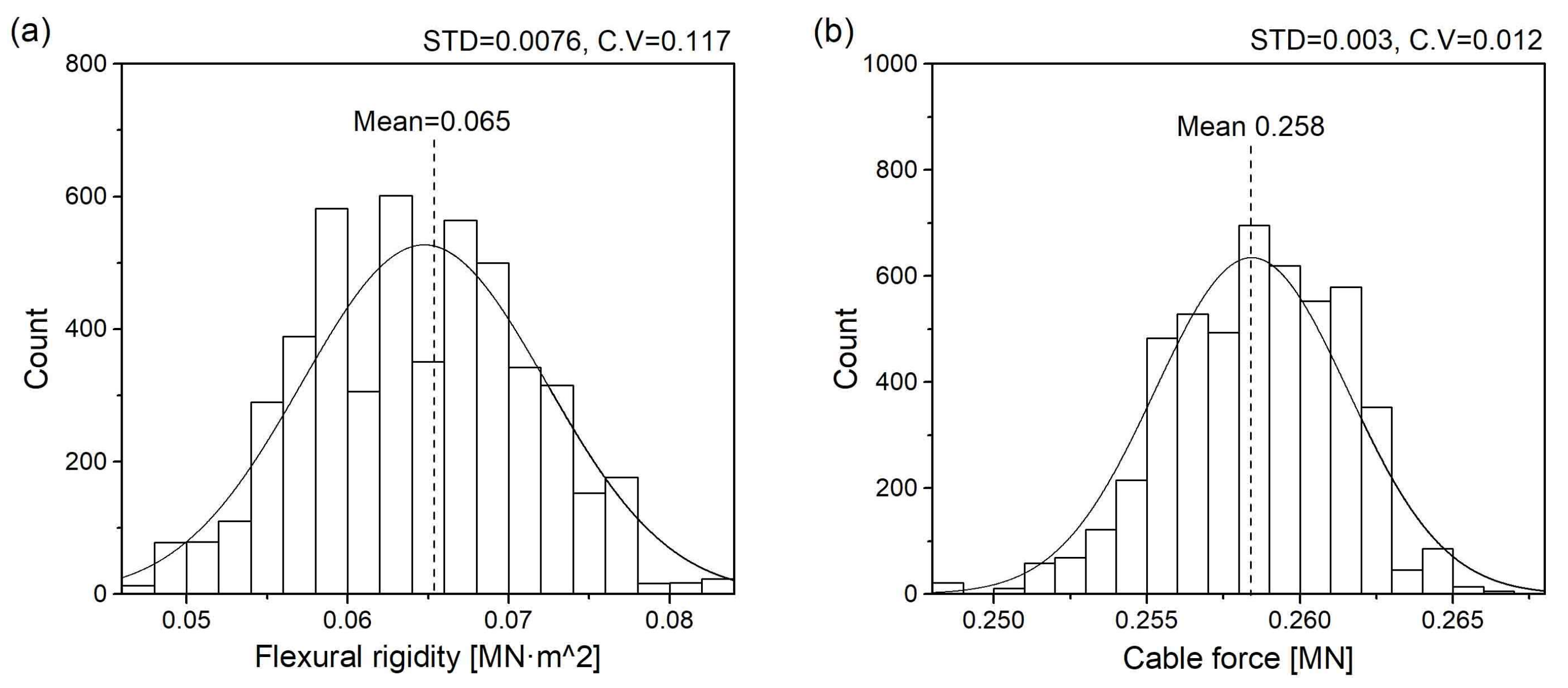
4. Feasibility Validation
4.1. Numerical Study
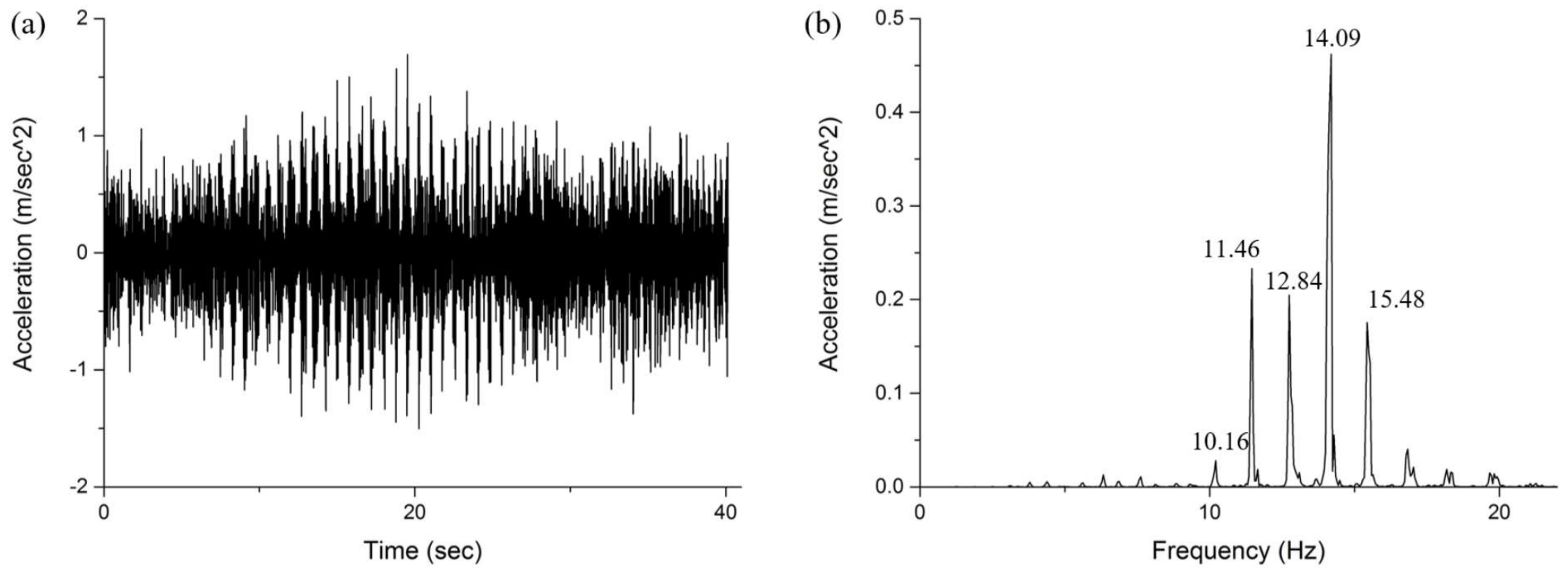
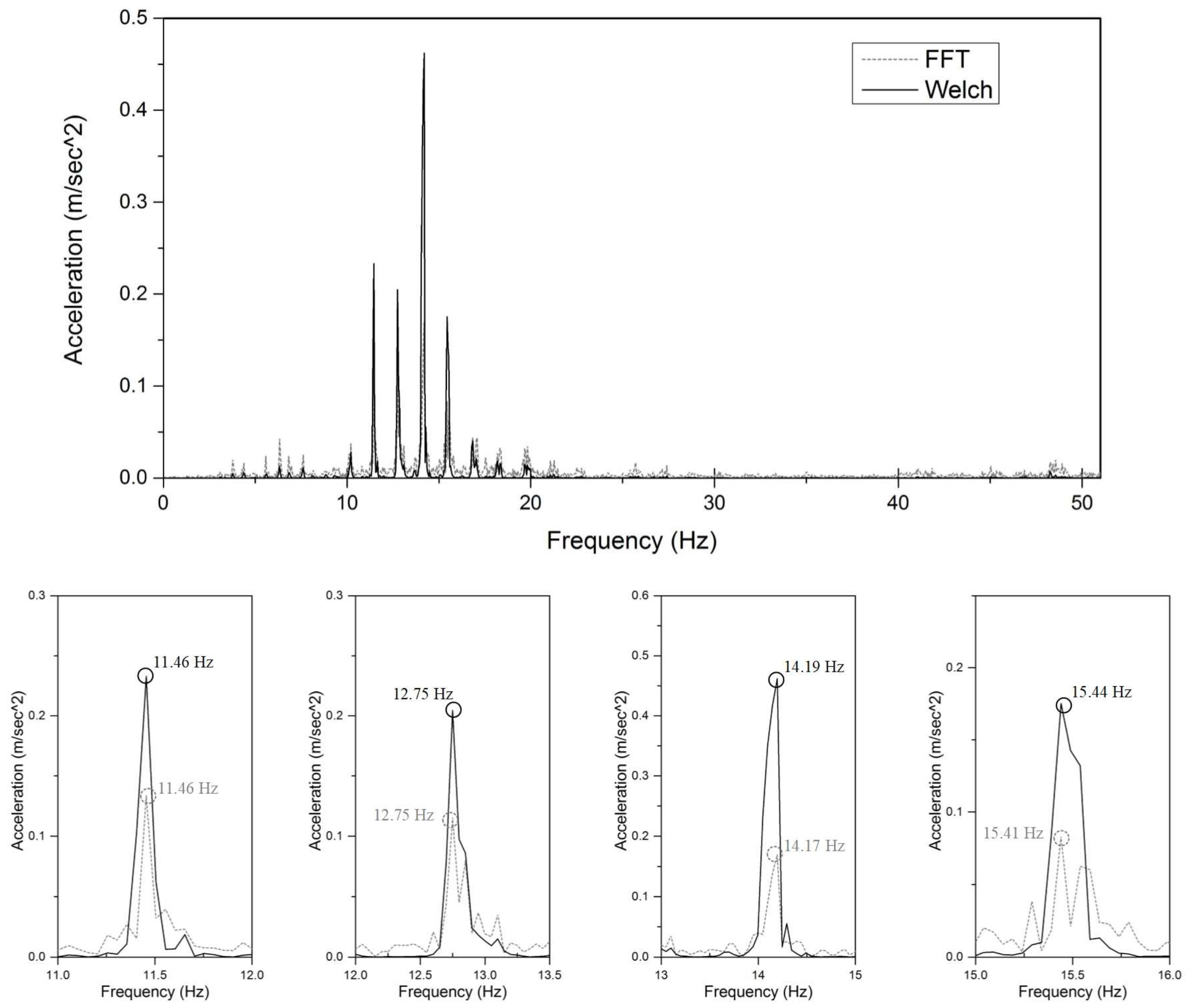
4.2. Field Application
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Russell, J.C.; Lardner, T.J. Experimental Determination of Frequencies and Tension for Elastic Cables. J. Eng. Mech. 1998, 124, 1067–1072. [Google Scholar] [CrossRef]
- Mordini, A.; Savov, K.; Wenzel, H. Damage Detection on Stay Cables using an Open Source-based Framework for Finite Element Model Updating. Struct. Heal. Monit. 2008, 7, 91–102. [Google Scholar] [CrossRef]
- Ma, L. A highly precise frequency-based method for estimating the tension of an inclined cable with unknown boundary conditions. J. Sound Vib. 2017, 409, 65–80. [Google Scholar]
- Wang, M.L.; Chen, Z.L.; Koontz, S.S.; Lloyd, G.M. Magnetoelastic permeability measurement for stress monitoring in steel tendons and cables. Proc. SPIE. Int. Soc. Opt. Eng. 2000, 3995, 492–500. [Google Scholar]
- Casas, J.R. A combined method for measuring cable forces: The cable-stayed Alamillo Bridge, Spain. Struct. Eng. Int. 1994, 4, 235–240. [Google Scholar] [CrossRef]
- Smith, S.W.; Campbell, J.E. Testing and model verification of the Maysville Kentucky Bridge stay cables. In Proceedings of the XX International Modal Analysis Conference, Los Angeles, CA, USA, 4–7 February 2002; pp. 1050–1056. [Google Scholar]
- Shimada, T. A Study on the Maintenance and Management of the Tensile Measurement for the Cable of Bridge. Ph.D. Thesis, Kobe University, Kobe, Japan, 1995. [Google Scholar]
- Zui, H.; Shinke, T.; Namita, Y.H. Practical formulas for estimation of cable tension by vibration method. J. Struct. Eng. 1996, 122, 651–656. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J. Practical Formula for Cable Tension Estimation by Vibration Method. J. Bridg. Eng. 2012, 17, 161–164. [Google Scholar] [CrossRef]
- Park, D.; Kim, N. Back analysis technique for tensile force on hanger cables of a suspension bridge. J. Vib. Control 2014, 20, 761–772. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Giakoumi, K.; Argyris, C.; Spyrou, L.A.; Panetsos, P. Bayesian estimation of tension in bridge hangers using modal frequency measurements. Struct. Monit. Maint. 2016, 3, 349–375. [Google Scholar] [CrossRef]
- Xie, X.; Li, X. Genetic Algorithm-based tension identification of hanger by solving inverse eigenvalue problem. Inverse Probl. Sci. Eng. 2014, 22, 966–987. [Google Scholar] [CrossRef]
- Mehrabi, A.B.; Tabatabai, H. Unified Finite Difference Formulation for Free Vibration. J. Struct. Eng. 1998, 124, 1313–1322. [Google Scholar] [CrossRef]
- Sansò, F.; Venuti, G. Integer variables estimation problems: The Bayesian approach. Ann. Geophys. 1997, 40, 1415–1431. [Google Scholar]
- Irvine, H.M. Cable Structures; The MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Brien, O.; Eugene, J.; Malekjafarian, A.; Obrien, E. Application of output-only modal method in monitoring of bridges using an instrumented vehicle. In Proceedings of the Civil Engineering Research in Ireland Conference, Belfast, UK, 28–29 August 2014. [Google Scholar]
- Ubertini, F.; Comanducci, G.; Cavalagli, N. Vibration-based structural health monitoring of a historic bell-tower using output-only measurements and multivariate statistical analysis. Struct. Heal. Monit. 2016, 15, 438–457. [Google Scholar] [CrossRef]
- Chen, J.; Kemna, A.; Hubbard, S.S. A comparison between Gauss-Newton and Markov chain Monte Carlo based methods for inverting spectral induced polarization data for Cole-Coleparameters. Geophysics 2008, 73, 247–259. [Google Scholar] [CrossRef]
- Beck, J.L. Bayesian system identification based on probability logic. Struct. Ctrl. Heal. Monit. 2010, 17, 825–847. [Google Scholar] [CrossRef]
- Erazo, K.; Nagarajaiah, S. An offline approach for output-only Bayesian identification of stochastic nonlinear systems using unscented Kalman filtering. J. Sound Vib. 2017, 397, 222–240. [Google Scholar] [CrossRef]
- Li, Z.; Feng, M.Q.; Luo, L.; Feng, D.; Xu, X. Statistical analysis of modal parameters of a suspension bridge based on Bayesian spectral density approach and shm data. Mech. Sys. Signal Proc. 2018, 98, 352–367. [Google Scholar] [CrossRef]
- Sun, H.; Büyüköztürk, O. Bayesian Model Updating Using Incomplete Modal Data without Mode Matching. Proc. SPIE 2016, 9805, 98050D. [Google Scholar]
- Barger, K.; Bunge, J. Objective Bayesian estimation for the number of species. Bayesian Anal. 2010, 5, 765–786. [Google Scholar] [CrossRef]
- Garcia, J.G.; Roncagliolo, P.A.; Carlos, H. A Bayesian technique for real and integer parameters estimation in linear models and its application to GNSS high precision positioning. IEEE Trans. Signal Process. 2016, 64, 923–933. [Google Scholar] [CrossRef]
- Liang, F.; Liu, C.; Carroll, R. Advanced Markov Chain Monte Carlo Methods: Learning from Past Samples; Wiley: New York, NY, USA, 2011; ISBN 1119956803. [Google Scholar]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–511. [Google Scholar] [CrossRef]
- Zhan, S.; Chen, M.; Li, Z.; Sun, W.; Li, W.J.; Zhang, G. Large bridge cable tension estimation with cyber vibration sensing system. In Proceedings of the IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems, Chengdu, China, 19–22 June 2016; pp. 121–125. [Google Scholar]




| Cable No. | ξ | N (MN) | EI (×106 N·m2) | L (m) |
|---|---|---|---|---|
| 1 | 20.0 | 0.8 | 0.2 | 10 |
| 2 | 40.0 | 0.32 | 0.5 | 50 |
| 3 | 70.7 | 0.5 | 1 | 100 |
| 4 | 198.0 | 0.392 | 0.1 | 100 |
| Cable No. | Model Order | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 24.2 | 38.3 | 54.5 (K1) | 73.4 (K2) | 95.2 (K3) | 120 (K4) | 148.4 | 180 |
| 2 | 3 | 4.5 (K1) | 6.1 (K2) | 7.8 (K3) | 9.7 (K4) | 11.7 | 13.8 | 16.1 |
| 3 | 1.8 | 2.8 | 3.7 | 4.7 | 5.7 (K1) | 6.7 (K2) | 7.8 (K3) | 8.8 (K4) |
| 4 | 1.6 (K1) | 2.4 (K2) | 3.2 (K3) | 4.1 (K4) | 4.9 | 5.7 | 6.5 | 7.3 |
| Length (m) | Diameter (mm) | Elastic Modulus (Pa) | Theoretical Sectional Area (mm2) | Mass per Unit Length (kg/m) |
|---|---|---|---|---|
| 110 | 56 | 1.1 × 1011 | 1490 | 13.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, S.; Li, Z.; Hu, J.; Liang, Y.; Zhang, G. Model Order Identification for Cable Force Estimation Using a Markov Chain Monte Carlo-Based Bayesian Approach. Sensors 2018, 18, 4187. https://doi.org/10.3390/s18124187
Zhan S, Li Z, Hu J, Liang Y, Zhang G. Model Order Identification for Cable Force Estimation Using a Markov Chain Monte Carlo-Based Bayesian Approach. Sensors. 2018; 18(12):4187. https://doi.org/10.3390/s18124187
Chicago/Turabian StyleZhan, Shaodong, Zhi Li, Jianmin Hu, Yiping Liang, and Guanglie Zhang. 2018. "Model Order Identification for Cable Force Estimation Using a Markov Chain Monte Carlo-Based Bayesian Approach" Sensors 18, no. 12: 4187. https://doi.org/10.3390/s18124187
APA StyleZhan, S., Li, Z., Hu, J., Liang, Y., & Zhang, G. (2018). Model Order Identification for Cable Force Estimation Using a Markov Chain Monte Carlo-Based Bayesian Approach. Sensors, 18(12), 4187. https://doi.org/10.3390/s18124187





