A Tellurium Oxide Microcavity Resonator Sensor Integrated On-Chip with a Silicon Waveguide
Abstract
1. Introduction
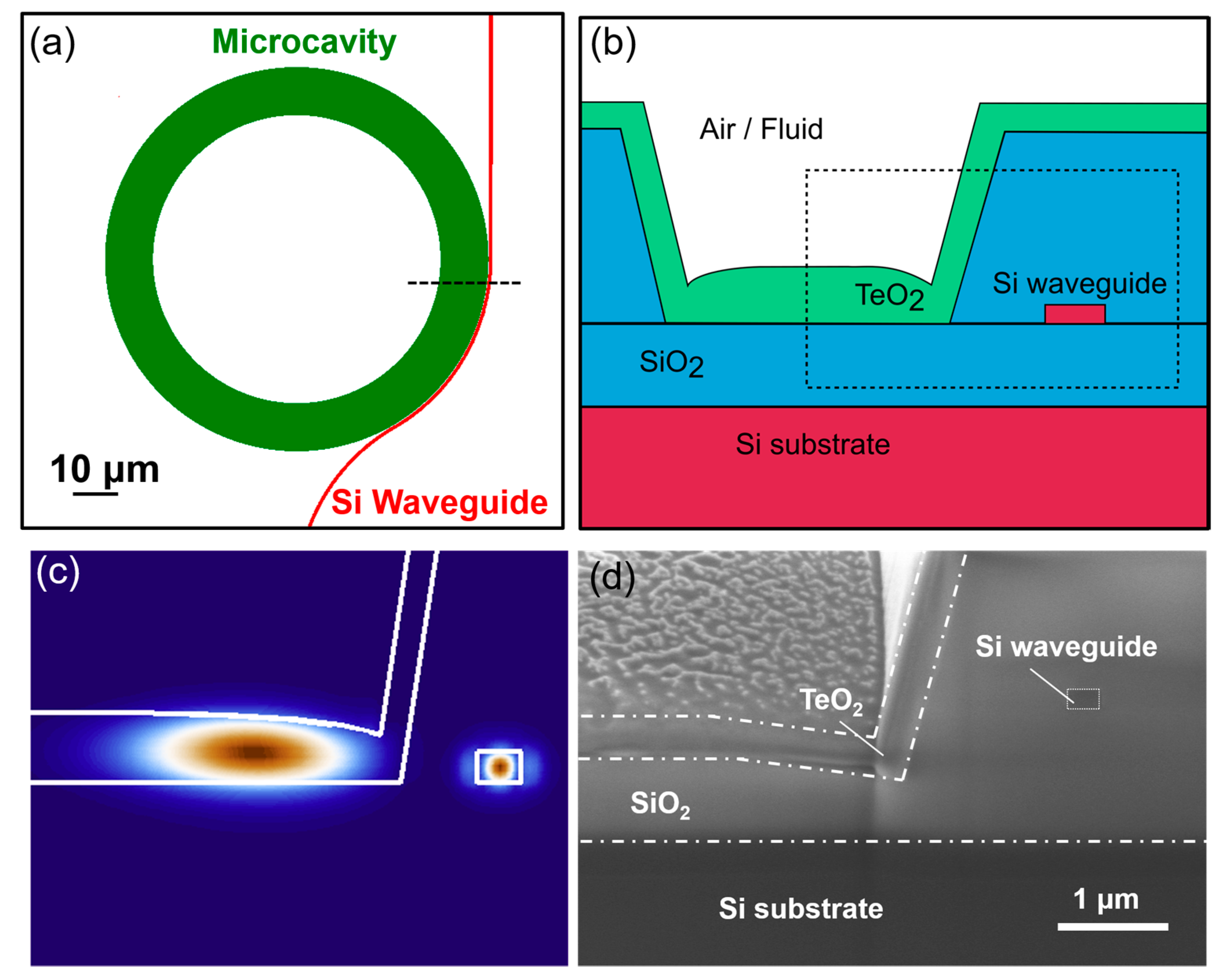
2. Microcavity Properties and Characterization
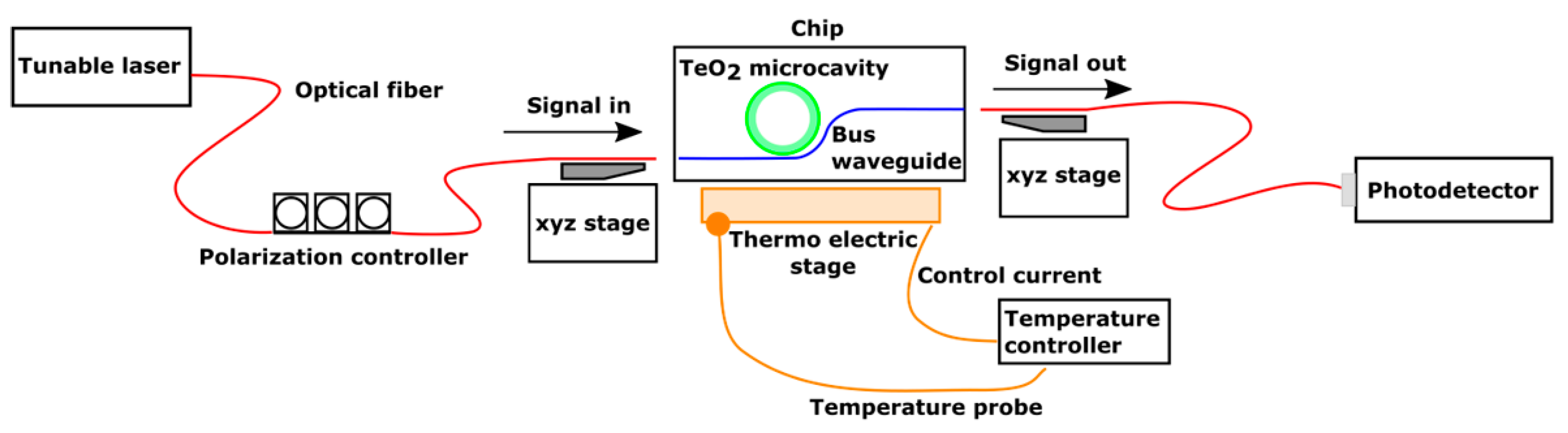
3. Sensing Experiments
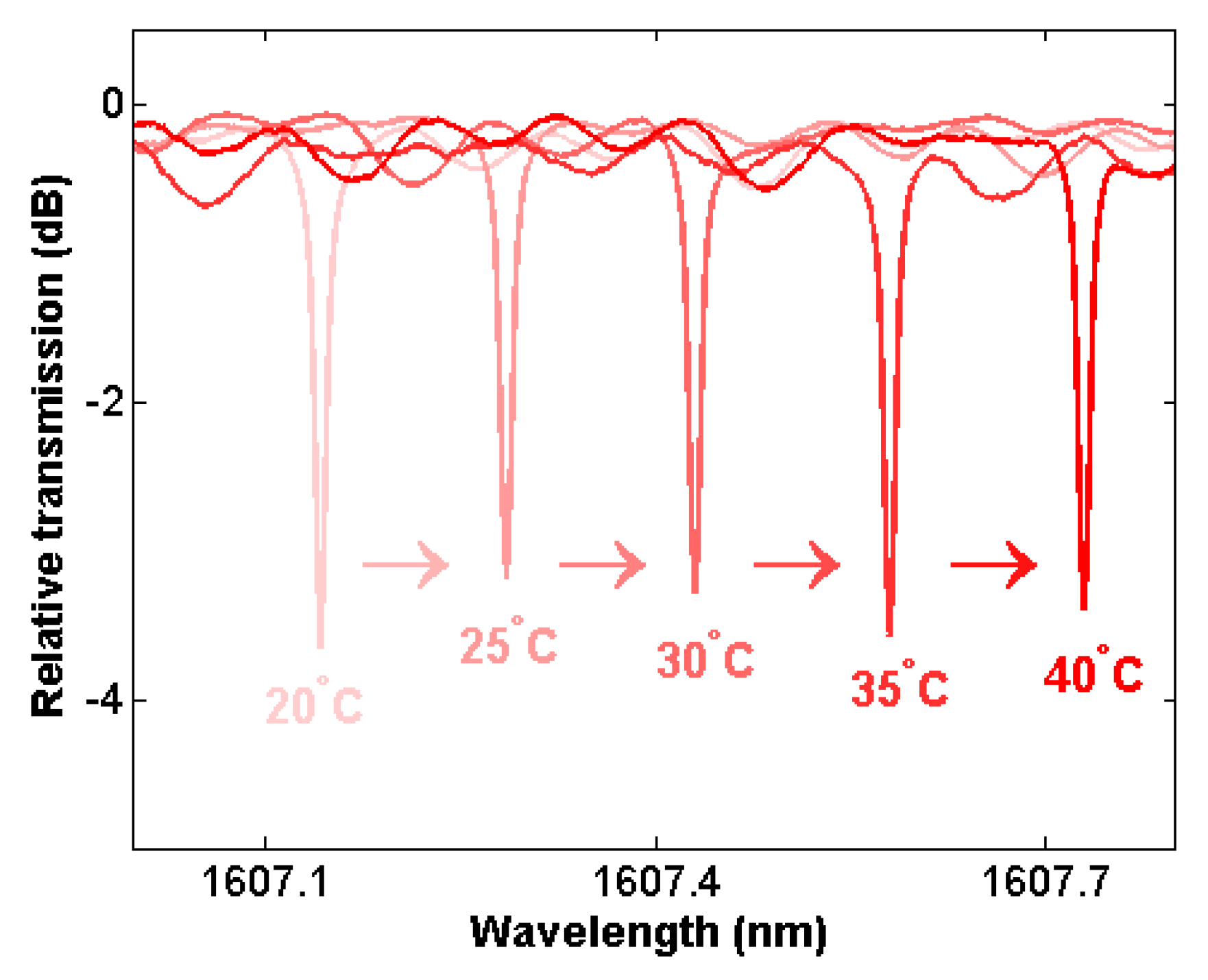
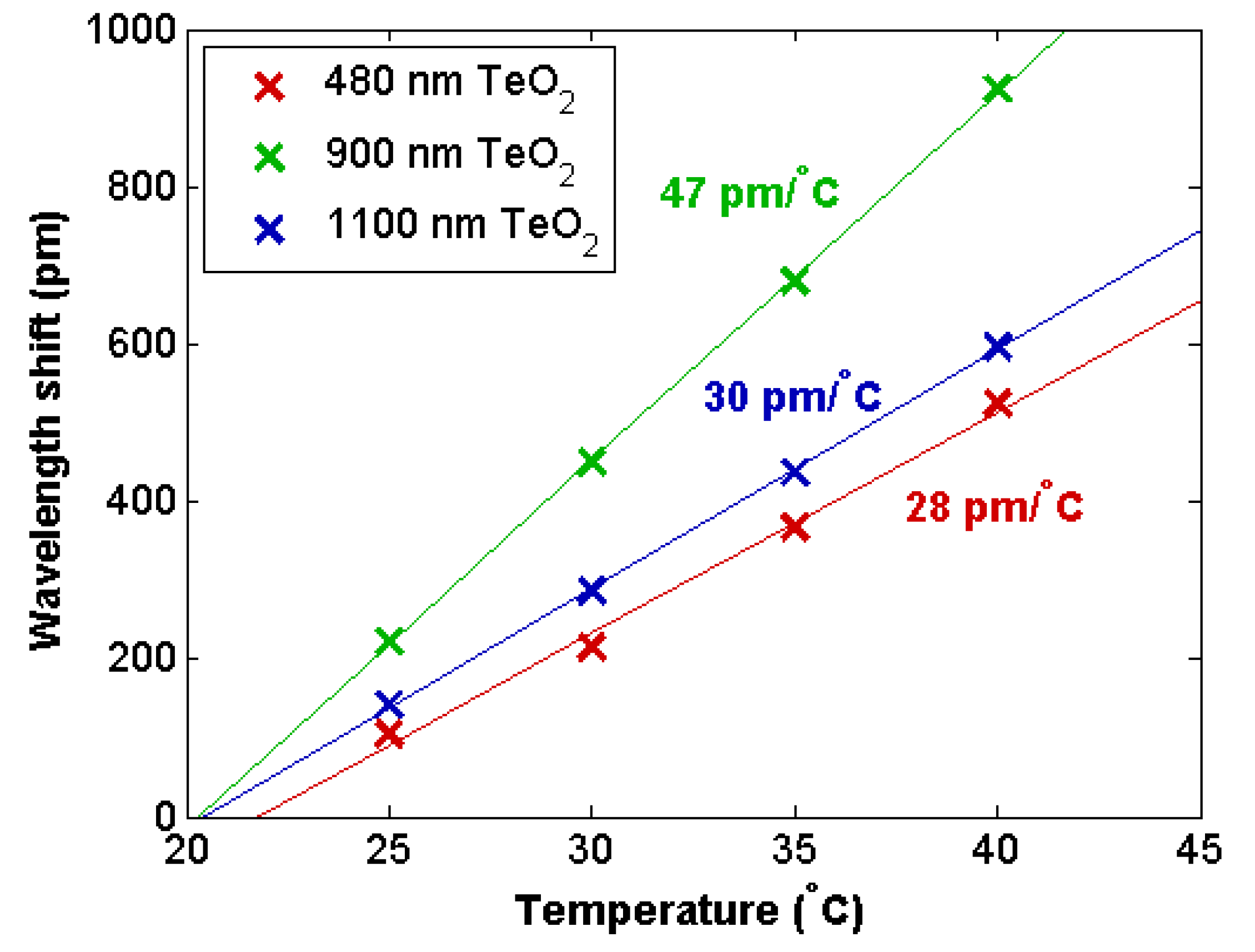
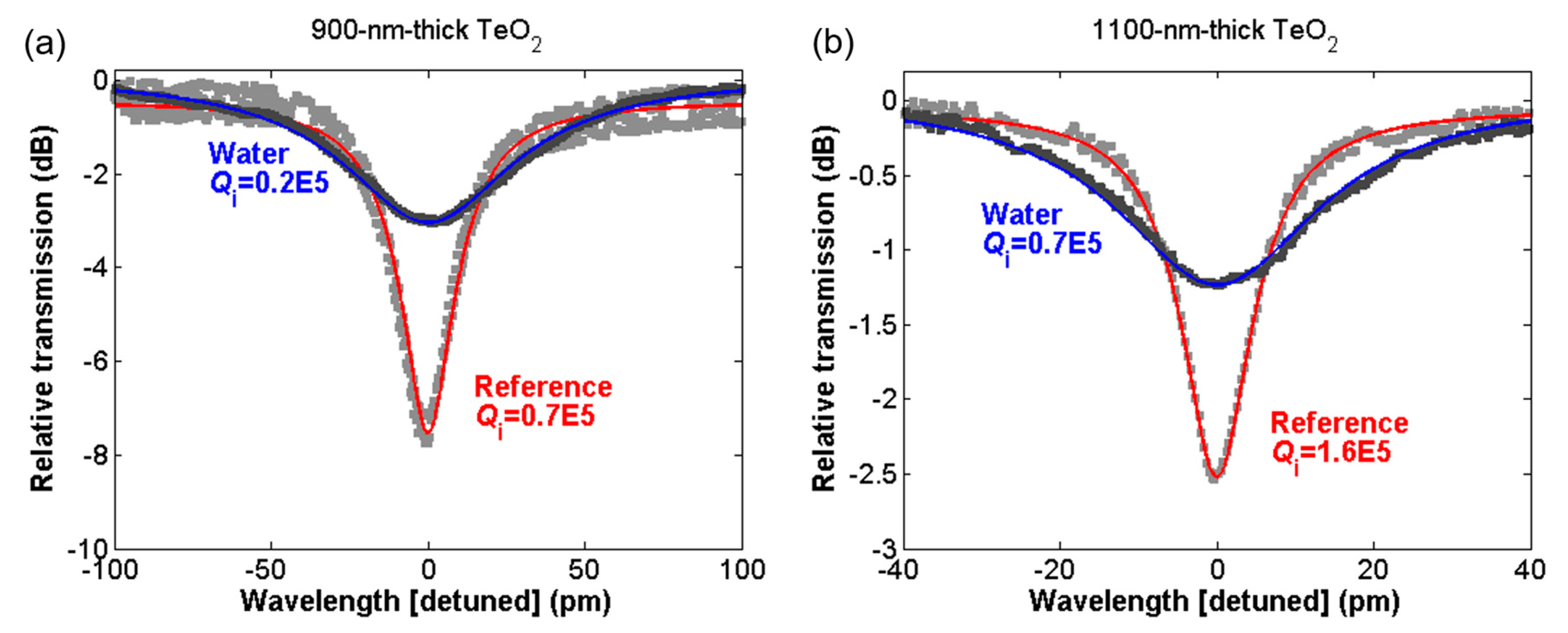
3.1. Thermal Sensing
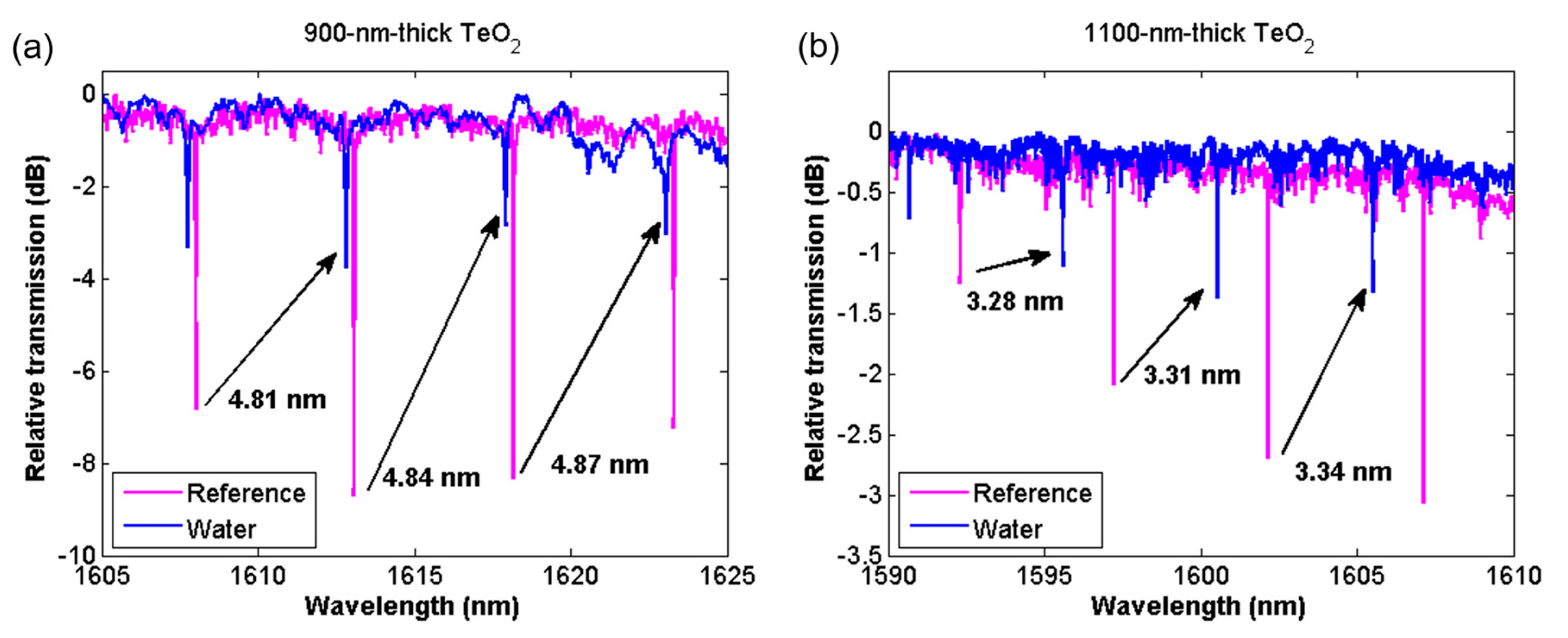
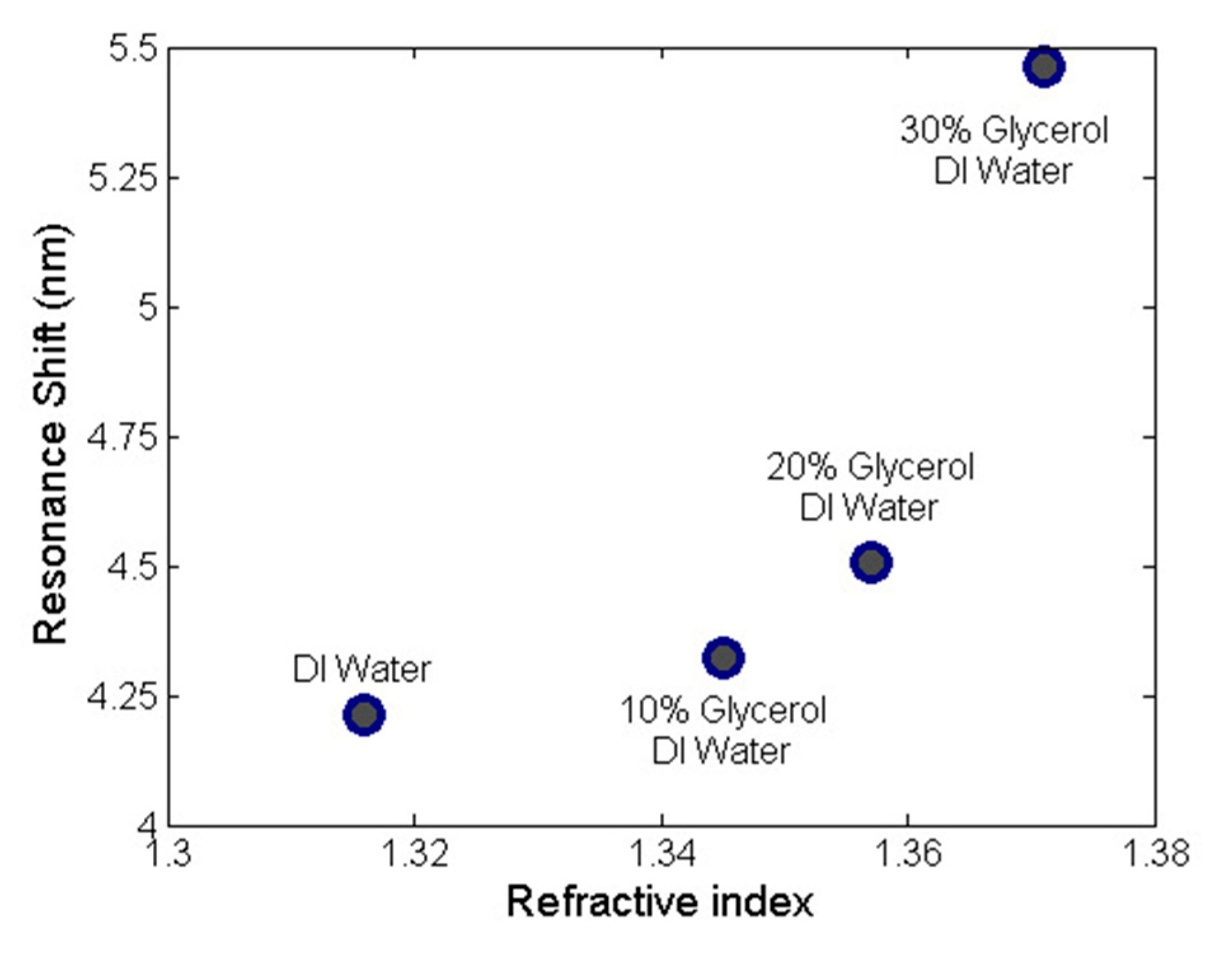
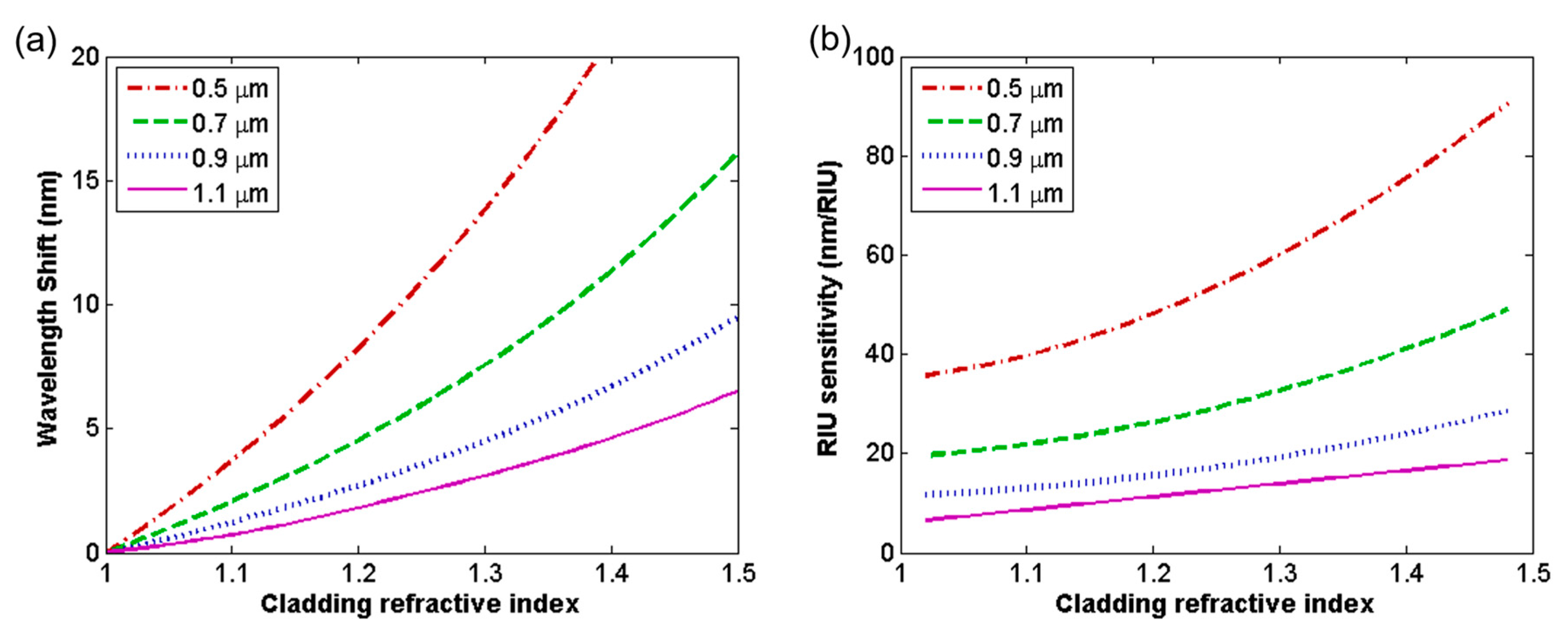
3.2. Evanescent Field Sensing
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gavela, A.F.; García, D.G.; Ramirez, J.C.; Lechuga, L.M. Last advances in silicon-based optical biosensors. Sensors 2016, 16, 285. [Google Scholar]
- De Vos, K.; Bartolozzi, I.; Schacht, E.; Bienstman, P.; Baets, R. Silicon-on-Insulator microring resonator for sensitive and label-free biosensing. Opt. Express 2007, 15, 7610–7615. [Google Scholar] [CrossRef] [PubMed]
- TalebiFard, S.; Schmidt, S.; Shi, W.; Wu, W.; Jaeger, N.A.F.; Kwok, E.; Ratner, D.M.; Chrostowski, L. Optimized sensitivity of Silicon-on-Insulator (SOI) strip waveguide resonator sensor. Biomed. Opt. Express 2017, 8, 500–511. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, S.; Flueckiger, J.; Wu, W.; Grist, S.M.; Talebi Fard, S.; Donzella, V.; Khumwan, P.; Thompson, E.R.; Wang, Q.; Kulik, P.; et al. Improving the performance of silicon photonic rings, disks, and Bragg gratings for use in label-free biosensing. Proc. SPIE 2014, 9166, 91660M. [Google Scholar]
- Chrostowski, L.; Grist, S.; Flueckiger, J.; Shi, W.; Wang, X.; Ouellet, E.; Yun, H.; Webb, M.; Nie, B.; Liang, Z.; et al. Silicon photonic resonator sensors and devices. Proc. SPIE 2012, 8236, 823620. [Google Scholar]
- Iqbal, M.; Gleeson, M.A.; Spaugh, B.; Tybor, F.; Gunn, W.G.; Hochberg, M.; Baehr-Jones, T.; Bailey, R.C.; Gunn, L.C. Label-free biosensor arrays based on silicon ring resonators and high-speed optical scanning instrumentation. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 654–661. [Google Scholar] [CrossRef]
- Kim, G.-D.; Lee, H.-S.; Park, C.-H.; Lee, S.-S.; Lim, B.T.; Bae, H.K.; Lee, W.-G. Silicon photonic temperature sensor employing a ring resonator manufactured using a standard CMOS process. Opt. Express 2010, 18, 22215–22221. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Hafezi, M.; Fan, J.; Taylor, J.M.; Strouse, G.F.; Ahmed, Z. Ultra-sensitive chip-based photonic temperature sensor using ring resonator structures. Opt. Express 2014, 22, 3098–3104. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-T.; Yu, M. Cascaded ring resonator-based temperature sensor with simultaneously enhanced sensitivity and range. Opt. Express 2016, 24, 9501–9510. [Google Scholar] [CrossRef] [PubMed]
- Janz, S.; Xu, D.-X.; Vachon, M.; Sabourin, N.; Cheben, P.; McIntosh, H.; Ding, H.; Wang, S.; Schmid, J.H.; Delâge, A.; et al. Photonic wire biosensor microarray chip and instrumentation with application to serotyping of Escherichia coli isolates. Opt. Express 2013, 21, 4623–4637. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhou, X.; Qiao, Z.; Zhang, J.; Zhang, C.; Xiang, T.; Shui, L.; Shi, Y.; Liu, L. Integrated optical chemical sensor based on an SOI ring resonator using phase-interrogation. IEEE Photonics J. 2014, 6, 1–7. [Google Scholar]
- Lo, S.M.; Hu, S.; Gaur, G.; Kostoulas, Y.; Weiss, S.M.; Fauchet, P.M. Photonic crystal microring resonator for label-free biosensing. Opt. Express 2017, 25, 7046–7054. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.; Wang, X.; Frandsen, L.H. Optical temperature sensor with enhanced sensitivity by employing hybrid waveguides in a silicon Mach-Zehnder interferometer. Opt. Express 2016, 24, 16349–16356. [Google Scholar] [CrossRef] [PubMed]
- Girault, P.; Lorrain, N.; Poffo, L.; Guendouz, M.; Lemaitre, J.; Carré, C.; Gadonna, M.; Bosc, D.; Vignaud, G. Integrated polymer micro-ring resonators for optical sensing applications. J. Appl. Phys. 2015, 117, 104504. [Google Scholar] [CrossRef]
- Zhang, D.; Men, L.; Chen, Q. Femtosecond laser fabricated polymer microring resonator for sensing applications. Electron. Lett. 2018, 54, 888–890. [Google Scholar] [CrossRef]
- Pucker, G.; Samusenko, A.; Ghulinyan, M.; Pasquardini, L.; Chalyan, T.; Guider, R.; Gandolfi, D.; Adami, A.; Lorenzelli, L.; Pavesi, L. An integrated optical biosensor platform. SPIE Newsroom 2016. [Google Scholar] [CrossRef]
- Ksendzov, A.; Lin, Y. Integrated optics ring-resonator sensors for protein detection. Opt. Lett. 2005, 30, 3344–3346. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Li, Z.; Yi, H.; Zhou, Z.; Yu, J. Microring resonator for glucose sensing applications. Front. Optoelectron. China 2009, 2, 304–307. [Google Scholar] [CrossRef]
- Wang, J.; Yao, Z.; Poon, A.W. Silicon-nitride-based integrated optofluidic biochemical sensors using a coupled-resonator optical waveguide. Front. Mater. 2015, 2, 1–13. [Google Scholar] [CrossRef]
- Madden, S.J.; Vu, K.T. Very low loss reactively ion etched Tellurium Dioxide planar rib waveguides for linear and non-linear optics. Opt. Express 2009, 17, 17645–17651. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Shaw, M.J.; Vawter, G.A.; Hadley, G.R.; Esherick, P.; Sullivan, C.T. High-Q microring resonator for biochemical sensors. Proc. SPIE 2005, 5728, 83–92. [Google Scholar]
- Hu, J.; Sun, X.; Agarwal, A.; Kimerling, L.C. Design guidelines for optical resonator biochemical sensors. J. Opt. Soc. Am. B 2009, 26, 1032–1041. [Google Scholar] [CrossRef]
- Righini, G.C.; Dumeige, Y.; Féron, P.; Ferrari, M.; Nunzi Conti, G.; Ristic, D.; Soria, S. Whispering gallery mode microresonators: Fundamentals and applications. Riv. Nuovo Cimento 2011, 34, 435–488. [Google Scholar]
- Foreman, M.R.; Swaim, J.D.; Vollmer, F. Whispering gallery mode sensors. Adv. Opt. Photonics 2015, 7, 168–240. [Google Scholar] [CrossRef] [PubMed]
- Vu, K.; Madden, S. Tellurium dioxide Erbium doped planar rib waveguide amplifiers with net gain and 2.8 dB/cm internal gain. Opt. Express 2010, 18, 19192–19200. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Song, F.; Jiang, S.; Peyghambarian, N.; Kuwata-Gonokami, M.; Xu, L. Fiber-taper-coupled L-band Er3+-doped tellurite glass microsphere laser. Appl. Phys. Lett. 2003, 82, 1497–1499. [Google Scholar] [CrossRef]
- Sasagawa, K.; Yonezawa, Z.; Iwai, R.; Ohta, J.; Nunoshita, M. S-band Tm3+-doped tellurite glass microsphere laser via a cascade process. Appl. Phys. Lett. 2004, 85, 4325–4327. [Google Scholar] [CrossRef]
- Ruan, Y.; Boyd, K.; Ji, H.; Francois, A.; Ebendorff-Heidepriem, H.; Munch, J.; Monro, T.M. Tellurite microspheres for nanoparticle sensing and novel light sources. Opt. Express 2014, 22, 11995–12006. [Google Scholar] [CrossRef] [PubMed]
- Vanier, F.; Côte, F.; El Amraoui, M.; Messaddeq, Y.; Peter, Y.-A.; Rochette, M. Low-threshold lasing at 1975 nm in thulium-doped tellurite glass microspheres. Opt. Lett. 2015, 40, 5227–5230. [Google Scholar] [CrossRef] [PubMed]
- Ostby, E.P.; Vahala, K.J. Yb-doped glass microcavity laser operation in water. Opt. Lett. 2009, 34, 1153–1155. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Özdemir, Ş.K.; Zhu, J.; Kim, W.; Yang, L. Detecting single viruses and nanoparticles using whispering gallery microlasers. Nat. Nanotechnol. 2011, 6, 428–432. [Google Scholar] [CrossRef] [PubMed]
- Bradley, J.D.B.; Hosseini, E.S.; Purnawirman; Su, Z.; Adam, T.N.; Leake, G.; Coolbaugh, D.; Watts, M.R. Monolithic erbium-and ytterbium-doped microring lasers on silicon chips. Opt. Express 2014, 22, 12226–12237. [Google Scholar] [CrossRef] [PubMed]
- Su, Z.; Li, N.; Magden, E.S.; Byrd, M.; Purnawirman; Adam, T.N.; Leake, G.; Coolbaugh, D.; Bradley, J.D.B.; Watts, M.R. Ultra-compact and low-threshold thulium microcavity laser monolithically integrated on silicon. Opt. Lett. 2016, 41, 5708–5711. [Google Scholar] [CrossRef] [PubMed]
- Frankis, H.C.; Bradley, J.D.B. Reactively sputtered tellurium oxide films for integrated photonics. In Proceedings of the Photonics North, Ottawa, ON, Canada, 6–8 June 2017. Paper MATERIALS-54. [Google Scholar]
- Honma, T.; Ito, N.; Komatsu, T.; Dimitrov, V. Thermo-optic properties and electronic polarizability in alkali tellurite glasses. J. Am. Ceram. Soc. 2010, 93, 3223–3229. [Google Scholar] [CrossRef]
- Yoshie, T.; Tang, L.; Su, S.Y. Optical microcavity: Sensing down to single molecules and atoms. Sensors 2011, 11, 1972–1991. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.-X.; Vachon, M.; Densmore, A.; Ma, R.; Delâge, A.; Janz, S.; Lapointe, J.; Li, Y.; Lopinski, G.; Zhang, D.; et al. Label-free biosensor array based on silicon-on-insulator ring resonators addressed using a WDM approach. Opt. Lett. 2010, 35, 2771–2773. [Google Scholar] [CrossRef] [PubMed]
- Su, Z.; Li, N.; Frankis, H.C.; Magden, E.S.; Adam, T.N.; Leake, G.; Coolbaugh, D.; Bradley, J.D.B.; Watts, M.R. High-Q-factor Al2O3 micro-trench cavities integrated with silicon nitride waveguides on silicon. Opt. Express 2018, 26, 11161–11170. [Google Scholar] [CrossRef] [PubMed]
- Pietralunga, S.M.; Lanata, M.; Ferè, M.; Piccinin, D.; Cusmai, G.; Torregiani, M.; Martinelli, M. High-contrast waveguides in sputtered pure TeO2 glass thin films. Opt. Express 2008, 16, 21662–21670. [Google Scholar] [CrossRef] [PubMed]
- Vasiliev, A.; Malik, A.; Muneeb, M.; Kuyken, B.; Baets, R.; Roelkens, G. On-chip mid-infrared photothermal spectroscopy using suspended silicon-on-insulator microring resonators. ACS Sens. 2016, 1, 1301–1307. [Google Scholar] [CrossRef]
| Figure of Merit | 480-nm-Thick TeO2 Resonator | 900-nm-Thick TeO2 Resonator | 1100-nm-Thick TeO2 Resonator |
|---|---|---|---|
| Extinction Ratio | 2 dB | 9 dB | 3 dB |
| Free Spectral Range | 5.1 nm | 5.1 nm | 4.9 nm |
| Thermal Sensitivity | 28 pm/°C | 47 pm/°C | 30 pm/°C |
| Q Factor (in Air) | 0.4 × 105 | 0.7 × 105 | 1.6 × 105 |
| Q Factor (in Water) | - | 0.2 × 105 | 0.7 × 105 |
| Evanescent Field Sensitivity | - | 15.4 nm/RIU | 10.6 nm/RIU |
| Limit of Detection | - | 5.2 × 10−3 RIU | 2.2 × 10−3 RIU |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frankis, H.C.; Su, D.; Bonneville, D.B.; Bradley, J.D.B. A Tellurium Oxide Microcavity Resonator Sensor Integrated On-Chip with a Silicon Waveguide. Sensors 2018, 18, 4061. https://doi.org/10.3390/s18114061
Frankis HC, Su D, Bonneville DB, Bradley JDB. A Tellurium Oxide Microcavity Resonator Sensor Integrated On-Chip with a Silicon Waveguide. Sensors. 2018; 18(11):4061. https://doi.org/10.3390/s18114061
Chicago/Turabian StyleFrankis, Henry C., Daniel Su, Dawson B. Bonneville, and Jonathan D. B. Bradley. 2018. "A Tellurium Oxide Microcavity Resonator Sensor Integrated On-Chip with a Silicon Waveguide" Sensors 18, no. 11: 4061. https://doi.org/10.3390/s18114061
APA StyleFrankis, H. C., Su, D., Bonneville, D. B., & Bradley, J. D. B. (2018). A Tellurium Oxide Microcavity Resonator Sensor Integrated On-Chip with a Silicon Waveguide. Sensors, 18(11), 4061. https://doi.org/10.3390/s18114061






