Message Integration Authentication in the Internet-of-Things via Lattice-Based Batch Signatures
Abstract
1. Introduction
1.1. Batch Signature
1.2. Lattice-Based Signature
1.3. Our Contributions
- We propose lattice-based batch signature schemes for the first time. Our schemes possess a general property, that is, our construction can be combined with any existing lattice-based signature scheme.
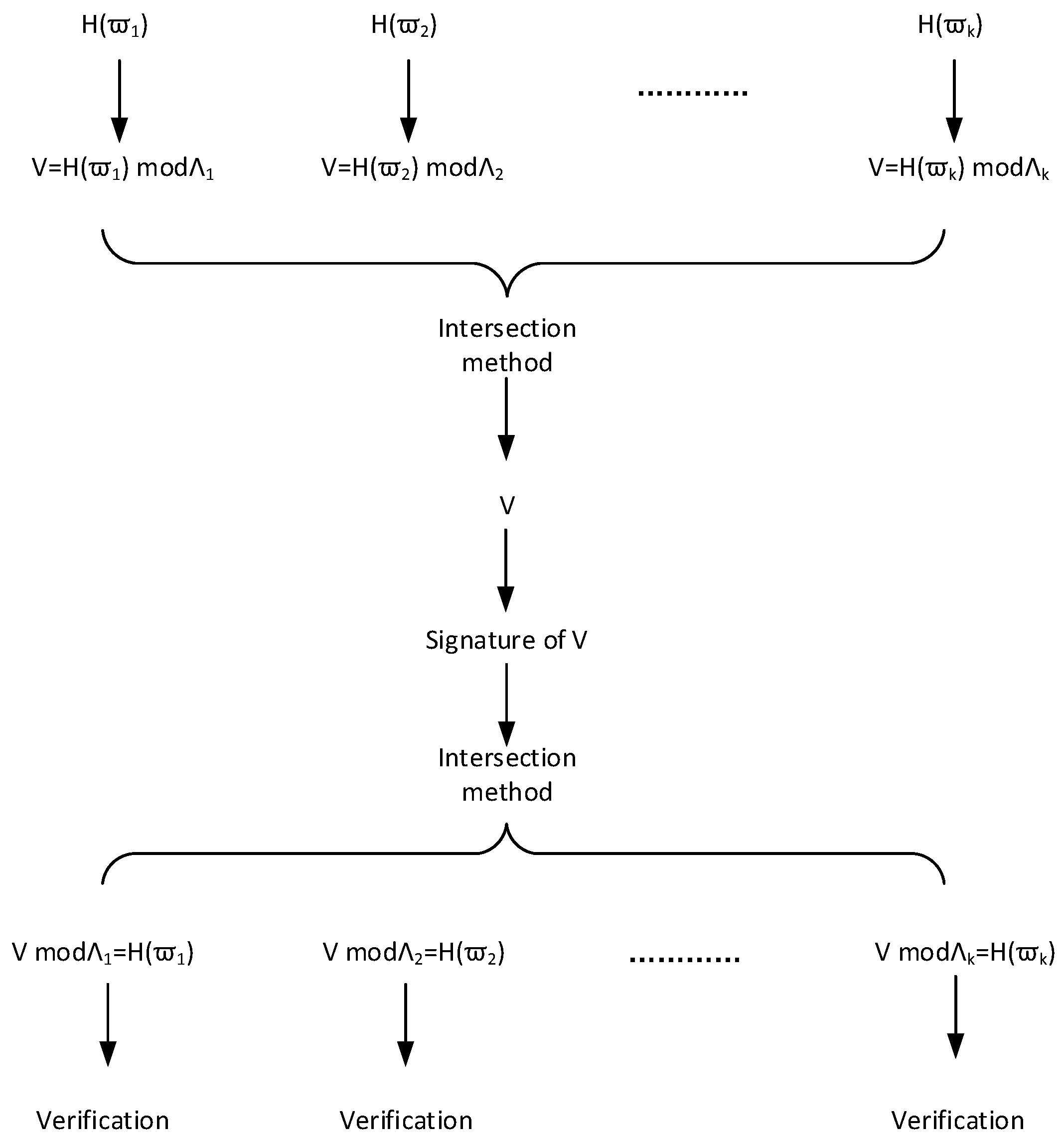
- The technique we use is an extension of the intersection method from [27]. The intersection method is as follows: for —dimensional integer lattices and such that and , there exists a short vector , which belongs to and can be viewed as a signature of and .We demonstrate this technique with a concrete example in terms of . In detail, let , with k primes . Because are different primes, and . Therefore, for k messages , there exists a short vector , which binds and can be viewed as their batch signature.
- With the intersection method as core technique, we give two batch signature schemes based on hash-and-sign paradigm and Fiat–Shamir transformation, as well as a lattice-based batch signature scheme based on binary tree.
1.4. Organization
2. Preliminaries
- (length-compressing):
- (hard to find collisions): For all PPT A, there exists a negligible function ϵ such that for all security parameters,
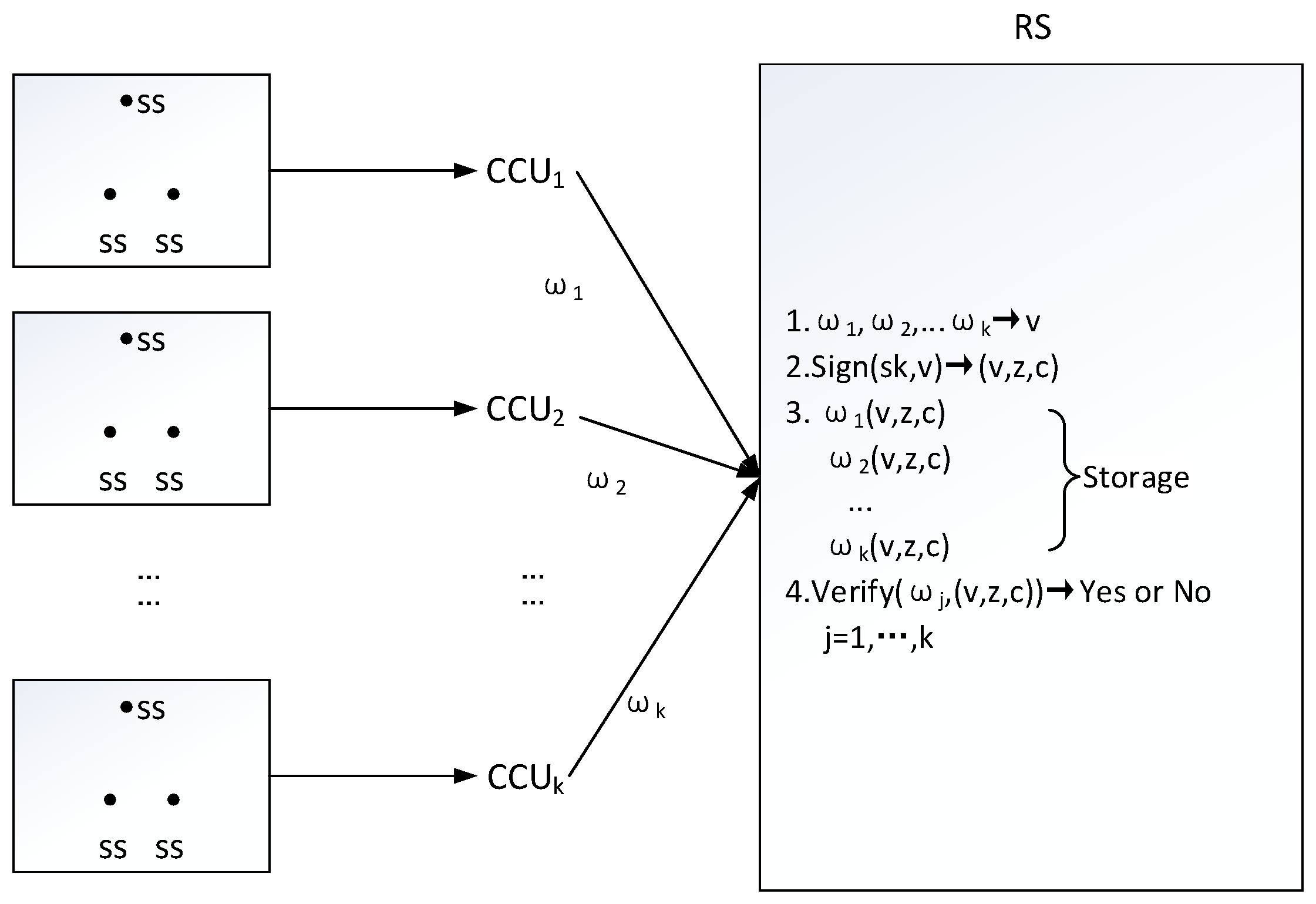
3. System Definition and Threat Model
3.1. Definition of Batch Signature System
- Setup(): Inputting security parameter , this algorithm determines necessary system public parameters .
- KeyGen(): With security parameter and system parameters as above, this algorithm provides public verification key and secret signing key .
- Sign(): Given signing key and messages set , this algorithm computes batch signature e.
- Verify(): Given message and its signature e associated with verification key , this algorithm tells whether the j-th message has gained valid authentication, and outputs 1 if the answer is yes, otherwise outputs 0.
3.2. Threat Model
- Initialization: In this period, challenger executes algorithms Setup and KeyGen, provides system public parameters and public verification key for adversary .
- Signing queries: In this stage, adversary selects a set of messages , sends the messages’ set to challenger for the associated signature. Challenger invokes Sign algorithm, returns the result to adversary . Adversary may repeat the query polynomial times in his favorite manner.
- Forgery: Once adversary terminates signing queries, he offers a new message-signature pair .
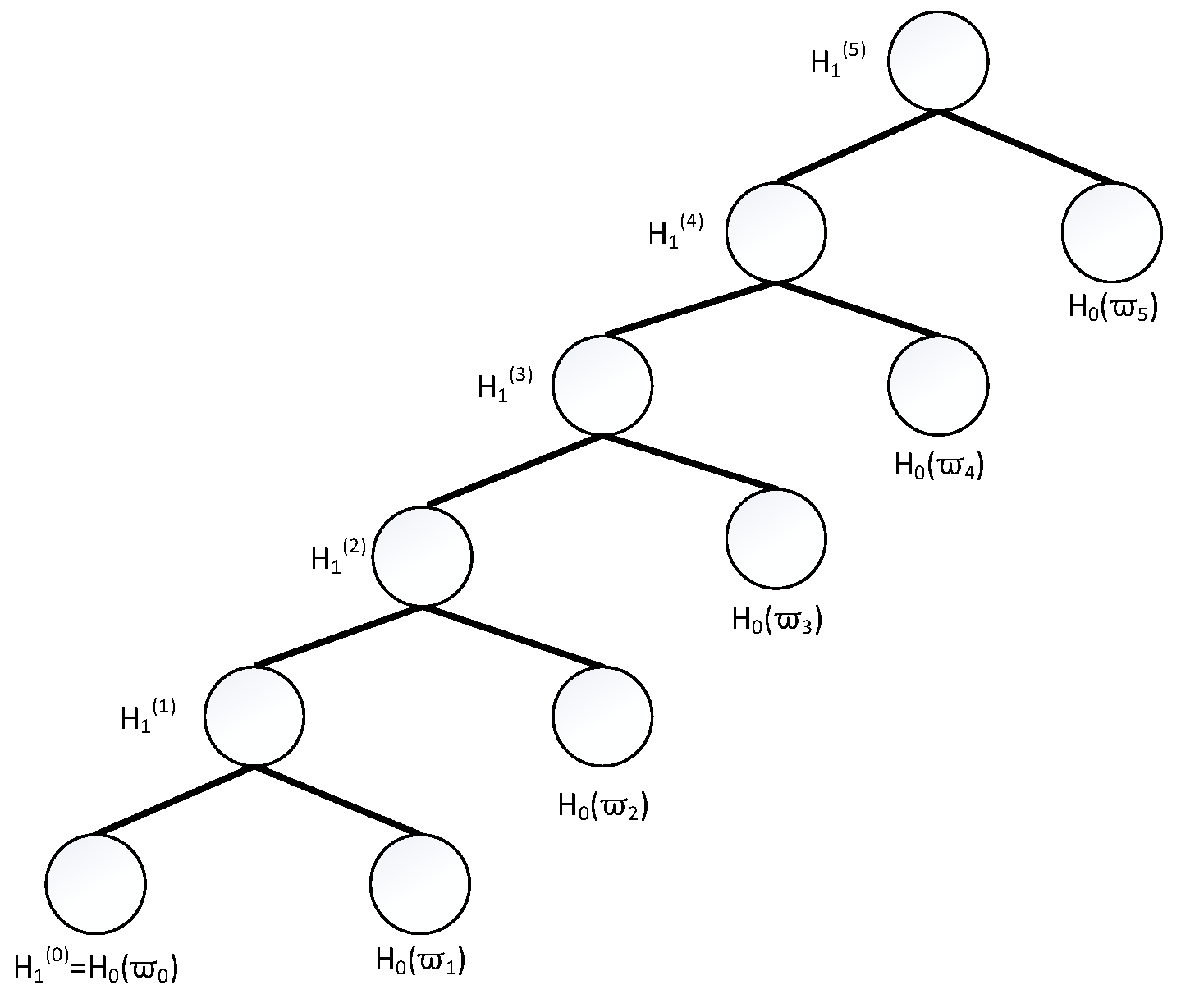
4. Lattice-Based Batch Signature with Binary Tree
4.1. Proposed Construction
- Setup(): In this stage, system parameters are provided with knowledge of security parameter .
- n is a polynomial of , is a polynomial of n, , .
- k is the number of messages to batch sign, and is the Gaussian parameter.
- and are two collision resistant hash functions.
- KeyGen(): With system parameters as above, public verification key and secret signing key are obtained as follows. Invoke trapdoor generation algorithm TrapGen to get a uniform and random matrix , and the short basis for lattice with .Finally output , .
- Sign(): Given and the set of messages , the following steps lead to batch signature on such messages.
- Compute , ,⋯, , let , and execute for-loop as follows.for to :
- Compute SamplePre.
- For , compute its brother . Firstly, , the left are shown in the next for-loop.for to :Here, for ’s brother , its first entry denotes ’s brother note, its second entry denotes the brother locates on ’s left or right .
- For , compute its residue . At first,,the left are shown in the next for-loop.for to :When , .Here, ’s residue includes ’s brother and all of its ancestor nodes’s brothers.
- For , its signature is .
- Verify(): Given message and its signature associated with verification key ,
- should be recovered firstly.(1) If ,,for to :When for-loop terminates, is obtained.(2) If ,,for to :When for-loop terminates, is obtained.
- Check whether and . If both relations are true, return 1 and accept the message-signature pair ; otherwise, return 0 and reject the message-signature pair.
4.2. Security Analysis
- Initialization: In this period, challenger executes setup algorithm to set system parameters, he sets public verification key , sends all of them to adversary .
- Hash queries: Challenger creates a list to save the binary tree for k messages, and sets .When adversary sends a set of messages to challenger for hash values. searches list ,If do not exist in list , chooses , sets . Then randomly picks , , sets for to , here . saves in the list .If exist in list , does nothing.At last, returns to adversary .
- Signature queries: In this stage, adversary selects a set of messages , sends the messages’ set to challenger for the associated signature. Challenger firstly searches list for the messages’ set. If it exists, returns to adversary . If the messages’ set does not exist, executes hash query firstly. Adversary may repeat the query polynomial times in his favorite manner.
- Forgery: Once adversary terminates signing queries, he forges a valid message-signature pair .
5. Lattice-Based Batch Signature Based on Hash-and-Sign Paradigm
5.1. Design
- Setup(): In this stage, system parameters are provided with knowledge of security parameter .
- n is a polynomial of , is a polynomial of n, , .
- k is the number of messages to batch sign, and is the Gaussian parameter.
- is a collision resistant hash function.
- KeyGen(): With system parameters as above, public verification key and secret signing key are obtained in the following manners.
- Invoke trapdoor generation algorithm TrapGen to get a uniform and random matrix , and the short basis for lattice with .
- Compute k different lattices , such that and , which takes q as modulus.Then , .
- Sign(): Given and the set of messages , the following steps lead to batch signature on such messages.
- Construct equations:compute its solution .
- Invoke preimage sampleable algorithm SamplePre to get the signature .
- Verify(: For the j-th message and the signature , validation involves the following two relations:
- .
- .If they are both true, accept message ; otherwise, reject it.
5.2. Security Analysis
- Initialization: In this period, challenger sets appropriate system parameters, lets public verification key , sends all of them to adversary .
- Hash queries: Challenger creates a list to save the hash values for k messages, and sets .When adversary sends a set of messages to challenger for hash values. searches list .If exist in list , returns directly.If do not exist in list , samples , sets , and lets , . Then saves in list , and returns to adversary .
- Signing queries: In this stage, adversary selects a set of messages , sends the messages’ set to challenger for the associated signature. Challenger searches list for messages .If the messages exist in list , challenger returns directly.If the messages do not exist in list , Challenger firstly executes Hash query, then returns to adversary .
- Forgery: Once adversary terminates signing queries, he offers a new message-signature pair .Challenger searches in list , then computes as the solution to the SIS instance .Because message-signature pair is valid, adversary has not made signing query on , and hash query on has been done. Given , according to preimage min-entropy property of hash function [23], the min-entropy of is , so that with overwhelming probability. Because , . depends on the validity of forged signature. Therefore, .
6. Lattice-Based Batch Signature Based on FS Transformation
6.1. Design
- Setup(n): In this stage, system parameters are provided with knowledge of security parameter n.
- q may be , d may be 1, r may be 512.
- , satisfies .
- s may be , and M may be .
- and are collision resistant hash functions, where is the 1-norm of vector , namely, it is the sum of the absolute values of each element of vector .
- KeyGen(n): With system parameters as above, public verification key and secret signing key are obtained in the following manners.
- Select randomly as secret signing key.
- Select , compute as public verification key.
- Compute k different lattices , such that and , which takes q as modulus.Then , .
- Sign(): Given and the set of messages , the following steps lead to batch signature on such messages.
- Construct equations:compute its solution .
- Sample randomly, compute .
- Let , output as signature with probability .
- Verify(: For the j-th message and the signature , validation involves the following three relations:
- .
- .
- .If they are true, accept message ; otherwise, reject it.
6.2. Security Analysis
7. Efficiency Comparison and the Application to IoT
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gubbi, J.; Buyya, R.; Marusic, S.; Palaniswami, M. Internet of Things (IoT): A vision, architectural elements, and future directions. Future Gener. Comput. Syst. 2013, 29, 1645–1660. [Google Scholar] [CrossRef]
- Bennett, T.R.; Savaglio, C.; Lu, D.; Massey, H.; Wang, X.; Wu, J.; Jafari, R. MotionSynthesis Toolset (MoST): A Toolset for Human Motion Data Synthesis and Validation. In Proceedings of the 4th ACM MobiHoc Workshop on Pervasive Wireless Healthcare (MobileHealth ’14), Philadelphia, PA, USA, 11 August 2014; pp. 25–30. [Google Scholar] [CrossRef]
- Li, S.; Xu, L.D.; Zhao, S. The internet of things: A survey. Inf. Syst. Front. 2015, 17, 243–259. [Google Scholar] [CrossRef]
- Fortino, G.; Russo, W.; Savaglio, C.; Viroli, M.; Zhou, M. Modeling Opportunistic IoT Services in Open IoT Ecosystems. In Proceedings of the 18th Workshop “From Objects to Agents” (WOA 2017), Scilla (RC), Italy, 15–16 June 2017; pp. 90–95. [Google Scholar]
- Diffie, W.; Hellman, M.E. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Goldwasser, S.; Micali, S.; Yao, A.C. On Signatures and Authentication. In Advances in Cryptology: Proceedings of CRYPTO ’82, Santa Barbara, CA, USA, 23–25 August 1982; Chaum, D., Rivest, R.L., Sherman, A.T., Eds.; Plenum Press: New York, NY, USA, 1982; pp. 211–215. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L.M. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems (Reprint). Commun. ACM 1983, 26, 96–99. [Google Scholar] [CrossRef]
- Huang, X.; Liu, J.K.; Tang, S.; Xiang, Y.; Liang, K.; Xu, L.; Zhou, J. Cost-Effective Authentic and Anonymous Data Sharing with Forward Security. IEEE Trans. Comput. 2015, 64, 971–983. [Google Scholar] [CrossRef]
- Liang, K.; Chu, C.; Tan, X.; Wong, D.S.; Tang, C.; Zhou, J. Chosen-ciphertext secure multi-hop identity-based conditional proxy re-encryption with constant-size ciphertexts. Theor. Comput. Sci. 2014, 539, 87–105. [Google Scholar] [CrossRef]
- Ning, J.; Cao, Z.; Dong, X.; Liang, K.; Ma, H.; Wei, L. Auditable σ-Time Outsourced Attribute-Based Encryption for Access Control in Cloud Computing. IEEE Trans. Inf. Forensics Secur. 2018, 13, 94–105. [Google Scholar] [CrossRef]
- Zhou, J.; Duan, H.; Liang, K.; Yan, Q.; Chen, F.; Yu, F.R.; Wu, J.; Chen, J. Securing Outsourced Data in the Multi-Authority Cloud with Fine-Grained Access Control and Efficient Attribute Revocation. Comput. J. 2017, 60, 1210–1222. [Google Scholar] [CrossRef]
- Shao, J.; Lu, R.; Lin, X.; Liang, K. Secure bidirectional proxy re-encryption for cryptographic cloud storage. Pervasive Mob. Comput. 2016, 28, 113–121. [Google Scholar] [CrossRef]
- Gamal, T.E. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Fiat, A. Batch RSA. In Proceedings of the Advances in Cryptology—CRYPTO ’89, 9th Annual International Cryptology Conference, Santa Barbara, CA, USA, 20–24 August 1989; pp. 175–185. [Google Scholar] [CrossRef]
- M’Raïhi, D.; Naccache, D. Batch Exponentiation: A Fast DLP-Based Signature Generation Strategy. In Proceedings of the 3rd ACM Conference on Computer and Communications Security (CCS ’96), New Delhi, India, 14–16 March 1996; pp. 58–61. [Google Scholar] [CrossRef]
- Pavlovski, C.; Boyd, C. Efficient batch signature generation using tree structures. In Proceedings of the International Workshop on Cryptographic Techniques and E-Commerce (CrypTEC), Hong Kong, China, 5–8 July 1999; Volume 99, pp. 70–77. [Google Scholar]
- Cheng, W.C.; Chou, C.; Golubchik, L. Performance of Batch-Based Digital Signatures. In Proceedings of the 10th International Workshop on Modeling, Analysis, and Simulation of Computer and Telecommunication Systems (MASCOTS 2002), Fort Worth, TX, USA, 11–16 October 2002; p. 291. [Google Scholar] [CrossRef]
- Korkmaz, T.; Tek, S. Analyzing Response Time of Batch Signing. J. Internet Serv. Inf. Secur. 2011, 1, 70–85. [Google Scholar]
- Boyd, C.; Foo, E.; Pavlovski, C. Efficient Electronic Cash Using Batch Signatures. In Proceedings of the Information Security and Privacy, 4th Australasian Conference, ACISP’99, Wollongong, NSW, Australia, 7–9 April 1999; pp. 244–257. [Google Scholar] [CrossRef]
- Youn, T.; Park, Y.; Kwon, T.; Kwon, S.; Lim, J. Efficient Flexible Batch Signing Techniques for Imbalanced Communication Applications. IEICE Trans. 2008, 91-D, 1481–1484. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Ajtai, M. Generating Hard Instances of Lattice Problems (Extended Abstract). In Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 99–108. [Google Scholar] [CrossRef]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for hard lattices and new cryptographic constructions. In Proceedings of the 40th Annual ACM Symposium on Theory of Computing, Victoria, BC, Canada, 17–20 May 2008; pp. 197–206. [Google Scholar] [CrossRef]
- Alwen, J.; Peikert, C. Generating Shorter Bases for Hard Random Lattices. Theory Comput. Syst. 2011, 48, 535–553. [Google Scholar] [CrossRef]
- Micciancio, D.; Peikert, C. Trapdoors for Lattices: Simpler, Tighter, Faster, Smaller. In Advances in Cryptology—EUROCRYPT 2012—31st Annual International Conference on the Theory and Applications of Cryptographic Techniques; Lecture Notes in Computer Science; Pointcheval, D., Johansson, T., Eds.; Springer: Cambridge, UK, 2012; Volume 7237, pp. 700–718. [Google Scholar] [CrossRef]
- Lyubashevsky, V. Lattice Signatures without Trapdoors. In Advances in Cryptology—EUROCRYPT 2012—31st Annual International Conference on the Theory and Applications of Cryptographic Techniques; Lecture Notes in Computer Science; Pointcheval, D., Johansson, T., Eds.; Springer: Cambridge, UK, 2012; Volume 7237, pp. 738–755. [Google Scholar] [CrossRef]
- Boneh, D.; Freeman, D.M. Homomorphic Signatures for Polynomial Functions. In Advances in Cryptology—EUROCRYPT 2011—30th Annual International Conference on the Theory and Applications of Cryptographic Techniques; Lecture Notes in Computer Science; Paterson, K.G., Ed.; Springer: Tallinn, Estonia, 2011; Volume 6632, pp. 149–168. [Google Scholar] [CrossRef]
- Bellare, M.; Rogaway, P. Collision-Resistant Hashing: Towards Making UOWHFs Practical. In Proceedings of the Advances in Cryptology—CRYPTO ’97, 17th Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 1997; pp. 470–484. [Google Scholar] [CrossRef]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (Leveled) Fully Homomorphic Encryption without Bootstrapping. TOCT 2014, 6, 13. [Google Scholar] [CrossRef]
- Howe, J.; Pöppelmann, T.; O’Neill, M.; O’Sullivan, E.; Güneysu, T. Practical Lattice-Based Digital Signature Schemes. ACM Trans. Embed. Comput. Syst. 2015, 14, 41. [Google Scholar] [CrossRef]
- Alkadri, N.A.; Buchmann, J.; Bansarkhani, R.; Krämer, J. A Framework to Select Parameters for Lattice-Based Cryptography. Cryptology ePrint Archive, Report 2017/615. Available online: https://eprint.iacr.org/2017/615 (accessed on 26 June 2017).
- Yuan, Y.; Cheng, C.M.; Kiyomoto, S.; Miyake, Y.; Takagi, T. Portable implementation of lattice-based cryptography using JavaScript. Int. J. Netw. Comput. 2016, 6, 309–327. [Google Scholar] [CrossRef]
- Longa, P.; Naehrig, M. Speeding up the number theoretic transform for faster ideal lattice-based cryptography. In Proceedings of the International Conference on Cryptology and Network Security, Milan, Italy, 14–16 November 2016; pp. 124–139. [Google Scholar]
- Yuce, M.R.; Ng, S.W.P.; Myo, N.L.; Khan, J.Y.; Liu, W. Wireless Body Sensor Network Using Medical Implant Band. J. Med. Syst. 2007, 31, 467–474. [Google Scholar] [CrossRef] [PubMed]
| Scheme (Size/Computation) | Our 1st Scheme (with Binary Tree) | Our 2nd Scheme (With Intersection Method) | Our 3rd Scheme (With FS Transformation) |
|---|---|---|---|
| signature | |||
| 3+ | |||
| Anti-quantum | √ | √ | √ |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Yin, W.; Wen, Q.; Liang, K.; Chen, L.; Chen, J. Message Integration Authentication in the Internet-of-Things via Lattice-Based Batch Signatures. Sensors 2018, 18, 4056. https://doi.org/10.3390/s18114056
Lu X, Yin W, Wen Q, Liang K, Chen L, Chen J. Message Integration Authentication in the Internet-of-Things via Lattice-Based Batch Signatures. Sensors. 2018; 18(11):4056. https://doi.org/10.3390/s18114056
Chicago/Turabian StyleLu, Xiuhua, Wei Yin, Qiaoyan Wen, Kaitai Liang, Liqun Chen, and Jiageng Chen. 2018. "Message Integration Authentication in the Internet-of-Things via Lattice-Based Batch Signatures" Sensors 18, no. 11: 4056. https://doi.org/10.3390/s18114056
APA StyleLu, X., Yin, W., Wen, Q., Liang, K., Chen, L., & Chen, J. (2018). Message Integration Authentication in the Internet-of-Things via Lattice-Based Batch Signatures. Sensors, 18(11), 4056. https://doi.org/10.3390/s18114056





