A Modified Extended Kalman Filter for a Two-Antenna GPS/INS Vehicular Navigation System
Abstract
1. Introduction
- Adaptive modification of noise covariance can treat dynamic model errors and measurement disturbance to reduce their impact on state estimation, especially when the statistics of both measured and predicted noise have to be adapted. With filter updating, positive feedback and numerical issues can be reduced by quantifying statistical measurement noise on a more granular level based on the corresponding quantifications of measurement reliability in the case of measurement outliers.
- The proposed method can accurately quantify measurement reliability. It is an evidence-based regulation method with the benefit of attenuating the impact of innovation perturbation. In addition to the assured stability of filter updating, the performance of the augmented measurement equation in state error feedback for precious measurements is improved.
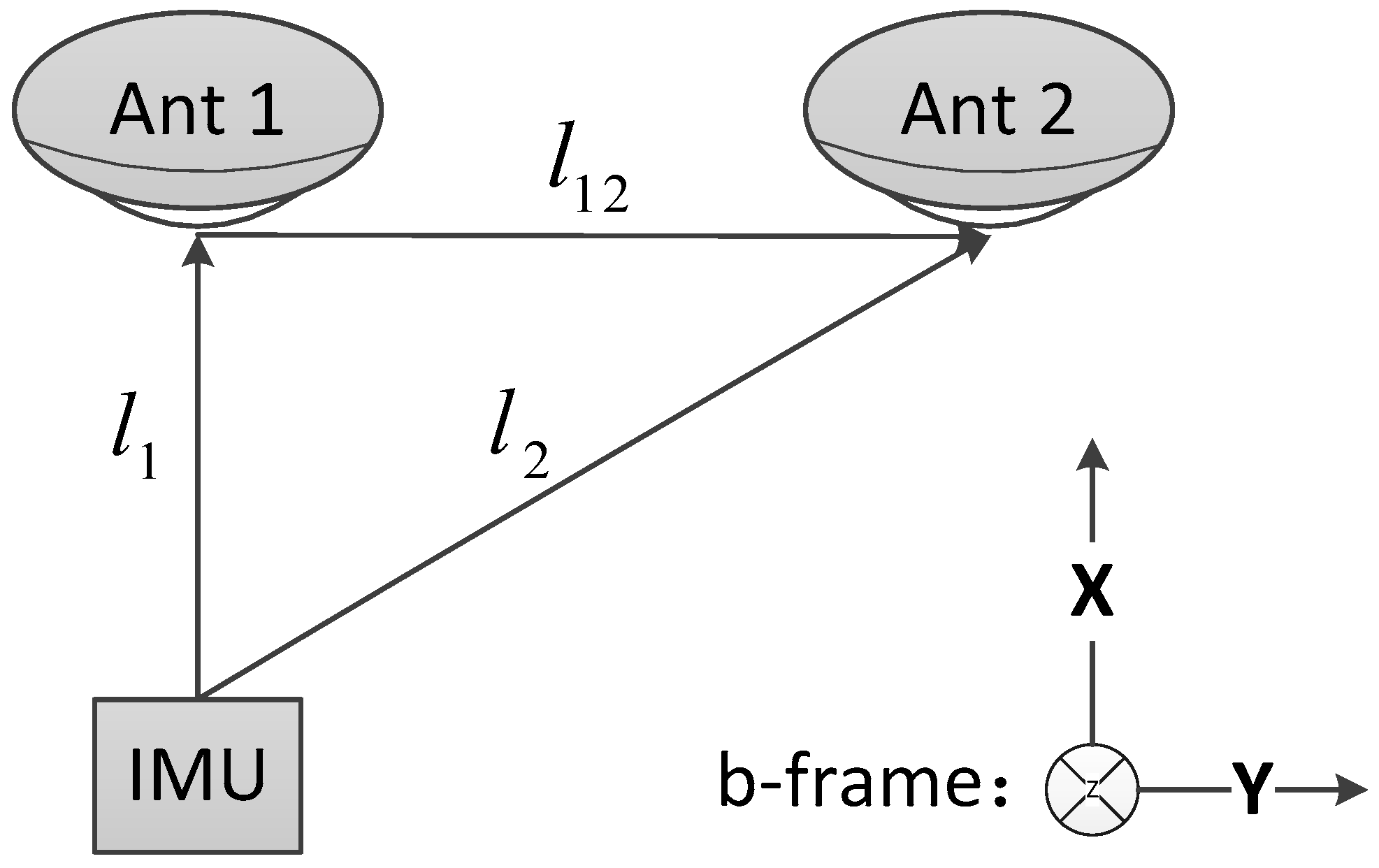
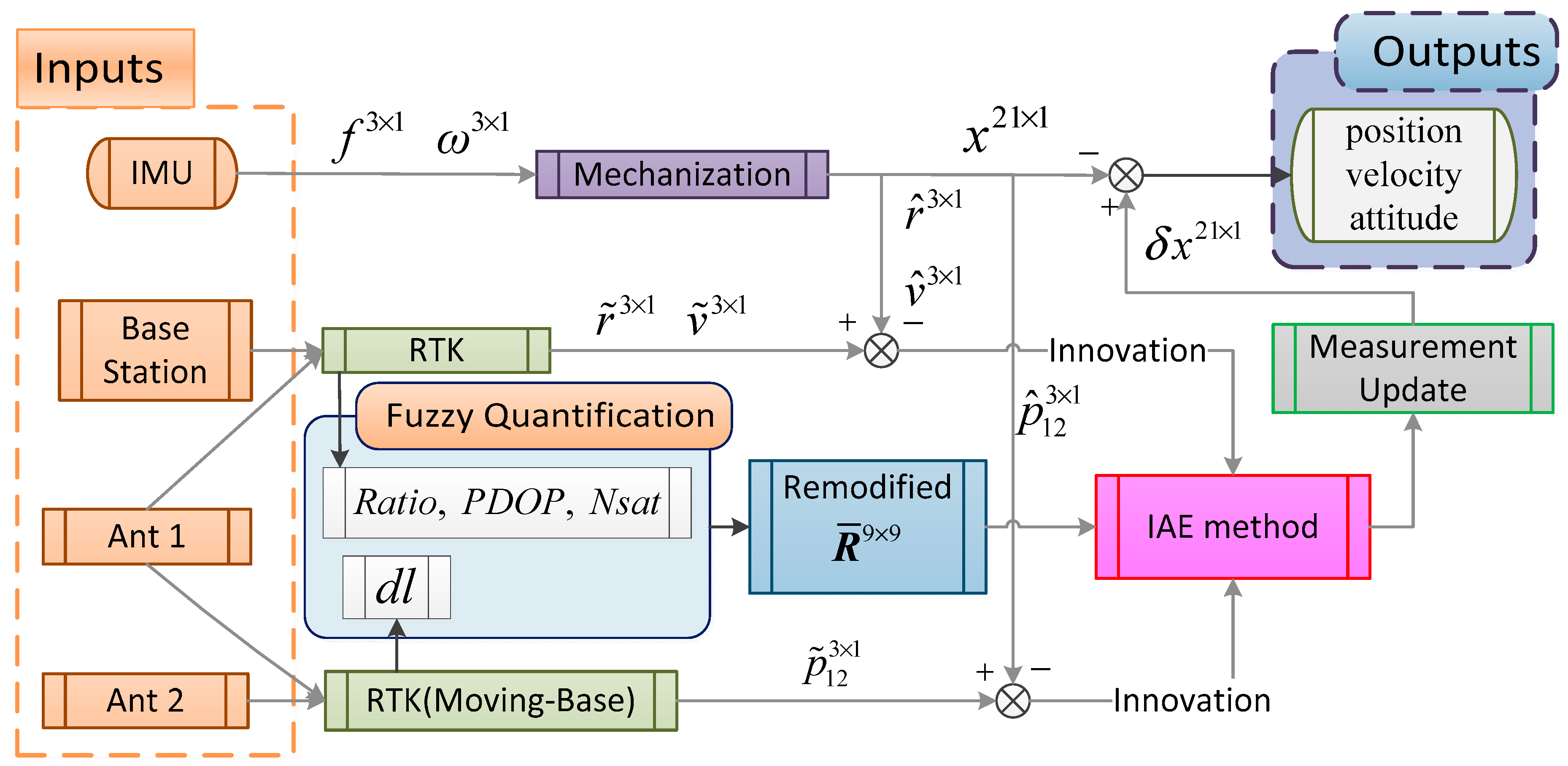
2. Two-Antenna GPS/INS
2.1. Inertial Dynamic Model
2.2. Measurement Model
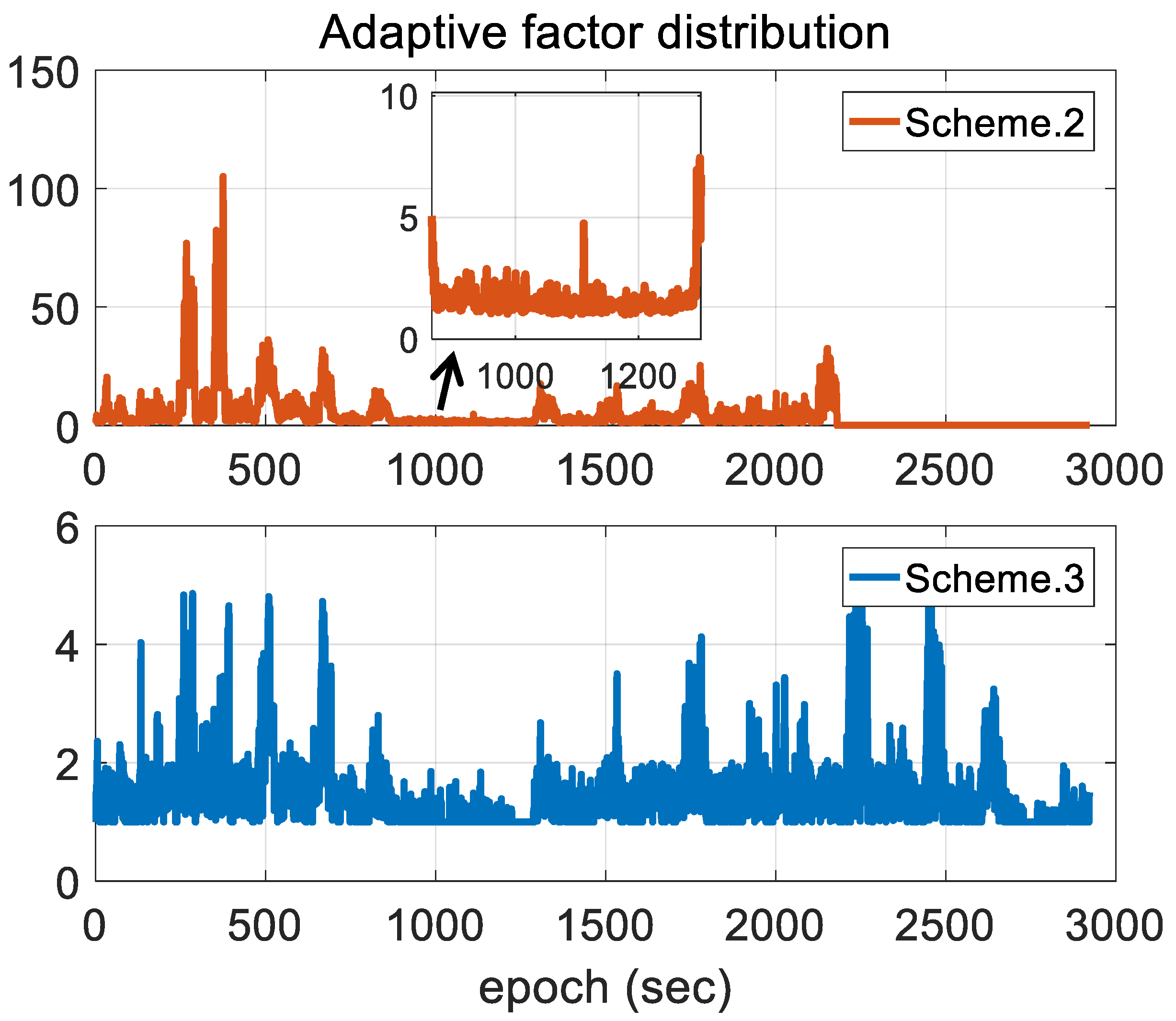
3. Adaptive Noise Covariance
3.1. Adaptive Process Noise Covariance
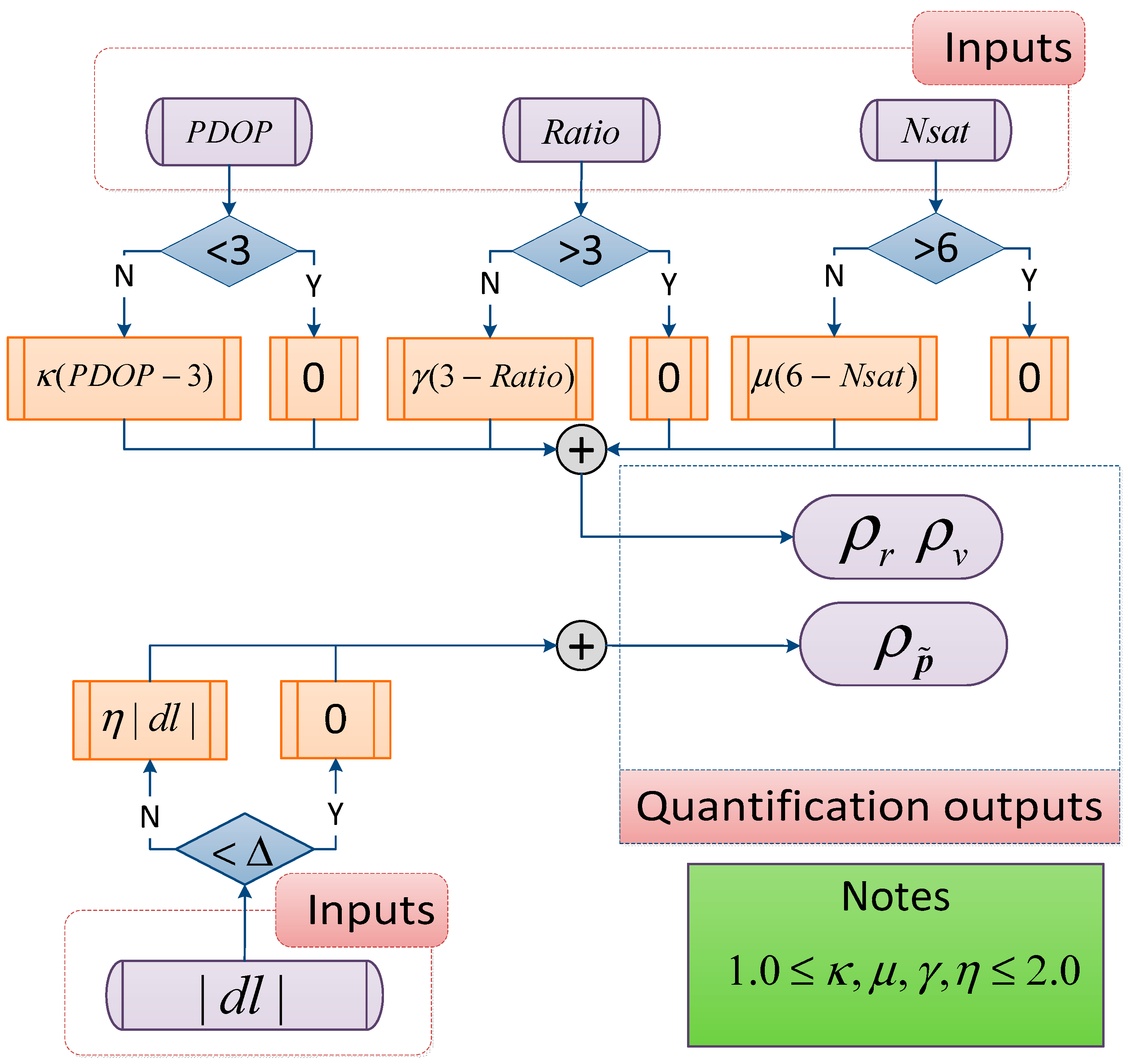
3.2. Adaptive Measurement Noise Covariance
- When tuning a Kalman filter, unknown uncertainties cannot be easily separated from the measurement noise. Although filter stability is ensured by assigning substantially larger state uncertainties, subjective assumption is introduced.
- The performance of measurement error equations in INS calibration is weakened when the measurement is in the steady state and cannot continually provide high-accuracy positioning and velocity results. Due to dynamic model errors and self-drawbacks of INS mechanization, INS cannot provide accurate state prediction. Due to low-accuracy a priori solutions or GPS outages, may be also extremely large even without a measurement outlier because Equation (27) cannot figure out the source of larger innovation deviation. Therefore, can be less than 1.0, and the impact of matrix error is increased. According to Equations (21) and (23), a small matrix error produces unresponsive state estimates, while of a too-large error magnitude produces unstable, oscillatory state estimates [51].
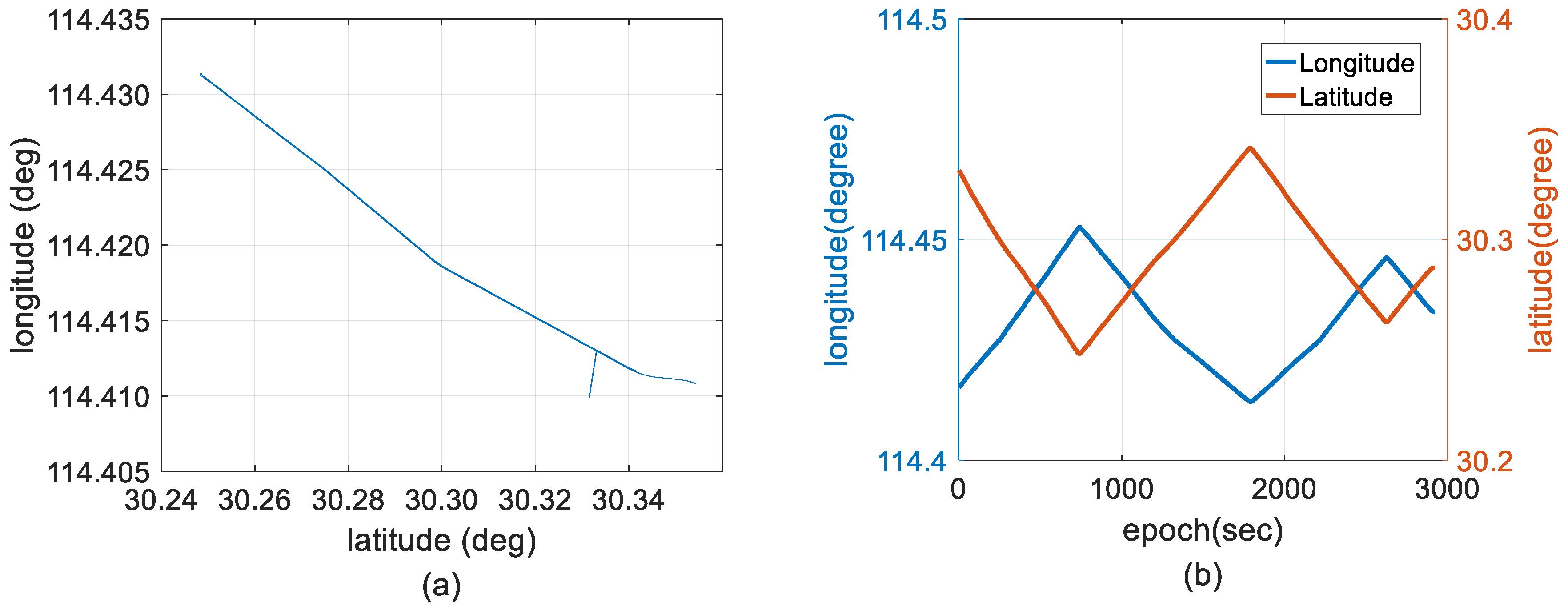
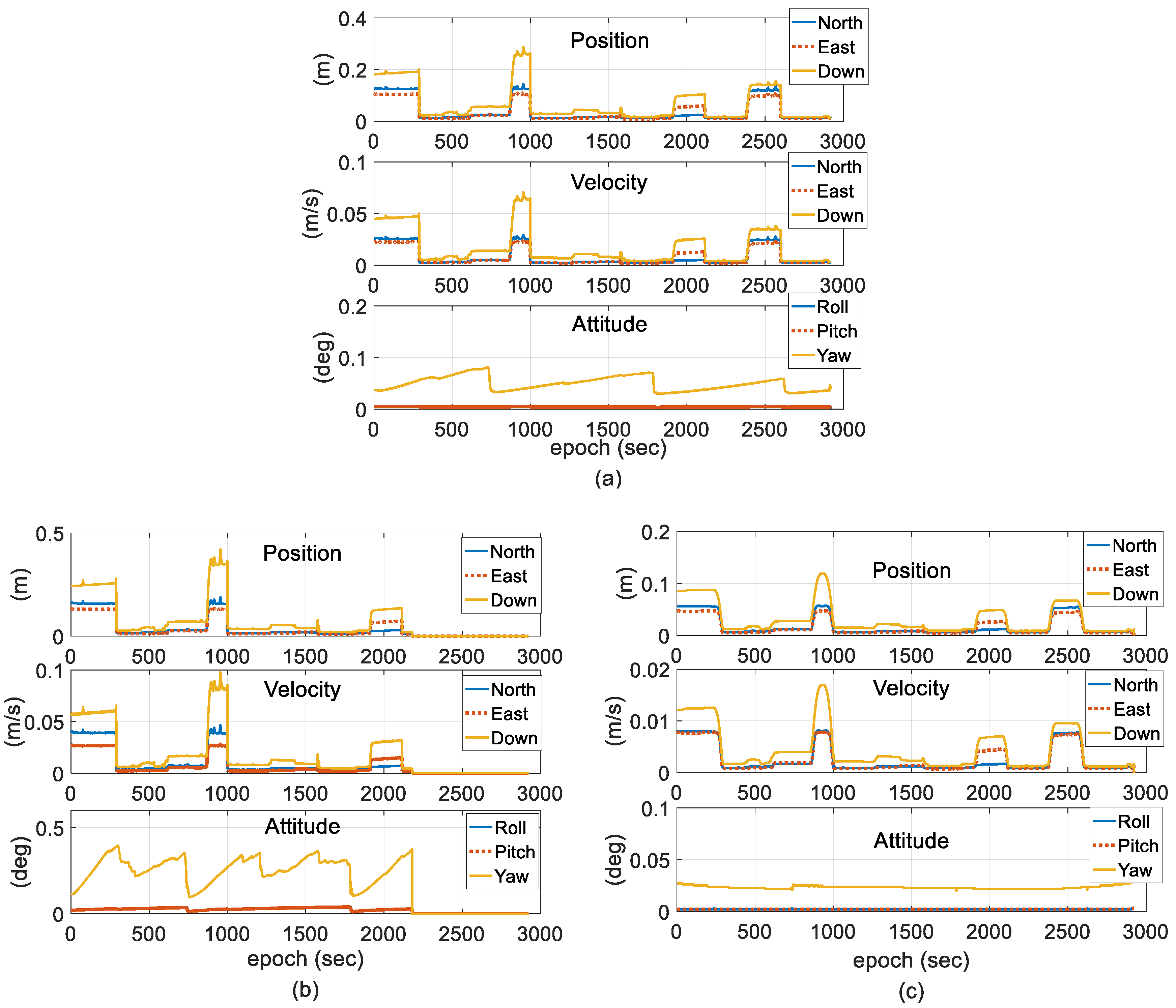
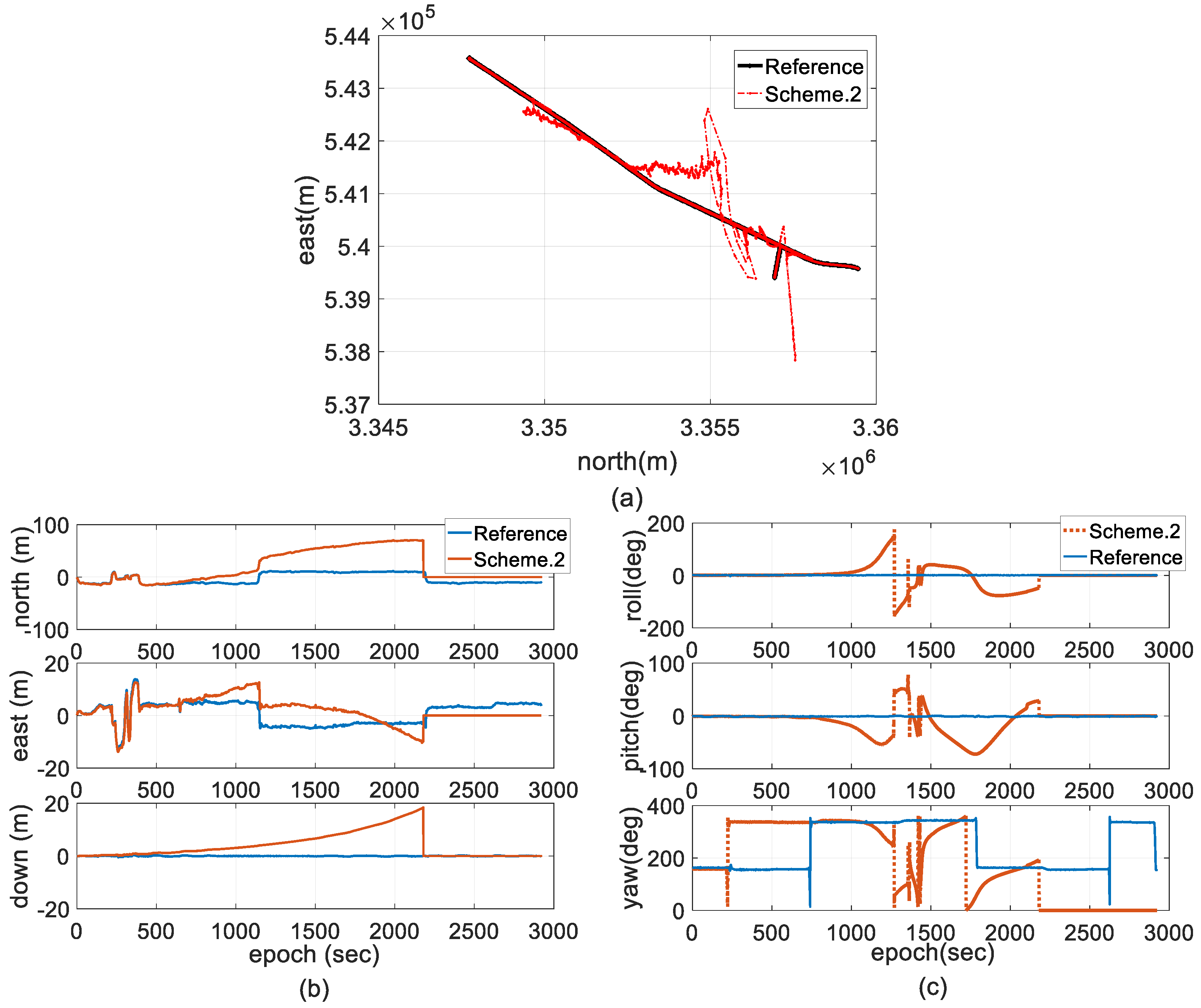
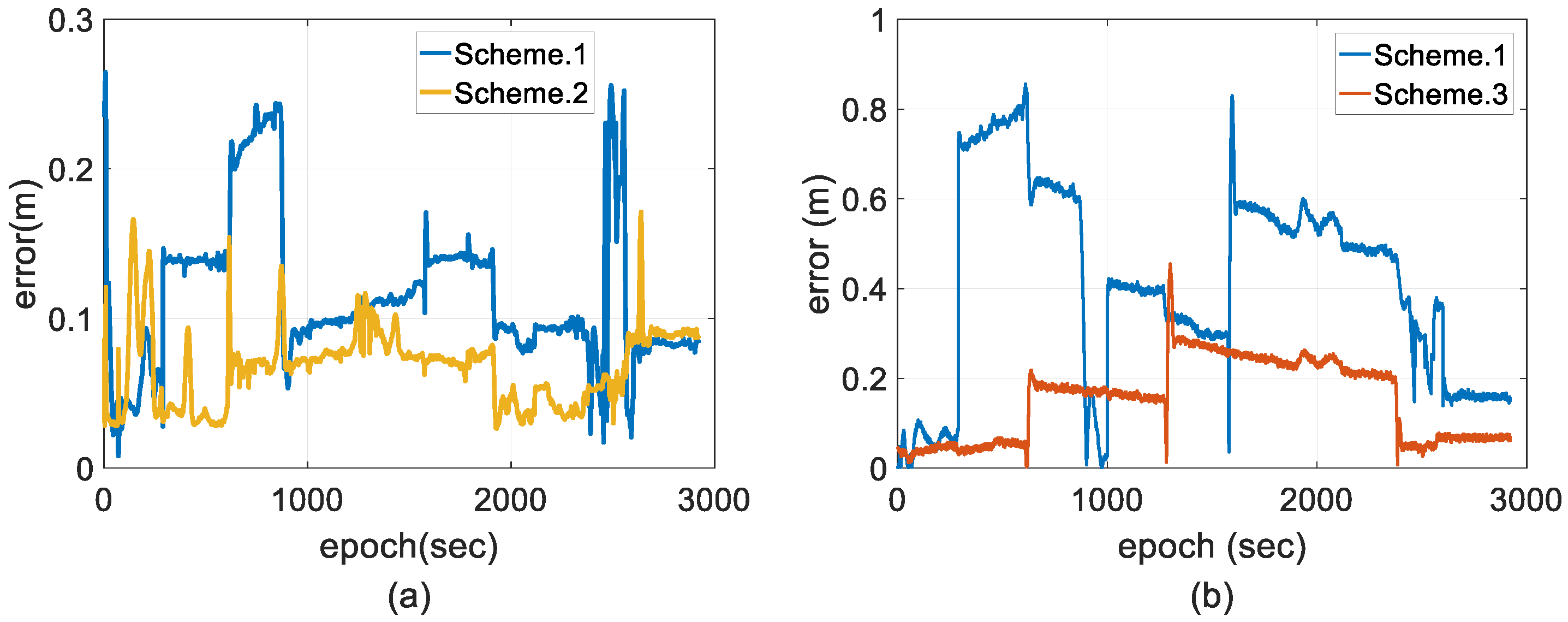
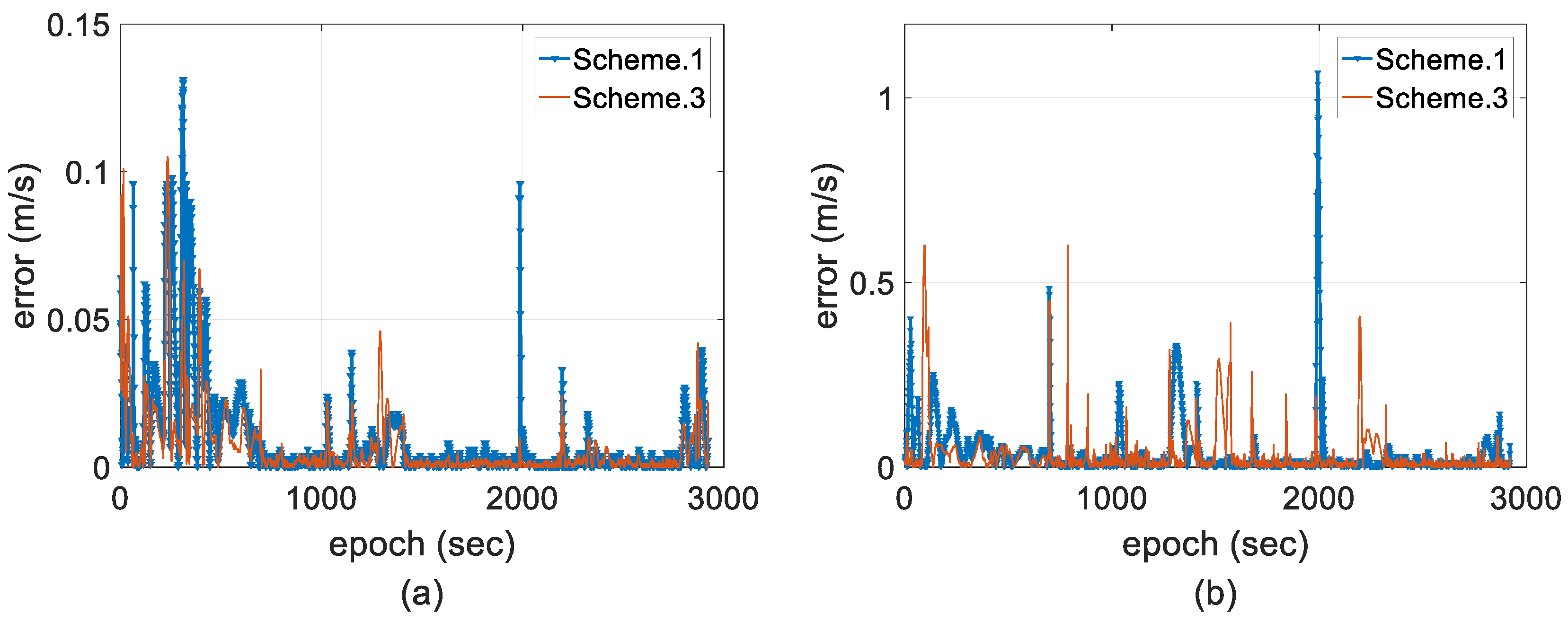
4. Field Test and Discussion
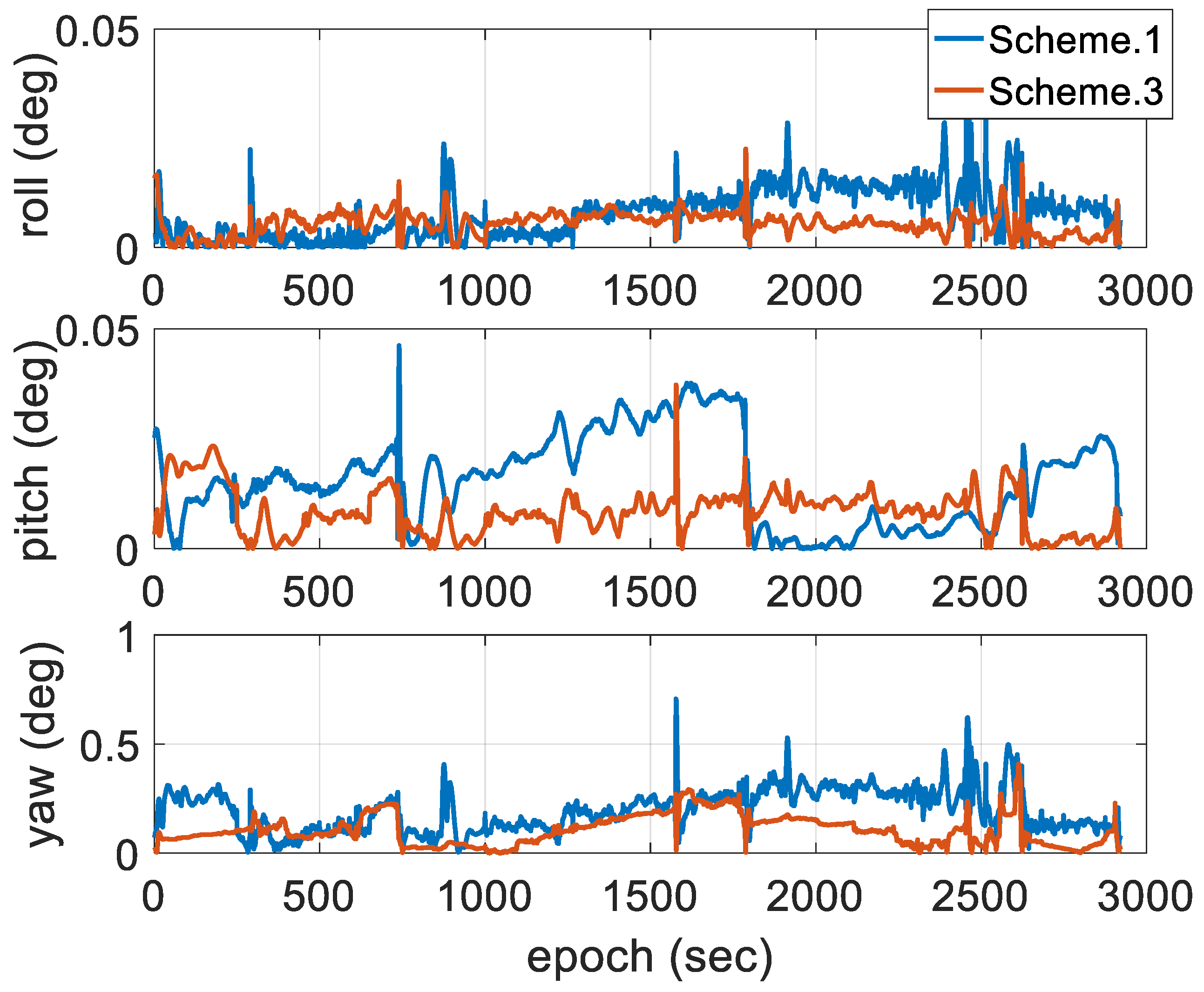
- Scheme 1: two-antenna GPS/INS using a forward EKF.
- Scheme 2: two-antenna GPS/INS using a forward EKF with adaptive modification of the process noise covariance based on Equation (27).
- Scheme 3: two-antenna GPS/INS using a forward EKF with adaptive modification of both the process and measurement noise covariance, which is the proposed method.
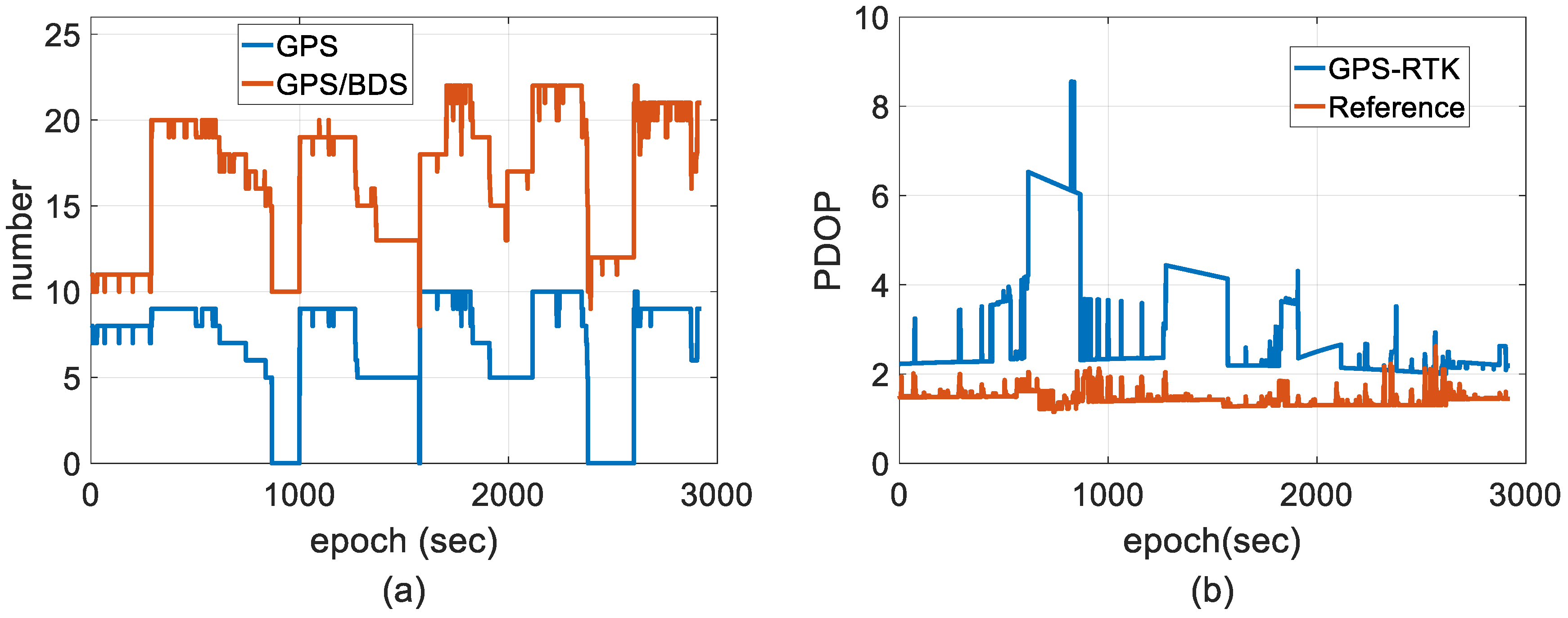
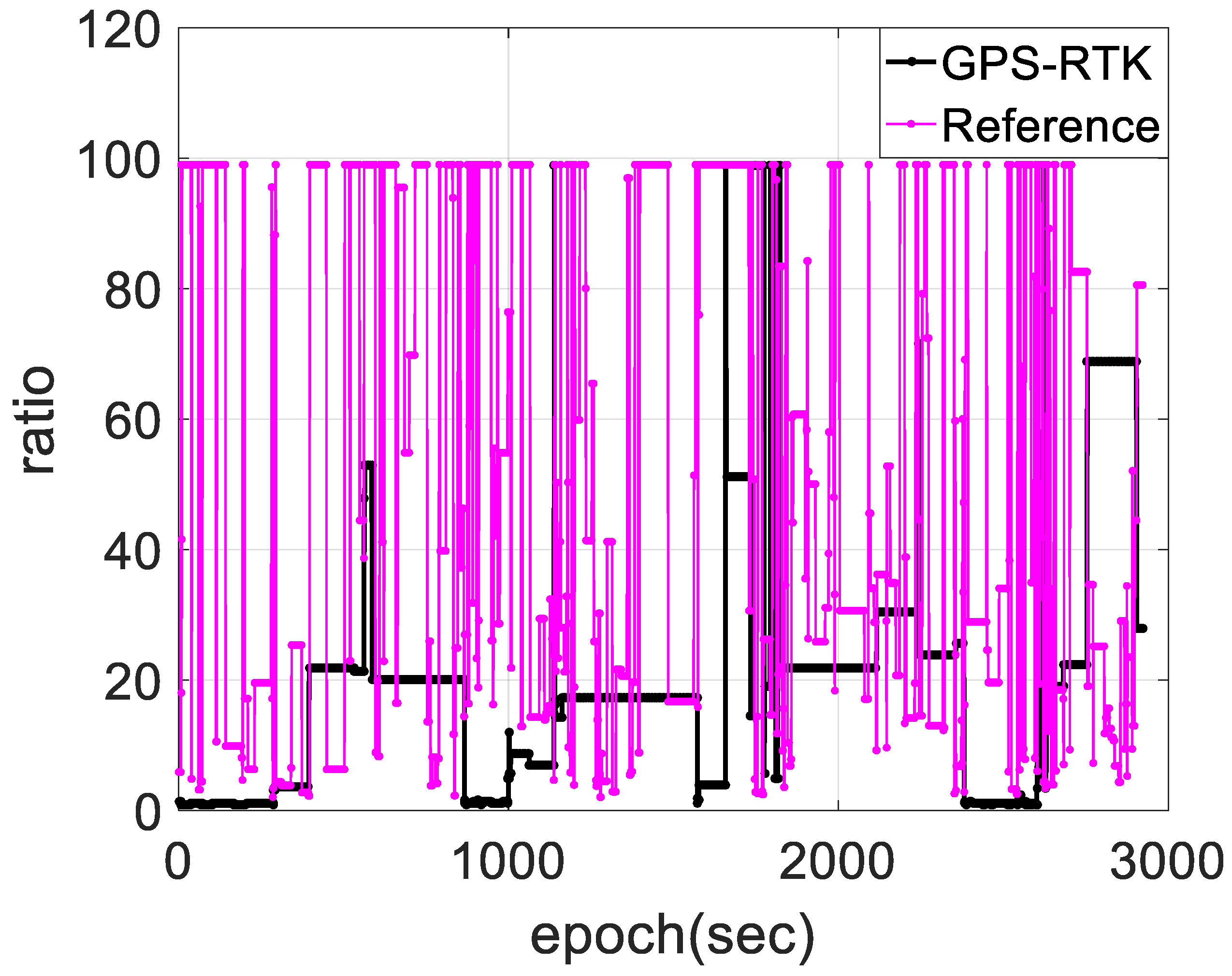
4.1. Reliability of the Measurements
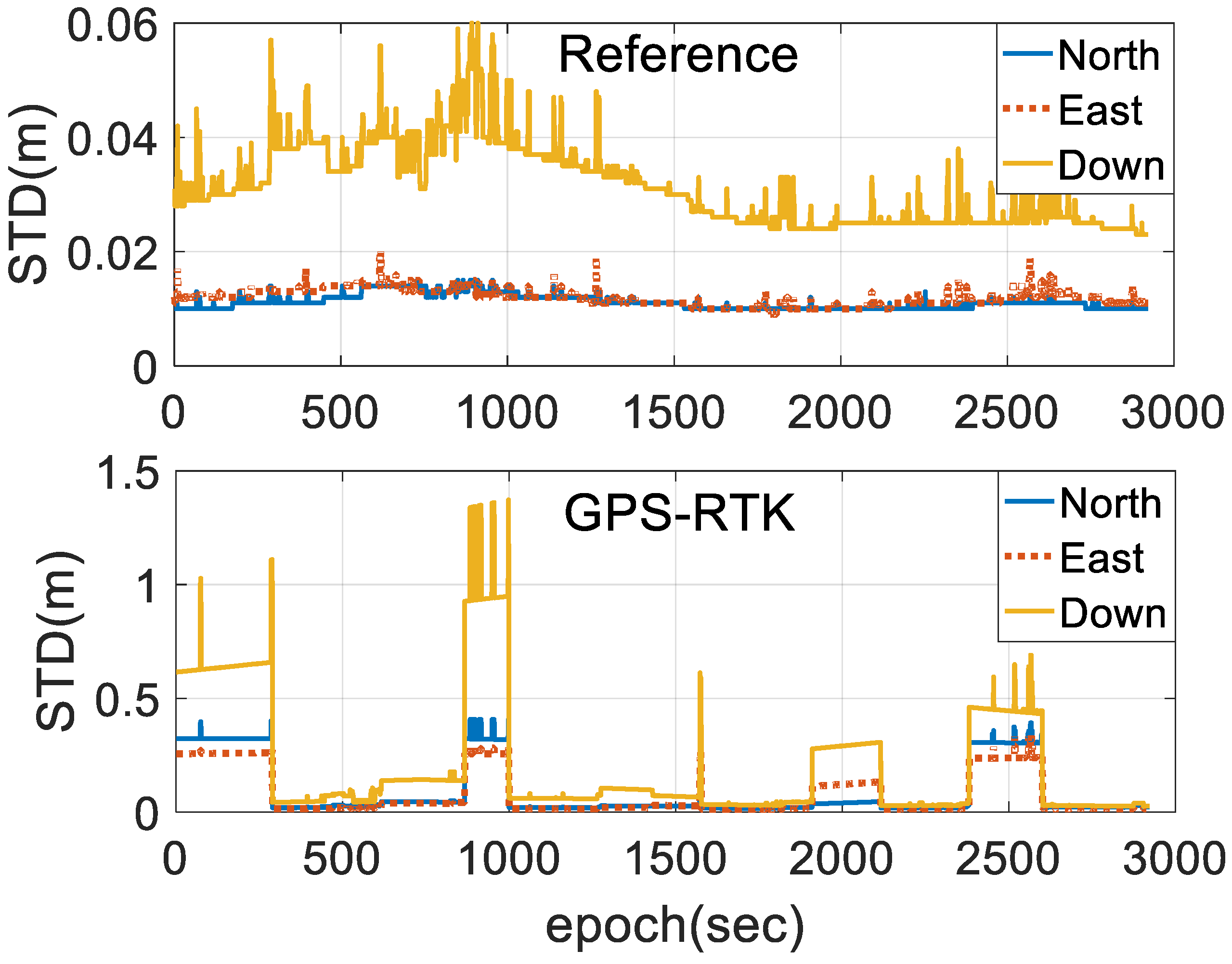
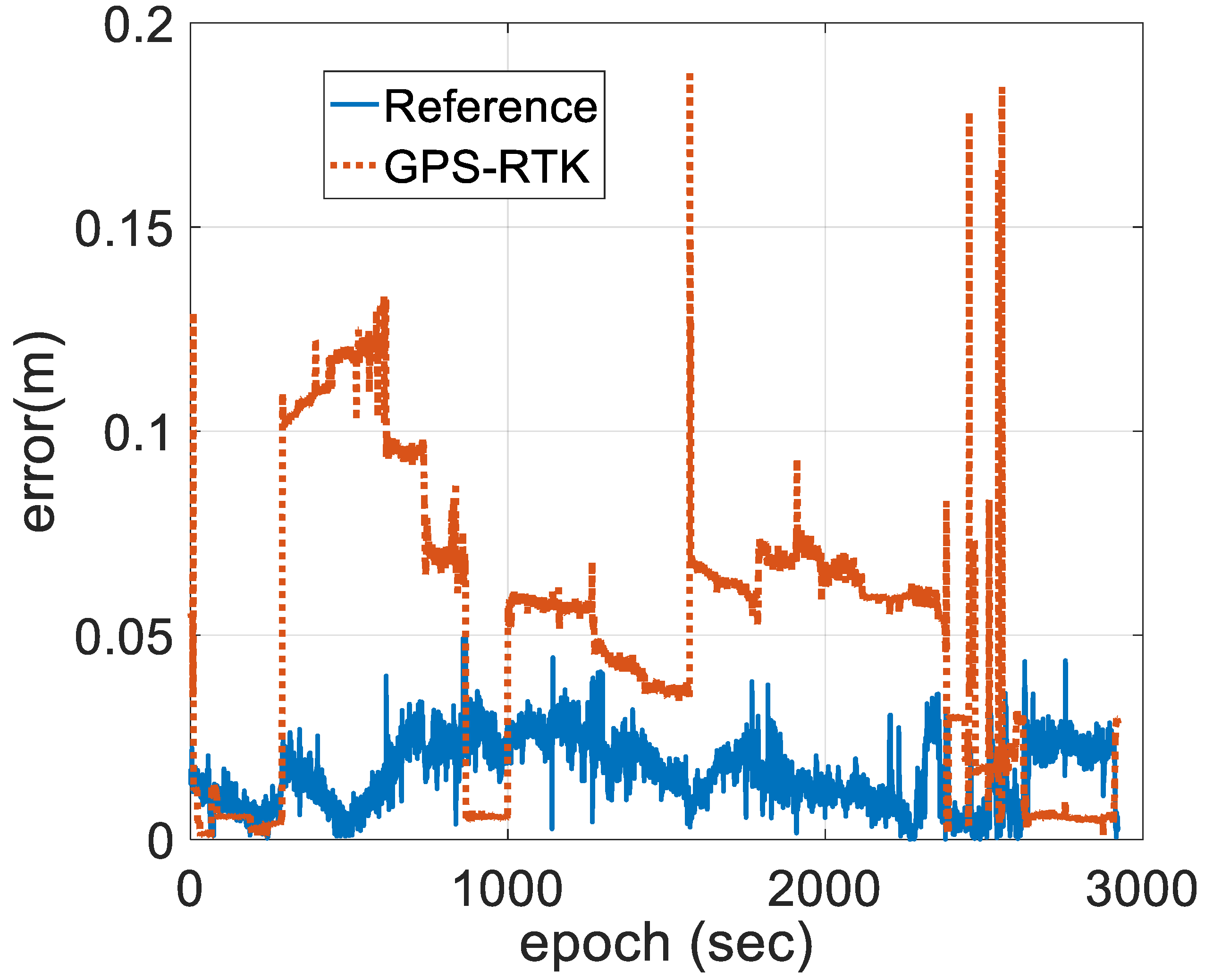
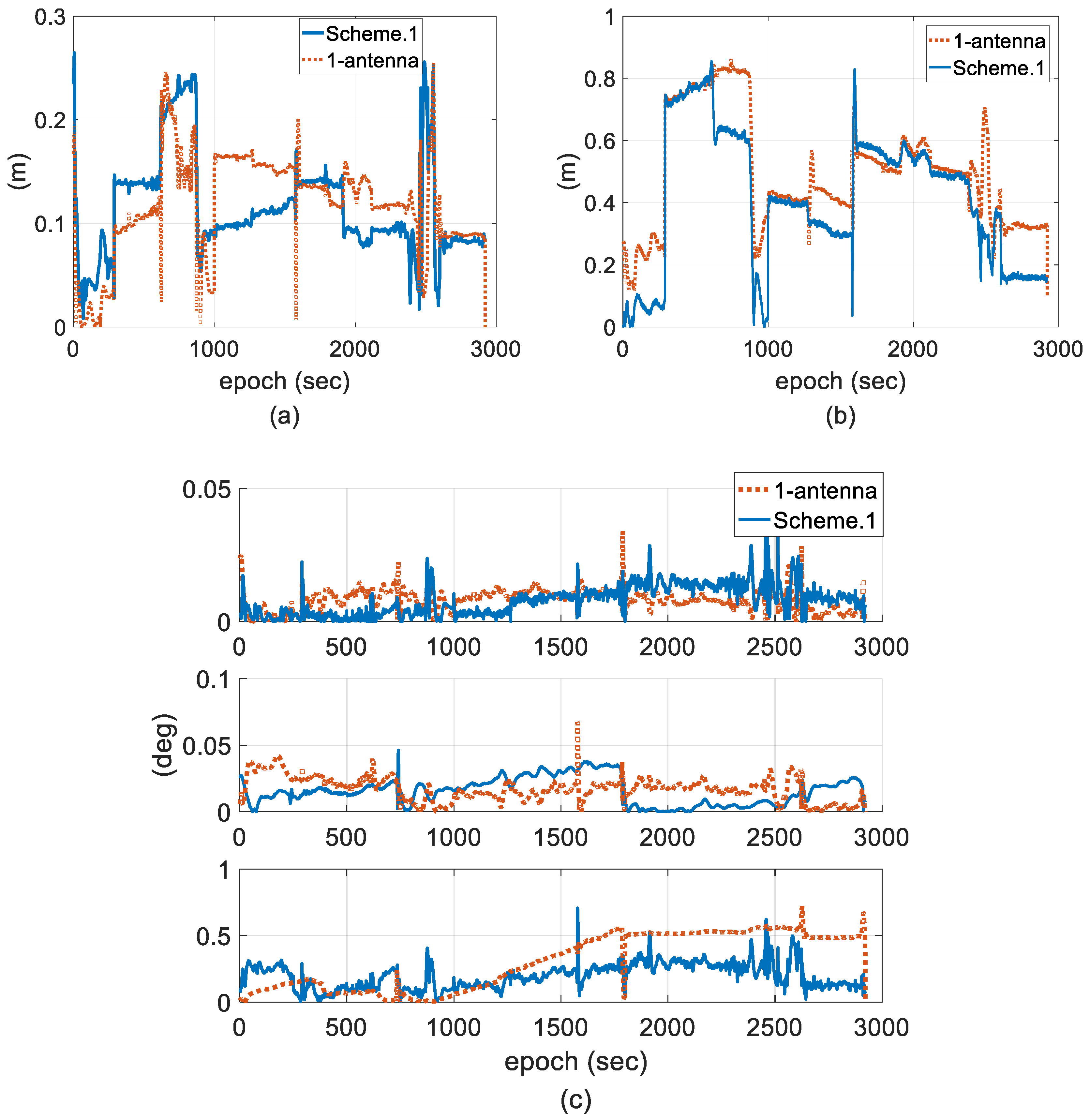
4.2. Experimental Results and Discussion
5. Conclusions
- The conventional EKF adopted in two-antenna GPS/INS integration cannot give a comparative performance in terms of the accuracy and stability of the state estimation because the corresponding noise covariance cannot be tuned by the filter algorithm itself in the case of dynamic model error and measurement outliers in harsh environments.
- Adaptive modification of the noise covariance process depends on the assumption that measurements are accurate and stable or measurement noise follows well-known statistical characteristics. Under unknown measurement uncertainties, the innovation sequence can be distorted by measurement outliers, and the contribution of measurement outliers is increased, which results in a more serious issue concerning the positive feedback on the state estimation and even the instability of the Kalman gain computation.
- The proposed method not only considers the dynamic model errors but also appropriately tunes the contribution of the measurements on the state estimates based on the quantitative reliability of the GPS-RTK solutions in detail. Filter crashes and positive feedback are completely resisted. By using the proposed approach, the two-antenna GPS/INS-integrated navigation system maintains a stable and smaller error magnitude over the long term, which reveals that tuning measurement noise covariance based on measurement outlier detection and unknown uncertainty compensation plays a very important role in stable state estimation.
Author Contributions
Funding
Conflicts of Interest
References
- He, H.; Li, J.; Yang, Y.; Xu, J.; Guo, H.; Wang, A. Performance assessment of single- and dual-frequency BeiDou/GPS single-epoch kinematic positioning. GPS Solut. 2014, 18, 393–403. [Google Scholar] [CrossRef]
- Vigneau, W.; Carcanague, S.; Julien, O.; Macabiau, C. Low-Cost, Single-Frequency GPS/GLONASS RTK for Road Users. In Proceedings of the Ion Pacific PNT Meeting, Honolulu, HI, USA, 23–25 April 2013; pp. 168–184. [Google Scholar]
- Teunissen, P.J.G.; Odolinski, R.; Odijk, D. Instantaneous BeiDou + GPS RTK positioning with high cut-off elevation angles. J. Geod. 2014, 88, 335–350. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J. Low-cost, high-precision, single-frequency GPS—BDS RTK positioning. GPS Solut. 2017, 21, 1315–1330. [Google Scholar] [CrossRef]
- Han, H.; Wang, J.; Wang, J.; Tan, X. Performance analysis on carrier phase-based tightly-coupled GPS/BDS/INS integration in GNSS degraded and denied environments. Sensors 2015, 15, 8685–8711. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Li, Y.; Wu, Y.; Rizos, C. An enhanced MEMS-INS/GNSS integrated system with fault detection and exclusion capability for land vehicle navigation in urban areas. GPS Solut. 2014, 18, 593–603. [Google Scholar] [CrossRef]
- Lee, J.Y.; Kim, H.S.; Choi, K.H.; Lim, J.; Chun, S.; Lee, H.K. Adaptive GPS/INS integration for relative navigation. GPS Solut. 2016, 20, 63–75. [Google Scholar] [CrossRef]
- Han, H.; Wang, J.; Wang, J.; Moraleda, A.H. Reliable partial ambiguity resolution for single-frequency GPS/BDS and INS integration. GPS Solut. 2016, 21, 251–264. [Google Scholar] [CrossRef]
- Chiang, K.W.; Lin, C.A.; Peng, K.Y. The performance analysis of an AKF based tightly-coupled INS/GNSS sensor fusion scheme with non-holonomic constraints for land vehicular applications. Appl. Mech. Mater. 2013, 284, 1956–1960. [Google Scholar] [CrossRef]
- Niu, X.; Li, B.; Ziedan, N.I.; Guo, W.; Liu, J. Analytical and simulation-based comparison between traditional and Kalman filter-based phase-locked loops. GPS Solut. 2016, 21, 123–135. [Google Scholar] [CrossRef]
- Magill, D.T. Optimal adaptive estimation of sampled stochastic processes. IEEE Trans. Autom. Control 1963, 10, 434–439. [Google Scholar] [CrossRef]
- Kotecha, J.H.; Djuric, P.M. Gaussian particle filtering. IEEE Trans. Signal Process. 2003, 51, 2592–2601. [Google Scholar] [CrossRef]
- Maiz, C.S.; Molanes-Lopez, E.M.; Djuric, P.M. A Particle Filtering Scheme for Processing Time Series Corrupted by Outliers. IEEE Trans. Signal Process. 2012, 60, 4611–4627. [Google Scholar] [CrossRef]
- Martino, L.; Read, J.; Elvira, V.; Louzada, F. Cooperative parallel particle filters for online model selection and applications to urban mobility. Dig. Signal Process. 2017, 60, 172–185. [Google Scholar] [CrossRef]
- Martino, L.; Elvira, V.; Camps-Valls, G. Group Importance Sampling for Particle Filtering and MCMC. Dig. Signal Process. 2017, 82, 133–151. [Google Scholar] [CrossRef]
- Chadli, M.; Davoodi, M.; Meskin, N. Distributed state estimation, fault detection and isolation filter design for heterogeneous multi-agent linear parameter-varying systems. IET Control Theory Appl. 2017, 11, 254–262. [Google Scholar] [CrossRef]
- Castillo, I.; Edgar, T.F.; Fernández, B.R. Robust model-based fault detection and isolation for nonlinear processes using sliding modes. Int. J. Robust Nonlinear Control 2015, 22, 89–104. [Google Scholar] [CrossRef]
- Hajshirmohamadi, S.; Davoodi, M.; Meskin, N.; Sheikholeslam, F. Event-triggered fault detection and isolation for discrete-time linear systems. IET Control Theory Appl. 2016, 10, 526–533. [Google Scholar] [CrossRef]
- Mehra, R.K. On the identification of variances and adaptive Kalman filtering. IEEE Trans. Autom. Control 1970, 15, 175–184. [Google Scholar] [CrossRef]
- Mehra, R.K. On-line identification of linear dynamic systems with applications to Kalman filtering. IEEE Trans. Autom. Control 1970, 16, 12–21. [Google Scholar] [CrossRef]
- Gao, Z.; Shen, W.; Zhang, H.; Ge, M.; Niu, X. Application of Helmert variance component based adaptive Kalman filter in multi-GNSS PPP/INS tightly coupled integration. Remote Sens. 2016, 8, 553. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Innovation-based adaptive Kalman filter for INS/GPS. In Proceedings of the Annual Meeting of the Institute of Navigation, Denver, CO, USA, 1–3 June 1998; p. 414. [Google Scholar]
- Lin, S.G. Assisted adaptive extended Kalman filter for low-cost single-frequency GPS/SBAS kinematic positioning. GPS Solut. 2015, 19, 215–223. [Google Scholar] [CrossRef]
- Liu, X.G.; Shan, W.U.; Wang, X.M.; Ting-Ting, P.U. Design of color noise filter in GOCE satellite gravimetry mission. Prog. Geophys. 2012, 27, 856–860. [Google Scholar]
- Yang, Y.X.; Ren, X.; Yan, X.U. Main progress of adaptively robust filter with applications in navigation. J. Navig. Position. 2013, 1, 9–15. [Google Scholar]
- Yang, Y.; Gao, W. An optimal adaptive Kalman filter. J. Geod. 2006, 80, 177–183. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, T. An adaptive Kalman filter combining variance component estimation with covariance matrix estimation based on moving window. Geomat. Inf. Sci. Wuhan Univ. 2003, 28, 714–718. [Google Scholar]
- Yang, Y.; Cui, X. Adaptively robust filter with multi adaptive factors. Empire Surv. Rev. 2013, 40, 260–270. [Google Scholar] [CrossRef]
- Xu, T.L. Adaptive Kalman Filter for INS/GPS Integrated Navigation System. Appl. Mech. Mater. 2013, 336, 332–335. [Google Scholar] [CrossRef]
- Han, H.Z. Research on the Key Models of INS Aided BDS/GPS High Precision Kinematic Positioning [D]; China University of Mining and Technology: Xuzhou, China, 2017. [Google Scholar]
- Narasimhappa, M.; Sabat, S.L.; Peesapati, R.; Nayak, J. An innovation based random weighting estimation mechanism for denoising fiber optic gyro drift signal. Int. J. Light Electron Opt. 2014, 125, 1192–1198. [Google Scholar] [CrossRef]
- Marzaki, M.H.; Tajjudin, M.; Rahiman, M.H.F.; Adnan, R. Performance of FOPI with error filter based on controllers performance criterion (ISE, IAE and ITAE). In Proceedings of the 10th Asian Control Conference (ASCC), Kota Kinabalu, Malaysia, 31 May–3 June 2015; pp. 1–6. [Google Scholar]
- Xie, S.; Chen, D.; Chu, X.; Liu, C. Identification of ship response model based on improved multi-innovation extended Kalman filter. J. Harbin Eng. Univ. 2018. [Google Scholar] [CrossRef]
- Safarinejadian, B.; Yousefi, M. Static alignment of inertial navigation systems using an adaptive multiple fading factors Kalman filter. Syst. Sci. Control Eng. 2015, 3, 351–359. [Google Scholar] [CrossRef]
- Farrell, J.A.; Tan, H.S.; Yang, Y. Carrier phase GPS-aided INS-based vehicle lateral control. J. Dyn. Syst. Meas. Control 2003, 125, 339–353. [Google Scholar] [CrossRef]
- Rui, H.; Ebinuma, T. A Low-Cost Tightly Coupled GPS/INS for Small UAVs Augmented with Multiple GPS Antennas. Navigation 2009, 56, 35–44. [Google Scholar]
- Emel’yantsev, G.I.; Blazhnov, B.A.; Stepanov, A.P. Specific Features of Constructing a Dual-Mode GNSS Gyrocompass as a Tightly-Coupled Integrated System. Gyroscopy Navig. 2018, 9, 97–105. [Google Scholar] [CrossRef]
- Farrell, J.A.; Givargis, T.D.; Barth, M.J. Real-time differential carrier phase GPS-aided INS. IEEE Trans. Control Syst. Technol. 2000, 8, 709–721. [Google Scholar] [CrossRef]
- Davari, N.; Gholami, A. An asynchronous adaptive direct Kalman filter algorithm to improve underwater navigation system performance. IEEE Sens. J. 2017, 17, 1061–1068. [Google Scholar] [CrossRef]
- Knight, D.T. Rapid development of tightly-coupled GPS/INS systems. IEEE Aerosp. Electron. Syst. Mag. 1997, 12, 14–18. [Google Scholar] [CrossRef]
- Chen, X.; Shen, C.; Zhao, Y. Study on GPS/INS System Using Novel Filtering Methods for Vessel Attitude Determination. Math. Probl. Eng. 2013, 2013, 289–325. [Google Scholar] [CrossRef]
- Chiang, K.W.; Huang, Y.W. An intelligent navigator for seamless INS/GPS integrated land vehicle navigation applications. Appl. Soft Comput. J. 2008, 8, 722–733. [Google Scholar] [CrossRef]
- Shin, E.H. Estimation Techniques for Low-Cost Inertial Navigation. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2005. [Google Scholar]
- Scherzinger, B. Inertial navigator error models for large heading uncertainty. In Proceedings of the Position, Location and Navigation Symposium, Atlanta, GA, USA, 22–25 April 1996; pp. 477–484. [Google Scholar]
- Bruder, S.; El-Osery, A. Low-Cost Inertial Navigation. Control and Systems Engineering; Springer International Publishing: Cham, Switzerland, 2015; pp. 231–259. [Google Scholar]
- Budiyono, A. Principles of GNSS, inertial, and multi-sensor integrated navigation systems. Ind. Robot 2013, 67, 191–192. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 1995; Volume 8, pp. 127–132. [Google Scholar]
- Kratz, W. A substitute of l’Hospital’s rule for matrices. Proc. Am. Math. Soc. 1987, 99, 395–402. [Google Scholar]
- Li, T.; Zhang, H.; Gao, Z.; Chen, Q.; Niu, X. High-Accuracy Positioning in Urban Environments Using Single-Frequency Multi-GNSS RTK/MEMS-IMU Integration. Remote Sens. 2018, 10, 205. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, inertial, and multisensor integrated navigation systems, 2nd edition [Book review]. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 26–27. [Google Scholar] [CrossRef]
- Cai, C.S.; Dai, W.J.; Kuang, C.L. Calculation and Analysis of PDOP for Combined GPS/GLONASS Systems. Bull. Surv. Mapp. 2011, 6, 214–233. [Google Scholar]
- Sun, H.; Hao, X.; Feng, W.; Yin, J. Inter-satellite links topology scenario based on minimum PDOP criterion. J. Beijing Univ. Aeronaut. Astronaut. 2011, 37, 1245–1249. [Google Scholar]
- Xu, J. Modeling and Evaluation of Effects of Fault Satellites Distribution on PDOP Availability of Navigation Constellation. Acta Aeronaut. Astronaut. Sin. 2008, 29, 1139–1143. [Google Scholar]
- Liang, L.; Li, Z.; Yuan, H.; Wang, L.; Hou, Y. Integrity monitoring-based ratio test for GNSS integer ambiguity validation. GPS Solut. 2016, 20, 573–585. [Google Scholar]
- Hou, Y.; Verhagen, S.; Wu, J. An Efficient Implementation of Fixed Failure-Rate Ratio Test for GNSS Ambiguity Resolution. Sensors 2016, 16, 945. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Luo, Z.; Yao, C. Simplified Autocovariance Least-Squares Method for Constant Acceleration Model. Acta Geod. Cartogr. Sin. 2014, 43, 1144–1150. [Google Scholar]
- Bao, Y.B.; Hong, Z.; Zhang, C.-Q. The Application of RTS Smooth Filter Algorithm in Post Attitude Determination. Aerosp. Control Appl. 2015, 41, 18–22. [Google Scholar]
- Hwang, J.S.; Han, H.C. A Study on Shipborne Gravity Data Correction Using Kalman RTS Filter. Trans. Korean Inst. Electr. Eng. 2010, 43, 343–348. [Google Scholar]
- Yang, Y.C.; Farrell, J.A. Two antennas GPS-aided INS for attitude determination. IEEE Trans. Control Syst. Technol. 2003, 11, 905–918. [Google Scholar] [CrossRef]
| Parameters | Accelerometer | Gyroscope |
|---|---|---|
| Range | ±10 g | ±300 °/s |
| Random Walk | 0.1 m/s/ | 0.03 deg |
| Instability | 25 m Gal | 0.5 °/h |
| Mean Error (ME) | Root Mean Square Error (RMSE) | Max Error (MAX) | |
|---|---|---|---|
| Roll (°) | 0.009 | 0.006 | 0.042 |
| Pitch (°) | 0.016 | 0.010 | 0.046 |
| Yaw (°) | 0.197 | 0.098 | 0.707 |
| Horizontal Position (m) | 0.120 | 0.180 | 0.397 |
| Vertical Position (m) | 0.411 | 0.221 | 0.856 |
| Horizontal Velocity (m/s) | 0.010 | 0.018 | 0.131 |
| Vertical Velocity(m/s) | 0.039 | 0.083 | 1.068 |
| ME | RMSE | MAX | |
|---|---|---|---|
| Roll (°) | 0.005 | 0.003 | 0.023 |
| Pitch (°) | 0.008 | 0.005 | 0.037 |
| Yaw (°) | 0.106 | 0.068 | 0.408 |
| Horizontal Position (m) | 0.060 | 0.080 | 0.171 |
| Vertical Position (m) | 0.151 | 0.090 | 0.456 |
| Horizontal Velocity (m/s) | 0.007 | 0.013 | 0.105 |
| Vertical Velocity (m/s) | 0.034 | 0.067 | 0.600 |
| Position Error | ≤0.05 m | ≤0.10 m | ≤0.15 m |
|---|---|---|---|
| Scheme 1 (%) | 2.00 | 10.75 | 51.87 |
| Scheme 3 (%) | 28.04 | 92.87 | 99.04 |
| Position Error | ≤0.10 m | ≤0.20 m | ≤0.30 m |
|---|---|---|---|
| Scheme 1 (%) | 12.01 | 25.30 | 31.77 |
| Scheme 3 (%) | 39.88 | 63.16 | 99.18 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Y.; Xu, A.; Sui, X.; Wang, Y. A Modified Extended Kalman Filter for a Two-Antenna GPS/INS Vehicular Navigation System. Sensors 2018, 18, 3809. https://doi.org/10.3390/s18113809
Hao Y, Xu A, Sui X, Wang Y. A Modified Extended Kalman Filter for a Two-Antenna GPS/INS Vehicular Navigation System. Sensors. 2018; 18(11):3809. https://doi.org/10.3390/s18113809
Chicago/Turabian StyleHao, Yushi, Aigong Xu, Xin Sui, and Yulei Wang. 2018. "A Modified Extended Kalman Filter for a Two-Antenna GPS/INS Vehicular Navigation System" Sensors 18, no. 11: 3809. https://doi.org/10.3390/s18113809
APA StyleHao, Y., Xu, A., Sui, X., & Wang, Y. (2018). A Modified Extended Kalman Filter for a Two-Antenna GPS/INS Vehicular Navigation System. Sensors, 18(11), 3809. https://doi.org/10.3390/s18113809




