Pressure Monitoring Cell for Constrained Battery Electrodes
Abstract
:1. Introduction
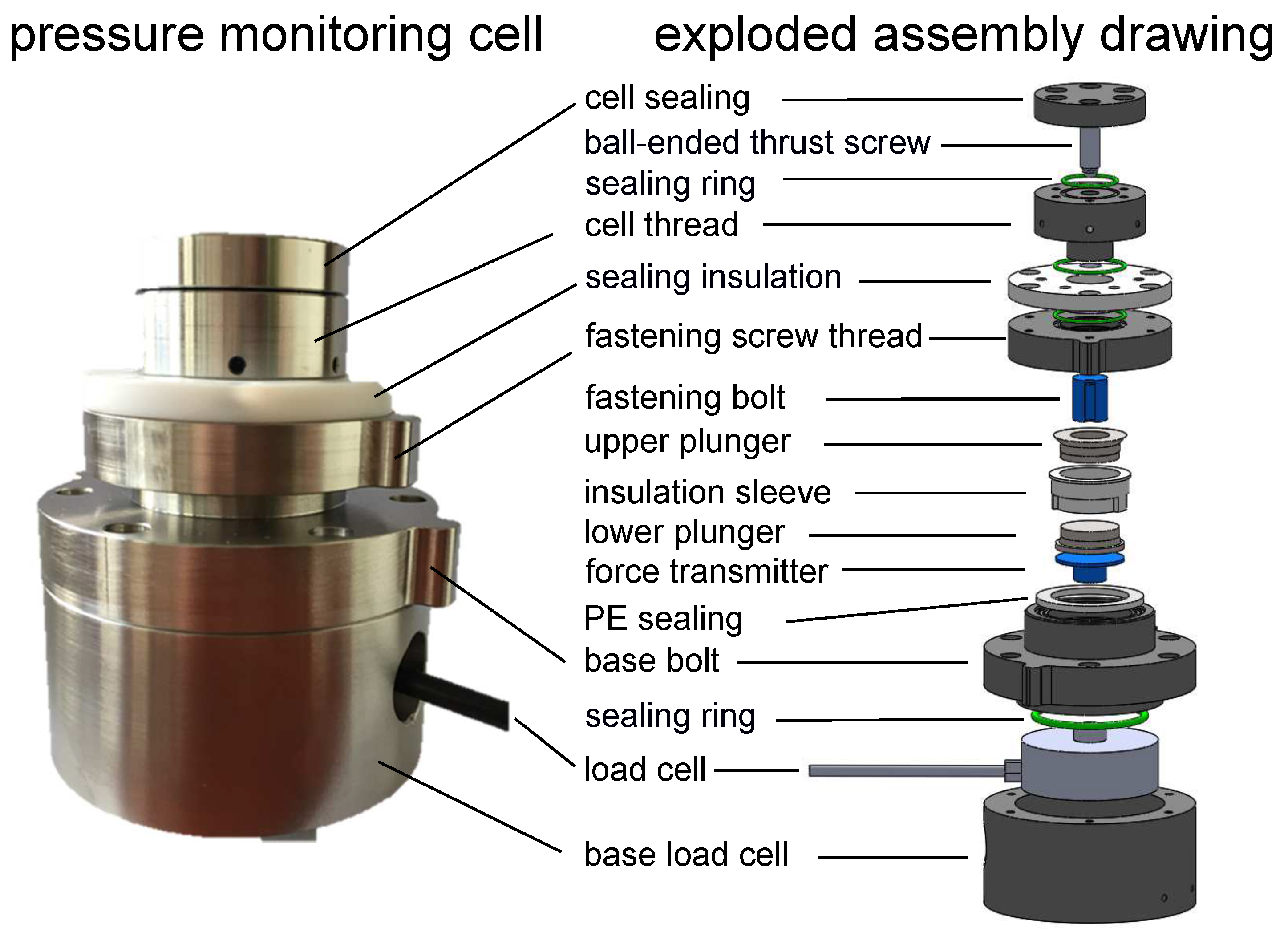
2. Method and Working Principle
2.1. Test Cell Setup
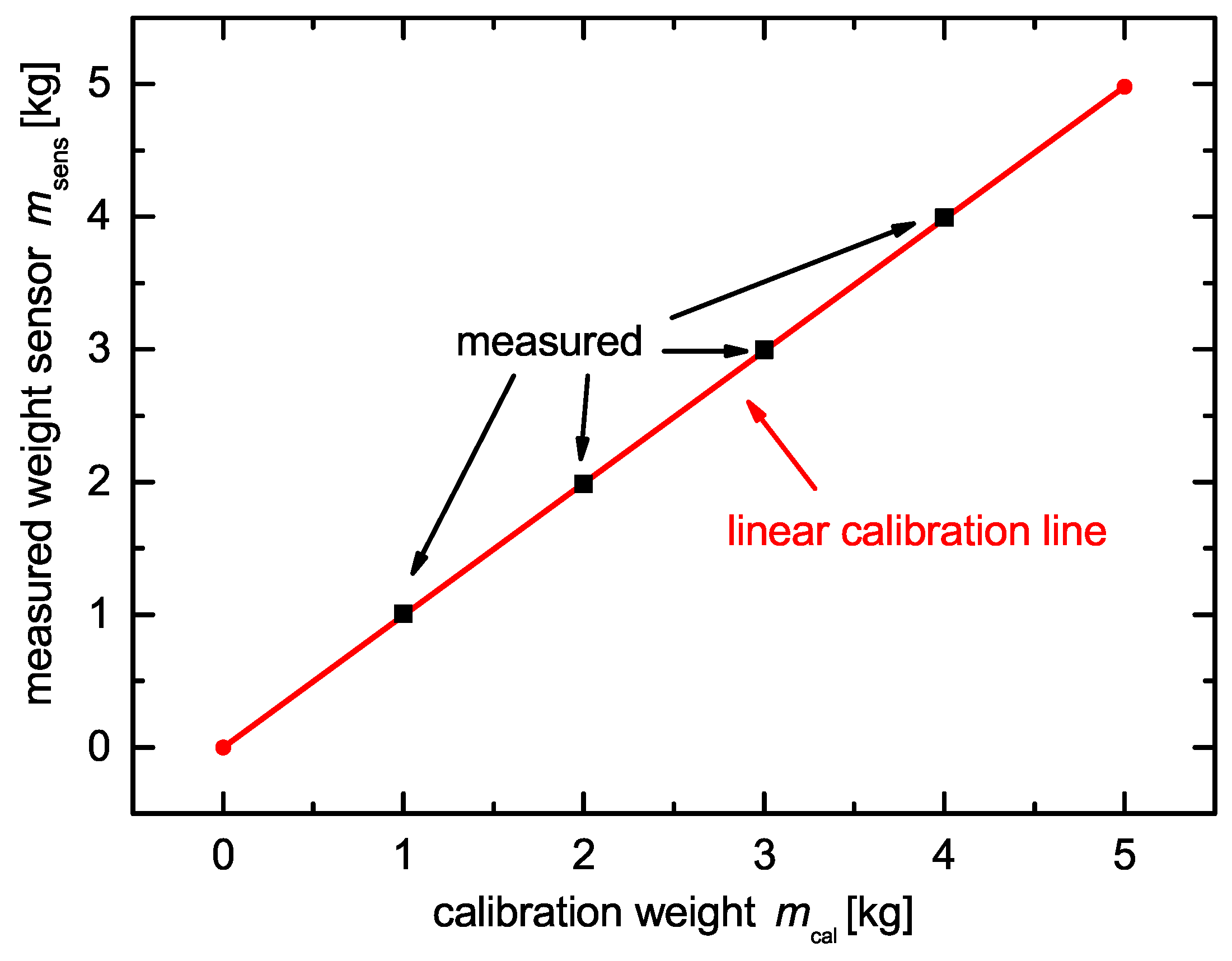
2.2. Load Cell and Data Acquisition
3. Results and Discussion
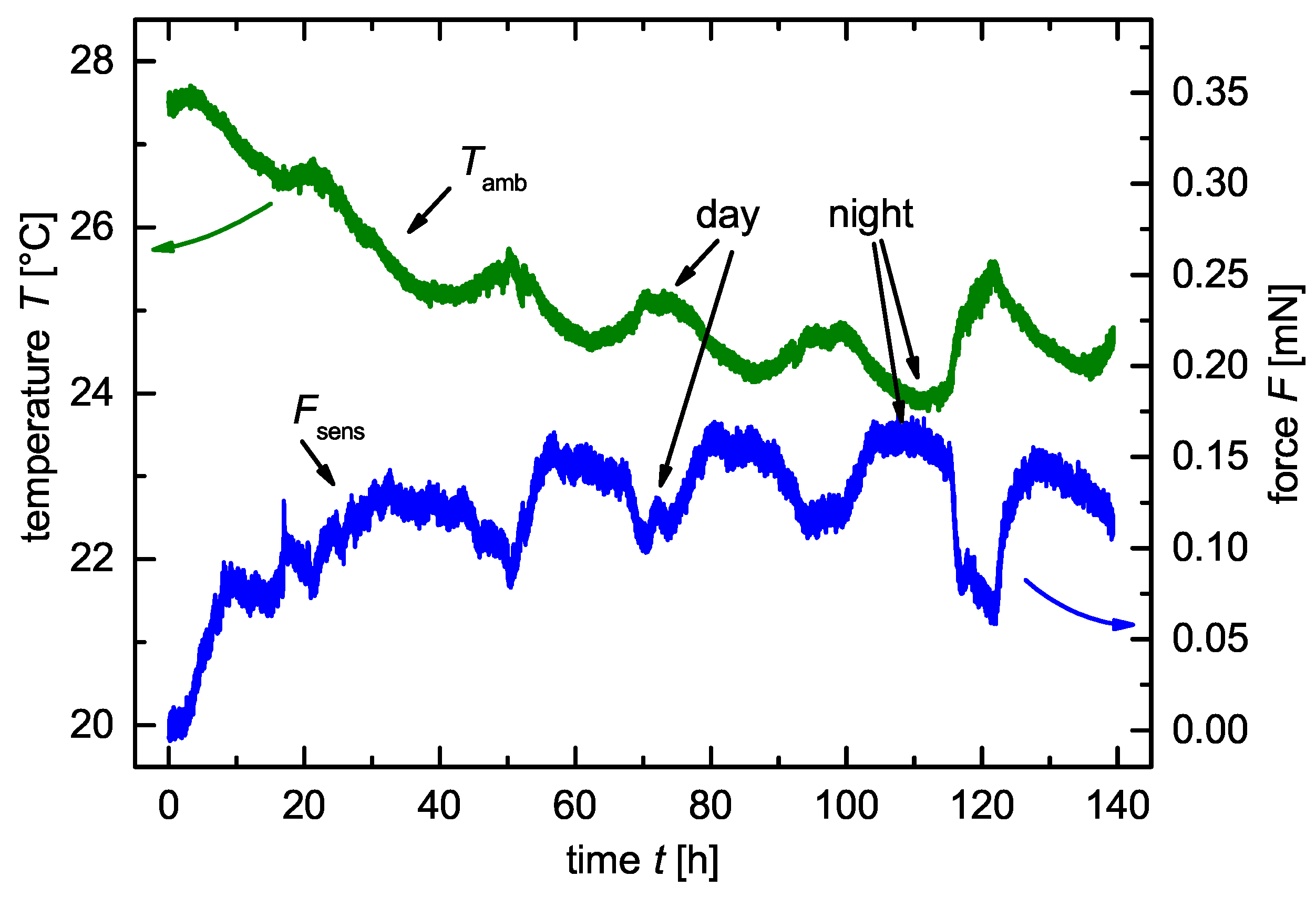
3.1. Temperature Sensitivity
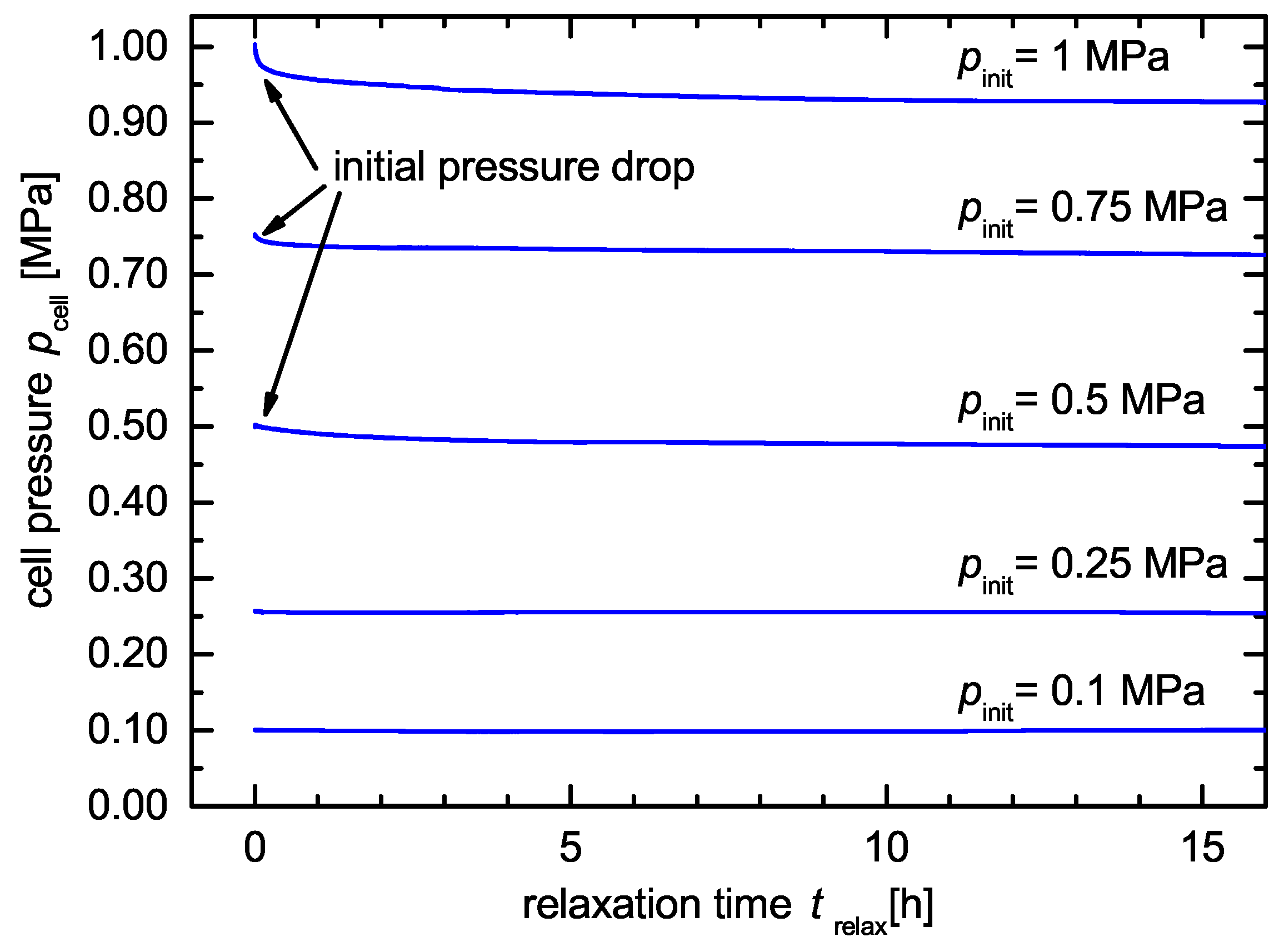
3.2. Mechanical Relaxation
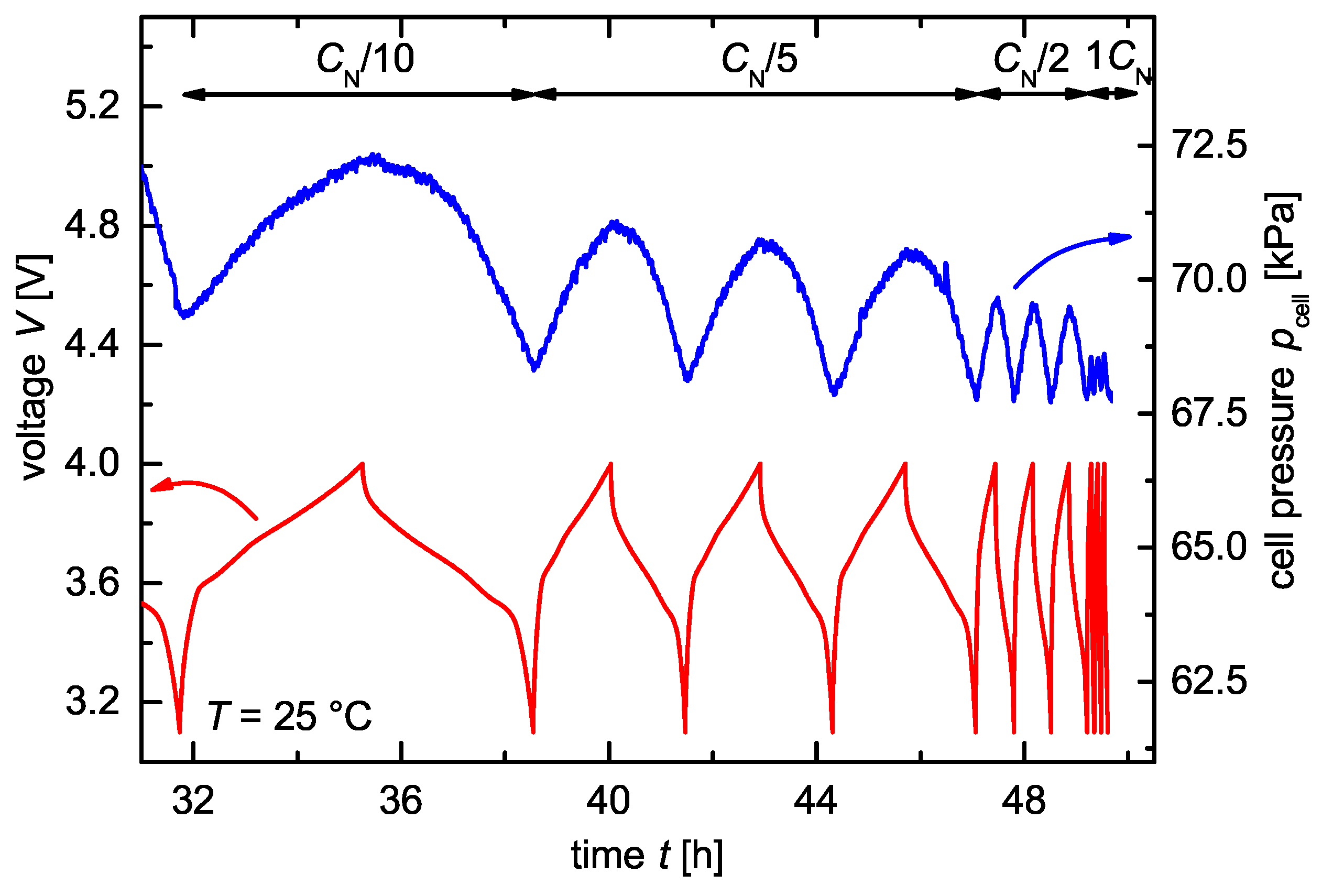
3.3. Cell Pressure
4. Conclusions
Funding
Conflicts of Interest
References
- Armand, M.; Tarascon, J. Building better batteries. Nature 2008, 451, 652–657. [Google Scholar] [CrossRef] [PubMed]
- Braga, M.H.; Grundish, N.S.; Murchison, A.J.; Goodenough, J.B. Alternative strategy for a safe rechargeable battery. Energy Environ. Sci. 2017, 10, 331–336. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Kim, Y. Challenges for rechargeable Li batteries. Chem. Mater. 2010, 22, 587–603. [Google Scholar] [CrossRef]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-ion battery materials: Present and future. Mater. Today 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Peled, E.; Menkin, S. Review—SEI: Past, Present and Future. J. Electrochem. Soc. 2017, 164, A1703–A1719. [Google Scholar] [CrossRef] [Green Version]
- Tarascon, J.M.; Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar] [CrossRef] [PubMed]
- Mancini, M.; Nobili, F.; Tossici, R.; Wohlfahrt-Mehrens, M.; Marassi, R. High performance, environmentally friendly and low cost anodes for lithium-ion battery based on TiO2 anatase and water soluble binder carboxymethyl cellulose. J. Power Sources 2011, 196, 9665–9671. [Google Scholar] [CrossRef]
- Angulakshmi, N.; Nahm, K.S.; Nair, J.R.; Gerbaldi, C.; Bongiovanni, R.; Penazzi, N.; Stephan, A.M. Cycling profile of MgAl2O4-incorporated composite electrolytes composed of PEO and LiPF6 for lithium polymer batteries. Electrochim. Acta 2013, 90, 179–185. [Google Scholar] [CrossRef]
- Bitsch, B.; Dittmann, J.; Schmitt, M.; Scharfer, P.; Schabel, W.; Willenbacher, N. A novel slurry concept for the fabrication of lithium-ion battery electrodes with beneficial properties. J. Power Sources 2014, 265, 81–90. [Google Scholar] [CrossRef] [Green Version]
- Woodford, W.H.; Carter, W.C.; Chiang, Y.M. Design criteria for electrochemical shock resistant battery electrodes. Energy Environ. Sci. 2012, 5, 8014. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. State of health and charge measurements in lithium-ion batteries using mechanical stress. J. Power Sources 2014, 269, 7–14. [Google Scholar] [CrossRef]
- Rieger, B.; Schlueter, S.; Erhard, S.V.; Schmalz, J.; Reinhart, G.; Jossen, A. Multi-scale investigation of thickness changes in a commercial pouch type lithium-ion battery. J. Energy Storage 2016, 6, 213–221. [Google Scholar] [CrossRef]
- Mohan, S.; Kim, Y.; Siegel, J.B.; Samad, N.A.; Stefanopoulou, A.G. A Phenomenological Model of Bulk Force in a Li-Ion Battery Pack and Its Application to State of Charge Estimation. J. Electrochem. Soc. 2014, 161, A2222–A2231. [Google Scholar] [CrossRef] [Green Version]
- Cannarella, J.; Arnold, C.B. Stress evolution and capacity fade in constrained lithium-ion pouch cells. J. Power Sources 2014, 245, 745–751. [Google Scholar] [CrossRef]
- Deshpande, R.; Verbrugge, M.; Cheng, Y.T.; Wang, J.; Liu, P. Battery Cycle Life Prediction with Coupled Chemical Degradation and Fatigue Mechanics. J. Electrochem. Soc. 2012, 159, A1730–A1738. [Google Scholar] [CrossRef]
- Ohzuku, T.; Iwakoshi, Y.; Sawai, K. Formation of Lithium-Graphite Intercalation Compounds in Nonaqueous Electrolytes and Their Application as a Negative Electrode for a Lithium Ion ( Shuttlecock ) Cell. J. Am. Chem. Soc. 1993, 140, 2490–2498. [Google Scholar]
- Yoon, W.S.; Yoon, K.; Mcbreen, J.; Yang, X.Q. A comparative study on structural changes of LiCo1/3N1/3Mn1/3O2 and LiNi0.8Co0.15Al0.05O2 during first charge using in situ XRD. Electrochem. Commun. 2006, 8, 1257–1262. [Google Scholar] [CrossRef]
- Liu, Q.; He, H.; Li, Z.F.; Liu, Y.; Ren, Y.; Lu, W.; Lu, J.; Stach, E.A.; Xie, J. Rate-dependent, Li-ion insertion/deinsertion behavior of LiFePO4 cathodes in commercial 18650 LiFePO4 cells. ACS Appl. Mater. Interfaces 2014, 6, 3282–3289. [Google Scholar] [CrossRef] [PubMed]
- Oh, K.Y.; Siegel, J.B.; Secondo, L.; Kim, S.U.; Samad, N.A.; Qin, J.; Anderson, D.; Garikipati, K.; Knobloch, A.; Epureanu, B.I.; et al. Rate dependence of swelling in lithium-ion cells. J. Power Sources 2014, 267, 197–202. [Google Scholar] [CrossRef]
- Singer, J.P.; Kropp, T.; Kuehnemund, M.; Birke, K.P. Pressure Characteristics and Chemical Potentials of Constrained LiFePO4/C6Cells. J. Electrochem. Soc. 2018, 165, A1348–A1356. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singer, J.P.; Sämann, C.; Gössl, T.; Birke, K.P. Pressure Monitoring Cell for Constrained Battery Electrodes. Sensors 2018, 18, 3808. https://doi.org/10.3390/s18113808
Singer JP, Sämann C, Gössl T, Birke KP. Pressure Monitoring Cell for Constrained Battery Electrodes. Sensors. 2018; 18(11):3808. https://doi.org/10.3390/s18113808
Chicago/Turabian StyleSinger, Jan Patrick, Christian Sämann, Tobias Gössl, and Kai Peter Birke. 2018. "Pressure Monitoring Cell for Constrained Battery Electrodes" Sensors 18, no. 11: 3808. https://doi.org/10.3390/s18113808
APA StyleSinger, J. P., Sämann, C., Gössl, T., & Birke, K. P. (2018). Pressure Monitoring Cell for Constrained Battery Electrodes. Sensors, 18(11), 3808. https://doi.org/10.3390/s18113808





