Parallel Computation of EM Backscattering from Large Three-Dimensional Sea Surface with CUDA
Abstract
1. Introduction
2. Electromagnetic Backscattering from an Electrically Large Sea Surface
2.1. Slope-Deterministic Kirchhoff Approximation Model (SDKAM)
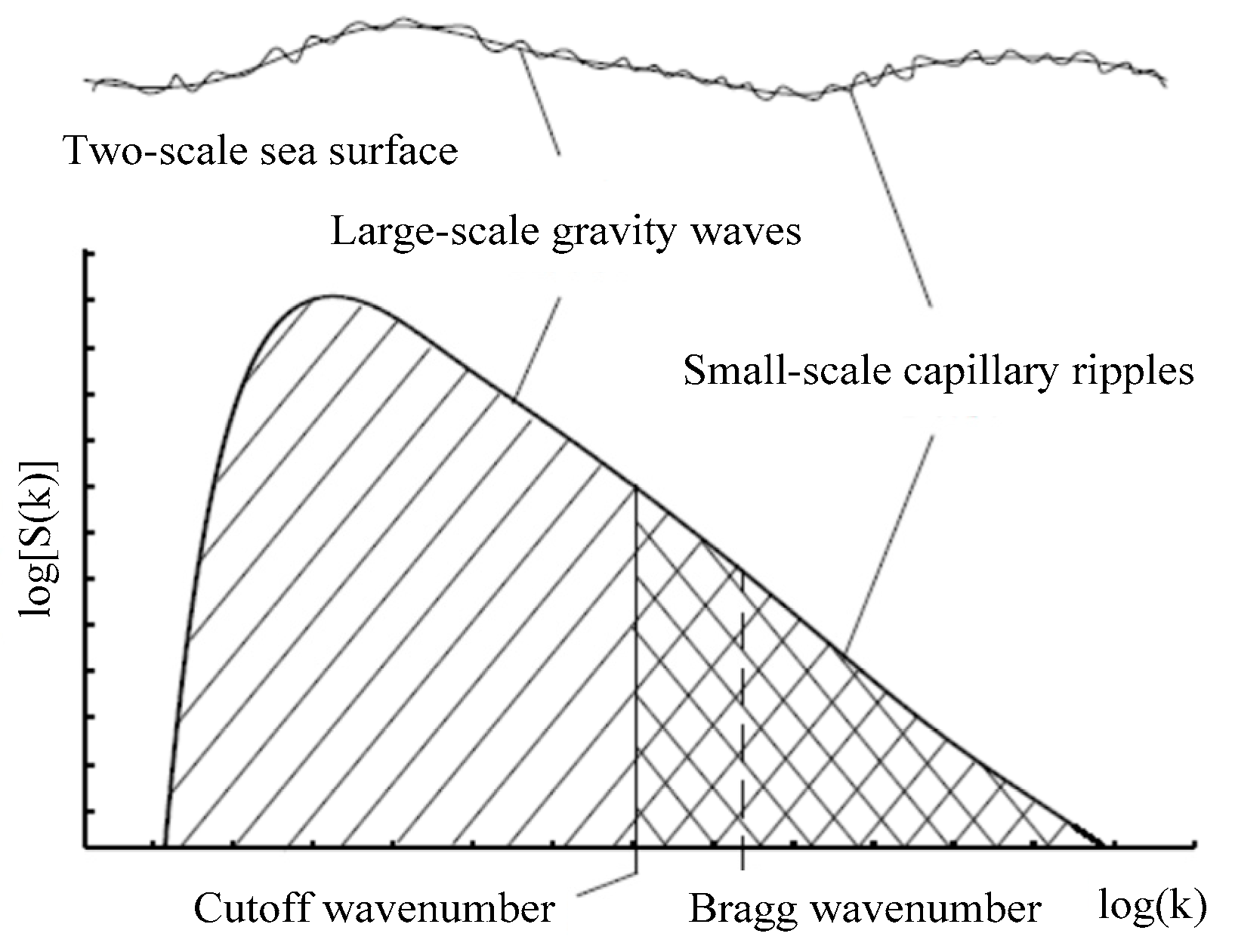
2.2. Slope-Deterministic Two-Scale Model (SDTSM)
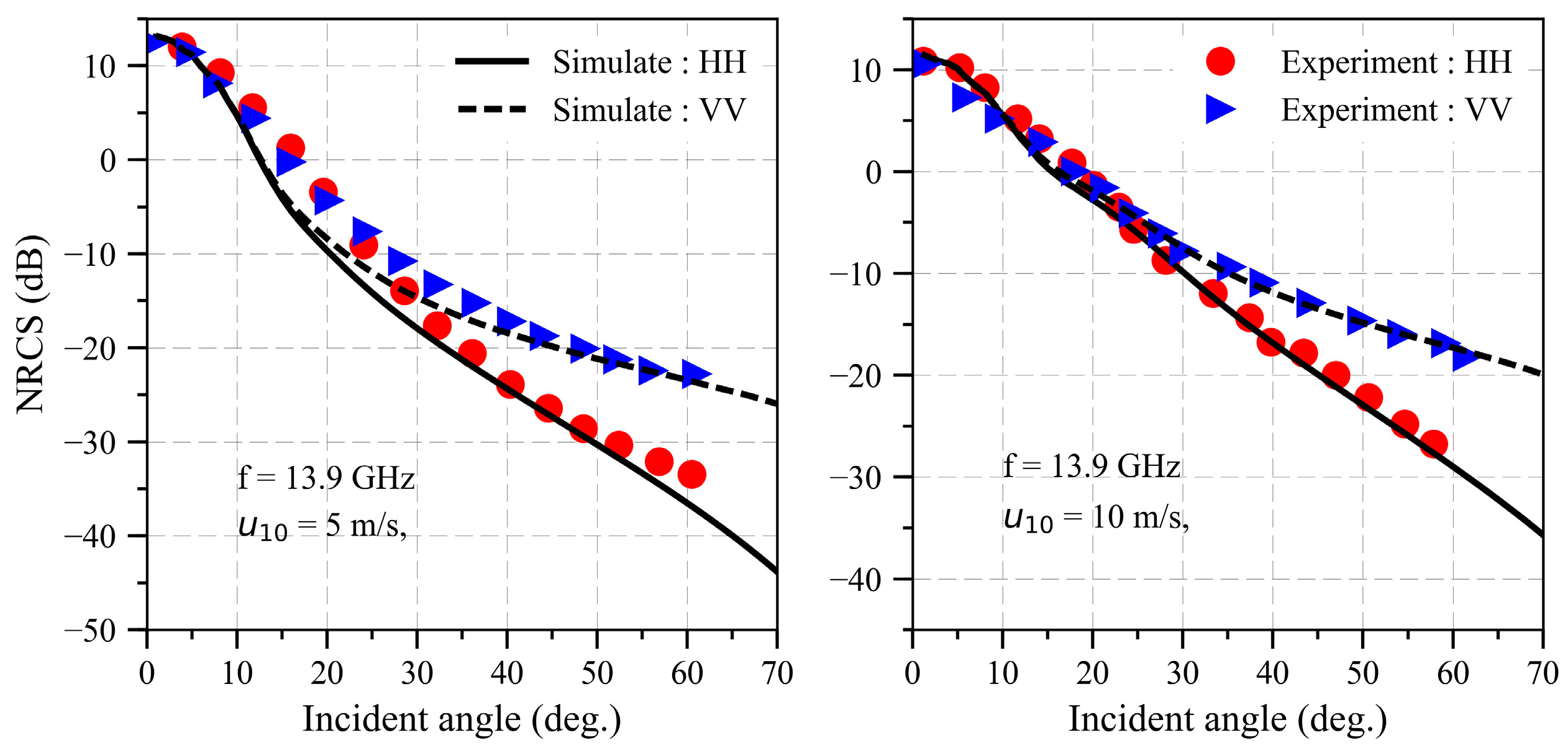
2.3. Slope-Deterministic Composite Scattering Model (SDCSM)
3. NVIDIA Tesla K80 GPU Features and GPU-Based SDCSM Implemented
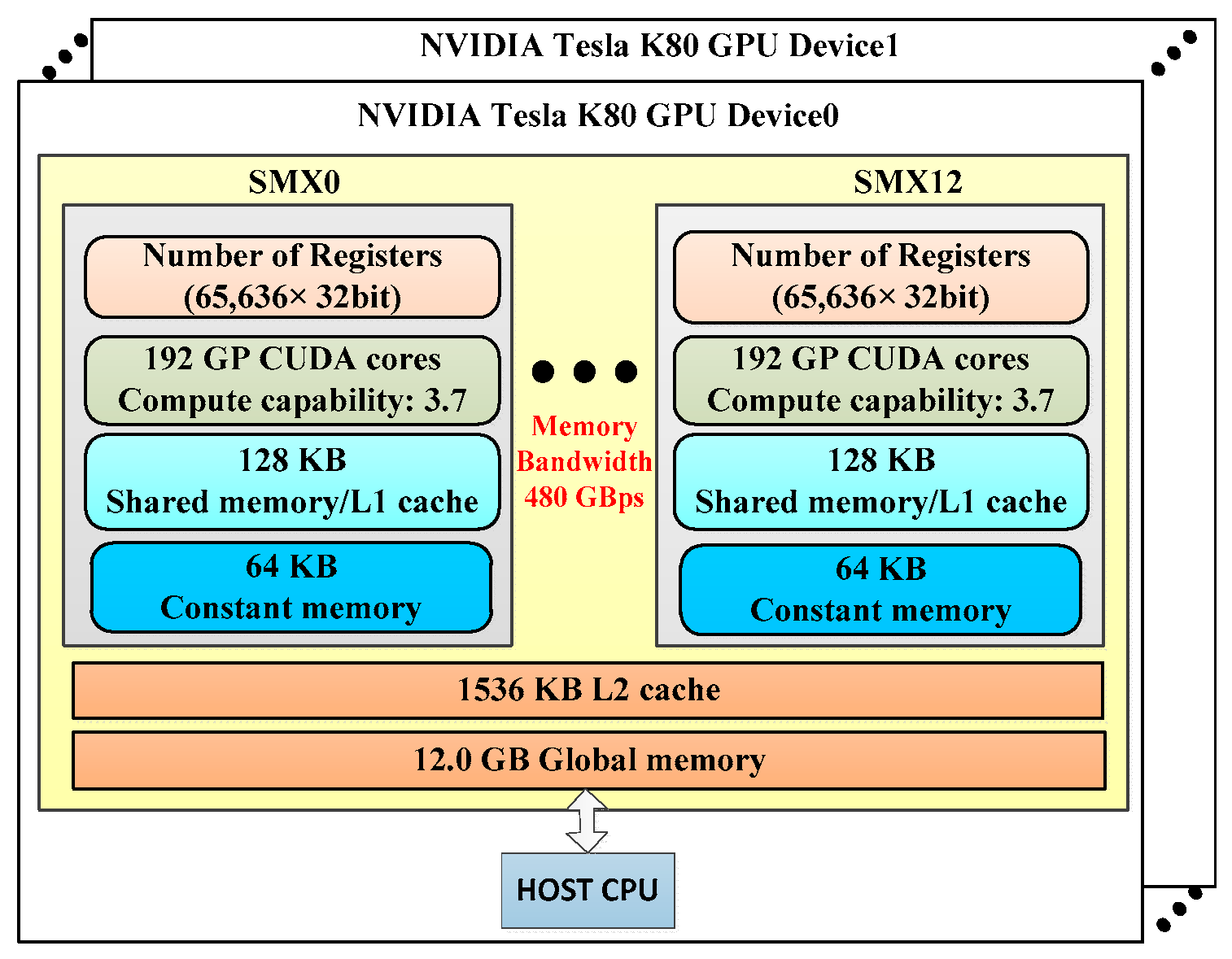
3.1. NVIDIA Tesla K80 GPU Haredare Resource
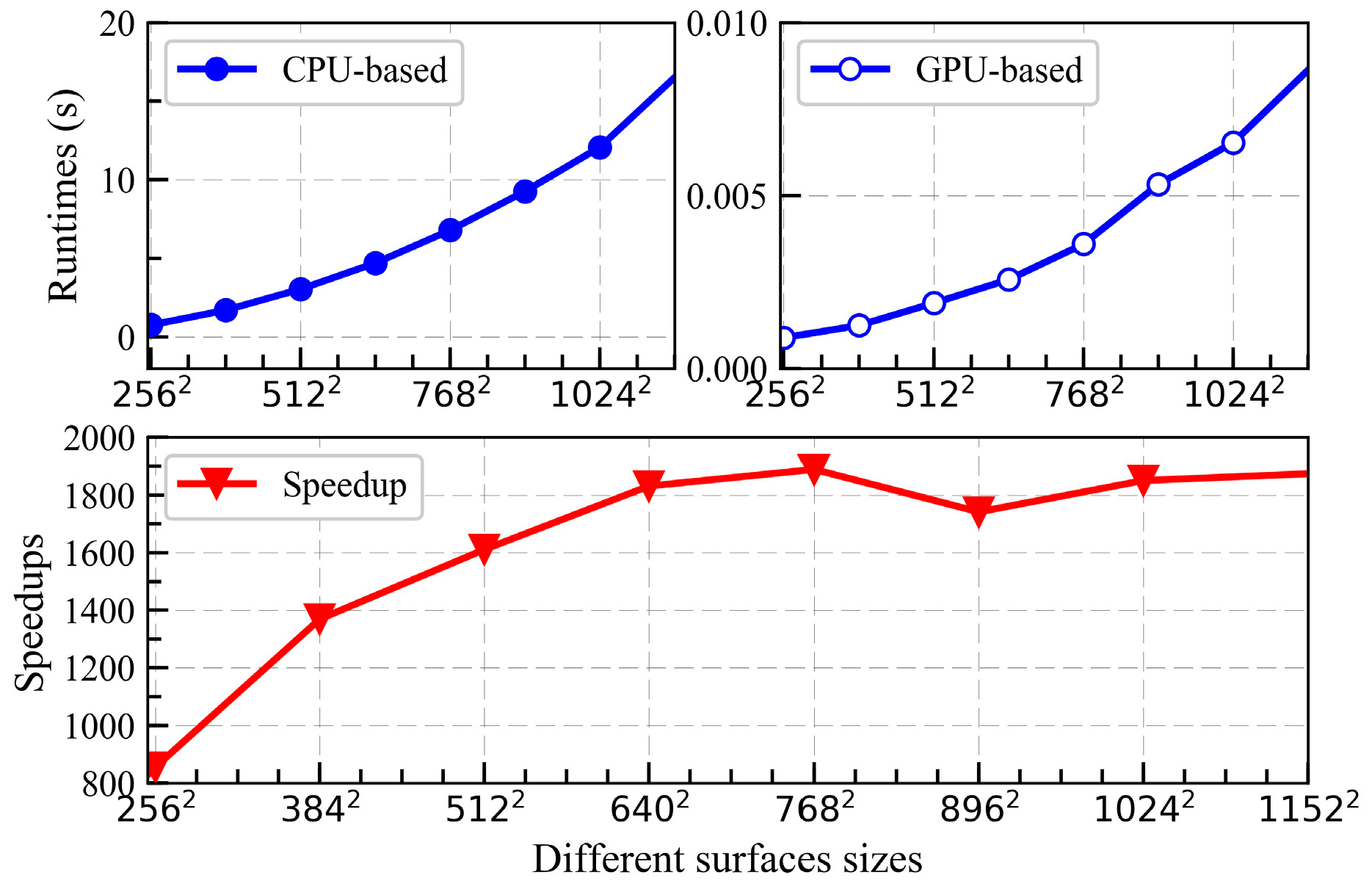
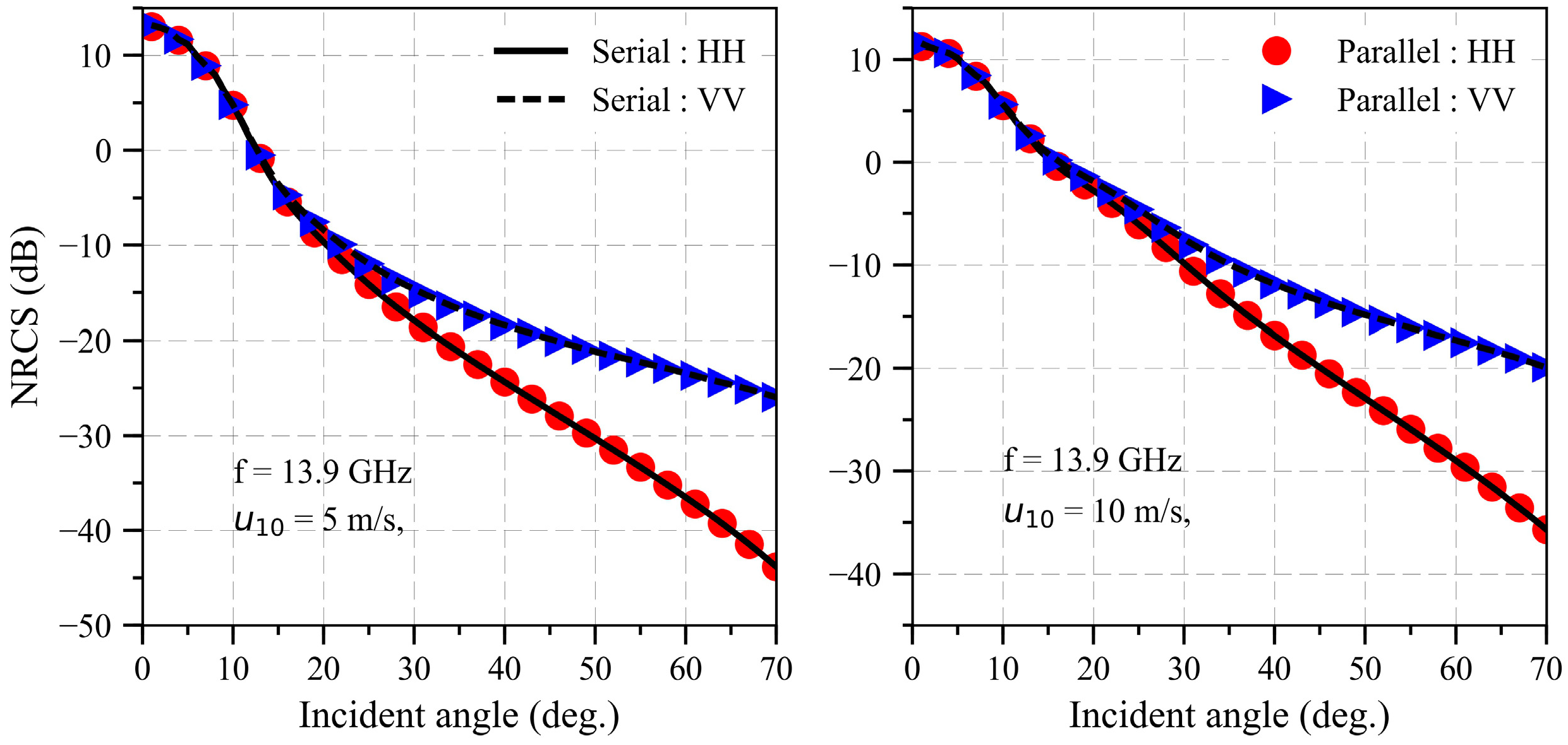
3.2. SDCSM Parallel Computing with CUDA
- Initialize the size of electrically large sea surface , the spatial step of the sea surface , the wind speed , the wind direction , the incident and scattering angles and , the incident and scattering azimuth angles and , the frequency , the grid and block sizes corresponding to the CUDA program.
- Transfer the electrically large sea surface data from the CPU to the GPU.
- Compute the NRCS of individual triangular meshing on the electrically large sea surface independently in parallel on the GPU by all threads within a block.
- Copy the results from the GPU back to the CPU.
4. Initial Parallel Implemented and Further Optimization
4.1. Initial Parallel Implemented
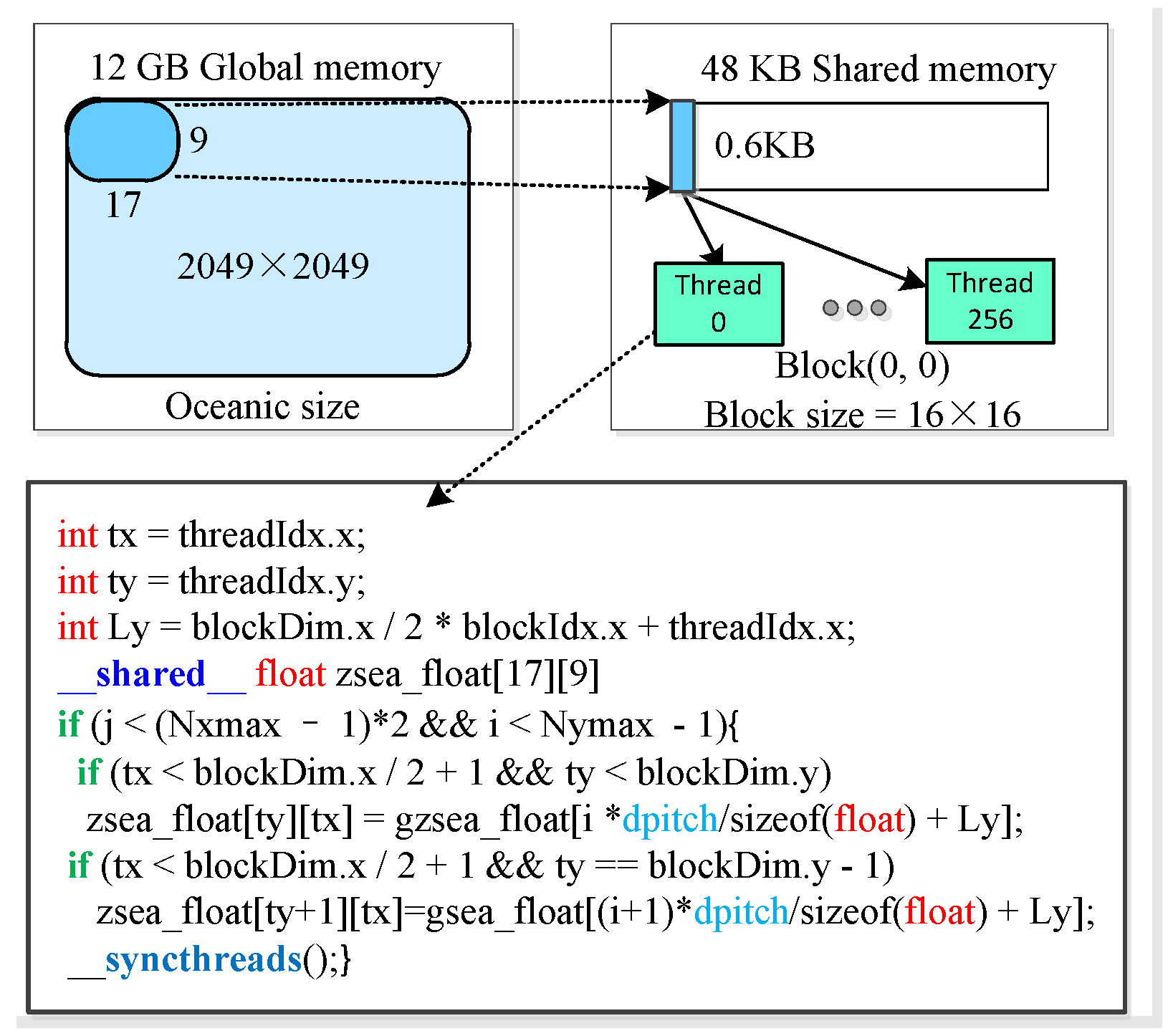
4.2. Further Optimization with Coalesced Global Memory Access
4.3. Further Optimization with Constant Memory
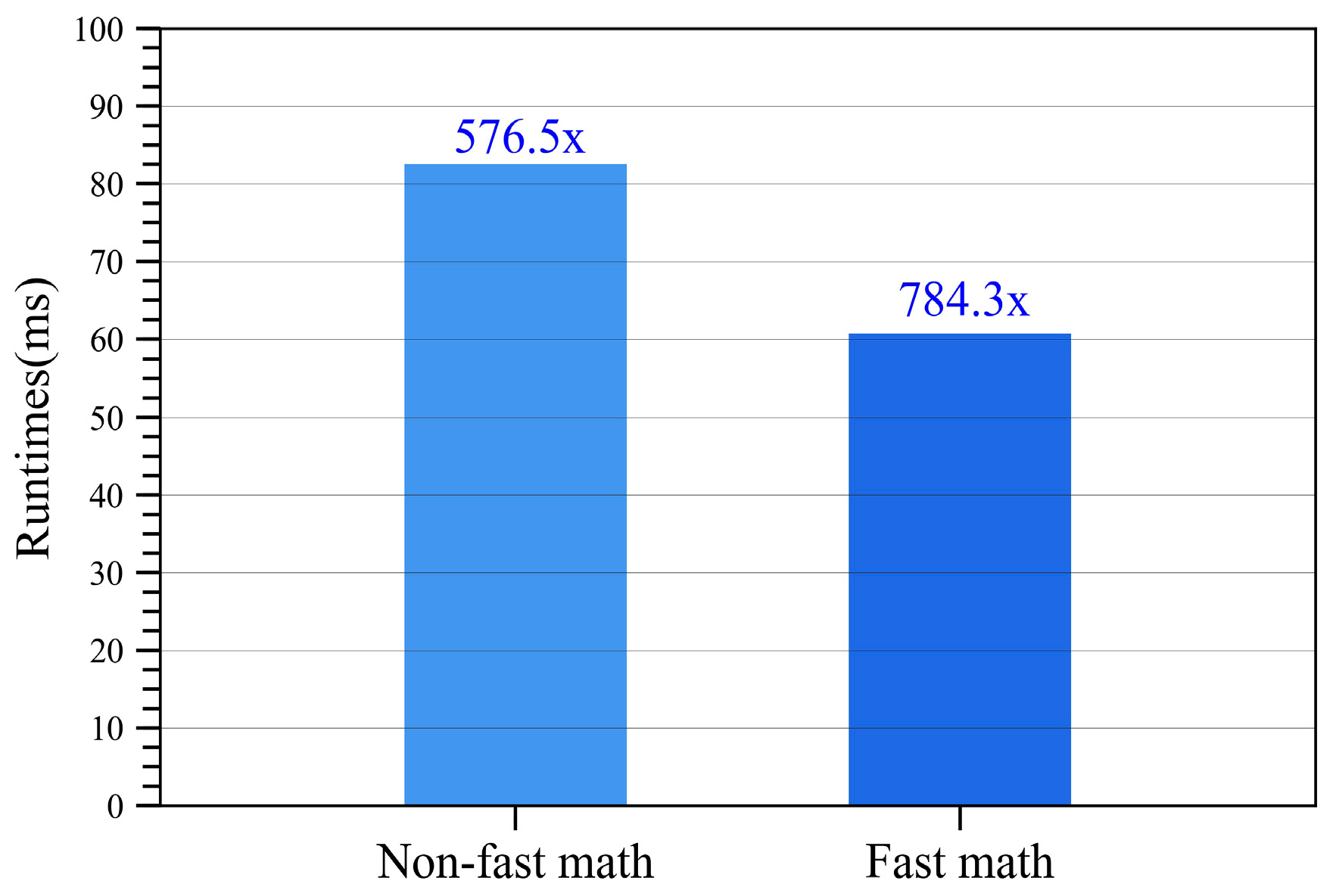
4.4. Further Optimization with Fast Math Compiler Option
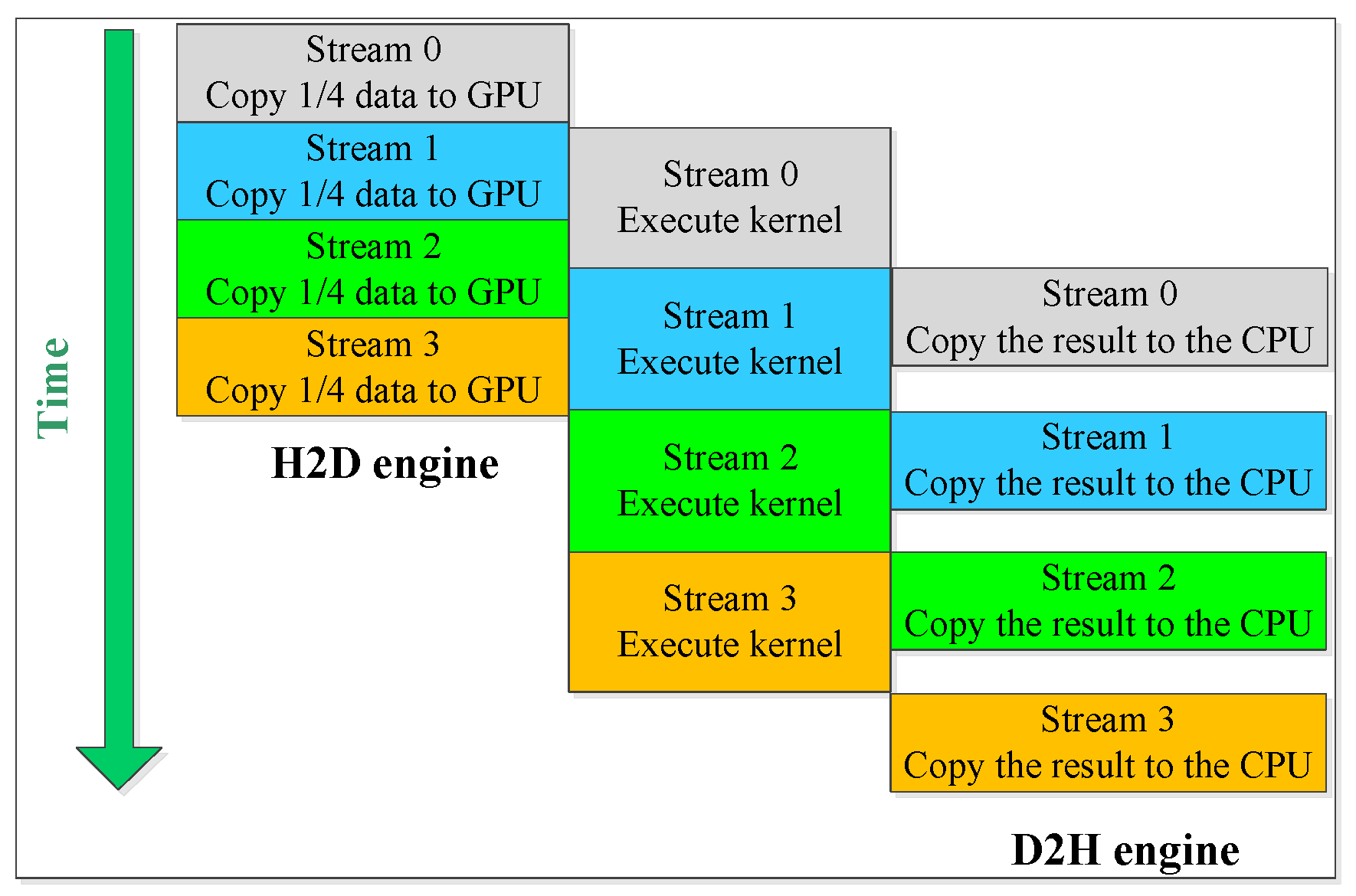
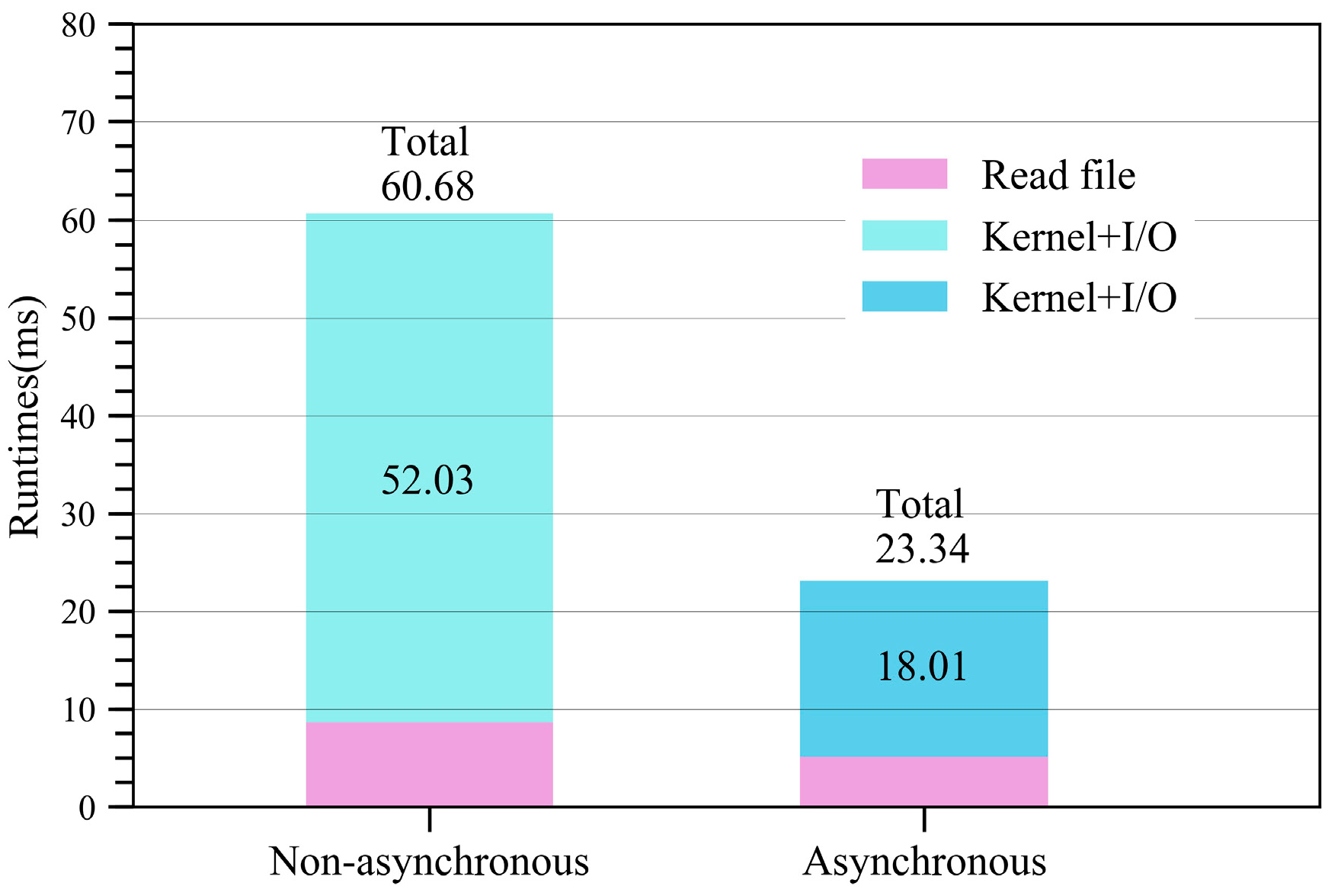
4.5. Further Optimization with Asynchronous Data Transfer (ADT)
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alper, W.R.; Bruening, C. On the relative importance of motion-related contribution to the SAR imaging mechanism of ocean surface waves. IEEE Trans. Geosci. Remote Sens. 1986, 24, 873–885. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Fan, W.; Nie, D. Facet-based investigation on microwave backscattering from sea surface with breaking waves: Sea spikes and SAR imaging. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2313–2325. [Google Scholar] [CrossRef]
- Li, X.; Xu, X. Scattering and Doppler spectral analysis for two-dimensional linear and nonlinear sea surface. IEEE Trans. Geosci. Remote Sens. 2011, 49, 603–611. [Google Scholar] [CrossRef]
- Joung, S.J.; Shelton, J. 3 Dimensional ocean wave model using directional wave spectra for limited capacity computers. In Proceedings of the OCEANS 91 Proceedings, Honolulu, HA, USA, 1–3 October 1991. [Google Scholar]
- Linghu, L.; Wu, J.; Huang, B.; Wu, Z.; Shi, M. GPU-accelerated massively parallel computation of electromagnetic scattering of a time-evolving oceanic surface model I: Time-evolving oceanic surface generation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 1–11. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive; Artech House: Norwood, MA, USA, 1986. [Google Scholar]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surface; Artech House: Norwood, MA, USA, 1963. [Google Scholar]
- Rice, S.O. Reflection of electromagnetic waves from slightly rough surface. Commun. Pure Appl. Math. 1951, 4, 351–378. [Google Scholar] [CrossRef]
- Bourlier, C.; Berginc, G. Microwave analytical backscattering models from randomly rough anisotropic sea surface-comparison with experimental data in C and Ku bands. PIER 2002, 37, 31–78. [Google Scholar] [CrossRef]
- Bourlier, C. Azimuthal harmonic coefficients of the microwave backscattering from a non-Gaussian ocean surface with the first-order SSA method. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2600–2611. [Google Scholar] [CrossRef]
- Bass, F.G.; Fuks, I.M. Wave Scattering from Statistically Rough Surface; Pergamon Press Oxford: New York, NY, USA, 1979; pp. 418–442. [Google Scholar]
- Wu, Z.; Zhang, J.; Guo, L.; Zhou, P. An improved two-scale mode with volume scattering for the dynamic ocean surface. PIER 2009, 89, 39–46. [Google Scholar] [CrossRef]
- Fung, A.K.; Lee, K. A semi-empirical sea-spectrum model for scattering coefficient estimation. IEEE J. Ocea. Eng. 1982, 7, 166–176. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, M.; Zhao, Y.; Luo, W. An efficient slope-deterministic facet model for SAR imagery simulation of marine scene. IEEE Trans. Antennas Propag. 2010, 58, 3751–3756. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, M.; Nie, D. Robust semi-deterministic facet model for fast estimation on EM scattering from ocean-like surface. PIER 2009, 18, 347–363. [Google Scholar] [CrossRef]
- Lee, C.A.; Gasster, S.D.; Plaza, A.; Chang, C.-I.; Huang, B. Recent developments in high performance computing for remote sensing: A review. IEEE J. Sel. Top. Appl. Earth Observ. 2011, 4, 508–527. [Google Scholar] [CrossRef]
- Wilt, N. The CUDA Handbook: A Comprehensive Guide to GPU Programming, 1st ed; Addision-Wesley: Crawfordsville, IN, USA, 2013. [Google Scholar]
- Sanders, J.; Kandrot, E. CUDA by Example: An Introduction to General-Purpose GPU Programming, 1st ed; Addision-Wesley: Ann Arbor, MI, USA, 2010. [Google Scholar]
- Su, X.; Wu, J.; Huang, B.; Wu, Z. GPU-accelerated computation of electromagnetic scattering of a double-layer vegetation model. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2013, 6, 1799–1806. [Google Scholar] [CrossRef]
- Wu, J.; Deng, L.; Jeon, G. Image autoregressive interpolation model using GPU-parallel optimization. IEEE Trans. Ind. Inf. 2017, 14, 426–436. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, M.; Wei, P.; Yuan, X. CUDA-based SSA method in application to calculating EM scattering from large two-dimensional rough surface. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 1372–1382. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, M.; Wei, P.; Nie, D. Spectral decomposition modeling method and its application to EM scattering calculation of large rough surface with SSA method. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 1848–1854. [Google Scholar] [CrossRef]
- Guo, X.; Wu, J.; Wu, Z.; Huang, B. Parallel computation of aerial target reflection of background infrared radiation: Performance comparison of OpenMP, OpenACC, and CUDA implementations. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 1653–1662. [Google Scholar] [CrossRef]
- Mielikainen, J.; Huang, B.; Huang, H.A.; Goldberg, M.D. Improved GPU/CUDA based parallel weather and research forecast (WRF) single moment 5-class (WSM5) cloud microphysics. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 1256–1265. [Google Scholar] [CrossRef]
- Plant, W.J. Studies of backscattered sea return with a CW, dual-frequency, X-band radar. IEEE Trans. Antennas Propag. 1977, 25, 28–36. [Google Scholar] [CrossRef]
- Fuks, I.M. Theory of radio wave scattering at a rough sea surface. Soviet Radiophys. 1966, 9, 513–519. [Google Scholar] [CrossRef]
- Brown, G.S. Backscattering from a Gaussian-distributed, perfectly conducting rough surface. IEEE Trans. Antennas Propag. 1985, 10, 445–451. [Google Scholar] [CrossRef]
- Efouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Voronovich, A.G.; Avorotni, V.U. Theoretical model for scattering of radar signals in Ku- and C-bands from a rough sea surface with breaking waves. Wave Random Complex Media 2001, 11, 247–269. [Google Scholar] [CrossRef]






| Total Time | Read File | Execution Time | I/O | |
|---|---|---|---|---|
| Serial program (ms) | 47,593.6 | -- | -- | -- |
| Parallel program (ms) | 86.31 | 8.663 | 39.99 | 37.657 |
| speedup | 551.4× | -- | -- | -- |
| CPU Runtime (ms) | GPU-Runtime (ms) | Speedup | |
|---|---|---|---|
| Serial program | 47,593.6 | -- | -- |
| Initial Parallel program | 86.31 | 551.4x | |
| Utilizing shared memory | 84.03 | 566.4x |
| CPU Runtime (ms) | GPU-Runtime (ms) | Speedup | |
|---|---|---|---|
| Serial program | 47,593.6 | -- | -- |
| Non-optimized | 84.03 | 566.4× | |
| Optimized | 82.56 | 576.5× |
| Variable | Variable Description | Non-Fast Math | Fast Math | ||
|---|---|---|---|---|---|
| MAE | MAE/Mean | MAE | MAE/Mean | ||
| The NRCS for HH polarization | |||||
| The NRCS for VV polarization | |||||
| CPU Runtime (ms) | GPU-Runtime (ms) | Speedup | |
|---|---|---|---|
| Serial program | 47,593.6 | -- | -- |
| Non-optimized | 60.68 | 784.3× | |
| Optimized | 23.34 | 2039.1× |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Linghu, L.; Wu, J.; Wu, Z.; Wang, X. Parallel Computation of EM Backscattering from Large Three-Dimensional Sea Surface with CUDA. Sensors 2018, 18, 3656. https://doi.org/10.3390/s18113656
Linghu L, Wu J, Wu Z, Wang X. Parallel Computation of EM Backscattering from Large Three-Dimensional Sea Surface with CUDA. Sensors. 2018; 18(11):3656. https://doi.org/10.3390/s18113656
Chicago/Turabian StyleLinghu, Longxiang, Jiaji Wu, Zhensen Wu, and Xiaobing Wang. 2018. "Parallel Computation of EM Backscattering from Large Three-Dimensional Sea Surface with CUDA" Sensors 18, no. 11: 3656. https://doi.org/10.3390/s18113656
APA StyleLinghu, L., Wu, J., Wu, Z., & Wang, X. (2018). Parallel Computation of EM Backscattering from Large Three-Dimensional Sea Surface with CUDA. Sensors, 18(11), 3656. https://doi.org/10.3390/s18113656





