Design and Experimental Validation of a Multiple-Frequency Microwave Tomography System Employing the DBIM-TwIST Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Antenna Design and Characterization
2.2. Array Setup and Data Acquisition Process
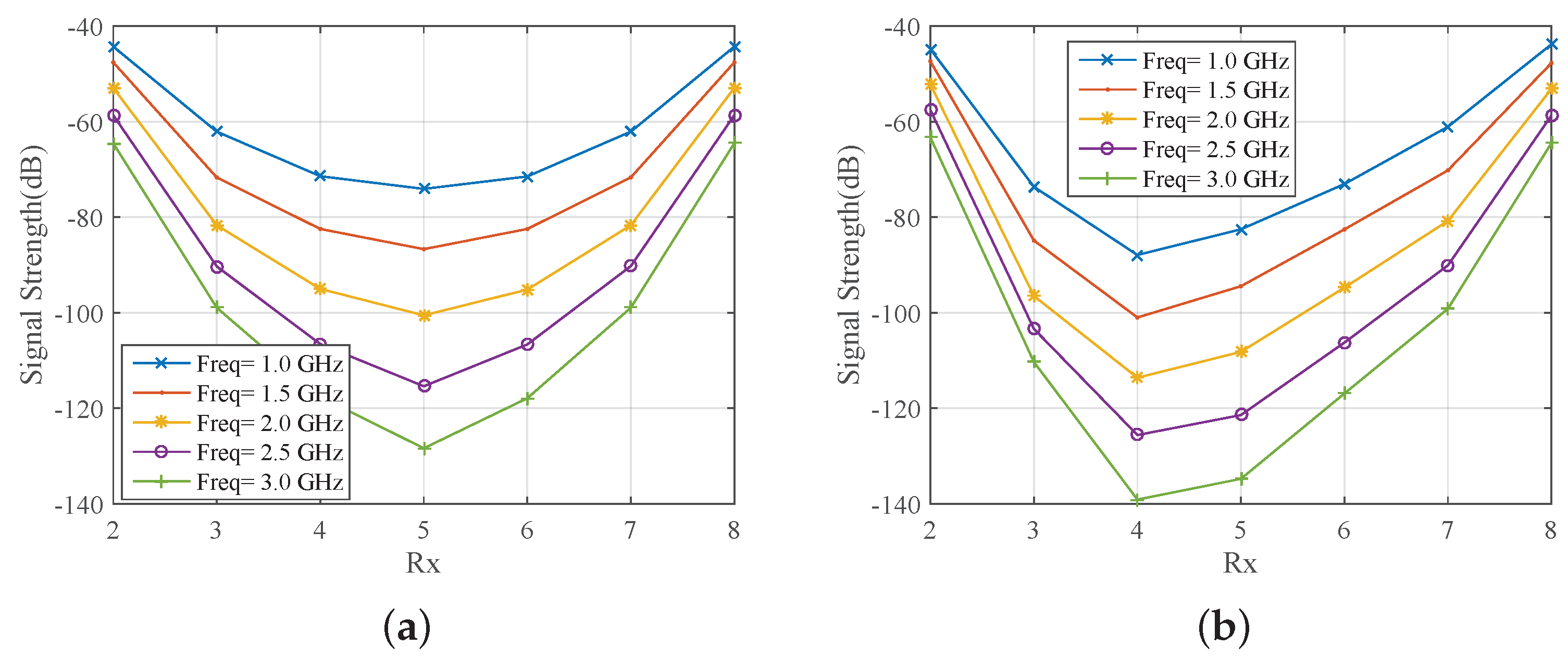
2.3. System Sensitivity Evaluation Using Numerical Simulations
3. Results
3.1. Comparison of CST and Experimental Results
3.2. Reconstructions Using the DBIM-TwIST Algorithm
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Semenov, S. Microwave tomography: Review of the progress towards clinical applications. Philos. Transact. A Math. Phys. Eng. Sci. 2009, 367, 3021–3042. [Google Scholar] [CrossRef] [PubMed]
- Winters, D.W.; Shea, J.D.; Kosmas, P.; Van Veen, B.D.; Hagness, S.C. Three-dimensional microwave breast imaging: Dispersive dielectric properties estimation using patient-specific basis functions. IEEE Trans. Med. Imaging 2009, 28, 969–981. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, S.; Lau, R.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251. [Google Scholar] [CrossRef] [PubMed]
- Foster, K.R.; Schwan, H.P. Dielectric properties of tissues and biological materials: A critical review. CRC Crit. Rev. Biomed. Eng. 1989, 17, 25–104. [Google Scholar]
- Lazebnik, M.; McCartney, L.; Popovic, D.; Watkins, C.B.; Lindstrom, M.J.; Harter, J.; Sewall, S.; Magliocco, A.; Booske, J.H.; Okoniewski, M.; et al. A large-scale study of the ultrawideband microwave dielectric properties of normal breast tissue obtained from reduction surgeries. Phys. Med. Biol. 2007, 52, 2637. [Google Scholar] [CrossRef] [PubMed]
- Lahri, R.; Rahman, M.; Wright, M.; Kosmas, P.; Thanou, M. Zinc oxide nanoparticles as contrast-enhancing agents for microwave imaging. Med. Phys. 2018, 45, 3820–3830. [Google Scholar] [CrossRef] [PubMed]
- Shea, J.D.; Kosmas, P.; Hagness, S.C.; Veen, B.D.V. Contrast-enhanced microwave breast imaging. In Proceedings of the 13th International Symposium on Antenna Technology and Applied Electromagnetics (ANTEM/URSI), Banff, AB, Canada, 15–18 February 2009; pp. 1–4. [Google Scholar]
- Semenov, S.Y.; Corfield, D.R. Microwave tomography for brain imaging: Feasibility assessment for stroke detection. Int. J. Antennas Propag. 2008, 2008. [Google Scholar] [CrossRef]
- Mohammed, B.J.; Abbosh, A.M.; Mustafa, S.; Ireland, D. Microwave System for Head Imaging. IEEE Trans. Instrum. Meas. 2014, 63, 117–123. [Google Scholar] [CrossRef]
- Meaney, P.M.; Fanning, M.W.; Li, D.; Poplack, S.P.; Paulsen, K.D. A clinical prototype for active microwave imaging of the breast. IEEE Trans. Microw. Theory Tech. 2000, 48, 1841–1853. [Google Scholar]
- Semenov, S.Y.; Svenson, R.H.; Boulyshev, A.E.; Souvorov, A.E.; Borisov, V.Y.; Sizov, Y.; Starostin, A.N.; Dezern, K.R.; Tatsis, G.P.; Baranov, V.Y. Microwave tomography: Two-dimensional system for biological imaging. IEEE Trans. Biomed. Eng. 1996, 43, 869–877. [Google Scholar] [CrossRef] [PubMed]
- Gilmore, C.; Mojabi, P.; Zakaria, A.; Ostadrahimi, M.; Kaye, C.; Noghanian, S.; Shafai, L.; Pistorius, S.; LoVetri, J. A wideband microwave tomography system with a novel frequency selection procedure. IEEE Trans. Biomed. Eng. 2010, 57, 894–904. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Yuan, M.; Stang, J.; Bresslour, E.; George, R.T.; Ybarra, G.A.; Joines, W.T.; Liu, Q.H. Active microwave imaging II: 3-D system prototype and image reconstruction from experimental data. IEEE Trans. Microw. Theory Tech. 2008, 56, 991–1000. [Google Scholar]
- Casu, M.R.; Vacca, M.; Tobon, J.A.; Pulimeno, A.; Sarwar, I.; Solimene, R.; Vipiana, F. A COTS-based microwave imaging system for breast-cancer detection. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 804–814. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Fhager, A.; He, Z.; Persson, M.; Linner, P.; Zirath, H. Development of a time domain microwave system for medical diagnostics. IEEE Trans. Instrum. Meas. 2014, 63, 2931–2939. [Google Scholar] [CrossRef]
- Fear, E.C.; Bourqui, J.; Curtis, C.; Mew, D.; Docktor, B.; Romano, C. Microwave breast imaging with a monostatic radar-based system: A study of application to patients. IEEE Trans. Microw. Theory Tech. 2013, 61, 2119–2128. [Google Scholar] [CrossRef]
- Porter, E.; Coates, M.; Popovic, M. An early clinical study of time-domain microwave radar for breast health monitoring. IEEE Trans. Biomed. Eng. 2016, 63, 530–539. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Bond, E.J.; Veen, B.D.V.; Hagness, S.C. An overview of ultra-wideband microwave imaging via space-time beamforming for early-stage breast-cancer detection. IEEE Antennas Propag. Mag. 2005, 47, 19–34. [Google Scholar]
- Song, H.; Kono, H.; Seo, Y.; Azhari, A.; Somei, J.; Suematsu, E.; Watarai, Y.; Ota, T.; Watanabe, H. A radar-based breast cancer detection system using CMOS integrated circuits. IEEE Access 2015, 3, 2111–2121. [Google Scholar] [CrossRef]
- Klemm, M.; Craddock, I.J.; Leendertz, J.A.; Preece, A.; Benjamin, R. Radar-based breast cancer detection using a hemispherical antenna array—Experimental results. IEEE Trans. Antennas Propag. 2009, 57, 1692–1704. [Google Scholar] [CrossRef]
- Meaney, P.M.; Shubitidze, F.; Fanning, M.W.; Kmiec, M.; Epstein, N.R.; Paulsen, K.D. Surface wave multipath signals in near-field microwave imaging. Int. J. Biomed. Imag. 2012, 2012, 8. [Google Scholar] [CrossRef] [PubMed]
- Semenov, S.Y.; Svenson, R.H.; Bulyshev, A.E.; Souvorov, A.E.; Nazarov, A.G.; Sizov, Y.E.; Posukh, V.G.; Pavlovsky, A.; Repin, P.N.; Starostin, A.N.; et al. Three-dimensional microwave tomography: Initial experimental imaging of animals. IEEE Trans. Biomed. Eng. 2002, 49, 55–63. [Google Scholar] [CrossRef] [PubMed]
- Mobashsher, A.T.; Mahmoud, A.; Abbosh, A.M. Portable wideband microwave imaging system for intracranial hemorrhage detection using improved back-projection algorithm with model of effective head permittivity. Sci. Rep. 2016, 6, 20459. [Google Scholar] [CrossRef] [PubMed]
- Miao, Z.; Kosmas, P. Microwave breast imaging based on an optimized two-step iterative shrinkage-thresholding method. In Proceedings of the 2015 9th European Conference on Antennas and Propagation (EuCAP), Lisbon, Portugal, 12–17 April 2015; pp. 1–4. [Google Scholar]
- Miao, Z.; Kosmas, P. Multiple-frequency DBIM-TwIST algorithm for microwave breast imaging. IEEE Trans. Antennas Propag. 2017, 65, 2507–2516. [Google Scholar] [CrossRef]
- Scapaticci, R.; Kosmas, P.; Crocco, L. Wavelet-based regularization for robust microwave imaging in medical applications. IEEE Transac. Biomed. Eng. 2015, 62, 1195–1202. [Google Scholar] [CrossRef] [PubMed]
- Meaney, P.M.; Fox, C.J.; Geimer, S.D.; Paulsen, K.D. Electrical characterization of glycerin: Water mixtures: Implications for use as a coupling medium in microwave tomography. IEEE Trans. Microw. Theory Tech. 2017, 65, 1471–1478. [Google Scholar] [CrossRef] [PubMed]
- Gilmore, C.; Zakaria, A.; LoVetri, J.; Pistorius, S. A study of matching fluid loss in a biomedical microwave tomography system. Med. Phys. 2013, 40, 023101. [Google Scholar] [CrossRef] [PubMed]
- Fox, C.J.; Meaney, P.M.; Shubitidze, F.; Potwin, L.; Kmiec, M.; Paulsen, K.D. Characterization of an implicitly resistively-loaded monopole antenna in lossy liquid media. Int. J. Antennas Propag. 2008, 2008, 580782. [Google Scholar] [CrossRef] [PubMed]
- Gilmore, C.; Zakaria, A.; Pistorius, S.; LoVetri, J. Microwave imaging of human forearms: Pilot study and image enhancement. J. Biomed. Imag. 2013, 2013, 19. [Google Scholar] [CrossRef] [PubMed]
- Meaney, P.M.; Pendergrass, S.A.; Fanning, M.W.; Paulsen, K.D. Importance of using a reduced contrast coupling medium in 2D microwave breast imaging. J. Electromagn. Waves Appl. 2003, 17, 333–355. [Google Scholar] [CrossRef]
- Bindu, G.; Lonappan, A.; Thomas, V.; Aanandan, C.; Mathew, K. Dielectric studies of corn syrup for applications in microwave breast imaging. Prog. Electromagn. Res. 2006, 59, 175–186. [Google Scholar] [CrossRef]
- Romeo, S.; Di Donato, L.; Bucci, O.M.; Catapano, I.; Crocco, L.; Scarfì, M.R.; Massa, R. Dielectric characterization study of liquid-based materials for mimicking breast tissues. Microw. Opt. Technol. Lett. 2011, 53, 1276–1280. [Google Scholar] [CrossRef]
- Bucci, O.; Crocco, L.; Scapaticci, R.; Bellizzi, G. On the design of phased arrays for medical applicatios. Proc. IEEE 2016, 104, 633–648. [Google Scholar] [CrossRef]
- Shea, J.D.; Kosmas, P.; Hagness, S.C.; Van Veen, B.D. Three-dimensional microwave imaging of realistic numerical breast phantoms via a multiple-frequency inverse scattering technique. Med. Phys. 2010, 37, 4210–4226. [Google Scholar] [CrossRef] [PubMed]
- Chandra, R.; Zhou, H.; Balasingham, I.; Narayanan, R.M. On the opportunities and challenges in microwave medical sensing and imaging. IEEE Trans. Biomed. Eng. 2015, 62, 1667–1682. [Google Scholar] [CrossRef] [PubMed]












© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahsan, S.; Guo, Z.; Miao, Z.; Sotiriou, I.; Koutsoupidou, M.; Kallos, E.; Palikaras, G.; Kosmas, P. Design and Experimental Validation of a Multiple-Frequency Microwave Tomography System Employing the DBIM-TwIST Algorithm. Sensors 2018, 18, 3491. https://doi.org/10.3390/s18103491
Ahsan S, Guo Z, Miao Z, Sotiriou I, Koutsoupidou M, Kallos E, Palikaras G, Kosmas P. Design and Experimental Validation of a Multiple-Frequency Microwave Tomography System Employing the DBIM-TwIST Algorithm. Sensors. 2018; 18(10):3491. https://doi.org/10.3390/s18103491
Chicago/Turabian StyleAhsan, Syed, Ziwen Guo, Zhenzhuang Miao, Ioannis Sotiriou, Maria Koutsoupidou, Efthymios Kallos, George Palikaras, and Panagiotis Kosmas. 2018. "Design and Experimental Validation of a Multiple-Frequency Microwave Tomography System Employing the DBIM-TwIST Algorithm" Sensors 18, no. 10: 3491. https://doi.org/10.3390/s18103491
APA StyleAhsan, S., Guo, Z., Miao, Z., Sotiriou, I., Koutsoupidou, M., Kallos, E., Palikaras, G., & Kosmas, P. (2018). Design and Experimental Validation of a Multiple-Frequency Microwave Tomography System Employing the DBIM-TwIST Algorithm. Sensors, 18(10), 3491. https://doi.org/10.3390/s18103491





