1. Introduction
The development and scientific research of advanced perceptual systems has notably grown during the last decades, and has experienced a tremendous rise in recent years due to the availability of increasingly sophisticated sensors, the use of computing nodes with higher and higher computational power, and the advent of powerful algorithmic strategies based on deep learning (all of them actually entering the mass consumer market). The aim of perceptual systems is to automatically analyze complex and rich information taken from different sensors in order to obtain refined information on the sensed environment and the activities being carried out within them. The scientific works in these environments cover research areas ranging from basic sensor technologies to signal processing and pattern recognition. They also open the pathway to the idea of systems being able to analyze human activities, providing us with advanced interaction capabilities and services.
In this context, the localization of humans (being the most interesting element for perceptual systems) is a fundamental task that needs to be addressed so that the systems can actually start to provide higher level information on the activities being carried out. Without a precise localization, further advanced interactions between humans and their physical environment cannot be fulfilled successfully.
The scientific community has devoted a huge amount of effort to building robust and reliable indoor localization systems based on different sensors [
1,
2,
3]. Non-invasive technologies are preferred in this context, so that no electronic or passive devices need to be carried by humans for localization. The two non-invasive technologies that have been mainly used in indoor localization are those based on video systems and acoustic sensors.
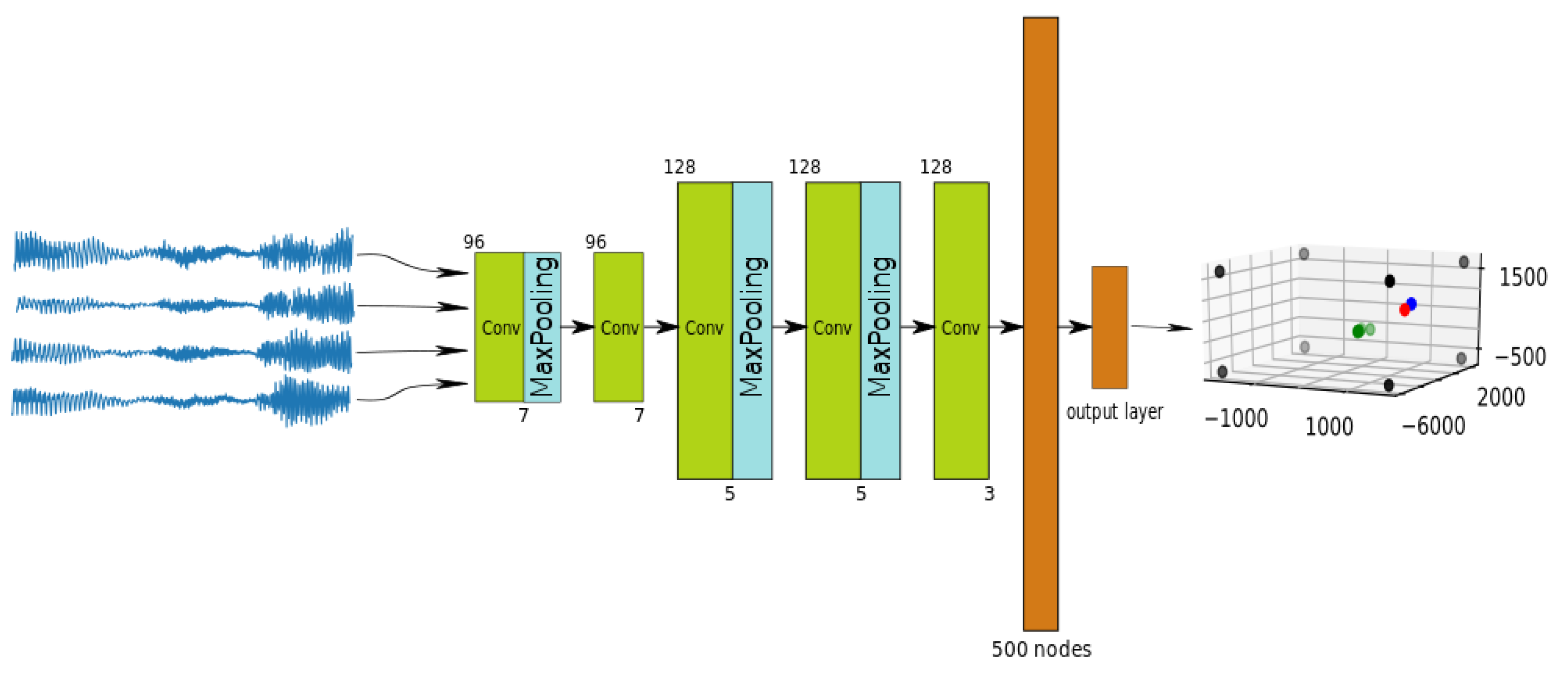
This paper focuses on audio-based localization from unknown wide-band audio sources (e.g., the human voice) captured by a set of microphone arrays placed in known positions. The main objective of the paper is to directly use the signals captured by the microphone arrays to automatically obtain the position of the acoustic source detected in the given environment.
Even though there have been a lot of proposals in this area, Acoustic Source Localization (ASL) is still a hot research topic. This paper proposes a Convolutional Neural Network (CNN) architecture that is trained end-to-end to solve the acoustic localization problem. Our CNN takes the raw signals captured by the microphones as input and delivers the 3D position of the acoustic source as its output.
The idea of using neural networks for sound processing is not new and has gained popularity in recent years (especially for speech recognition [
4]). In the context of ASL, deep learning methods have been recently developed [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. Most of these works focus on obtaining the Direction of Arrival (DOA) of the acoustic source. They also feed the network with feature vectors extracted from the audio signals. To the best of our knowledge, this is the first work in the literature that directly uses the speech signal as input and aims to directly estimating the source position coordinates in the room in three-dimensional space. The avoidance of hand-crafted features has been proven to increase the accuracy of classifications and regression methods based on Convolutional Neural Networks in other fields, such as in computer vision [
19,
20].
Our proposal is evaluated using both semi-synthetic and real data, and outperforms traditional solutions based on Steered Response Power (
SRP) [
21] (that are still being actively used in state-of-the-art systems [
22,
23,
24,
25]), and also shows better results than a very recent proposal based on a Convolutional Recurrent Neural Network [
18].
The rest of the paper is organized as follows.
Section 2 includes a review study of the state-of-the-art in acoustic source localization with special emphasis on the use of deep learning approaches.
Section 3 describes the CNN-based proposal, with details on the training and fine tuning strategies. The experimental work is detailed in
Section 4, and
Section 5 summarizes the main conclusions and contributions of the paper and gives some ideas for future work.
2. State of the Art
The literature contains many approaches to address the acoustic source localization (ASL) problem. According to the classical literature review on this topic, these approaches can be broadly divided into three categories [
26,
27]: time delay based, beamforming based, and high-resolution spectral estimation based methods. This taxonomy relies on the fact that ASL has traditionally been considered a signal processing problem based on the definition of a signal propagation model [
26,
27,
28,
29,
30,
31,
32,
33,
34], but, more recently, the range of proposals in the literature has also considered strategies based on exploiting the optimization techniques and mathematical properties of related measurements [
35,
36,
37,
38,
39], and also the use of machine learning strategies [
40,
41,
42], aimed at obtaining direct mapping from specific features to source locations [
43], an area in which deep learning approaches are starting to be applied and that will be further described later in this section.
Time delay based methods (also referred to as
indirect methods), compute the time difference of arrivals (TDOAs) across various combinations of pairs of spatially separated microphones, usually using the Generalized Correlation Function (GCC) [
28]. In a second step, the TDOAs are combined with knowledge of the microphones’ positions to generate a position estimation [
26,
44].
Beamforming based techniques [
23,
27,
30,
34] attempt to estimate the position of the source by optimizing a spatial statistic associated with each position, such as in the Steered Response Power (
SRP) approach, in which the statistic is based on the signal power received when the microphone array is steered in the direction of a specific location.
SRP-PHAT is a widely used algorithm for speaker localization that is based on beamforming and was first proposed in Ref. [
21] (although the formulation is virtually identical to the
Global Coherence Field (GCF) described in Ref. [
45]), it combines the robustness of the SRP approach with Phase Transform (PHAT) filtering, which increases the robustness of the algorithm to signal and room conditions, making it an ideal strategy for realistic speaker localization systems [
31,
32,
46,
47,
48]. There are other beamforming based methods such as the Minimum Variance Distortionless Response (MVDR) [
33], which is the most widely used adaptive beamformer.
Regarding spectral estimation based methods, the multiple signal classification algorithm (MUSIC) [
49] has been widely used, as it is able to handle arbitrary geometries and multiple simultaneous narrowband sources. MUSIC’s performance can be affected when the task has a low signal-to-noise ratio and by reverberant environments [
27]. It also requires a good estimate of the number of active sources in the multiple source scenario.
In the past few years, deep learning approaches [
50] have taken the lead in different signal processing and machine learning fields, such as computer vision [
20,
51] and speech recognition [
52,
53,
54], and, in general, in any area in which complex relationships between observed signals and the underlying processes generating them need to be discovered.
The idea of using neural networks for ASL is not new. Back in the early nineties and in the first decade of the current century, works such as Refs. [
40,
55,
56] proposed the use of neural network techniques in this area. However, an evaluation of realistic and extensive datasets was not viable at this time, and the proposals were somewhat limited in scope.
With the advent and huge increase of applications of deep neural networks in all areas of machine learning, promising works have also been proposed for ASL [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
57,
58,
59,
60,
61]. This is mainly due to the sophisticated capabilities and more careful implementation details of network architectures and the availability of advanced hardware architectures with increased computational capacity.
The main differences between the different proposals for the use of neural networks for ASL reside in the architectures, input features, network output (target), and the experimental setup (using real or simulated data).
With respect to the information given to the neural network, several works have used features that are physically related to the ASL problem. Some of the proposals have used features derived from the GCC or related functions which actually make sense, as these correlation function are closely related to the TDOAs which are used in traditional methods to generate position estimations. The published works have used either the GCC or GCC-PHAT coefficients directly [
6,
17], as well as features derived from them [
11,
58] or from the correlation matrix [
5,
60], or even combined with others, such as cepstral coefficients [
9]. Other works have focused on exploiting binaural cues [
13,
57,
59], and even trying to discover binaural features using a CNN [
16]. Others have employed narrowband SRP values [
14]. The latter approach goes one step further from correlation related values, as the SRP function actually integrates multiple GCC estimations in such a way that acoustic energy maps can be easily generated from them.
As opposed to the previously described works that used refined features that are directly related to the localization problem, others used frequency domain features directly [
8,
12,
18,
61]. In some cases, these were generated from spectrograms of general time–frequency representations [
7,
10]. These approaches represent a step forward compared with previous ones, as they give the network the responsibility of automatically learning the relationships between spectral cues and location-related information [
15]. In this last reference, the authors combined both strategies, as they used spectral features but calculated them in a cross-spectral fashion, that is, they combined the values from all of the available microphones in the so-called Cross Spectral Map (CSM).
In none of the referenced works did the authors use the raw acoustic signal directly, and we are interested in evaluating the capabilities of CNN architectures in directly exploiting this raw input information. At this point, we must mention that the works using spectral features directly derived from linear and fully recoverable transforms [
7,
8,
10,
12,
18,
61], such as the STFT spectrum (thus containing the same amount of information than the time-domain signals), also used raw acoustic information. We do not claim that the use of time domain signals is better than using frequency domain, or cross-spectral features, but we want to exploit the windowed time domain signal without further preprocessing as an input to the network to assess whether its feasibility is a valid input feature in the ASL task.
Regarding the estimation target, most works have been oriented towards estimating the Direction of Arrival (DOA) of the acoustic sources [
6,
7,
11,
12,
14,
58], or the DOA-related measurements, such as the azimuth angle [
13,
57,
59,
61], the elevation angle [
16], or the position bearing and range [
9]. Some of the proposals posed the problem not as a direct estimation (regression) but as a classification problem among a predefined set of possible position related values [
5,
8,
10,
60,
61] (azimuth, positions in a predefined grid, etc.). Other works tried to estimate a
clean acoustic source map [
15] or to learn time frequency masks as a preprocessing stage prior to ASL [
62].
In only two of the referenced works [
17,
18] the authors try to directly find out the coordinate values of the acoustic sources. In Ref. [
17], the source coordinates were estimatedin a bidimensional space, and in Ref. [
18], a three-dimensional space was considered, but the estimated position was calculated as the
x,
y, and
z axis coordinates of the DOA on a unit sphere around the microphone. In our proposal, we are again interested in further evaluating the capabilities of CNN architectures to directly generate the generic cartesian coordinates in a full three-dimensional space.
With respect to the number of active sources considered in the ASL task, most works have considered the single source case, but in the last couple of years, the multi-source localization scenario has also been addressed [
7,
12,
18]. We focus on the single source case, as our target is to evaluate the feasibility of the end-to-end approach by estimating the three-dimensional cartesian coordinates of the source position.
Finally, regarding the experimental setup, most previous works used simulated data either for training or for training and testing [
5,
6,
7,
8,
10,
11,
13,
14,
15,
16,
57,
58,
59,
60,
61,
62], usually by convolving clean (anechoic) speech with impulse responses (room, head-related, or DOA-related (azimuth, elevation)). Only some of them actually used real recordings [
9,
11,
14,
17,
57,
58], which in our opinion is a must to be able to assess the actual impact of the proposals under real conditions.
So, in this paper, we describe a CNN architecture in which we directly exploit the raw acoustic signal to be provided to the neural network, with the objective of directly estimating the coordinates of the three-dimensional position of an acoustic source in a given environment. This is the reason why we refer to this strategy as end-to-end, considering the full coverage of the ASL problem. The proposal is evaluated using both semi-synthetic and real data from a publicly available database.
4. Experimental Work
In this section, we describe the datasets used in both steps of the training strategy described in
Section 3.3, and the details associated with them. We then define the general conditions of the experimental setup and the error metrics used for comparing our proposal with other state-of-the-art methods, and finally, we present our experimental results, starting from the baseline performance that we aimed to improve.
4.1. Datasets
4.1.1. IDIAP AV16.3 Corpus: For Testing and Fine Tuning
We evaluated our proposal with the audio recordings from the AV16.3 database [
66], an audio-visual corpus recorded in the
Smart Meeting Room of the IDIAP research institute in Switzerland. We also used the physical layout of this room for our semi-synthetic data generation process.
The
IDIAP Smart Meeting Room is a 3.6 m × 8.2 m × 2.4 m rectangular room with a centrally located rectangular table that measures 4.8 m × 1.2 m. On the table’s surface, there are two circular microphone arrays of 0.1 m radius, each of them composed by eight regularly distributed microphones, as shown in
Figure 2. The centers of both arrays are separated by a distance of 0.8 m. The middle point between them is considered to be the origin of the coordinate reference system. A detailed description of the meeting room can be found in Ref. [
67].
The dataset is composed of several sequences of recordings, synchronously sampled at 16 KHz, with a wide range of experimental conditions in the number of speakers involved and their activity. Some of the available audio sequences are assigned a corresponding annotation file that contains the real ground truth positions (3D coordinates) of the speaker’s mouth at every time frame in which that speaker was talking. The segmentation of acoustic frames with speech activity was first checked manually at certain time instances by a human operator in order to ensure its correctness, and later, this was extended to cover the rest of the recording time by means of interpolation techniques. The frame shift resolution was defined to be 40 ms. The complete dataset is fully accessible online at Ref. [
68].
In this paper, we focused on the annotated sequences of this dataset that featured a single speaker, whose main characteristics are shown in
Table 2. This allowed us to directly compare our performance with the method presented in Ref. [
35] that was proven to achieve better results than the
SRP-PHAT algorithm. Note that the first three sequences involved a speaker who remained static while speaking at different positions, and the last two ones involved a moving speaker; all of the speakers were different. We refer to these sequences as
s01,
s02,
s03,
s11, and
s15 for brevity.
Depending on the sequence being considered, the distances between the speakers and the microphone arrays had maximum, minimum, and average values in the intervals (209, 243) cm, (46, 156) cm and (118, 192) cm, respectively.
4.1.2. Albayzin Phonetic Corpus: For Semi-Synthetic Dataset Generation
The Albayzin Phonetic Corpus [
69] consists of three sub-corpora of 16 kHz 16 bits signals, recorded by 304 Castilian Spanish speakers in a professional recording studio using high quality, close-talk microphones.
We used this dataset to generate semi-synthetic data, as described in
Section 3.3.1. From the three sub-corpora, we only used the so-called
phonetic corpus [
70], which is composed of 6800 utterances of phonetically balanced sentences. This phonetical balance characteristic makes this dataset perfect for generating our semi-synthetic data, as it covers all possible acoustic contexts.
4.2. Training and Fine Tuning Details
In the semi-synthetic dataset generation procedure, described in
Section 3.3.1, we generated random positions (
) with uniformly distributed values in the following intervals:
m,
m and
m, which corresponded to the possible distributions of the speaker’s mouth positions in the
IDIAP room [
66].
Regarding the optimization strategy for the loss function described by Equation (
4), we employed the
ADAM [
71] optimizer (variant of SGD with a variable learning rate) along 200 epochs with a batch size of 100 samples. The learning rate of the
ADAM optimizer was fixed at
, and the other parameters were set with the recommended values in accordance with Ref. [
71] (
,
and
). A total of 7200 different frames of input data per epoch were randomly generated during the training phase, and another 800 were generated for validation.
The experiments were performed with three different window lengths (80 ms, 160 ms, and 320 ms), and the training phase was run once per window length, obtaining three different network models. In each training session, 200 audio recordings were randomly chosen and 40 different windows were randomly extracted from each. In the same way, 200 acoustic source position vectors () were randomly generated, so each position generated 40 windows of the same signal.
For the fine tuning procedure described in
Section 3.3.2, we mainly used sequences
s11 and
s15 that feature a speaker moving in the room while speaking, as well as sequences
s01,
s02 and
s03 in a final experiment. The
ADAM optimizer was also used for fine tuning. In this case, we fixed the learning rate at
, while the rest of the parameters were set to the recommended values.
As described in
Section 4.6, we also carried out experiments to assess the relevance of adding additional sequences (
s01,
s02, and
s03) to complement the fine tuning data provided by
s11 and
s15. We also refer to gender and height issues in the fine tuning and evaluation data.
4.3. Experimental Setup
In our experiments, sequences s01, s02, and s03 were used to test the performance of our network, and as explained above, to complement sequences s11 and s15 for fine tuning.
In this work, we used a simple microphone array configuration to evaluate our proposal in a resource-restricted environment, as was done in Ref. [
35]. In order to do so, we used four microphones (numbers 1, 5, 11, and 15, out of the 16 available in the AV16.3 dataset), grouped in two microphone pairs. This configuration of four microphones is the same as that selected in Ref. [
35] to provide two orthogonal microphone pairs. The selected microphone pair configurations are shown in
Figure 2c, in which microphones of the same color are considered to belong to the same microphone pair. We assessed the results related to the length of the acoustic frame for 80 ms, 160 ms, and 320 ms to precisely assess to what extent the improvements were consistent with varying acoustic time resolutions.
The main interest of our experimental work was to assess whether the end-to-end CNN based approach (that we will refer to as CNN) could be competitive with other traditional localization methods. We compared this CNN approach with the standard
SRP-PHAT method and the recent strategy proposed in Ref. [
35] that we refer to as GMBF. This GMBF method is based on fitting a generative model to the GCC-PHAT signals using sparse constraints, and it was associated with significant improvements over
SRP-PHAT in the
IDIAP dataset [
35,
72]. The GMBF fitting procedure does not require training, as opposed to the CNN approach. We also compare our method with another very recently published ASL strategy based on a Convolutional Recurrent Neural Network (CRNN) [
18], with a similar scope.
After providing the baseline results of the comparison between SRP-PHAT, GMBF, and our proposal without applying the fine tuning procedure, we then describe three experiments, that we briefly summarize here:
In the first experiment, we evaluate the performance improvements when using a single sequence for the fine tuning procedure.
In the second experiment, we evaluate the impact of adding an additional fine tuning sequence.
In the third experiment, we evaluate the final performance improvements when also adding static sequences to the refinement process.
After these experiments, we evaluate the differences between the semi-synthetic training plus the fine tuning approach versus just training the network from scratch, to validate the contribution of the fine tuning strategy.
Finally, we provide a comparison between our proposal and that described in Ref. [
18], for which the authors kindly provided the source code [
73].
4.4. Evaluation Metrics
Our CNN based approach yielded a set of spatial coordinates that are estimations of the current speaker’s position as time instant k. These position estimates were compared, by means of the Euclidean distance, to the ones labeled in a transcription file containing the real positions, (ground truth), of the speaker.
We evaluated performance by adopting the same metric used in Ref. [
35] and developed under the CHIL project [
74]. It is known as MOTP (
Multiple Object Tracking Precision) and is defined as
where
denotes the total number of position estimations along time,
the estimated position vector, and
is the labeled ground truth position vector.
We compared our experimental results, and that of the GMBF method, with that of
SRP-PHAT by measuring the relative improvement in MOTP which is defined as follows:
4.5. Baseline Results
The baseline results for sequences
s01,
s02 and
s03 are shown in
Table 3 as well as the evaluated time window sizes (in all the tables showing results in this paper,
bold font highlights the best ones for a given data sequence and window length). The table shows the results achieved by the
SRP-PHAT standard algorithm strategy (column SRP), the alternative described in Ref. [
35] (column GMBF), and the proposal in this paper without applying the fine tuning procedure (column CNN). We also show the relative improvements of GMBF and CNN compared with SRP-PHAT.
The main conclusions from the baseline results are as follows:
The MOTP values improved as the frame size increased, as expected, given that better correlation values will be estimated for longer window signal lengths. The best MOTP values for the standard SRP-PHAT algorithm were around 69 cm, and for the GMBF, around 48 cm.
The average MOTP value for the standard SRP-PHAT algorithm was between 76 cm and 96 cm, and for the GMBF, it was between 59 cm and 78 cm.
The GMBF strategy, as described in Ref. [
35], achieves very relevant improvements compared with SRP-PHAT, with average relative improvements of around
and peak improvement values of almost
.
Our CNN strategy, which, at this point, is only trained with semi-synthetic data, was shown to be very far from reaching SRP-PHAT or GMBF in terms of performance. This result leads us to think that there are other effects that are only present in real data such as reverberation that are affecting the network, as they have not been properly modeled in the training data. This could be addressed by introducing simulation algorithms that can model room propagation effects (such as the image source method [
64,
75]) to generate more realistic semi-synthetic data. This will be evaluated in future work.
So, given the discussion above, we decided to apply the fine tuning strategy discussed in
Section 3.3.2 with the experimental details described in
Section 4.2. The results shown in
Table 3 were compared with those obtained by our CNN method under different fine tuning (and training) conditions, and they are described below.
4.6. Results and Discussion
The first experiment in which we applied the fine tuning procedure used s15 as the fine tuning subset.
Table 4 shows the results obtained by GMBF (column GMBF) and CNN with this fine tuning strategy (column CNNf15 ). The results in the table shown that CNNf15 is, most of the time, better than the
SRP-PHAT baseline (except in two cases for
s03 in which there was a slight degradation). The average performance showed a consistent improvement in CNNf15 compared with SRP-PHAT, between
and
. However, CNNf15 was still behind GMBF in all cases but one (for
s02 and 80 ms).
Our conclusion is that the fine tuning procedure is able to effectively complement the trained models from synthetic data, leading to results that outperform SRP-PHAT. This is specially relevant due to the following points.
The amount of fine tuning data is limited (only 36 s, corresponding to 436 frames, as shown in
Table 2), thus opening the path to further improvements with a limited data recording effort.
The speaker used for fine tuning was mostly moving while speaking, while in the testing sequences, the speakers are static while speaking. This means that the fine tuning material included far more active positions than the testing sequences, and the network was able to extract the relevant information for the tested positions.
The improvements obtained by our CNN decrease for longer signal window sizes suggest that the speake’sr speed (and thus, the displacement of the speaker across the signal window) might be having an impact on the results. We evaluated the average speed of the speakers for the moving speaker sequences, m/s for s11, and m/s for seq15. They do not seem to have a significant relevant impact on position estimation. We also evaluated the source displacement distribution within individual signal frames across the different sequences. The average displacement distances were 4–6 cm for the 80 ms window, 7–11 cm for the 160 ms window and 15–20 cm for the 320 ms window. When we considered the maximum displacement distances, these values turned out to be 7–27 cm for the 80 ms window, 14–34 cm for the 160 ms window, and 28–46 cm for the 320 ms case. These displacements could have a visible impact on the results, and they might be the reason for the lower improvements achieved by our method for longer window sizes.
The speaker used for fine tuning was male, and the obtained results for male speakers (sequences s01 and s03) and the female one (sequence s02) do not seem to show any gender-dependent bias, which means that the gender issue does not seem to play a role in the adequate adaptation of the network models.
In spite of the relevant improvements with the fine tuning approach, they are still far from making this method suitable for further competitive exploitation in the ASL scenario (provided we have the GMBF alternative), so we next aimed to increase the amount of fine tuning material.
In our third experiment, we applied the fine tuning procedure using an additional moving speaker sequence, that is, by including s15 and s11 in the fine tuning subset.
Table 5 shows the results obtained by GMBF and CNN after fine tuning with
s15 and
s11 (CNNf15+11 columns). In this case, additional improvements over using only
s15 for fine tuning occurred, and there was only one case in which CNNf15+11 did not outperform SRP-PHAT (with a marginal degradation of
).
The CNN based approach again showed an average, consistent improvement compared with SRP-PHAT of between and .
In this case, the newly added sequence (s11, with a duration of only 33 s) for fine tuning corresponded to a randomly moving male speaker, and the results show that its addition contributed to further improvements in the CNN based proposal, but it was still behind GMBF in all cases but two, but with results getting closer. This suggests that a further increment in the fine tuning material should be considered.
Our last experiment consisted of fine tuning the network, including additional static speaker sequences. To assure that the training (including fine tuning) and testing material were fully independent, we fine-tuned with
s15,
s11 and with the static sequences that were not tested in each experiment run, as shown in
Table 6.
Table 7 shows the results obtained for this fine tuning scenario. The main conclusions were as follows:
The CNN based method exhibited much better average behavior than GMBF for all window sizes. The average absolute improvement against SRP-PHAT for the CNN was more than 10 points higher than for GMBF, reaching in the CNN case and in GMBF.
Considering the individual sequences, CNN was shown to be significantly better than GMBF for sequences s01 and s02, and slightly worse for s03.
Considering the best individual result, the maximum improvement for the CNN was (s01, 320 ms), while the top result for GMBF was (s03, 320 ms).
The effect of adding static sequences was shown to be beneficial, as expected, provided that the acoustic tuning examples were generated from similar, but not identical, positions, as the speakers had varying heights and their positions in the room were not strictly equal from sequence to sequence.
The improvements obtained were significant and came at the cost of additional fine tuning sequences. However, this extra cost was still reasonable, as the extra fine tuning material is of limited duration, around 400 s on average ( min).
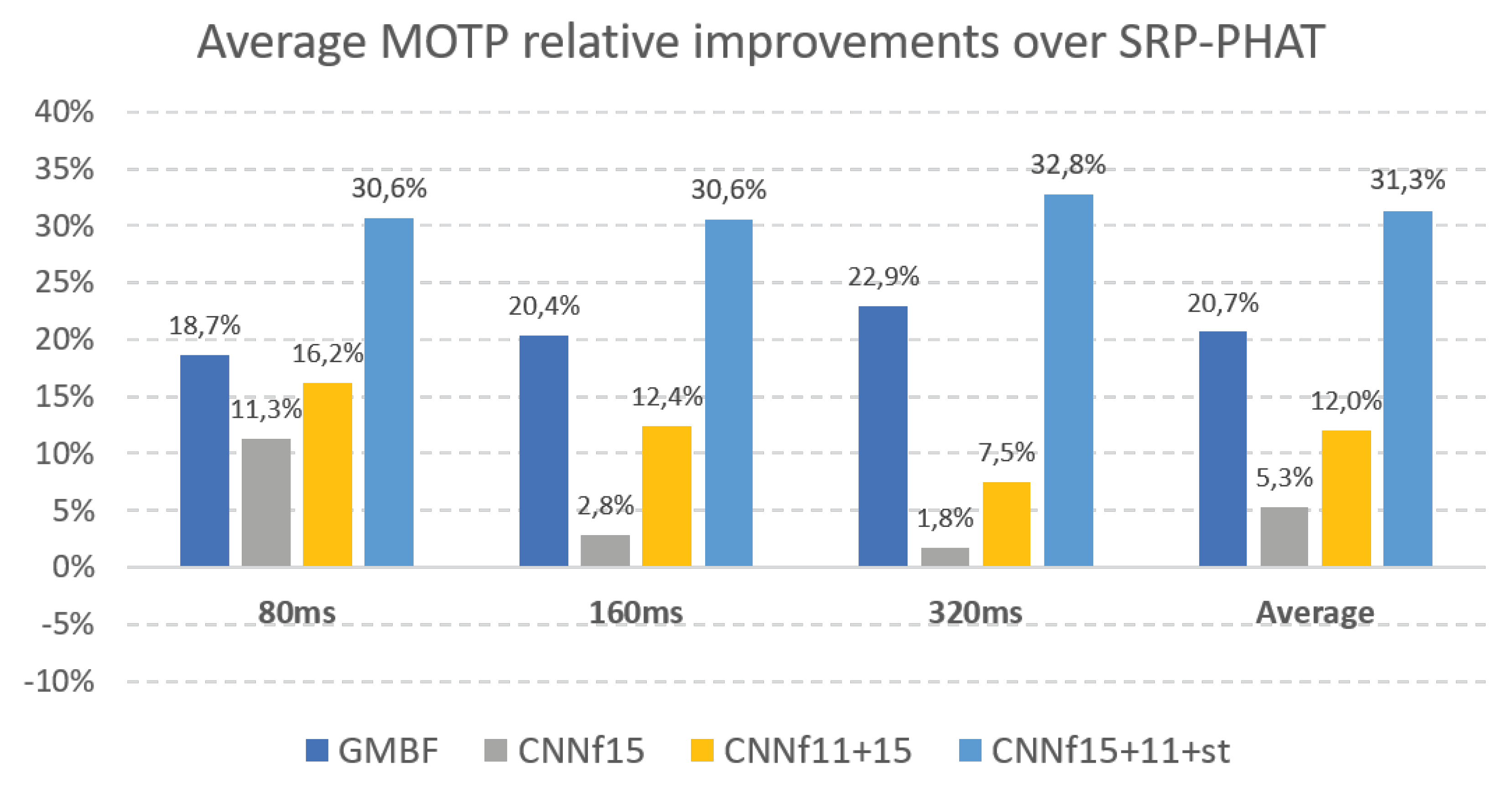
Finally, to summarize,
Figure 3 shows the average MOTP relative improvements over
SRP-PHAT obtained by our CNN proposal using different fine tuning subsets and its comparison with the GMBF results for all of the signal window sizes.
From the results obtained by our proposal, it is clear that the highest contribution to the improvements from the bare CNN training was the fine tuning procedure with limited data (CNNf15, compare
Table 3 and
Table 4), while the use of additional fine tuning material consistently improved the results (
Table 5 and
Table 7). It is again worth noticing that these improvements were consistently independent of the height and gender of the considered speaker and whether there was a match or not between the static or dynamic activity of the speakers being used in the fine tuning subsets. This suggests that the network actually learns the acoustic cues that are related to the localization problem. Thus, we conclude that our proposal is a suitable and promising strategy for solving the ASL task.
4.7. Validation of the Fine Tuning Strategy
When comparing the results of
Table 3 and
Table 4, and given the large improvement when applying the fine tuning strategy, it could be assumed that the initial training with semi-synthetic data is limited. Based on this argument, we ran additional training experiments in which we just trained the network
from scratch with the same sequences used in the experiments shown in
Table 4,
Table 5 and
Table 7, with the objective of assessing the actual effect of combining semi-synthetic training and fine tuning versus just training with real room data. The training strategy and parameters were the same as those used when training the network from semi-synthetic data, and they are described in
Section 4.2.
Table 8 shows a comparison between these two options using different sequences. The figures shown are the average values across all testing sequences for each case. The results for the training from scratch approach are included in column tr−sc, and those for our proposed combined semi-synthetic training and fine tuning strategy are included in column tr+ft.
When using
s15 in the training and fine tuning procedures (first row of
Table 8), the average improvement of the tr+ft approach varied between
and
with an average improvement over all window lengths of
, while the tr−sc average improvement varied between
and
with an average value of
.
When using
s15 and
s11 in the training and fine tuning procedures (second row of
Table 8), the average improvement of the tr+ft approach varied between
and
with an average improvement over all window lengths of
, while the tr−sc average improvement varied between
and
with an average value of
.
Finally, when using the sequences described in
Table 6 (third row of
Table 8), the average improvement of the tr+ft approach varied between
and
with an average improvement over all window lengths of
, while the tr−sc average improvement varied between
and
with an average value of
.
So, in all of the evaluated cases, the combined semi-synthetic training and fine tuning approach clearly outperformed the training from scratch strategy, thus validating our methodology.
4.8. Comparison with Deep Learning Methods
In this section, we also provide a comparison between our proposal and a recent deep learning ASL method known as SELDnet [
18], for which the source code is available in Ref. [
73]. SELDnet is a CRNN architecture that uses the signal spectrum of the audio signals as inputs (phase and magnitude components of the spectrogram calculated on each audio channel) and is able to deal with multiple overlapping sound events.
SELDNet generates two different outputs:
Classification output: The first output of the SELDnet is able to classify the sound events among a list of classes for each consecutive frame in the input audio signals.
Regression output: The second output estimates the DOA vector detected on each of the consecutive frames in the audio input. This vector is parametrized as the x, y, and z axis coordinates of the DOA on a unit sphere around the microphone, which is claimed to lead to a network that learns better than one that uses a parametrization based on angles.
As suggested by the authors, we used the default values of the SELDnet design parameters regarding the feature extraction, network model, and training process, and in order to carry out the comparison with our method, the following issues were taken into account:
SELDnet uses an audio window of size for each microphone and extracts consecutive overlapped frames to compute the spectral components that are used as inputs. To compare this with our network, we performed experiments with different values of : 80 ms, 160 ms, and 320 ms.
Due to the fact that we used sequences of audio where only a single speaker appeared simultaneously, we assigned the same label (“speech”) to all the audio windows used for training.
We needed SELDnet to infer the coordinates of the target source, instead of the DOA vector. This only required us to change the target output during training, as the network model does not change it at all. Our spatial coordinates were also normalized in the interval which is compatible with the regression output of the SELDnet. The final output coordinates were again denormalized back to metric coordinates to proceed with the MOTP calculations.
We followed the same experimental procedure as in our proposal (initial semi-synthetic training followed by fine tuning) in a resource-restricted scenario using only two microphone pairs. The experimental conditions were those for which we got the best performance (included in
Table 7), that is, using the testing and fine tuning sequences described in
Table 6.
Table 9 shows the relative improvements of the proposal in Ref. [
18] (column SELDnet) and our CNN approach (column CNNf15+11+st) over SRP-PHAT.
It can be clearly seen that the SELDnet produced worse results than our CNN approach in terms of localization accuracy and it actually performed worse than the standard SRP-PHAT algorithm.