Energy Efficient Hybrid Routing Protocol Based on the Artificial Fish Swarm Algorithm and Ant Colony Optimisation for WSNs
Abstract
1. Introduction
2. Related Work
2.1. Hierarchical Routing Algorithm
2.2. ACO-Based Routing
2.3. Hybrid SI-Based Routing
2.4. Artificial Fish Swarm Algorithm
- Preying behaviour: This is a basic biological behaviour that tends toward food; generally the Artificial Fish (AF) perceives the concentration of food in water to determine the movement by vision or other sense and then chooses the tendency.
- Swarming behaviour: The AF will assemble in groups naturally in the moving process, which is considered a living habit, in order to guarantee the existence of the colony and avoid dangers.
- Follow behaviour: In the moving process of the artificial fish swarm, when a single AF or several ones find food, the neighbourhood partners will trail behind and reach the food quickly.
- A novel AFSA-based initial route discovery algorithm is proposed. The AFSA algorithm achieves a comparatively better global optimisation performance in the early stage and can obtain higher quality routes quickly [12,14]. We utilise these feasible routes as a heuristic factor for the ACO routing algorithm in our hybrid routing protocol, which can improve the power efficiency of the entire hybrid swarm intelligent routing protocol.
- We propose a hybrid route discovery algorithm, which combines the crowd factor in AFSA and the pseudo-random proportional route select model in ACO-based routing algorithms. The introduction of the crowd factor can effectively prevent the routing algorithm from falling into a local optimum and find the optimal path finally.
- Propose an improved pheromone trail update method based on energy levels and path length to prolong the network lifetime.
3. Protocol Specification
3.1. Network Model
- All nodes are isomorphic;
- Links are symmetric. If the target’s transmitted power is known, nodes can calculate the approximate distance of senders according to the Received Signal Strength Indication (RSSI);
- Depending on the recipient’s distance, the node can adjust its transmit power.
- We use a first radio model as described in [3].
3.2. Protocol Overview
- First, AFSA is initialised for each AF to perform preying, swarming and following behaviours from the source node to the sink node.
- After several iterations, a selection of satisfactory routes to the sink node is obtained through the AFSA algorithm.
- Initialise the pheromone information of the ACO routing algorithm using the satisfactory routes obtained by AFSA.
- At some variable interval, a Forward Ant (FANT) is launched from the source node toward the sink node.
- Each FANT chooses the next node according to a probabilistic state transition rule integrated with the crowd factor in AFSA.
- Once FANT reaches the sink node, a Backward Ant (BANT) is created, which moves back along the route that the FANT had previously traversed.
- During the BANT travel, it will modify the amount of pheromone on the path by applying the pheromone updating rule.
- Once a BANT arrives at the source node, the next iteration will begin after some interval.
3.3. Initial Route Establishment
3.3.1. Preying Behaviour
3.3.2. Swarming Behaviour
3.3.3. Following Behaviour
3.4. Hybrid Route Discovery
3.5. Global Pheromone Update Strategy
- The shorter path (less hops) will get a larger pheromone increment.
- When the minimum energy value in this path is larger, the pheromone increment is also larger, which avoids more data traffic routed through this path.
- The average energy of a relatively high path will get more attention, and therefore will attract more data flow.
- The closer the node is, the more pheromones are obtained.
4. Performance Analysis
4.1. Simulation Model and Parameters
4.2. Evaluation Metric
4.3. Simulation Results
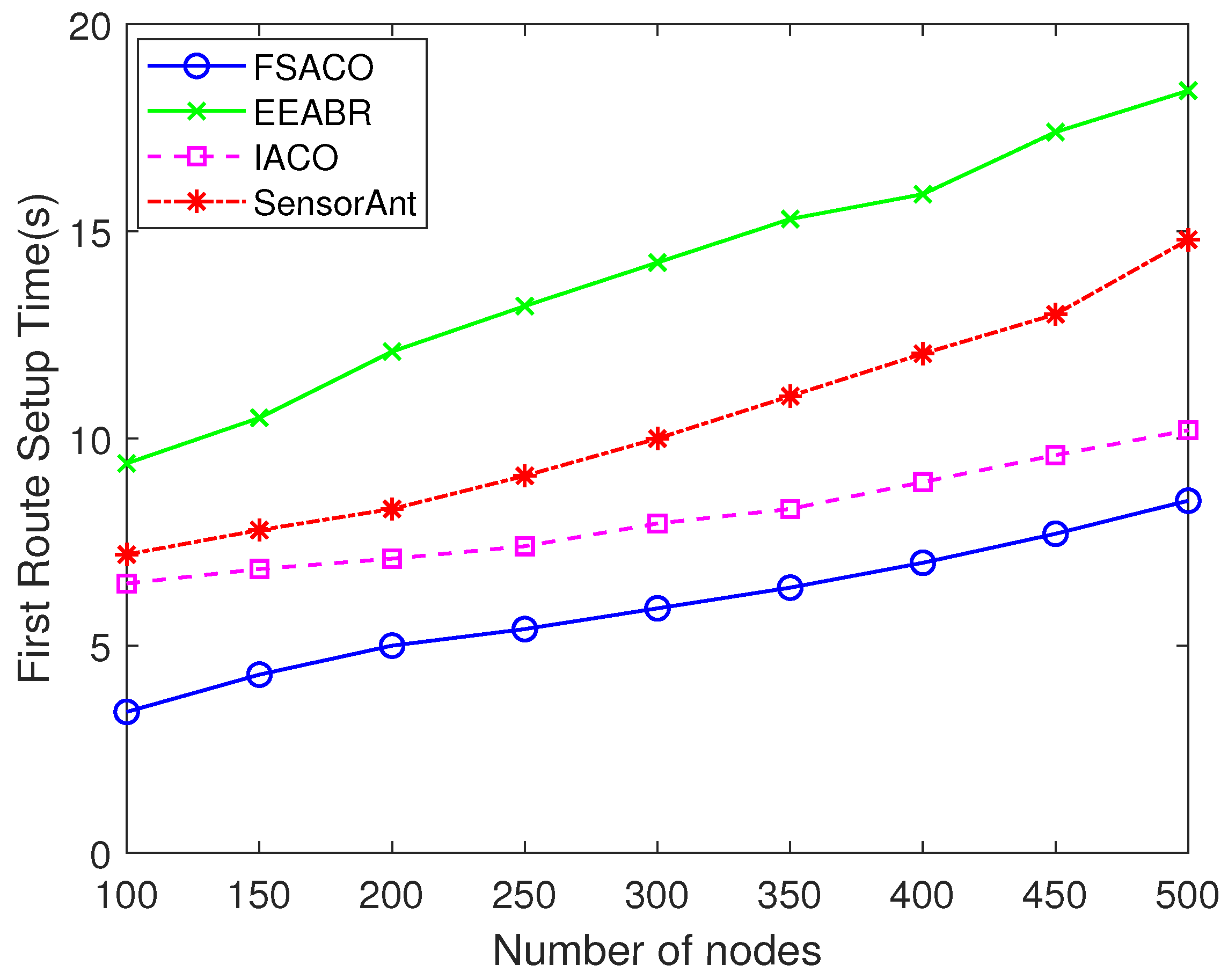
4.3.1. Route Setup Time
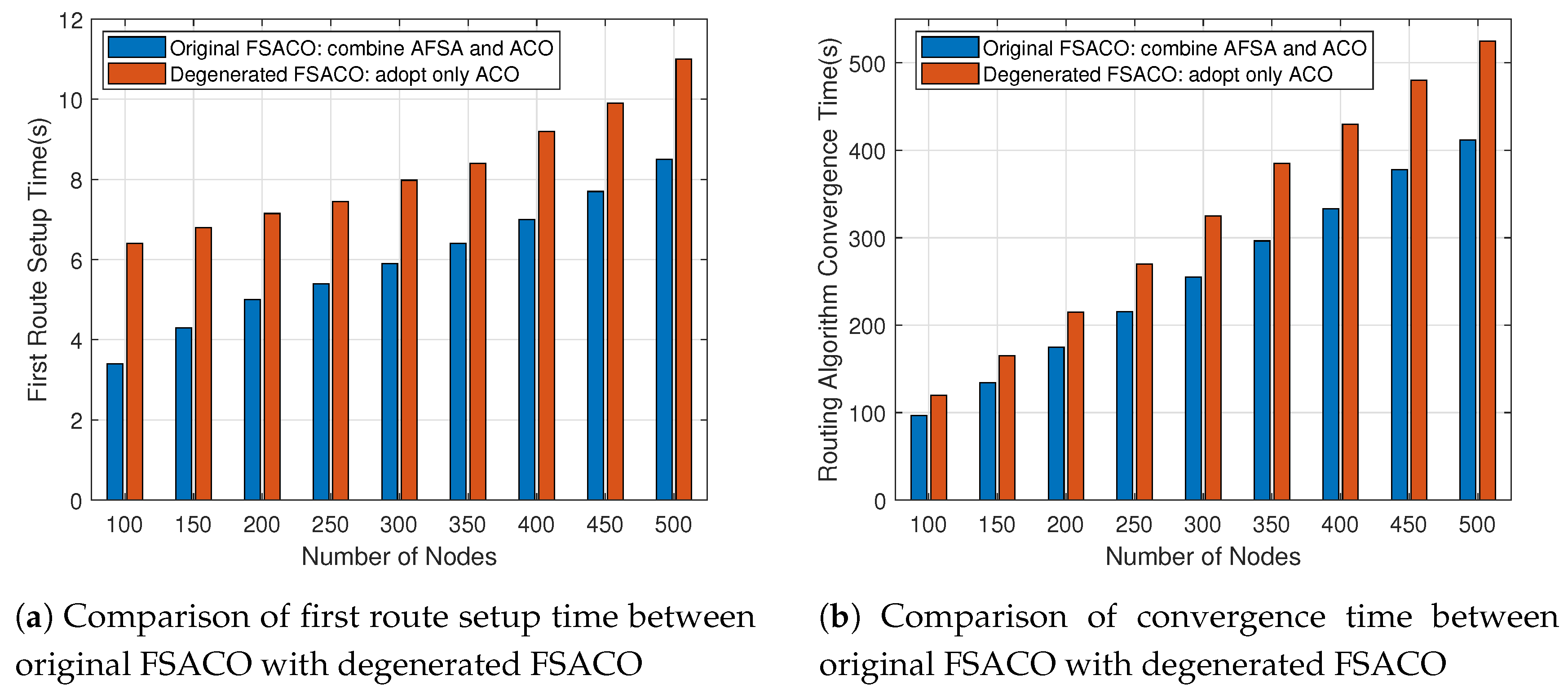
4.3.2. Convergence Time
4.3.3. Energy Consumption
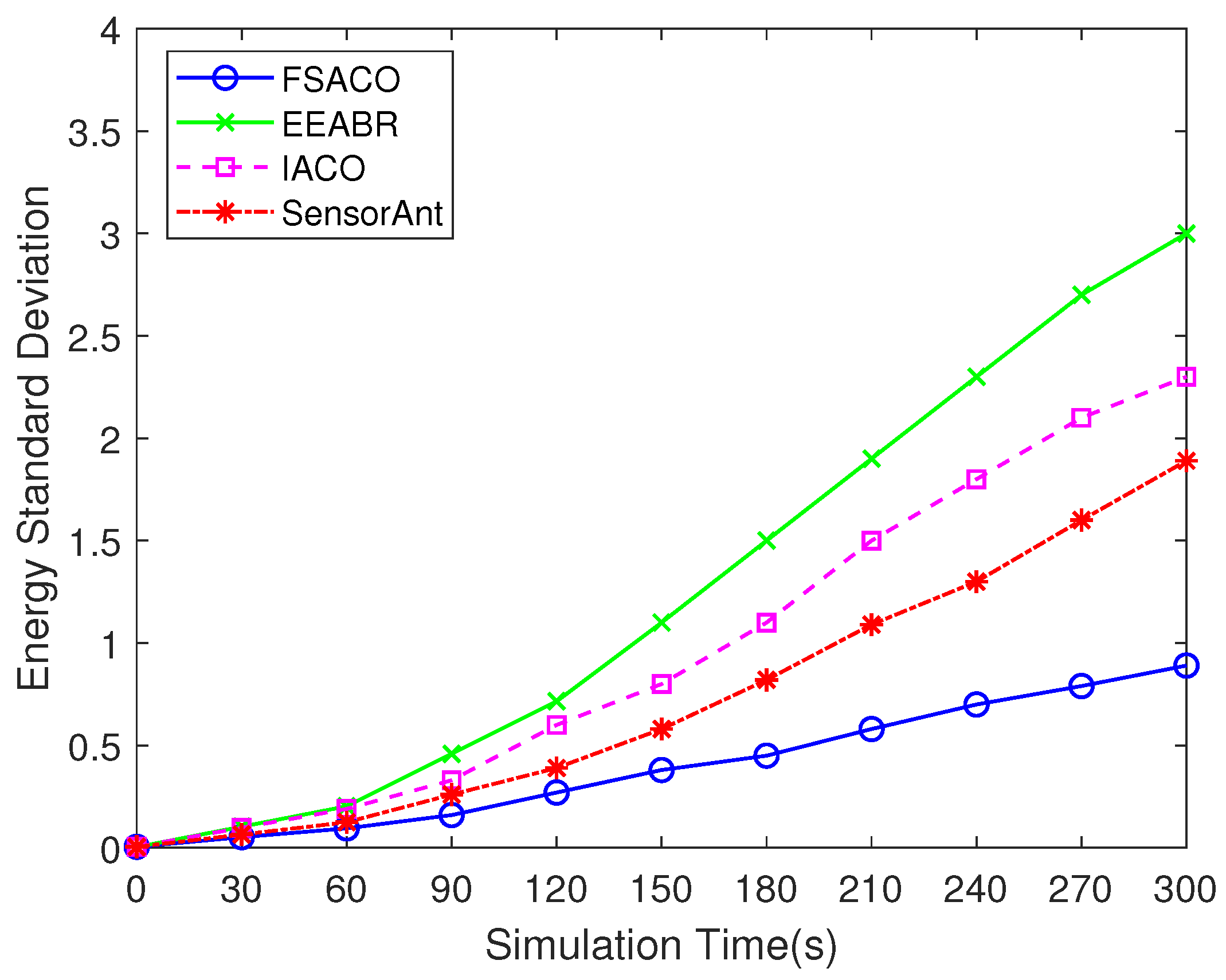
4.3.4. Energy Standard Deviation
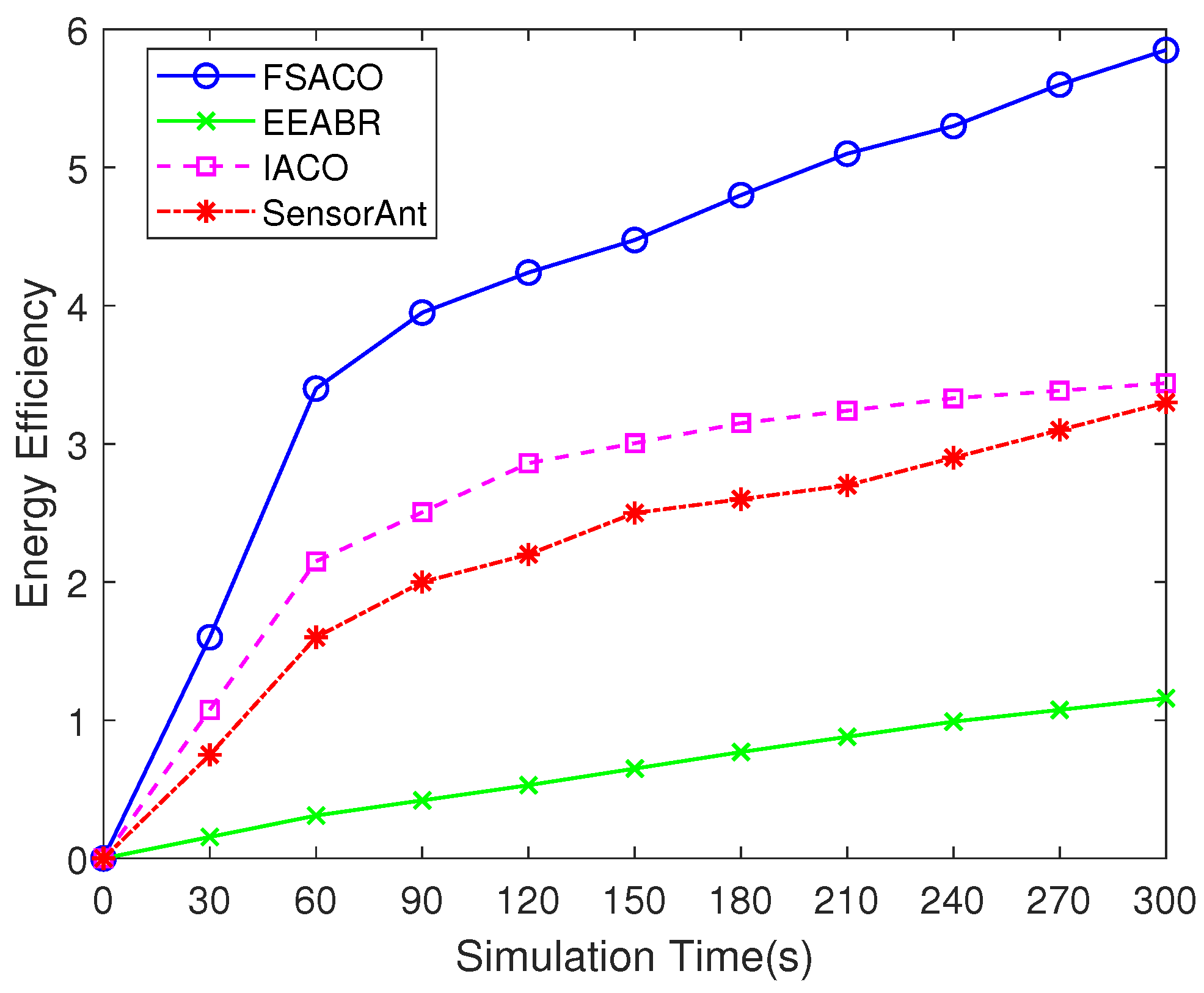
4.3.5. Energy Efficiency
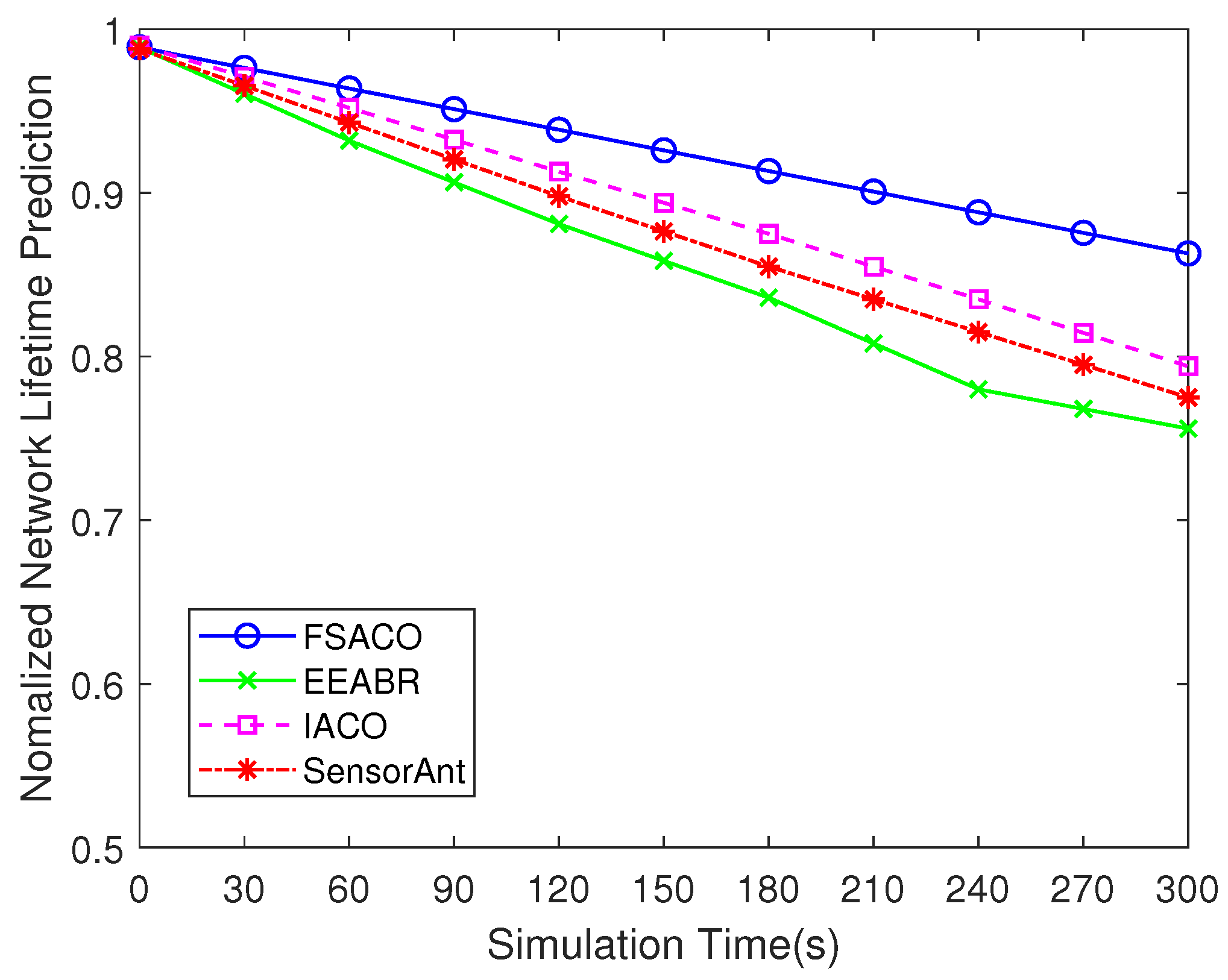
4.3.6. Network Lifetime Prediction
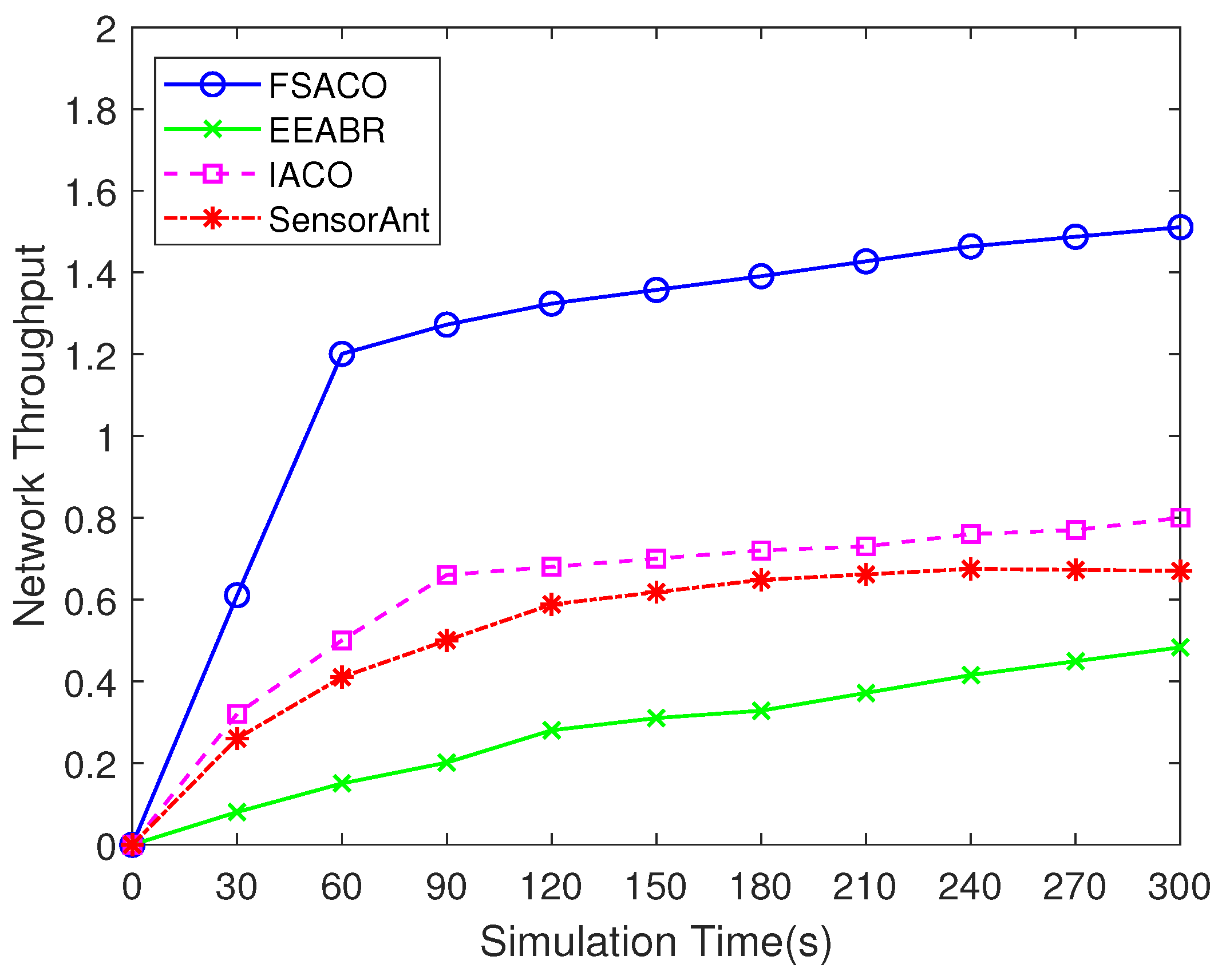
4.3.7. Network Throughput
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pantazis, N.A.; Nikolidakis, S.A.; Vergados, D.D. Energy-efficient routing protocols in wireless sensor networks: A survey. IEEE Commun. Surv. Tutor. 2013, 15, 551–591. [Google Scholar] [CrossRef]
- Lin, C.R.; Gerla, M. Adaptive clustering for mobile wireless networks. IEEE J. Sel. Areas Commun. 1997, 15, 1265–1275. [Google Scholar] [CrossRef]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Mitsis, G.; Papavassiliou, S. Interest-aware energy collection & resource management in machine to machine communications. Ad Hoc Netw. 2018, 68, 48–57. [Google Scholar]
- Tsiropoulou, E.E.; Paruchuri, S.T.; Baras, J.S. Interest, energy and physical-aware coalition formation and resource allocation in smart IoT applications. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar]
- Dorigo, M.; Birattari, M. Ant colony optimization. In Encyclopedia of Machine Learning; Springer: Berlin, Germany, 2011; pp. 36–39. [Google Scholar]
- Di Caro, G.; Dorigo, M. AntNet: Distributed stigmergetic control for communications networks. J. Artif. Intell. Res. 1998, 9, 317–365. [Google Scholar] [CrossRef]
- Di Caro, G.; Dorigo, M. Ant Colony Optimization and Its Application to Adaptive Routing in Telecommunication Networks. Ph.D. Thesis, Université libre de Bruxelles, Faculté des Sciences AppliquéEs, Brussels, Belgium, 2004. [Google Scholar]
- Zhang, Y.; Kuhn, L.D.; Fromherz, M.P. Improvements on ant routing for sensor networks. In International Workshop on Ant Colony Optimization and Swarm Intelligence; Springer: Berlin, Germany, 2004; pp. 154–165. [Google Scholar]
- Camilo, T.; Carreto, C.; Silva, J.S.; Boavida, F. An energy-efficient ant-based routing algorithm for wireless sensor networks. In International Workshop on Ant Colony Optimization and Swarm Intelligence; Springer: Berlin, Germany, 2006; pp. 49–59. [Google Scholar]
- Blum, C.; Li, X. Swarm intelligence in optimization. In Swarm Intelligence; Springer: Berlin, Germany, 2008; pp. 43–85. [Google Scholar]
- Li, X.-L. An optimizing method based on autonomous animats: Fish-swarm algorithm. Syst. Eng.-Theory Pract. 2002, 22, 32–38. [Google Scholar]
- Li, X. A New Intelligent Optimization-Artificial Fish Swarm Algorithm. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2003. [Google Scholar]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M.; Toosi, A.N. Artificial fish swarm algorithm: A survey of the state-of-the-art, hybridization, combinatorial and indicative applications. Artif. Intell. Rev. 2014, 42, 965–997. [Google Scholar] [CrossRef]
- Gerla, M.; Tsai, J.T.-C. Multicluster, mobile, multimedia radio network. Wirel. Netw. 1995, 1, 255–265. [Google Scholar] [CrossRef]
- Dorigo, M.; Stützle, T. The ant colony optimization metaheuristic: Algorithms, applications, and advances. In Handbook of Metaheuristics; Springer: Berlin, Germany, 2003; pp. 250–285. [Google Scholar]
- Kar, A.K. Bio inspired computing—A review of algorithms and scope of applications. Exp. Syst. Appl. 2016, 59, 20–32. [Google Scholar] [CrossRef]
- Chang, J.-H.; Tassiulas, L. Maximum lifetime routing in wireless sensor networks. IEEE/ACM Trans. Netw. 2004, 12, 609–619. [Google Scholar] [CrossRef]
- Habibi, J.; Aghdam, A.G.; Ghrayeb, A. A framework for evaluating the best achievable performance by distributed lifetime-efficient routing schemes in wireless sensor networks. IEEE Trans. Wirel. Commun. 2015, 14, 3231–3246. [Google Scholar] [CrossRef]
- Sun, Y.; Dong, W.; Chen, Y. An improved routing algorithm based on ant colony optimization in wireless sensor networks. IEEE Commun. Lett. 2017, 21, 1317–1320. [Google Scholar] [CrossRef]
- Shamsan Saleh, A.M.; Mohd Ali, B.; Rasid, M.F.A.; Ismail, A. A self-optimizing scheme for energy balanced routing in wireless sensor networks using sensorant. Sensors 2012, 12, 11307–11333. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.; Xun, Y.; Zhou, T.; Li, W. An energy aware ant colony algorithm for the routing of wireless sensor networks. In Intelligent Computing and Information Science; Springer: Berlin, Germany, 2011; pp. 395–401. [Google Scholar]
- Mohajerani, A.; Gharavian, D. An ant colony optimization based routing algorithm for extending network lifetime in wireless sensor networks. Wirel. Netw. 2016, 22, 2637–2647. [Google Scholar] [CrossRef]
- Liu, X. A novel transmission range adjustment strategy for energy hole avoiding in wireless sensor networks. J. Netw. Comput. Appl. 2016, 67, 43–52. [Google Scholar] [CrossRef]
- Gajjar, S.; Sarkar, M.; Dasgupta, K. FAMACROW: Fuzzy and ant colony optimization based combined mac, routing, and unequal clustering cross-layer protocol for wireless sensor networks. Appl. Soft Comput. 2016, 43, 235–247. [Google Scholar] [CrossRef]
- Kaur, S.; Mahajan, R. Hybrid meta-heuristic optimization based energy efficient protocol for wireless sensor networks. Egypt. Inf. J. 2018. [Google Scholar] [CrossRef]
- Leabi, S.K.; Abdalla, T.Y. Energy Efficient Routing Protocol for Maximizing the Lifetime in WSNs Using Ant Colony Algorithm and Artificial Immune System. Int. J. Adv. Comput. Sci. Appl. 2016, 7. [Google Scholar] [CrossRef]
- Khoshkangini, R.; Zaboli, S.; Conti, M. Efficient routing protocol via ant colony optimization (ACO) and breadth first search (BFS). In Proceedings of the 2014 IEEE International Conference on Internet of Things (iThings), and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom), Taipei, Taiwan, 1–3 September 2014; pp. 374–380. [Google Scholar]
- Rosset, V.; Paulo, M.A.; Cespedes, J.G.; Nascimento, M.C. Enhancing the reliability on data delivery and energy efficiency by combining swarm intelligence and community detection in large-scale WSNs. Exp. Syst. Appl. 2017, 78, 89–102. [Google Scholar] [CrossRef]
- Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev. E 2007, 76, 036106. [Google Scholar] [CrossRef] [PubMed]
- Gui, T.; Ma, C.; Wang, F.; Wilkins, D.E. Survey on swarm intelligence based routing protocols for wireless sensor networks: An extensive study. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 1944–1949. [Google Scholar]
- Zungeru, A.M.; Ang, L.-M.; Seng, K.P. Classical and swarm intelligence based routing protocols for wireless sensor networks: A survey and comparison. J. Netw. Comput. Appl. 2012, 35, 1508–1536. [Google Scholar] [CrossRef]
- Saleem, M.; Di Caro, G.A.; Farooq, M. Swarm intelligence based routing protocol for wireless sensor networks: Survey and future directions. Inf. Sci. 2011, 181, 4597–4624. [Google Scholar] [CrossRef]
- Iyengar, S.S.; Wu, H.-C.; Balakrishnan, N.; Chang, S.Y. Biologically inspired cooperative routing for wireless mobile sensor networks. IEEE Syst. J. 2007, 1, 29–37. [Google Scholar] [CrossRef]
- Xiao, J.; Zheng, X.; Wang, X.; Huang, Y. A modified artificial fish-swarm algorithm. In Proceedings of the Sixth World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 3456–3460. [Google Scholar]
- Baba, Y.; Ugweje, O.C.; Koyunlu, G. Development and analysis of a modified Artificial Fish Swarm Algorithm. In Proceedings of the 2017 13th International Conference on Electronics, Computer and Computation (ICECCO), Abuja, Nigeria, 28–29 November 2017; pp. 1–6. [Google Scholar]
- Awadel-Bayoumy, M.; Rashad, M.; Elsoud, M.; El-dosuky, M. FAFSA: Fast Artificial Fish Swarm Algorithm. Int. J. Inf. Sci. Intell. Syst. 2013, 2, 60–70. [Google Scholar]
- Tsai, H.-C.; Lin, Y.-H. Modification of the fish swarm algorithm with particle swarm optimization formulation and communication behaviour. Appl. Soft Comput. 2011, 11, 5367–5374. [Google Scholar] [CrossRef]
- Adnan, M.A.; Razzaque, M.A.; Ahmed, I.; Isnin, I.F. Bio-mimic optimization strategies in wireless sensor networks: A survey. Sensors 2013, 14, 299–345. [Google Scholar] [CrossRef] [PubMed]
- Liao, T.; Socha, K.; de Oca, M.A.M.; Stützle, T.; Dorigo, M. Ant colony optimization for mixed-variable optimization problems. IEEE Trans. Evolut. Comput. 2014, 18, 503–518. [Google Scholar] [CrossRef]
- Li, X.-L.; Qian, J.-X. Studies on artificial fish swarm optimization algorithm based on decomposition and coordination techniques. J. Circuits Syst. 2003, 1, 1–6. [Google Scholar]
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278. [Google Scholar] [CrossRef]


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Dimension of topology | 1000 | Number of nodes | 100–500 |
| Nodes placement | Random | Mobility | Static |
| Traffic | Constant Bit Rate (CBR) | Simulation time | 300 s |
| MAC layer | IEEE 802.11 | Initial energy | 1000 J |
| Metric | EEABR | IACO | SensorAnt | FSACO |
|---|---|---|---|---|
| Route Setup Time | 9.4 | 6.5 | 7.2 | 3.4 |
| Convergence Time | 136 | 120.5 | 135.2 | 96.8 |
| Energy Consumption (J) | 134.55 | 97.65 | 127.22 | 85 |
| Energy Efficiency | 1.16 | 3.44 | 3.3 | 5.85 |
| Energy Standard Deviation | 3 | 2.3 | 1.89 | 0.89 |
| Lifetime Prediction | 0.76 | 0.79 | 0.775 | 0.86 |
| Network Throughput | 0.48 | 0.8 | 0.67 | 1.511 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Keegan, B.; Mtenzi, F. Energy Efficient Hybrid Routing Protocol Based on the Artificial Fish Swarm Algorithm and Ant Colony Optimisation for WSNs. Sensors 2018, 18, 3351. https://doi.org/10.3390/s18103351
Li X, Keegan B, Mtenzi F. Energy Efficient Hybrid Routing Protocol Based on the Artificial Fish Swarm Algorithm and Ant Colony Optimisation for WSNs. Sensors. 2018; 18(10):3351. https://doi.org/10.3390/s18103351
Chicago/Turabian StyleLi, Xinlu, Brian Keegan, and Fredrick Mtenzi. 2018. "Energy Efficient Hybrid Routing Protocol Based on the Artificial Fish Swarm Algorithm and Ant Colony Optimisation for WSNs" Sensors 18, no. 10: 3351. https://doi.org/10.3390/s18103351
APA StyleLi, X., Keegan, B., & Mtenzi, F. (2018). Energy Efficient Hybrid Routing Protocol Based on the Artificial Fish Swarm Algorithm and Ant Colony Optimisation for WSNs. Sensors, 18(10), 3351. https://doi.org/10.3390/s18103351





