Surface-Plasmon-Resonance-Based Optical-Fiber Micro-Displacement Sensor with Temperature Compensation
Abstract
1. Introduction
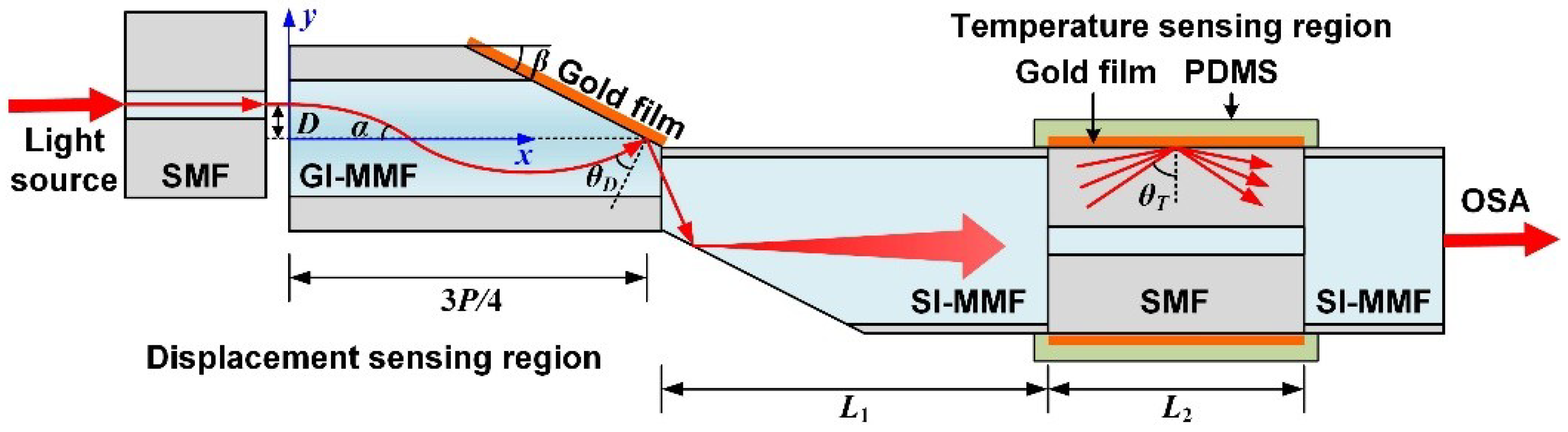
2. Sensor Structure Design and Sensing Principle
2.1. Sensor Structure
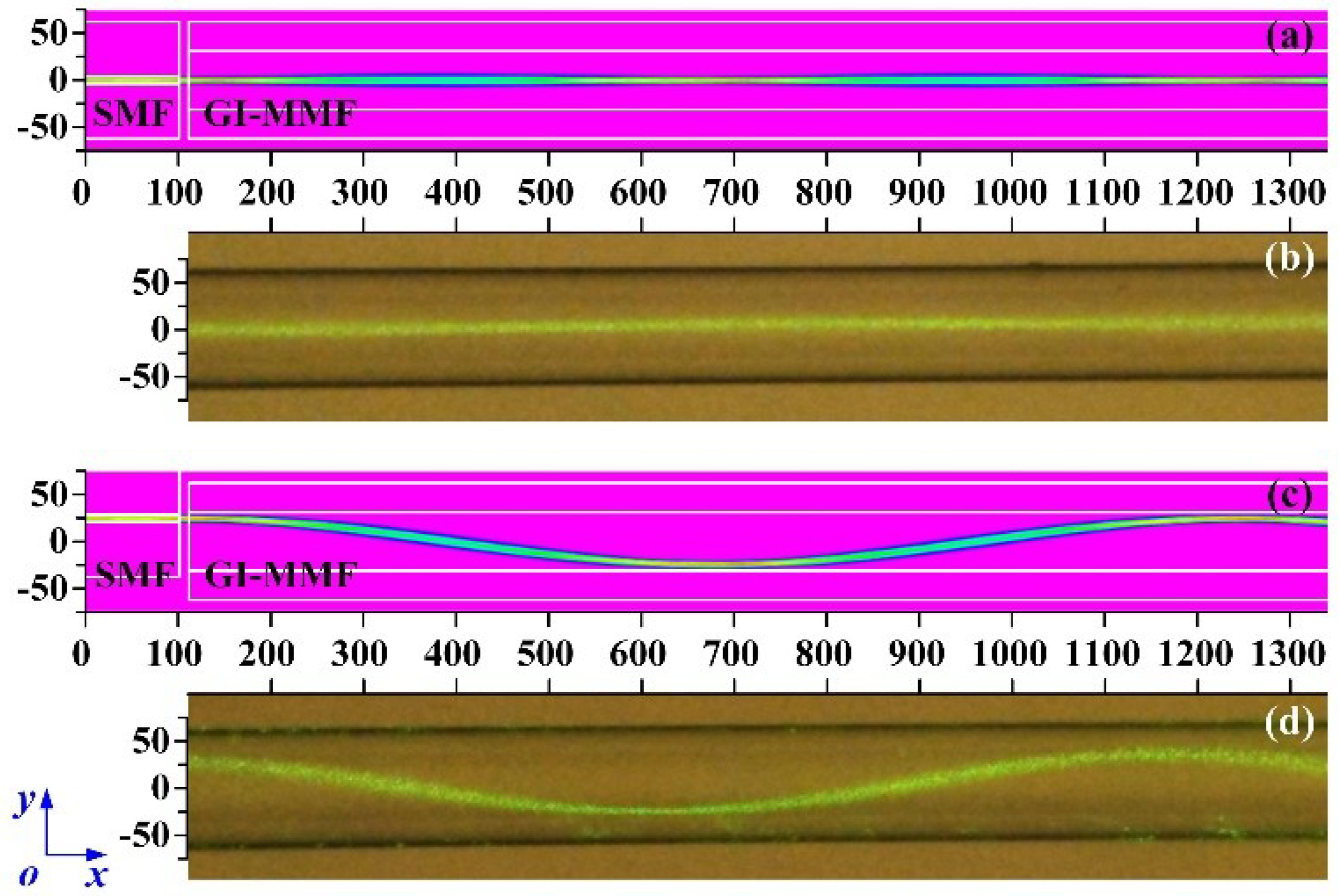
2.2. Propagation Characteristics of the Light Beam in the GI-MMF
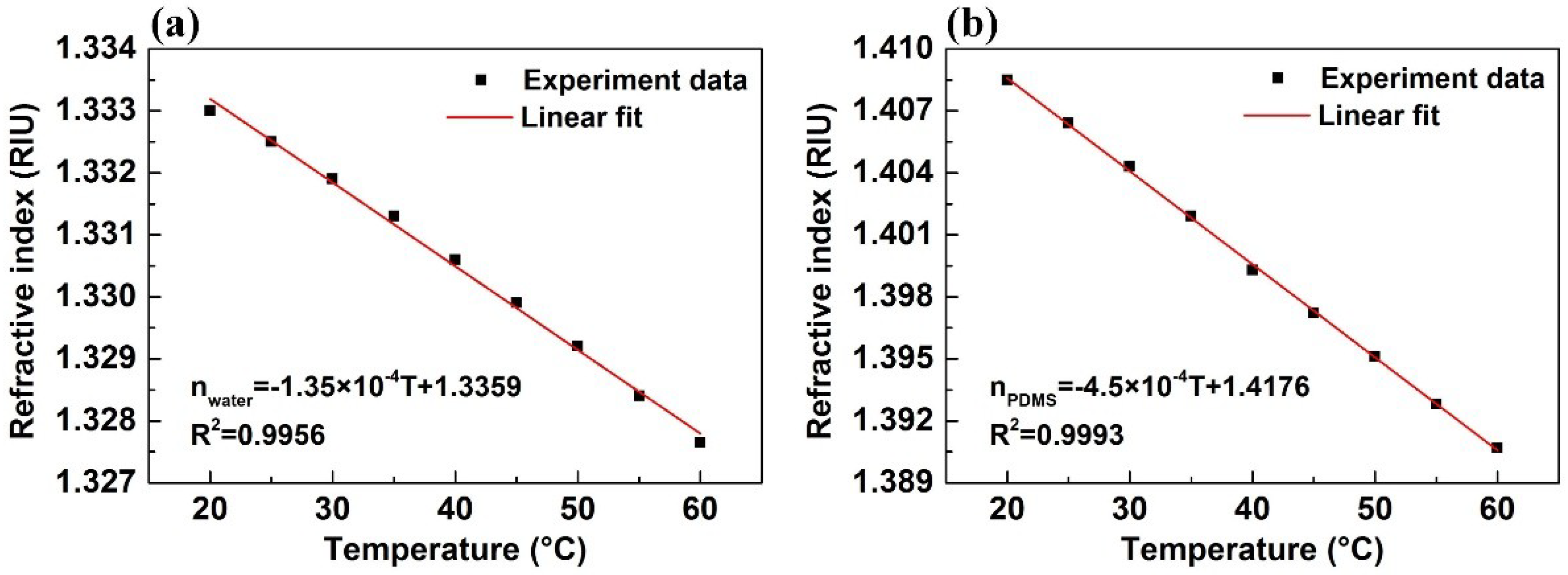
2.3. Temperature Characteristics of the PDMS and Water
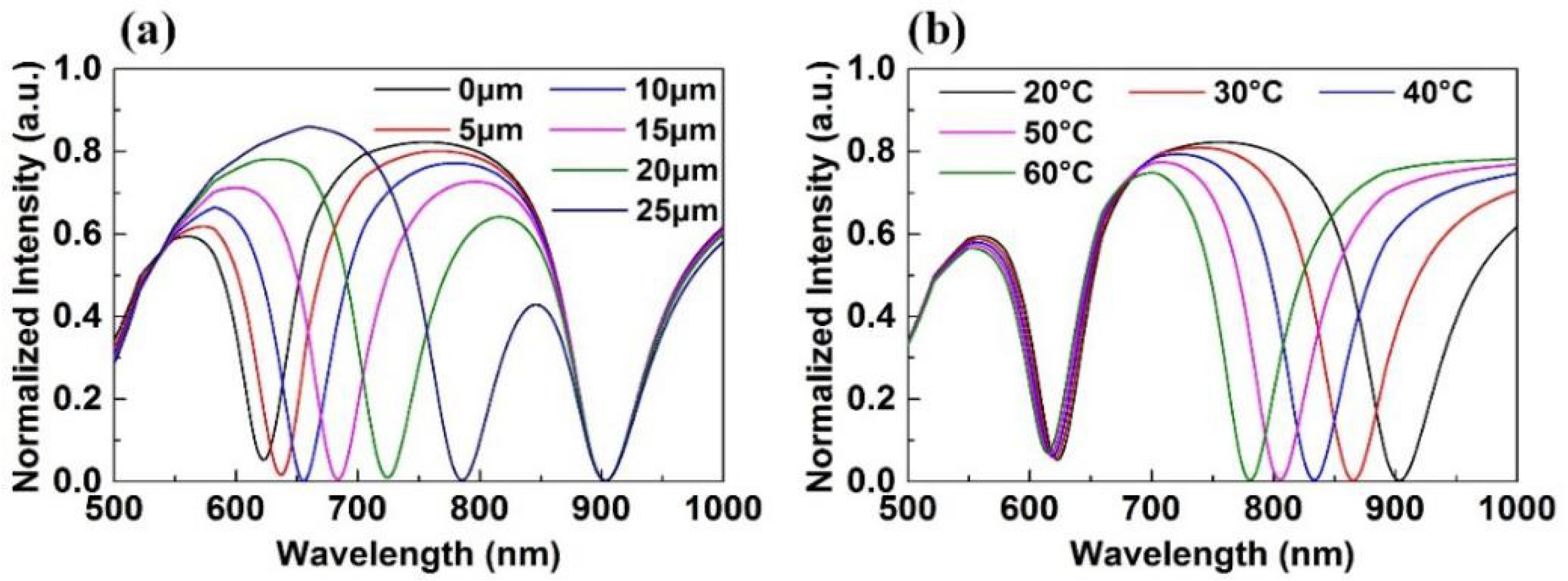
2.4. Spectrum Simulation
3. Experimental Preparation
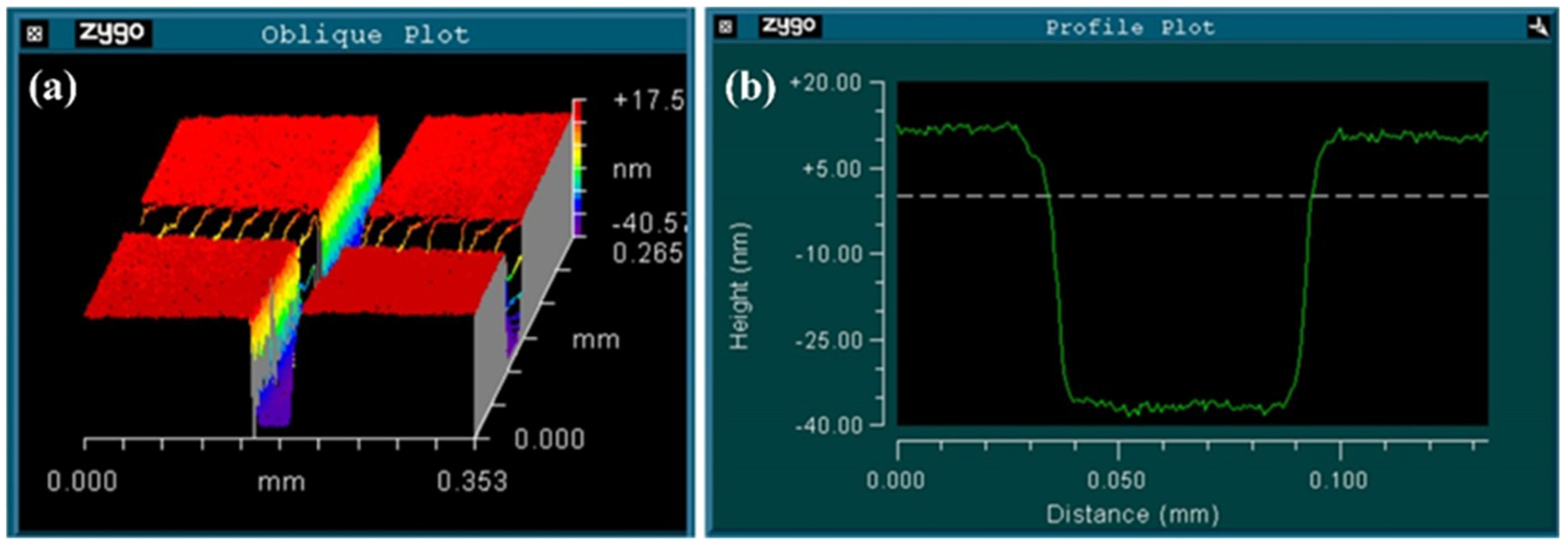
3.1. Fabrication of the Micro-Displacement Sensor
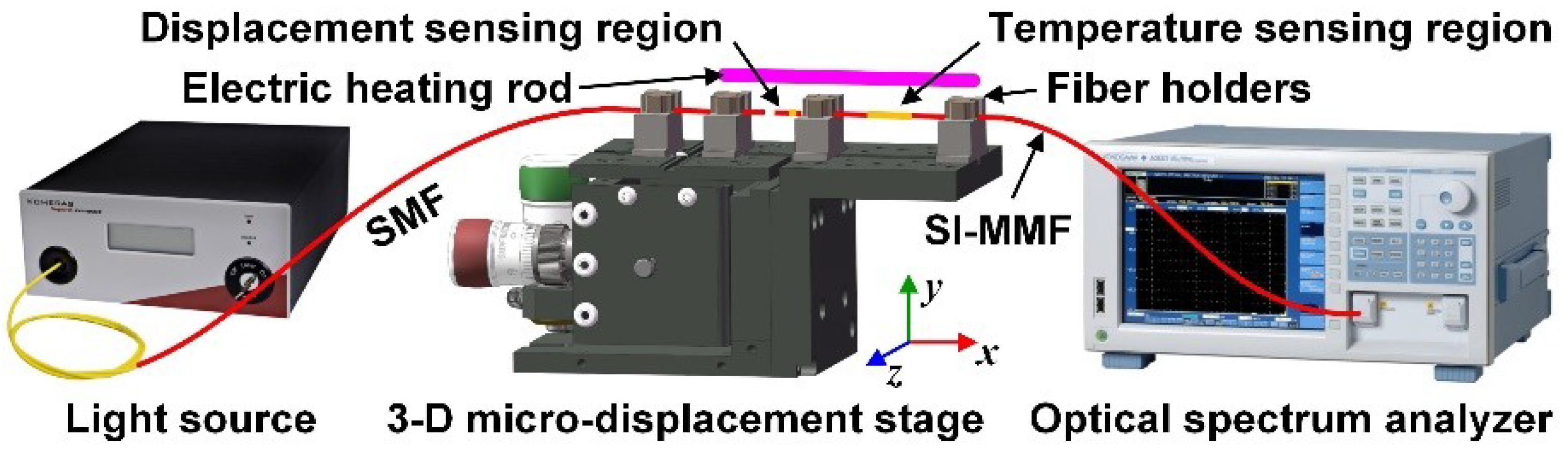
3.2. Experimental Set-Up
4. Results and Discussion
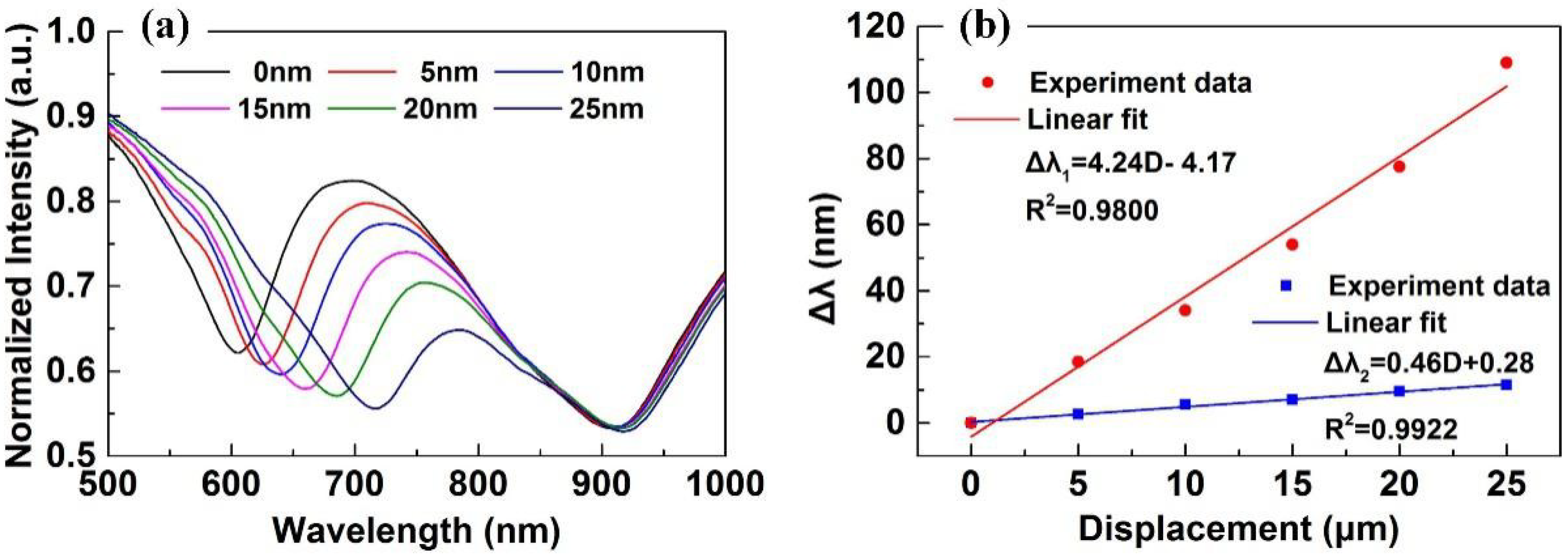
4.1. Displacement Experiment
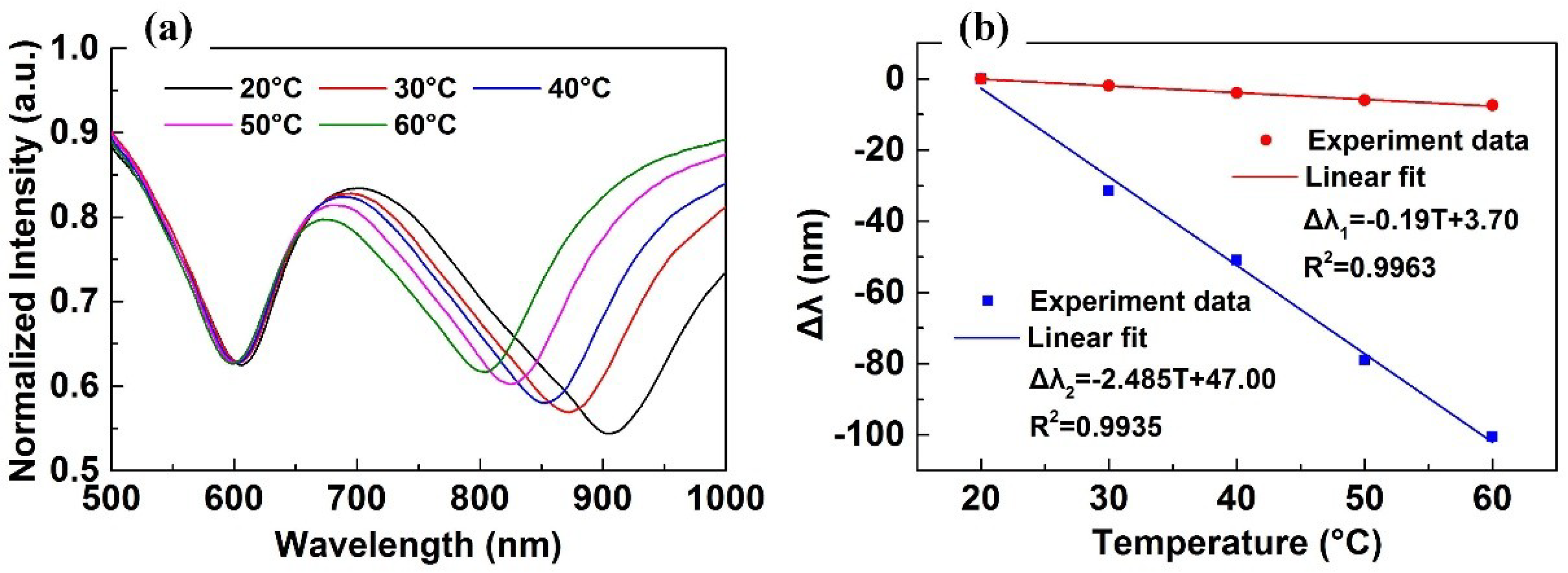
4.2. Temperature Experiment
4.3. Temperature Compensation by Means of the Sensing Matrix
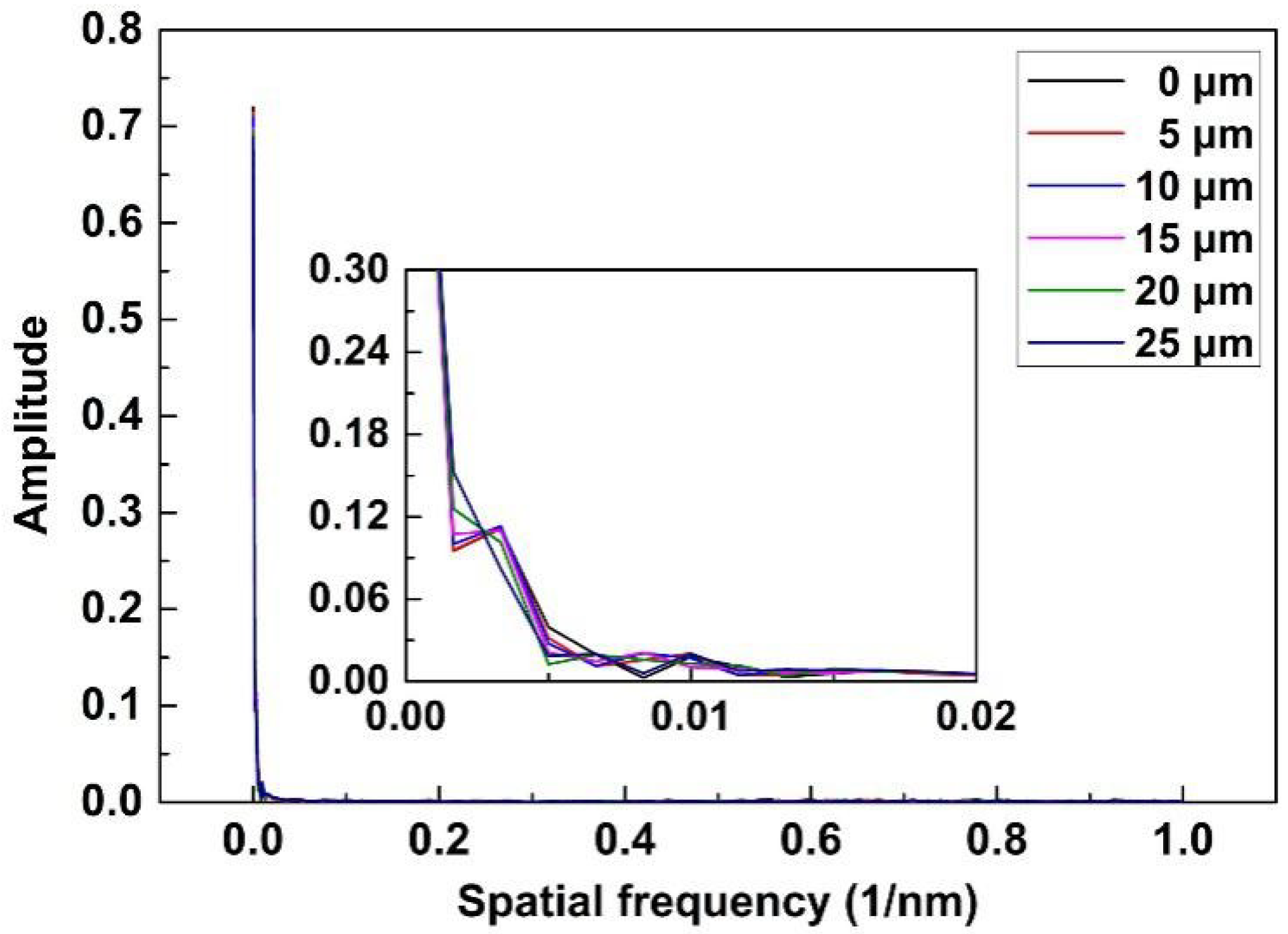
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ng, J.H.; Zhou, X.Q.; Yang, X.F.; Hao, J.Z. A simple temperature-insensitive fiber Bragg grating displacement sensor. Opt. Commun. 2007, 273, 398–401. [Google Scholar] [CrossRef]
- Zhong, C.; Shen, C.Y.; Li, K.; Dong, X.Y.; Jin, Y.X.; Wang, J.F. Temperature-Insensitive Fiber Bragg Grating Tiny Displacement Sensor. Sens. Lett. 2012, 10, 1472–1475. [Google Scholar] [CrossRef]
- Qi, L.; Zhao, C.L.; Wang, Y.P.; Kang, J.; Zhang, Z.X.; Jin, S.Z. Compact micro-displacement sensor with high sensitivity based on a long-period fiber grating with an air-cavity. Opt. Express 2013, 21, 3193–3200. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.M.; Li, X.W.; Zou, W.W.; Li, X.; Hong, Z.H.; Chen, J.P. Temperature-Insensitive Microdisplacement Sensor Based on Locally Bent Microfiber Taper Modal Interferometer. IEEE Photonics J. 2012, 4, 772–778. [Google Scholar] [CrossRef]
- Chen, J.P.; Zhou, J.; Yuan, X.C. MZ Interferometer Constructed by Two S-Bend Fibers for Displacement and Force Measurements. IEEE Photonic Technol. Lett. 2014, 26, 837–840. [Google Scholar] [CrossRef]
- Bravo, M.; Pinto, A.M.R.; Lopez-Amo, M.; Kobelke, J.; Schuster, K. High precision micro-displacement fiber sensor through a suspended-core Sagnac interferometer. Opt. Lett. 2012, 37, 202–204. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Hatta, A.M.; Wang, P.F.; Semenova, Y.; Farrell, G. Use of a Bent Single SMS Fiber Structure for Simultaneous Measurement of Displacement and Temperature Sensing. IEEE Photonic Technol. Lett. 2011, 23, 130–132. [Google Scholar] [CrossRef]
- Xu, Z.F.; Cao, L.C.; Gu, C.; He, Q.S.; Jin, G.F. Micro displacement sensor based on line-defect resonant cavity in photonic crystal. Opt. Express 2006, 14, 298–305. [Google Scholar] [CrossRef] [PubMed]
- Homola, J. Surface plasmon resonance sensors for detection of chemical and biological species. Chem. Rev. 2008, 108, 462–493. [Google Scholar] [CrossRef] [PubMed]
- Singh, P. SPR Biosensors: Historical Perspectives and Current Challenges. Sens. Actuators B Chem. 2016, 229, 110–130. [Google Scholar] [CrossRef]
- Miranda-Castro, R.; de-los-Santos-Alvarez, N.; Miranda-Ordieres, A.J.; Lobo-Castanon, M.J. Harnessing Aptamers to Overcome Challenges in Gluten Detection. Biosensors 2016, 6, 16. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Liu, Q.; Chen, S.M.; Cheng, F.; Wang, H.Q.; Peng, W. Surface Plasmon Resonance Biosensor Based on Smart Phone Platforms. Sci. Rep. 2015, 5, 12864. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.Y.; Chen, K.H.; Chen, J.H. Measurement of small displacement based on surface plasmon resonance heterodyne interferometry. Opt. Lasers Eng. 2011, 49, 811–815. [Google Scholar] [CrossRef]
- Wang, S.F.; Chen, C.T.; Kao, F.H.; Chu, Y.; Liao, Y.P.; Lay, S.R.; Liu, A.L. Theoretical Analyses and Experimental Evaluation of a Small-Displacement Sensor Based on Surface Plasmon Resonance Technology. Sens. Mater. 2014, 26, 371–377. [Google Scholar]
- Wang, X.M.; Zhao, C.L.; Wang, Y.R.; Shen, C.Y.; Dong, X.Y. A Highly Sensitive Fibre-Optic Nano-Displacement Sensor Based on Surface Plasmon Resonance. J. Lightwave Technol. 2016, 34, 2324–2330. [Google Scholar] [CrossRef]
- Zhu, Z.D.; Liu, L.; Liu, Z.H.; Zhang, Y.; Zhang, Y.X. High-precision micro-displacement optical-fiber sensor based on surface plasmon resonance. Opt. Lett. 2017, 42, 1982–1985. [Google Scholar] [CrossRef] [PubMed]
- Iga, M.; Seki, A.; Watanabe, K. Hetero-core structured fiber optic surface plasmon resonance sensor with silver film. Sens. Actuators B Chem. 2004, 101, 368–372. [Google Scholar] [CrossRef]
- Roy, D. Surface plasmon resonance spectroscopy of dielectric coated gold and silver films on supporting metal layers: Reflectivity formulas in the Kretschmann formalism. Appl. Spectrosc. 2001, 55, 1046–1052. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Liu, Z.H.; Wei, Y.; Zhang, Y.; Zhang, Y.X.; Zhao, E.M.; Yang, J.; Yuan, L.B. Twin-core fiber SPR sensor. Opt. Lett. 2015, 40, 2826–2829. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.H.; Wei, Y.; Zhang, Y.; Liu, C.L.; Zhang, Y.X.; Zhao, E.M.; Yang, J.; Liu, C.Y.; Yuan, L.B. Distributed fiber surface plasmon resonance sensor based on the incident angle adjusting method. Opt. Lett. 2015, 40, 4452–4455. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.H.; Wei, Y.; Zhang, Y.; Sun, B.; Zhao, E.M.; Zhang, Y.X.; Yang, J.; Yuan, L.B. A novel surface plasmon resonance sensor based on fiber butt-joint technology. Sens. Actuators B Chem. 2015, 221, 1330–1334. [Google Scholar] [CrossRef]
- Zhu, Z.D.; Liu, L.; Liu, Z.H.; Zhang, Y.; Zhang, Y.X. Surface-plasmon-resonance-based optical-fiber temperature sensor with high sensitivity and high figure of merit. Opt. Lett. 2017, 42, 2948–2951. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, L.V.; Hwang, D.; Moon, S.; Moon, D.S.; Chung, Y. High temperature fiber sensor with high sensitivity based on core diameter mismatch. Opt. Express 2008, 16, 11369–11375. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.Y.; Kim, M.J.; Lee, B.H. All-fiber Mach-Zehnder type interferometers formed in photonic crystal fiber. Opt. Express 2007, 15, 5711–5720. [Google Scholar] [CrossRef] [PubMed]

| Sensor Type | Sensitivity | Range | Resolution |
|---|---|---|---|
| FBG [2] | 0.55 nm/mm | 0–0.5 mm | 36 μm |
| LPFG [3] | 0.22 nm/μm | 0–140 μm | 90 nm |
| OFMI [4] | −0.1 nm/μm | 0–30 μm | 0.2 μm |
| OFMZI [5] | −1.533 nm/μm | 0–80 μm | 13 nm |
| SMS structure [7] | 5.89 pm/μm | 0–600 μm | 3.4 μm |
| Otto-SPR structure [15] | 31.45 nm/nm | 0–10 nm | 0.6 pm |
| This paper | 4.24 nm/μm | 0–25 μm | 5 nm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Wu, P.; Zhu, Z.; Liu, L.; Liu, C.; Hu, J.; Wang, S.; Zhang, Y. Surface-Plasmon-Resonance-Based Optical-Fiber Micro-Displacement Sensor with Temperature Compensation. Sensors 2018, 18, 3210. https://doi.org/10.3390/s18103210
Wei Y, Wu P, Zhu Z, Liu L, Liu C, Hu J, Wang S, Zhang Y. Surface-Plasmon-Resonance-Based Optical-Fiber Micro-Displacement Sensor with Temperature Compensation. Sensors. 2018; 18(10):3210. https://doi.org/10.3390/s18103210
Chicago/Turabian StyleWei, Yong, Ping Wu, Zongda Zhu, Lu Liu, Chunlan Liu, Jiangxi Hu, Shifa Wang, and Yonghui Zhang. 2018. "Surface-Plasmon-Resonance-Based Optical-Fiber Micro-Displacement Sensor with Temperature Compensation" Sensors 18, no. 10: 3210. https://doi.org/10.3390/s18103210
APA StyleWei, Y., Wu, P., Zhu, Z., Liu, L., Liu, C., Hu, J., Wang, S., & Zhang, Y. (2018). Surface-Plasmon-Resonance-Based Optical-Fiber Micro-Displacement Sensor with Temperature Compensation. Sensors, 18(10), 3210. https://doi.org/10.3390/s18103210





