Underdetermined Wideband DOA Estimation for Off-Grid Sources with Coprime Array Using Sparse Bayesian Learning
Abstract
:1. Introduction
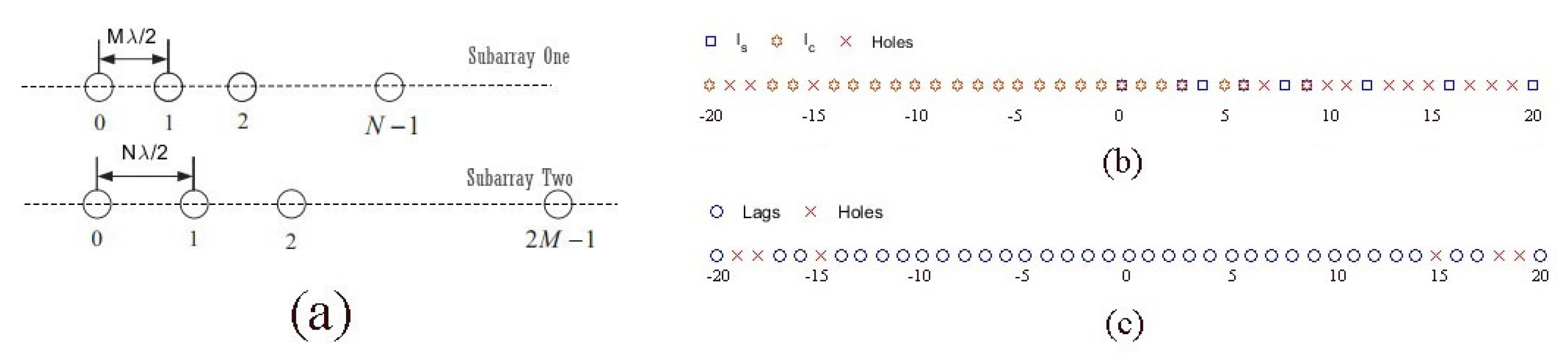
2. Wideband Signal Model for Coprime Array
3. Sparse Bayesian Learning with Off-Grid Sources
3.1. Off-Grid Formulation
3.2. Sparse Bayesian Learning Algorithm
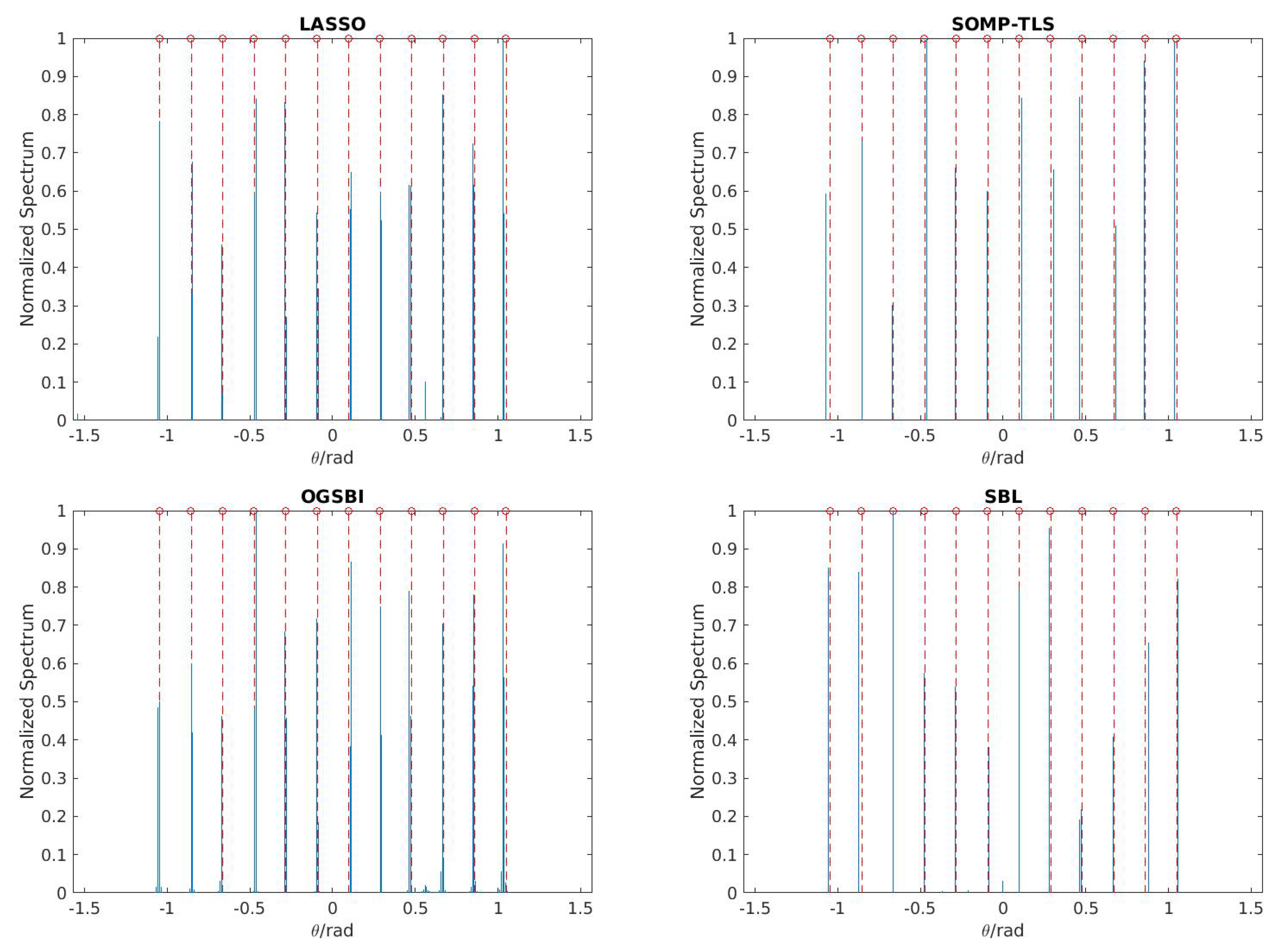
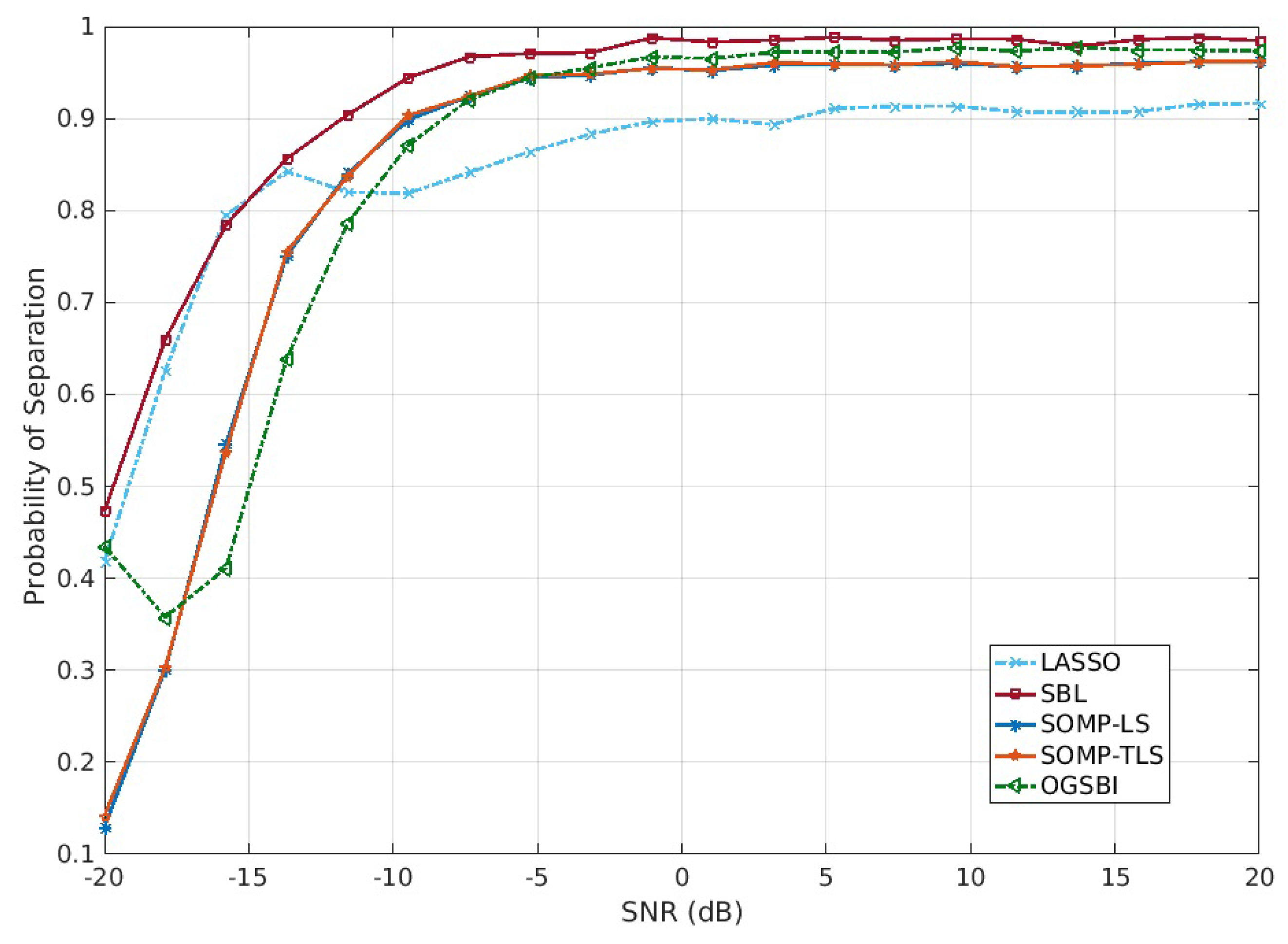
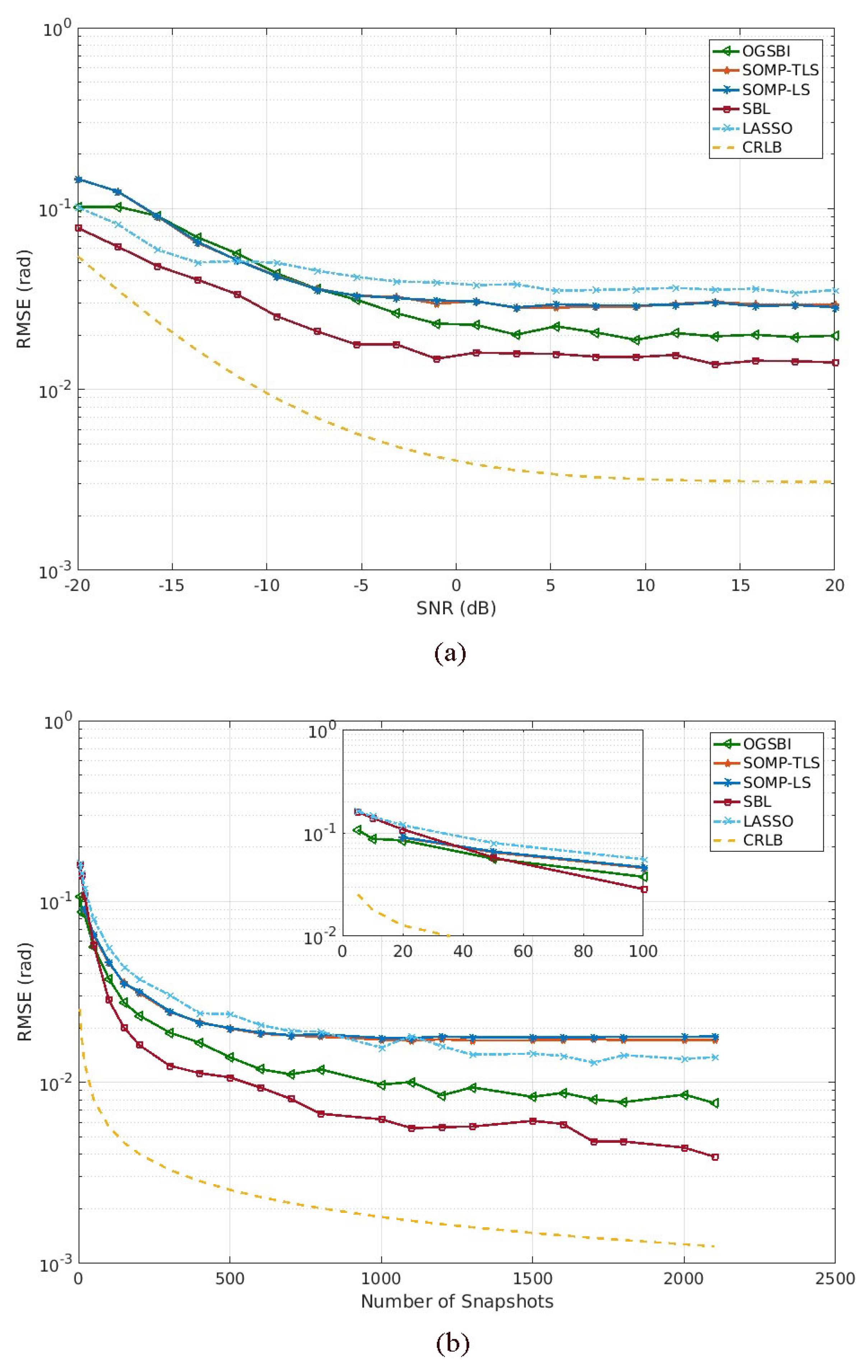
4. Simulation Result
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing With Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 2011, 59, 573–587. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Why does direct-MUSIC on sparse-arrays work? In Proceedings of the 2013 Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 2013; pp. 2007–2011. [Google Scholar]
- Tan, Z.; Nehorai, A. Sparse Direction of Arrival Estimation Using Co-Prime Arrays with Off-Grid Targets. IEEE Signal Process. Lett. 2014, 21, 26–29. [Google Scholar] [CrossRef]
- Zhao, T.; Eldar, Y.C.; Nehorai, A. Direction of arrival estimation using co-prime arrays: A super resolution viewpoint. IEEE Trans. Signal Process. 2014, 62, 5565–5576. [Google Scholar]
- Shen, Q.; Liu, W.; Cui, W. Low-Complexity Direction-of-Arrival Estimation Based on Wideband Co-Prime Arrays. IEEE Trans. Audio Speech Lang. Process. 2015, 23, 1445–1456. [Google Scholar] [CrossRef]
- BouDaher, E.; Jia, Y.; Ahmad, F.; Amin, M.G. Multi-Frequency Co-Prime Arrays for High-Resolution Direction-of-Arrival Estimation. IEEE Trans. Signal Process. 2015, 64, 3797–3808. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Liu, Z.M.; Huang, Z.T.; Zhou, Y.Y. An Efficient Maximum Likelihood Method for Direction-of-Arrival Estimation via Sparse Bayesian Learning. IEEE Trans. Wirel. Commun. 2012, 11, 1–11. [Google Scholar] [CrossRef]
- Hu, N.; Ye, Z.F.; Xu, X.; Bao, M. DOA Estimation for Sparse Array via Sparse Signal Reconstruction. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 760–773. [Google Scholar] [CrossRef]
- Chi, Y.; Scharf, L.L.; Pezeshki, A.; Calderbank, A.R. Sensitivity to Basis Mismatch in Compressed Sensing. IEEE Trans. Signal Process. 2011, 59, 2182–2195. [Google Scholar] [CrossRef]
- Shen, Q.; Cui, W.; Liu, W.; Wu, S.; Zhang, Y.D.; Amin, M.G. Underdetermined wideband DOA estimation of off-grid sources employing the difference co-array concept. Signal Process. 2017, 130, 299–304. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, L.; Bi, G.; Wan, C.; Zhang, L.; Zhang, H. Novel Wideband DOA Estimation Based on Sparse Bayesian Learning With Dirichlet Process Priors. IEEE Trans. Signal Process. 2016, 64, 275–289. [Google Scholar] [CrossRef]
- Gerstoft, P.; Xenaki, A.; Mecklenbräuker, C.F.; Zochmann, E. Multiple snapshot compressive beamforming. In Proceedings of the 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 1774–1778. [Google Scholar]
- Gerstoft, P.; Mecklenbräuker, C.F.; Xenaki, A.; Nannuru, S. Multisnapshot Sparse Bayesian Learning for DOA. IEEE Signal Process. Lett. 2016, 23, 1469–1473. [Google Scholar] [CrossRef]
- Kay, L.G.; Santosh, N.; Gerstoft, P.; William, S.H. Multi-frequency sparse Bayesian learning for robust matched field processing. J. Acoust. Soc. Am. 2017, 141, 3411–3420. [Google Scholar]
- Nannuru, S.; Gemba, K.L.; Gerstoft, P.; Mecklenbräuker, C.F. Multi-frequency sparse Bayesian learning with uncertainty models. arXiv, 2017; arXiv:1704.00436. [Google Scholar]
- Zhang, Z.L.; Rao, B.D. Sparse signal recovery in the presence of correlated multiple measurement vectors. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 3986–3989. [Google Scholar]
- Zhang, Z.L.; Rao, B.D. Sparse Signal Recovery With Temporally Correlated Source Vectors Using Sparse Bayesian Learning. IEEE J. Sel. Top. Signal Process. 2011, 5, 912–926. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Rao, B.D. Extension of SBL Algorithms for the Recovery of Block Sparse Signals with Intra-Block Correlation. IEEE Trans. Signal Process. 2013, 61, 2009–2015. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Wipf, D.P.; Rao, B.D. Sparse Bayesian learning for basis selection. IEEE Trans. Signal Process. 2004, 52, 2153–2164. [Google Scholar] [CrossRef]
- Robert, T. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B 1994, 58, 267–288. [Google Scholar]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized Coprime Array Configurations for Direction-of-Arrival Estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar] [CrossRef]
- Hu, N.; Sun, B.; Zhang, Y.; Dai, J.S.; Wang, J.J.; Chang, C. Underdetermined DOA Estimation Method for Wideband Signals Using Joint Nonnegative Sparse Bayesian Learning. IEEE Signal Process. Lett. 2017, 24, 535–539. [Google Scholar] [CrossRef]
- Gretsistas, A.; Plumbley, M.D. An alternating descent algorithm for the off-grid DOA estimation problem with sparsity constraints. In Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 Auguest 2012; pp. 874–878. [Google Scholar]
- Yang, Z.; Xie, L.H.; Zhang, C.S. Off-Grid Direction of Arrival Estimation Using Sparse Bayesian Inference. IEEE Trans. Signal Process. 2013, 61, 38–43. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Trees, H.L.V. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Shaghaghi, M.; Vorobyov, S.A. Cramer-Rao Bound for Sparse Signals Fitting the Low-Rank Model with Small Number of Parameters. IEEE Signal Process. Lett. 2015, 22, 1497–1501. [Google Scholar] [CrossRef]
- Liu, C.L.; Vaidyanathan, P.P. Cramer-Rao bounds for coprime and other sparse arrays, which find more sources than sensors. Digit. Signal Process. 2017, 61, 43–61. [Google Scholar] [CrossRef]
- Wang, M.; Nehorai, A. Coarrays, MUSIC, and the Cramer-Rao Bound. IEEE Trans. Signal Process. 2017, 65, 933–946. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Liu, Y.; Liu, J.; Yu, Z. Underdetermined Wideband DOA Estimation for Off-Grid Sources with Coprime Array Using Sparse Bayesian Learning. Sensors 2018, 18, 253. https://doi.org/10.3390/s18010253
Qin Y, Liu Y, Liu J, Yu Z. Underdetermined Wideband DOA Estimation for Off-Grid Sources with Coprime Array Using Sparse Bayesian Learning. Sensors. 2018; 18(1):253. https://doi.org/10.3390/s18010253
Chicago/Turabian StyleQin, Yanhua, Yumin Liu, Jianyi Liu, and Zhongyuan Yu. 2018. "Underdetermined Wideband DOA Estimation for Off-Grid Sources with Coprime Array Using Sparse Bayesian Learning" Sensors 18, no. 1: 253. https://doi.org/10.3390/s18010253
APA StyleQin, Y., Liu, Y., Liu, J., & Yu, Z. (2018). Underdetermined Wideband DOA Estimation for Off-Grid Sources with Coprime Array Using Sparse Bayesian Learning. Sensors, 18(1), 253. https://doi.org/10.3390/s18010253



