High-Temperature Sensor Based on Fabry-Perot Interferometer in Microfiber Tip
Abstract
:1. Introduction
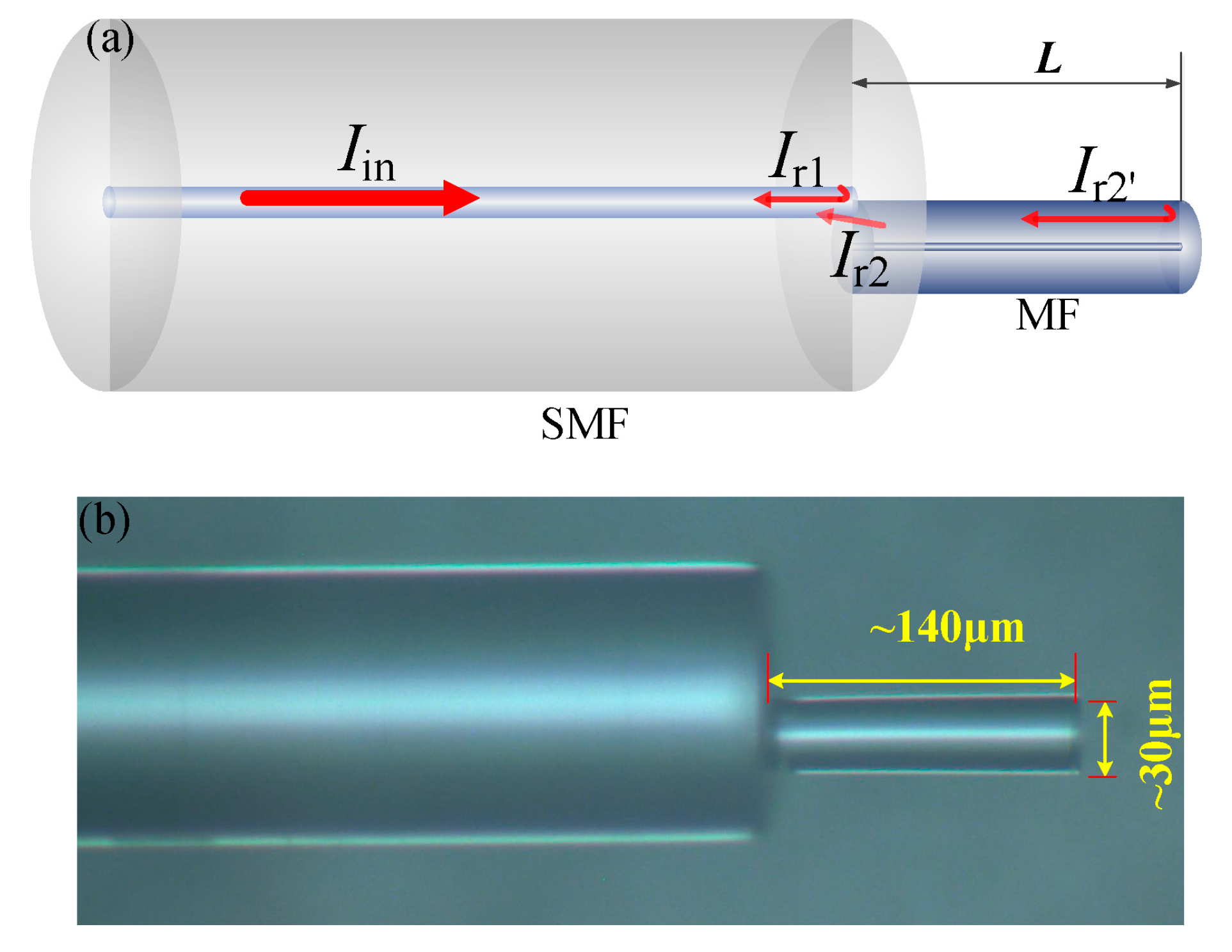
2. Structure and Theory
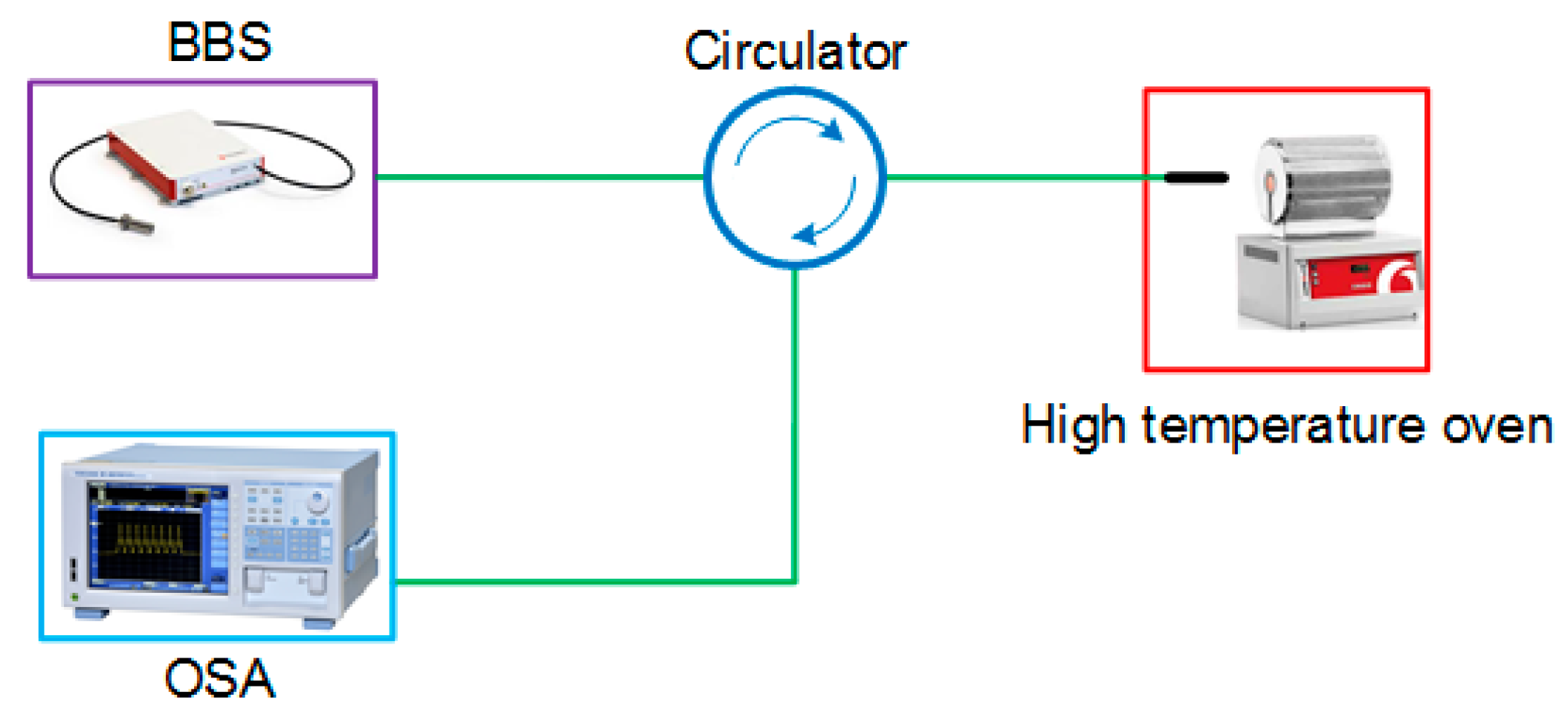
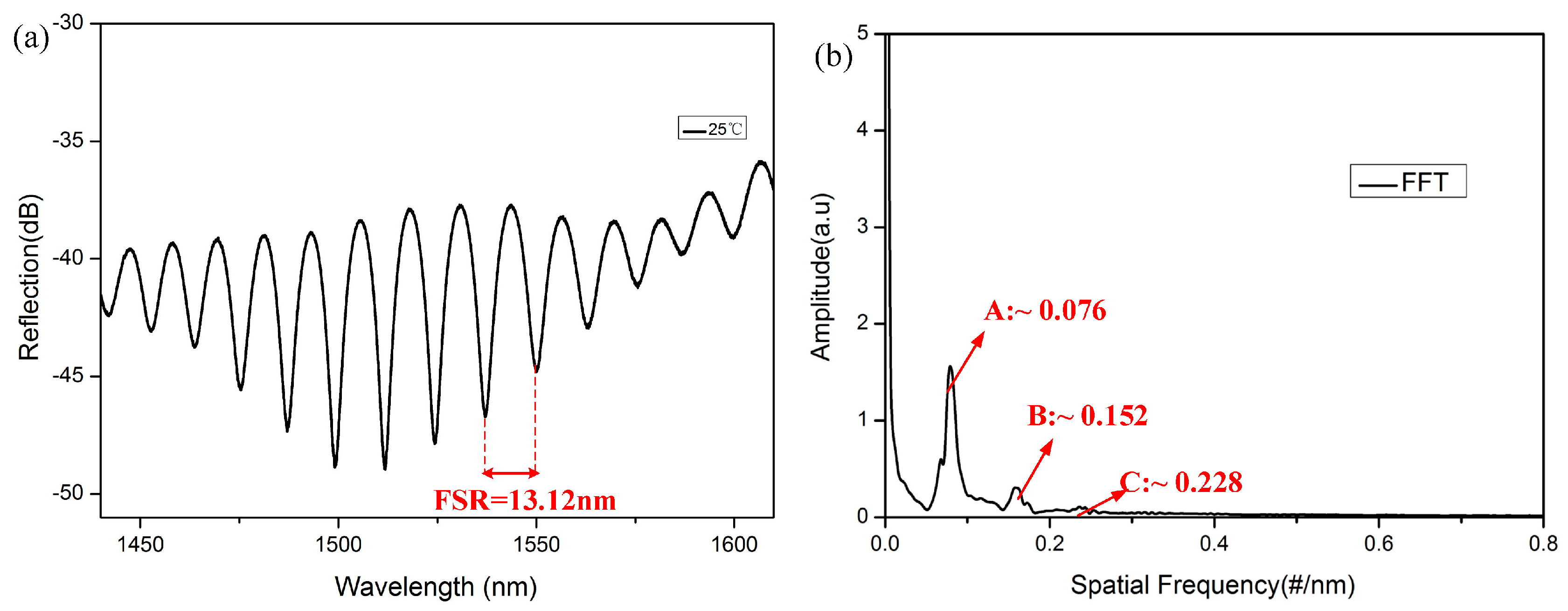
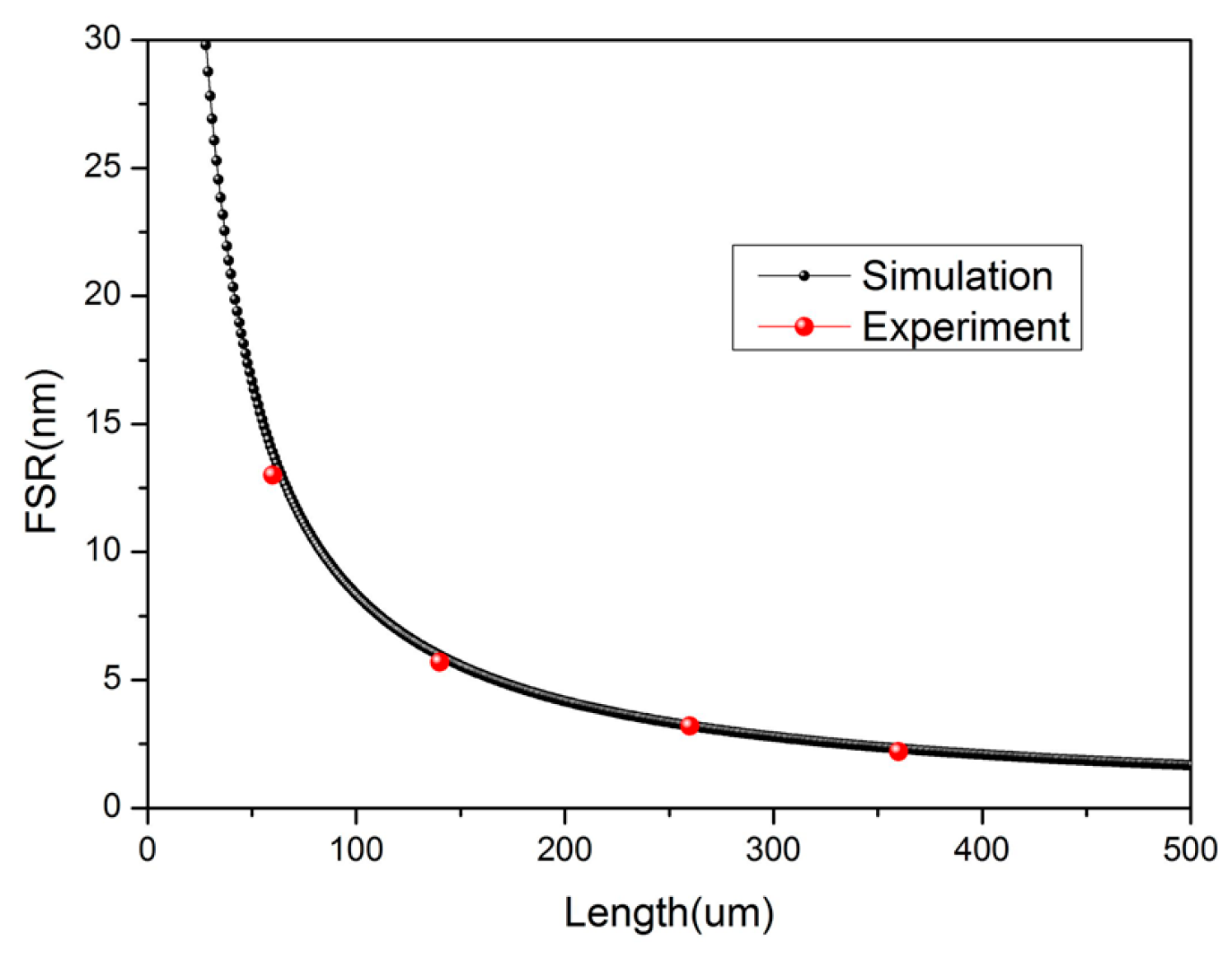
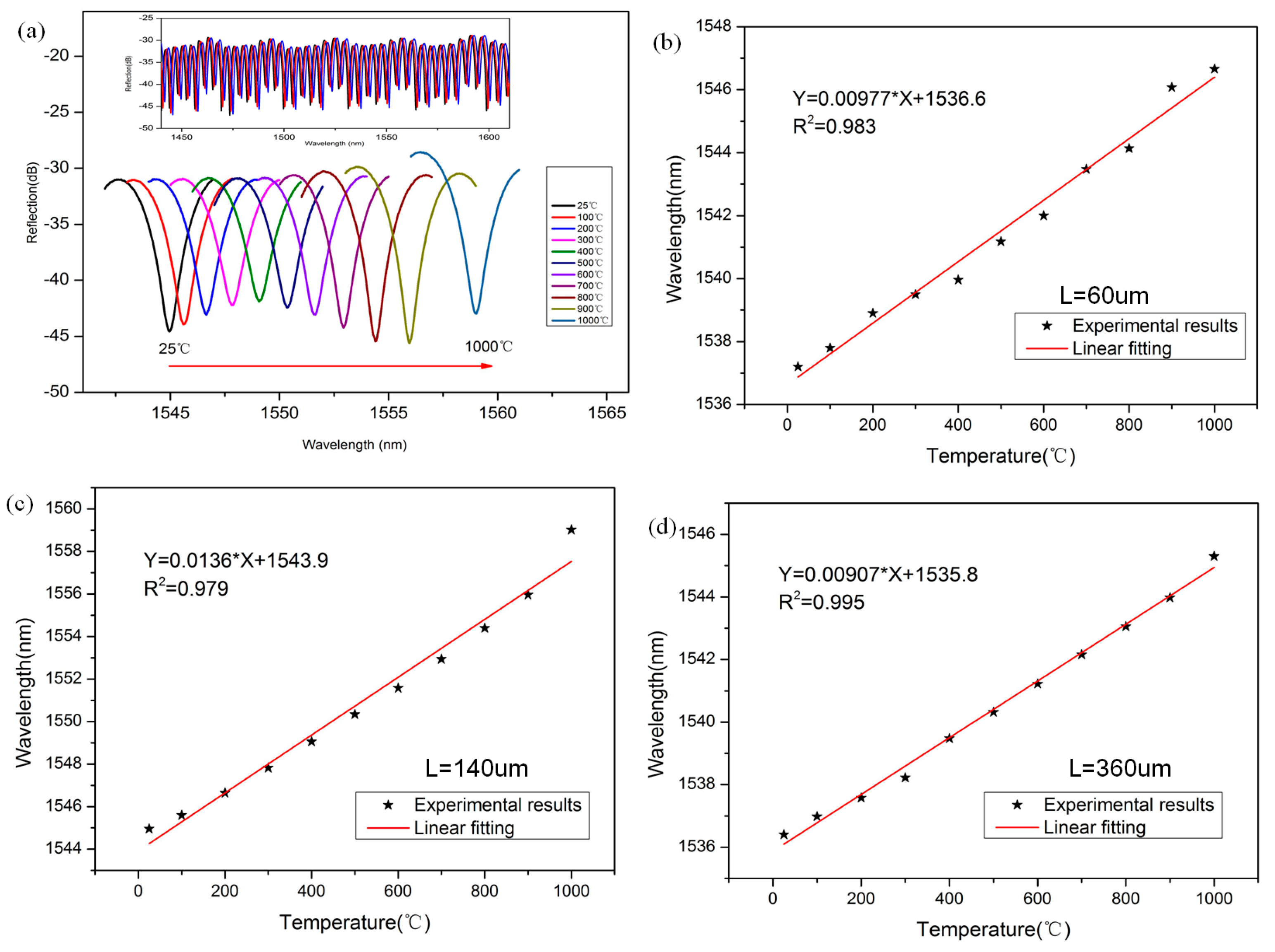
3. Experiment and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, M.; Peng, J.; Wang, G.; Dai, J. Fiber optic sensors based on nano-films. In Fiber Optic Sensors: Current Status and Future Possibilities; Matias, I.R., Ikezawa, S., Corres, J., Eds.; Springer: Cham, Switzerland, 2016; Volume 21. [Google Scholar]
- Barrera, D.; Finazzi, V.; Villatoro, J.; Sales, S.; Pruneri, V. Performance of a high-temperature sensor based on regenerated fiber bragg gratings. In Proceedings of the 21st International Conference on Optical Fibre Sensors (OFS21), Ottawa, ON, Canada, 15–19 May 2011; pp. 775381–775384. [Google Scholar] [CrossRef]
- Tian, Z.; Yu, Z.; Liu, B.; Wang, A. Sourceless optical fiber high temperature sensor. Opt. Lett. 2016, 41, 195–198. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Shen, X.; Wu, J.; Peng, J.; Yang, L.; Li, J.; Li, H.; Dai, N. All fiber M-Z interferometer for high temperature sensing based on a hetero-structured cladding solid-core photonic bandgap fiber. Opt. Express 2016, 24, 21693–21699. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, Y.; Liao, C.; Wang, D.; Yang, M.; Lu, P. High-temperature sensing using miniaturized fiber in-line mach–zehnder interferometer. IEEE Photonics Technol. Lett. 2010, 22, 39–41. [Google Scholar] [CrossRef]
- Yuan, L.; Wei, T.; Han, Q.; Wang, H.; Huang, J.; Jiang, L.; Xiao, H. Fiber inline michelson interferometer fabricated by a femtosecond laser. Opt. Lett. 2012, 37, 4489–4491. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Liu, T.; Jiang, J.; Liu, K.; Wang, S.; Zou, S.; Wu, F. Assembly-free-based fiber-optic micro-michelson interferometer for high temperature sensing. IEEE Photonics Technol. Lett. 2016, 28, 625–628. [Google Scholar] [CrossRef]
- Rao, Y.-J.; Duan, D.-W.; Fan, Y.-E.; Ke, T.; Xu, M. High-temperature annealing behaviors of CO2 laser pulse-induced long-period fiber grating in a photonic crystal fiber. J. Lightwave Technol. 2010, 28, 1530–1535. [Google Scholar] [CrossRef]
- Rao, Y.-J.; Ran, Z.-L.; Liao, X.; Deng, H.-Y. Hybrid LPFG/MEFPI sensor for simultaneous measurement of high-temperature and strain. Opt. Express 2007, 15, 14936–14941. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Xie, Z.; Song, Y.; Yin, K.; Chu, D.; Duan, J.A. High temperature-sensitivity sensor based on long period fiber grating inscribed with femtosecond laser transversal-scanning method. Chin. Opt. Lett. 2017, 15, 090602. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, L.; Lan, X.; Kaur, A.; Huang, J.; Xiao, H. High-temperature fiber-optic fabry–perot interferometric pressure sensor fabricated by femtosecond laser. Opt. Lett. 2013, 38, 4609–4612. [Google Scholar] [CrossRef] [PubMed]
- Mathew, J.; Schneller, O.; Polyzos, D.; Havermann, D.; Carter, R.M.; MacPherson, W.N.; Hand, D.P.; Maier, R.R. In-fiber fabry–perot cavity sensor for high-temperature applications. J. Lightwave Technol. 2015, 33, 2419–2425. [Google Scholar] [CrossRef]
- Chen, P.; Shu, X.; Cao, H.; Sugden, K. Ultra-sensitive refractive index sensor based on an extremely simple femtosecond-laser-induced structure. Opt. Lett. 2017, 42, 1157–1160. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, M.S.; Coelho, L.; Schuster, K.; Kobelke, J.; Santos, J.L.; Frazão, O. Fabry–perot cavity based on a diaphragm-free hollow-core silica tube. Opt. Lett. 2011, 36, 4029–4031. [Google Scholar] [CrossRef] [PubMed]
- Coviello, G.; Finazzi, V.; Villatoro, J.; Pruneri, V. Thermally stabilized pcf-based sensor for temperature measurements up to 1000 °C. Opt. Express 2009, 17, 21551–21559. [Google Scholar] [CrossRef] [PubMed]
- Antonio-Lopez, J.E.; Eznaveh, Z.S.; LiKamWa, P.; Schülzgen, A.; Amezcua-Correa, R. Multicore fiber sensor for high-temperature applications up to 1000 °C. Opt. Lett. 2014, 39, 4309–4312. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Fu, H.; Qureshi, K.K.; Guan, B.-O.; Tam, H.-Y. High-pressure and high-temperature characteristics of a fabry–perot interferometer based on photonic crystal fiber. Opt. Lett. 2011, 36, 412–414. [Google Scholar] [CrossRef] [PubMed]
- Warren-Smith, S.C.; Nguyen, L.V.; Lang, C.; Ebendorff-Heidepriem, H.; Monro, T.M. Temperature sensing up to 1300 °C using suspended-core microstructured optical fibers. Opt. Express 2016, 24, 3714–3719. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, L.V.; Warren-Smith, S.C.; Ebendorff-Heidepriem, H.; Monro, T.M. Interferometric high temperature sensor using suspended-core optical fibers. Opt. Express 2016, 24, 8967–8977. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Sheng, Q.; Dam, D.; Hua, J.; Hou, W.; Han, M. Self-gauged fiber-optic micro-heater with an operation temperature above 1000 °C. Opt. Lett. 2017, 42, 1412–1415. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Han, M.; Hou, W. High-resolution and fast-response fiber-optic temperature sensor using silicon fabry-pérot cavity. Opt. Express 2015, 23, 7237–7247. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Cooper, K.L.; Pickrell, G.R.; Wang, A. High-temperature fiber-tip pressure sensor. J. Lightwave Technol. 2006, 24, 861–869. [Google Scholar] [CrossRef]
- Ferreira, M.S.; Bierlich, J.; Unger, S.; Schuster, K.; Santos, J.L.; Frazão, O. Post-processing of fabry–pérot microcavity tip sensor. IEEE Photonics Technol. Lett. 2013, 25, 1593–1596. [Google Scholar] [CrossRef]
- Wei, T.; Han, Y.; Li, Y.; Tsai, H.-L.; Xiao, H. Temperature-insensitive miniaturized fiber inline fabry-perot interferometer for highly sensitive refractive index measurement. Opt. Express 2008, 16, 5764–5769. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhao, Z.; Chen, N.; Pang, F.; Chen, Z.; Liu, Y.; Wang, T. Temperature characteristics of silicon core optical fiber fabry–perot interferometer. Opt. Lett. 2015, 40, 1362–1365. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Zhang, W.; Bai, Z.-Y.; Zhang, H.; Lin, W.; Wang, L.; Li, J. Microfiber-enabled in-line fabry–pérot interferometer for high-sensitive force and refractive index sensing. J. Lightwave Technol. 2014, 32, 1682–1688. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, W.; Geng, P.; Xue, X.; Zhang, H.; Bai, Z. Highly sensitive in-fiber refractive index sensor based on down-bitaper seeded up-bitaper pair. IEEE Photonics Technol. Lett. 2012, 24, 1878–1881. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, W.; Bai, Z.; Zhang, H.; Geng, P.; Lin, W.; Li, J. Ultrasensitive refractive index sensor based on microfiber-assisted u-shape cavity. IEEE Photonics Technol. Lett. 2013, 25, 1815–1818. [Google Scholar] [CrossRef]
- Song, B.; Zhang, H.; Liu, B.; Lin, W.; Wu, J. Label-free in-situ real-time DNA hybridization kinetics detection employing microfiber-assisted mach-zehnder interferometer. Biosens. Bioelectron. 2016, 81, 151–158. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Xiong, S.; Gao, S.; Zhang, H.; Wan, L.; Huang, X.; Huang, B.; Feng, Y.; Liu, W.; Li, Z. High-Temperature Sensor Based on Fabry-Perot Interferometer in Microfiber Tip. Sensors 2018, 18, 202. https://doi.org/10.3390/s18010202
Chen Z, Xiong S, Gao S, Zhang H, Wan L, Huang X, Huang B, Feng Y, Liu W, Li Z. High-Temperature Sensor Based on Fabry-Perot Interferometer in Microfiber Tip. Sensors. 2018; 18(1):202. https://doi.org/10.3390/s18010202
Chicago/Turabian StyleChen, Zhenshi, Songsong Xiong, Shecheng Gao, Hui Zhang, Lei Wan, Xincheng Huang, Bingsen Huang, Yuanhua Feng, Weiping Liu, and Zhaohui Li. 2018. "High-Temperature Sensor Based on Fabry-Perot Interferometer in Microfiber Tip" Sensors 18, no. 1: 202. https://doi.org/10.3390/s18010202
APA StyleChen, Z., Xiong, S., Gao, S., Zhang, H., Wan, L., Huang, X., Huang, B., Feng, Y., Liu, W., & Li, Z. (2018). High-Temperature Sensor Based on Fabry-Perot Interferometer in Microfiber Tip. Sensors, 18(1), 202. https://doi.org/10.3390/s18010202




