Fast Alignment of SINS for Marching Vehicles Based on Multi-Vectors of Velocity Aided by GPS and Odometer
Abstract
:1. Introduction
2. New Alignment Mechanism Based on the GPS and the Odometer
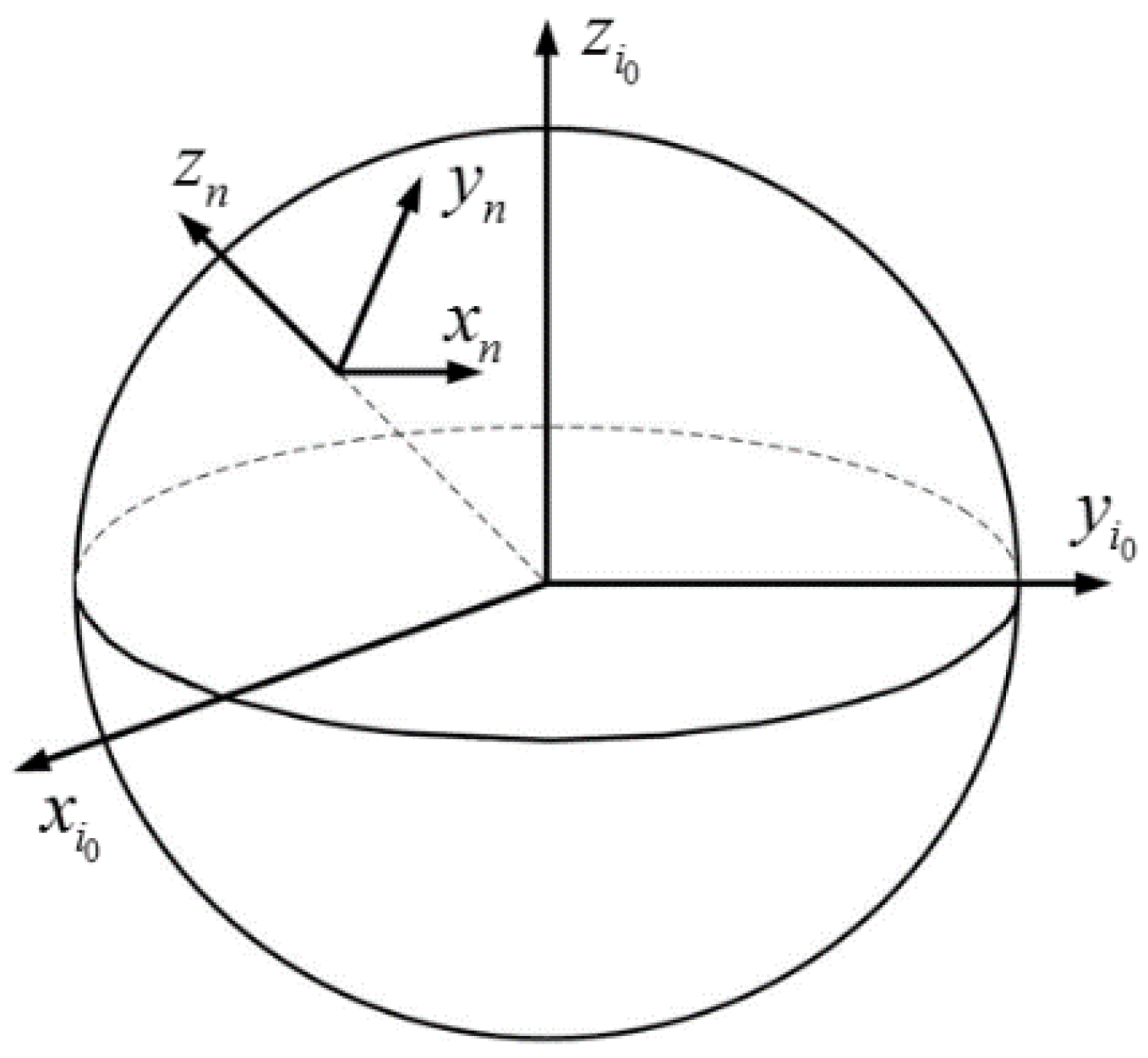
2.1. Coordinate Frame Definitions
- The frame is the Earth-fixed coordinate frame, whose origin is the center of the Earth. The axis is in the equatorial plane and points to the prime meridian, and the axis is parallel to the rotation axis of the Earth. The axis completes the right-handed coordinate system.
- The frame is also the Earth-fixed coordinate frame, whose origin is the center of the Earth. The axis is in the equatorial plane, and points to the meridian of the vehicle’s position at the beginning of initial alignment, and the axis is parallel to the rotation axis of the Earth. The axis completes the right-handed coordinate system.
- The frame is formed by fixing the frame at the beginning of alignment in inertial space.
- The frame is the instantaneous navigation coordinate frame, which is the local level coordinate frame. The axis points to the east, the axis points to the north, and the axis points upwards.
- The frame is the instantaneous body coordinate frame, which is defined as the common “Right–Forward–Up” frame.
- The frame is formed by fixing the frame at the beginning of alignment in the inertial space.
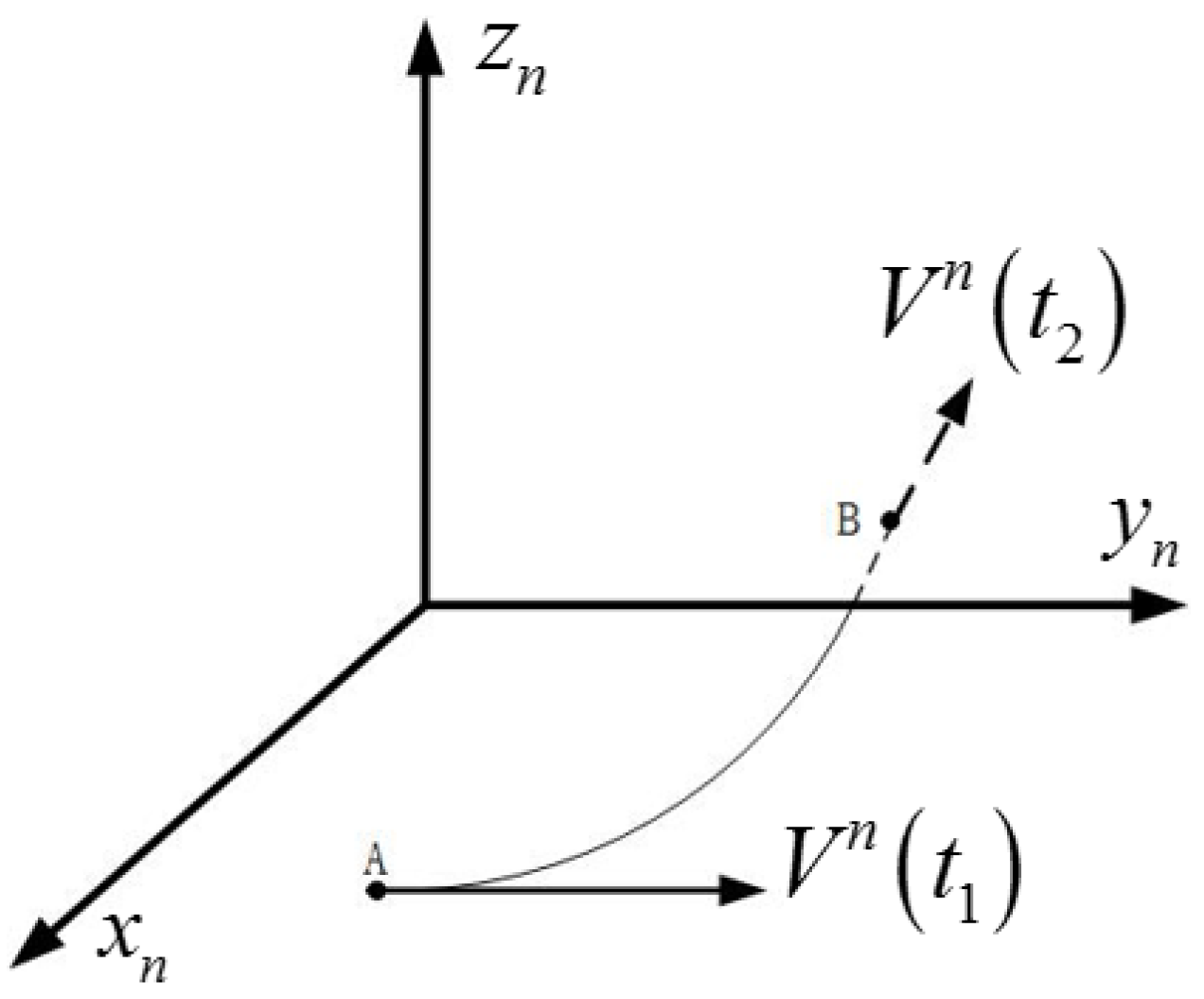
2.2. Constructing Nonlinear Vectors by Turning Movement
2.3. Alignment Algorithm
3. Error Analysis and the Improved Alignment Method
3.1. Error Analysis
3.2. Improved Method
4. Simulation and Vehicle Test
4.1. Simulation
4.1.1. Simulation Settings
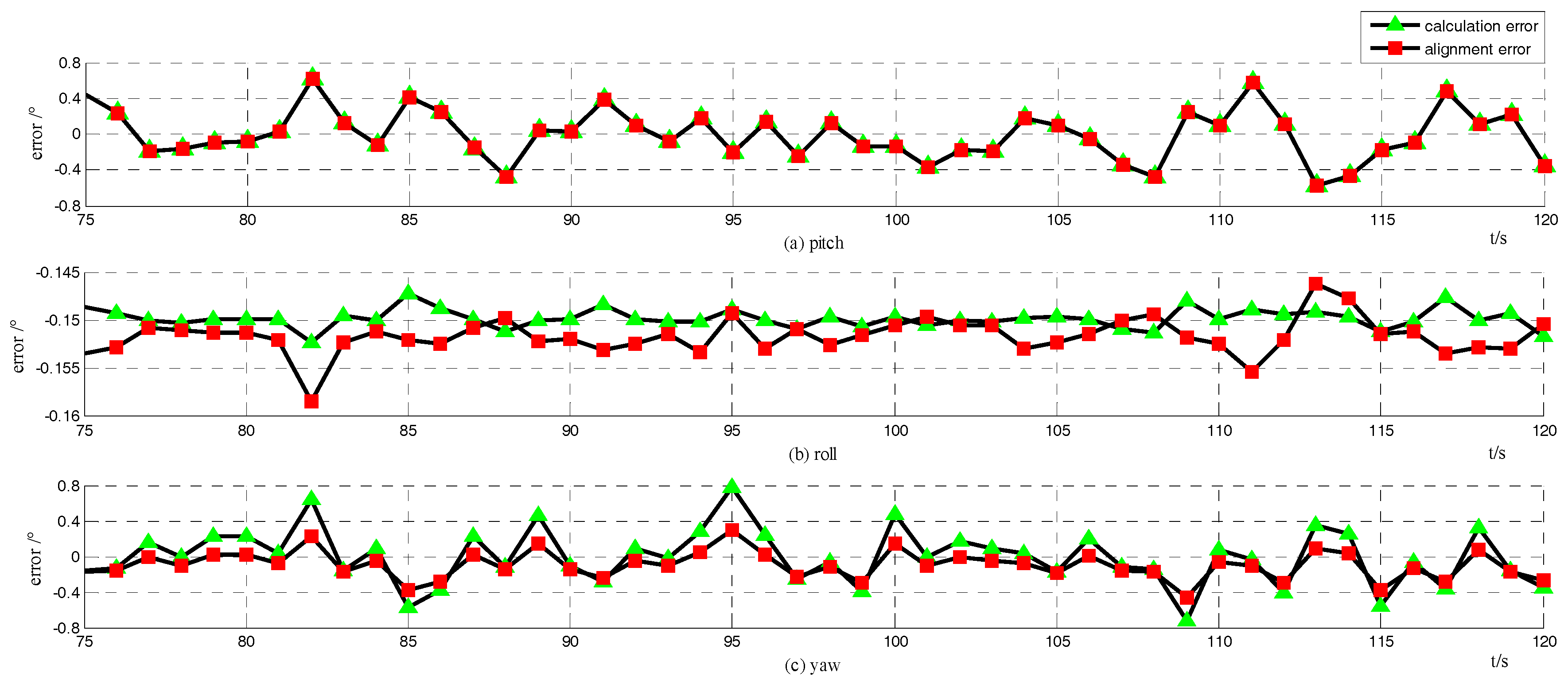
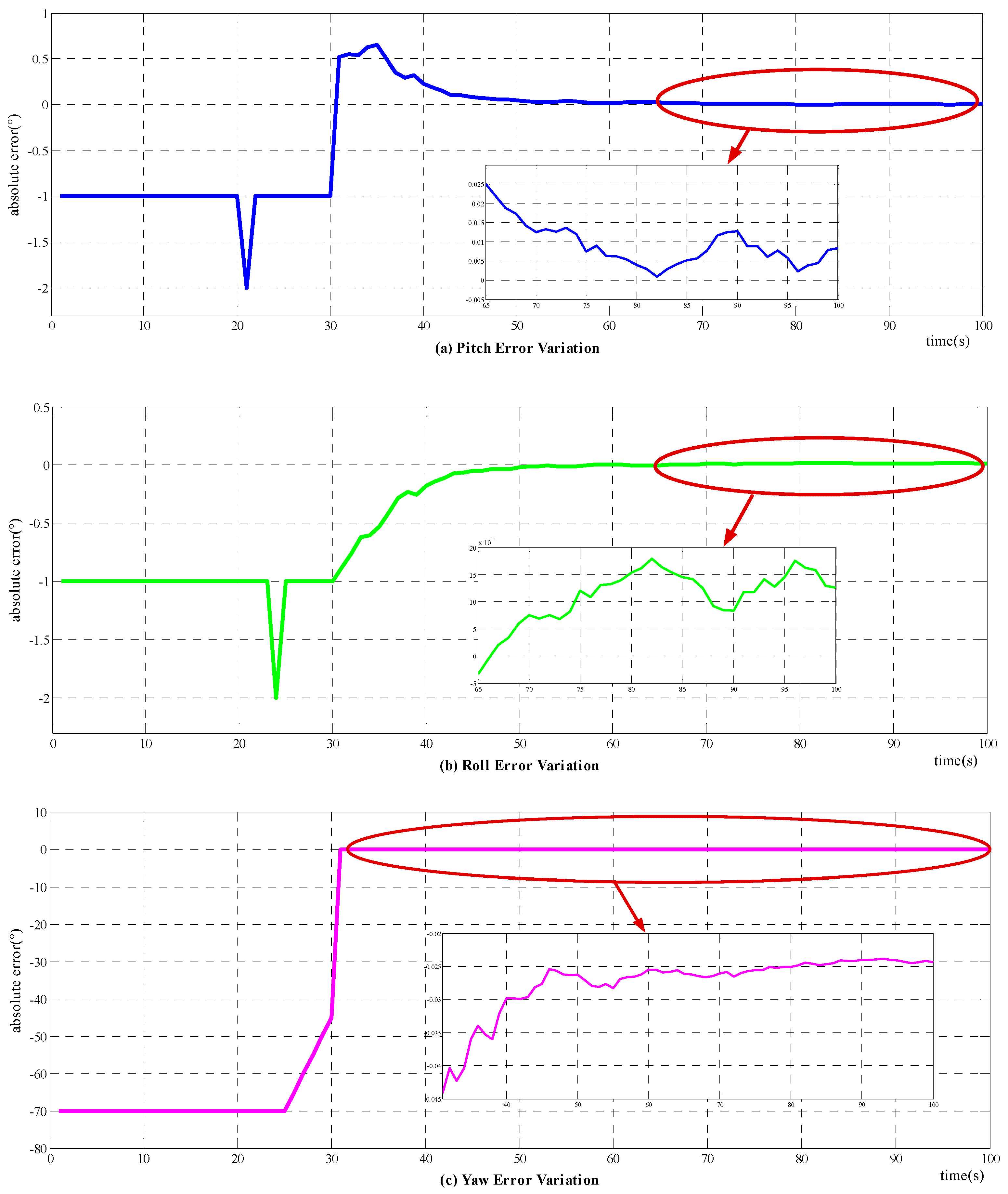
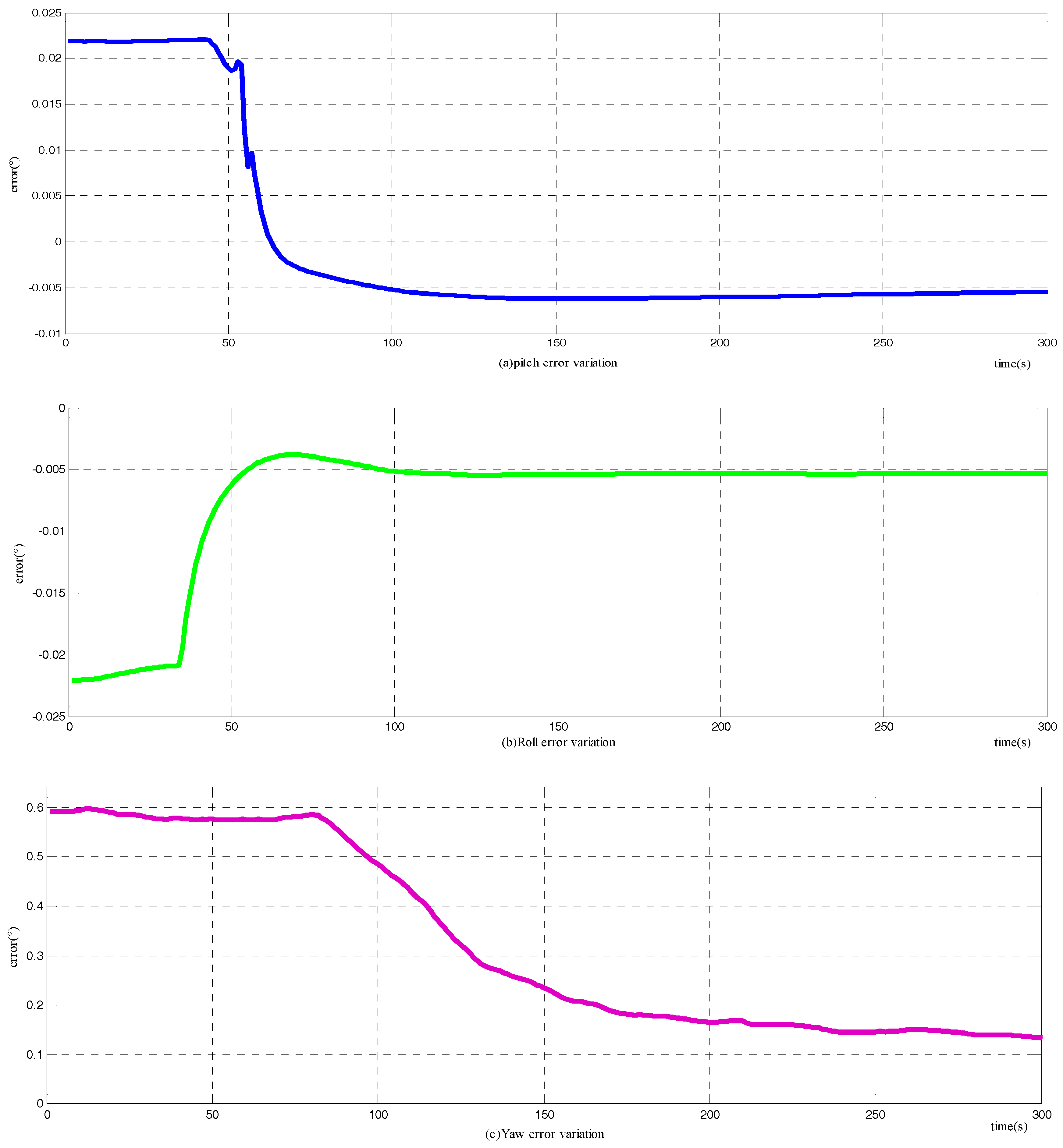
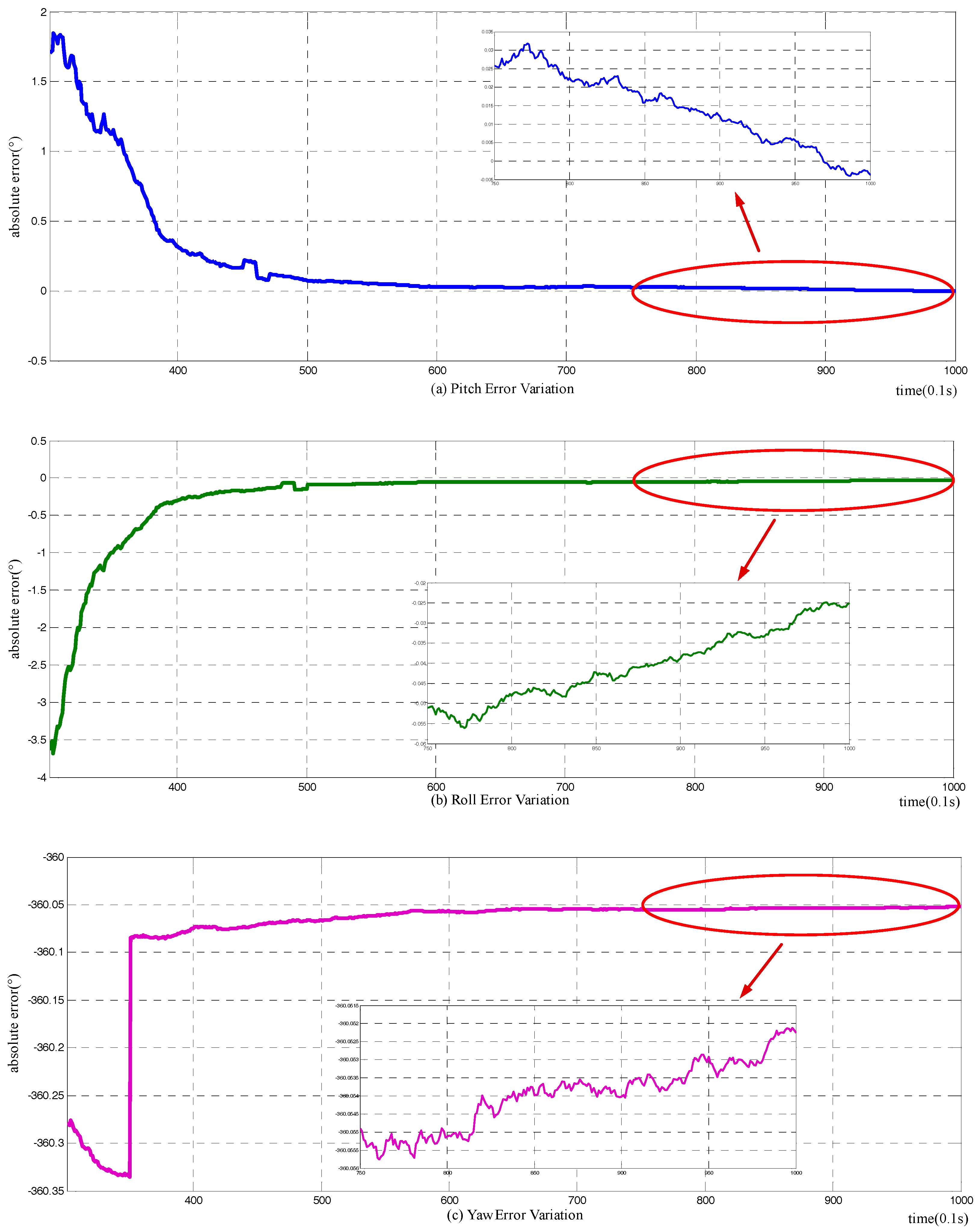
4.1.2. Simulation Results and Analysis
Error Analysis Validation
Alignment Mechanism Validation
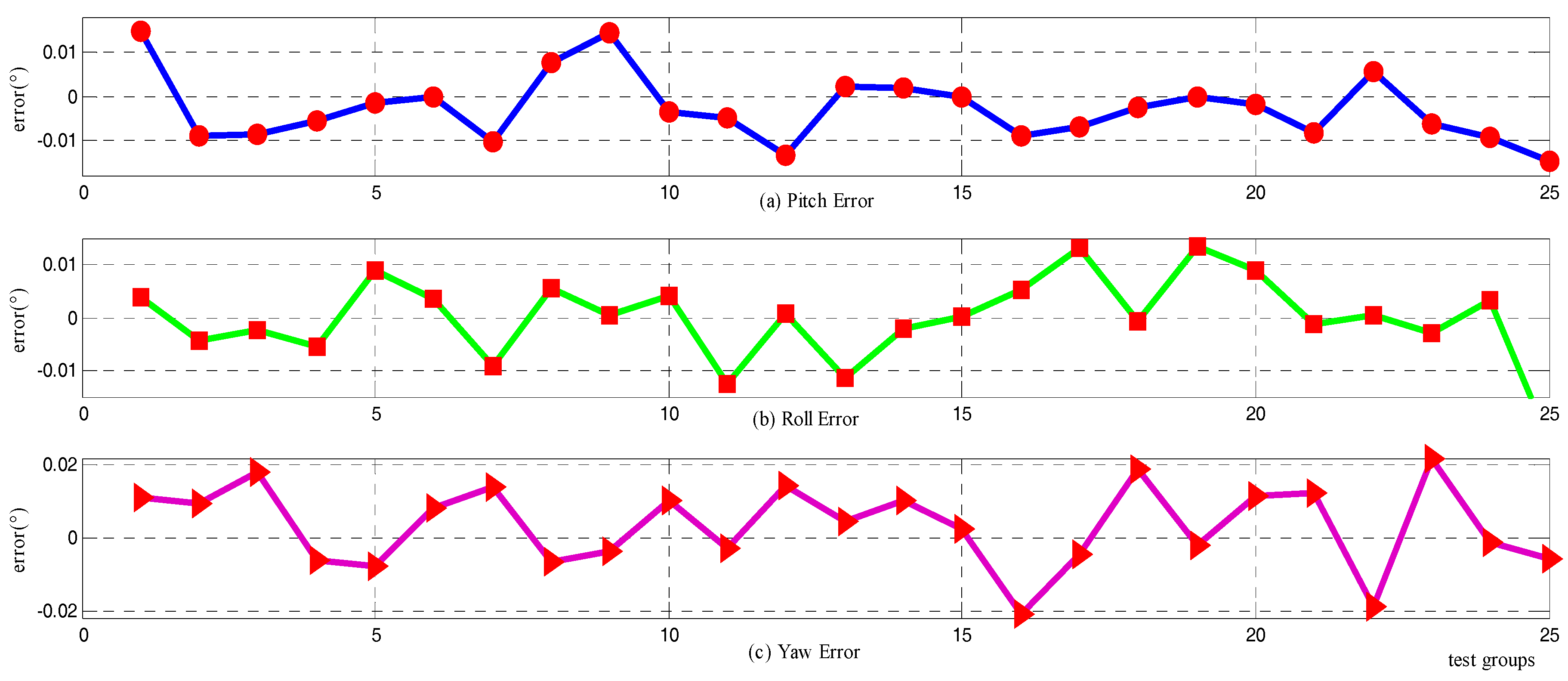
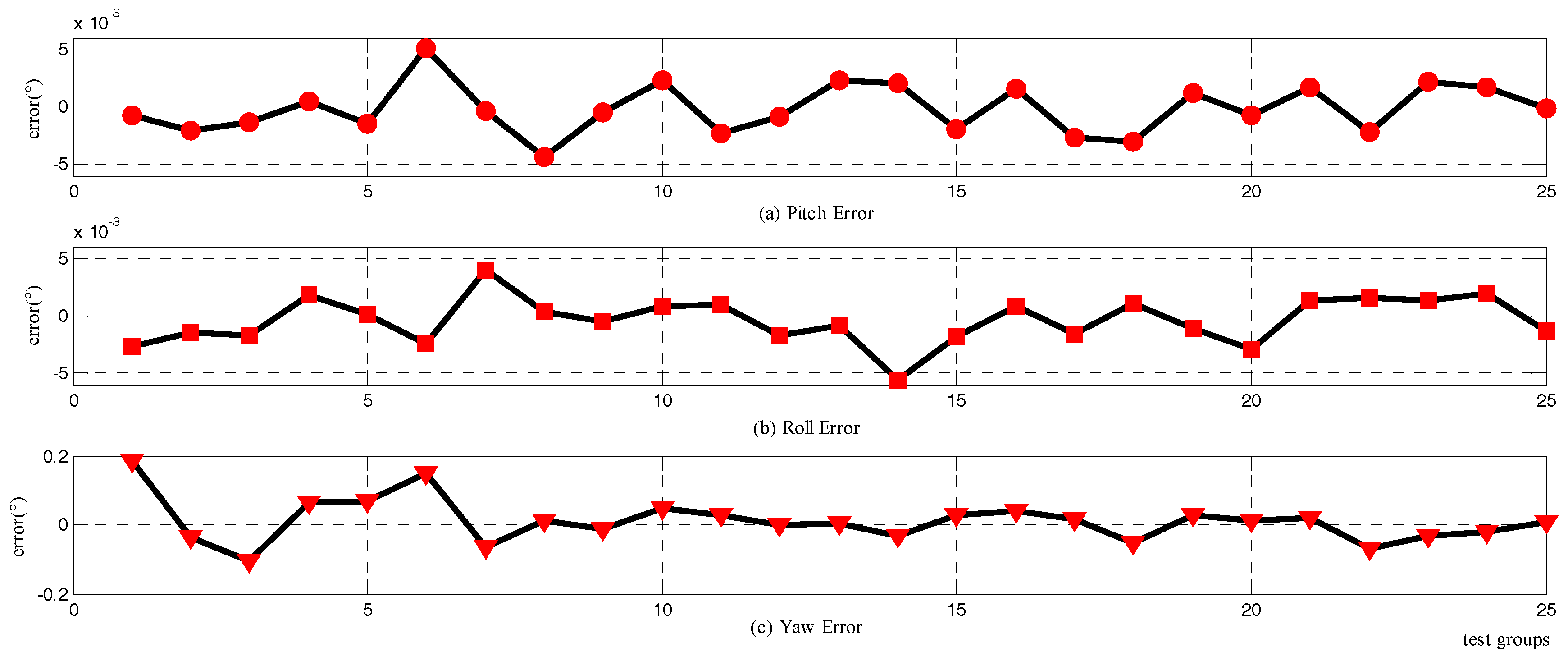
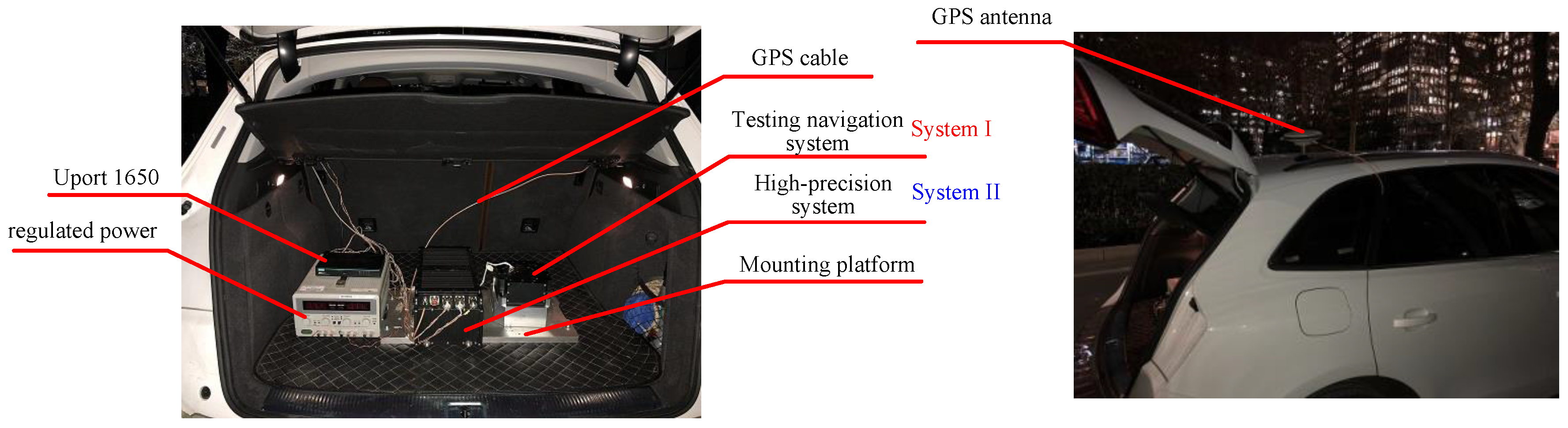
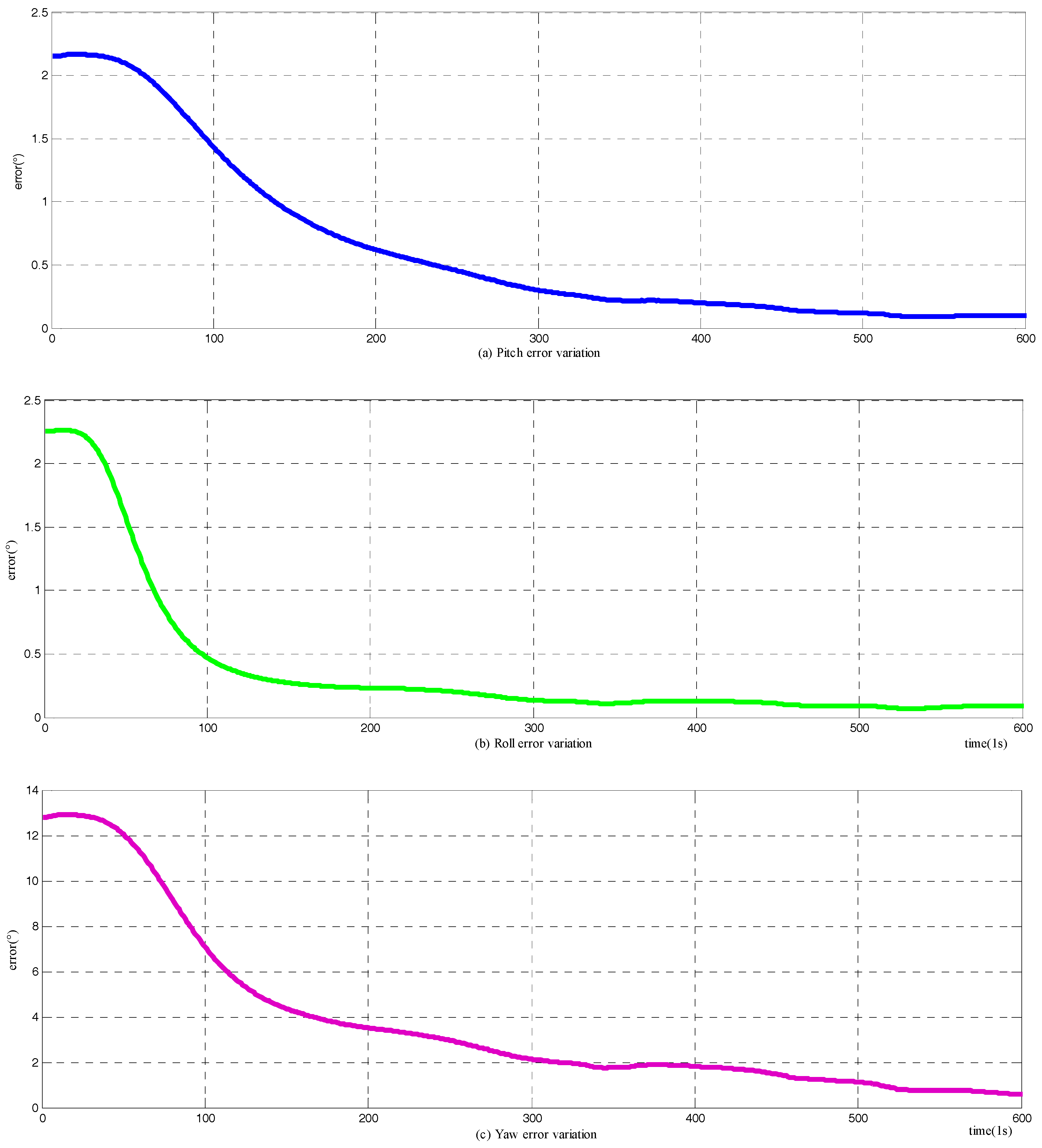
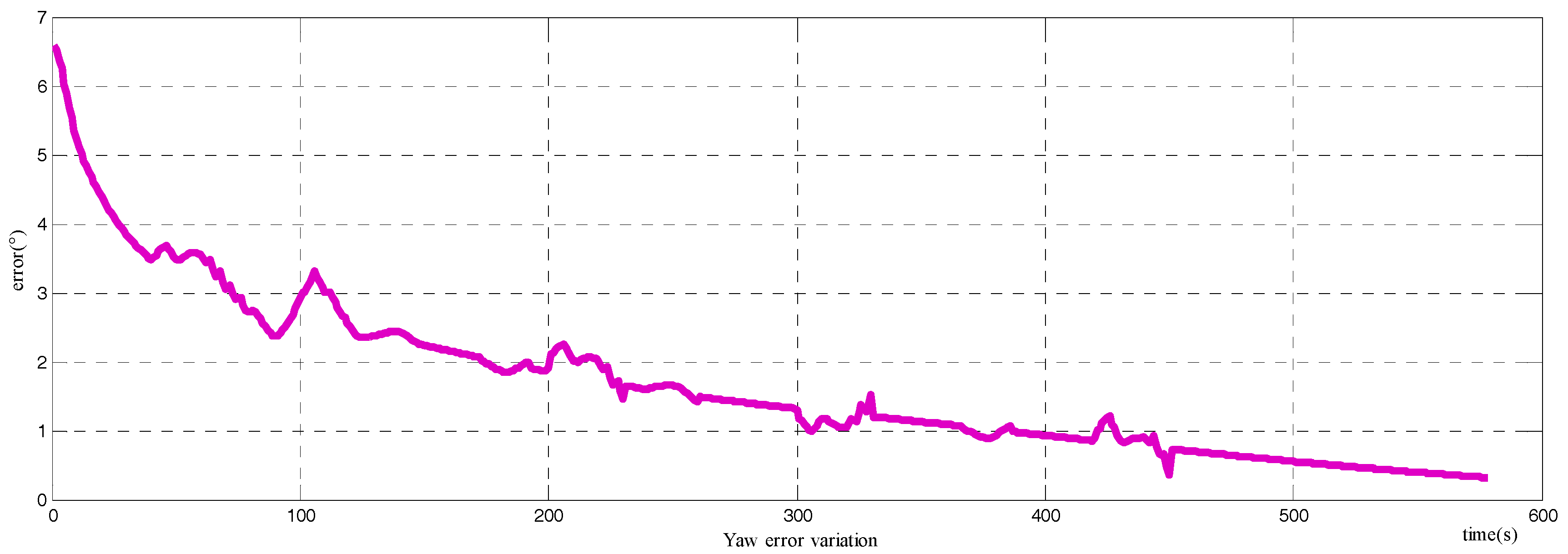
4.2. Vehicle Test
- (a)
- The testing navigation system (simplified as System I) and the reference system (simplified as System II) were mounted in the testing car, as shown in Figure 8. The receiver of the GPS is integrated in the navigation system, the information from the GPS can be shared by System I and System II. The velocity information from the odometer is pulse signal, which can be collected by System I immediately.
- (b)
- The misalignment of the two systems could be obtained through optical sighting, as these two systems had installed the optical prism. The misalignment must be compensated when processing the output data.
- (c)
- System I and System II were launched simultaneously and with a strick on the mounting platform. System II would start its alignment and navigation procedure in normal mode. The testing carrier could moving out after the alignment of System II finished. All of the data from System I and System II, including the inertial sensor, the GPS, and the odometer, should be saved in the computer for further processing.
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Gaho, A.A.; Qureshi, M.S. The generic investigation of initial alignment of SINS. J. Space Technol. 2012, 1, 11–16. [Google Scholar]
- Yu, H.; Wu, W.; Wu, M.; Yu, M.; Hao, M. Stochastic observability-based analytic optimization of SINS multiposition alignment. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2181–2192. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, F.; Zhang, Y.; Liu, H.; Min, H. Central difference particle filter applied to transfer alignment for SINS on missiles. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 375–387. [Google Scholar] [CrossRef]
- Titterton, D.; Weston, J.L. Strapdown Inertial Navigation Technology; IET: Stevenage, UK, 2004. [Google Scholar]
- Jiang, Y.F. Error analysis of analytic coarse alignment methods. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 334–337. [Google Scholar] [CrossRef]
- Pecht, E.; Mintchev, M.P. Observability analysis for INS alignment in horizontal drilling. IEEE Trans. Instrum. Meas. 2007, 56, 1935–1945. [Google Scholar] [CrossRef]
- Jiancheng, F.; Sheng, Y. Study on innovation adaptive EKF for in-flight alignment of airborne POS. IEEE Trans. Instrum. Meas. 2011, 60, 1378–1388. [Google Scholar] [CrossRef]
- Wu, M.; Wu, Y.; Hu, X.; Hu, D. Optimization-based alignment for inertial navigation systems: Theory and algorithm. Aerosp. Sci. Technol. 2011, 15, 1–17. [Google Scholar] [CrossRef]
- Sun, F.; Sun, W.; Wu, L. Coarse alignment based on IMU rotational motion for surface ship. In Proceedings of the 2010 IEEE/ION Position Location and Navigation Symposium (PLANS), Indian Wells, CA, USA, 4–6 May 2010; pp. 993–998. [Google Scholar]
- Yu, H.; Zhu, H.; Gao, D.; Yu, M.; Wu, W. A stationary north-finding scheme for an azimuth rotational IMU utilizing a linear state equality constraint. Sensors 2015, 15, 4368–4387. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.G.; Park, C.; Park, H.W. Multiposition alignment of strapdown inertial navigation system. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 1323–1328. [Google Scholar] [CrossRef]
- Dai, H.; Dai, S.; Cong, Y.; Zhao, G.; Wu, G. Rapid transfer alignment of laser SINS using quaternion based angular measurement. Optik-Int. J. Light Electron Opt. 2013, 124, 4364–4368. [Google Scholar] [CrossRef]
- Wendel, J.; Metzger, J.; Trommer, G.F. Rapid transfer alignment in the presence of time correlated measurement and system noise. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; pp. 1–12. [Google Scholar]
- Hao, Y.; Xiong, Z.; Wang, W.; Sun, F. Rapid transfer alignment based on unscented Kalman filter. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar] [CrossRef]
- Groves, P.D. Optimising the transfer alignment of weapon INS. J. Navig. 2003, 56, 323–335. [Google Scholar] [CrossRef]
- Liu, X.; Xu, X.; Liu, Y.; Wang, L. A fast and high-accuracy transfer alignment method between M/S INS for ship based on iterative calculation. Measurement 2014, 51, 297–309. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Y. New rapid transfer alignment method for SINS of airborne weapon systems. J. Syst. Eng. Electron. 2014, 25, 281–287. [Google Scholar] [CrossRef]
- Sun, F.; Sun, W. Mooring alignment for marine SINS using the digital filter. Measurement 2010, 43, 1489–1494. [Google Scholar] [CrossRef]
- Lv, S.; Xie, L.; Chen, J. New techniques for initial alignment of strapdown inertial navigation system. J. Frankl. Inst. 2009, 346, 1021–1037. [Google Scholar]
- El-Sheimy, N.; Nassar, S.; Noureldin, A. Wavelet de-noising for IMU alignment. Aerosp. Electron. Syst. Mag. 2004, 19, 32–39. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Gao, J.; Li, B.; Zhou, F. A vondrak low pass filter for IMU sensor initial alignment on a disturbed base. Sensors 2014, 14, 23803–23821. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhao, Y.; Liu, X.; Yang, Y.; Song, Q.; Liu, Z. An improved self-alignment method for strapdown inertial navigation system based on gravitational apparent motion and dual-vector. Rev. Sci. Instrum. 2014, 85, 125108. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Ben, Y.; Yang, J. Coarse alignment for Fiber Optic Gyro SINS with external velocity aid. Optik-Int. J. Light Electron Opt. 2014, 125, 4241–4245. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Song, Q.; Yang, Y.; Liu, Y.; Wang, L. A novel self-alignment method for SINS based on three vectors of gravitational apparent motion in inertial frame. Measurement 2015, 62, 47–62. [Google Scholar] [CrossRef]
- Ma, L.; Wang, K.; Shao, M. Initial alignment on moving base using GPS measurements to construct new vectors. Measurement 2013, 46, 2405–2410. [Google Scholar] [CrossRef]
- Gu, D.; El-Sheimy, N.; Hassan, T.; Syed, Z. Coarse alignment for marine SINS using gravity in the inertial frame as a reference. In Proceedings of the 2008 IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; pp. 961–965. [Google Scholar]
- Silson, P.M.G.; Jordan, S. A novel inertial coarse alignment method. In Proceedings of the AIAA Guidance, Navigation and Control Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Feng, S.; Tong, C. Accuracy analysis of coarse alignment based on gravity in inertial frame. Chin. J. Sci. Instrument. 2011, 32, 2409–2415. [Google Scholar]
- Han, S.; Wang, J. A novel initial alignment scheme for low-cost INS aided by GPS for land vehicle applications. J. Navig. 2010, 63, 663–680. [Google Scholar] [CrossRef]
- Chang, L.B.; He, H.Y.; Qin, F.J. In-Motion Initial Alignment for Odometer-Aided Strapdown Inertial Navigation System Based on Attitude Estimation. IEEE Sens. J. 2017, 17, 766–773. [Google Scholar] [CrossRef]
- Zhao, C.; Qin, Y.; Yan, G. On-the-move alignment for strap-down inertial navigation system. In Proceedings of the International Conference on Information and Automation, Changsha, China, 20–23 June 2008; pp. 1428–1432. [Google Scholar]
- Sun, F.; Lan, H.; Yu, C.; El-Sheimy, N.; Zhou, G.; Cao, T.; Liu, H. A robust self-alignment method for ship’s strapdown INS under mooring conditions. Sensors 2013, 13, 8103–8139. [Google Scholar] [CrossRef] [PubMed]
- Jianping, M.A. A new GPS aided initial alignment algorithm for SINS on moving base. Chin. J. Sens. Actuators 2010, 23, 1656–1661. [Google Scholar]
| Gyro | Bias | 0.1 °/h |
| Random Walk | ||
| Updating Frequency | 1 kHz | |
| Accelerometer | Bias | 500 μg |
| Updating Frequency | 1 kHz | |
| GPS | Velocity accuracy | 0.03 m/s (RMS) |
| Horizontal position accuracy | 2 m (RMS) | |
| Updating Frequency | 10 Hz | |
| Odometer bias | Scale Factor | 0.2% |
| Updating Frequency | 10 Hz |
| Statistics | Pitch (°) | Roll (°) | Yaw (°) | |
|---|---|---|---|---|
| Mean | Alignment error | −0.0036 | −0.1516 | −0.0969 |
| Calculation error | −0.0036 | −0.1497 | −0.0065 | |
| Std | Alignment error | 0.2823 | 0.0019 | 0.1574 |
| Calculation error | 0.2819 | 9.8 × 10−4 | 0.3137 | |
| Gyro | Bias | 0.01 °/h |
| Random Walk | ||
| Updating Frequency | 1 kHz | |
| Accelerometer | Bias | 50 μg |
| Updating Frequency | 1 kHz |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Ran, L.; Song, L. Fast Alignment of SINS for Marching Vehicles Based on Multi-Vectors of Velocity Aided by GPS and Odometer. Sensors 2018, 18, 137. https://doi.org/10.3390/s18010137
Zhang C, Ran L, Song L. Fast Alignment of SINS for Marching Vehicles Based on Multi-Vectors of Velocity Aided by GPS and Odometer. Sensors. 2018; 18(1):137. https://doi.org/10.3390/s18010137
Chicago/Turabian StyleZhang, Chunxi, Longjun Ran, and Lailiang Song. 2018. "Fast Alignment of SINS for Marching Vehicles Based on Multi-Vectors of Velocity Aided by GPS and Odometer" Sensors 18, no. 1: 137. https://doi.org/10.3390/s18010137
APA StyleZhang, C., Ran, L., & Song, L. (2018). Fast Alignment of SINS for Marching Vehicles Based on Multi-Vectors of Velocity Aided by GPS and Odometer. Sensors, 18(1), 137. https://doi.org/10.3390/s18010137




