Abstract
Data authenticated aggregation is always a significant issue for wireless sensor networks (WSNs). The marine sensors are deployed far away from the security monitoring. Secure data aggregation for marine WSNs has emerged and attracted the interest of researchers and engineers. A multi-signature enables the data aggregation through one signature to authenticate various signers on the acknowledgement of a message, which is quite fit for data authenticated aggregation marine WSNs. However, most of the previous multi-signature schemes rely on the technique of bilinear pairing involving heavy computational overhead or the management of certificates, which cannot be afforded by the marine wireless sensors. Combined with the concept of identity-based cryptography, a few pairing-free identity-based multi-signature (IBMS) schemes have been designed on the basis of the integer factorization problem. In this paper, we propose two efficient IBMS schemes that can be used to construct provably secure data authenticated aggregation protocols under the cubic residue assumption, which is equal to integer factorization. We also employ two different methods to calculate a cubic root for the cubic residue number during the signer’s private key extraction. The algorithms are quite efficient compared to the previous work, especially for the algorithms of the multi-signature generation and its verification.
1. Introduction
In most of the wireless sensor networks (WSNs), the significant issue for data collection or data aggregation always lies in the center of data transmission, both in the academia and in the industry [1,2,3]. In most scenarios of marine WSNs, all the nearby wireless sensors send their data, such as the temperature, pressure, salinity, and potential of hydrogen (pH value) in the chemistry of the environmental monitoring ocean, to a central node, which is located at a base station or a buoy for data collection, as shown in Figure 1. The central node further sends the aggregated data through the long-distance data transmission networks, such as vessel-based or satellite-based networks [4]. However, marine sensors are always deployed far away from the security monitoring. Thus, the secure data aggregation for marine sensor networks has emerged and attracted the interest of researchers and engineers. In order to mitigate the malicious attackers injecting false data, it is quite necessary for each central node to authenticate these sensing measurements from the nearby sensors in the ocean observation system [5].
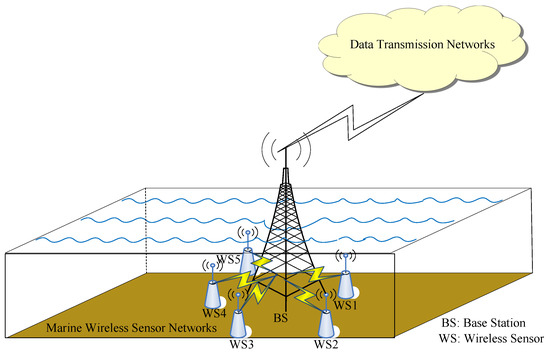
Figure 1.
Data collection in marine wireless sensor networks (WSNs).
Generally, a digital signature often provides the properties of authenticity and non-repudiation through checking the signed acknowledgments from senders [6]. However, in WSNs, the international standards for broadcasting authentication are very vulnerable to signature verification flooding attacks, as the excessive requests for signature verification must run out of the computational resources of those victims [7]. The scenario seems worse, as the marine wireless sensors are powered by a limited battery and cannot afford these overloaded requests in an oceanic environment. To optimize the communication and computational overhead, a variant of digital signature, named multi-signature, permits various signers to sign on a message individually and aggregate partial signatures to a compact signature [8].
A multi-signature can play a significant role in authenticating different sensors’ data by checking a single compact signature to cut down the communication bandwidth for marine wireless devices, as the transmission of one-bit data consumes more energy than the arithmetic operations on several bits [9]. This seems a promising way to solve the data authentication in a multi-user scenario. Since the primitive has been proposed, multi-signature schemes have been paid attention to by most of the network designers and industry engineers. However, in the past years, most of the work on multi-signature schemes has been constructed by relying on the assumed existence of public key infrastructure (PKI) [10,11]; the heavy burdens of the digital public key certificate management bring high communication overhead and storage overhead when PKI is applied and implemented in the wireless networks. The cases become worse when the sensors are deployed in the marine environments (denoted as Problem 1).
To overcome the weakness brought by PKI, identity-based cryptography emerges as a novel cryptographic primitive and a powerful alternative to traditional certificate-based cryptography, which has been raised early on in [12] and is further specifically designed in [13,14]. Identity-based cryptography makes some public, known information a public key, such as the device’s number, IP address, or a username, to mitigate the management problem for the public key certificates. In the extreme case that the bandwidth is a bottleneck, the identities of the signers often appear in the head of the communication packets, instead of in the transmission of the heavy public keys. Inspired by this concept, the first identity-based multi-signature (IBMS) scheme, proposed in [15], uses a mathematical technique named “bilinear mapping”, such as is used in [13], and is proved to be secure, relying on discrete logarithm (DL) assumptions or computational Diffie–Hellman (CDH) assumptions. Because the operation of bilinear mapping involves too much computational overhead [16,17], many bilinear mapping techniques are not suitable for the battery-limited sensors in marine WSNs (denoted as Problem 2).
As a consequence, there is great interest for cryptographic researchers to design pairing-free identity-based cryptographic schemes [18]. The first non-pairing IBMS scheme was proposed in [19] with three-round interactive communications and under R. Rivest, A. Shamir, L. Adleman (RSA) assumptions. Later, a communication efficiency-improved IBMS scheme under RSA assumptions was presented in [20] with two-round interactive communications. Yang et al. [21] proposed an efficient improved IBMS scheme that aims to save the computational resources and communication bandwidth. Even if the RSA assumption approaches the integer factorization assumptions, unfortunately, the RSA assumption has not yet been proved equal to the factorization assumption (denoted as Problem 3).
To satisfy the application requirements and to avoid security concerns in cryptrography, it is common practice to construct alternative cryptographic schemes under a weaker assumption—integer factorization. Recently, cryptographic researchers have been focused on finding a new construction that is proved to be secure directly on the basis of factorization. Chai [22] gave an instance of an identity-based digital signature relying on the quadratic residue assumption. Following this, Wei et al. [6] proposed IBMS schemes using quadratic residue assumptions, under weaker assumptions and a strengthened security model, achieving advantages in the computational consumption and transmission overhead. Xing [23] and Wang [24] presented identity-based signature schemes under the cubic residue assumptions. Wang proposed several signature variants relying on cubic residues, including identity-based ring signature [25], identity-based proxy multi-signature (IBPMS) [26] and threshold ring signature [27]. Wei [28] considered an identity-based multi-proxy signature (IBMPS) scheme for use in a cloud-based data authentication protocol. Zhang [29] proposed a secure multi-entity delegated authentication protocol based on an identity-based multi-proxy multi-signature (IBMPMS) for mobile cloud computing. Unfortunately, none considered constructing IBMS schemes directly based on cubic residues (denoted as Problem 4).
Facing the above problems, this work constructs IBMS schemes relying on the cubic residue assumption equal to integer factoring. Our schemes have merits not only in the efficiency aspect, where we do not rely on the bilinear pairing maps or over exponentiations, but also in the security aspect, where we prove them to be secure under a weaker assumption of factoring to achieve stronger security. The contributions for this paper can be summarized as follows.
- We have proposed two efficient IBMS schemes, denoted as IBMSCR−1 and IBMSCR−2, which are suitable for data aggregation among the sensors and collectors in marine WSNs.
- We formally define the security of IBMS and prove IBMSCR−1 to be secure, relying on the cubic residues in a random oracle model. The computational cost of IBMSCR−1 is lower, as the exponentiations are cubic exponentials.
- To enhance efficiency, the total computational cost of IBMSCR−2 is almost four-fifths that of IBMSCR−1 in implementation. We also prove the security of IBMSCR−2 on the basis of the cubic residues equalling integer factoring in the random oracle model.
The organization of this paper is as follows. Section 2 gives necessary preliminaries, and Section 3 gives the formal definition of the security model. In Section 4 and Section 5, we propose two concrete IBMS schemes, IBMSCR−1 and IBMSCR−2, as well as outline their correctness and full security proof. Section 6 gives the performance comparison. Section 7 gives the conclusion for the paper.
2. Preliminaries
Some fundamental concepts are introduced simply, for further explaining the construction and security proof.
2.1. Cubic Residue
We first introduce the definition of the cubic residue.
Definition 1
(Cubic residue [23]). For an integer , a cubic residue modulo N, , if for some .
Because the module N is a product for unknown p and q, it is difficult to obtain x from a cubic residue c, that is, the difficulty of obtaining x from c is equal to the factorization of N.
2.2. Cubic Residue Symbol in Eisenstein Ring
Following the work in [23,30,31], we let denote a complex root of , which means that is a cubic root of 1. We also have , where is the conjugate complex of . The Eisenstein ring is defined as the set . We introduce the cubic residue symbol as follows:
For a prime p in where p is not associated to , we have
where is defined as the norm of p.
2.3. Some Useful Theorems
Theorem 1
(Factorization Theorem [23]). Let , where p and q are large primes. Let c be a cubic residue modulo N, and and be c’s two cubic roots modulo N; that is, and . N can be factored by taking in polynomial time, where is the greatest common divisor of x and y.
Theorem 1 is easily validated, as if , we have . There must exist an integer k such that . If , cannot be a multiple of N at the same time; must contain a non-trivial divisor of N, which is p or q. Therefore, the integer N can be factored by Theorem 1. However, the two cubic roots satisfying cannot lead directly to factoring the integer N.
The following theorem shows a solution to compute a -th root of a cubic residue without factoring N.
Theorem 2.
Let , , c be a cubic residue modulo N, and satisfy
Then we can easily calculate the cubic root y; that is, .
Because , we can denote ; following this,
We take the -th root and obtain
Because , we have
Let ; then we have
Theorem 2 can be used in the security proof for IBMSCR−1. We introduce the following Theorem [24,29] regarding the cubic residue used in the security proof for IBMSCR−2.
Theorem 3
(Cubic residue construction [24,29]). If p and q are two primes with and or , it is easy to produce a cubic residue modulo N. Let be a non-cubic modulo q, for any ; we can compute that , , , , and
We can construct a cubic residue C modulo N; that is, .
Theorem 4.
Let p, q, N, C, and η be defined as in Theorem 3; we can calculate a cubic root s of by Note that .
3. Formal Definition and Security Model
3.1. Formal Definition
We assume that there exist n distinct signers, named , to authenticate a message m by cooperatively generating a multi-signature . The signer is denoted as .
Theorem 5.
A typical IBMS scheme is always made up of six algorithms, that is, Setup, Extra, Sign, Verify, MSign, and MVerify. We describe each of them as follows.
- Setup: Setup(1). The algorithm is controlled by the key generator center (KGC). The KGC generates the system’s master public keys mpk and master secret keys msk when it is given the security parameter k.
- Extra: Extra (mpk, msk, ID). The algorithm is also controlled by the KGC, given msk, mpk, and a user’s identity ID, such as a string. It returns the private key through secure channels.
- Sign: Sign (mpk, sk, m, ID): The signer uses its private key sk, the identity ID, and the message to be signed m to generate a signature σ on m.
- Verify: Verify (mpk, ID, m, σ): The algorithm takes the signer’s identity ID, the data m, and a candidate signature σ. If σ is a valid signature, it returns 1. Otherwise, it returns 0.
- MSign: MSign (mpk, sk, m, IDSet). The signer with the private sk joins in the multi-signing algorithm, which needs additional parameters, including a message m and an identity set containing all the identities of the signers. After several rounds of interactive communication, MSign generates a multi-signature mσ.
- MVerify: MVerify (mpk, IDSet, m, mσ). The algorithm returns 1 if mσ is a valid multi-signature on the message m by authenticating the signers in IDSet.
Correctness. When all of the participating signers honestly and correctly execute the algorithm MSign using the private keys, derived from the algorithm Extra, each of the signers will end the algorithm by obtaining a local multi-signature such that
where all and are generated by the algorithm Setup and includes n identities for any messages .
3.2. Security Model
This considers an extreme case: the adversary compromising the participants and leaving only one honest user, denoted . The user is controlled by the challenger . When the game starts, gives the honest identity of and allows to compromise the other signers’ private keys. It also assume that a secure channel between the signers is not guaranteed. All of the communication among the signers can be eavesdropped upon. provides a hash oracle, a key extraction oracle and a multi-sign oracle. ’s final target is to successfully forge a multi-signature.
Definition 2.
Considering the games between and .
- Setup: executes the algorithm to generate the master public keys mpk and sends mpk to .
- Query: : is allowed to query to in an adaptive way.
- -
- Extraction-query (mpk, ID). executes Extra to obtain and sends to when asks for the private key of .
- -
- Multi-signature query (mpk, m, IDSet) obtains a multi-signature and sends to when asks for the multi-signature on m and .
- -
- Hash-query. chooses the returned values by itself and sends to when asks.
- Forgery. makes a multi-signature as a forgery, that is, on for , which contains at least one uncompromised user’s identity; meanwhile, never sends to the multi-signature query.
Definition 3 (Attack Goals).
The advantage in breaking the problems is defined as
Definition 4 (Unforgeability).
An adversary breaks the scheme if executes for a time of t at most, and makes at most hash queries, extraction queries, and multi-signature queries with n participants, and is at least ϵ. An IBMS scheme has unforgeability if there exists no attacker that breaks it.
4. Concrete Construction of IBMSCR-1
4.1. Construction
Inspired by the previous work [6,22,23], we propose a concrete identity-based multi-signature scheme (IBMSCR−1) with three-round interactive communications among the marine sensors and the generation of a single multi-signature as an authenticated tag.
- Setup : The key generator center inputs security parameters k and ℓ, and then:
- Chooses two random primes p and q, such that and . Without loss of generality, we assume that , .
- Chooses two random primes and from the Eisenstein ring , s.t. the norms satisfy and .
- Computes . We let , , and then compute . Note that , and .
- Chooses a random number such that .
- Computes .
- Selects three hash functions , , and such that , and .
As a result of the step Setup, the master secret key is , which is securely stored, and the public parameter is .
- Extra (mpk, msk, ID): KGC inputs the identity , computes the hash value of as and obtains a first symbol such thatWe let and we have . Following this, KGC computes a second symbol such thatWe let . It is easy to find that , as Finally, KGC extracts the private key as a -th root of :KGC sends as well as () to signer secretly. Note that . Following this, we denote .
- Sign and verify: These two algorithms can be derived from [23].
- MSign : For simplicity, IBMSCR−1 is described from the ’s point of view. Given the ’s private key , the message m and the identity set , executes the following algorithm from Algorithm 1. MSign generates as the multi-signature.
- MVerify (mpk, IDSet, m, mσ). The algorithm verifies by the following three steps.
- (1)
- For , it computes .
- (2)
- It computes .
- (3)
- It checks whetheris satisfied. If Equation (2) is satisfied, MVerify returns 1. This means is valid. Otherwise MVerify returns 0.
4.2. Correctness
The correctness follows:
We have .
| Algorithm 1: The MSign Algorithm in IBMS CR−1. |
| Input: the master public key , the private key , the identity set , the message to be signed m; Output: a multi-signature . 1. Each randomly selects and computes and . 2. only broadcasts to other signers () in and keeps temporarily. 3. After receiving from (), then broadcasts to other . 4. After receiving from , checks whether for is satisfied. 5. If one of these fails, the algorithm stops, which means the attackers have mixed invalid partial signatures. Otherwise, sets , , and . 6. broadcasts to other . 7. After receiving from , aggregates these by . 8. Each locally generates a multi-signature . Return ; |
4.3. Security Proof
IBMSCR−1 is provably secure under the factorization in the random oracle model.
Theorem 6.
If the factorization problem is -hard, IBMSCR−1 is -secure against existential forgery attackers under the adaptively chosen message attack and chosen identity attack. We have estimates for and as follows:
Proof.
We assume is given a factorization instance N for a product of unknown p and q, and obtain the result of p or q with a non-negligible probability. plays with as follows.
Firstly, selects , such as a non-cubic residue and a secure parameter (the length of ℓ has been discussed and suggested in [22]), and sends to as . manages several lists: one signature list and three hash lists.
Then, starts to answer according to ’s queries, as follows.
- -Query : manages a list . When requests the identity , answers as . in two bits and is used as a secret key. When asks on , answers if has existed in the -list. Otherwise, randomly selects and , calculatesand returns the answer to , adding to the -list.
- -Query : manages a list . When asks on R, answers if R has existed in the -list. Otherwise, randomly selects , adds into the -list and returns .
- -Query : manages a list . When asks on , returns if has existed in the -list. Otherwise, randomly selects , returns , and adds to the -list.
- Extraction query : executes an additional -query if does not yet exist in the -list and returns s and .
- Multi-signature queries: checks in the -list for whether exists. If is already in the -list, has obtained the private key of and simulates the game as the real algorithm MSign using the secret key . Otherwise, does not have the private key of and executes the following steps:
- -
- plays as , and randomly chooses , broadcasting to other signers. also waits to receive from others; it randomly selects and , and calculatesIf already exists in the -list, stops. Otherwise, sets in the -list. looks up such that where . If for some i the record is found, also stops. Otherwise, calculates and sets , or stops if the entry has already existed.
- -
- sends to other signers. After receiving from the signers, verifies that . ends up with the protocol if one of these does not satisfy this, which means has to guess the results of the hash value. If for some i, stops. sends to the signers, receives , and calculates . Finally, sends to .
At the end of the game, generates a multi-signature on message . calculates
and makes an additional query . We let denote the honest IDSet, that is, never compromised. If succeeded in forgery, that is,
- MVerify
- has never queried to the signature oracle then checks the -list. If the multi-signature is valid, we can obtain
We let and produce .
To factor N by applying the rewinding technique, plays with once again using the random tapes, which are the same as for the first time. Because previously recorded the transcripts, obtains the same results for ’s queries.
When queries for , randomly selects an alternative answer instead of w, as, in the second run, the - and -query are equal to those of the first round.
generates and such that
By , and , we have
Because and , we can obtain . According to Theorem 2, can calculate a cubic root where . Meanwhile, checks the -list to search for an entry in which and calculates .
Therefore, . If , N can be factored by Theorem 1. Otherwise, cannot factor N. The probability that is 2/3.
Finally, we calculate the probability that returns a valid result. Because most of the simulation game is similar to in [6], we set , and as the probability to factor N by , the probability to forge a multi-signature in practice by and the probability to succeed in the first run before the rewinding technique by , respectively.
We have
Furthermore, according to the forking lemma [32], we can easily obtain
The probability that succeeds to factor N is
☐
5. Concrete Construction of IBMSCR−2
Inspired by the related work [24,26,29], we give a more efficient IBMS construction (named IBMSCR−2), whose computational overhead in MSign and MVerify is much lower than for those in IBMSCR−1.
5.1. Construction
- Setup : Given the security parameters, Setup can be executed as follows.
- (1)
- KGC chooses random primes p and q where and or , and calculates the product .
- (2)
- A non-cubic residue a is selected such that .
- (3)
- Several computational parameters are computed:
- (4)
- Three hash functions and are picked up, where :, :.
Finally, the algorithm Setup outputs and . KGC keeps secretly.
- Extra ): KGC computes as follows:
- (1)
- KGC computes and set sa symbol according to and :KGC denotes .
- (2)
- KGC calculatesand securely distributes to the signer. We have . Following this, we denote the identity by .
- Sign and verify: These two algorithms can be derived from [29].
- MSign : Given the ’s private key , the message m and the identity set , executes the following algorithm in Algorithm 2. MSign generates the multi-signature .
- MVerify . The algorithm verifies by the following three steps:
- (1)
- For , it computes .
- (2)
- It computes .
- (3)
- It checks whetheris satisfied. If Equation (13) is satisfied, MVerify returns 1. This means is valid. Otherwise MVerify returns 0.
| Algorithm 2: The MSign algorithm in IBMSCR−2. |
| Input: the master public key , the private key , the identity set , the message to be signed m; Output: a multi-signature . 1. Each randomly selects and calculates and . 2. Each broadcasts to co-signers (). 3. After obtaining from , broadcasts to other . 4. After receiving from other signers, checks whether for is satisfied. 5. If one of these fails, the algorithm stops, which means the attackers have mixed invalid partial signatures. Otherwise, sets , , and . 6. broadcasts to other . 7. After receiving from , aggregates these by . 8. Each locally generates a multi-signature . Return ; |
5.2. Correctness
The correctness is as follows:
5.3. Security Proof
IBMSCR−2 is secure under the factorization in the random oracle model.
Theorem 7.
If integer factorization is -hard, our IBMSCR−2 scheme is -secure against existential forgery in the random oracle model.
Because most of the simulation game between and is the same, we give the security proof simply.
Proof.
When it is given an integer factorization instance N, returns p or q if succeeds in forging a multi-signature.
sends to . maintains several lists (, , , ).
- -Query. manages a list . sends to if exists when queries the hash value of . Otherwise, randomly selects and , sets , returns , and adds to .
- The -query, -query and extraction query are similar to IBMSCR−1.
- The multi-signature query is similar to IBMSCR−1, except that Equation (5) changes to
At the end of the game, forges with on . calculates
and queries to the hash oracle. If the forgery is valid, we obtain that
because . returns .
We also apply the rewinding technique to factor N. At last, obtains and such that
Because , , and , we have
Because , two cases emerge:
- If , we denote for an integer k. Therefore, , that is, satisfies .
- If , we denote for an integer k. Therefore, , that is, satisfies .
From the discussion above, calculates a cubic root where . Meanwhile searches the entries in the -list where and calculates . Therefore, we have . If , we can factor N by Theorem 1 with a probability that of 2/3.
Thus, we have finished the proof. ☐
6. Performance Comparisons
The comparison of security assumptions for related works are given in Table 1. These schemes are provably secure on the basis of different hardness assumptions (such as CDH, DL, RSA, quadratic residues, and cubic residues). The aim of these schemes is to find new constructions under simpler hardness assumptions.

Table 1.
The comparison of related work on the security assumptions.
We denote , , and as the operation of scalar multiplication, map-to-point hash function, bilinear pairing, and modular exponentiation, respectively. We ran each of the above operations in a personal computer and used their times from [33] to calculate the total computational cost in the running time (milliseconds), as shown in the columns of Table 2.

Table 2.
The comparison of related work of IBMS on the computational performance.
We have also compared related works on the basis of the cubic residues for the computational performance evaluation in Table 3. For consistency, we used the modular exponentiation times to evaluate the Sign and Verify algorithms.

Table 3.
The comparison of related work on computational performance based on the cubic residues.
7. Conclusions
Data authenticated aggregation is always a significant issue for marine WSNs. Most data authenticated aggregation is based on the multi-signature, which relies on the technique of bilinear pairing involving heavy computational overhead or the management of certificates beyond marine wireless sensors. We have constructed two efficient IBMS schemes (IBMSCR−1 and IBMSCR−2) based on cubic residues, which are much more suitable for data authenticated aggregation in marine WSNs. Without employing the heavy overload of a bilinear pairing technique, our schemes have been designed efficiently. Our schemes have been proven to be secure under chosen identity attacks and chosen message attacks, relying only on the hardness of the integer factorization assumptions.
Acknowledgments
This work was supported by the Natural Science Foundation of China (NSFC grant nos. 61402282, 61672339 and 41671431), the Shanghai Youth Talent Development Program (grant no. 14YF1410400), and the Shanghai Local University Capacity Enhancement Program (grant no. 15590501900).
Author Contributions
The work was conducted under the cooperation of authors. Lifei Wei conceived the scheme 1, and wrote the partial paper; Lei Zhang conceived the scheme 2 and wrote the partial paper, Dongmei Huang guided the study and reviewed the manuscript; Kai Zhang conceived the security proof and wrote the partial paper; Liang Dai gave the figures and verified the results; Guojian Wu introduced the background of marine sensor networks.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bosman, H.; Iacca, G.; Tejada, A.; Wortche, H.J.; Liotta, A. Spatial anomaly detection in sensor networks using neighborhood information. Inform. Fusion J. 2017, 33, 41–56. [Google Scholar] [CrossRef]
- Bosman, H.; Iacca, G.; Tejada, A.; Wortche, H.J.; Liotta, A. Ensembles of incremental learners to detect anomalies in ad hoc sensor networks. Ad Hoc Netw. 2015, 35, 14–36. [Google Scholar] [CrossRef]
- Ahn, J.; Green, M.; Hohenberger, S. Synchronized aggregate signatures: New definitions, constructions and applications. In Proceedings of the 17th ACM Conference on Computer and Communications Security (CCS 2010), Chicago, IL, USA, 4–8 October 2010. [Google Scholar]
- Wei, L.; Zhang, L.; Huang, D.; Zhang, K. Efficient and Provably Secure Identity-based Multi-Signature Schemes for Data Aggregation in Marine Wireless Sensor Networks. In Proceedings of the 14th IEEE International Conference on Networking, Sensing and Control (ICNSC 2017), Calabria, Italy, 16–18 May 2017. [Google Scholar]
- Huang, D.; Zhao, D.; Wei, L.; Wang, Z.; Du, Y. Modeling and analysis in marine big data: Advances and challenges. Math. Probl. Eng. 2015, 2015, 1–13. [Google Scholar] [CrossRef]
- Wei, L.; Cao, Z.; Dong, X. Secure identity-based multisignature schemes under quadratic residue assumptions. Secur. Commun. Netw. 2013, 6, 689–701. [Google Scholar] [CrossRef]
- Hsiao, H.; Studer, A.; Chen, C.; Perrig, A.; Bai, F.; Bellur, B.; Iyer, A. Flooding-resilient broadcast authentication for vanets. In Proceedings of the 17th Annual International Conference on Mobile Computing and Networking (MOBICOM 2011), Las Vegas, NV, USA, 20–22 September 2011. [Google Scholar]
- Itakura, K.; Nakamura, K. A public-key cryptosystem suitable for digital multisignatures. NEC Res. Dev. 1983, 71, 1–8. [Google Scholar]
- Barr, K.C.; Asanovic, K. Energy-aware lossless data compression. ACM Trans. Comput. Syst. 2006, 24, 250–291. [Google Scholar] [CrossRef]
- Bagherzandi, A.; Cheon, J.; Jarecki, S. Multisignatures secure under the discrete logarithm assumption and a generalized forking lemma. In Proceedings of the 15th ACM Conference on Computer and Communications Security (CCS 2008), Alexandria, VA, USA, 27–31 October 2008. [Google Scholar]
- Ma, C.; Weng, J.; Li, Y.; Deng, R. Efficient discrete logarithm based multi-signature scheme in the plain public key model. Des. Codes Cryptogr. 2010, 54, 121–133. [Google Scholar] [CrossRef]
- Shamir, A. Identity-based cryptosystems and signature schemes. In Proceedings of the 4th International Cryptology Conference (CRYPTO 1984), Santa Barbara, CA, USA, 19–22 August 1984. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-based encryption from the Weil pairing. SIAM J. Comput. 2003, 32, 586–615. [Google Scholar]
- Cocks, C. An Identity Based Encryption Scheme Based on Quadratic Residues. In Proceedings of the 8th IMA International Conference on Cryptography and Coding, Cirencester, UK, 17–19 December 2001. [Google Scholar]
- Gentry, C.; Ramzan, Z. Identity-based aggregate signatures. In Proceedings of the 9th International Conference on Theory and Practice of Public-Key Cryptography (PKC 2006), New York, NY, USA, 24–26 April 2006. [Google Scholar]
- Lu, R.; Lin, X.; Zhu, H.; Liang, X.; Shen, X. BECAN: A Bandwidth-Efficient Cooperative Authentication Scheme for Filtering Injected False Data in Wireless Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 32–43. [Google Scholar]
- Zhang, K.; Wei, L.; Li, X.; Qian, H. Provably Secure Dual-Mode Publicly Verifiable Computation Protocol in Marine Wireless Sensor Networks. In Proceedings of the 10th International Conference on Wireless Algorithms, Systems, and Applications (WASA 2017), Guilin, China, 19–21 June 2017. [Google Scholar]
- Lu, Y.; Li, J. A Pairing-Free Certificate-Based Proxy Re-encryption Scheme for Secure Data Sharing in Public Clouds. Future Gener. Comput. Syst. 2016, 62, 140–147. [Google Scholar] [CrossRef]
- Bellare, M.; Neven, G. Identity-Based Multi-signatures from RSA. In Proceedings of the Cryptographers Track at the RSA Conference (CT-RSA 2007), San Francisco, CA, USA, 5–9 February 2007. [Google Scholar]
- Bagherzandi, A.; Jarecki, S. Identity-Based Aggregate and Multi-Signature Schemes Based on RSA. In Proceedings of the 13th International Conference on Practice and Theory in Public Key Cryptography (PKC 2010), Paris, France, 26–28 May 2010; pp. 480–498. [Google Scholar]
- Yang, F.; Lo, J.; Liao, C. Improving an efficient id-based rsa multisignature. J. Ambient Intell. Hum. Comput. 2011, 4, 249–254. [Google Scholar] [CrossRef]
- Chai, Z.; Cao, Z.; Dong, X. Identity-based signature scheme based on quadratic residues. Sci. China Inform. Sci. 2007, 50, 373–380. [Google Scholar] [CrossRef]
- Xing, D.; Cao, Z.; Dong, X. Identity based signature scheme based on cubic residues. Sci. China Inform. Sci. 2011, 54, 2001–2012. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Zheng, S.; Yang, Y.; Hu, Z. Provably secure and efficient identity-based signature scheme based on cubic residues. Int. J. Netw. Secur. 2012, 14, 33–38. [Google Scholar]
- Wang, F.; Lin, C. Secure and efficient identity-based proxy multisignature using cubic residues. J. Univ. Electr. Sci. Technol. China 2013, 42, 778–783. [Google Scholar]
- Wang, F.; Chang, C.-C.; Lin, C.; Chang, S.-C. Secure and efficient identity-based proxy multi-signature using cubic residues. Int. J. Netw. Secur. 2016, 18, 90–98. [Google Scholar]
- Wang, F.; Lin, C.; Lian, G. Efficient identtiy based threshold ring signature based on cubic residues. J. Wuhan Univ. (Nat. Sci.) 2013, 59, 75–81. [Google Scholar]
- Wei, L.; Zhang, L.; Zhang, K.; Dong, M. An Efficient and Secure Delegated Multi-Authentication Protocol for Mobile Data Owners in Cloud. In Proceedings of the 10th International Conference on Wireless Algorithms, Systems, and Applications (WASA15), Qufu, China, 10–12 August 2015. [Google Scholar]
- Zhang, L.; Wei, L.; Huang, D.; Zhang, K.; Dong, M.; Ota, K. Medaps: Secure multi-entities delegated authentication protocols for mobile cloud computing. Secur. Commun. Netw. 2016, 9, 3777–3789. [Google Scholar] [CrossRef]
- Damgard, I.; Frandsen, G. Efficient algorithms for gcd and cubic residuosity in the ring of Eisenstein integers. J. Symb. Comput. 2005, 39, 643–652. [Google Scholar] [CrossRef]
- Benhamouda, F.; Herranz, J.; Joye, M.; Libert, B. Efficient cryptosystems from 2k. J. Cryptol. 2016, 1–31. [Google Scholar]
- Coron, J. On the exact security of full domain hash. In Proceedings of the 20th Annual International Cryptology Conference (CRYPTO 2000), Santa Barbara, CA, USA, 20–24 August 2000. [Google Scholar]
- He, D.; Chen, J.; Zhang, R. An efficient and provably-secure certificateless signature scheme without bilinear pairings. Int. J. Commun. Syst. 2012, 25, 1432–1442. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).