Joint Resource Optimization for Cognitive Sensor Networks with SWIPT-Enabled Relay
Abstract
:1. Introduction
- Firstly, we derive the transmission rate expression of AF CSNs with energy harvesting relay by considering the interference caused by the relay sensor node, which was ignored in [18].
- Secondly, an algorithm is proposed to obtain the closed-form optimal value of transmit power and power splitting ratio—unlike [17], in which the optimal energy harvesting duration was derived through the simulation.
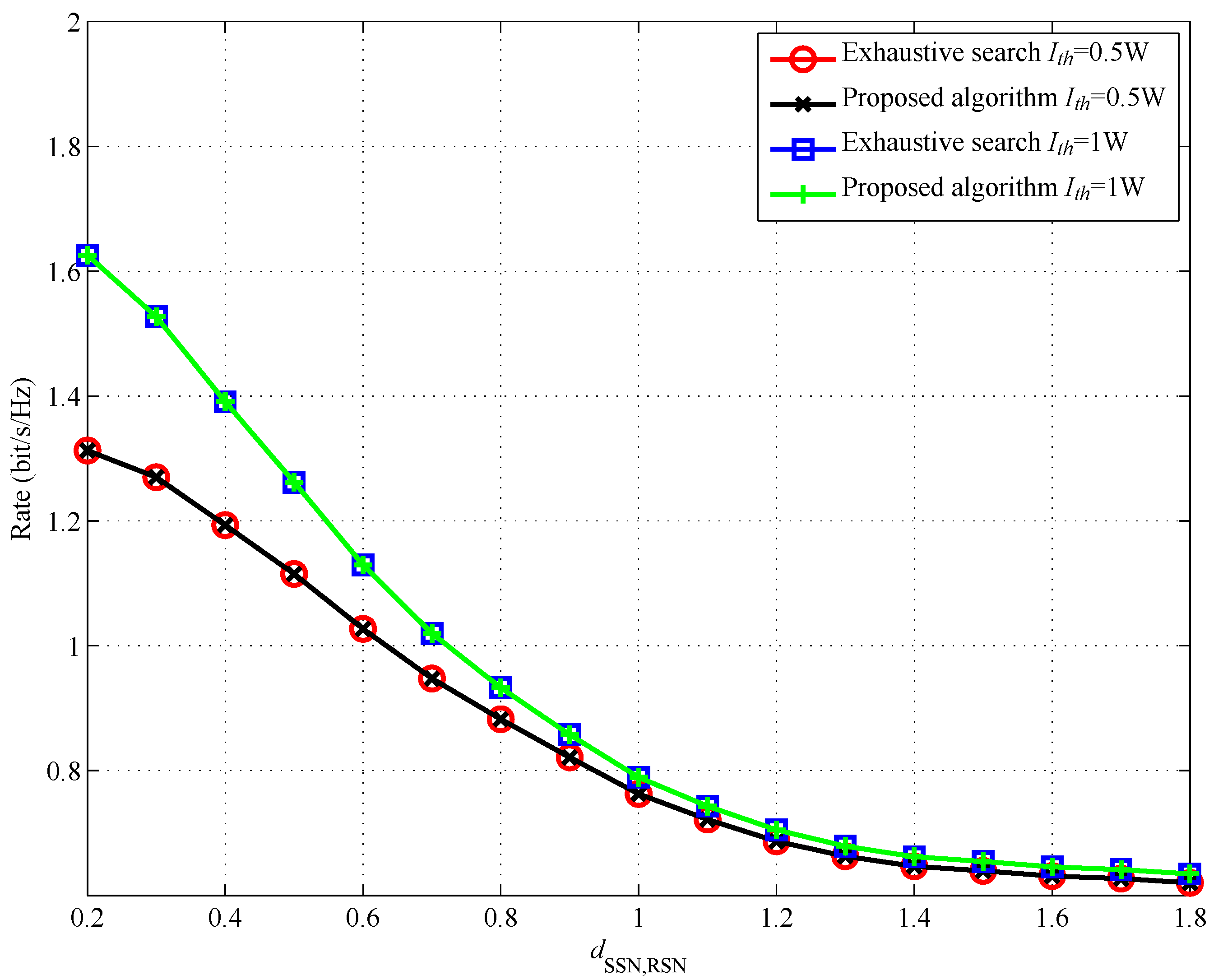
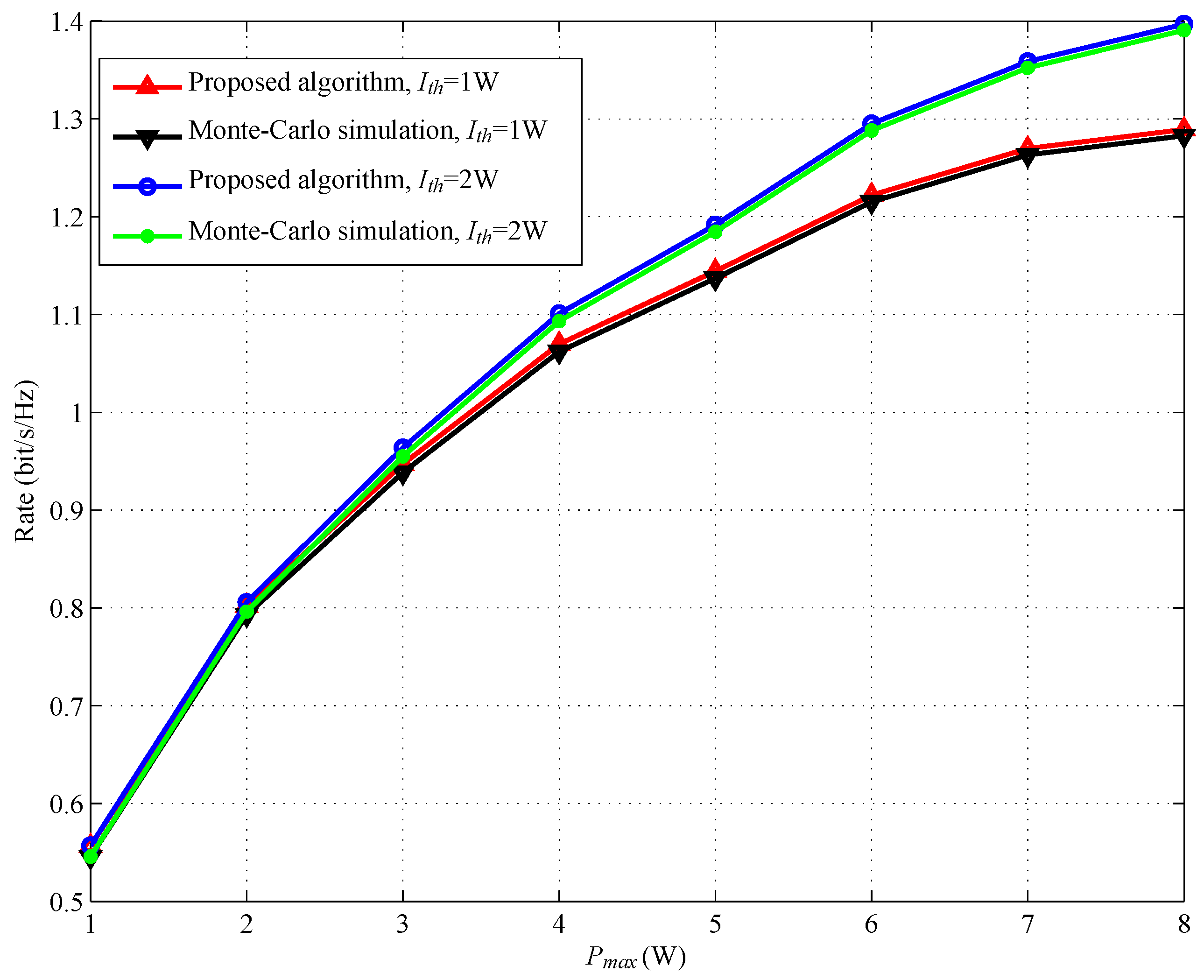
- Finally, we show that there is no performance gap between our proposed algorithm and exhaustive search method.
2. System Model and Problem Formulation
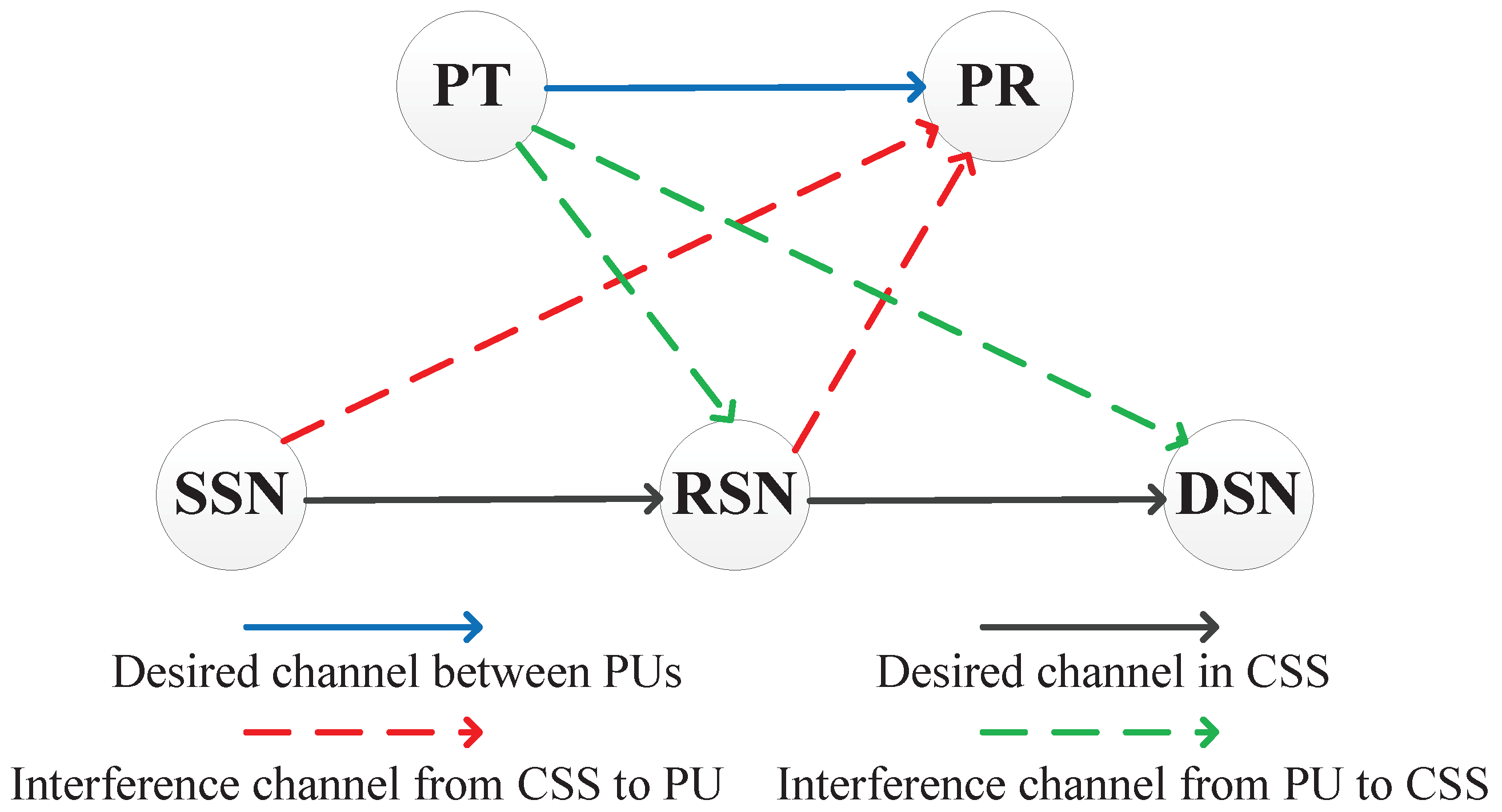
2.1. System Model
2.2. Problem Formulation
3. Joint Optimization of Transmit Power and Power Allocation Ratio
3.1. Finding the with Fixed
3.2. Finding
| Algorithm 1 Proposed Algorithm for Joint Optimization Problem. | ||||
| 1. | if | |||
| 2. | if then | |||
| 3. | and | |||
| 4. | else | |||
| 5. | if or then | |||
| 6. | and substituting into obtains the optimal value of | |||
| 7. | else | |||
| 8. | and substituting into obtains the optimal value of | |||
| 9. | end if | |||
| 10. | end if | |||
| 11. | else | |||
| 12. | if then | |||
| 13. | and | |||
| 14. | else | |||
| 15. | if or then | |||
| 16. | and substituting into obtains the optimal value of | |||
| 17. | else | |||
| 18. | and substituting into obtains the optimal value of | |||
| 19. | end if | |||
| 20. | end if | |||
| 21. | end if | |||
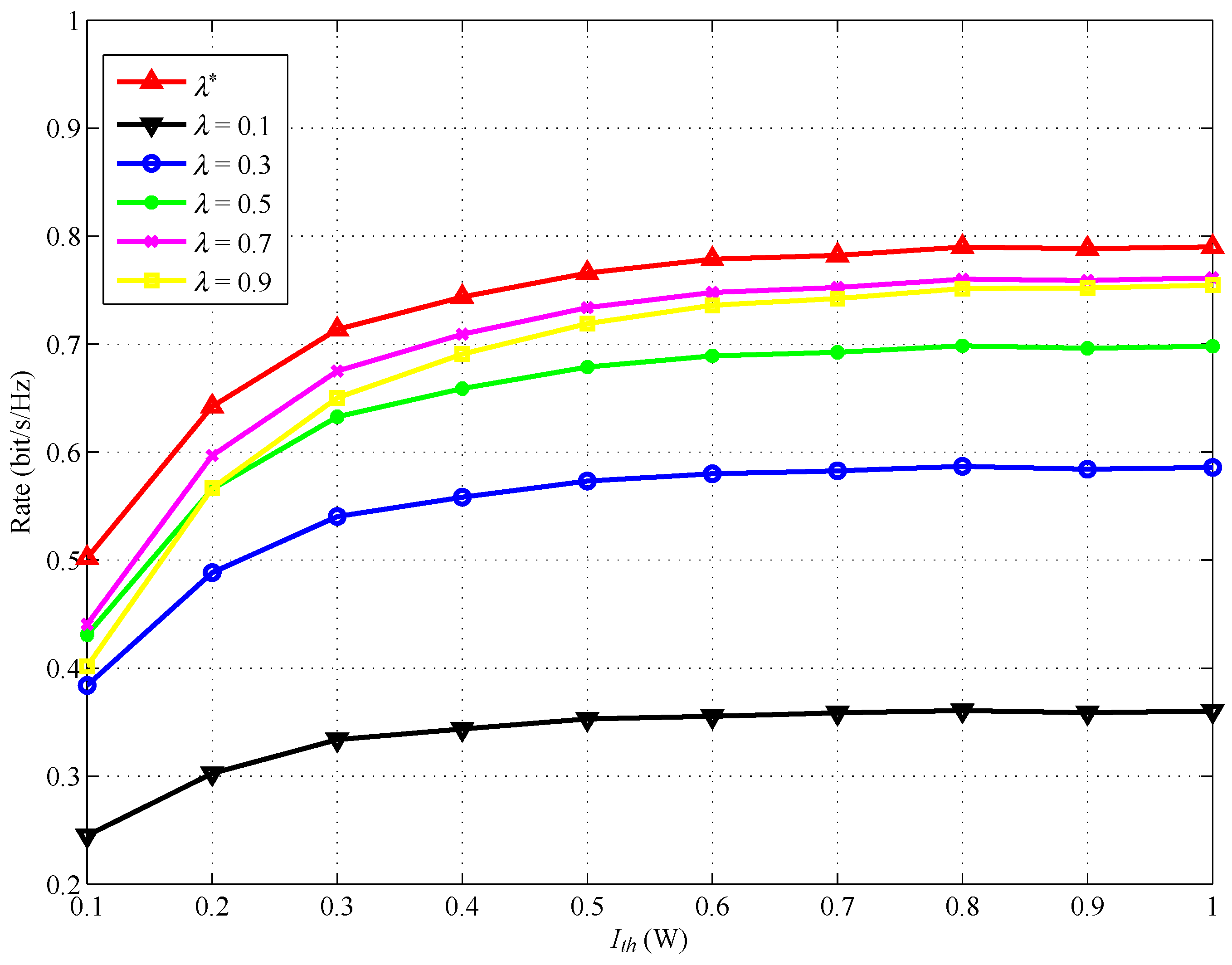
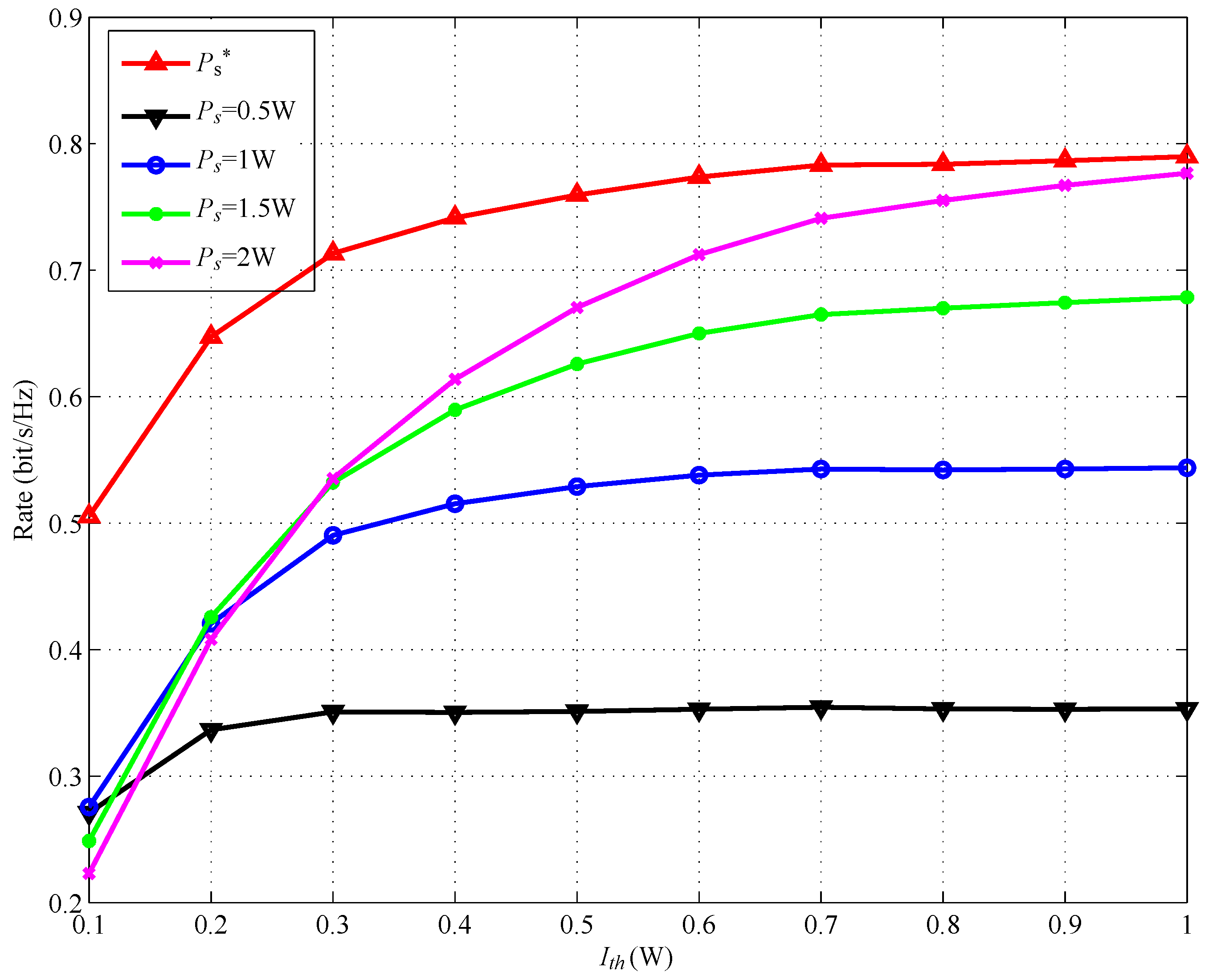
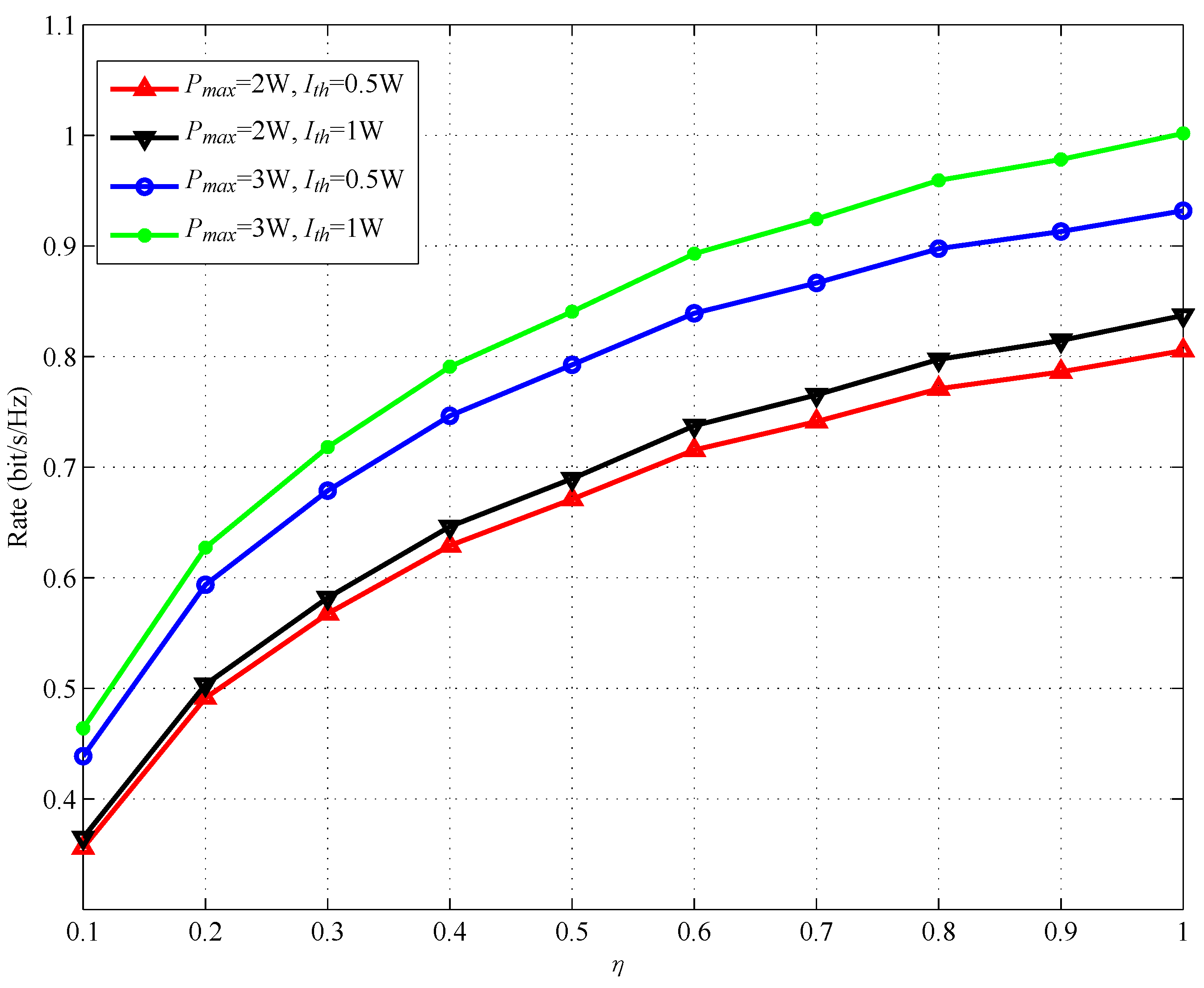
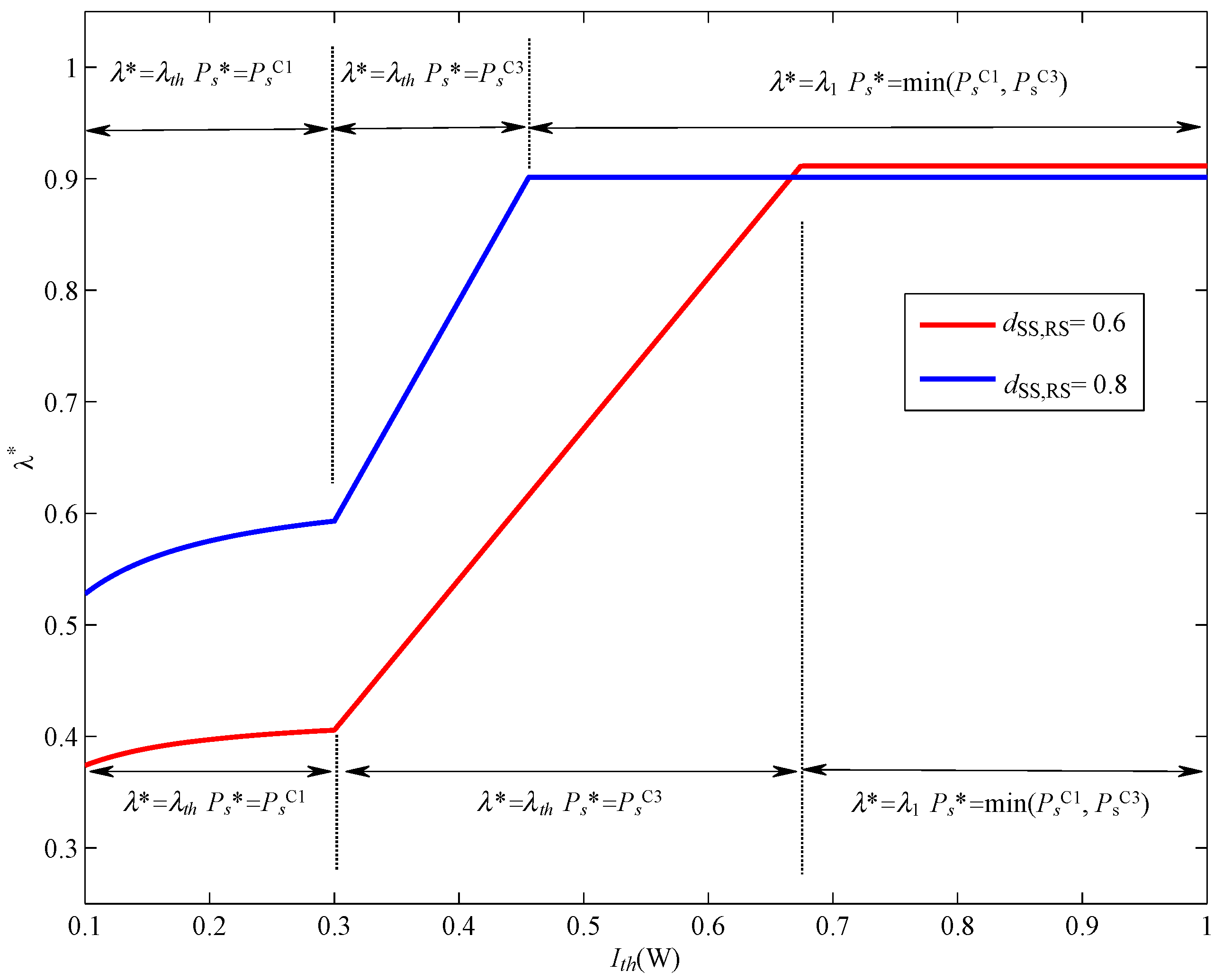
4. Simulation Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, Y.; Mousavifar, S.A.; Deng, Y.; Leung, C.; Elkashlan, M. Wireless energy harvesting in a cognitive relay network. IEEE Trans. Wirel. Commun. 2016, 15, 2498–2508. [Google Scholar] [CrossRef]
- Akan, O.B.; Karli, O.B.; Ergul, O. Cognitive radio sensor networks. IEEE Netw. 2009, 23, 34–40. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, Z.; Ren, J.; Ning, Z.; Awad, K.M.; Zhou, H.; Shen, X. Energy harvesting-aided spectrum sensing and data transmission in heterogeneous cognitive radio sensor network. IEEE Trans. Veh. Technol. 2017, 66, 831–843. [Google Scholar] [CrossRef]
- Sudevalayam, S.; Kulkarni, P. Energy harvesting sensor nqodes: survey and implications. IEEE Commun. Surv. Tutor. 2011, 13, 443–461. [Google Scholar] [CrossRef]
- Ho, C.K.; Zhang, R. Optimal energy allocation for wireless communications with energy harvesting constraints. IEEE Trans. Signal Process. 2012, 60, 4808–4818. [Google Scholar] [CrossRef]
- Chalasani, S.; Conrad, J. A survey of energy harvesting sources for embedded systems. In Proceedings of the IEEE SoutheastCon, Huntsville, AL, USA, 3–6 April 2008; pp. 442–447. [Google Scholar]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless networks with RF energy harvesting: A contemporary survey. IEEE Commun. Surv. Tutor. 2015, 17, 757–789. [Google Scholar] [CrossRef]
- Varshney, L.R. Transporting information and energy simultaneously. In Proceedings of the Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1612–1616. [Google Scholar]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless information and power transfer: architecture design and rate-energy tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, R.; Chua, K.C. Wireless information transfer with opportunistic energy harvesting. IEEE Trans. Wirel. Commun. 2013, 12, 288–300. [Google Scholar] [CrossRef]
- Lee, S.; Huang, K.; Zhang, R. Cognitive energy harvesting and transmission from a network perspective. In Proceedings of the 2012 IEEE Communication Systems, Singapore, 21–23 November 2012; pp. 225–229. [Google Scholar]
- Guo, S.; Wang, F.; Yang, Y.; Xiao, B. Energy-efficient cooperative for simultaneous wireless information and power transfer in clustered wireless sensor networks. IEEE Trans. Commun. 2015, 63, 4405–4417. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying protocols for wireless energy harvesting and information processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Ding, Z.G.; Esnaola, I.; Sharif, B.; Poor, H.V. Wireless information and power transfer in cooperative networks with spatially random relays. IEEE Trans. Wirel. Commun. 2014, 13, 4400–4453. [Google Scholar] [CrossRef]
- Mousavifar, S.A.; Liu, Y.; Leung, C.; Elkashlan, M.; Duong, T.Q. Wireless energy harvesting and spectrum sharing in cognitive radio. In Proceedings of the IEEE 80th Vehicular Technology Conference, Vancouver, BC, Canada, 14–17 September 2014; pp. 1–5. [Google Scholar]
- Lu, X.; Xu, W.; Li, S.; Liu, Z.; Lin, J. Simultaneous wireless information and power transfer for cognitive two-way relaying networks. In Proceedings of the Personal, Indoor, and Mobile Radio Communication (PIMRC), Washington, DC, USA, 2–5 September 2014; pp. 748–752. [Google Scholar]
- Im, G.; Lee, J.H. Outage probability of underlay cognitive radio networks with SWIPT-enabled relay. In Proceedings of the IEEE 82nd Vehicular Technology Conference, Boston, MA, USA, 6–9 September 2015; pp. 1–5. [Google Scholar]
- Singh, S.; Modem, S.; Prakriya, S. Optimization of cognitive two-way networks with energy harvesting relays. IEEE Commun. Lett. 2017, 21, 1381–1384. [Google Scholar] [CrossRef]
- Ju, M.; Kim, I.M. Relay selection with ANC and TDBC protocols in bidirectional relay networks. IEEE Trans. Commun. 2010, 58, 3500–3511. [Google Scholar] [CrossRef]

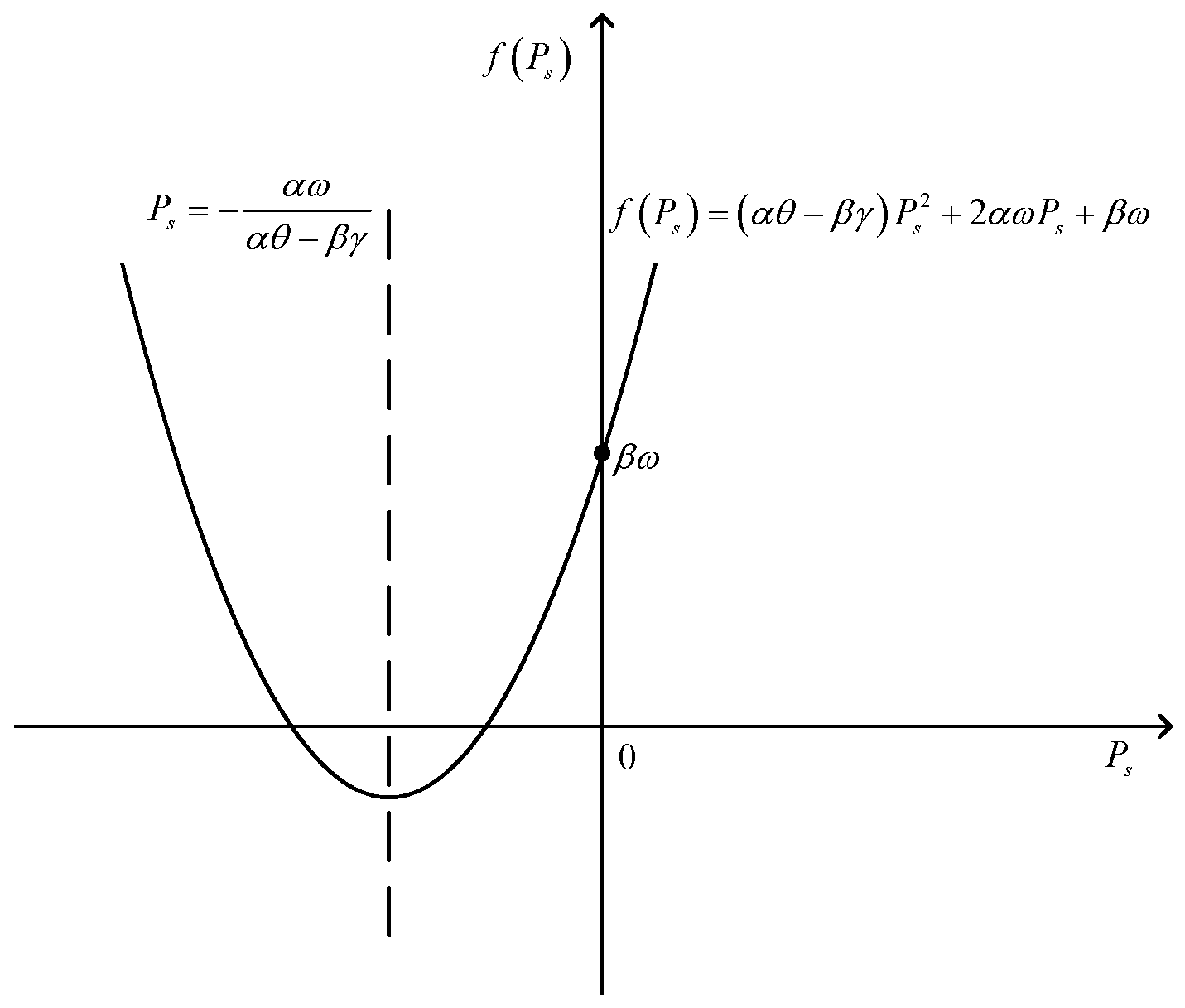
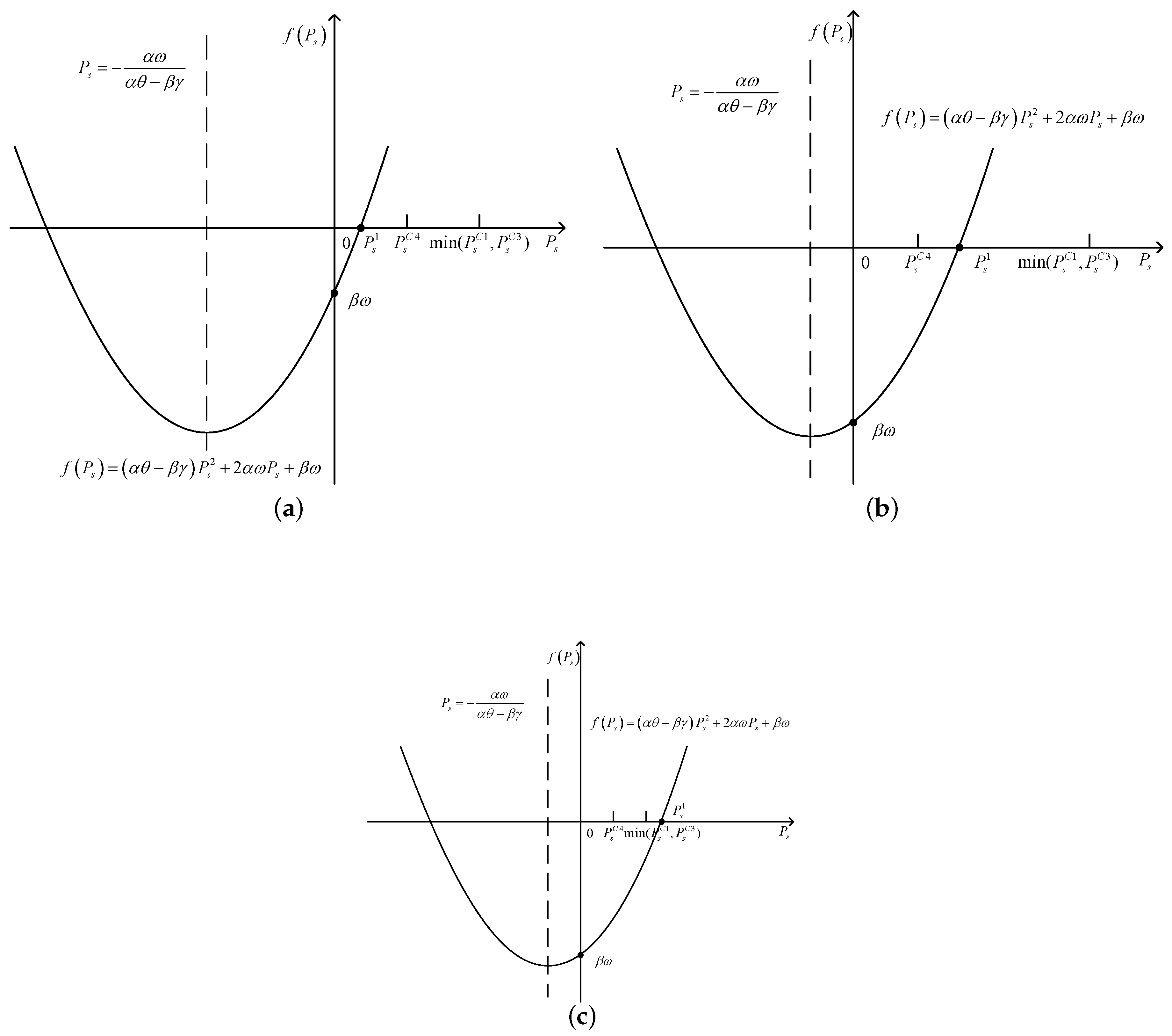

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Lin, Y.; Peng, H.; Nan, T.; Liu, X. Joint Resource Optimization for Cognitive Sensor Networks with SWIPT-Enabled Relay. Sensors 2017, 17, 2093. https://doi.org/10.3390/s17092093
Lu W, Lin Y, Peng H, Nan T, Liu X. Joint Resource Optimization for Cognitive Sensor Networks with SWIPT-Enabled Relay. Sensors. 2017; 17(9):2093. https://doi.org/10.3390/s17092093
Chicago/Turabian StyleLu, Weidang, Yuanrong Lin, Hong Peng, Tian Nan, and Xin Liu. 2017. "Joint Resource Optimization for Cognitive Sensor Networks with SWIPT-Enabled Relay" Sensors 17, no. 9: 2093. https://doi.org/10.3390/s17092093
APA StyleLu, W., Lin, Y., Peng, H., Nan, T., & Liu, X. (2017). Joint Resource Optimization for Cognitive Sensor Networks with SWIPT-Enabled Relay. Sensors, 17(9), 2093. https://doi.org/10.3390/s17092093





