Real-Time Two-Dimensional Magnetic Particle Imaging for Electromagnetic Navigation in Targeted Drug Delivery
Abstract
:1. Introduction
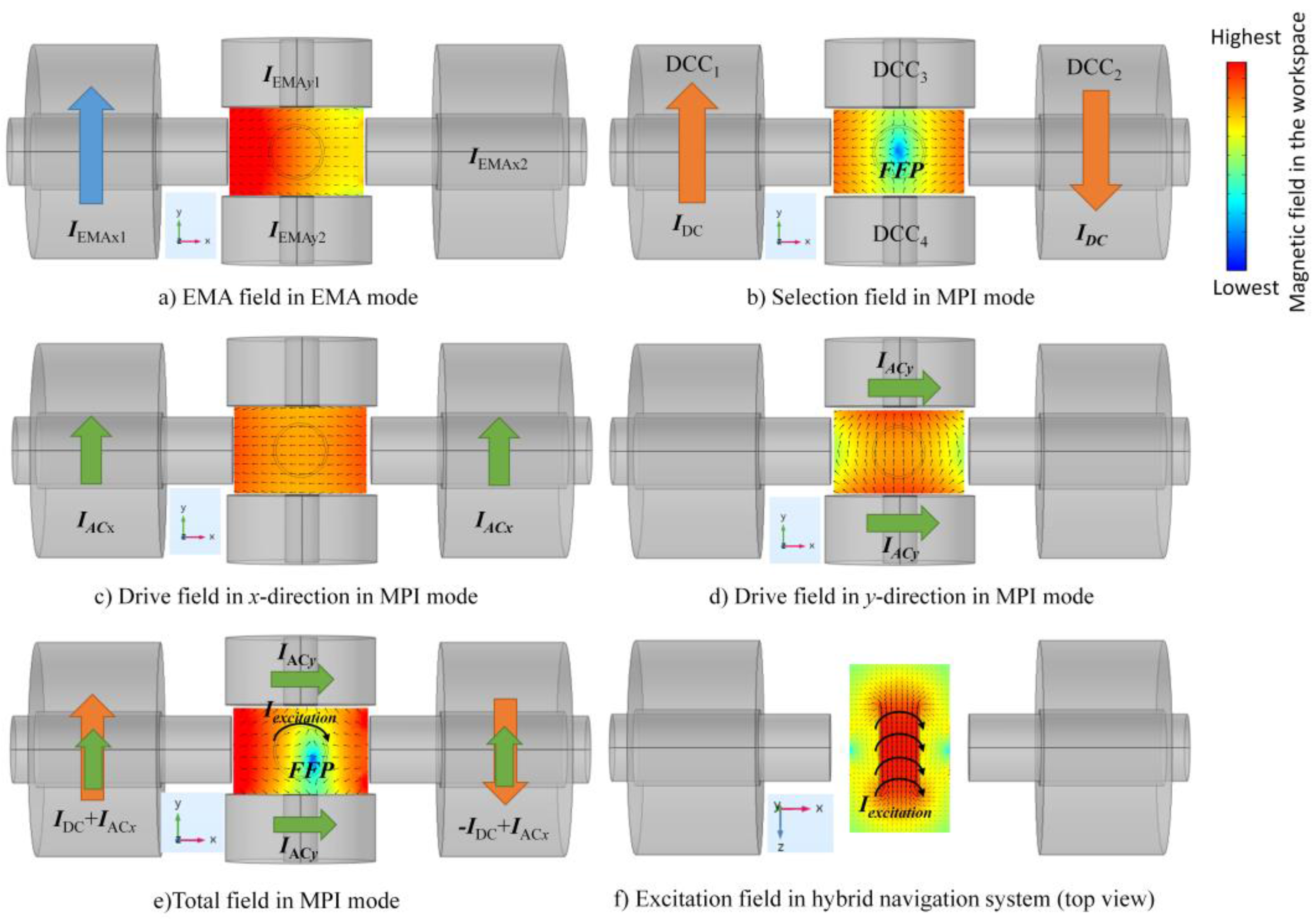
2. Two-Dimensional MNP Navigation System
3. Two-Dimensional AM MPI Signal and Image Reconstruction
3.1. Generation of an FFP and Its Movement in the FOV
3.2. Low-Amplitude, High-Frequency Excitation Field
3.3. Total Magnetic Field
3.4. Magnetization of Particles
3.5. Signal Produced by 2D AM MPI
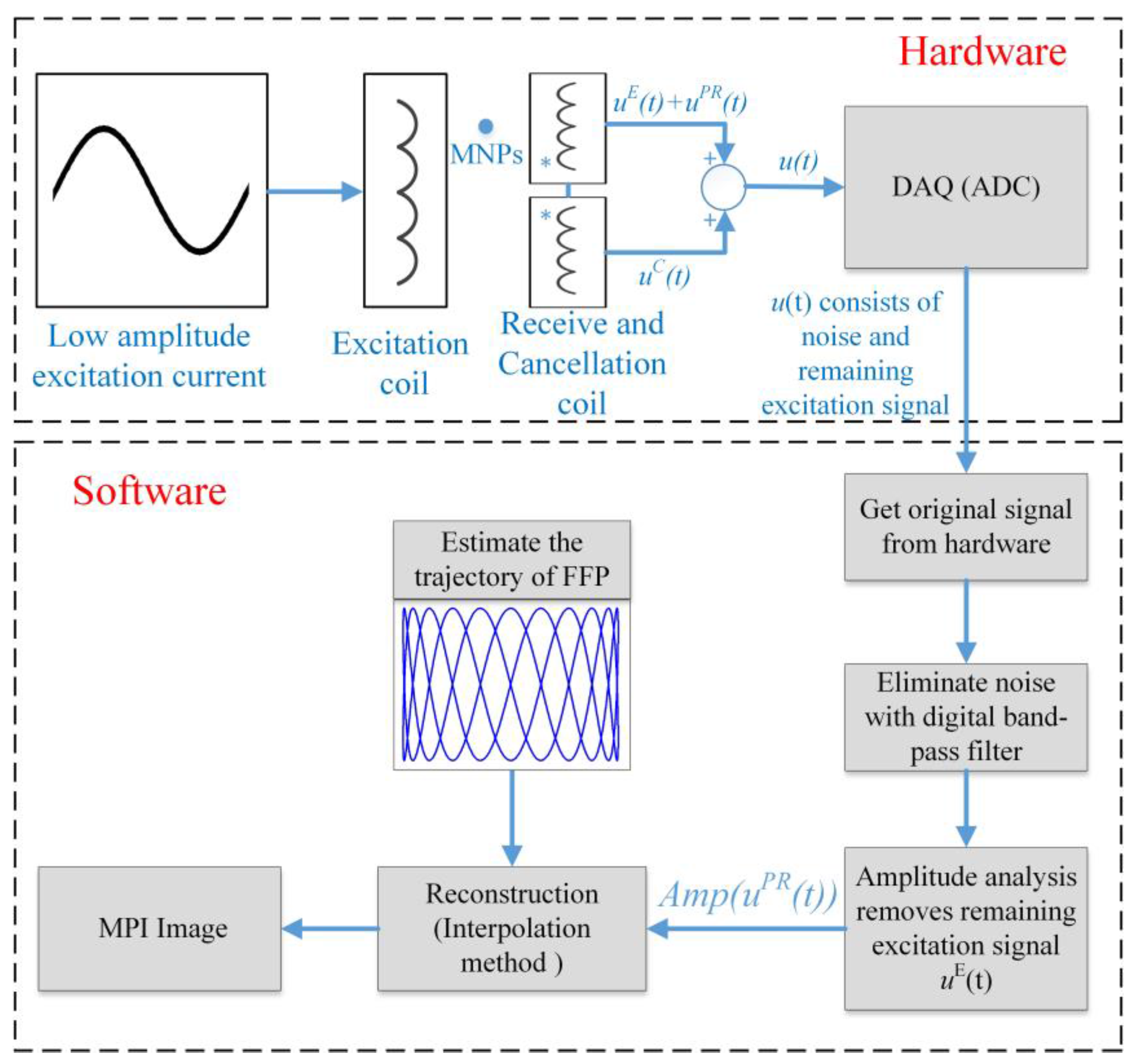
3.6. Signal Processing
3.7. Reconstruction of 2D AM MPI
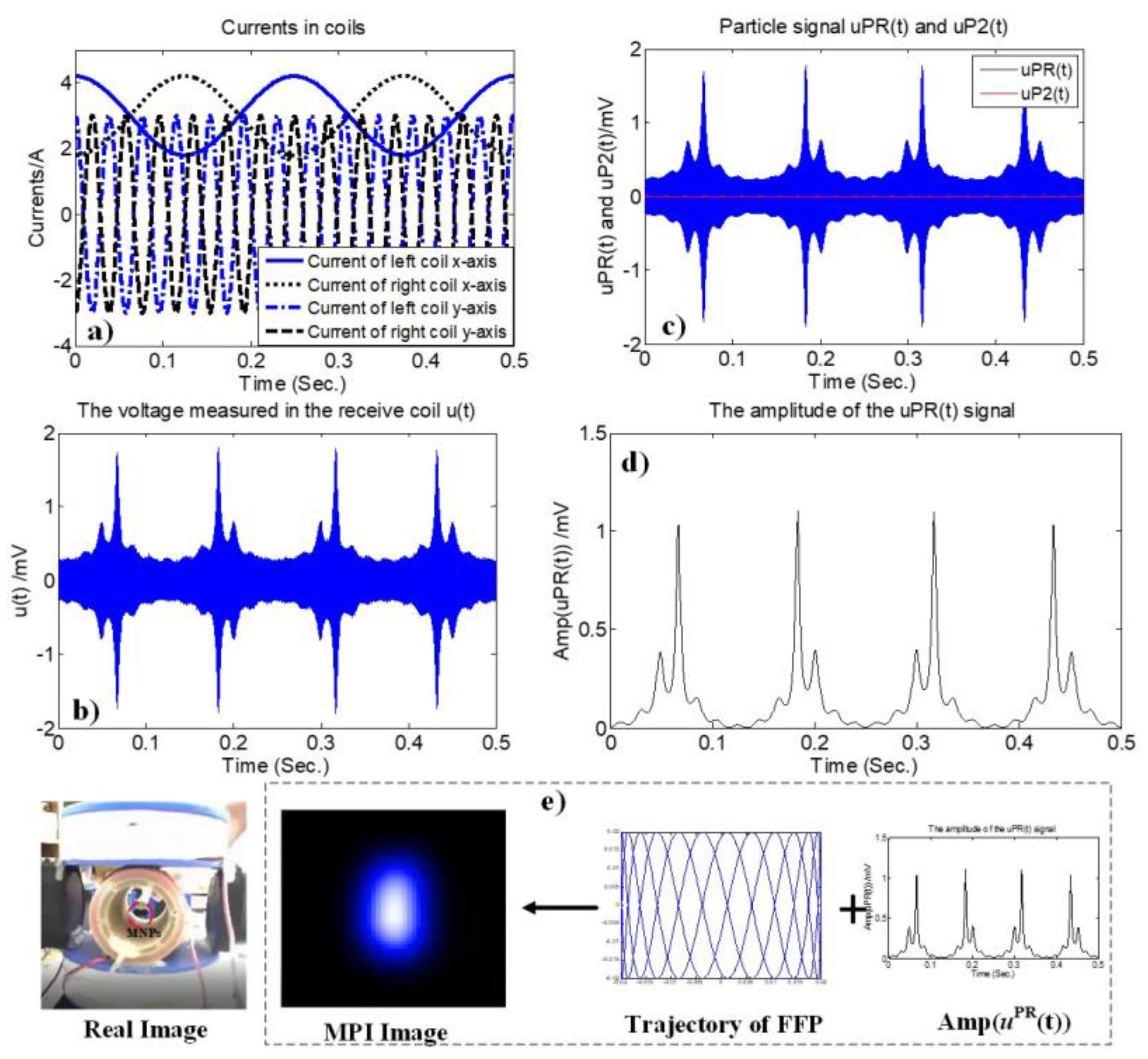
4. Results and Discussion
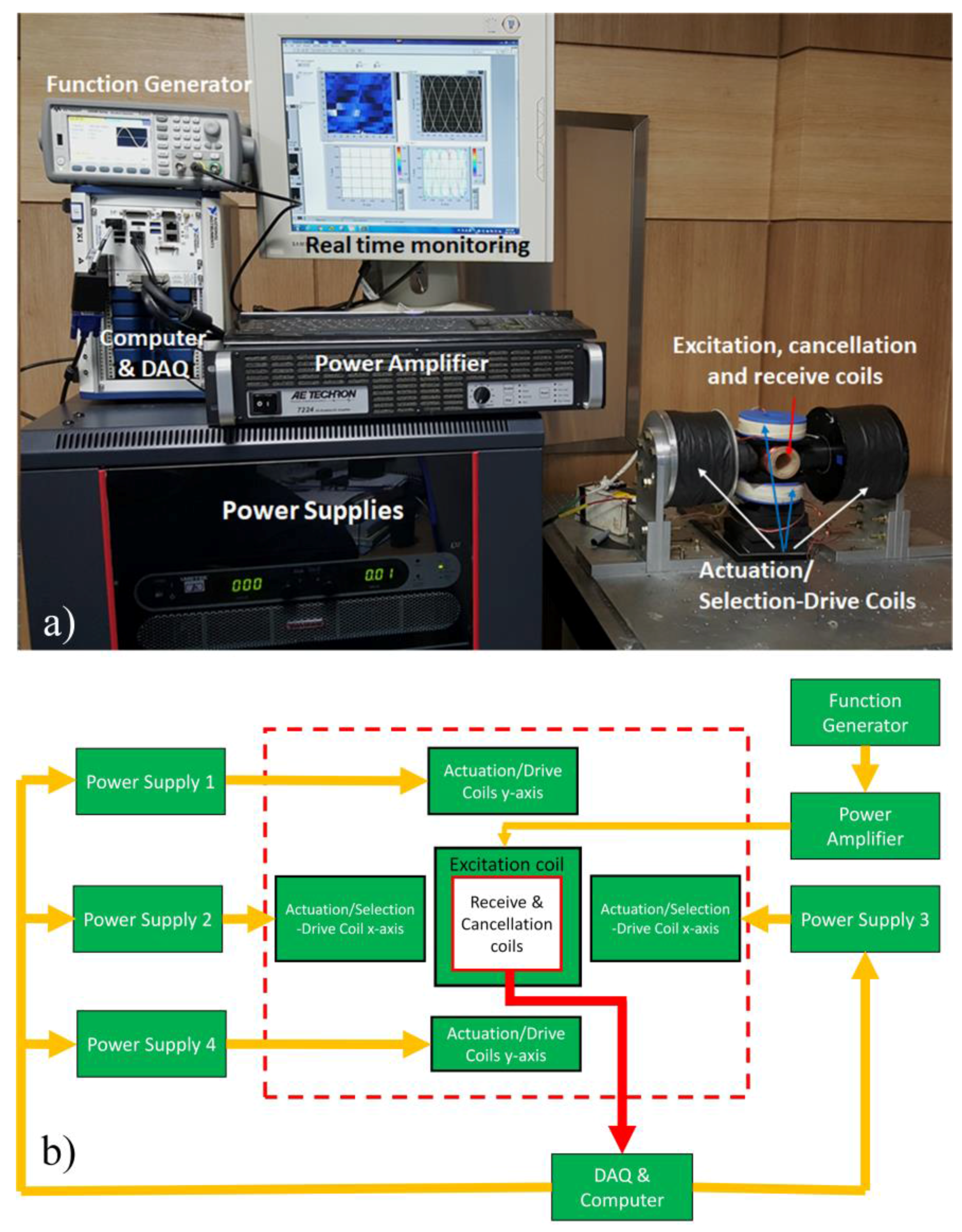
4.1. Experimental Setup
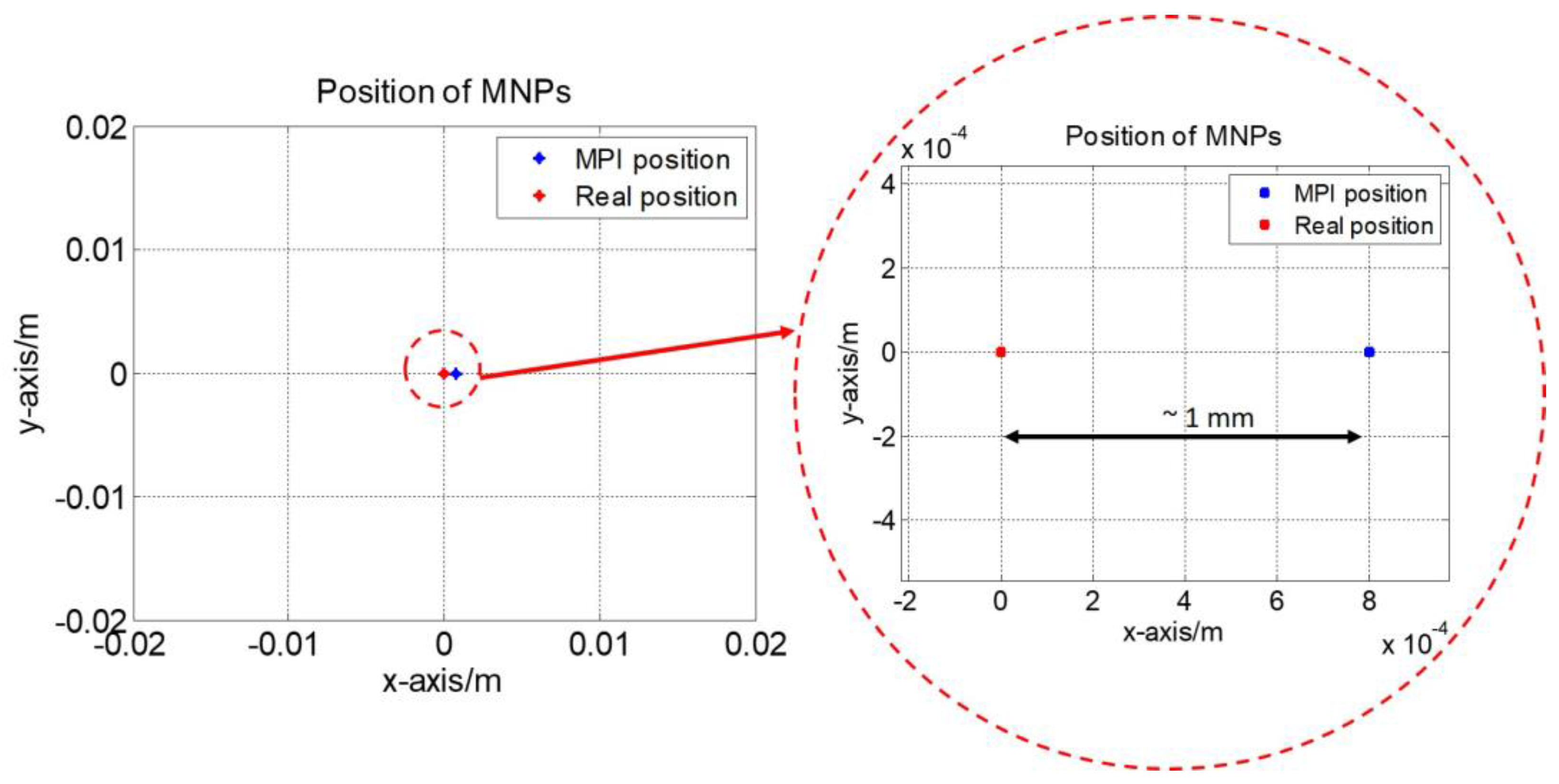
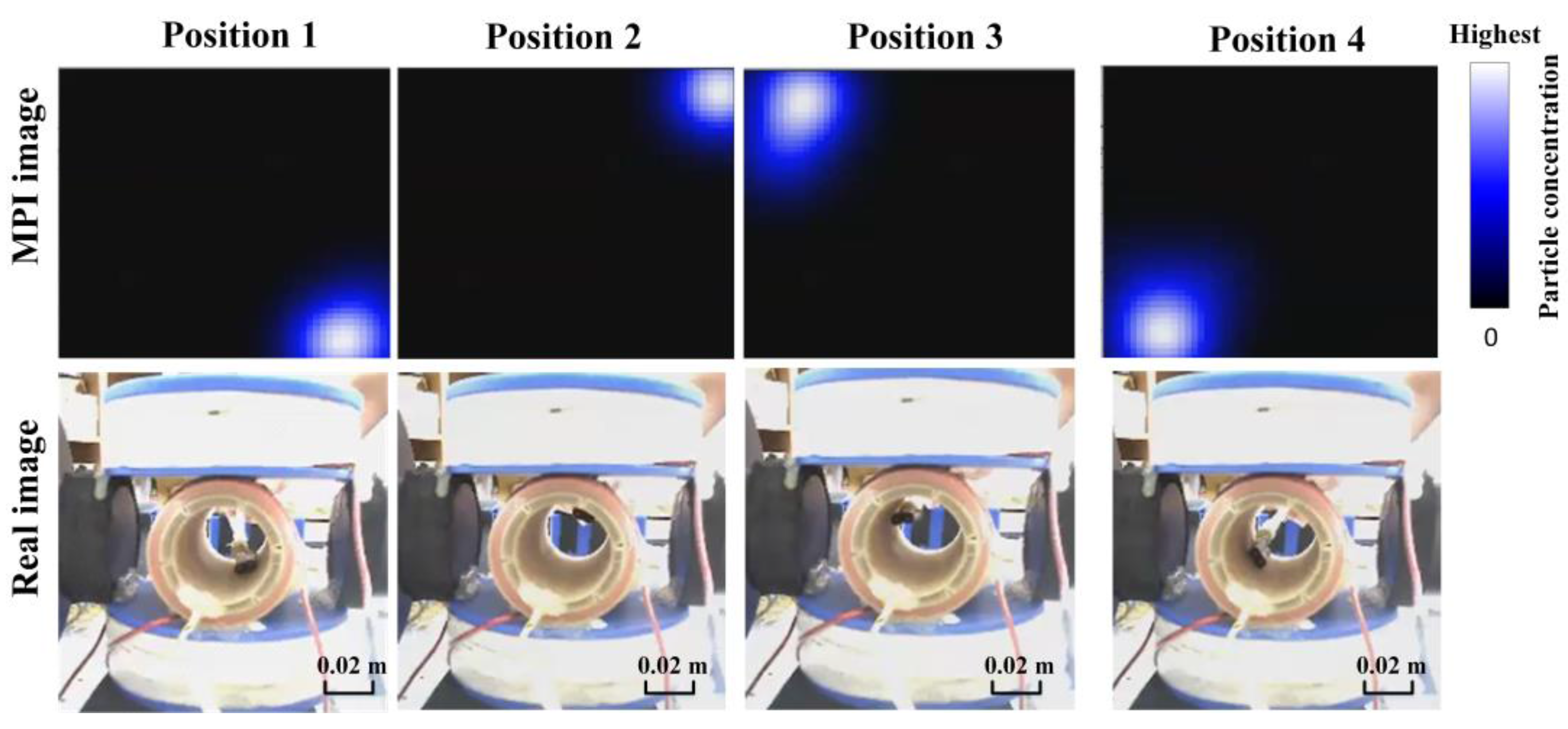
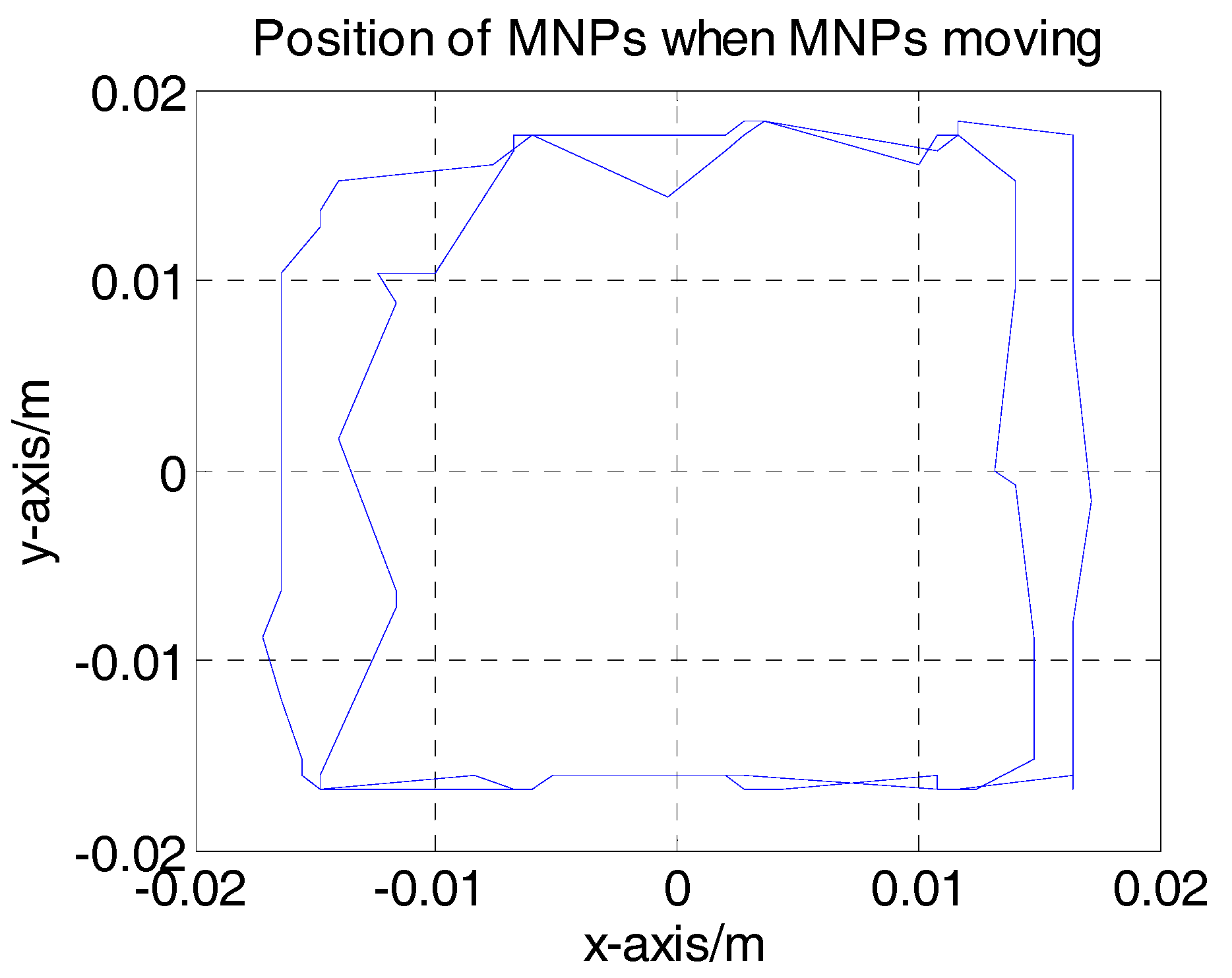
4.2. Two-Dimensional Real-Time AM MPI Monitoring
4.3. Discussions for the Developed 2D MPI System
5. Conclusions
Supplementary Materials
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bertrand, N.; Wu, J.; Xu, X.; Kamaly, N.; Farokhzad, O.C. Cancer nanotechnology: The impact of passive and active targeting in the era of modern cancer biology. Adv. Drug Deliv. Rev. 2014, 66, 2–25. [Google Scholar] [CrossRef] [PubMed]
- Steichen, S.D.; Caldorera-Moore, M.; Peppas, N.A. A review of current nanoparticle and targeting moieties for the delivery of cancer therapeutics. Eur. J. Pharm. Sci. 2013, 48, 416–427. [Google Scholar] [CrossRef] [PubMed]
- Bar, J.; Herbst, R.S.; Onn, A. Targeted drug delivery strategies to treat lung metastasis. Expert Opin. Drug Deliv. 2009, 6, 1003–1016. [Google Scholar] [CrossRef] [PubMed]
- Torchilin, V.P. Passive and active drug targeting: Drug delivery to tumors as an example. In Drug Delivery; Springer: Berlin/Heidelberg, Germany, 2010; pp. 3–53. [Google Scholar]
- Choi, H.; Cha, K.; Choi, J.; Jeong, S.; Jeon, S.; Jang, G.; Park, J.-O.; Park, S. Ema system with gradient and uniform saddle coils for 3D locomotion of microrobot. Sens. Actuators A Phys. 2010, 163, 410–417. [Google Scholar] [CrossRef]
- Jeong, S.; Choi, H.; Choi, J.; Yu, C.; Park, J.-O.; Park, S. Novel electromagnetic actuation (ema) method for 3-dimensional locomotion of intravascular microrobot. Sens. Actuators A Phys. 2010, 157, 118–125. [Google Scholar] [CrossRef]
- Kummer, M.P.; Abbott, J.J.; Kratochvil, B.E.; Borer, R.; Sengul, A.; Nelson, B.J. Octomag: An electromagnetic system for 5-dof wireless micromanipulation. IEEE Trans. Robot. 2010, 26, 1006–1017. [Google Scholar] [CrossRef]
- Tehrani, M.D.; Yoon, J.-H.; Kim, M.O.; Yoon, J. A novel scheme for nanoparticle steering in blood vessels using a functionalized magnetic field. IEEE Trans. Biomed. Eng. 2015, 62, 303–313. [Google Scholar] [CrossRef] [PubMed]
- Hoshiar, A.K.; Le, T.-A.; Amin, F.U.; Kim, M.O.; Yoon, J. Studies of aggregated nanoparticles steering during magnetic-guided drug delivery in the blood vessels. J. Magn. Magn. Mater. 2017, 427, 181–187. [Google Scholar] [CrossRef]
- Amin, F.U.; Hoshiar, A.K.; Do, T.D.; Noh, Y.; Shah, S.A.; Khan, M.S.; Yoon, J.; Kim, M.O. Osmotin-loaded magnetic nanoparticles with electromagnetic guidance for the treatment of alzheimer’s disease. Nanoscale 2017, 9, 10619–10632. [Google Scholar] [CrossRef] [PubMed]
- Khalil, I.S.; Ferreira, P.; Eleutério, R.; de Korte, C.L.; Misra, S. Magnetic-based closed-loop control of paramagnetic microparticles using ultrasound feedback. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 3807–3812. [Google Scholar]
- Khalil, I.S.; Keuning, J.D.; Abelmann, L.; Misra, S. Wireless magnetic-based control of paramagnetic microparticles. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; pp. 460–466. [Google Scholar]
- Martel, S. Combining pulsed and dc gradients in a clinical mri-based microrobotic platform to guide therapeutic magnetic agents in the vascular network. Int. J. Adv. Robot. Syst. 2013, 10, 30. [Google Scholar] [CrossRef]
- Mathieu, J.B.; Martel, S. Steering of aggregating magnetic microparticles using propulsion gradients coils in an mri scanner. Magn. Reson. Med. 2010, 63, 1336–1345. [Google Scholar] [CrossRef] [PubMed]
- Latulippe, M.; Martel, S. Dipole field navigation: Theory and proof of concept. IEEE Trans. Robot. 2015, 31, 1353–1363. [Google Scholar] [CrossRef]
- Bigot, A.; Tremblay, C.; Soulez, G.; Martel, S. Temperature response of a magnetic resonance imaging coil insert for the navigation of theranostic agents in complex vascular networks. IEEE Trans. Magn. 2014, 50, 1–7. [Google Scholar] [CrossRef]
- Mathieu, J.-B.; Beaudoin, G.; Martel, S. Method of propulsion of a ferromagnetic core in the cardiovascular system through magnetic gradients generated by an mri system. IEEE Trans. Biomed. Eng. 2006, 53, 292–299. [Google Scholar] [CrossRef] [PubMed]
- Yesin, K.B.; Vollmers, K.; Nelson, B.J. Modeling and control of untethered biomicrorobots in a fluidic environment using electromagnetic fields. Int. J. Robot. Res. 2006, 25, 527–536. [Google Scholar] [CrossRef]
- Tehrani, M.D.; Kim, M.O.; Yoon, J. A novel electromagnetic actuation system for magnetic nanoparticle guidance in blood vessels. IEEE Trans. Magn. 2014, 50, 1–12. [Google Scholar] [CrossRef]
- Gleich, B.; Weizenecker, J. Tomographic imaging using the nonlinear response of magnetic particles. Nature 2005, 435, 1214–1217. [Google Scholar] [CrossRef] [PubMed]
- Borgert, J.; Schmidt, J.D.; Schmale, I.; Rahmer, J.; Bontus, C.; Gleich, B.; David, B.; Eckart, R.; Woywode, O.; Weizenecker, J. Fundamentals and applications of magnetic particle imaging. J. Cardiovasc. Comput. Tomogr. 2012, 6, 149–153. [Google Scholar] [CrossRef] [PubMed]
- Heyn, C.; Bowen, C.V.; Rutt, B.K.; Foster, P.J. Detection threshold of single spio-labeled cells with fiesta. Magn. Reson. Med. 2005, 53, 312–320. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, A.; Dadkhah, M.; Kim, M.O.; Yoon, J. A novel design of an MPI-based guidance system for simultaneous actuation and monitoring of magnetic nanoparticles. IEEE Trans. Magn. 2015, 51, 1–5. [Google Scholar] [CrossRef]
- Zhang, X.; Le, T.-A.; Yoon, J. Development of a magnetic nanoparticles guidance system for interleaved actuation and MPI-based monitoring. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 5279–5284. [Google Scholar]
- Zhang, X.; Le, T.-A.; Yoon, J. Development of a real time imaging-based guidance system of magnetic nanoparticles for targeted drug delivery. J. Magn. Magn. Mater. 2017, 427, 345–351. [Google Scholar] [CrossRef]
- Knopp, T.; Buzug, T.M. Magnetic Particle Imaging: An Introduction to Imaging Principles and Scanner Instrumentation; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Nothnagel, N.; Rahmer, J.; Gleich, B.; Halkola, A.; Buzug, T.M.; Borgert, J. Steering of magnetic devices with a magnetic particle imaging system. IEEE Trans. Biomed. Eng. 2016, 63, 2286–2293. [Google Scholar] [CrossRef] [PubMed]
- Schulz, V.; Straub, M.; Mahlke, M.; Hubertus, S.; Lammers, T.; Kiessling, F. A field cancellation signal extraction method for magnetic particle imaging. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, I.N.; Stepanov, P.Y.; Fricke, S.T.; Probst, R.; Urdaneta, M.; Warnow, D.; Sanders, H.; Glidden, S.C.; McMillan, A.; Starewicz, P.M. Increasing the oscillation frequency of strong magnetic fields above 101 khz significantly raises peripheral nerve excitation thresholds. Med. Phys. 2012, 39, 2578–2583. [Google Scholar] [CrossRef] [PubMed]
- Goodwill, P.W.; Conolly, S.M. Multidimensional x-space magnetic particle imaging. IEEE Trans. Med. Imaging 2011, 30, 1581–1590. [Google Scholar] [CrossRef] [PubMed]
- Le, T.-A.; Asl, H.J.; Do, T.D.; Kim, M.O.; Yoon, J. Band-stop filter analysis and design for 1D magnetic particle imaging hybrid system. J. Nanosci. Nanotechnol. 2016, 16, 8492–8495. [Google Scholar] [CrossRef]
- Lehmann, T.M.; Gonner, C.; Spitzer, K. Survey: Interpolation methods in medical image processing. IEEE Trans. Med. Imaging 1999, 18, 1049–1075. [Google Scholar] [CrossRef] [PubMed]
- Eberbeck, D.; Wiekhorst, F.; Wagner, S.; Trahms, L. How the size distribution of magnetic nanoparticles determines their magnetic particle imaging performance. Appl. Phys. Lett. 2011, 98, 182502. [Google Scholar] [CrossRef]
- Goodwill, P.W.; Conolly, S.M. The x-space formulation of the magnetic particle imaging process: 1-D signal, resolution, bandwidth, SNR, SAR, and magnetostimulation. IEEE Trans. Med. Imaging 2010, 29, 1851–1859. [Google Scholar] [CrossRef] [PubMed]
- Panagiotopoulos, N.; Duschka, R.L.; Ahlborg, M.; Bringout, G.; Debbeler, C.; Graeser, M.; Kaethner, C.; Lüdtke-Buzug, K.; Medimagh, H.; Stelzner, J. Magnetic particle imaging: Current developments and future directions. Int. J. Nanomed. 2015, 10, 3097. [Google Scholar] [CrossRef] [PubMed]
- Mason, E.E.; Cooley, C.Z.; Cauley, S.F.; Griswold, M.A.; Conolly, S.M.; Wald, L.L. Design analysis of an MPI human functional brain scanner. Int. J. Magn. Part. Imaging 2017, 3. [Google Scholar] [CrossRef]
- Ng, K.-H.; Ahmad, A.C.; Nizam, M.; Abdullah, B. Magnetic resonance imaging: Health effects and safety. In Proceedings of the International Conference on Non-Ionizing Radiation at UNITEN (ICNIR2003) Electromagnetic Fields and Our Health, Kuala Lumpur, Malaysia, 20–23 October 2003. [Google Scholar]
- Hartwig, V.; Giovannetti, G.; Vanello, N.; Lombardi, M.; Landini, L.; Simi, S. Biological effects and safety in magnetic resonance imaging: A review. Int. J. Environ. Res. Public Health 2009, 6, 1778–1798. [Google Scholar] [CrossRef] [PubMed]
| Turns | Inner Diameter | Outer Diameter | Coil Length | Wire | |
|---|---|---|---|---|---|
| Actuation/selection-drive coil (x-axis) | 5000 | 0.070 m | 0.190 m | 0.070 m | 1 mm copper wire |
| Actuation/drive coil (y-axis) | 260 | 0.040 m | 0.126 m | 0.030 m | Litz wire |
| Receive coil | 400 | 0.042 m | Single layer | 0.060 m | Litz wire |
| Cancellation coil | 200 | 0.042 m | Single layer | 0.015 m | Litz wire |
| Excitation coil | 44 | 0.050 m | Single layer | 0.110 m | Litz wire |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.-A.; Zhang, X.; Hoshiar, A.K.; Yoon, J. Real-Time Two-Dimensional Magnetic Particle Imaging for Electromagnetic Navigation in Targeted Drug Delivery. Sensors 2017, 17, 2050. https://doi.org/10.3390/s17092050
Le T-A, Zhang X, Hoshiar AK, Yoon J. Real-Time Two-Dimensional Magnetic Particle Imaging for Electromagnetic Navigation in Targeted Drug Delivery. Sensors. 2017; 17(9):2050. https://doi.org/10.3390/s17092050
Chicago/Turabian StyleLe, Tuan-Anh, Xingming Zhang, Ali Kafash Hoshiar, and Jungwon Yoon. 2017. "Real-Time Two-Dimensional Magnetic Particle Imaging for Electromagnetic Navigation in Targeted Drug Delivery" Sensors 17, no. 9: 2050. https://doi.org/10.3390/s17092050
APA StyleLe, T.-A., Zhang, X., Hoshiar, A. K., & Yoon, J. (2017). Real-Time Two-Dimensional Magnetic Particle Imaging for Electromagnetic Navigation in Targeted Drug Delivery. Sensors, 17(9), 2050. https://doi.org/10.3390/s17092050






