Conditional Variational Autoencoder for Prediction and Feature Recovery Applied to Intrusion Detection in IoT
Abstract
:1. Introduction
2. Related Works
3. Work Description
3.1. Selected Dataset
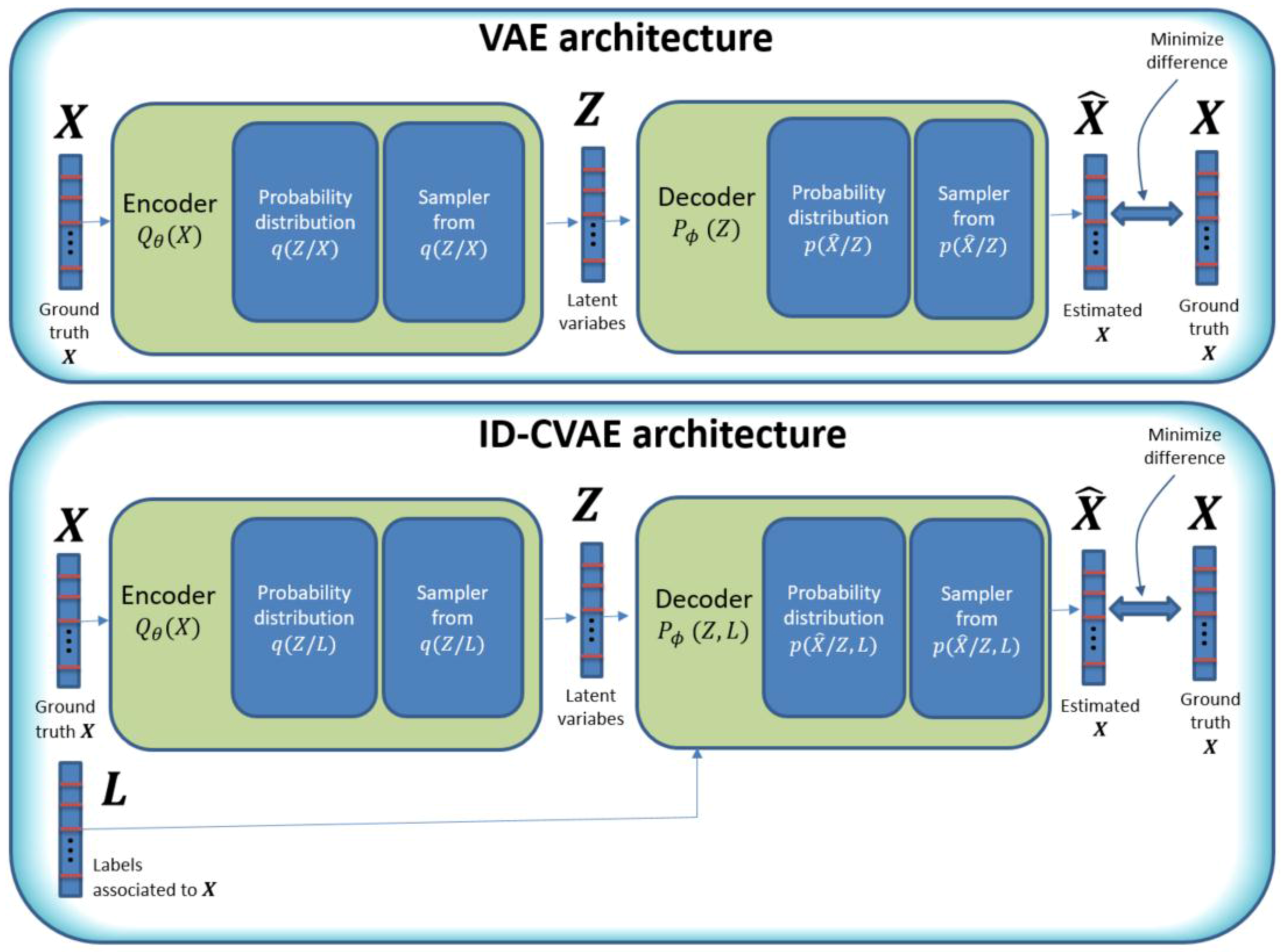
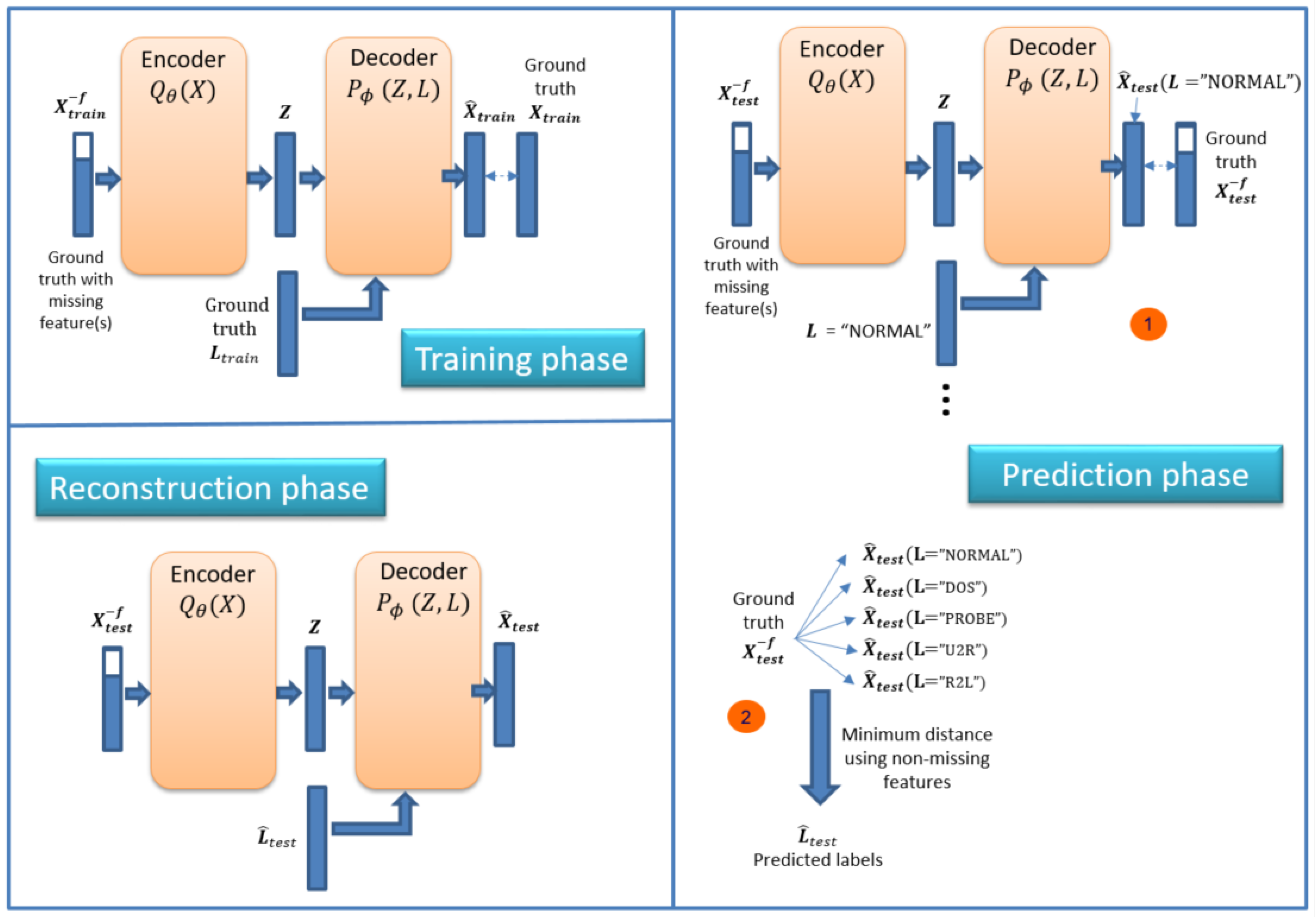
3.2. Methodology
- Add extra information into the decoder block which is important to create the required binding between the vector of features and labels.
- Perform classification with a single training step, with all training data.
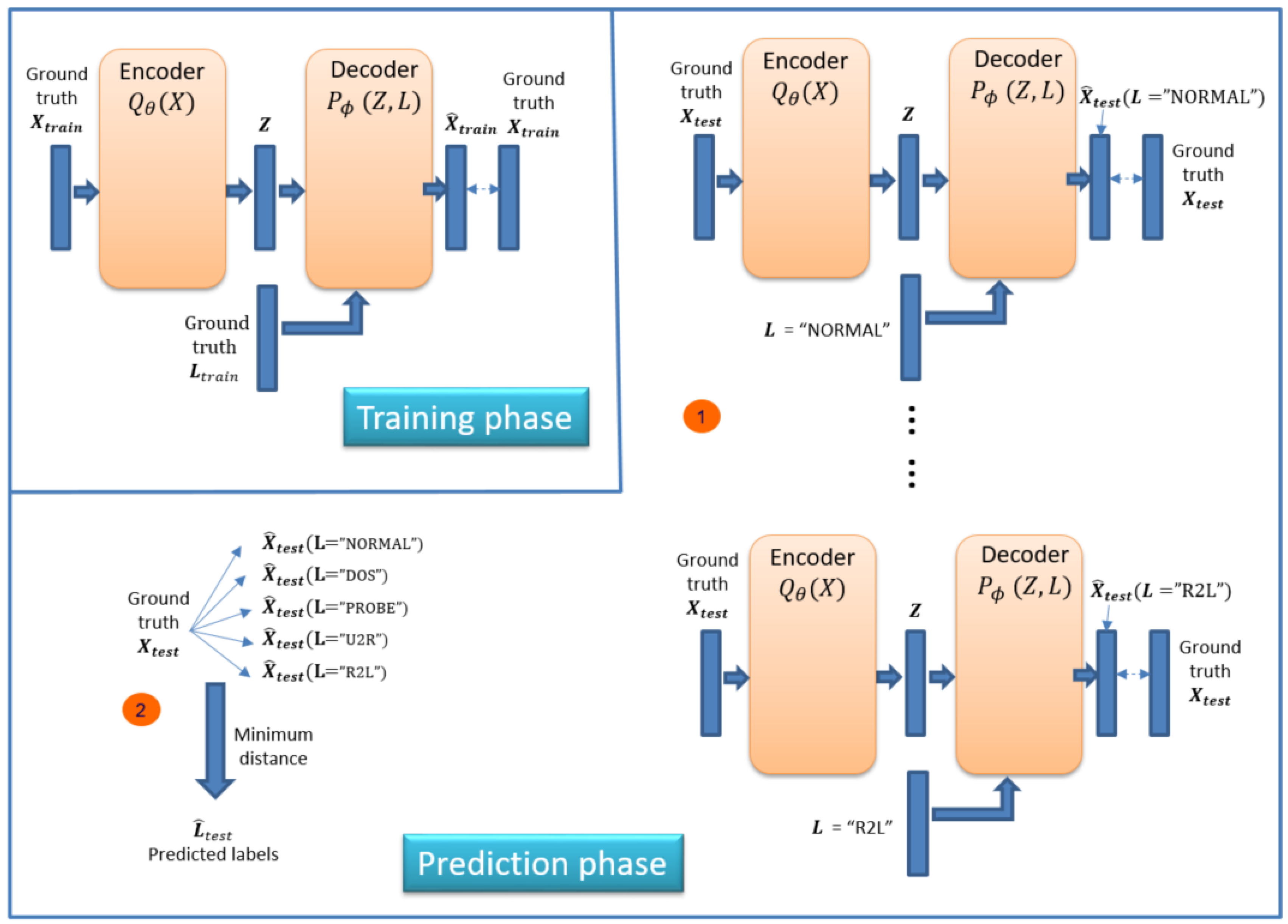
- Perform feature reconstruction. An ID-CVAE will learn the distribution of features values using a mapping to the latent distributions, from which a later feature recovery can be performed, in the case of incomplete input samples (missing features).
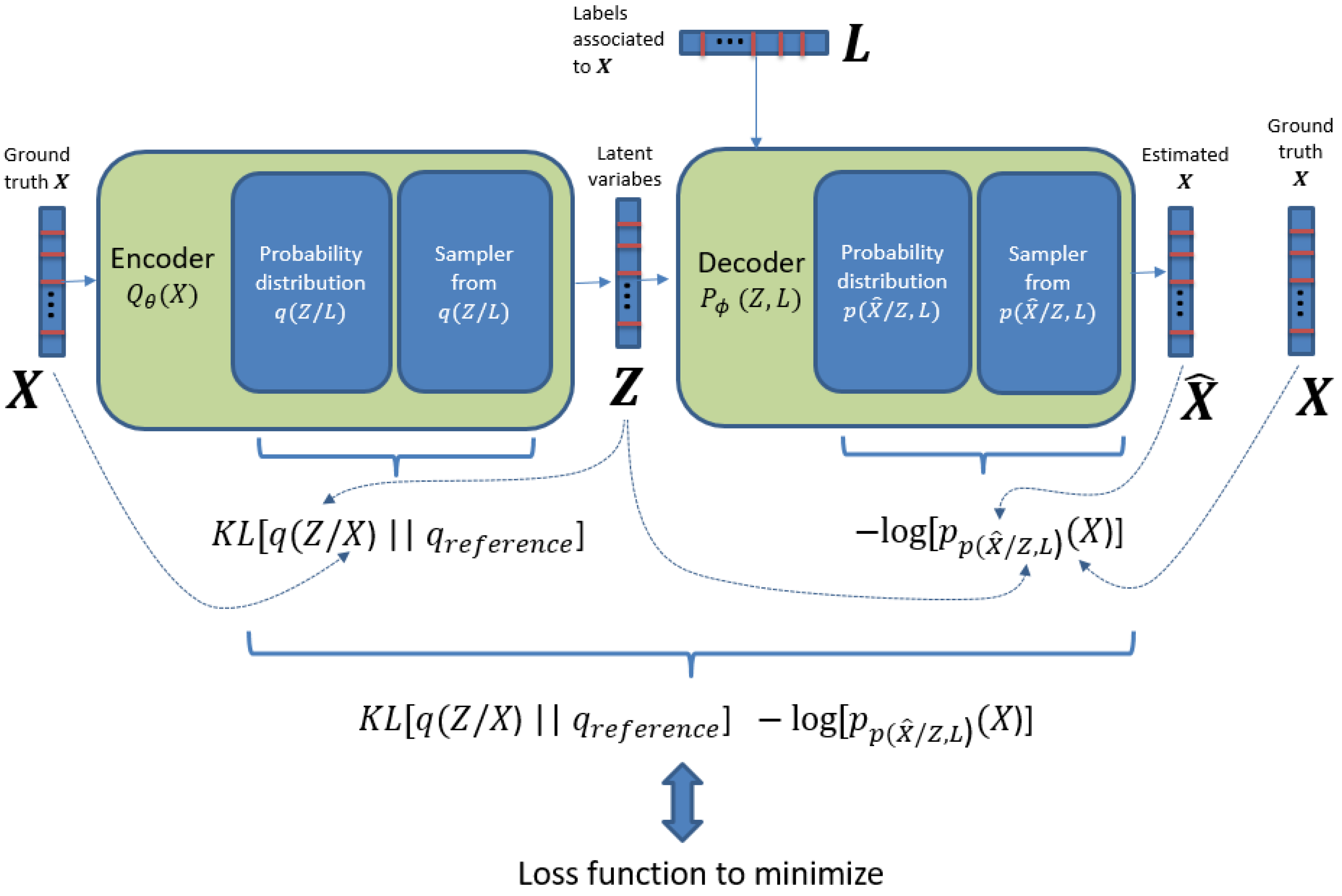
3.3. Model Details
4. Results
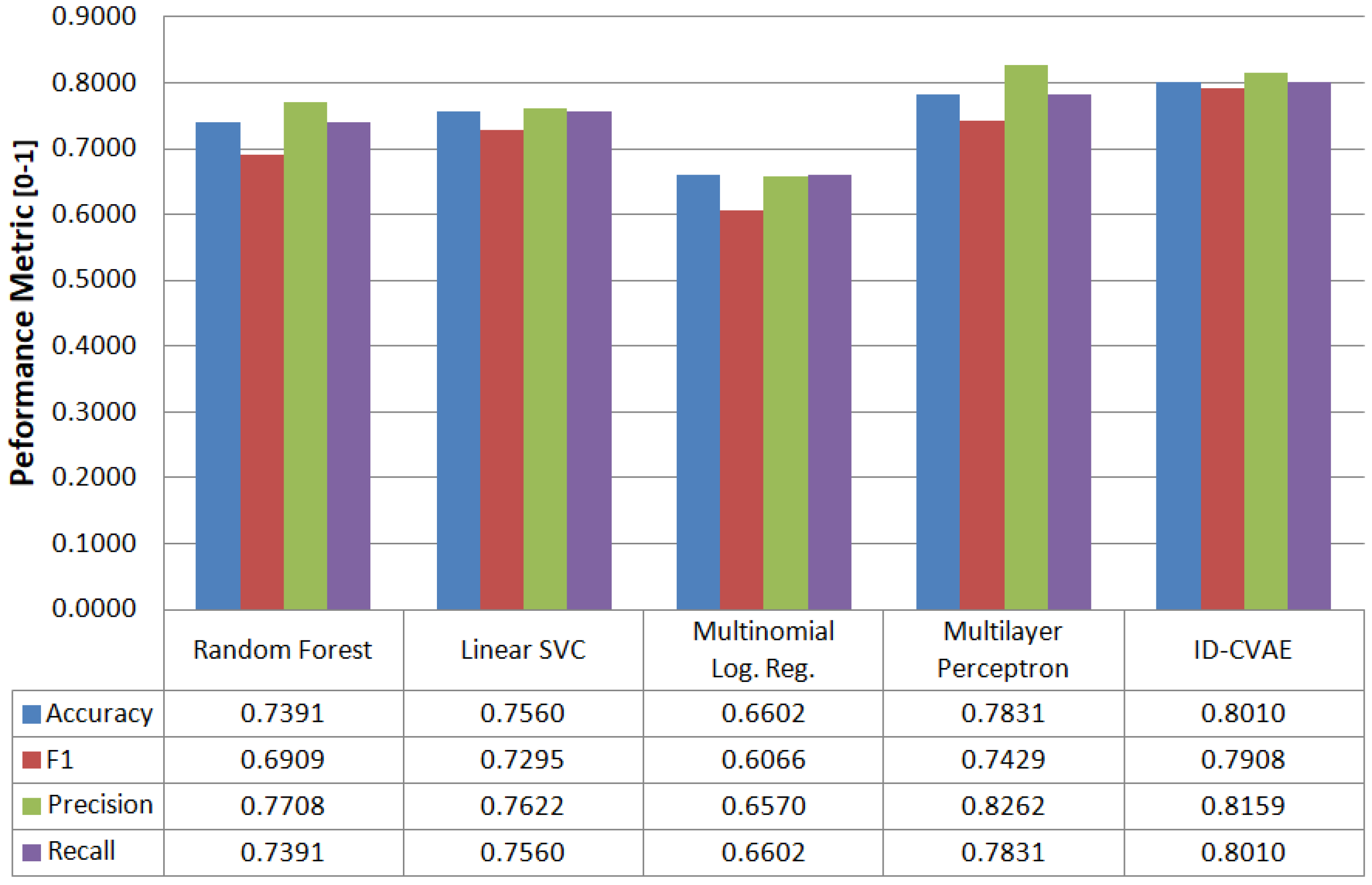
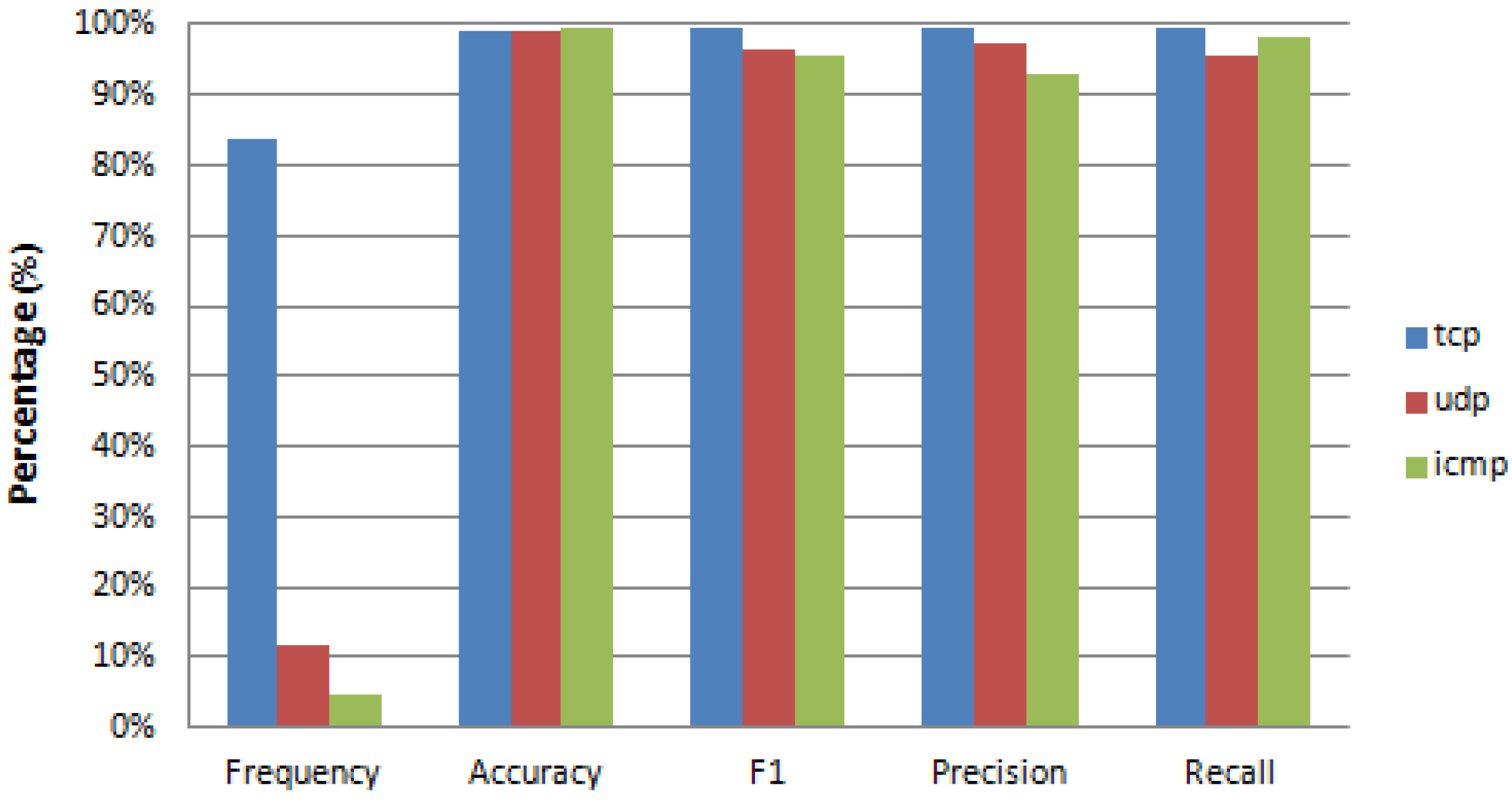
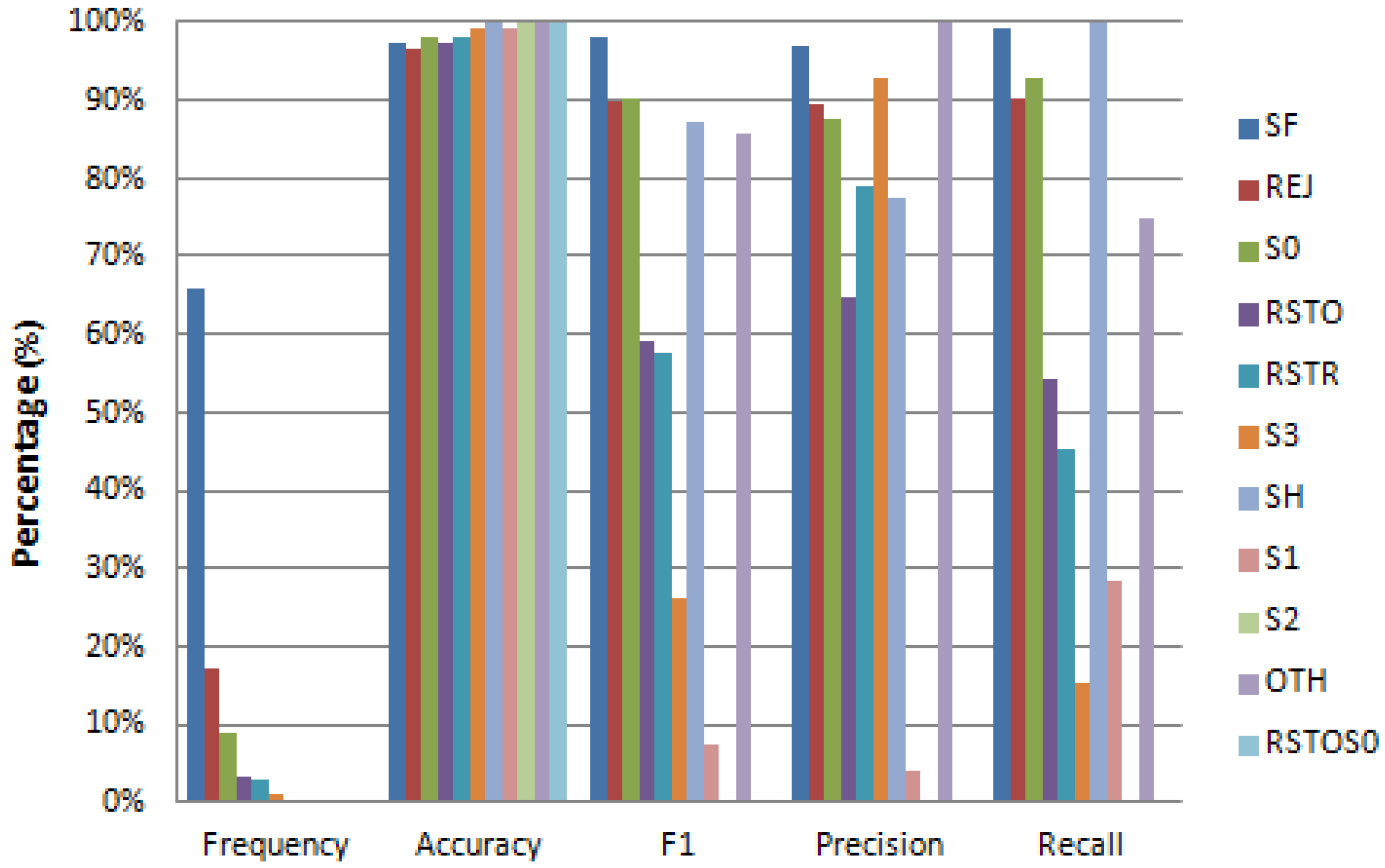
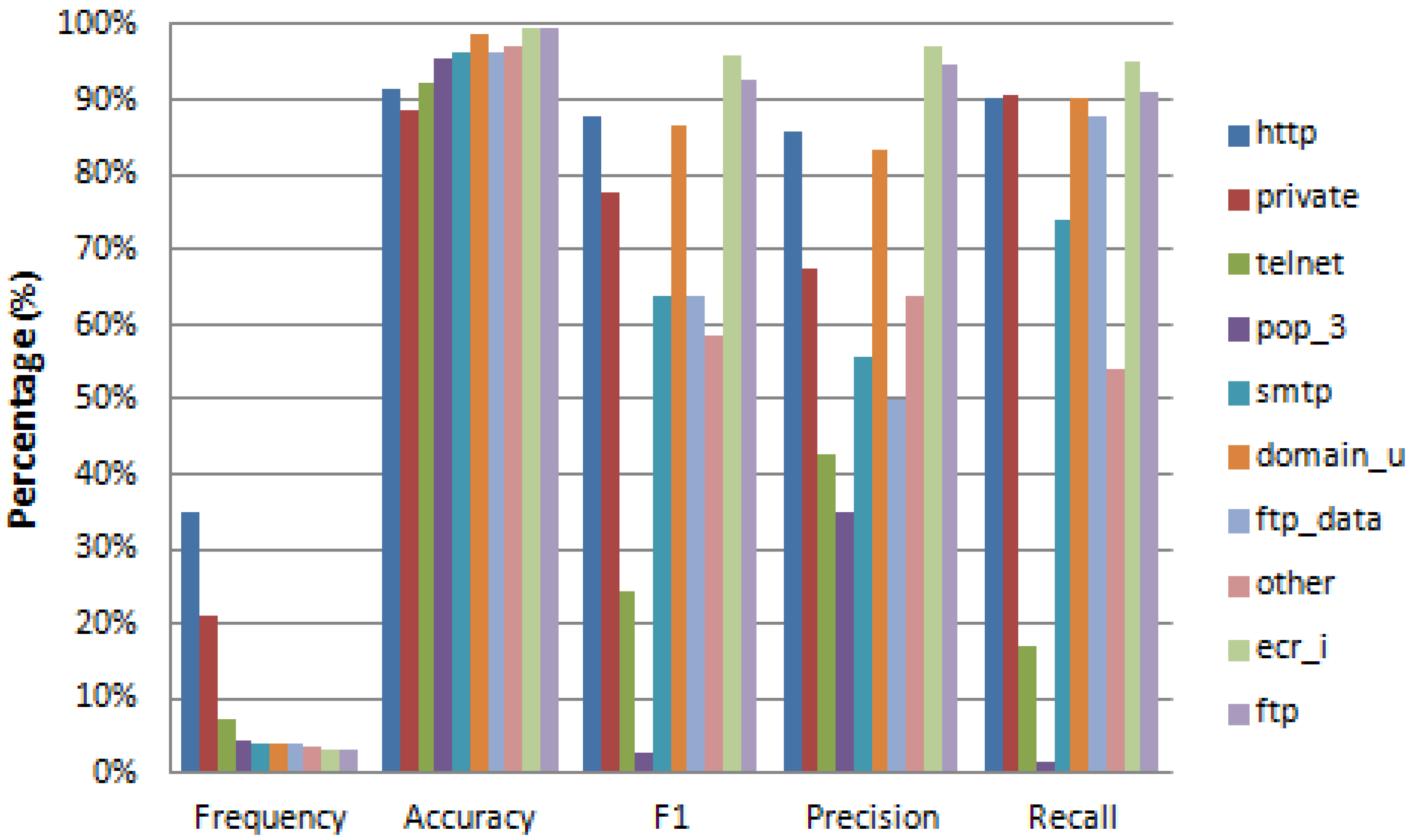
4.1. Classification
4.2. Feature Reconstruction
4.3. Model Training
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zarpelo, B.B.; Miani, R.S.; Kawakani, C.T.; de Alvarenga, S.C. A survey of intrusion detection in Internet of Things. J. Netw. Comput. Appl. 2017, 84, 25–37. [Google Scholar] [CrossRef]
- Bhuyan, M.H.; Bhattacharyya, D.K.; Kalita, J.K. Network Anomaly Detection: Methods, Systems and Tools. In IEEE Communications Surveys & Tutorials; IEEE: Piscataway, NJ, USA, 2014; Volume 16, pp. 303–336. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Outlier Analysis; Springer: New York, NY, USA, 2013; pp. 10–18. ISBN 978-1-4614-639-5. [Google Scholar]
- Kingma, D.P.; Rezende, D.J.; Mohamed, S.; Welling, M. Semi-supervised learning with deep generative models. In Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS’14), Montreal, QC, Canada, 8–13 December 2014; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; MIT Press: Cambridge, MA, USA, 2014; pp. 3581–3589. [Google Scholar]
- Sohn, K.; Yan, X.; Lee, H. Learning structured output representation using deep conditional generative models. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NIPS’15), Montreal, QC, Canada, 7–12 December 2015; Cortes, C., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; MIT Press: Cambridge, MA, USA, 2015; pp. 3483–3491. [Google Scholar]
- Fekade, B.; Maksymyuk, T.; Kyryk, M.; Jo, M. Probabilistic Recovery of Incomplete Sensed Data in IoT. IEEE Int. Things J. 2017, 1. [Google Scholar] [CrossRef]
- An, J.; Cho, S. Variational Autoencoder based Anomaly Detection using Reconstruction Probability; Seoul National University: Seoul, Korea, 2015. [Google Scholar]
- Suh, S.; Chae, D.H.; Kang, H.G.; Choi, S. Echo-state conditional Variational Autoencoder for anomaly detection. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1015–1022. [Google Scholar]
- Sölch, M. Detecting Anomalies in Robot Time Series Data Using Stochastic Recurrent Networks. Master’s Thesis, Department of Mathematics, Technische Universitat Munchen, Munich, Germany, 2015. [Google Scholar]
- Hodo, E.; Bellekens, X.; Hamilton, A. Threat analysis of IoT networks using artificial neural network intrusion detection system. In Proceedings of the 2016 International Symposium on Networks, Computers and Communications (ISNCC), Yasmine Hammamet, Tunisia, 11–13 May 2016; pp. 1–6. [Google Scholar]
- Kang, M.-J.; Kang, J.-W. Intrusion Detection System Using Deep Neural Network for In-Vehicle Network Security. PLoS ONE 2016, 11, e0155781. [Google Scholar] [CrossRef] [PubMed]
- Thing, V.L.L. IEEE 802.11 Network Anomaly Detection and Attack Classification: A Deep Learning Approach. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Ma, T.; Wang, F.; Cheng, J.; Yu, Y.; Chen, X. A Hybrid Spectral Clustering and Deep Neural Network Ensemble Algorithm for Intrusion Detection in Sensor Networks. Sensors 2016, 16, 1701. [Google Scholar] [CrossRef] [PubMed]
- Tavallaee, M.; Bagheri, E.; Lu, W.; Ghorbani, A.A. A detailed analysis of the KDD CUP 99 data set. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications, Ottawa, ON, Canada, 8–10 July 2009; pp. 1–6. [Google Scholar]
- Ingre, B.; Yadav, A. Performance analysis of NSL-KDD dataset using ANN. In Proceedings of the 2015 International Conference on Signal Processing and Communication Engineering Systems, Guntur, India, 2–3 January 2015; pp. 92–96. [Google Scholar]
- Ibrahim, L.M.; Basheer, D.T.; Mahmod, M.S. A comparison study for intrusion database (KDD99, NSL-KDD) based on self-organization map (SOM) artificial neural network. In Journal of Engineering Science and Technology; School of Engineering, Taylor’s University: Selangor, Malaysia, 2013; Volume 8, pp. 107–119. [Google Scholar]
- Wahb, Y.; ElSalamouny, E.; ElTaweel, G. Improving the Performance of Multi-class Intrusion Detection Systems using Feature Reduction. arXiv 2015, arXiv:1507.06692. [Google Scholar]
- Bandgar, M.; Dhurve, K.; Jadhav, S.; Kayastha, V.; Parvat, T.J. Intrusion Detection System using Hidden Markov Model (HMM). IOSR J. Comput. Eng. (IOSR-JCE) 2013, 10, 66–70. [Google Scholar] [CrossRef]
- Chen, C.-M.; Guan, D.-J.; Huang, Y.-Z.; Ou, Y.-H. Anomaly Network Intrusion Detection Using Hidden Markov Model. Int. J. Innov. Comput. Inform. Control 2016, 12, 569–580. [Google Scholar]
- Alom, M.Z.; Bontupalli, V.; Taha, T.M. Intrusion detection using deep belief networks. In Proceedings of the 2015 National Aerospace and Electronics Conference (NAECON), Dayton, OH, USA, 15–19 June 2015; pp. 339–344. [Google Scholar]
- Xu, J.; Shelton, C.R. Intrusion Detection using Continuous Time Bayesian Networks. J. Artif. Intell. Res. 2010, 39, 745–774. [Google Scholar]
- Hodo, E.; Bellekens, X.; Hamilton, A.; Tachtatzis, C.; Atkinson, R. Shallow and Deep Networks Intrusion Detection System: A Taxonomy and Survey. arXiv 2017, arXiv:1701.02145. [Google Scholar]
- Khan, S.; Lloret, J.; Loo, J. Intrusion detection and security mechanisms for wireless sensor networks. Int. J. Distrib. Sens. Netw. 2017, 10, 747483. [Google Scholar] [CrossRef]
- Alrajeh, N.A.; Lloret, J. Intrusion detection systems based on artificial intelligence techniques in wireless sensor networks. Int. J. Distrib. Sens. Netw. 2013, 9, 351047. [Google Scholar] [CrossRef]
- Han, G.; Li, X.; Jiang, J.; Shu, L.; Lloret, J. Intrusion detection algorithm based on neighbor information against sinkhole attack in wireless sensor networks. Comput. J. 2014, 58, 1280–1292. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv e-prints 2014, arXiv:1312.6114v10. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Sønderby, C.K.; Raiko, T.; Maaløe, L.; Sønderby, S.K.; Winther, O. Ladder Variational Autoencoders. ArXiv e-prints 2016, arXiv:1602.02282v3. [Google Scholar]
- Johnson, M.J.; Duvenaud, D.; Wiltschko, A.B.; Datta, S.R.; Adams, R.P. Structured VAEs: Composing Probabilistic Graphical Models and Variational Autoencoders. ArXiv e-prints 2016, arXiv:1603.06277v1. [Google Scholar]

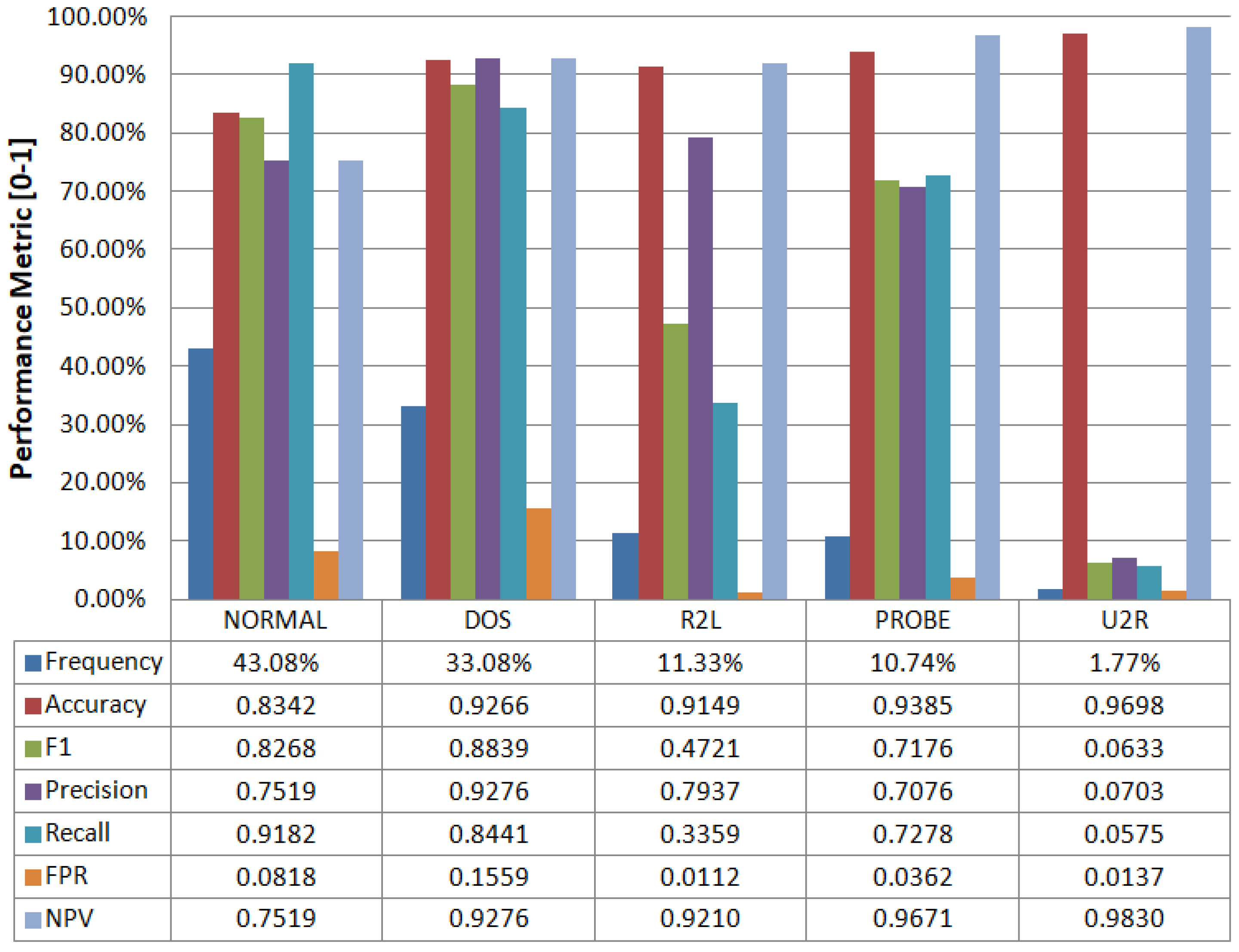

| Prediction | ||||||||
|---|---|---|---|---|---|---|---|---|
| DoS | Normal | Probe | R2L | U2R | Total | Percentage (%) | ||
| DoS | 6295 | 916 | 61 | 162 | 24 | 7458 | 33.08% | |
| Normal | 119 | 8917 | 610 | 36 | 29 | 9711 | 43.08% | |
| Probe | 368 | 252 | 1762 | 18 | 21 | 2421 | 10.74% | |
| Ground Truth | R2L | 4 | 1430 | 32 | 858 | 230 | 2554 | 11.33% |
| U2R | 0 | 345 | 25 | 7 | 23 | 400 | 1.77% | |
| Total | 6786 | 11860 | 2490 | 1081 | 327 | 22544 | 100.00% | |
| Percentage (%) | 30.10% | 52.61% | 11.05% | 4.80% | 1.45% | 100.00% | ||
| Model | Accuracy | F1 | Precision | Recall |
|---|---|---|---|---|
| Labels inserted in first layer of decoder | 0.7791 | 0.7625 | 0.7888 | 0.7791 |
| Labels inserted in second layer of decoder (ID-CVAE) | 0.8010 | 0.7908 | 0.8159 | 0.8010 |
| Labels inserted in third layer of decoder | 0.7547 | 0.7389 | 0.7584 | 0.7547 |
| Prediction | ||||||
|---|---|---|---|---|---|---|
| icmp | tcp | udp | Total | Percentage (%) | ||
| Ground Truth | icmp | 1022 | 19 | 2 | 1043 | 4.63% |
| tcp | 13 | 18791 | 76 | 18880 | 83.75% | |
| udp | 7 | 79 | 2535 | 2621 | 11.63% | |
| Total | 1042 | 18889 | 2613 | 22544 | 100.00% | |
| Percentage (%) | 4.62% | 83.79% | 11.59% | 100.00% | ||
| Label Value | Frequency | Accuracy | F1 | Precision | Recall | FPR | NPV |
|---|---|---|---|---|---|---|---|
| tcp | 83.75% | 0.9917 | 0.9950 | 0.9948 | 0.9953 | 0.0267 | 0.9757 |
| udp | 11.63% | 0.9927 | 0.9687 | 0.9701 | 0.9672 | 0.0039 | 0.9957 |
| icmp | 4.63% | 0.9982 | 0.9803 | 0.9808 | 0.9799 | 0.0009 | 0.9990 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopez-Martin, M.; Carro, B.; Sanchez-Esguevillas, A.; Lloret, J. Conditional Variational Autoencoder for Prediction and Feature Recovery Applied to Intrusion Detection in IoT. Sensors 2017, 17, 1967. https://doi.org/10.3390/s17091967
Lopez-Martin M, Carro B, Sanchez-Esguevillas A, Lloret J. Conditional Variational Autoencoder for Prediction and Feature Recovery Applied to Intrusion Detection in IoT. Sensors. 2017; 17(9):1967. https://doi.org/10.3390/s17091967
Chicago/Turabian StyleLopez-Martin, Manuel, Belen Carro, Antonio Sanchez-Esguevillas, and Jaime Lloret. 2017. "Conditional Variational Autoencoder for Prediction and Feature Recovery Applied to Intrusion Detection in IoT" Sensors 17, no. 9: 1967. https://doi.org/10.3390/s17091967
APA StyleLopez-Martin, M., Carro, B., Sanchez-Esguevillas, A., & Lloret, J. (2017). Conditional Variational Autoencoder for Prediction and Feature Recovery Applied to Intrusion Detection in IoT. Sensors, 17(9), 1967. https://doi.org/10.3390/s17091967






