Auxiliary Sensor-Based Borehole Transient Electromagnetic System for the Nondestructive Inspection of Multipipe Strings
Abstract
:1. Introduction
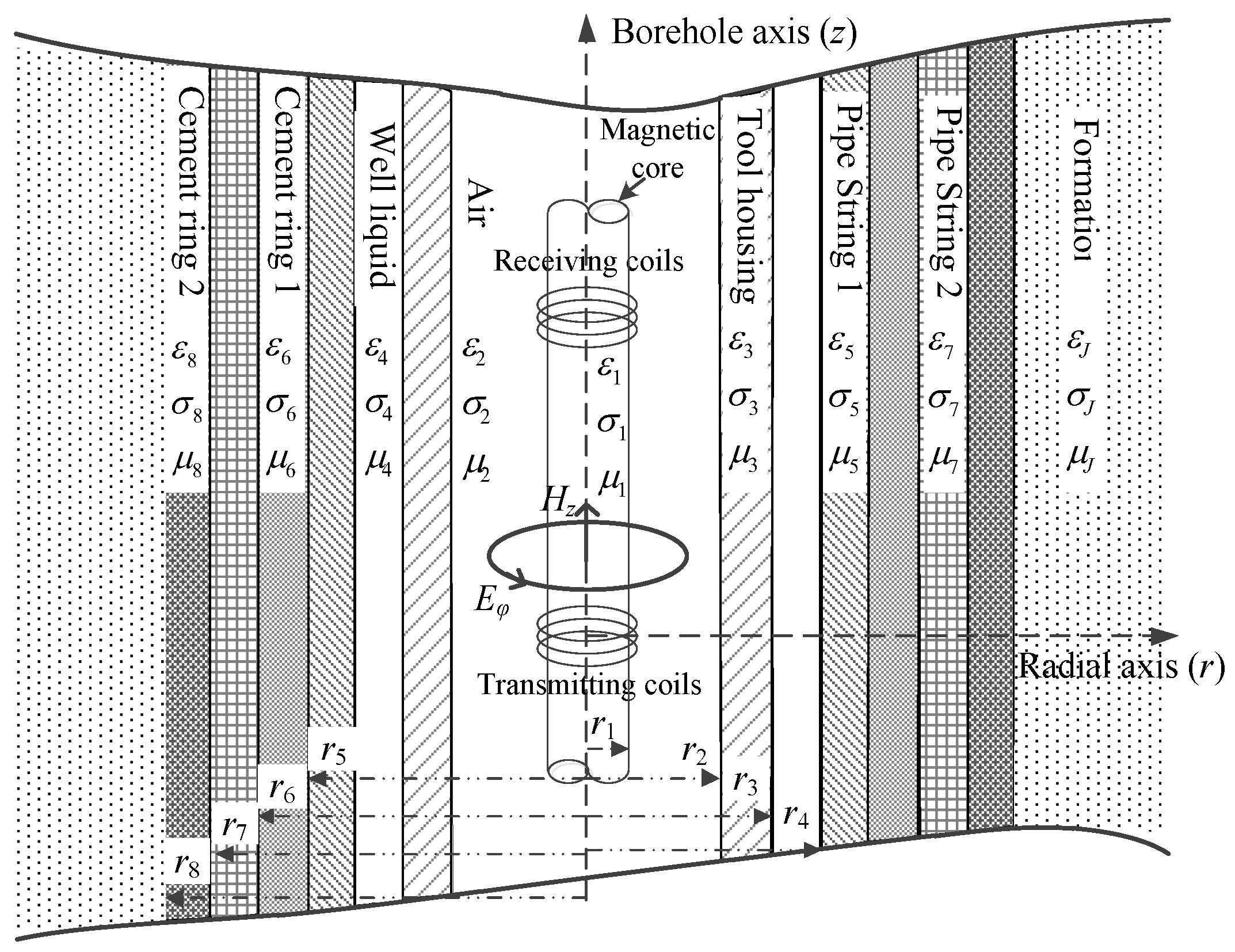
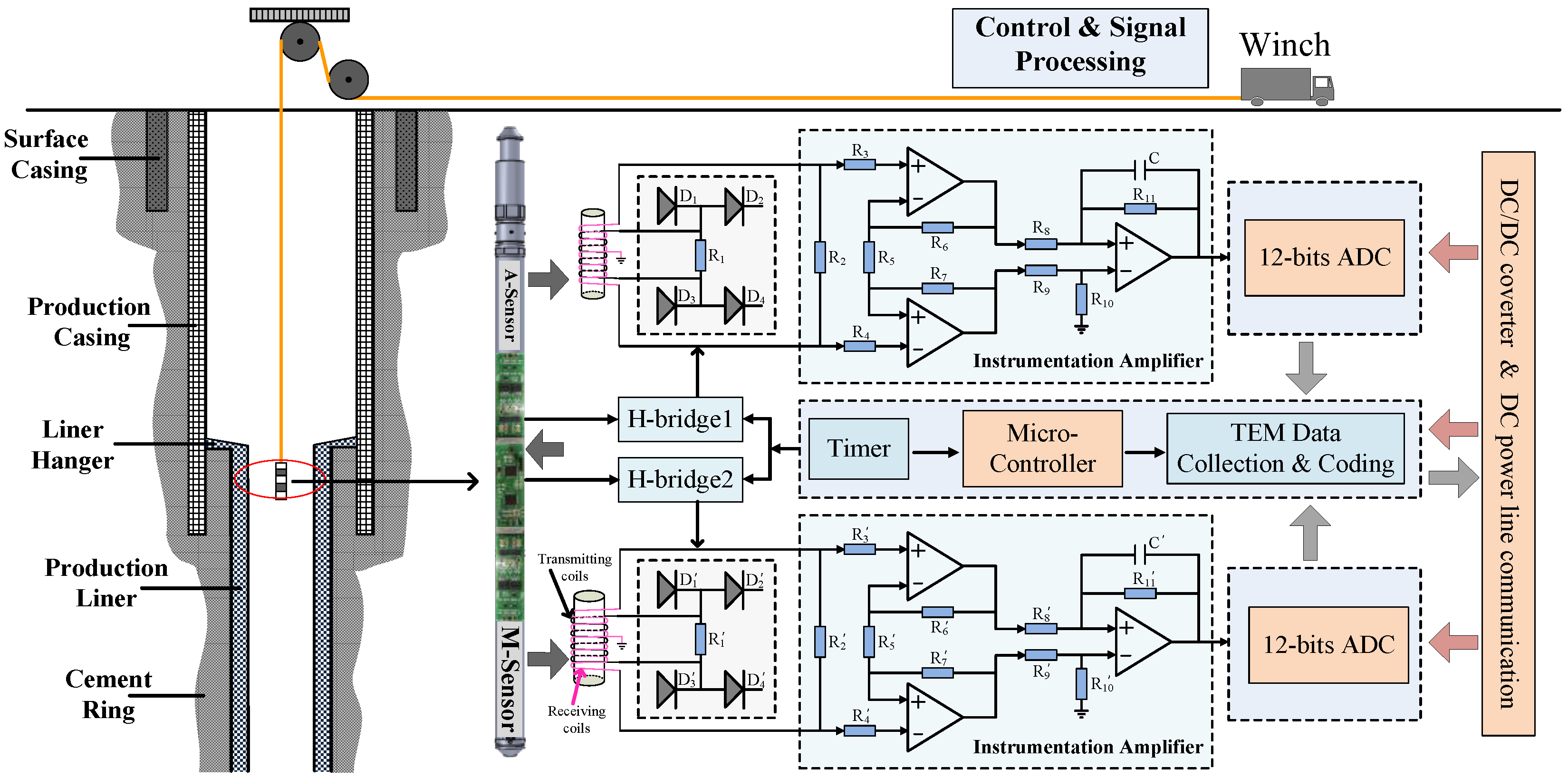
2. Borehole TEM System Model
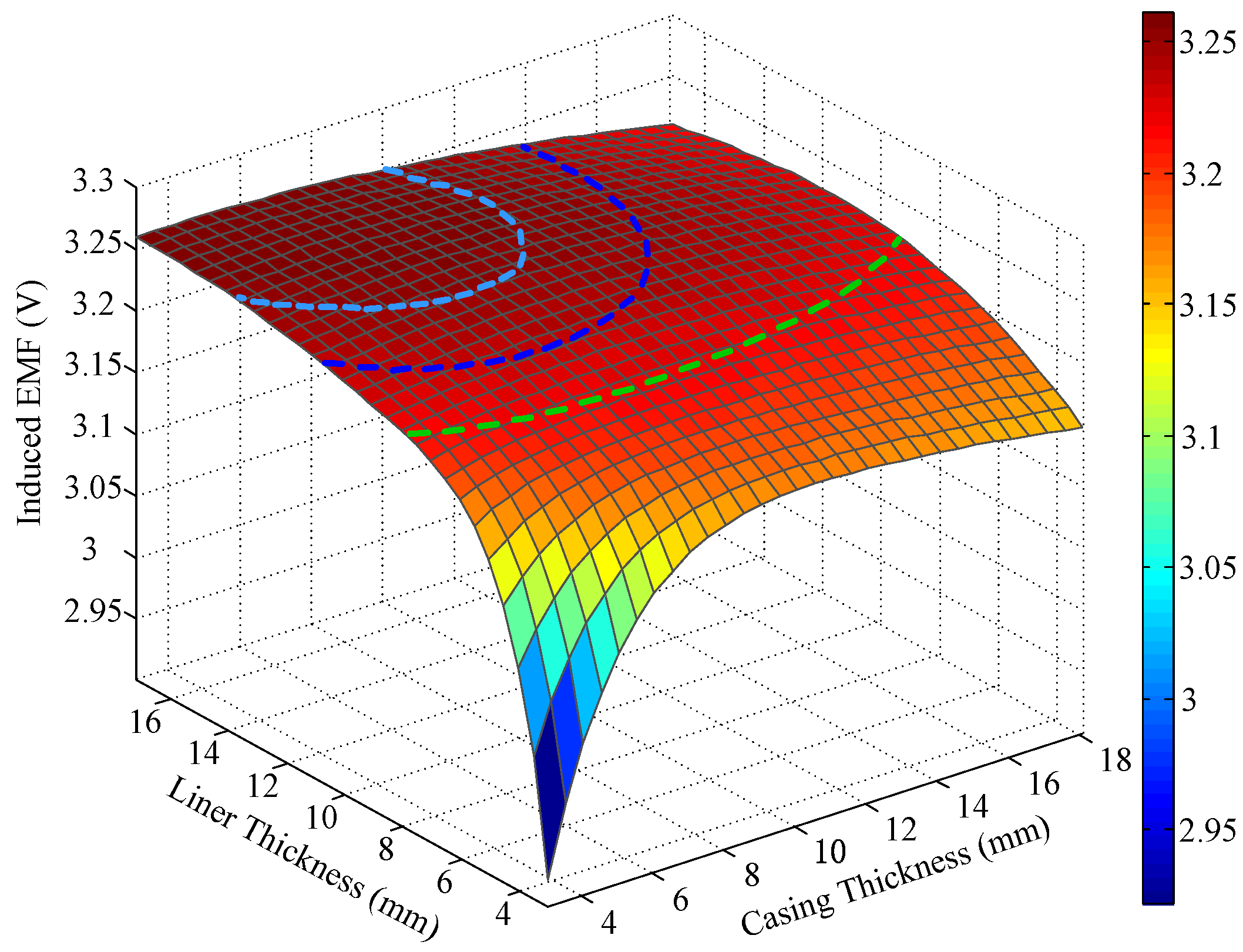
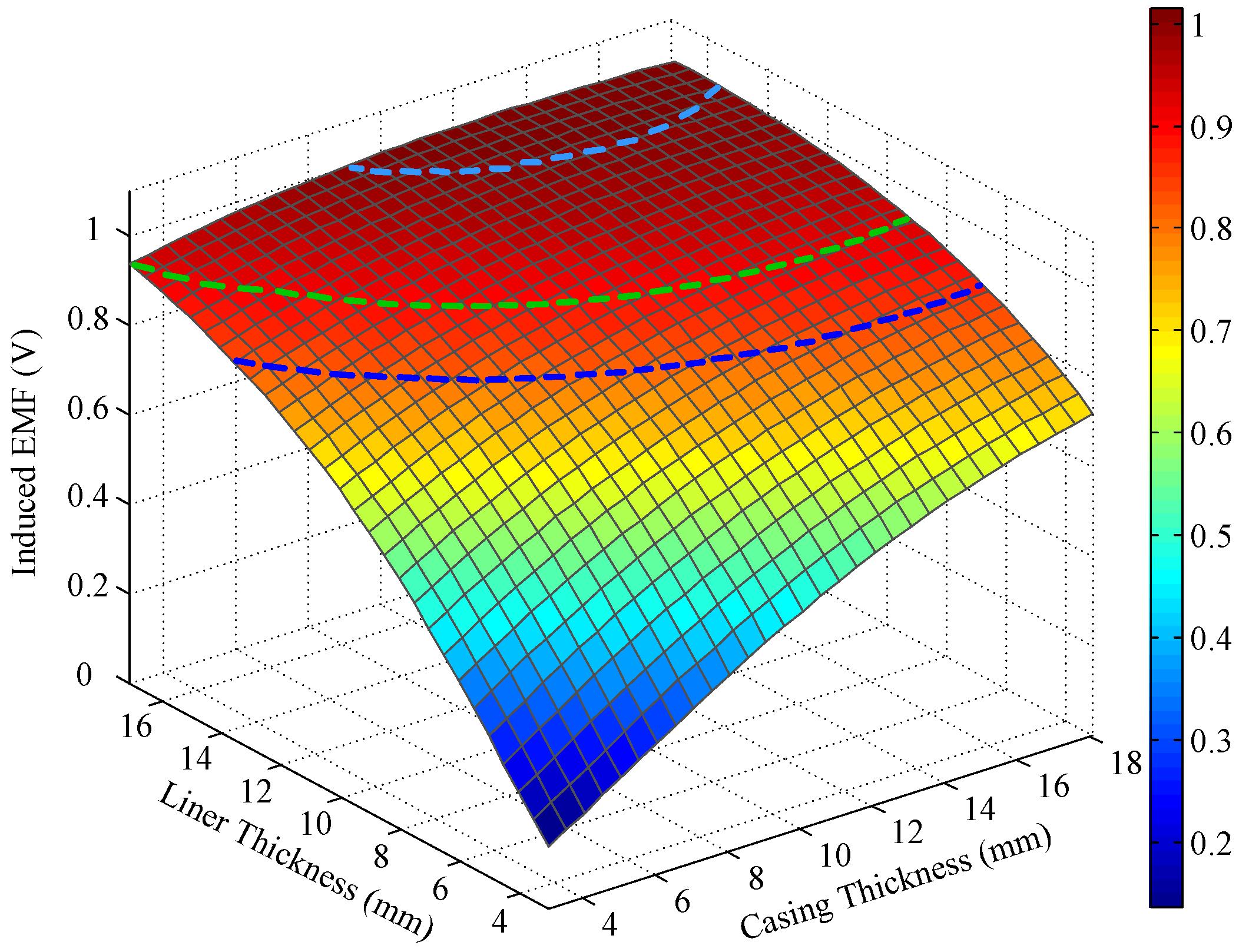
3. NDI of Multipipe Strings
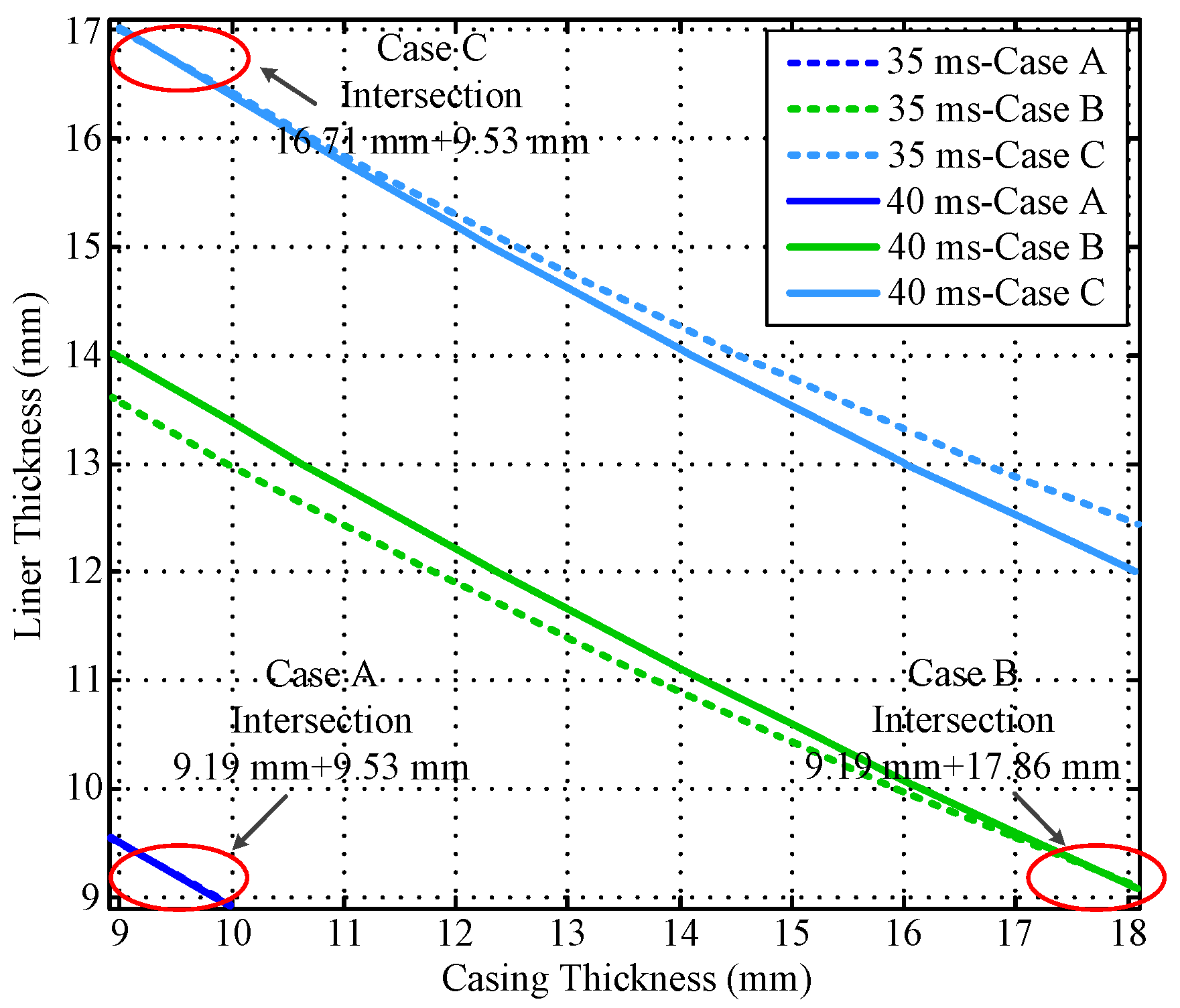
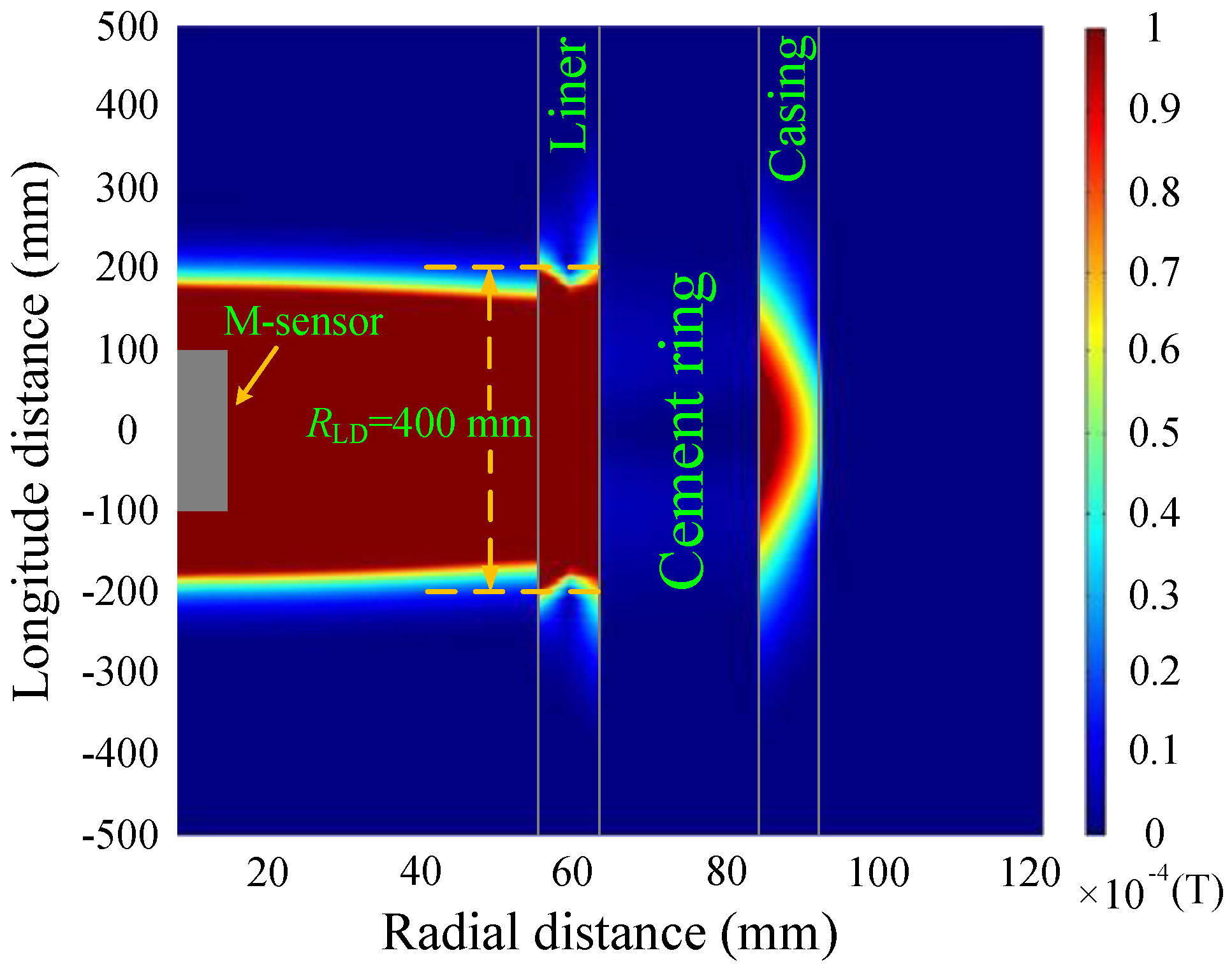
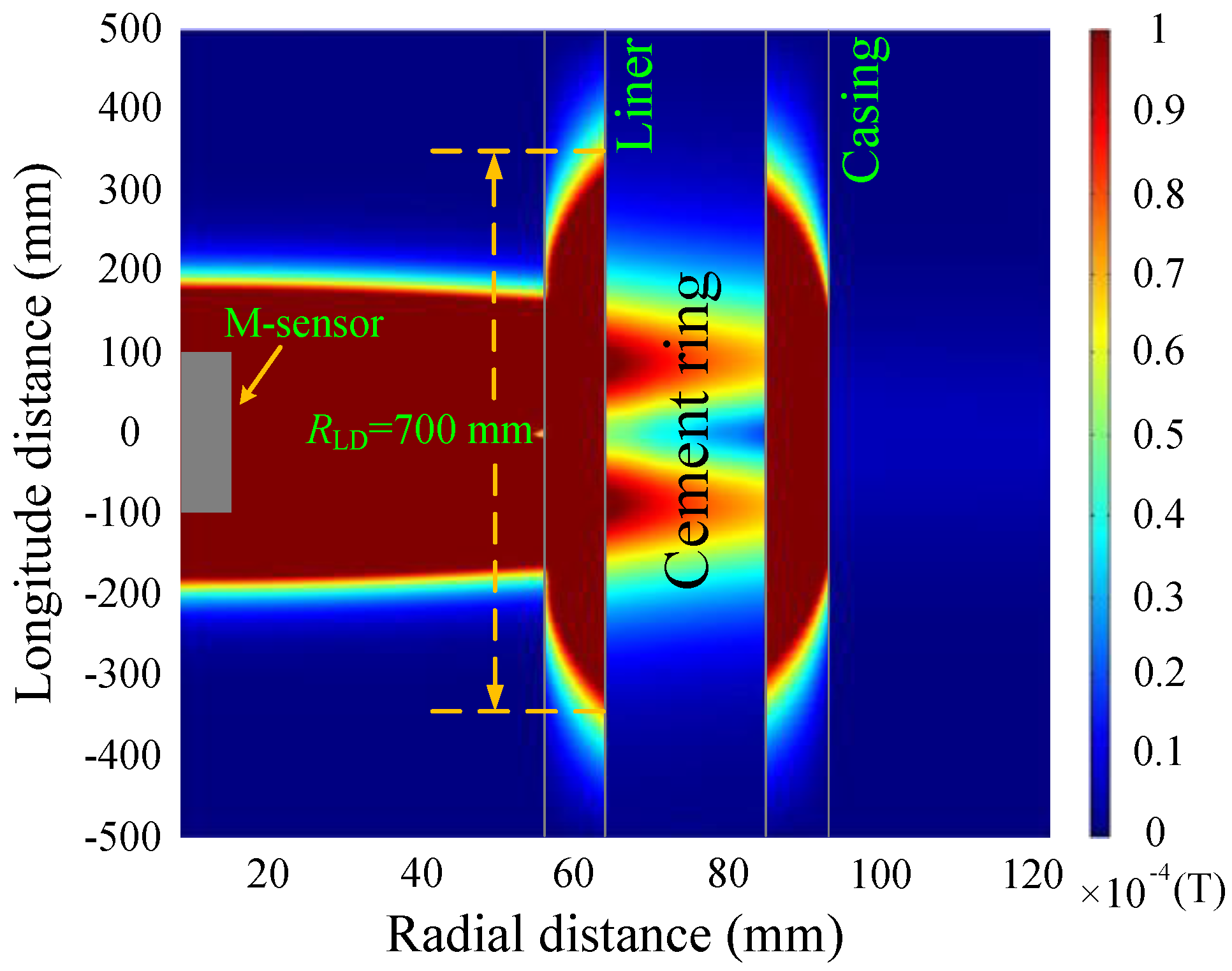
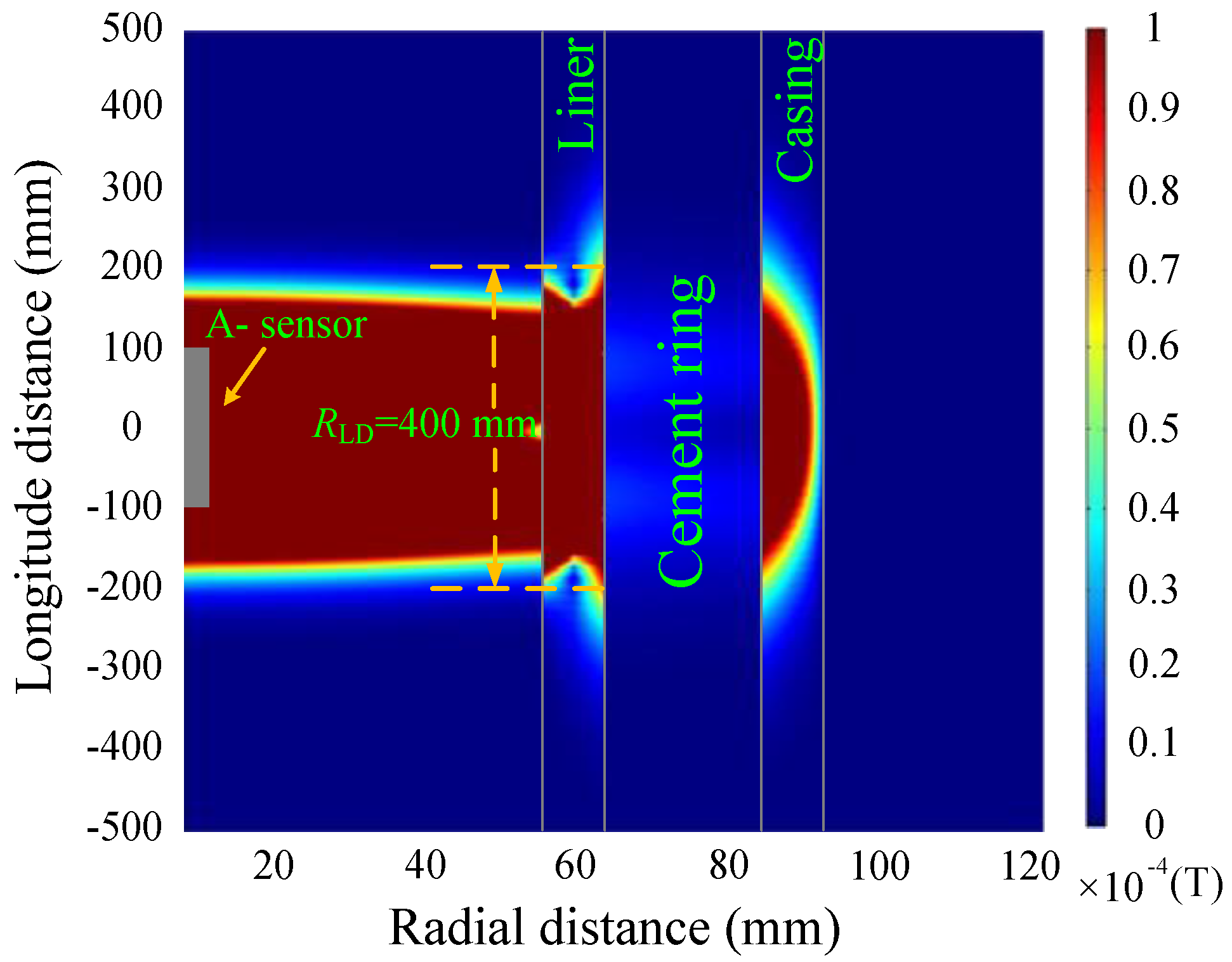
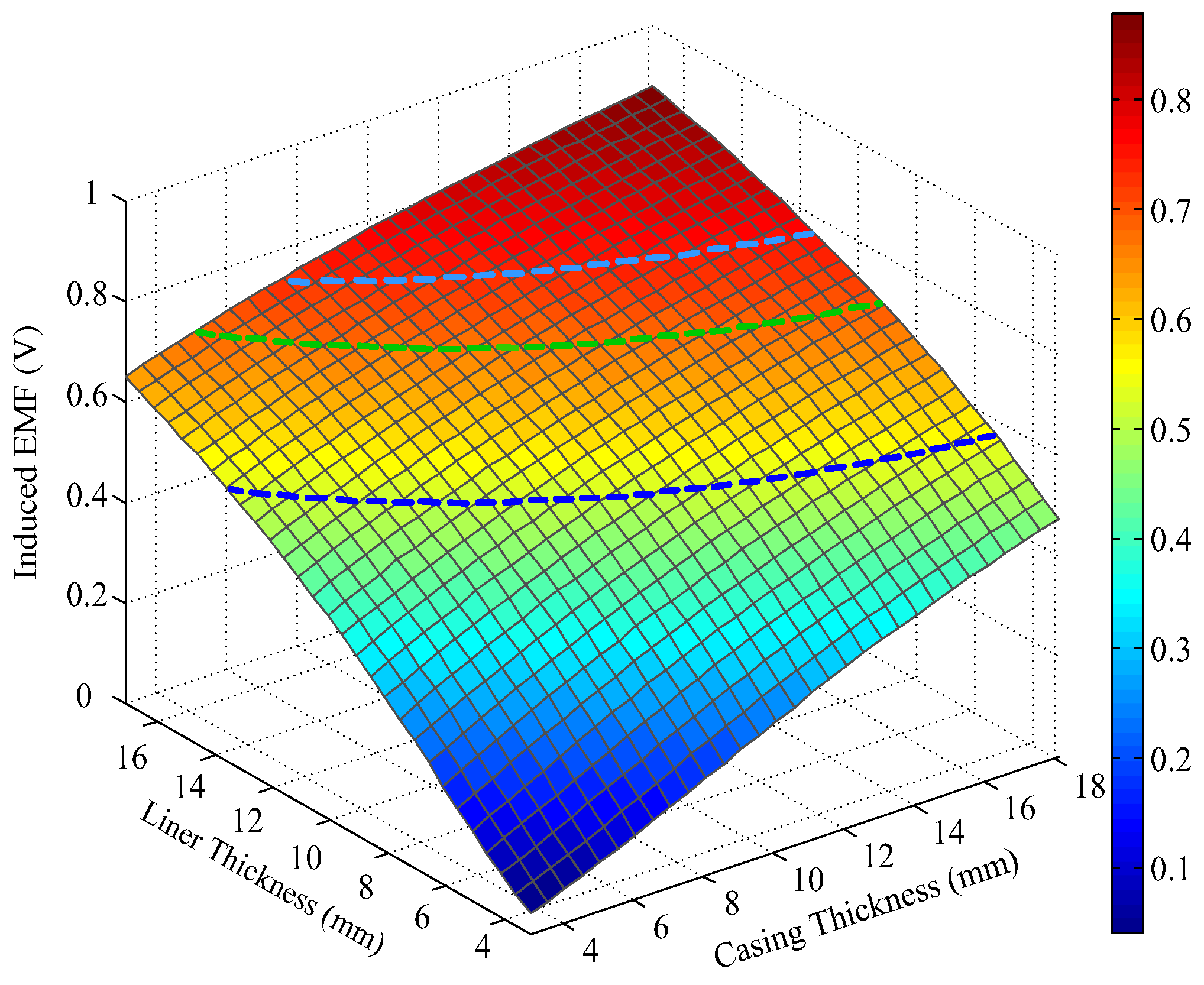
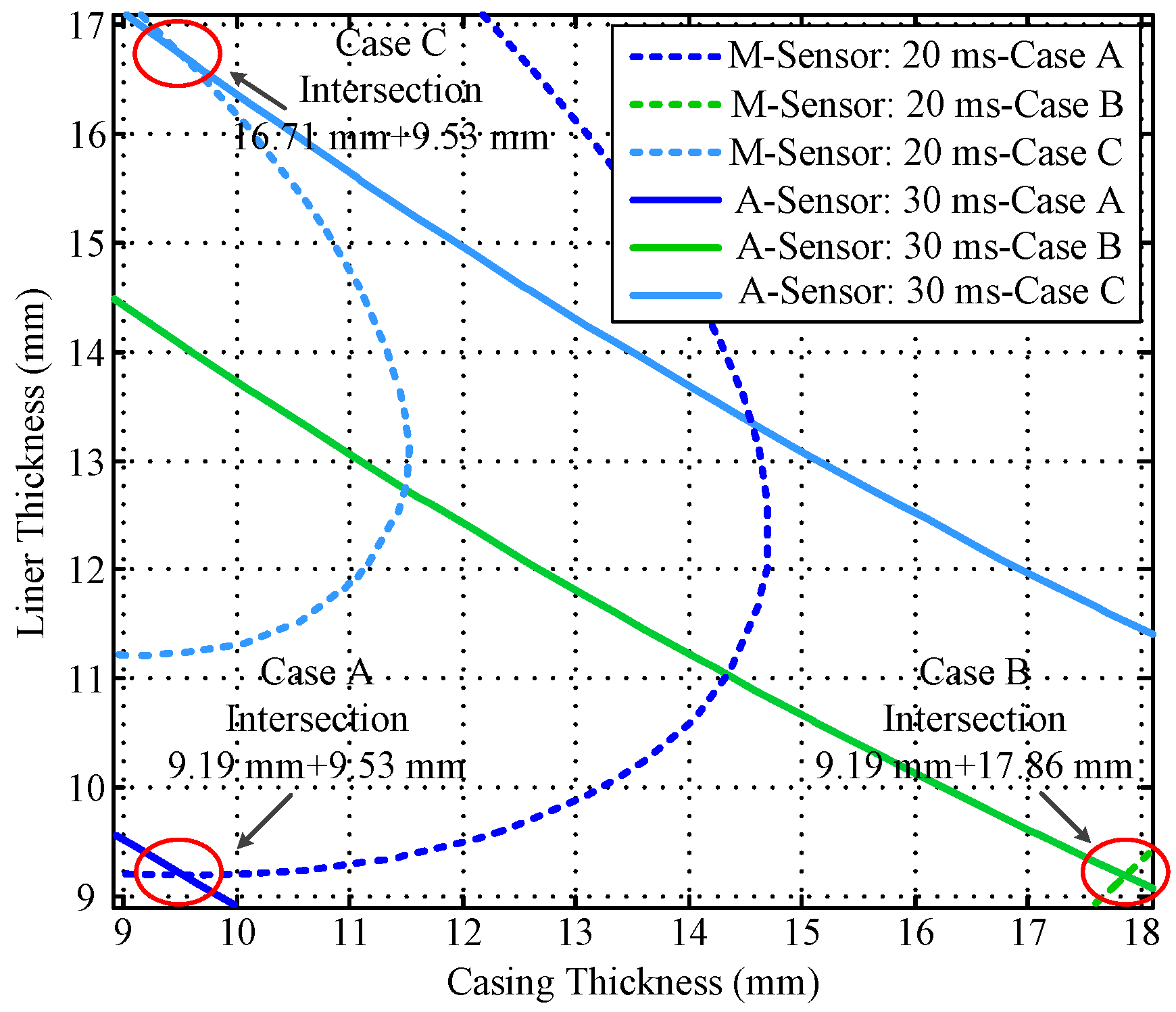
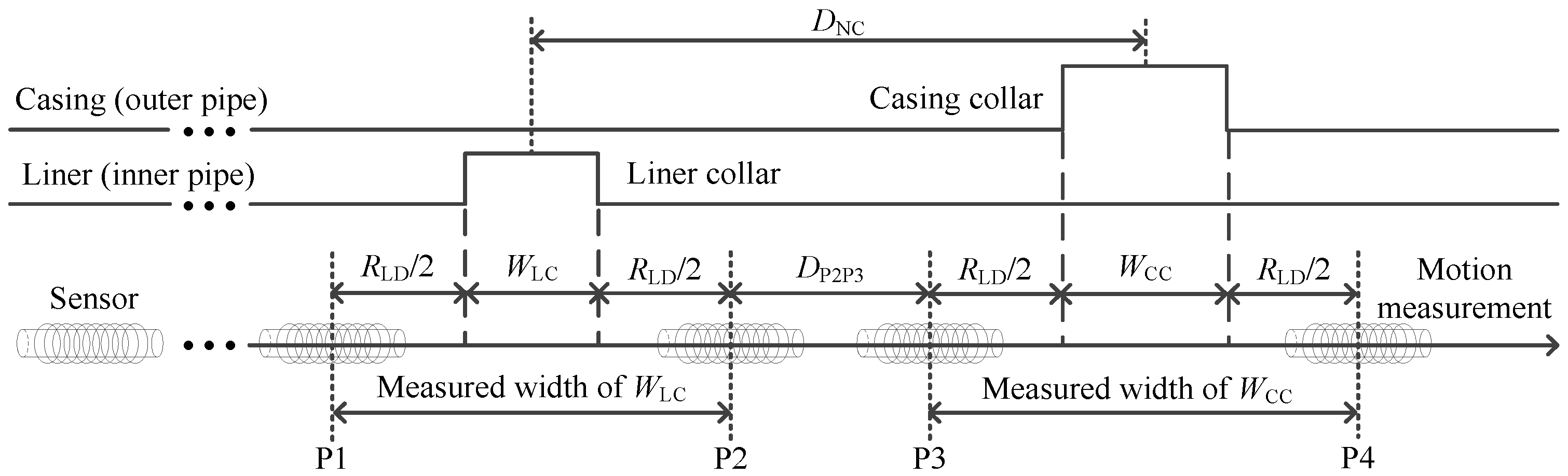
4. Auxiliary Sensor-Based NDI of Multipipe Strings
5. Field Experiments
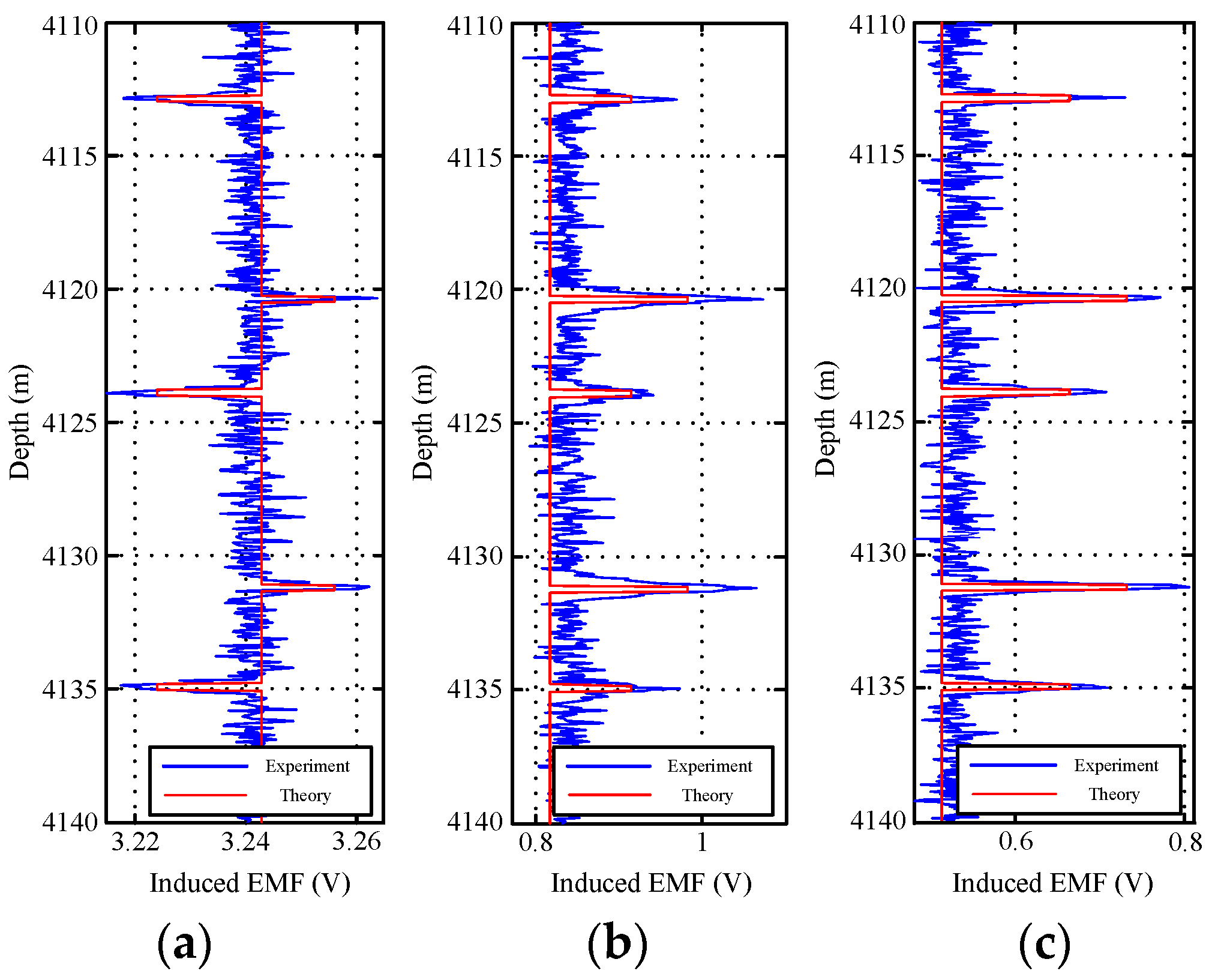
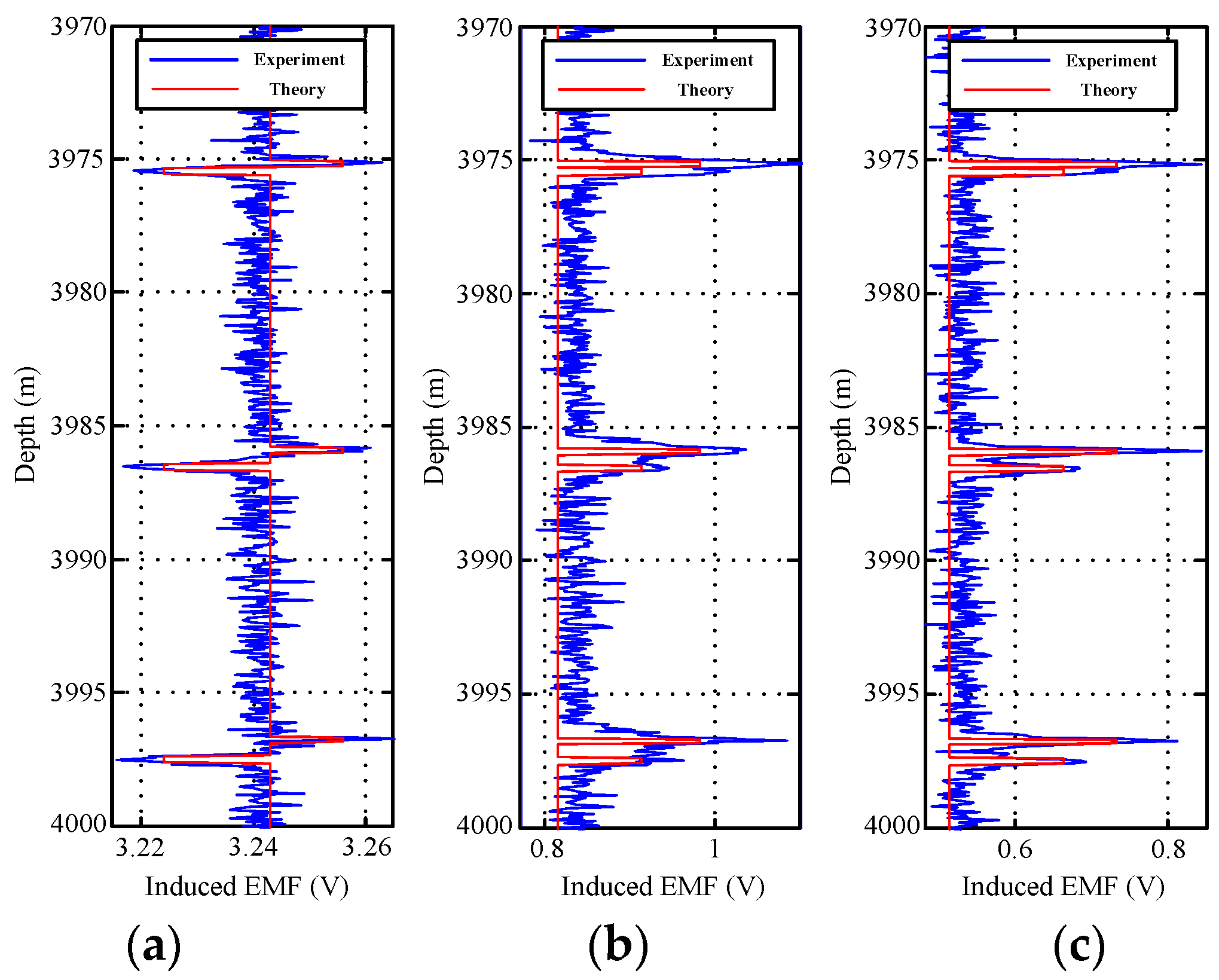
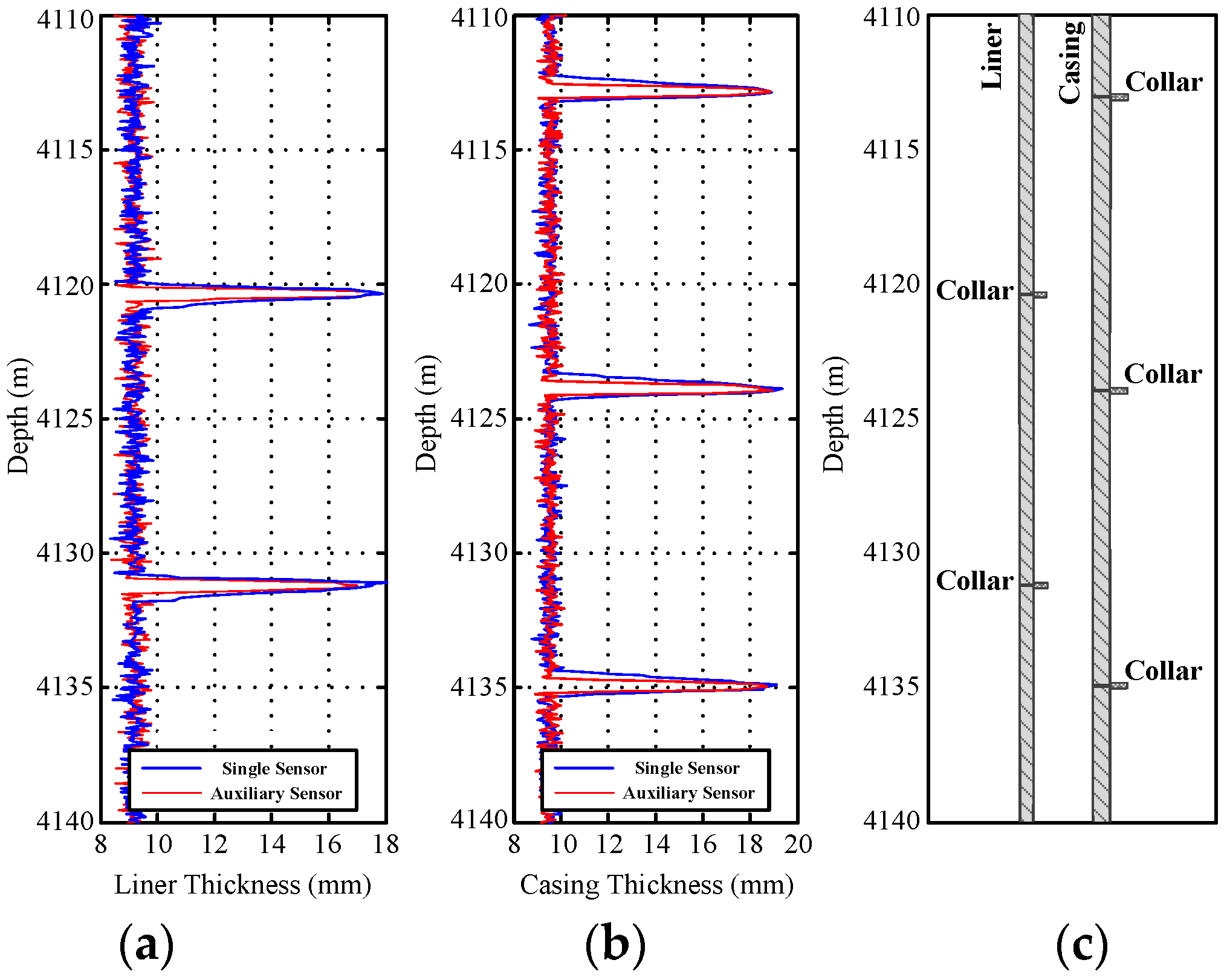
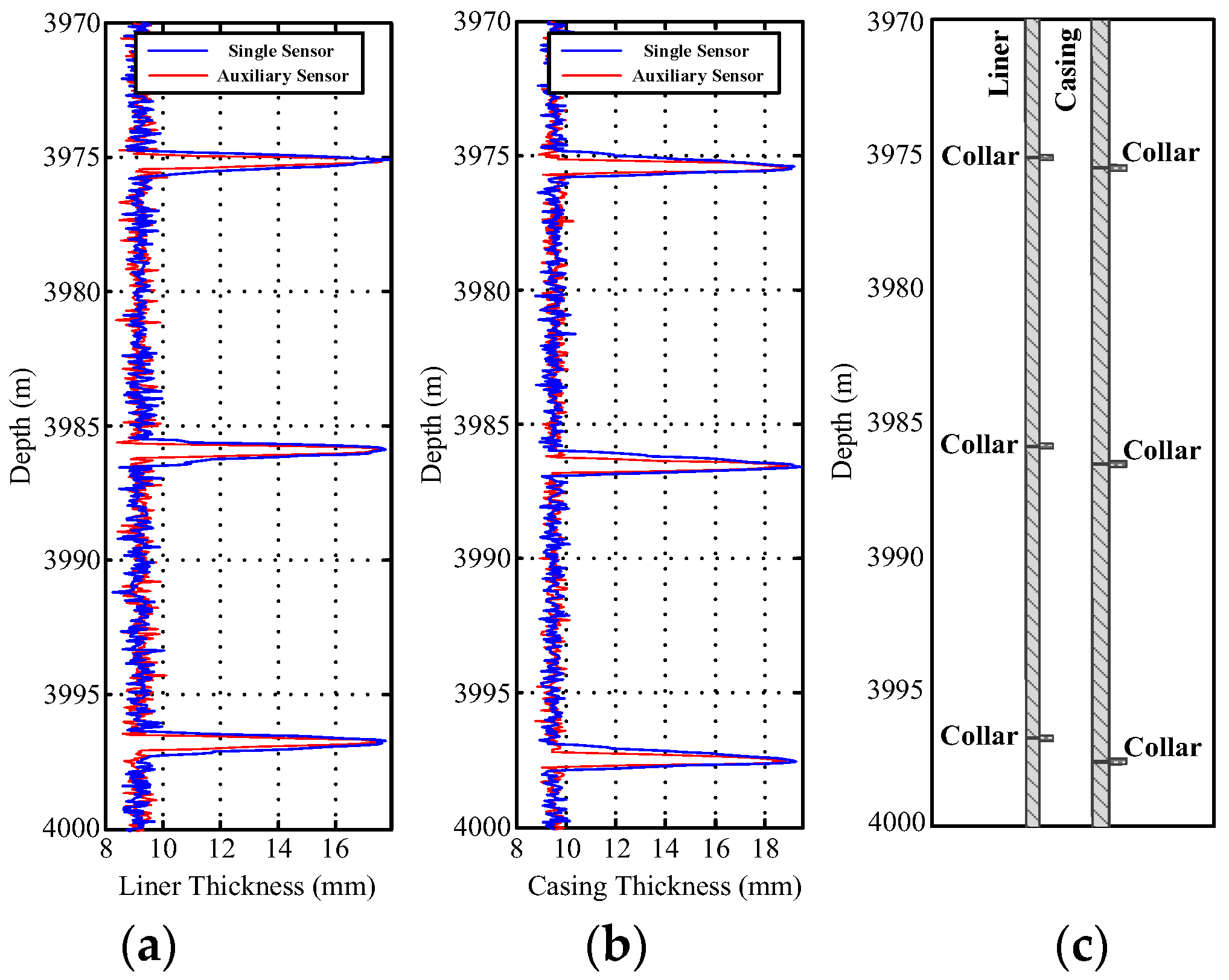
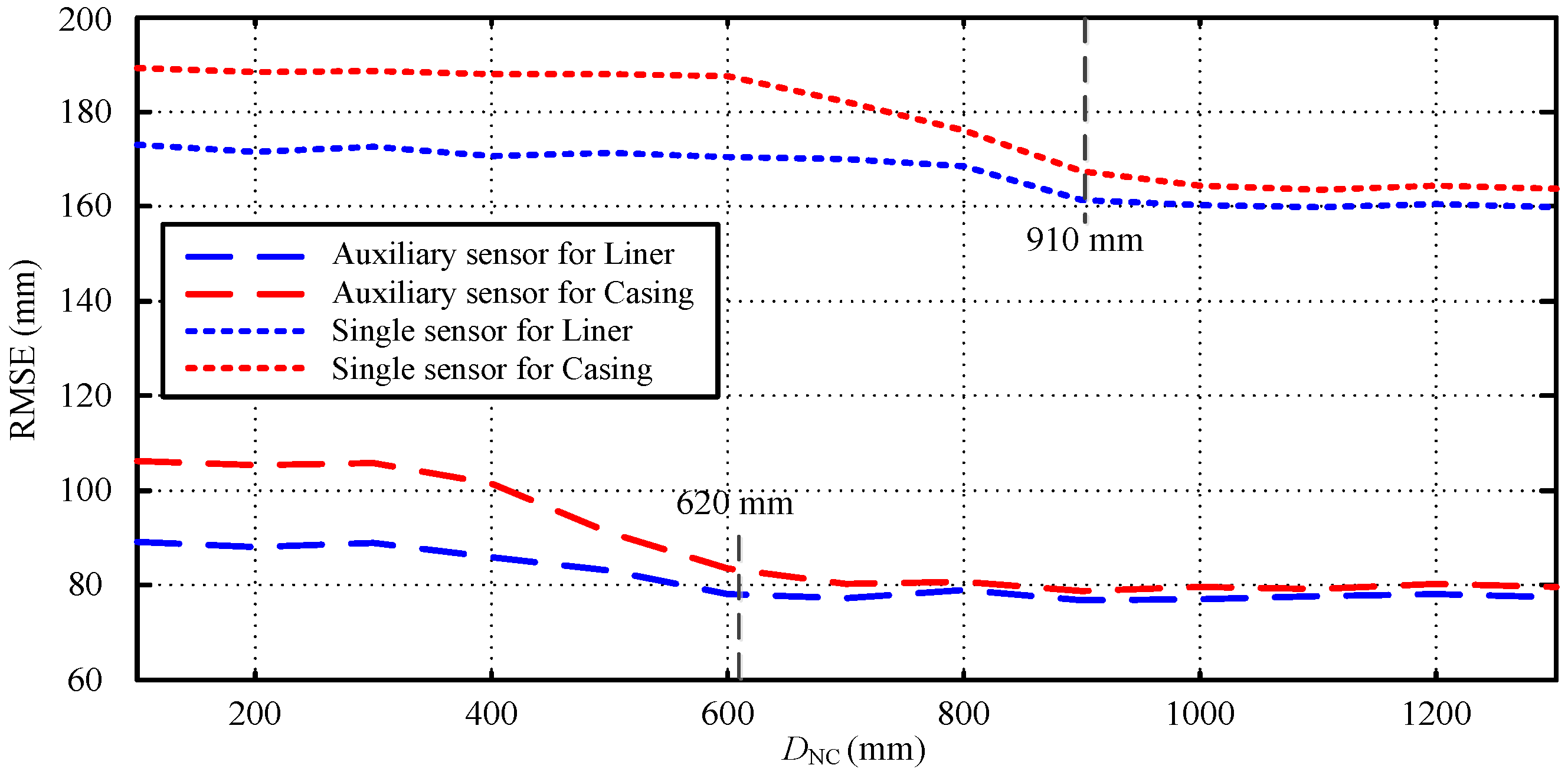
5.1. Experimental Results
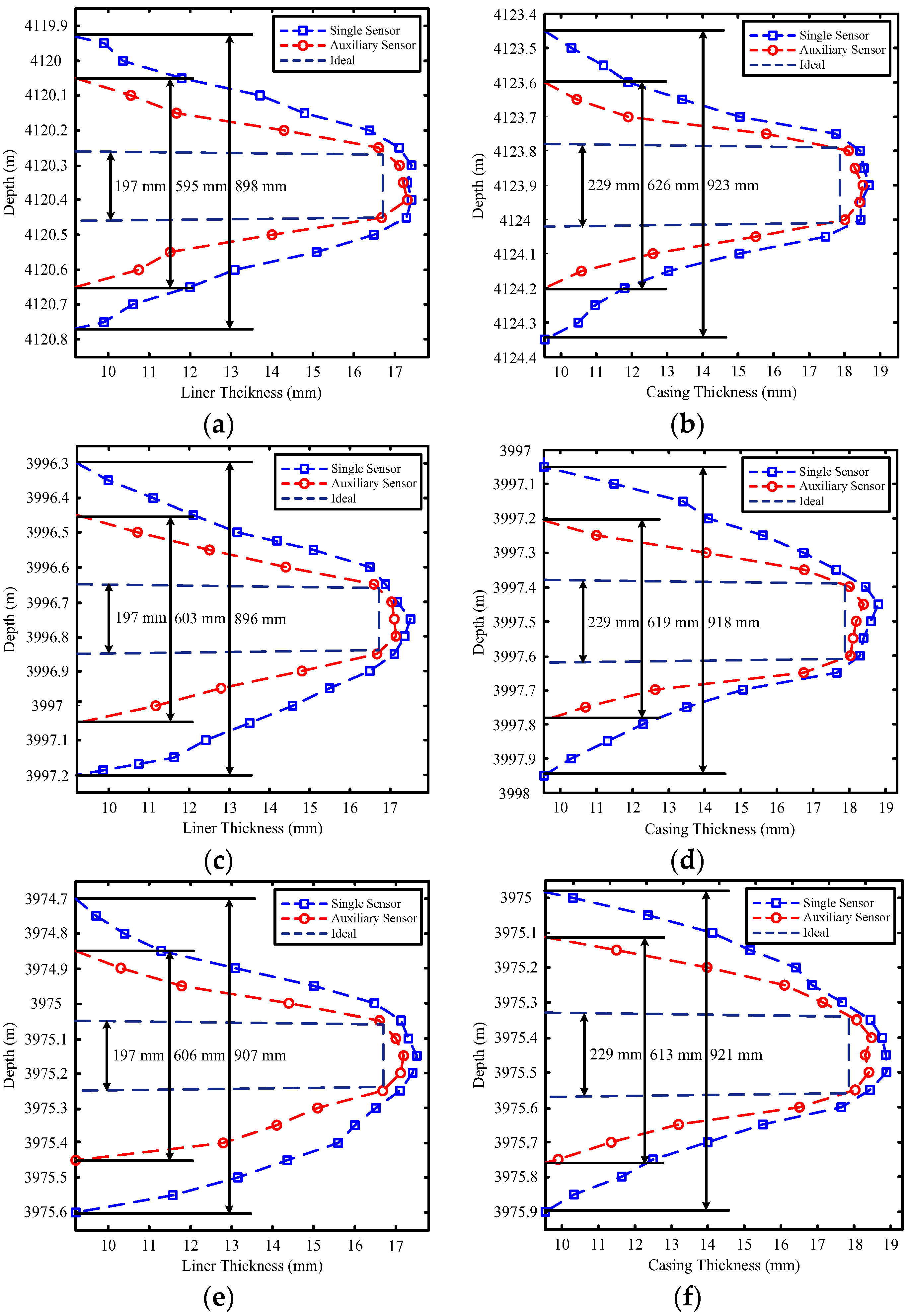
5.2. Analysis and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, C.; Liu, F.; Lin, J.; Zhu, K.; Wang, Y. An Optimized Air-Core Coil Sensor with a Magnetic Flux Compensation Structure Suitable to the Helicopter TEM System. Sensors 2016, 16, 508. [Google Scholar] [CrossRef] [PubMed]
- Danielsen, J.E.; Auken, E.; Jørgensen, F.; Jørgensen, F.; Søndergaard, V.; Sørensen, K.I. The application of the transient electromagnetic method in hydrogeophysical surveys. J. Appl. Geophys. 2003, 53, 181–198. [Google Scholar] [CrossRef]
- Ezersky, M.G.; Frumkin, A. Evaluation and mapping of Dead Sea coastal aquifers salinity using Transient Electromagnetic (TEM) resistivity measurements. C. R. Geosci. 2017, 349, 1–11. [Google Scholar] [CrossRef]
- Christiansen, A.V.; Auken, E.; Sørensen, K. The transient electromagnetic method. Groundw. Geophys. 2009, 179–226. [Google Scholar]
- Dang, B.; Yang, L.; Dang, R.; Xie, Y. Borehole electromagnetic induction system with noise cancelation for casing inspection. IEICE Electron. Express 2016, 13, 20160714. [Google Scholar] [CrossRef]
- Dutta, S.M.; Reiderman, A.; Schoonover, L.G. New Borehole Transient Electromagnetic System for Reservoir Monitoring. Petrophysics 2012, 53, 222–232. [Google Scholar]
- Spies, B.R. Electrical and electromagnetic borehole measurements: A review. Surv. Geophys. 1996, 17, 517–556. [Google Scholar] [CrossRef]
- Huang, S.; Wang, S. The Pulsed Eddy Current Testing. In New Technologies in Electromagnetic Non-Destructive Testing; Springer: Singapore, 2016. [Google Scholar]
- Mokros, S.G.; Underhill, P.R.; Morelli, J.E.; Krause, T.W. Pulsed Eddy Current Inspection of Wall Loss in Steam Generator Trefoil Broach Supports. IEEE Sens. J. 2017, 17, 444–449. [Google Scholar] [CrossRef]
- Garcíamartín, J.; Gómezgil, J.; Vázquezsánchez, E. Non-Destructive Techniques Based on Eddy Current Testing. Sensors 2011, 11, 2525–2565. [Google Scholar] [CrossRef] [PubMed]
- Park, D.G.; Kishore, M.B.; Kim, J.Y.; Jacobs, L.J.; Lee, D.H. Detection of Corrosion and Wall Thinning in Carbon Steel Pipe Covered With Insulation Using Pulsed Eddy Current. J. Magn. 2016, 21, 57–60. [Google Scholar] [CrossRef]
- Bateman, R.M. Casing Inspection Cased-Hole Log Analysis and Reservoir Performance Monitoring; Springer: New York, NY, USA, 2015; pp. 227–243. [Google Scholar]
- Technical Report on Equations and Calculations for Casing, Tubing, and Line Pipe used as Casing or Tubing; and Performance Properties Tables for Casing and Tubing, 7th ed.; American Petroleum Institute: Washington, DC, USA, 2008.
- Marinov, S.G. Improved Interpretation of the Downhole Casing Inspection Logs for Two Strings of Pipess Review of Progress in Quantitative Nondestructive Evaluation; Springer: Berlin, Germany, 1985; pp. 1673–1679. [Google Scholar]
- Zhang, S.; Guergueb, N.; Garcia, J.; Yateem, K.S.; Sethi, N. Successful Application of a New Electromagnetic Corrosion Tool for Well Integrity Evaluation in Old Wells Completed with Reduced Diameter Tubular. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2013. [Google Scholar]
- Fu, Y.; Yu, R.; Peng, X.; Ren, S. Investigation of casing inspection through tubing with pulsed eddy current. NDT E Int. 2012, 27, 353–374. [Google Scholar] [CrossRef]
- Krause, H.J.; Panaitov, G.I.; Zhang, Y. Conductivity tomography for non-destructive evaluation using pulsed eddy current with HTS SQUID magnetometer. IEEE Trans. Appl. Supercon. 2003, 13, 215–218. [Google Scholar] [CrossRef]
- Stott, C.A.; Underhill, P.R.; Babbar, V.K.; Krause, T.W. Pulsed Eddy Current Detection of Cracks in Multilayer Aluminum Lap Joints. IEEE Sens. J. 2015, 15, 956–962. [Google Scholar] [CrossRef]
- Desjardins, D.R.; Vallières, G.; Whalen, P.P.; Krause, T.W. Advances in transient (pulsed) eddy current for inspection of multi-layer aluminum structures in the presence of ferrous fasteners. Am. Inst. Phys. 2012, 1, 400–407. [Google Scholar]
- Dashevsky, A.; Yu, A. Principles of Induction Logging; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]

| Parameter | Value |
|---|---|
| Radius of the main sensor | 12 mm |
| Radius of the auxiliary sensor | 6 mm |
| Number of transmitting coil turns | 95 |
| Number of receiving coil turns | 980 |
| Wire diameter of the transmitting coils | 0.46 mm |
| Wire diameter of the receiving coils | 0.18 mm |
| Resistance of the transmitting coils of the A-sensor | 1.57 Ω |
| Resistance of the receiving coils of the A-sensor | 52.8 Ω |
| Resistance of the transmitting coils of the M-sensor | 3.12 Ω |
| Resistance of the receiving coils of the M-sensor | 105.1 Ω |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, B.; Yang, L.; Du, N.; Liu, C.; Dang, R.; Wang, B.; Xie, Y. Auxiliary Sensor-Based Borehole Transient Electromagnetic System for the Nondestructive Inspection of Multipipe Strings. Sensors 2017, 17, 1836. https://doi.org/10.3390/s17081836
Dang B, Yang L, Du N, Liu C, Dang R, Wang B, Xie Y. Auxiliary Sensor-Based Borehole Transient Electromagnetic System for the Nondestructive Inspection of Multipipe Strings. Sensors. 2017; 17(8):1836. https://doi.org/10.3390/s17081836
Chicago/Turabian StyleDang, Bo, Ling Yang, Na Du, Changzan Liu, Ruirong Dang, Bin Wang, and Yan Xie. 2017. "Auxiliary Sensor-Based Borehole Transient Electromagnetic System for the Nondestructive Inspection of Multipipe Strings" Sensors 17, no. 8: 1836. https://doi.org/10.3390/s17081836
APA StyleDang, B., Yang, L., Du, N., Liu, C., Dang, R., Wang, B., & Xie, Y. (2017). Auxiliary Sensor-Based Borehole Transient Electromagnetic System for the Nondestructive Inspection of Multipipe Strings. Sensors, 17(8), 1836. https://doi.org/10.3390/s17081836





