Two Hop Adaptive Vector Based Quality Forwarding for Void Hole Avoidance in Underwater WSNs
Abstract
1. Introduction
2. Related Works
- There is an inefficient void hole avoidance mechanism opted for in AHH-VBF that is further modified in the proposed scheme.
- Forwarder selection in 2hop-AHH-VBF is based on the potential neighbor number (PNN) of the forwarder node in the area towards the destination (ATD). Hence, it aims to optimize the forwarder selection criterion different from the AHH-VBF adopted.
- In QF-AHH-VBF, every node computes the composite priority function () to elect itself as a qualified node. The node that secures high among the PNN of a sender node is assigned the lowest holding time. Eventually, network throughput and end-to-end delay are achieved opting for this mechanism.
3. Proposed Schemes
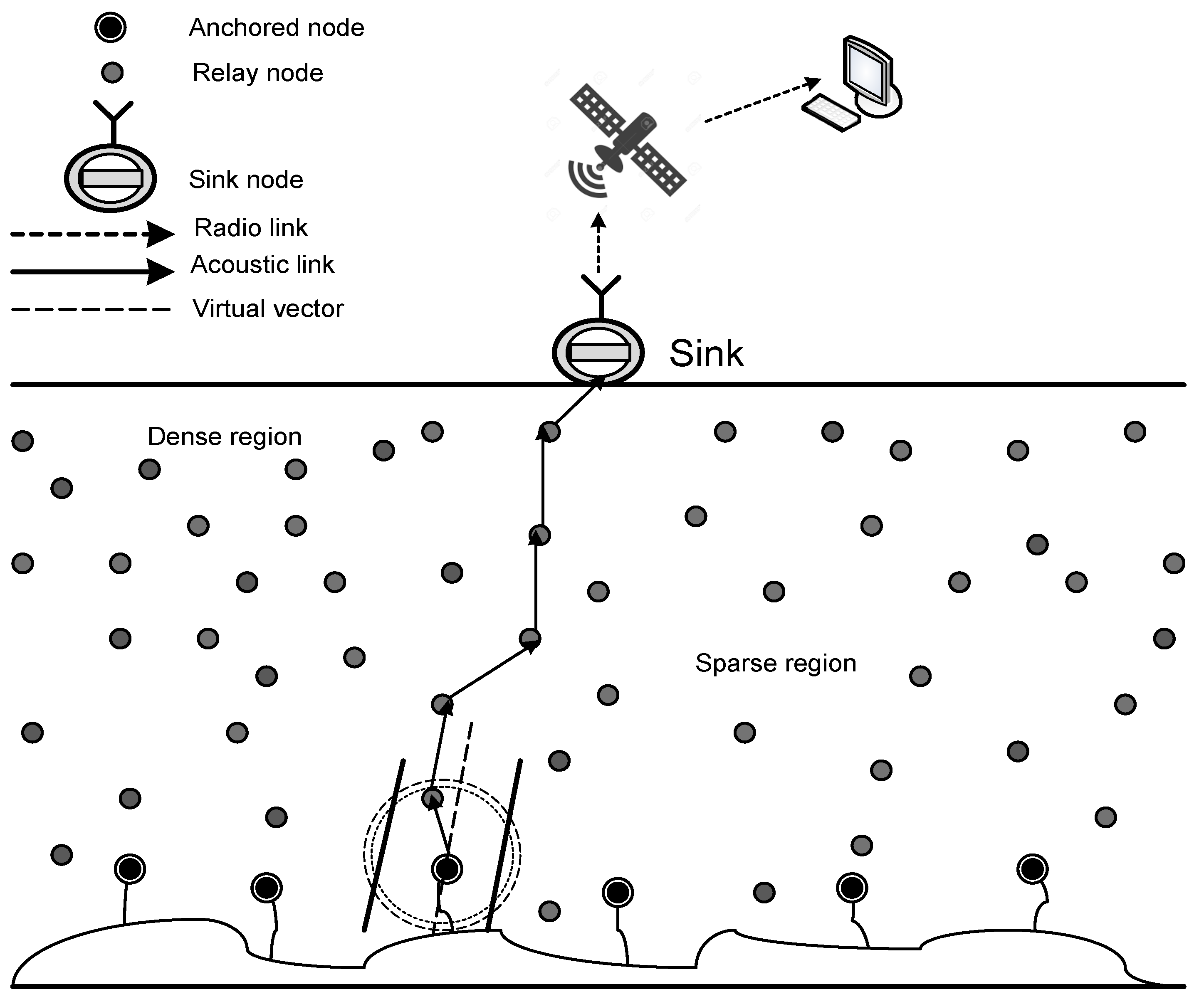
3.1. Network Architecture
3.2. Problem Definition
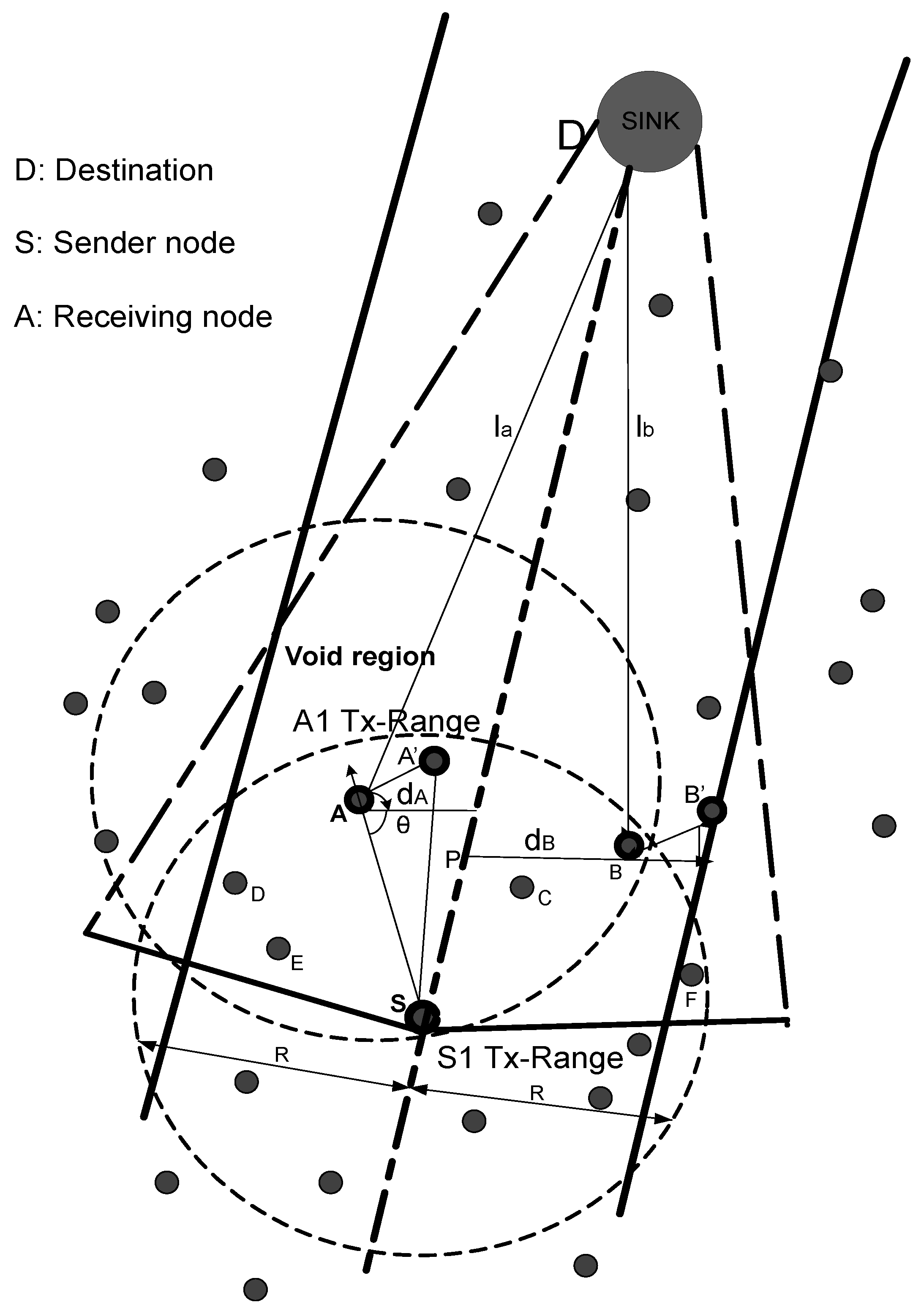
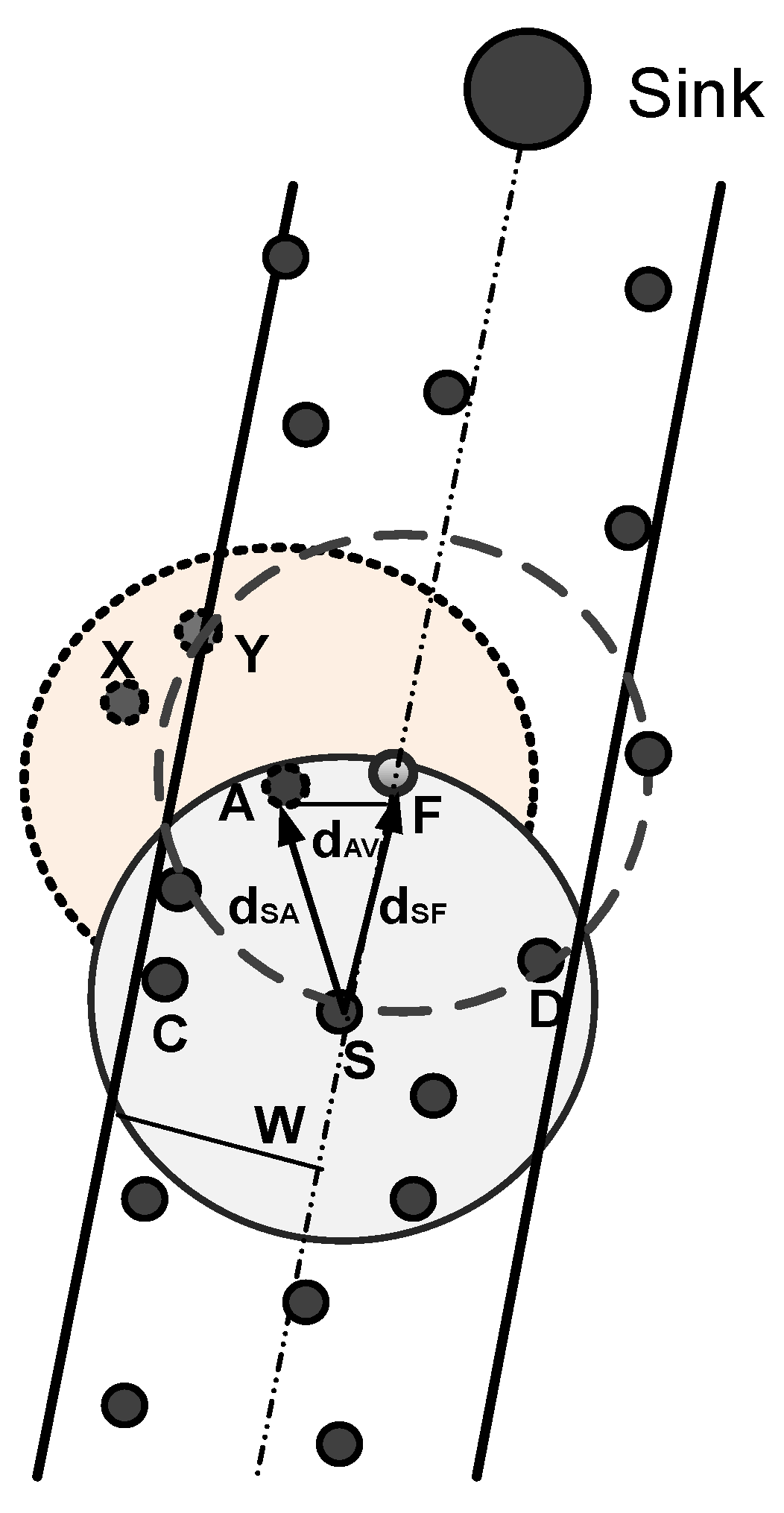
3.3. Two-Hop Adaptive Routing Scheme
3.4. Quality Forwarding for Forwarder Node Selection
3.5. Packet Types
4. Linear Programming-Based Mathematical Formulation
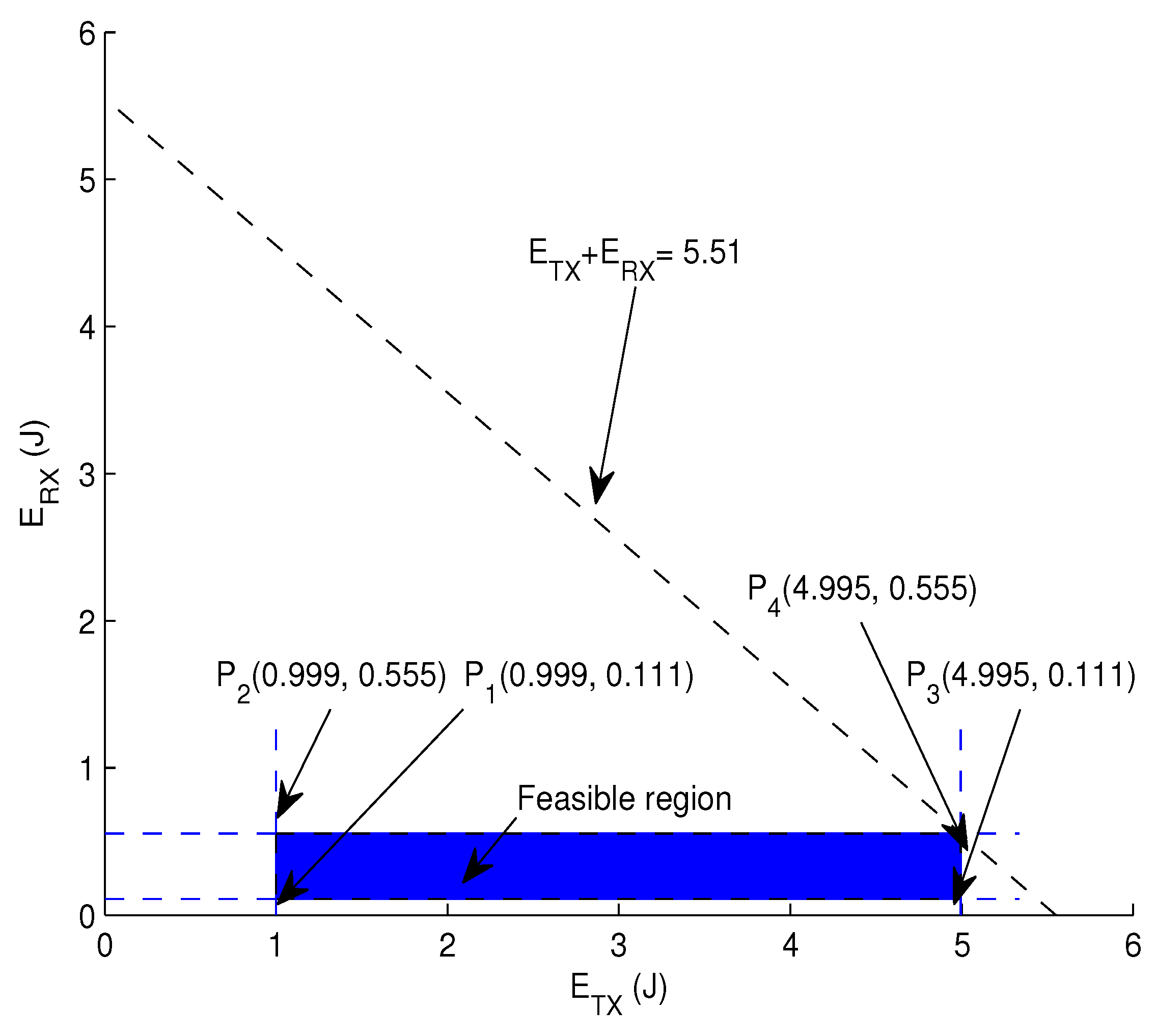
4.1. Energy Tax Minimization Using Linear Programming
- at J
- at J
- at J
- at J.
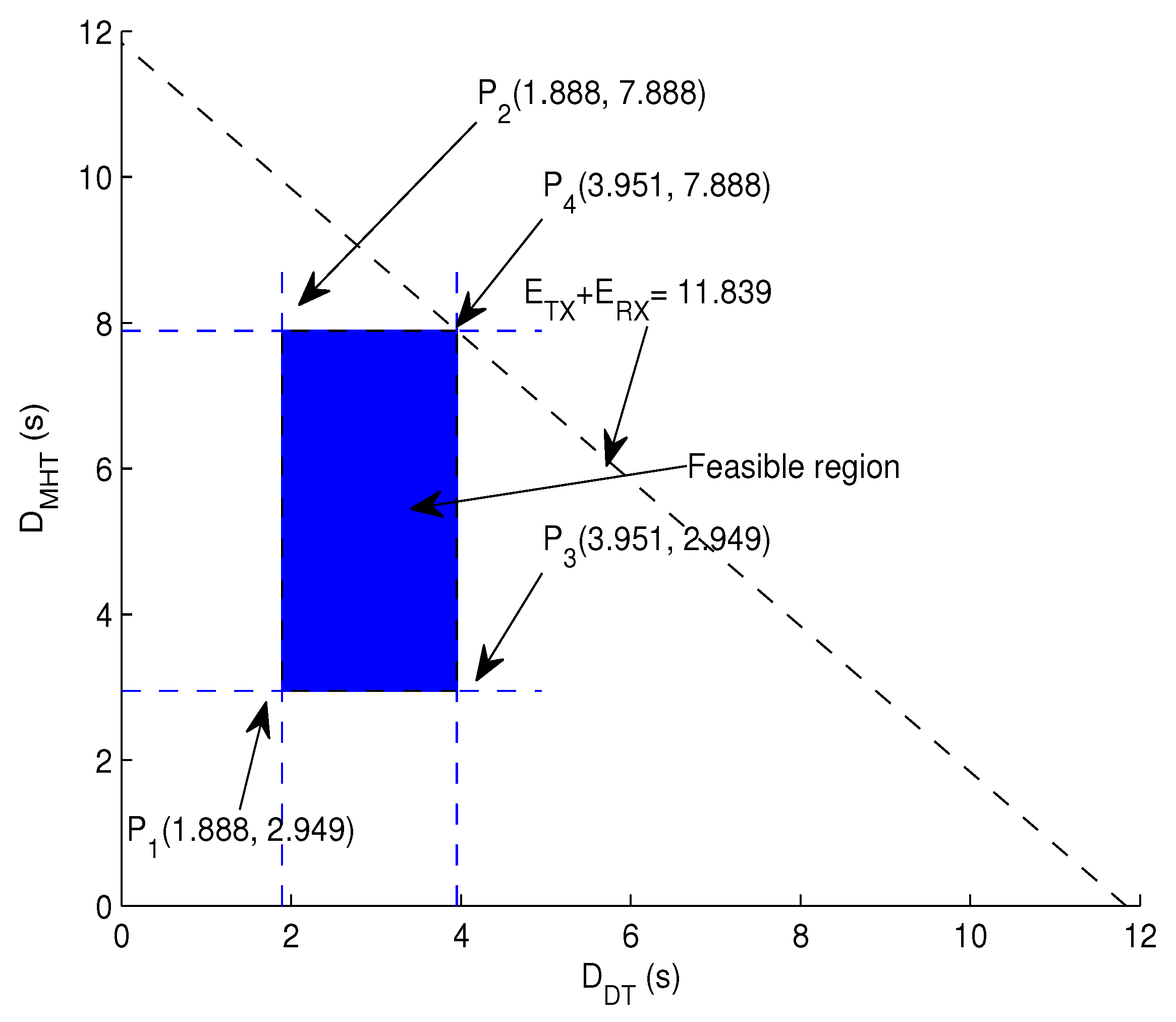
4.2. End-To-End Delay Minimization Using Linear Programming
- at
- at
- at
- at
- at C1:
- at C2:
- at C3:
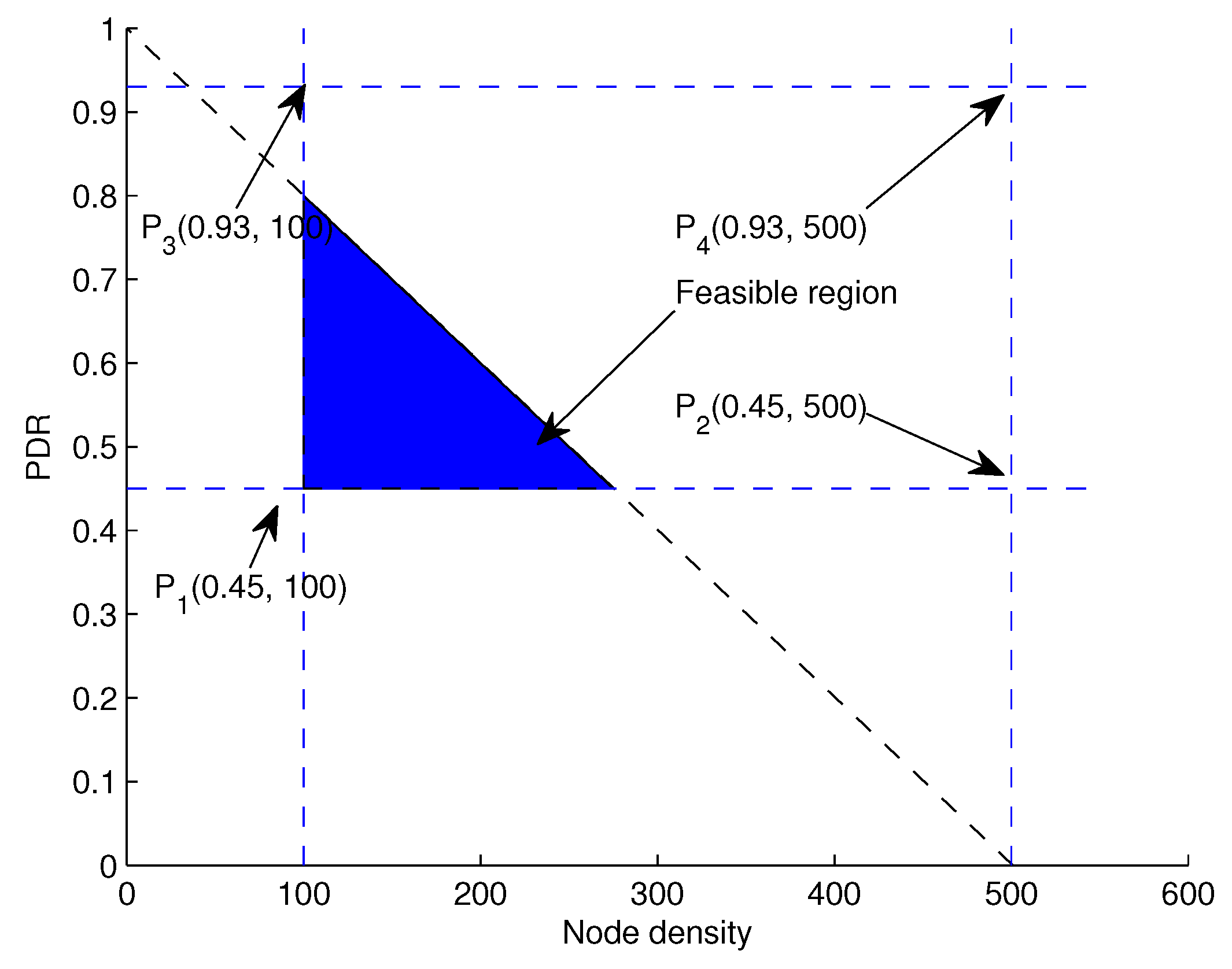
4.3. Throughput Maximization Using Linear Programming
- C1:
- C2:
- C3:,
- C4:. Feasible solution lies in the shaded region as can be seen in Figure 7.
5. Performance Evaluation
5.1. Performance Metrics
5.2. Discussion
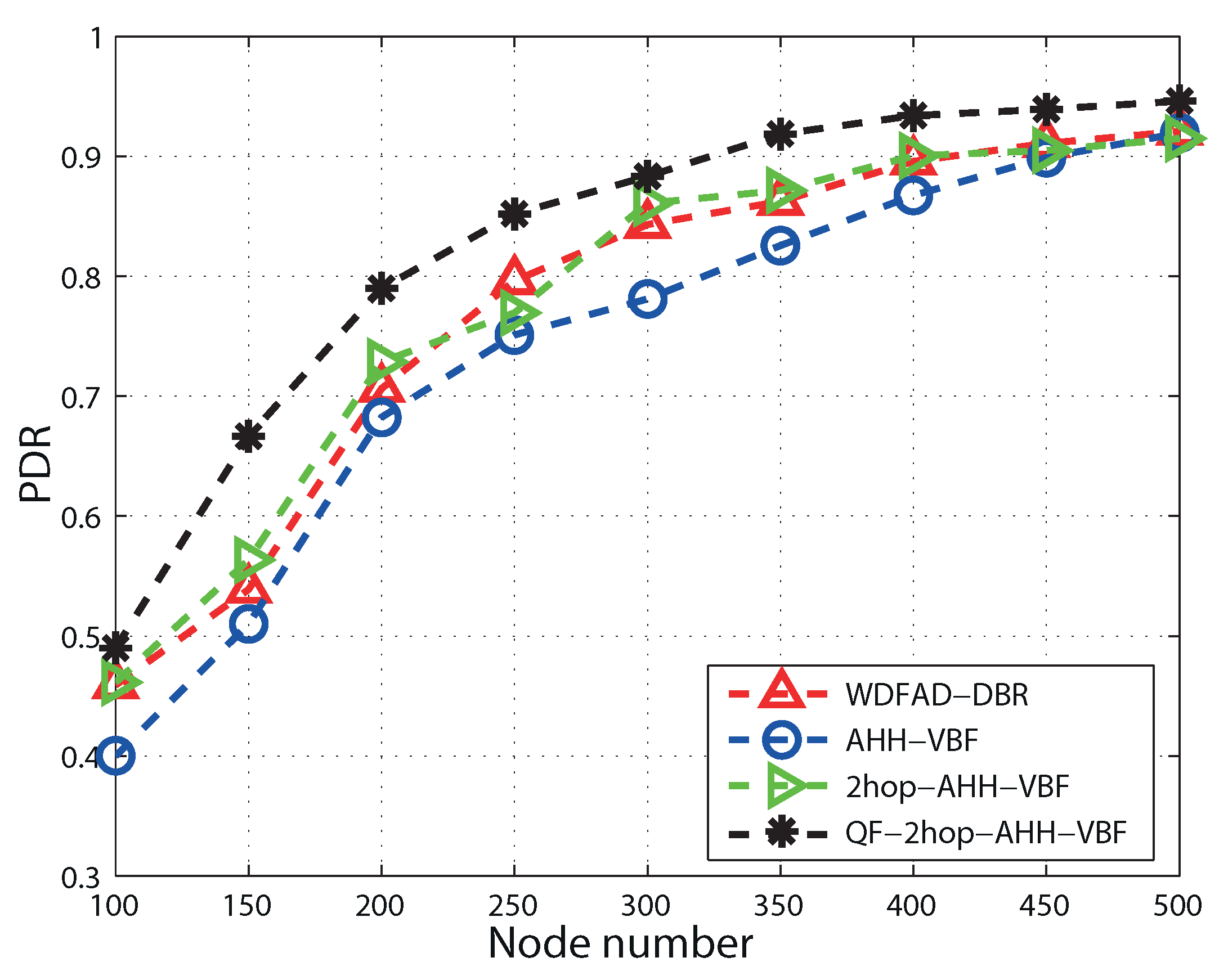
5.3. Packet Delivery Ratio
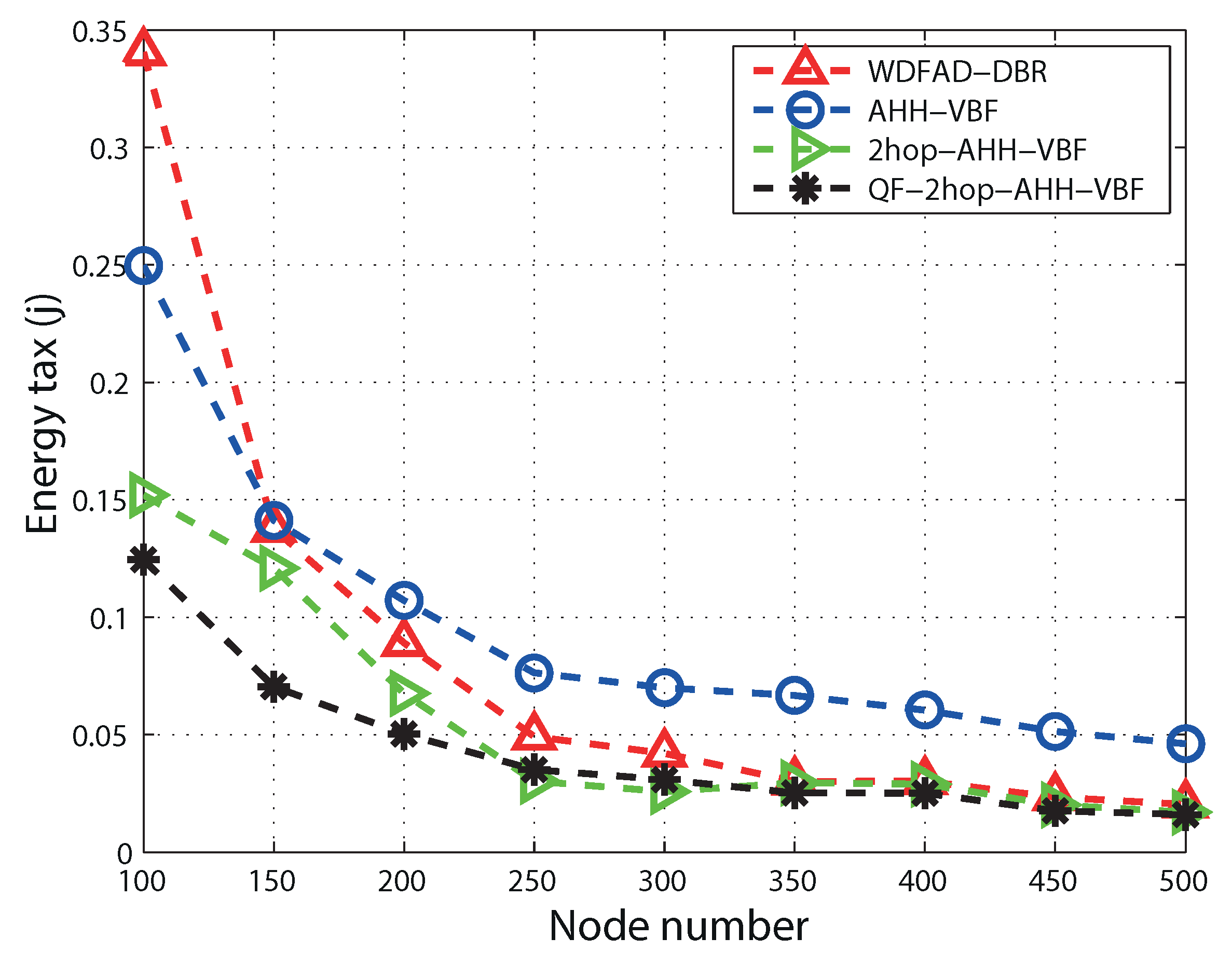
5.4. Energy Tax
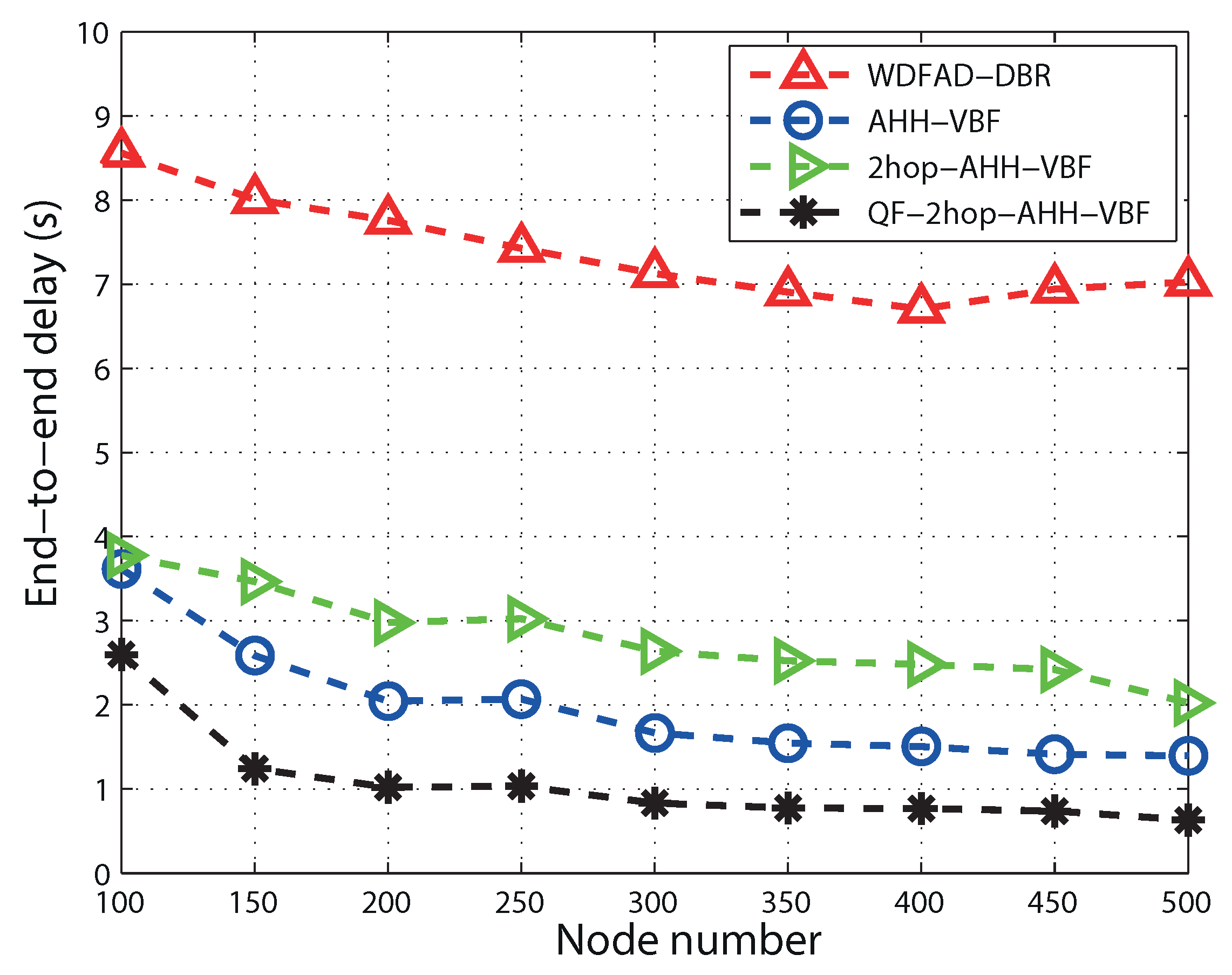
5.5. End-To-End Delay
6. Trade-Off Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Azam, I.; Javaid, N.; Ahmad, A.; Wadood, A.; Almogren, A.; Alamri, A. Balanced Load Distribution with Energy Hole Avoidance in Underwater WSNs. IEEE Access 2017. [Google Scholar] [CrossRef]
- Javaid, N.; Shah, M.; Ahmad, A.; Imran, M.; Khan, M.I.; Vasilakos, A.V. An Enhanced Energy Balanced Data Transmission Protocol for Underwater Acoustic Sensor Networks. Sensors 2016, 16, 487. [Google Scholar] [CrossRef] [PubMed]
- Akbar, M.; Javaid, N.; Khan, A.H.; Imran, M.; Shoaib, M.; Vasilakos, A. Efficient data gathering in 3D linear underwater wireless sensor networks using sink mobility. Sensors 2016, 16. [Google Scholar] [CrossRef] [PubMed]
- Larsson, P. Selection diversity forwarding in a multihop packet radio network with fading channel and capture. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 47–54. [Google Scholar] [CrossRef]
- Clausen, T.; Jacquet, P. Optimized Link State Routing Protocol (OLSR). 2003. Available online: http://www.rfc-editor.org/info/rfc3626 (accessed on 28 July 2017).
- Perkins, C.E.; Bhagwat, P. Highly dynamic destination-sequenced distance-vector routing (DSDV) for mobile computers. In ACM SIGCOMM Computer Communication Review; ACM: New York, NY, USA, 1994; pp. 234–244. [Google Scholar]
- Royer, E.M.; Perkins, C.E. Multicast operation of the ad-hoc on-demand distance vector routing protocol. In Proceedings of the 5th Annual ACM/IEEE International Conference on Mobile Computing and Networking, Seattle, WA, USA, 15–19 August 1999; ACM: New York, NY, USA, 1999; pp. 207–218. [Google Scholar]
- Johnson, D.B.; Maltz, D.A. Dynamic source routing in ad hoc wireless networks. In Mobile Computing; Springer: New York, NY, USA, 1996; pp. 153–181. [Google Scholar]
- Ayaz, M.; Abdullah, A. Hop-by-hop dynamic addressing based (H2-DAB) routing protocol for underwater wireless sensor networks. In Proceedings of the International Conference on Information and Multimedia Technology, Jeju Island, Korea, 16–18 December 2009; pp. 436–441. [Google Scholar]
- Domingo, M.C. A distributed energy-aware routing protocol for underwater wireless sensor networks. Wirel. Pers. Commun. 2011, 57, 607–627. [Google Scholar] [CrossRef]
- Liu, G.; Wei, C. A new multi-path routing protocol based on cluster for underwater acoustic sensor networks. In Proceedings of the 2011 International Conference on Multimedia Technology (ICMT), Hangzhou, China, 26–28 July 2011; pp. 91–94. [Google Scholar]
- Yan, H.; Shi, Z.J.; Cui, J.-H. DBR: Depth-based routing for underwater sensor networks. In Proceedings of the International Conference on Research in Networking, Singapore, 5–9 May 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 72–86. [Google Scholar]
- Wahid, A.; Kim, D. An energy efficient localization-free routing protocol for underwater wireless sensor networks. Int. J. Distrib. Sens. Netw. 2012, 8. [Google Scholar] [CrossRef]
- Yu, H.; Yao, N.; Wang, T.; Li, G.; Gao, Z.; Tan, G. WDFAD-DBR: Weighting depth and forwarding area division DBR routing protocol for UASNs. Ad Hoc Netw. 2016, 37, 256–282. [Google Scholar] [CrossRef]
- Majid, A.; Azam, I.; Khan, T.; Khan, Z.A.; Qasim, U.; Javaid, N. A reliable and interference-aware routing protocol for underwater wireless sensor networks. In Proceedings of the 2016 10th International Conference on Complex, Intelligent, and Software Intensive Systems (CISIS), Fukuoka, Japan, 6–8 July 2016; pp. 246–255. [Google Scholar]
- Xie, P.; Cui, J.-H.; Lao, L. VBF: Vector-based forwarding protocol for underwater sensor networks. In Proceedings of the International Conference on Research in Networking, Coimbra, Portugal, 15–19 May 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1216–1221. [Google Scholar]
- Xie, P.; Zhou, Z.; Nicolaou, N.; See, A.; Cui, J.-H.; Shi, Z. Efficient vector-based forwarding for underwater sensor networks. EURASIP J. Wirel. Commun. Netw. 2010, 2010. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Yao, N.; Liu, J. An adaptive routing protocol in underwater sparse acoustic sensor networks. Ad Hoc Netw. 2015, 34, 121–143. [Google Scholar] [CrossRef]
- Sudevalayam, S.; Kulkarni, P. Energy harvesting sensor nodes: Survey and implications. IEEE Commun. Surv. Tutor. 2011, 13, 443–461. [Google Scholar] [CrossRef]
- Knight, C.; Davidson, J.; Behrens, S. Energy options for wireless sensor nodes. Sensors 2008, 8, 8037–8066. [Google Scholar] [CrossRef] [PubMed]
- Syed, A.A.; Ye, W.; Heidemann, J.; Krishnamachari, B. Understanding spatio-temporal uncertainty in medium access with ALOHA protocols. In Proceedings of the Second Workshop on Underwater Networks, Montreal, QC, Canada, 14 September 2007; ACM: New York, NY, USA, 2007; pp. 41–48. [Google Scholar]
- Peng, Z.; Zhu, Y.; Zhou, Z.; Guo, Z.; Cui, J.H. COPE-MAC: A contention-based medium access control protocol with parallel reservation for underwater acoustic networks. In Proceedings of the OCEANS 2010 IEEE Sydney, Sydney, Australia, 24–27 May 2010; pp. 1–10. [Google Scholar]

| Techniques | Features | Parameters Achieved | Limitations |
|---|---|---|---|
| Proactive routing protocols (OLSR, DSDV, etc.) [5,6] | Routing tables are updated regularly to maintain routing information | Routes are always available | Large signaling overhead for establishing routing tables |
| Reactive routing protocols (AODV, DSR, etc.) [7,8] | Route discovery, Route maintenance | Bandwidth efficient, on demand approach | Higher latency, energy consumption |
| Beacon-based routing protocols such as H2-DAB [9] | Without location information, unique ID assignment to every node based on hop counts from sink | Improved reliability | Infeasible for low node mobility speed, high network overhead |
| Clustering routing [10,11] in UWSNs | Cluster head selection based on residual energy or location, nodes report data to cluster heads | Communication overhead minimization, efficient network management | Longer end-to-end delay, poor performance in time critical applications |
| DBR [12], depth-based routing protocol for UWSNs | Greedy forwarder selection, constant forwarding region all of the time | Energy conservation, network lifetime maximization | Inappropriate void hole avoidance mechanism, inefficient forwarder selection |
| EE-DBR [13], depth-based routing protocol for UWSNs | Energy conservation based routing protocol, depth-based routing protocol for UWSNs | Low end-to-end delay, energy tax | Inefficient void hole mechanism, large network overhead |
| WDFAD-DBR [14], depth-based routing protocol for UWSNs | Forwarder selection on the basis of two hop depth information, adaptive changes the forwarding area | Void hole avoidance, suppression of duplicate packets in local area network | Unnecessary energy consumption due to packet drop |
| Intar and Re-Intarrouting protocol [15], for UWSNs | One hop back transmission to avoid void hole, forwarder selection based on cost function | Void hole avoidance, high throughput | High accumulated propagation distance |
| VBF [16], location-based routing protocol for UWSNs | Confined forwarding area division to avoid packet duplication, directional forwarding along the virtual vector | High packet delivery ratio | Poor performance in sparse networks |
| HH-VBF [17], location-based routing protocol for UWSNs | Change in direction of pipeline hop-by-hop, directional forwarding | High network throughput | Inefficient void hole avoidance, poor performance in sparse networks |
| AHH-VBF [18], location-based routing protocol for UWSNs | Change in direction of pipeline, adaptive transmission range hop by hop | High network throughput, energy conservation | Inefficient forwarder selection |
| TWSN | UWSN |
|---|---|
| Radio signal | Acoustic signal |
| High bandwidth | Low Bandwidth |
| Low propagation delay | High propagation delay |
| Low location error rate | High location error rate |
| High data rate | Low data rate |
| Parameter | Value |
|---|---|
| Nodes | 100–500 Random deployment |
| Sinks | 1, on the surface |
| Network area | 3D region of 10 km × 10 km × 10 km |
| Max power for transmission | 90 dB re Pa |
| Max power for reception | 10 dB re Pa |
| Max Transmission range | 2000 m |
| Initial energy of each node | 100 Joule |
| Node mobility | 1–3 m/s |
| Data rate | 16 kbps |
| Data packet size | 111 bytes |
| Neighbor request packet size | 66 bytes |
| Acknowledgment packet size | 114 bytes |
| Center frequency | 12 kHz |
| Bandwidth | 4 kHz |
| Mobility model | Random walk mobility mode |
| Performance Parameters | 2hop-AHH-VBF Scheme | QF-2hop-AHH-VBF Scheme | WDFAD-DBR Scheme |
|---|---|---|---|
| PDR (%) | 2 | 5.6 | 2 |
| Energy tax (%) | 31.15 | −45 | −49.77 |
| End-to-end delay (%) | −21 | 28.5 | −56.13 |
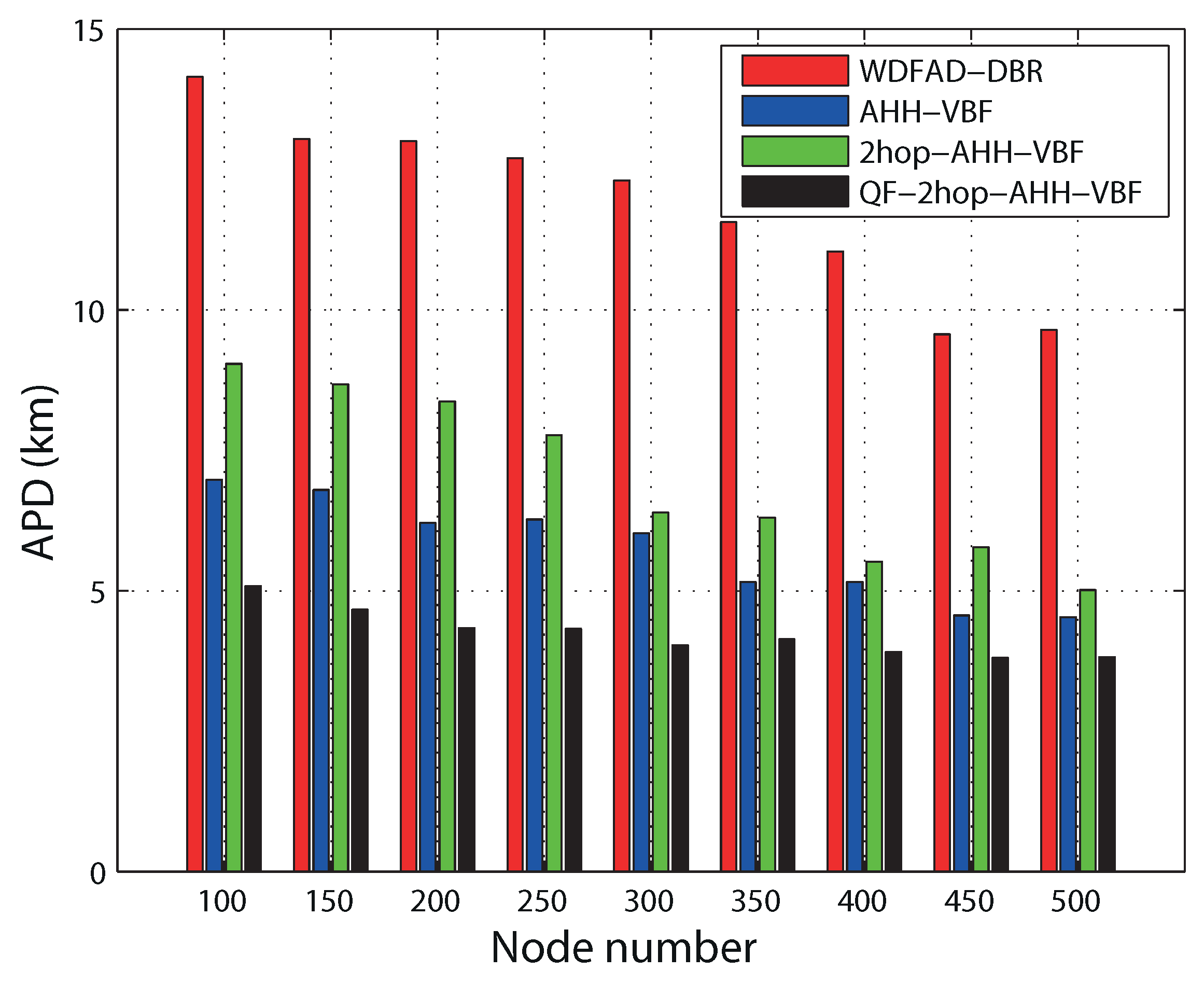
| APD (%) | −25 | 28 | −53 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javaid, N.; Ahmed, F.; Wadud, Z.; Alrajeh, N.; Alabed, M.S.; Ilahi, M. Two Hop Adaptive Vector Based Quality Forwarding for Void Hole Avoidance in Underwater WSNs. Sensors 2017, 17, 1762. https://doi.org/10.3390/s17081762
Javaid N, Ahmed F, Wadud Z, Alrajeh N, Alabed MS, Ilahi M. Two Hop Adaptive Vector Based Quality Forwarding for Void Hole Avoidance in Underwater WSNs. Sensors. 2017; 17(8):1762. https://doi.org/10.3390/s17081762
Chicago/Turabian StyleJavaid, Nadeem, Farwa Ahmed, Zahid Wadud, Nabil Alrajeh, Mohamad Souheil Alabed, and Manzoor Ilahi. 2017. "Two Hop Adaptive Vector Based Quality Forwarding for Void Hole Avoidance in Underwater WSNs" Sensors 17, no. 8: 1762. https://doi.org/10.3390/s17081762
APA StyleJavaid, N., Ahmed, F., Wadud, Z., Alrajeh, N., Alabed, M. S., & Ilahi, M. (2017). Two Hop Adaptive Vector Based Quality Forwarding for Void Hole Avoidance in Underwater WSNs. Sensors, 17(8), 1762. https://doi.org/10.3390/s17081762





