Load Identification for a Cantilever Beam Based on Fiber Bragg Grating Sensors
Abstract
:1. Introduction
2. Sensing Principle
3. Load Identification of a Linear Beam System
3.1. Identification Principle
3.1.1. Linear System Discretization
3.1.2. Kalman Filter
3.1.3. Linear Estimator
3.2. Numerical Simulations of a Linear Beam System
3.3. Experimental Verification of a Linear Beam System
4. Load Identification of a Nonlinear Beam System
4.1. Identification Principle
4.1.1. Nonlinear System Discretization
4.1.2. Cubature Kalman Filter
- (1)
- Calculate the cubature points:where is the prior estimated state. , is the ith column of the matrix [I (−1)I].
- (2)
- Calculate the propagated cubature points:
- (3)
- Calculate the predicted state and covariance matrix:
- (1)
- Calculate the cubature points:
- (2)
- Calculate the propagated cubature points:
- (3)
- Calculate the predicted state:
- (4)
- Calculate the innovation covariance matrix:
- (5)
- Calculate the cross-covariance matrix:
- (6)
- Calculate the Kalman gain:
- (7)
- Calculate the updated state:
- (8)
- Calculate the error covariance:
4.1.3. The Nonlinear Estimator
4.2. Numerical Simulations of a Nonlinear Beam System
4.3. Experimental Verification of a Nonlinear Beam System
5. Discussion
- (1)
- The proposed method of load identification is a recursive method that only needs the recent measurement values and the previously identified values to be kept in storage. This characteristic can save considerable memory and greatly decrease the system burden. The proposed method is based on a Kalman filter, and this can be helpful to control the beam structure by using optimal control theory after identifying the load.
- (2)
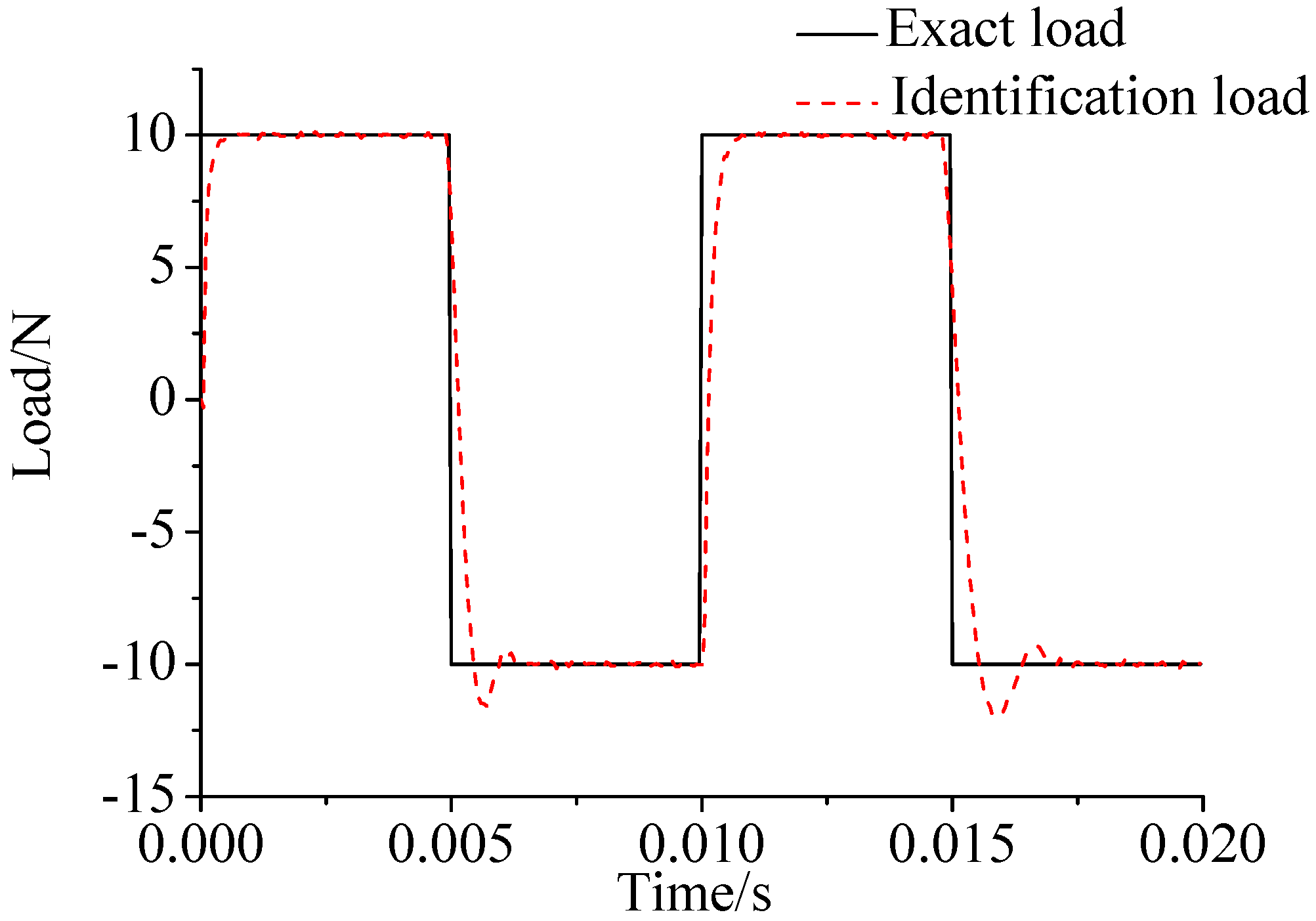
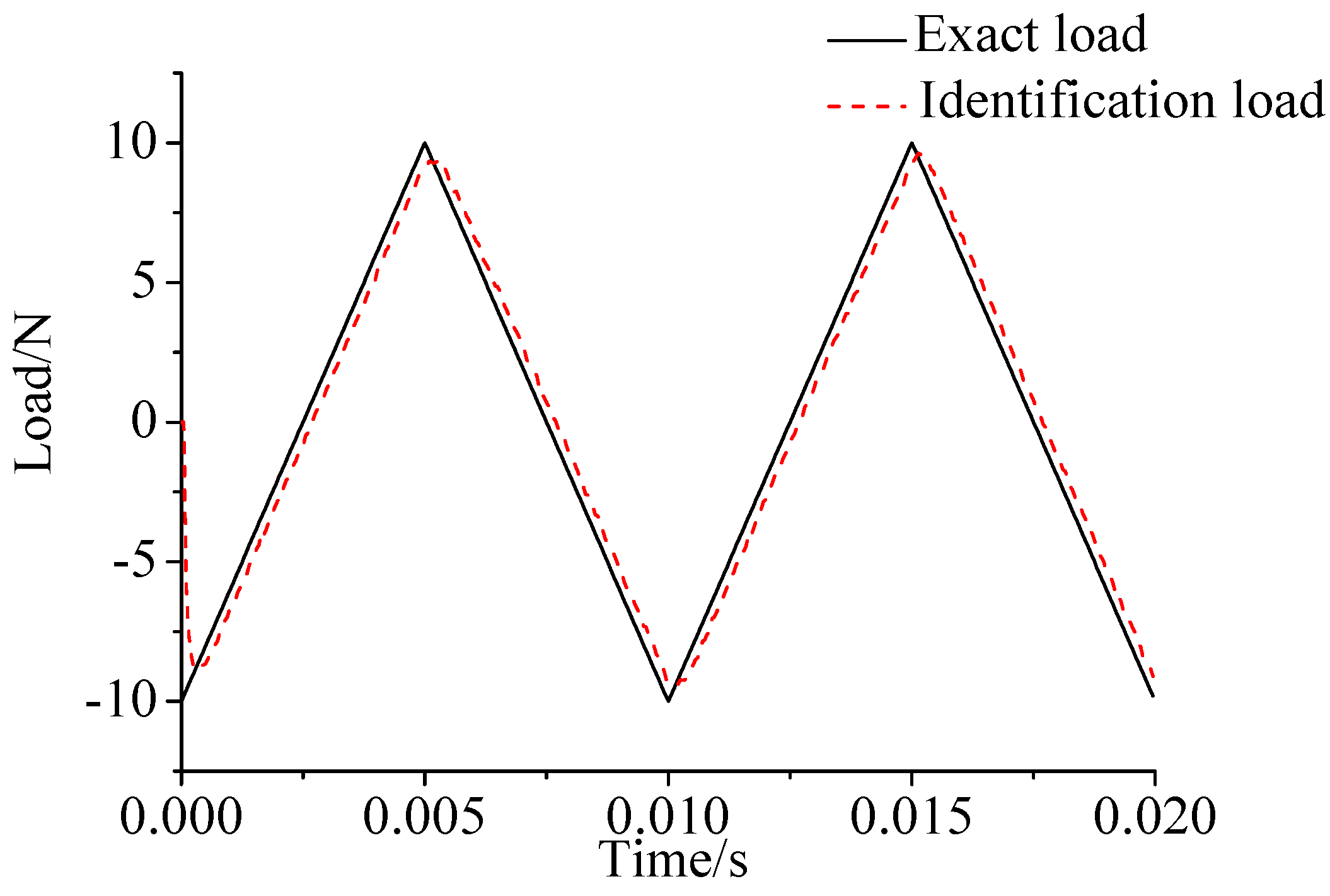
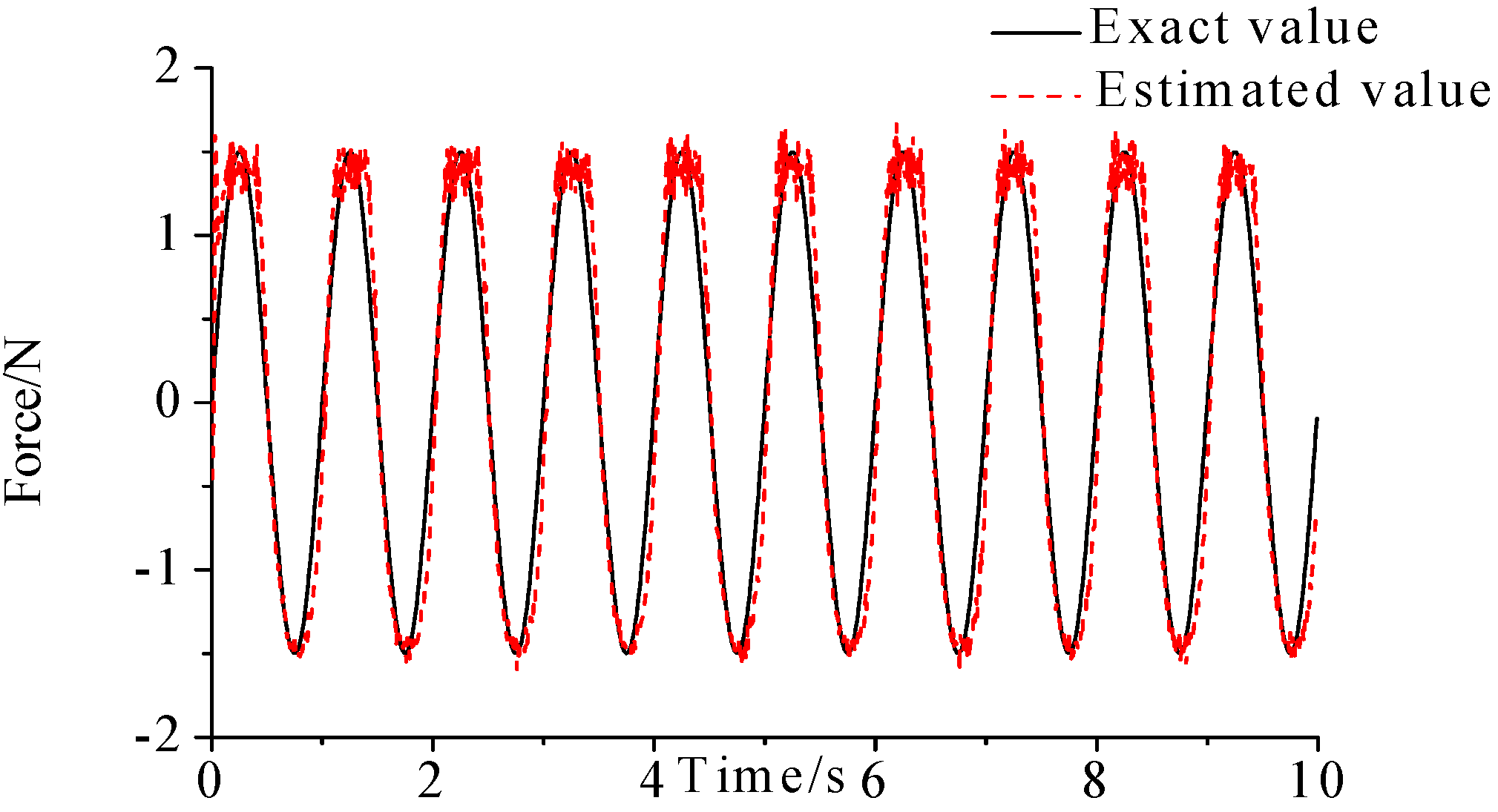
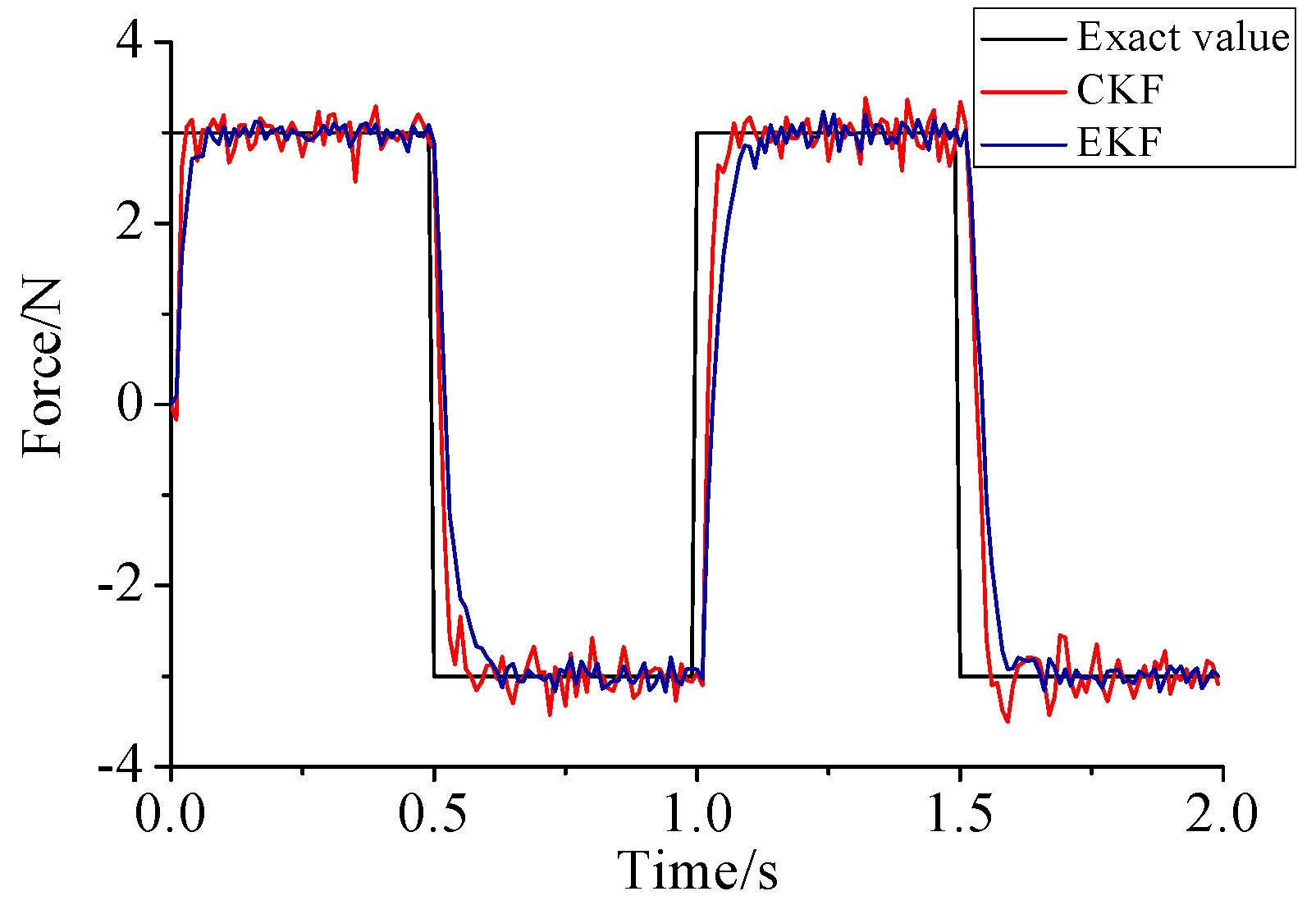
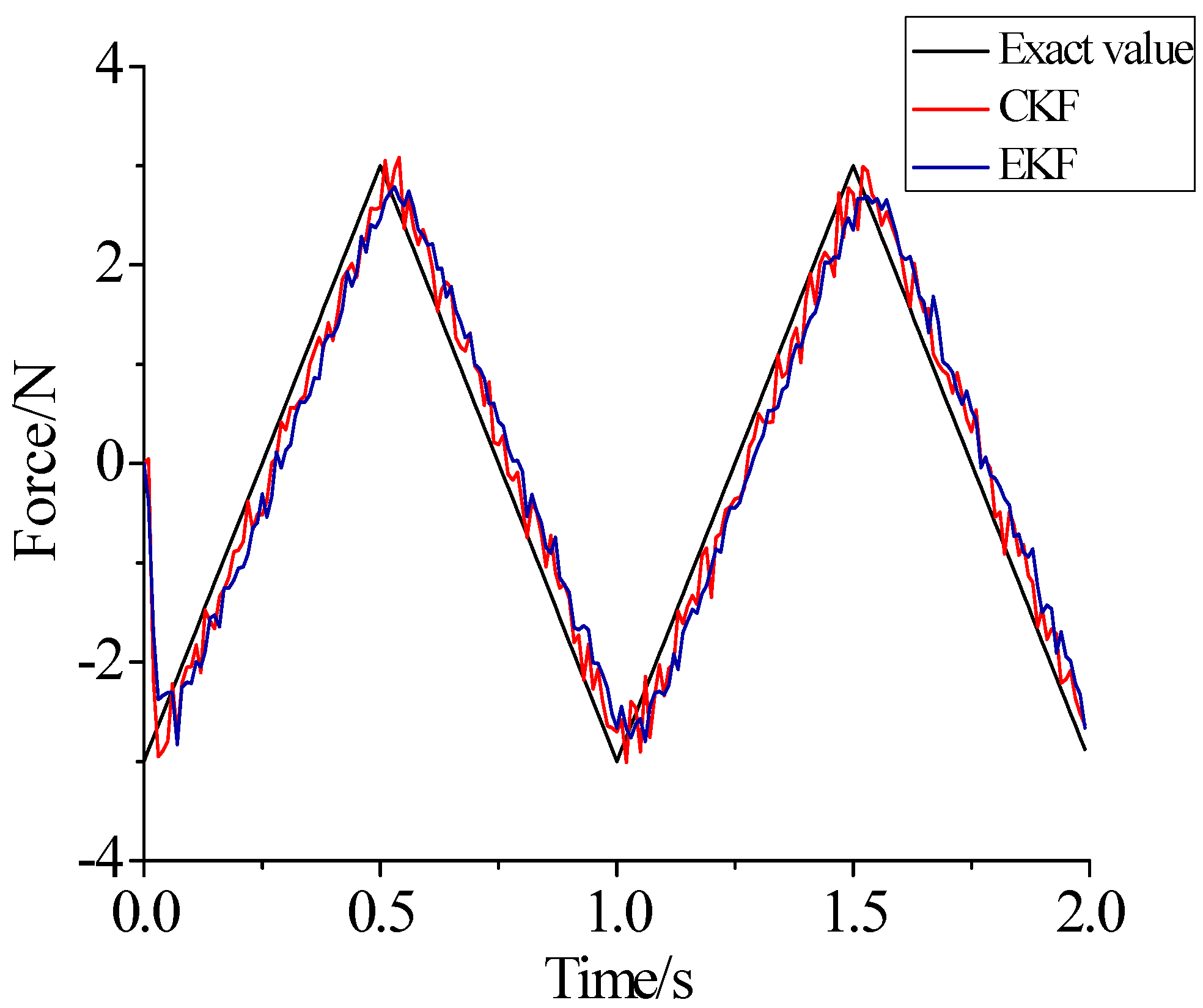
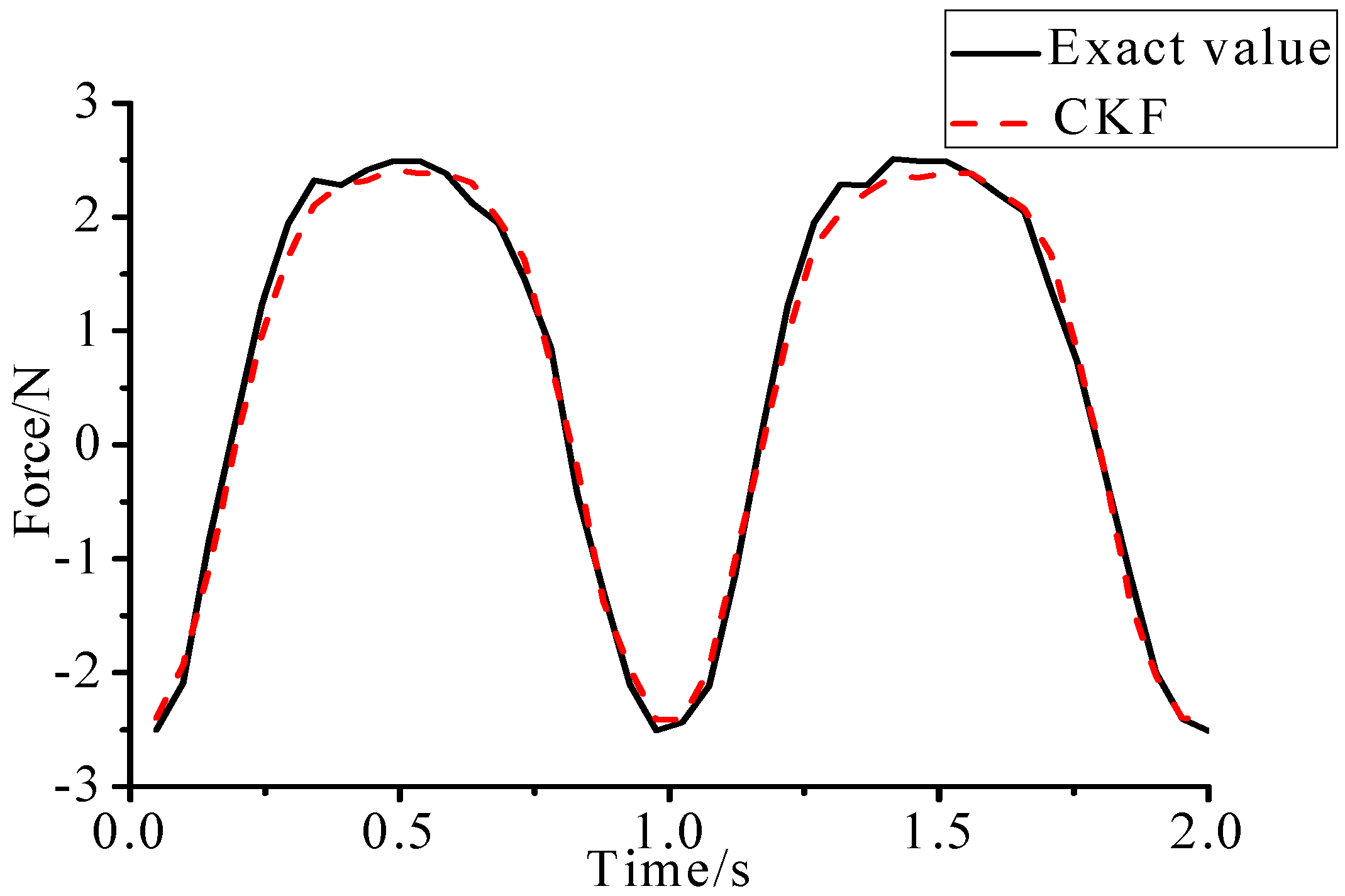
- As illustrated in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, Figure 11, Figure 12 and Figure 13, the identified load rapidly converges to the exact load. The identification performance of the sinusoidal load is better than that of the triangular load and rectangular load. As illustrated in Figure 9 and Figure 15, experimental results show that the load identification system based on FBG sensors has a good performance.
- (3)
- The proposed method of load identification is based on a Kalman filter. As a Kalman filter can only be used to estimate continuous signal and cannot be used to estimate a random signal, the proposed method cannot be used to identify a random load. The identification results show a little delay between the exact load and the identified load, but we can apply iterative algorithms to decrease the delay. The identified load rapidly converges to the exact load, but with large initial estimation errors. To improve the performance of the initial estimation, the initial values of P and should be set to large values.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
- k < n. = 0. = 0, so = 0
- k = n. = 0. = 0, so = 0
- k > n. , so
- k < n. = 0,
- k = n. = 0,
- k > n. ,
Appendix B
- k < n. = 0. = 0, so = 0
- k = n. = 0. = 0, so = 0
- k > n. , so
- k < n. = 0,
- k = n. = 0,
- k > n.
References
- Kazemi, A.A.; Bucher, C. Derivation of a new parametric impulse response matrix utilized for nodal wind load identification by response measurement. J. Sound Vib. 2015, 22, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Sun, X.; Li, K.; Jiang, C.; Han, X. A probability density function discretization and approximation method for the dynamic load identification of stochastic structures. J. Sound Vib. 2015, 357, 74–94. [Google Scholar] [CrossRef]
- Zhou, P.; Xu, S.; Wang, Z.; Guo, D. A load identification method for the grinding damage induced stress (GDIS) distribution in silicon wafers. Int. J. Mach. Tools Manuf. 2016, 107, 1–7. [Google Scholar] [CrossRef]
- Song, H.; Yu, K.; Li, X.; Han, J. Error estimation of load identification based on linear sensitivity analysis and interval technique. Struct. Multidiscip. Optim. 2017, 55, 423–436. [Google Scholar] [CrossRef]
- Airoldi, A.; Sala, G.; Evenblij, R.; Koimtzoglou, C.; Loutas, T.; Carossa, G.M.; Mastromauro, P.; Kanakis, T. Load Monitoring by Means of Optical Fibers and Strain Gages. In Smart Intelligent Aircraft Structures (SARISTU); Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Liu, J.; Sun, X.; Han, X.; Jiang, C.; Yu, D. Dynamic load identification for stochastic structures based on Gegenbauer polynomial approximation and regularization method. Mech. Syst. Signal Process. 2015, 56–57, 35–54. [Google Scholar] [CrossRef]
- Xue, X.; Chen, X.; Zhang, X.; Qiao, B. Hermitian plane wavelet finite element method: Wave propagation and load identification. Comput. Math. Appl. 2016. [Google Scholar] [CrossRef]
- Ma, C.; Tuan, P.; Lin, D.; Liu, C. A study of an inverse method for the estimation of impulsive loads. Int. J. Syst. Sci. 1998, 29, 663–672. [Google Scholar] [CrossRef]
- Ma, C.-K.; Ho, C.-C. An inverse method for the estimation of input forces acting on non-linear structural systems. J. Sound Vib. 2004, 275, 953–971. [Google Scholar] [CrossRef]
- Lin, D.-C. Input estimation for nonlinear systems. Inverse Probl. Sci. Eng. 2010, 18, 673–689. [Google Scholar] [CrossRef]
- Zhao, X.; Lv, X.; Wang, L.; Zhu, Y.; Dong, H.; Chen, W.; Li, J.; Ji, B.; Ding, Y. Research of concrete residual strains monitoring based on WLI and FBG following exposure to freeze–thaw tests. Cold Reg. Sci. Technol. 2015, 116, 40–48. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S.; Hurd, T.R. Cubature kalman filtering for continuous-discrete systems: Theory and simulations. IEEE Trans. Signal Process. 2010, 58, 4977–4993. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.; Yu, T.; Jian, H.; Liu, T. Design of adaptive robust square-root cubature Kalman filter with noise statistic estimator. Appl. Math. Comput. 2015, 256, 352–367. [Google Scholar] [CrossRef]
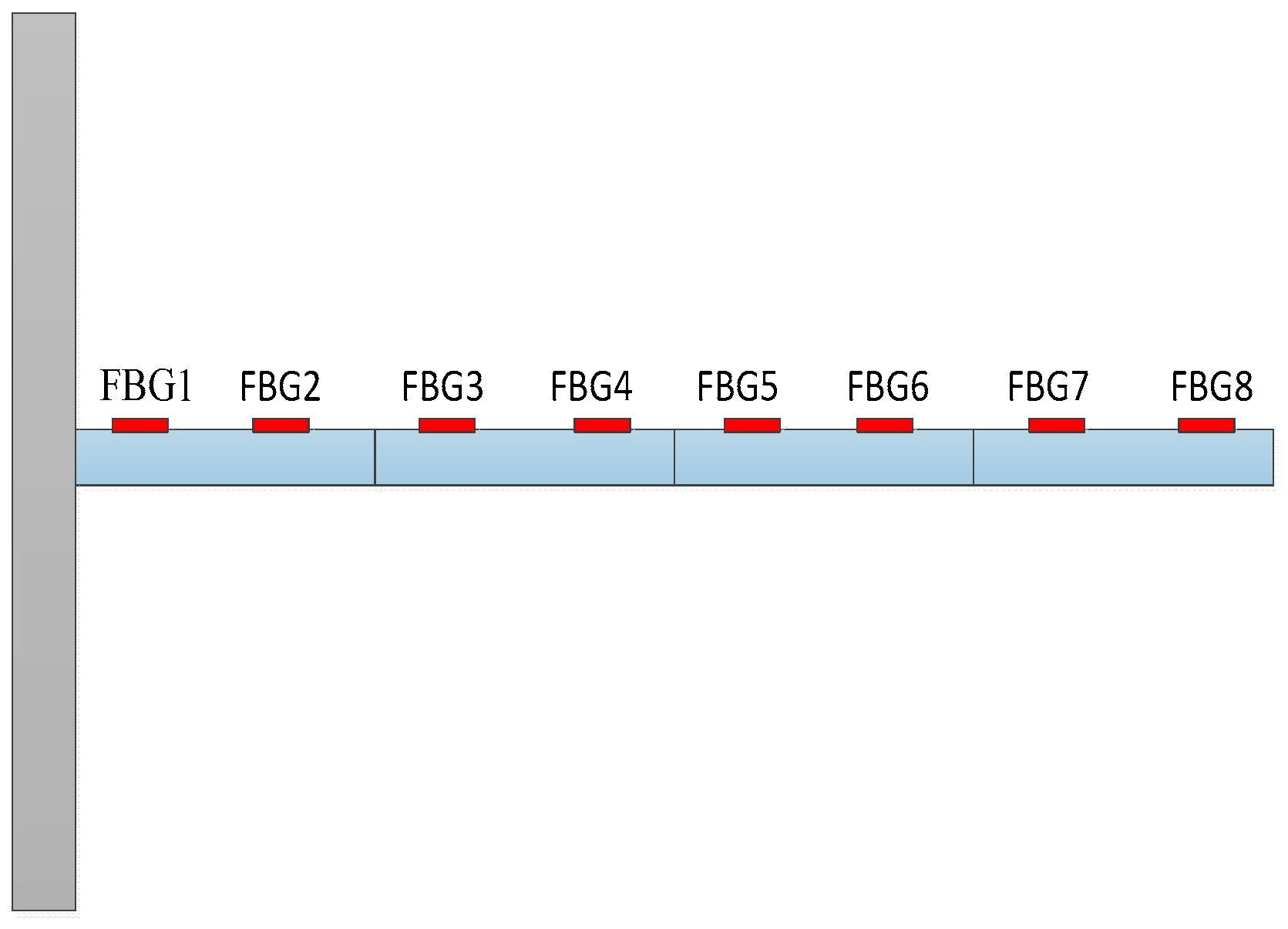
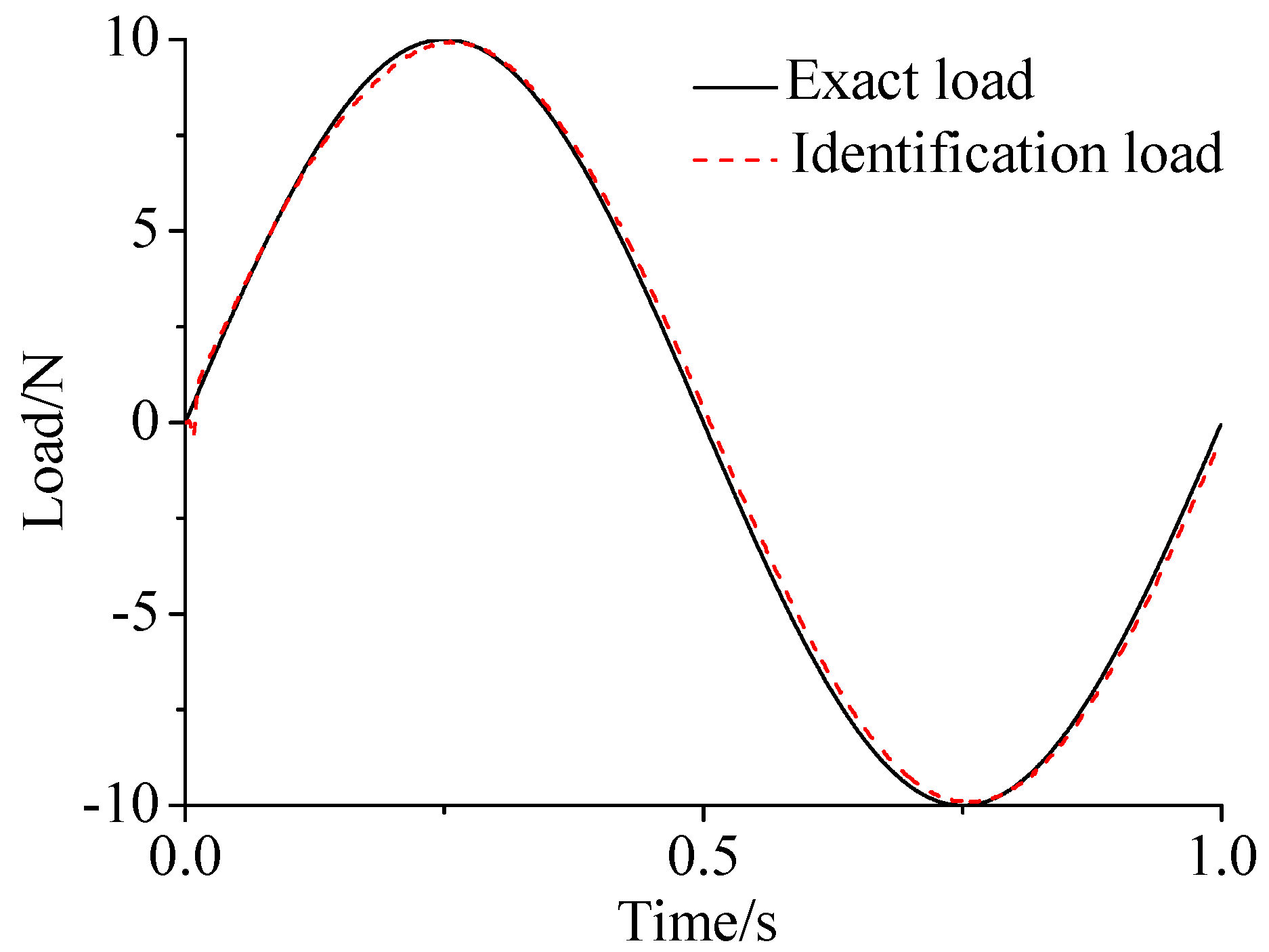
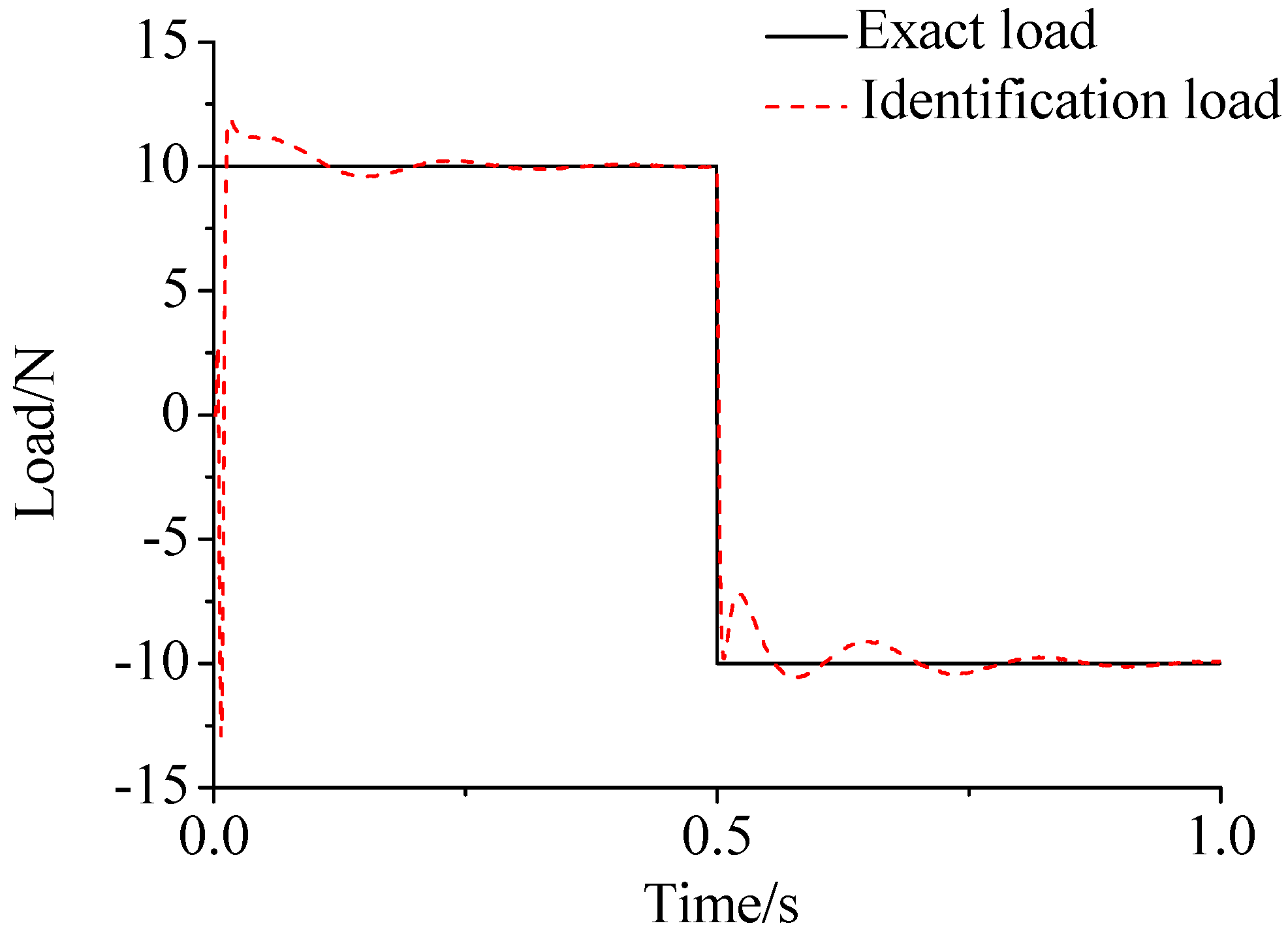
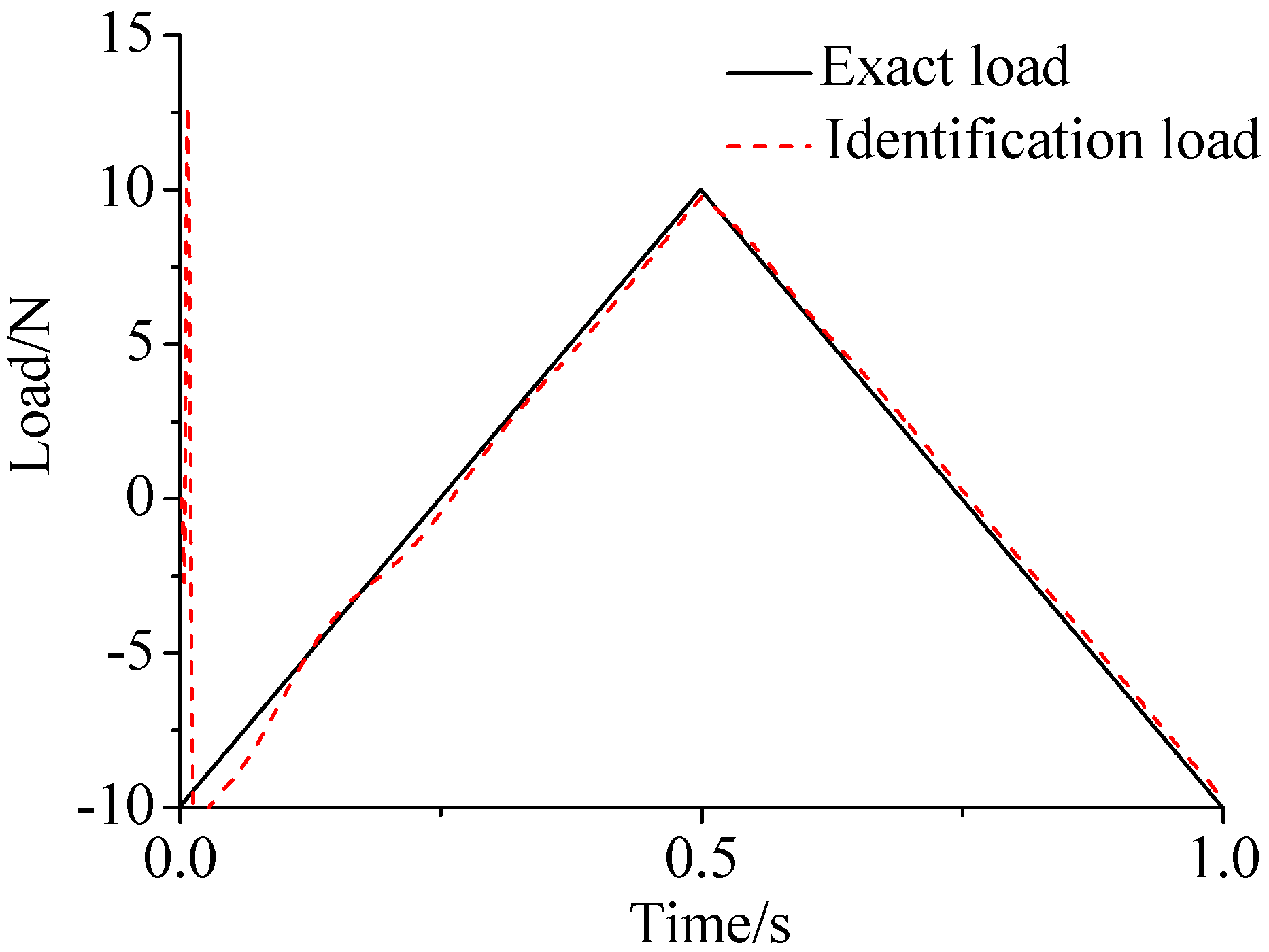


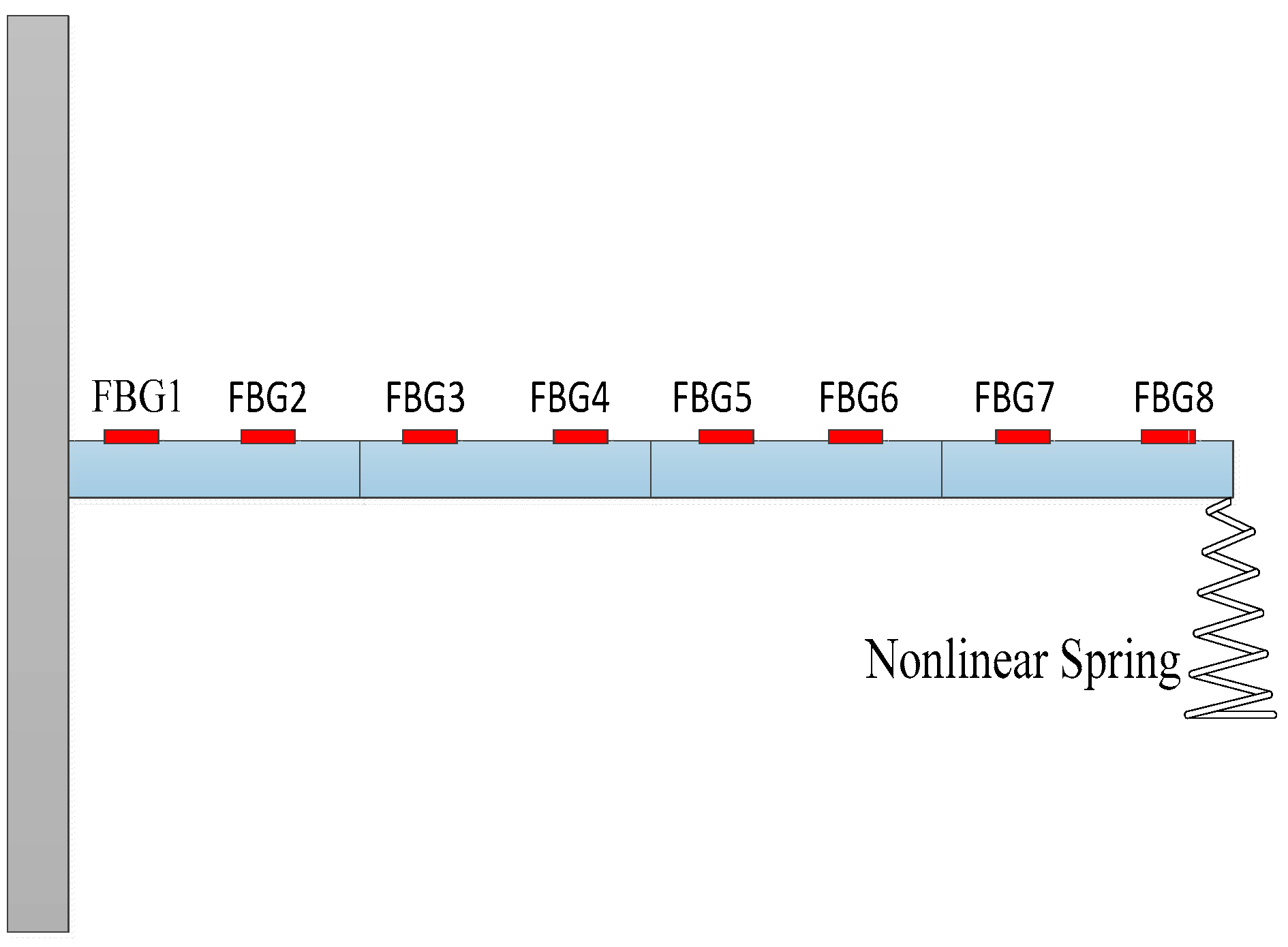


| Bernoulli–Euler Beam | |
|---|---|
| Material | 1540 |
| Density (kg/ ) | 2690 |
| Elastic modulus (GPa) | 68.9 |
| Length (m) | 0.64 |
| Width (m) | 0.03 |
| Height (m) | 0.003 |
| Units number | 4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Zhang, Y.; Liang, D. Load Identification for a Cantilever Beam Based on Fiber Bragg Grating Sensors. Sensors 2017, 17, 1733. https://doi.org/10.3390/s17081733
Song X, Zhang Y, Liang D. Load Identification for a Cantilever Beam Based on Fiber Bragg Grating Sensors. Sensors. 2017; 17(8):1733. https://doi.org/10.3390/s17081733
Chicago/Turabian StyleSong, Xuegang, Yuexin Zhang, and Dakai Liang. 2017. "Load Identification for a Cantilever Beam Based on Fiber Bragg Grating Sensors" Sensors 17, no. 8: 1733. https://doi.org/10.3390/s17081733
APA StyleSong, X., Zhang, Y., & Liang, D. (2017). Load Identification for a Cantilever Beam Based on Fiber Bragg Grating Sensors. Sensors, 17(8), 1733. https://doi.org/10.3390/s17081733




