Evaluation of Shifted Excitation Raman Difference Spectroscopy and Comparison to Computational Background Correction Methods Applied to Biochemical Raman Spectra
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Approach
2.2. Experimental Approach
3. Results
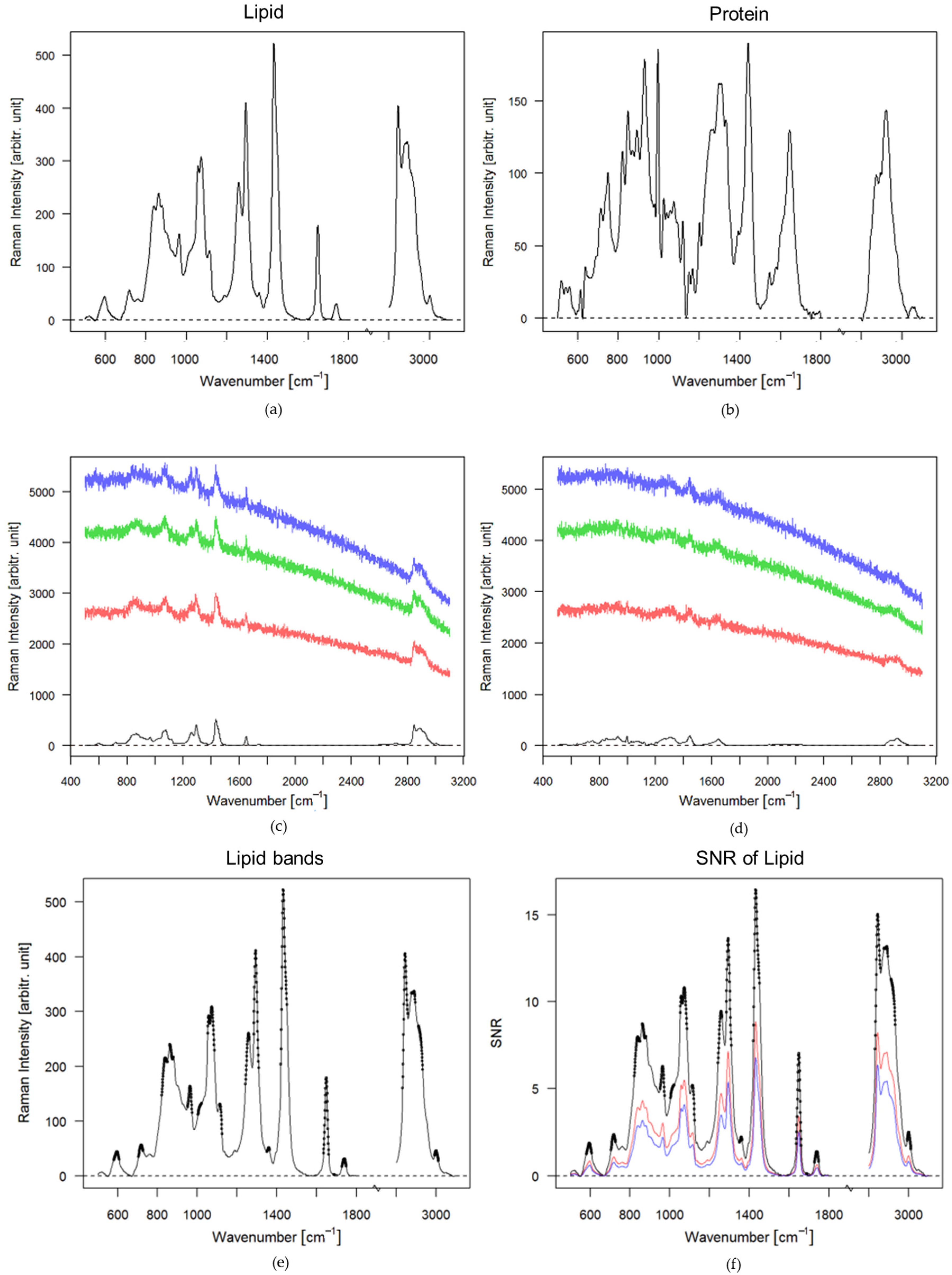
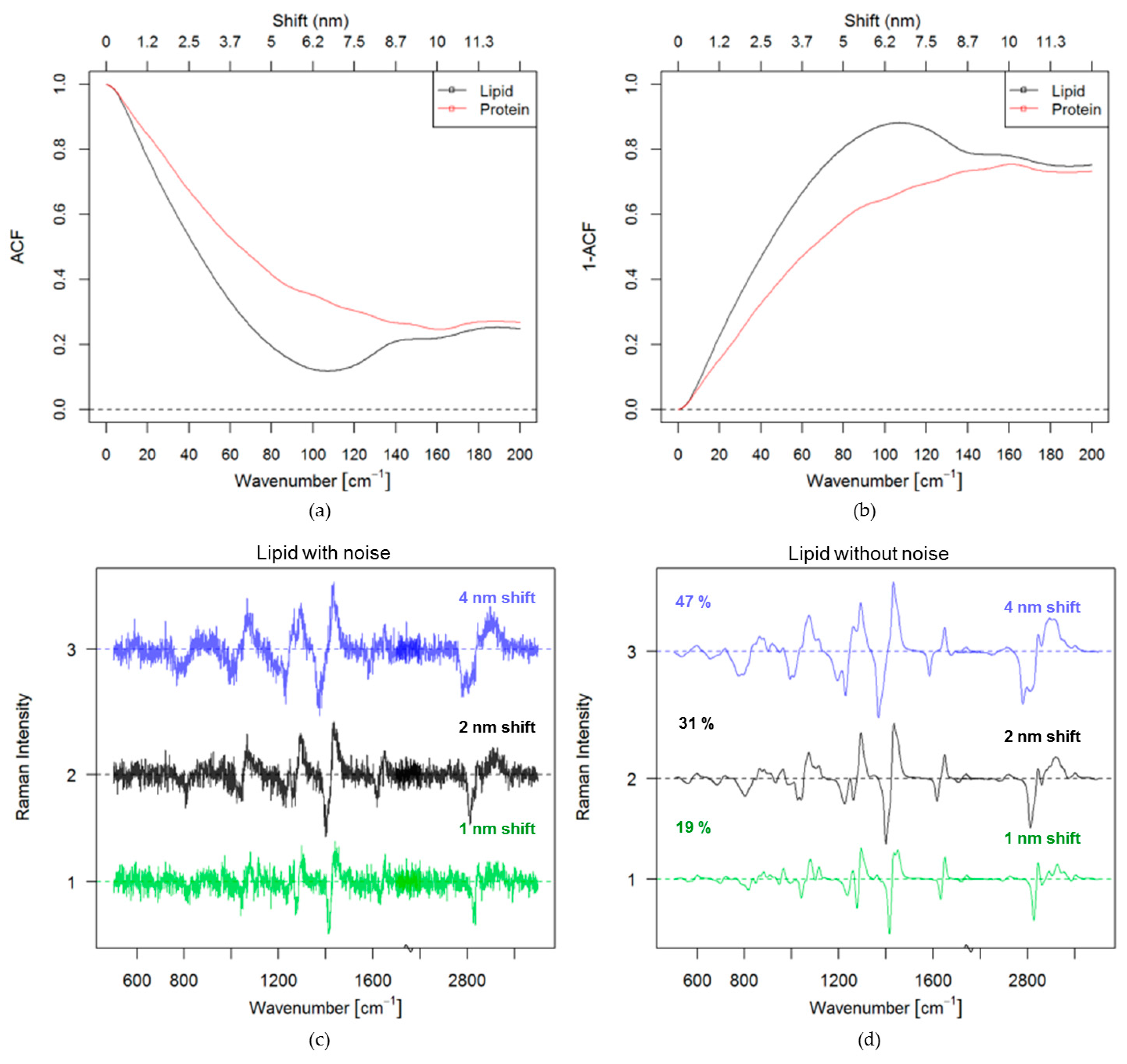
3.1. Theoretical Approach
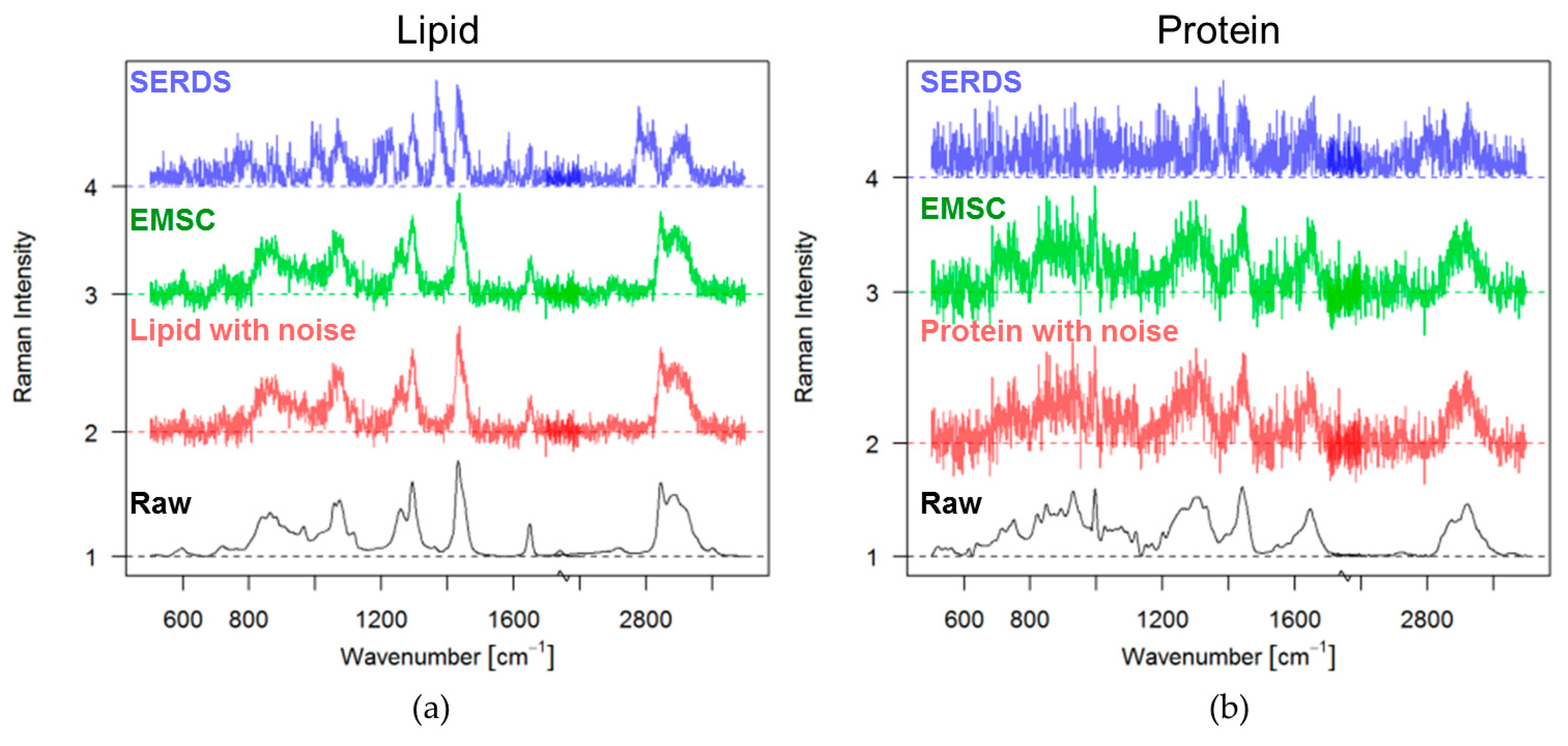
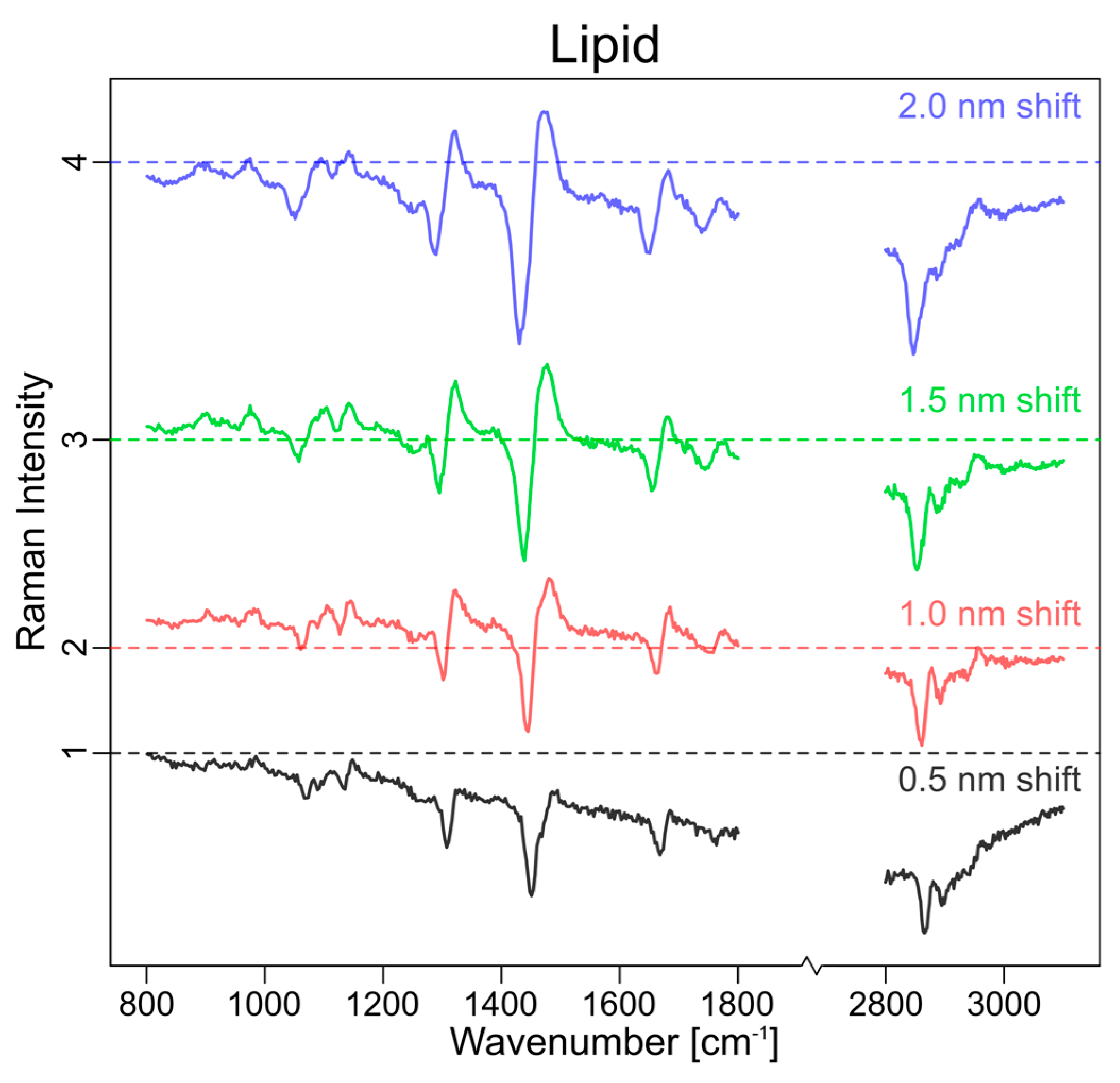
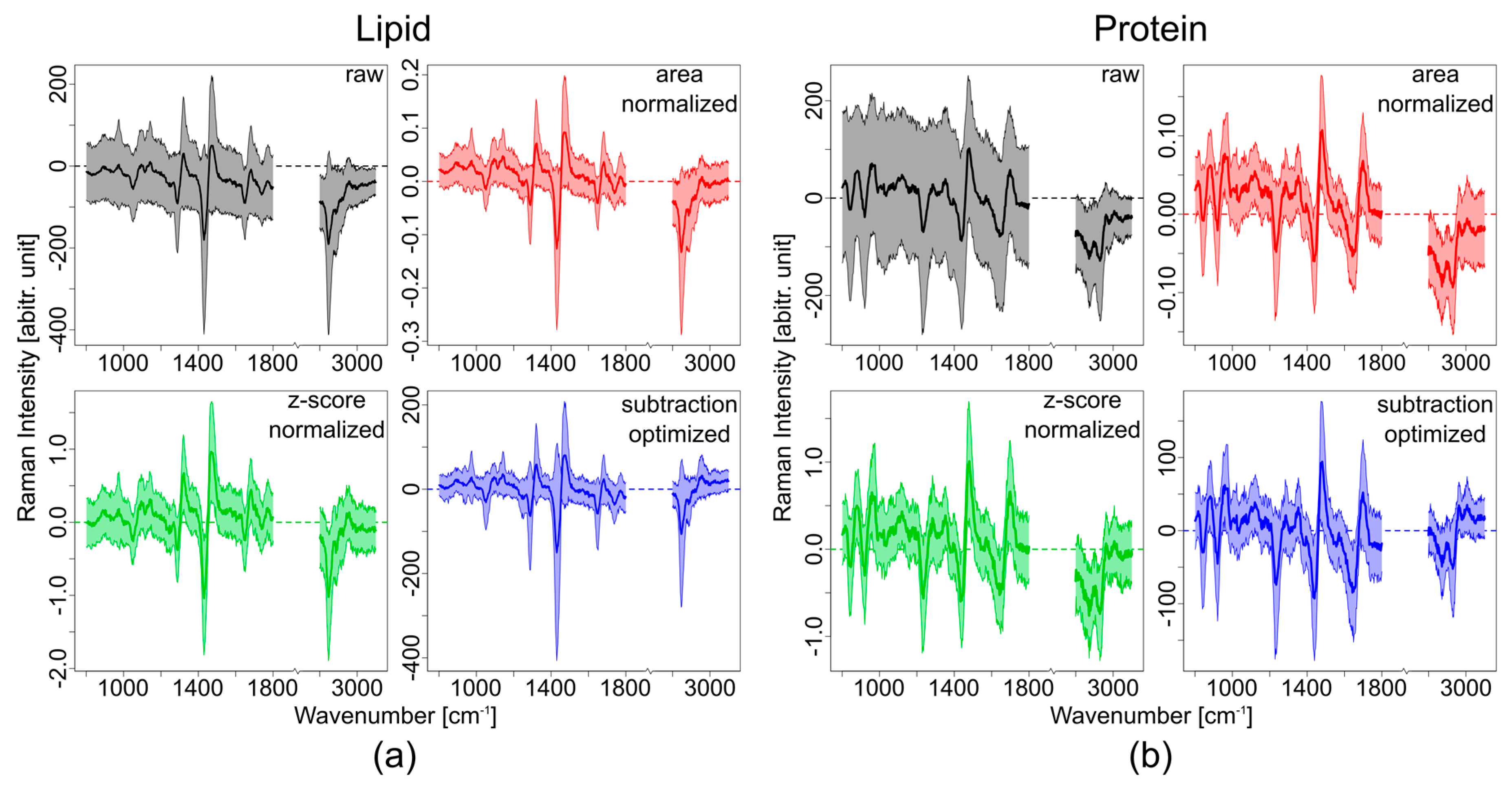
3.2. Experimental Approach
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Krafft, C.; Schie, I.; Meyer, T.; Schmitt, M.; Popp, J. Development in spontaneous and coherent Raman scattering microscopic imaging for biomedical applications. Chem. Soc. Rev. 2016, 45, 1819–1849. [Google Scholar] [CrossRef] [PubMed]
- Krafft, C.; Schmitt, M.; Schie, I.; Cialla-May, D.; Matthäus, C.; Bocklitz, T.; Popp, J. Label-free molecular imaging of biological cells and tissues by linear and non-linear Raman spectroscopic approaches. Angew. Chem. 2017, 56, 4392–4430. [Google Scholar] [CrossRef] [PubMed]
- Stone, N. The use of Raman spectroscopy to provide an estimation of the gross biochemistry asociated with urological pathologies. Anal. Bioanal. Chem. 2007, 387, 1657–1668. [Google Scholar] [CrossRef] [PubMed]
- Crow, P.; Uff, J.A.; Farmer, J.A.; Wright, M.P.; Stone, N. The use of Raman spectroscopy to identify and characterize transitional cell carcicoma in vitro. BJU Int. 2004, 93, 1232–1236. [Google Scholar] [CrossRef] [PubMed]
- Kerr, L.T.; Domikan, K.; Cullen, I.; Hennelly, B.M. Applications of Raman spectroscopy to the urinary bladder for cancer diagnostics. Photonics Lasers Med. 2014, 3, 193–224. [Google Scholar] [CrossRef]
- Crow, P.; Molckovsky, A.; Stone, N.; Uff, J.; Wilson, B.; Wongkeesong, L.-M. Assesment of fiberoptic Near-infrared Raman spectroscopy for diagnostics of bladder and prostate cancer. J. Urol. 2005, 65, 1126–1130. [Google Scholar] [CrossRef] [PubMed]
- Bergholt, M.S.; Zheng, W.; Ho, K.Y.; Teh, M.; Yeoh, K.G.; So, J.B.Y.; Shabbir, A.; Huang, Z. Fiberoptic confocal Raman spectroscopy for real-time in vivo diagnosis of dysplasia in Barrett’s esophagus. Gastroenterology 2014, 146, 27–32. [Google Scholar] [CrossRef] [PubMed]
- Eberhardt, K.; Stiebing, C.; Matthäus, C.; Schmitt, M.; Popp, J. Advantages and limitations of Raman spectroscopy for molecular diagnostics: An update. Expert Rev. Mol. Diagn. 2015, 15, 773–787. [Google Scholar] [CrossRef] [PubMed]
- Motz, J.T.; Gandhi, S.J.; Scepanovic, O.R.; Feld, M.S. Real-time Raman system for in vivo disease diagnosis. J. Biomed. Opt. 2005, 10, 031113. [Google Scholar] [CrossRef] [PubMed]
- Draga, R.O.P.; Grimbergen, M.C.M.; Vijverberg, P.L.M.; Bosch, J.L.H.R. In Vivo Bladder Cancer Daignosis by High-Volume Raman Spectroscopy. Anal. Chem. 2010, 82, 5993–5999. [Google Scholar] [CrossRef] [PubMed]
- De Jong, B.W.D.; Schut, T.C.B.; Wolffenbuttel, K.P.; Nijman, J.M.; Kok, D.J.; Puppels, G.J. Identification of bladder wall layers by Raman spectroscopy. J. Urol. 2002, 168, 1771–1778. [Google Scholar] [CrossRef]
- Monici, M. Cell and tissue autofluorescence research and diagnostic applications. Biotechnol. Annu. Rev. 2005, 11, 227–256. [Google Scholar] [PubMed]
- McCain, S.T.; Willett, R.M.; Brady, D.J. Multi-excitation Raman Spectroscopy Technique for Fluorescence Rejection. Opt. Express 2008, 16, 10975–10991. [Google Scholar] [CrossRef] [PubMed]
- Macdonald, A.M.; Wyeth, P. On the use of photobleaching to reduce fluorescence background in Raman spectroscopy to improve the reliability of pigment identification on painted textiles. J. Raman Spectrosc. 2006, 37, 830–835. [Google Scholar] [CrossRef]
- Zięba-Palus, J.; Michalska, A. Photobleaching as a useful technique in reducing of fluorescence in Raman spectra of blue automobile paint samples. Vib. Spectrosc. 2014, 74, 6–12. [Google Scholar] [CrossRef]
- Da Silva, M.A.; Riveiro, D.G.; Pereira, E.A.; Martin, A.A.; Fontes, A.; da Silva Martinho, H. Shifted-excitation difference spectroscopy for in vitro and in vivo biological samples analysis. Biomed. Opt. Express 2017, 1, 617–626. [Google Scholar]
- Zhang, Z.-M.; Chen, S.; Liang, Y.-Z.; Liu, Z.-X.; Zhang, Q.-M.; Ding, L.-X.; Yec, F.; Zhou, H. An intelligent background-correction algorithm for highly fluorescent samples in Raman spectroscopy. J. Raman Spectrosc. 2009, 41, 659–669. [Google Scholar] [CrossRef]
- Venables, B.; Hornik, K.; Maechler, M. Polynom: A Collection of Functions to Implement a Class for Univariate Polynomial Manipulations. R Package v 1.3-8. 2014. Available online: https://rdrr.io/github/eestileib/ComplexPoly/ (accessed on 26 July 2017).
- Kourkoumelis, N.; Polymeros, A.; Tzaphlidou, M. Background estimation of biomedical Raman spectra using a geometric approach. Spectrosc. Int. J. 2012, 27, 441–447. [Google Scholar] [CrossRef]
- Gautam, R.; Vanga, S.; Ariese, F.; Umapathy, S. Review of multidimensional data processing approaches for Raman and infrared spectroscopy. EPJ Tech. Instrum. 2015, 2, 8. [Google Scholar] [CrossRef]
- Lieber, C.A.; Mahadevan-Jansen, A. Automated Method for Subtraction of Fluorescence from Biological Raman Spectra. Appl. Spectrosc. 2003, 57, 1363–1367. [Google Scholar] [CrossRef] [PubMed]
- Cadusch, P.J.; Hlaing, M.M.; Wade, S.A.; MxArthur, S.L.; Stoddart, P.R. Improved methods for fluorescence background substraction from Raman spectra. Mater. Sci. 2013, 44, 1587–1595. [Google Scholar]
- Martens, H.; Nielsen, J.P.; Engelsen, S.B. Light scattering and ligth absorbance separated by extended multiplicative signal correction. Application to near-infrared transmission analysis of powder mixtures. Anal. Chem. 2003, 75, 593–604. [Google Scholar] [CrossRef]
- Mecozzi, M. A Polynomial Curve Fitting Method for Baseline Drift Correction in the Chromatographic Analysis of Hydrocarbons in Environmental Samples. APCBEE Procedia 2014, 10, 2–6. [Google Scholar] [CrossRef]
- Massart, D.L.; Vandeginste, B.G.M.; Buydens, L.C.M.; Jong, S.D.; Lewi, P.J.; Smeyers-Verbeke, J. Data Handling in Science and Technology, Handbook of Chemometrics and Qualimetrics, Vols. 20A and 20B; Elsevier: Amsterdam, The Netherland, 1997. [Google Scholar]
- Vinzi, V.E.; Chin, W.W.; Henseler, J.; Wang, H. Handbook of Partial Least Squares: Concepts, Methods and Applications; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Baek, S.J.; Park, A.; Ahn, Y.J.; Choo, J. Baseline correction using asymmetrically reweighted penalized least squares smoothing. Analyst 2014, 140, 17–38. [Google Scholar] [CrossRef] [PubMed]
- Liland, K.H.; Kohler, A.; Afseth, N.K. Model-based pre-processing in Raman spectroscopy of biological samples. J. Raman Spectrosc. 2015, 47, 643–650. [Google Scholar] [CrossRef]
- Hasegawaa, T.; Nishijoa, J.; Umemurab, J. Separation of Raman spectra from fluorescence emission background by principal component analysis. Chem. Phys. Lett. 2000, 317, 642–646. [Google Scholar] [CrossRef]
- Asfour, H.; Swift, L.M.; Sarvazyan, N.; Doroslovacki, M.; Kay, M.W. Signal Decomposition of Transmembrane Voltage-Sensitive Dye Fluorescence Using a Multiresolution Wavelet Analysis. IEEE Trans. Biomed. Eng. 2011, 58, 2083–2093. [Google Scholar] [CrossRef] [PubMed]
- Qu, H.-B.; Ou, D.-L.; Cheng, Y.-Y. Background correction in near-infrared spectra of plant extracts by orthogonal signal correction. J. Zhejiang Univ. Sci. B 2015, 6, 838–843. [Google Scholar] [CrossRef] [PubMed]
- Dennis, A. Photo-Bleaching and Automatic Baseline Correction for Raman Spectroscopy; R Package v 1.2-1; PerkinElmer: Waltham, MA, USA, 2007. [Google Scholar]
- Knorr, F.; Smith, Z.J.; Wachsmann-Hogiu, S. Development of a time-gated system for Raman spectroscopy of biological samples. J. Opt. Soc. Am. 2010, 18, 20049–20058. [Google Scholar] [CrossRef] [PubMed]
- Shreve, A.P.; Cherepy, N.J.; Mathies, R.A. Effective Rejection of Fluorescence Interference in Raman Spectroscopy Using a Shifted Excitation Difference Technique. Spectrosc. Tech. 1992, 46, 707. [Google Scholar] [CrossRef]
- De Luca, A.C.; Mazilu, M.; Riches, A.; Herrington, C.S.; Dholakia, K. Online Fluorescence Suppression in Modulated Raman Spectroscopy. Anal. Chem. 2010, 82, 738–745. [Google Scholar] [CrossRef] [PubMed]
- Dongy, S.; Melnik, E.D.; Ban, V.S.; Volodin, B.L. A novel Method for practical implementation of shifted-excitation Raman difference spectroscopy (SERDS). Spectroscopy 2012, 47, 198–209. [Google Scholar]
- Gebrekidan, M.T.; Knipfer, C.; Stelzle, F.; Popp, J.; Will, S.; Braeuer, A. A shifted-excitation Raman difference spectroscopy (SERDS) evaluation strategy for the efficient isolation of Raman spectra from extreme fluorescence interference. J. Raman Spectrosc. 2015, 47, 198–209. [Google Scholar] [CrossRef]
- Osticioli, I.; Zoppi, A.; Castellucci, E.M. Shift-Excitation Raman difference spectroscopy-difference deconvolution methods for the luminescence background rejection from Raman spectra of solid samples. Appl. Spectrosc. 2007, 61, 839–844. [Google Scholar] [CrossRef] [PubMed]
- Oshima, Y.; Komachi, Y.; Furihata, C.; Tashiro, H.; Sato, H. Fluorescence-suppressed Raman technique for quantitative analysis of protein solution using a micro-Raman probe, the shifted excitation method, and partial least squares regression analysis. Appl Spectrosc. 2006, 60, 964–970. [Google Scholar] [CrossRef] [PubMed]
- Dochow, S.; Ma, D.; Latka, I.; Bocklitz, T.; Hartl, B.; Bec, J.; Fatakdawala, H.; Marple, E.; Urmey, K.; Wachsmann-Hogiu, S.; et al. Combined fiber probe for fluorescence lifetime and Raman spectroscopy. Anal. Bioanal. Chem. 2015, 407, 8291–8301. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Short, M.; Braun, T.; Lui, H.; McLean, D.; Zeng, H. Clinical Raman measurements under special ambient lighting illumination. J. Biomed. Opt. 2014, 19, 111609. [Google Scholar] [CrossRef] [PubMed]
- Maiwald, M.; Müller, A.; Sumpf, B.; Erbert, G.; Tränkle, G. Capability of shifted excitation Raman difference spectroscopy under ambient daylight. Appl. Opt. 2015, 54, 5520–5524. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Carrabba, M.M.; Allen, F.S. Automated Fluorescence Rejection Using Shifted Excitation Raman Difference Spectroscopy. Appl. Spectrosc. 2002, 56, 834–845. [Google Scholar] [CrossRef]
- Dochow, S.; Bergner, N.; Krafft, C.; Clement, J.; Mazilu, M.; Praveen, B.B.; Ashok, P.C.; Marchington, R.; Dholakia, K.; Popp, J. Classification of Raman spectra of single cells with autofluorescence suppression by wavelength modulated excitation. Anal. Methods 2013, 5, 4608–4614. [Google Scholar] [CrossRef]
- Mazilu, M.; Luca, A.C.D.; Riches, A.; Herrington, C.S.; Dholakia, K. Optimal algorithm for fluorescence suppression of modulated Raman spectroscopy. Opt. Express 2010, 18, 11382–11395. [Google Scholar] [CrossRef] [PubMed]
- Krafft, C.; Dochow, S.; Bergner, N.; Clement, J.H.; Praveen, B.B.; Mazilu, M.; Marchington, R.; Dholakia, K.; Popp, J. Raman spectra of single cells with autofluorescence suppression by modulated wavelength excitation. In Proceedings of the Biomedical Vibrational Spectroscopy V: Advances in Research and Industry, San Francisco, CA, USA, 9 February 2012. [Google Scholar]
- Schmidt, H.; Sowoidnich, K.; Kronfeldt, H.-D. A Prototype Hand-Held Raman Sensor for the in situ Characterization of Meat Quality. Appl. Spectrosc. 2010, 64, 888–894. [Google Scholar] [CrossRef] [PubMed]
- Bell, S.E.J.; Bourguignon, E.S.O.; Dennis, A. Analysis of luminescent samples using subtracted shifted Raman spectroscopy. Analyst 1998, 123, 1729–1734. [Google Scholar] [CrossRef]
- Matousek, P.; Towrie, M.; Parker, A.W. Simple reconstruction algorithm for shifted excitation Raman difference spectroscopy. Appl. Spectrosc. 2005, 59, 848–851. [Google Scholar] [CrossRef] [PubMed]
- Willett, R. Multiscale reconstruction for photon-limited shifted excitation Raman spectroscopy. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing—ICASSP, Honolulu, HI, USA, 16–20 April 2007. [Google Scholar]
- Schmidt, H.; Kaiser, D.P.; Maiwald, M. Method for Generating and for Detecting a Raman Spectrum. U.S. Patent 8,310, 672, 28 June 2012. [Google Scholar]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Beleites, C.; Sergo, V. HyperSpec: A Package to Handle Hyperspectral Data Sets in R. R package v 0.98-20150805. 2015. [Google Scholar]
- Liland, K.H.; Mevik, B.-H. Baseline:Baseline Correction of Spectra. R Package v 1.2-1. 2015. Available online: https://cran.r-project.org/web/packages/baseline/index.html (accessed on 26 July 2017).
- Borchers, H.W. Pracma: Practical Numerical Math Functions. R Package v 1.9.9. 2017. Available online: https://www.rdocumentation.org/packages/pracma/versions/1.9.9 (accessed on 26 July 2017).
- Beleites, C. Ramancal: Calibration Routines for Raman Spectrometers. R Package v 0.1. 2013. [Google Scholar]
- Hyndman, R. (Partial) Autocorrelation and Cross Correlation Function Estimation. From Forecast v7.3. 2016. Available online: https://www.rdocumentation.org/packages/forecast/versions/7.3 (accessed on 26 July 2017).
- Hyndman, R.J. Forecast: Forecasting Functions for Time Series and Linear Models. 2017. Available online: https://rdrr.io/cran/forecast/ (accessed on 26 July 2017).
- Beleites, C. Cbmodels: Collection of “Combined” Models: PCA-LDA, PLS-LDA, PLS-LR as Well as EMSC. R Package v 0.5-20160412. 2016. [Google Scholar]
- McCreery, R.L. Raman Spectroscopy for Chemical Analysis; Wiley-interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Kiselev, R.; Schie, I.W.; Askrabic, S.; Krafft, C.; Popp, J. Design and first applications of a flexible Raman micro-spectroscopic system for biological imaging. Biomed. Spectrosc. Imaging 2016, 5, 115–127. [Google Scholar] [CrossRef]
- Ryabchykov, O. Spikes: Spike Correction of Raman Spectral Data. R Package v 1.0. 2016. [Google Scholar]
- Ryabchykov, O.; Bocklitz, T.; Ramoji, A.; Neugebauer, U.; Foerster, M.; Kroegel, C.; Bauer, M.; Kiehntopf, M.; Popp, J. Automatization of spike correction in Raman spectra of biological samples. Chemom. Intell. Lab. Syst. 2016, 155, 1–6. [Google Scholar] [CrossRef]
- Dhanoa, M.S.; Barnes, R.J.; Lister, S.J. Standard normal variate transformation and de-trending of near-infrared diffuse reflectance spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar]
- Slobodan, S. Pharmaceutical Applications of Raman Spectroscopy; John Wiley & Sons, Inc.: Sandwich, UK, 2008. [Google Scholar]
- Long, D.A. The Raman Effect: A Unified Treatment of the Theory of Raman Scattering by Molecules; John Wiley & Sons Ltd.: Bradford, UK, 2002. [Google Scholar]
- Maiwald, M.; Müller, A.; Sumpf, B.; Tränkle, G. A portable shifted excitation Raman difference spectroscopy system: Device and field demonstration. J. Raman Spectrosc. 2016, 47, 1180–1184. [Google Scholar] [CrossRef]
- De Luca, A.C.; Dholakia, K.; Mazilu, M. Modulated Raman Spectroscopy for Enhanced Cancer Diagnosis at the Cellular Level. Sensors 2015, 15, 13680–13704. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cordero, E.; Korinth, F.; Stiebing, C.; Krafft, C.; Schie, I.W.; Popp, J. Evaluation of Shifted Excitation Raman Difference Spectroscopy and Comparison to Computational Background Correction Methods Applied to Biochemical Raman Spectra. Sensors 2017, 17, 1724. https://doi.org/10.3390/s17081724
Cordero E, Korinth F, Stiebing C, Krafft C, Schie IW, Popp J. Evaluation of Shifted Excitation Raman Difference Spectroscopy and Comparison to Computational Background Correction Methods Applied to Biochemical Raman Spectra. Sensors. 2017; 17(8):1724. https://doi.org/10.3390/s17081724
Chicago/Turabian StyleCordero, Eliana, Florian Korinth, Clara Stiebing, Christoph Krafft, Iwan W. Schie, and Jürgen Popp. 2017. "Evaluation of Shifted Excitation Raman Difference Spectroscopy and Comparison to Computational Background Correction Methods Applied to Biochemical Raman Spectra" Sensors 17, no. 8: 1724. https://doi.org/10.3390/s17081724
APA StyleCordero, E., Korinth, F., Stiebing, C., Krafft, C., Schie, I. W., & Popp, J. (2017). Evaluation of Shifted Excitation Raman Difference Spectroscopy and Comparison to Computational Background Correction Methods Applied to Biochemical Raman Spectra. Sensors, 17(8), 1724. https://doi.org/10.3390/s17081724




