Dynamic Hierarchical Energy-Efficient Method Based on Combinatorial Optimization for Wireless Sensor Networks
Abstract
:1. Introduction
2. Related Work
3. The System Model
3.1. Network Model
- (1)
- The BS and all sensor nodes are stationary after deployment, and are equipped with a Global Positioning System (GPS) unit. Hence, these nodes are location-aware.
- (2)
- All properties for each sensor node are identical, while the BS is manually maintained and has enough energy to support continuous operations, with its energy denoted as .
- (3)
- Provided with sufficient energy, each node can control the transmission power according to the distance between the transmitter and the receiver.
- (4)
- The amount of transmission data is exactly equal for each sensor node of valid routes.
3.2. Sensor Energy Model
4. Proposed Protocol
4.1. Constructing the Hierarchical Network Structure
4.2. Establishing the Feasible Routing Set
4.3. Obtaining the Optimal Route
5. Performance Evaluation
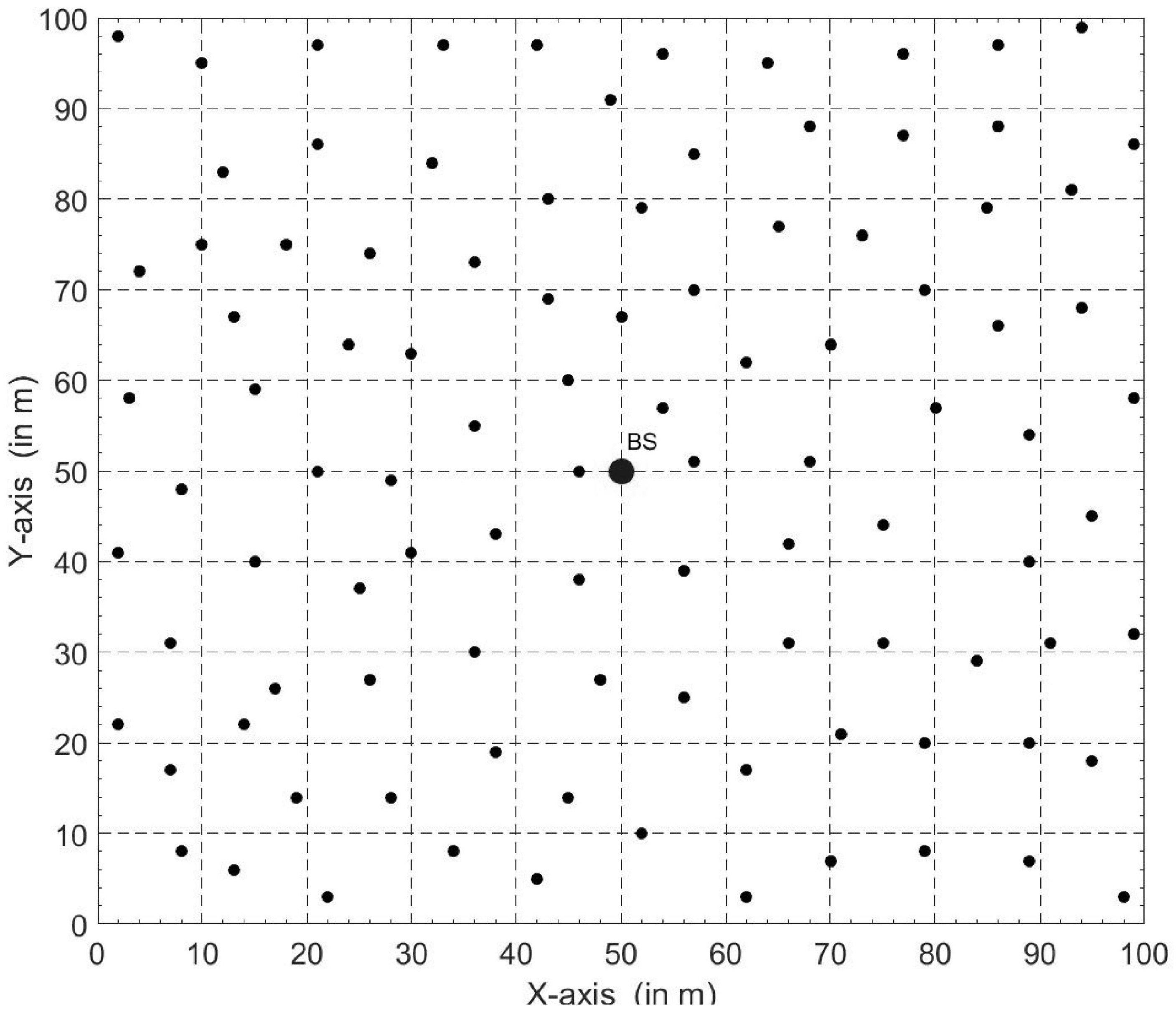
5.1. Experimental Setup
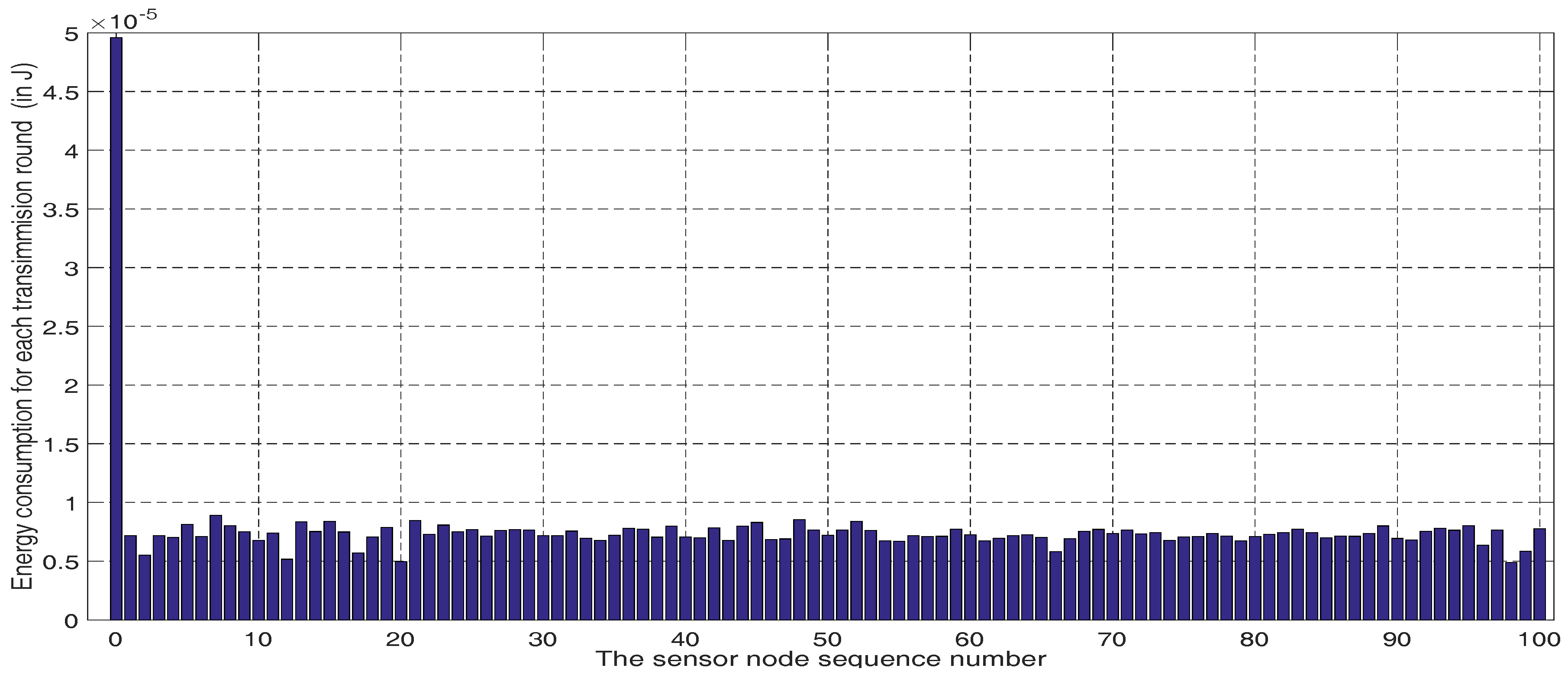
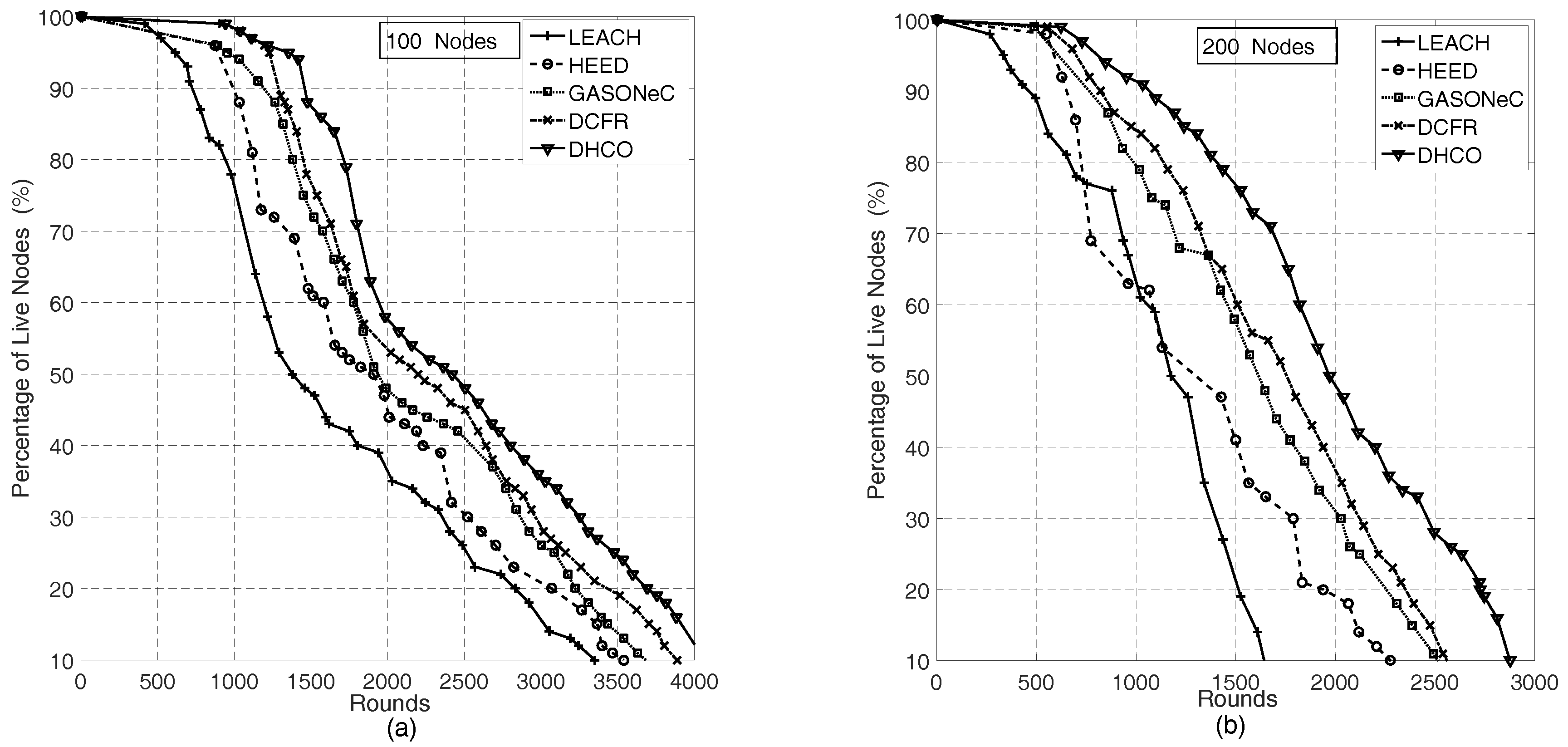
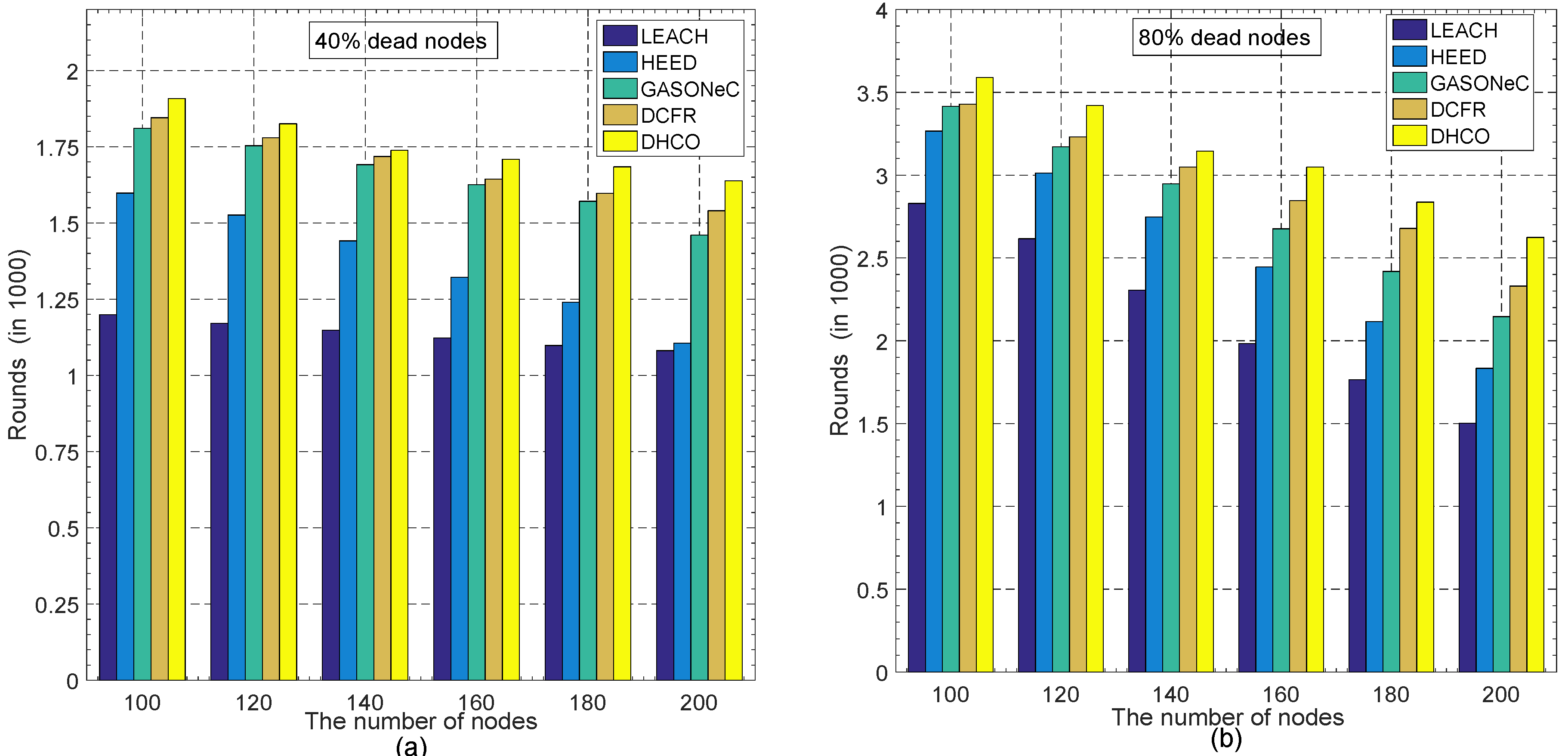
5.2. Node Energy Consumption and Wireless Sensor Network Longevity for the Dynamic Hierarchical Protocol Based on Combinatorial Optimization Algorithm
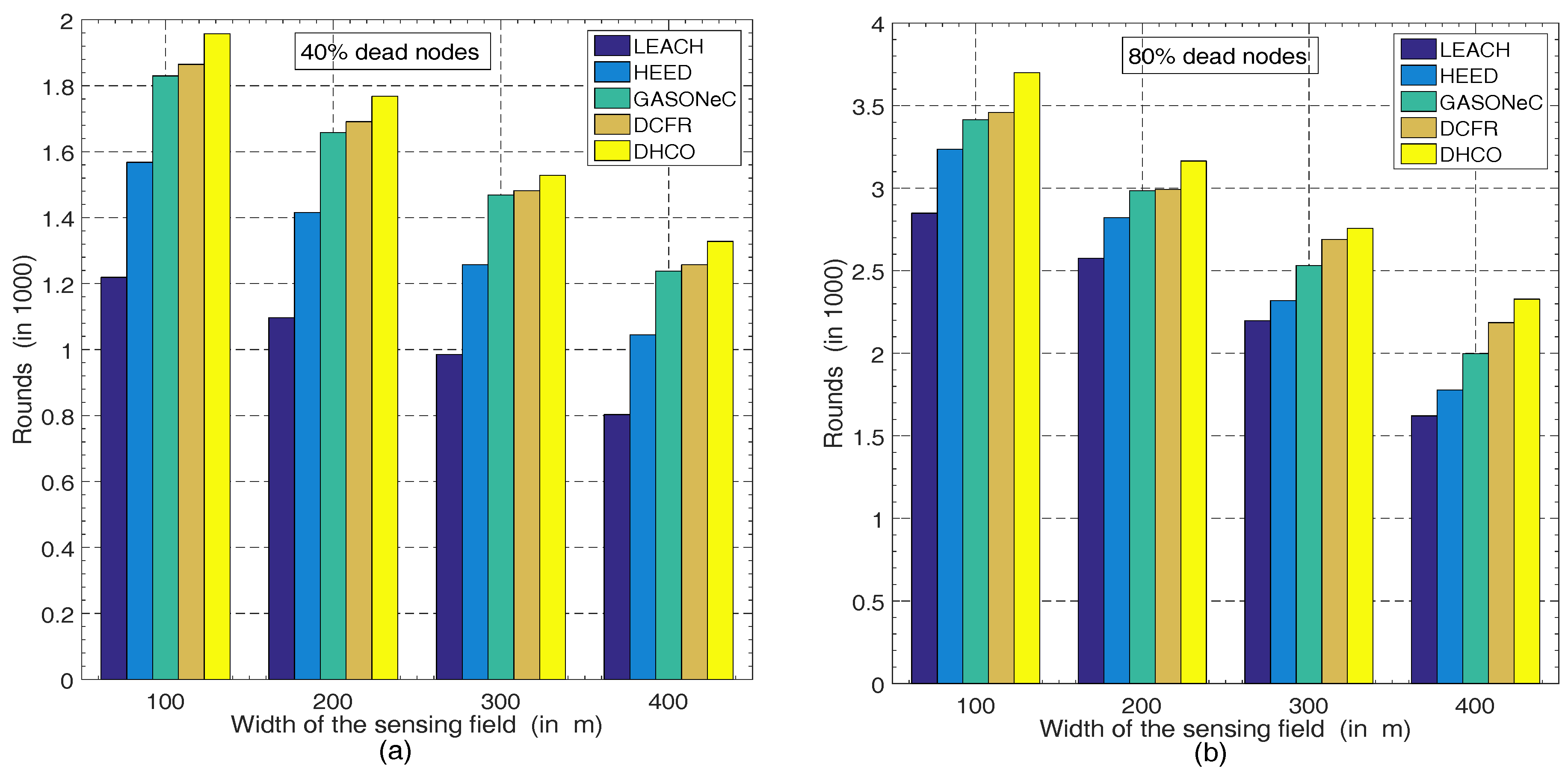
5.3. Wireless Sensor Network Longevity versus the Width of the Sensing Field and the Number of Sensor Nodes
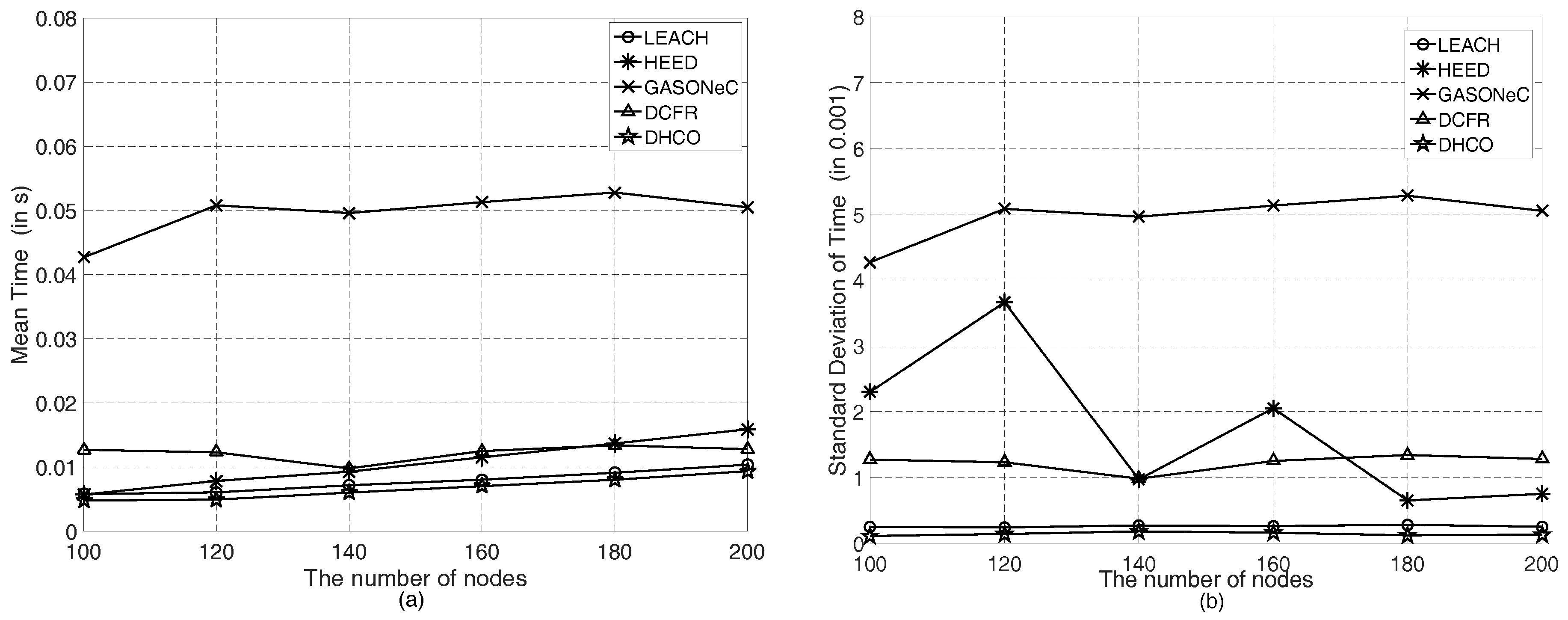
5.4. Efficiency and Computational Complexity Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Goyal, D.; Tripathy, M.R. Routing Protocols in Wireless Sensor Networks: A Survey. Proceedings of 2012 Second International Conference on Advanced Computing & Communication Technologies (ACCT), Rohtak, Haryana, India, 7–8 January 2012; pp. 474–480. [Google Scholar]
- Diaz, V.H.; Martinez, J.F.; Martinez, N.L.; Toro, R.M. Self-Adaptive Strategy Based on Fuzzy Control Systems for Improving Performance in Wireless Sensors Networks. Sensors 2015, 15, 24125–24142. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, K.; Inoue, N.; Tanigawa, Y.; Tode, H.; Watanabe, T. Fair Routing for Overlapped Cooperative Heterogeneous Wireless Sensor Networks. IEEE Sens. J. 2016, 16, 3981–3988. [Google Scholar] [CrossRef]
- Chiwewe, T.M.; Hancke, G.P. A Distributed Topology Control Technique for Low Interference and Energy Efficiency in Wireless Sensor Networks. IEEE Trans. Ind. Inf. 2012, 8, 11–19. [Google Scholar] [CrossRef]
- Sayyed, R.; Kundu, S.; Warty, C.; Nema, S. Resource Optimization using Software Defined Networking for Smart Grid Wireless Sensor Network. Proceedings of 2014 3rd International Conference on Eco-Friendly Computing and Communication Systems (ICECCS), Mangalore, India, 18–21 December 2014; pp. 200–205. [Google Scholar]
- Pantazis, N.A.; Nikolidakis, S.A.; Vergados, D.D. Energy-Efficient Routing Protocols in Wireless Sensor Networks: A Survey. IEEE Commun. Surv. Tutor. 2013, 15, 551–591. [Google Scholar] [CrossRef]
- Ramachandran, G.S.; Daniels, W.; Matthys, N.; Huygens, C.; Michiels, S.; Joosen, W.; Meneghello, J.; Lee, K.; Canete, E.; Rodriguez, M.D.; Hughes, D. Measuring and Modeling the Energy Cost of Reconfiguration in Sensor Networks. IEEE Sens. J. 2015, 15, 3381–3389. [Google Scholar] [CrossRef]
- Feng, R.J.; Li, T.L.; Wu, Y.F.; Yu, N. Reliable routing in wireless sensor networks based on coalitional game theory. IET Commun. 2016, 10, 1027–1034. [Google Scholar] [CrossRef]
- Azad, A.K.M.; Kamruzzaman, J. Energy-Balanced Transmission Policies for Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2011, 10, 927–940. [Google Scholar] [CrossRef]
- Younis, O.; Fahmy, S. HEED: A Hybrid, Energy-Efficient, Distributed Clustering Approach for Ad Hoc Sensor Networks. IEEE Trans. Mob. Comput. 2004, 3, 366–379. [Google Scholar] [CrossRef]
- Heinzelman, W.R.; Chandrakasan, A.P.; Balakrishnan, H. Energy-Efficient Communication Protocol for Wireless Microsensor Networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; pp. 1–10. [Google Scholar]
- Elhoseny, M.; Yuan, X.H.; Yu, Z.T.; Mao, C.L.; El-Minir, H.K.; Riad, A.M. Balancing Energy Consumption in Heterogeneous Wireless Sensor Networks Using Genetic Algorithm. IEEE Commun. Lett. 2015, 19, 2194–2197. [Google Scholar] [CrossRef]
- Smaragdakis, G.; Matta, I.; Matta, A. SEP: A Stable Election Protocol for Clustered Heterogeneous Wireless Sensor Networks. 2004. Available online: http://open.bu.edu/handle/2144/1548 (accessed on 17 July 2017).
- Elbhiri, B.; Saadane, R.; Fldhi, E.S.; Aboutajdine, D. Developed Distributed Energy-Efficient Clustering (DDEEC) for Heterogeneous Wireless Sensor Networks. In Proceedings of the 5th International Symposium on I/V Communications and Mobile Network (ISVC), Rabat, Morocco, 30 September–2 October 2010; pp. 1–4. [Google Scholar]
- Ren, J.; Zhang, Y.X.; Zhang, K.; Liu, A.F.; Chen, J.E.; Shen, X.M. Lifetime and Energy Hole Evolution Analysis in Data-Gathering Wireless Sensor Networks. IEEE Trans. Ind. Inform. 2016, 12, 788–800. [Google Scholar] [CrossRef]
- Lindsey, S.; Raghavendra, C.S. PEGASIS: Power-Efficient Gathering in Sensor Information Systems. In Proceedings of the IEEE on Aerospace Conference Proceedings, Big Sky, MT, USA, 9–16 March 2002; pp. 1125–1130. [Google Scholar]
- Li, C.F.; Ye, M.; Chen, G.H.; Wu, J. An Energy-Efficient Unequal Clustering Mechanism for Wireless Sensor Networks. In Proceedings of the 2nd IEEE International Conference on Mobile Ad-Hoc and Sensor Systems, Washington, DC, USA, 7 November 2005; pp. 604–611. [Google Scholar]
- Nadeem, Q.; Rasheed, M.B.; Javaid, N.; Khan, Z.A.; Maqsood, Y.; Din, A. M-GEAR: Gateway-Based Energy-Aware Multi-Hop Routing Protocol for WSNs. In Proceedings of the 2013 Eighth International Conference on Broadband and Wireless Computing, Communication and Applications (BWCCA), Compiegne, France, 28–30 October 2013; pp. 164–169. [Google Scholar]
- Lin, C.H.; Tsai, M.J. A Comment on “HEED: A Hybrid, Energy-Efficient, Distributed Clustering Approach for Ad Hoc Sensor Networks”. IEEE Trans. Mob. Comput. 2006, 5, 1471–1472. [Google Scholar]
- Shirmohammadi, M.M.; Faez, K.; Chhardoli, M. LELE: Leader Election with Load Balancing Energy in Wireless Sensor Network. In Proceedings of the CMC ’09. WRI International Conference on Communications and Mobile Computing, Yunnan, China, 6–8 January 2009; pp. 106–110. [Google Scholar]
- Yuan, X.H.; Elhoseny, M.; El-Minir, H.K.; Riad, A.M. A Genetic Algorithm-Based, Dynamic Clustering Method Towards Improved WSN Longevity. J Netw. Syst. Manag. 2017, 25, 21–46. [Google Scholar] [CrossRef]
- Liu, X.; He, D. Ant colony optimization with greedy migration mechanism for node deployment in wireless sensor networks. J. Netw. Comput. Appl. 2014, 39, 310–318. [Google Scholar] [CrossRef]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An Application-Specific Protocol Architecture for Wireless Microsensor Networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
- Tang, J.Q.; Yang, W.; Zhu, L.Y.; Wang, D.; Feng, X. An Adaptive Clustering Approach Based on Minimum Travel Route Planning for Wireless Sensor Networks with a Mobile Sink. Sensors 2017, 17, 964. [Google Scholar] [CrossRef] [PubMed]
- Taheri, H.; Neamatollahi, P.; Younis, O.M.; Naghibzadeh, S.; Yaghmaee, M.H. An Energy-aware Distributed Clustering Protocol in Wireless Sensor Networks using Fuzzy Logic. Ad Hoc Netw. 2012, 10, 1469–1481. [Google Scholar] [CrossRef]

| Properties | Values |
|---|---|
| Initial node energy | 0.5 J |
| Electronics energy, | 50 nJ/bit |
| Consumption loss for , | 10 pJ/bit/m |
| Consumption loss for , | 0.0013 pJ/bit/m |
| Data aggregation energy | 50 nJ/bit/signal |
| Packet size, l | 400 bit |
| The optimal communication radius, | 40 m |
| The threshold distance, | 75 m |
| The minimum residual node energy, | J |
| The initial probability p of being a CH | 0.05 |
| The maximum number of iterations in HEED | 12 |
| The population size in GASONeC | 30 |
| The generation size in GASONeC | 30 |
| The crossover probability in GASONeC | 0.8 |
| The mutation probability in GASONeC | 0.006 |
| Duty cycle in DCFR | 10% |
| Duration of a data period in DCFR | 10 s |
| Energy consumption rate for idle listening in DCFR | 0.88 mJ/s |
| Width of Square Region | Location of BS | Number of Nodes | Mean Time | Standard Deviation |
|---|---|---|---|---|
| 100 m | (50 m, 50 m) | 100 | 0.00479 s | 0.00011 |
| 100 m | (50 m, 50 m) | 120 | 0.00494 s | 0.00014 |
| 100 m | (50 m, 50 m) | 140 | 0.00603 s | 0.00018 |
| 100 m | (50 m, 50 m) | 160 | 0.00703 s | 0.00016 |
| 100 m | (50 m, 50 m) | 180 | 0.00803 s | 0.00012 |
| 100 m | (50 m, 50 m) | 200 | 0.00937 s | 0.00013 |
| 100 m | (100 m, 100 m) | 100 | 0.00417 s | 0.00015 |
| 100 m | (150 m, 150 m) | 100 | 0.00407 s | 0.00014 |
| 100 m | (200 m, 200 m) | 100 | 0.00393 s | 0.00009 |
| 100 m | (250 m, 250 m) | 100 | 0.00408 s | 0.00012 |
| 200 m | (50 m, 50 m) | 100 | 0.00409 s | 0.00015 |
| 300 m | (50 m, 50 m) | 100 | 0.00389 s | 0.00008 |
| 400 m | (50 m, 50m) | 100 | 0.00411 s | 0.00011 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Tang, H.; Cheng, Y.; Zhao, Q.; Yuan, B.L.a. Dynamic Hierarchical Energy-Efficient Method Based on Combinatorial Optimization for Wireless Sensor Networks. Sensors 2017, 17, 1665. https://doi.org/10.3390/s17071665
Chang Y, Tang H, Cheng Y, Zhao Q, Yuan BLa. Dynamic Hierarchical Energy-Efficient Method Based on Combinatorial Optimization for Wireless Sensor Networks. Sensors. 2017; 17(7):1665. https://doi.org/10.3390/s17071665
Chicago/Turabian StyleChang, Yuchao, Hongying Tang, Yongbo Cheng, Qin Zhao, and Baoqing Li andXiaobing Yuan. 2017. "Dynamic Hierarchical Energy-Efficient Method Based on Combinatorial Optimization for Wireless Sensor Networks" Sensors 17, no. 7: 1665. https://doi.org/10.3390/s17071665
APA StyleChang, Y., Tang, H., Cheng, Y., Zhao, Q., & Yuan, B. L. a. (2017). Dynamic Hierarchical Energy-Efficient Method Based on Combinatorial Optimization for Wireless Sensor Networks. Sensors, 17(7), 1665. https://doi.org/10.3390/s17071665







