An RFID-Based Smart Structure for the Supply Chain: Resilient Scanning Proofs and Ownership Transfer with Positive Secrecy Capacity Channels †
Abstract
:1. Introduction
- 1.
- 2.
- (1)
- Extend the notion of a grouping proof of integrity to a broader class of applications where items may be missing. The primary concern of the owner of a shipped pallet is to establish its integrity; however, if some tagged items are missing, then the owner wants a list of the missing items and proof that nothing else is missing (resiliency). Thus, based on the work published in [12], we present a two-round anonymous RFID scanning proof that supports tag privacy such that: (a) the verifier (owner) can authorize an untrusted reader (carrier) to scan a group of tagged items and either generate a proof of integrity, or if some tagged items are missing, identify these and prove that nothing else is missing, (b) the authorization is for one only scanning, (c) tagged items are untraceable while the group is not scanned, and (d) only the verifier (owner) can check the proof: unauthorized inspections or forged proofs will not be accepted.
- (2)
- Extend the implementation of positive secrecy capacity channels for provably secure OTP in [11] by using time-slot modulation, similar to the random-slotted medium access control protocol, to make it possible to implement them without requiring multi-level but binary detection.
2. Background
2.1. Brief Review of Grouping-Proofs
2.2. Brief Review of Group Codes
2.3. Brief Review of Ownership Transfer Protocols
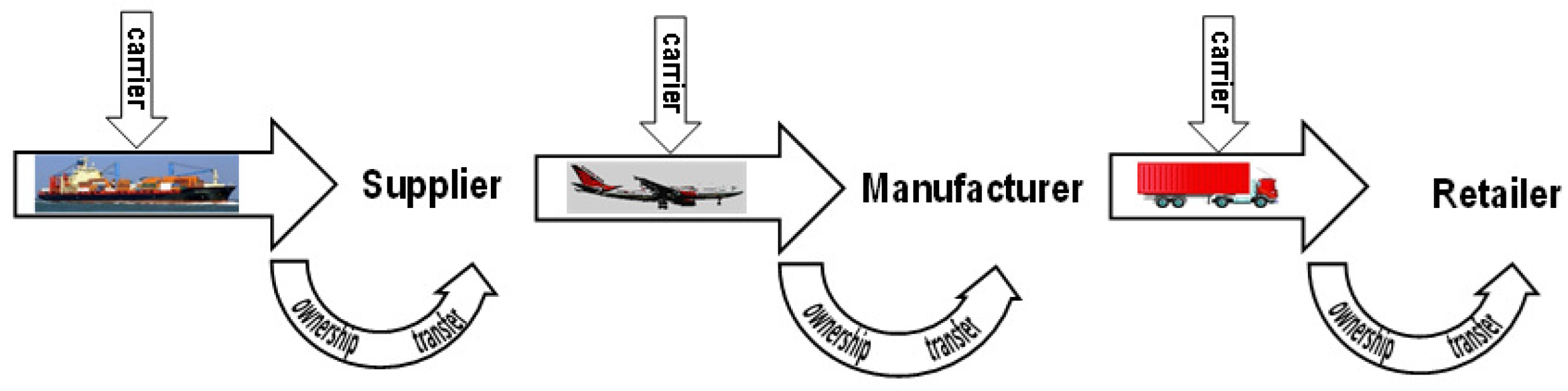
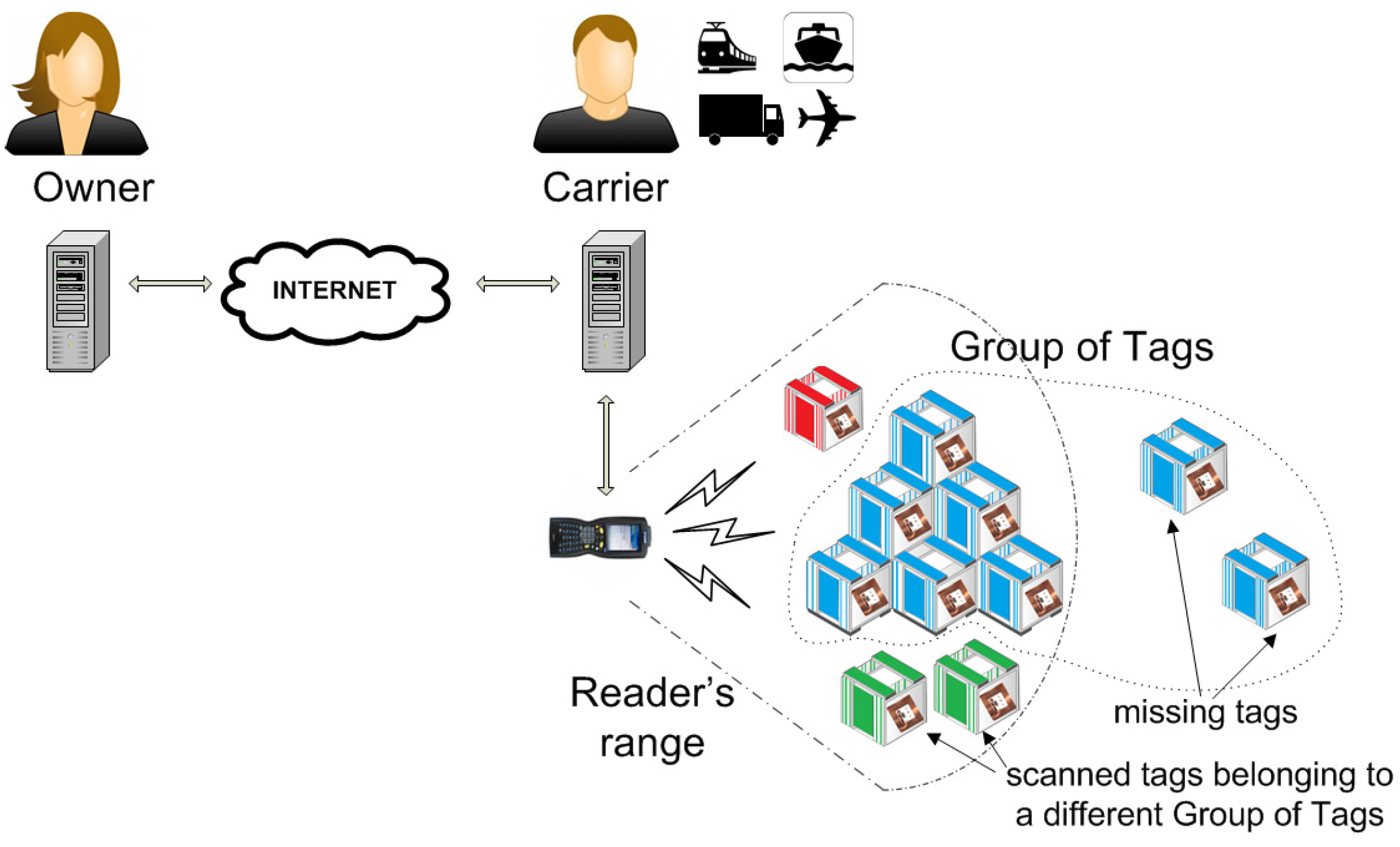
3. The Shipment Link
- 1.
- The owner of the pallet P (e.g., the supplier, manufacturer, retailer, etc.) can authorize an untrusted carrier to inspect P for integrity and identify any missing goods.
- 2.
- The authorization is for a certain number of inspections (or limited time) defined by a counter , and the contents of P are untraceable after the authorization expires. In particular, the carrier does not share any private keys with the tags and cannot access or even trace the tags beyond the lifetime of the counter .
- 3.
- The carrier can generate a grouping proof of integrity for the pallet P that (only) the owner can verify if no goods are missing; if some goods are missing, then the carrier can (a) identify the missing goods without requiring a packing list (or an external database) and (b) generate a scanning proof of presence for the remaining goods.
- 4.
- The grouping proof is generated only if the tags of the group were scanned simultaneously (during the same session defined by the activation time of the tags) within a time window defined by .
- a
- The tags of a pallet are not compromised. This does not mean that tags cannot be compromised; but if they are, then the corroborating evidence generated for a scanning proof is compromised.
- b
- Simultaneity. This is defined in terms of counters or timestamps provided by the owner.
- c
- Batch connectivity. The owner does not enjoy permanent connectivity with the carrier and is restricted to: (a) broadcasting a challenge that is valid for a (short) time span and, (b) checking responses from tags that are compiled and sent from time to time by untrusted readers.
- d
- Balanced loading. The tags of a pallet have similar hardware capabilities and the computation load per tag is balanced.
- e
- Messages must include destination information (possibly private) to allow for unicast/multicast communication. This is sometimes neglected by designers, but it is particularly important for checking anonymity: each message must contain information that allows tags to decide if they are the intended recipient.
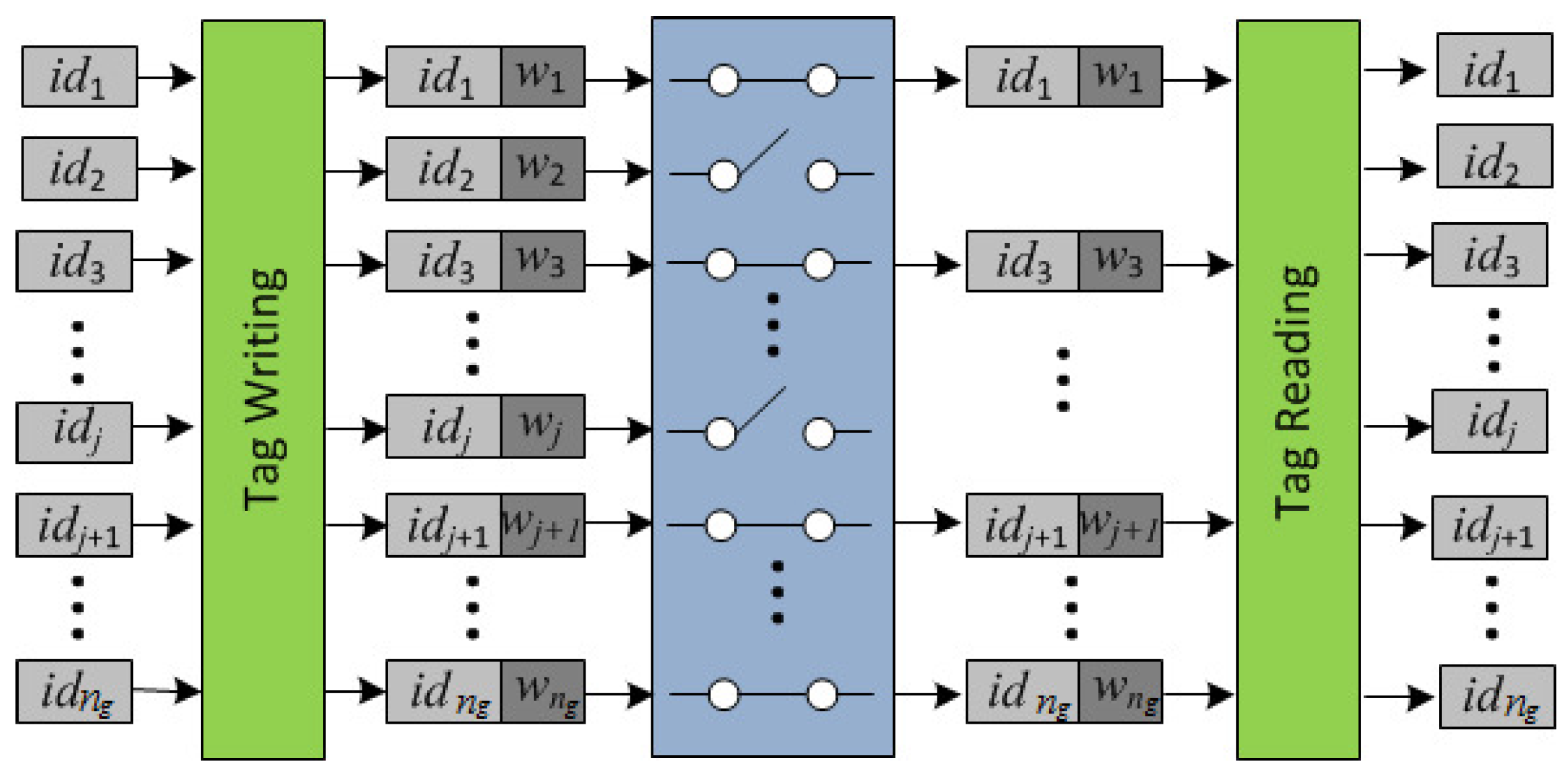
3.1. Extended Identifiers with Redundancy
3.2. Scanning Proof Description
- Round 1.
- The reader R of the carrier broadcasts to all tags in its range: , and sets a timer. Each in the range of R computes and checks the correctness of by verifying that and that the counter value . If any of these fail, returns two random values. Otherwise, it updates its counter to T, draws a random number and computes its authenticator . Then, it sends to R and sets a timer. The received nonces are used by the reader R to identify (singulate) tags in this session (session pseudonyms). R checks the correctness of every by verifying that , and if this holds, R stores them in a list . On timeout, R computes the request , where are the indices of the tags of pallet P that were scanned, and its authenticator . Thus, the first round incorporates the randomness provided by the owner’s challenge T and the randomness provided by the interrogated tags. This prevents replay attacks. The participation of “alien" tags does not affect the execution (availability is guaranteed) and information about the total number of tags or reply order is not leaked because tags do not follow any chaining structure. The scanning period is defined by the scanning request T of the reader, and simultaneity by the validity period of the nonces that is set by the scanned tags.
- Round 2.
- The reader R broadcasts the authenticated request to all tags in its range. Each in the range of R that has not timed out, checks that and if so, it computes: and its session authenticator , as well as a “proof of presence during the session” (a message authentication code), and its authenticator . Then, it encrypts its identifier with the “one-time-pad” key to get , sends to R: (, , , ), and timeouts. The reader R computes and retrieves the identifiers . Then, it checks (by exhaustive search) that for some value in the list , and that . If these are correct, R stores the identifiers in a list . On timeout, R checks that (that all tags singulated in Round 1 responded in Round 2), and if so, compiles the proof as evidence that the tags were scanned. Otherwise, R aborts the protocol. Then, using the control information, R checks that the cardinality of the group coincides with . If not, R finds the missing s by using the redundant information stored in the retrieved identifiers , provided that this is within the correction capabilities of the implemented forward error correction mechanism (i.e., the number of missing tags is no more than ). If there are no missing tags, then W becomes a grouping proof of integrity for pallet P that the reader R sends to the owner Own. Otherwise, R retrieves the list of identifiers , , of the missing goods, and sends Own the scanning proof of presence for the remaining goods.
3.3. Security Discussion
- 1.
- Traceability attacks (privacy). Unlinkability is related to the capability of linking interrogations after physical tracking is temporarily interrupted. Different formal models can be found in the literature (e.g., [48,49,50]). Intuitively, a protocol guarantees unlinkability, if no adversary can decide with advantage better than negligible whether two transmitted messages from different protocol executions are linked to the same tag . In the scanning proof, is untraceable because, in every session, it updates its counter and will draw a fresh (pseudo) random number after responding to the reader’s challenge T. Consequently, the responses of the same tag in different interrogations look random to an observer and cannot be linked. Tags do not follow a sequence to reply so that information about the order of a tag cannot be leaked.
- 2.
- Replay Attacks. The use of the counter T prevents replay attacks: if an adversarial reader re-uses T, the tags that received it earlier will have updated their counter and not respond.
- 3.
- Impersonation attacks. Impersonation attacks on tagged goods are prevented by using private keys . Impersonation attacks on a reader will not yield a valid proof since the owner will only accept proofs from authorized readers that have been given .
- 4.
- Forged proofs. The values can only be generated by someone who knows ; i.e., and the owner. Values from different sessions cannot be used to compile a proof since they involve the session nonces of interrogated tags and the challenge of the reader R () that depends on the counter T which specifies the validity time window. Note that all tags set timers in Round 1 of the protocol and will not respond after timeout.
- 5.
- De-synchronization attacks (DoS attacks). The adversary cannot compute a valid pair of values because this requires knowledge of the key k. On the other hand, if a protocol execution completes successfully, then all tags will share the same counter value. No tag will accept a previously used T. However, tags will accept future values of T, not necessarily the next value, so that even if they do not share the same counter value (e.g., because of an interrupted interrogation), there are no synchronization concerns.
4. Ownership Transfer Link
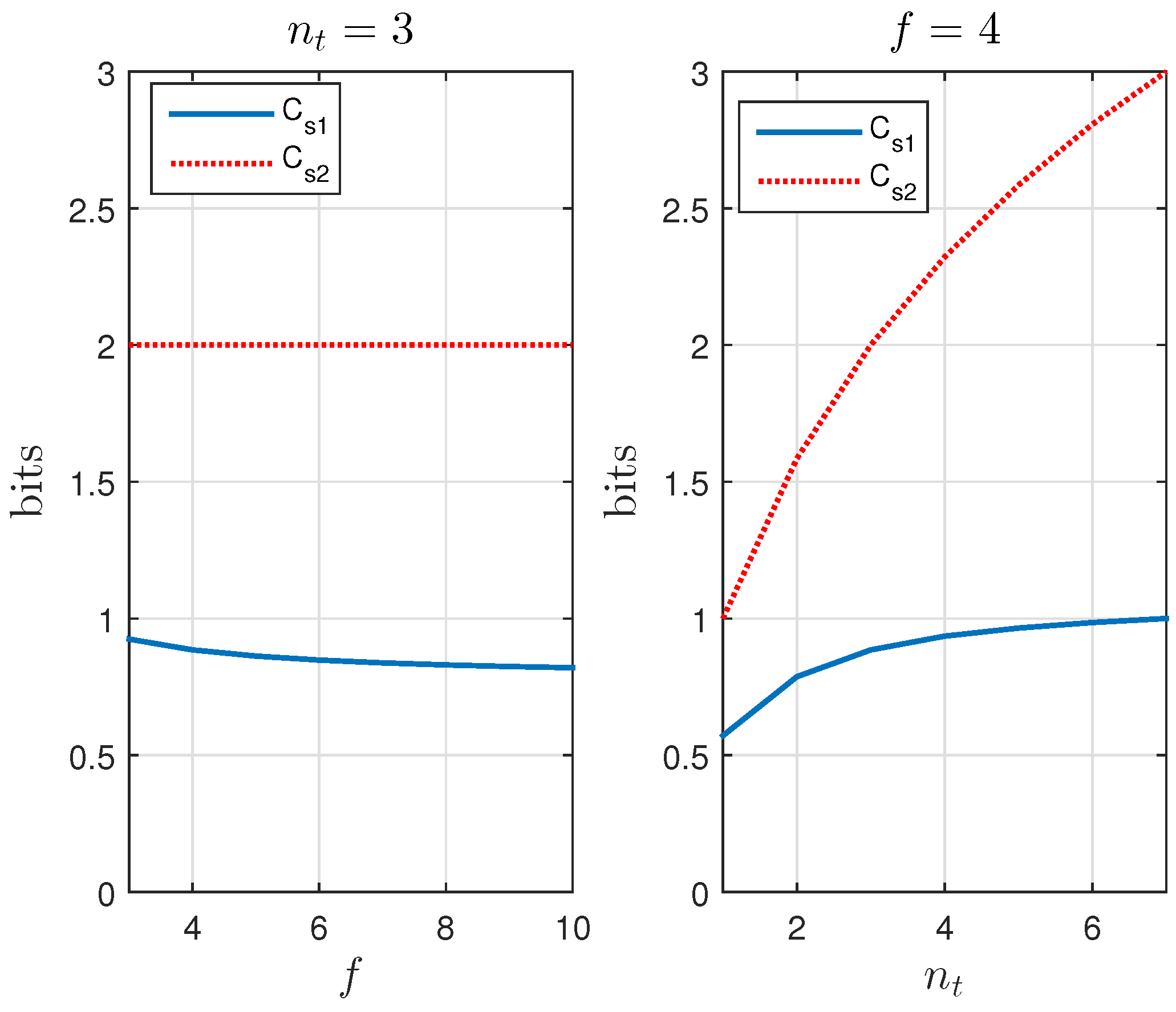
5. A KUP That Uses a Positive Secrecy Capacity Channel Adapted for the Supply Chain
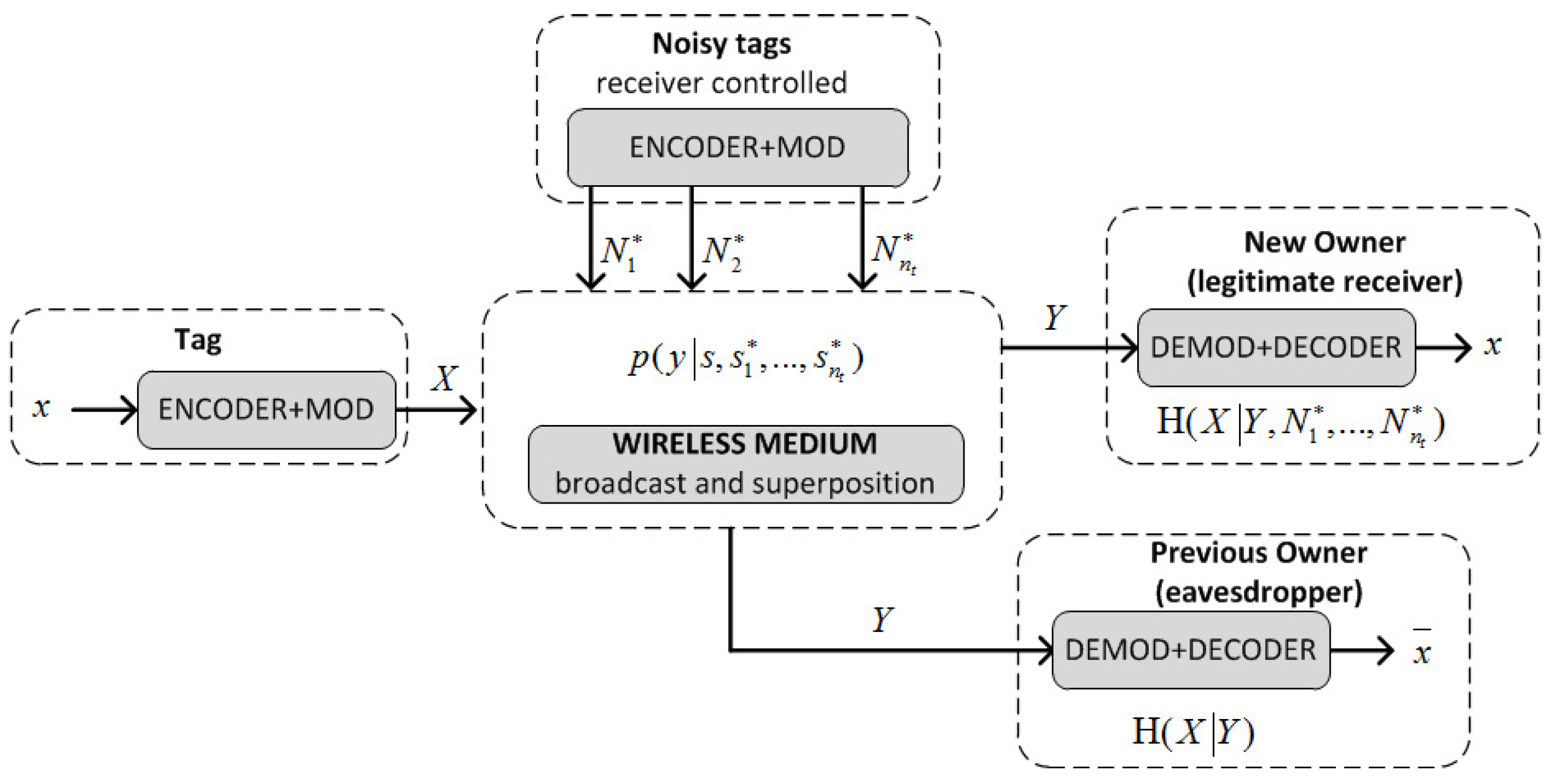
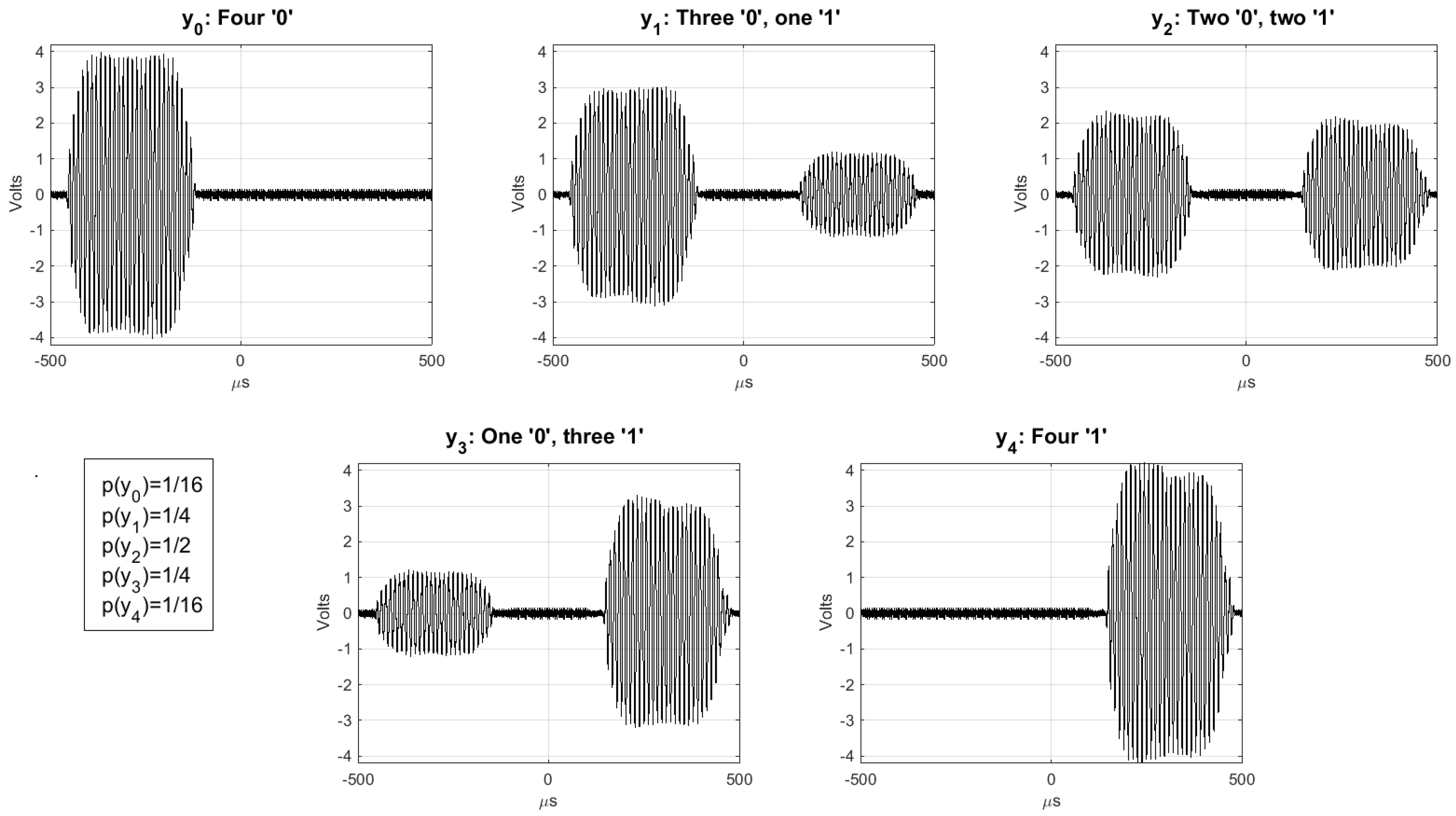
5.1. A Positive Secrecy Capacity Channel Based on Modified Random-Slotted Modulation
5.2. A KUP Based on a Positive Secrecy Capacity Channel with Modified Random-Slotted Modulation
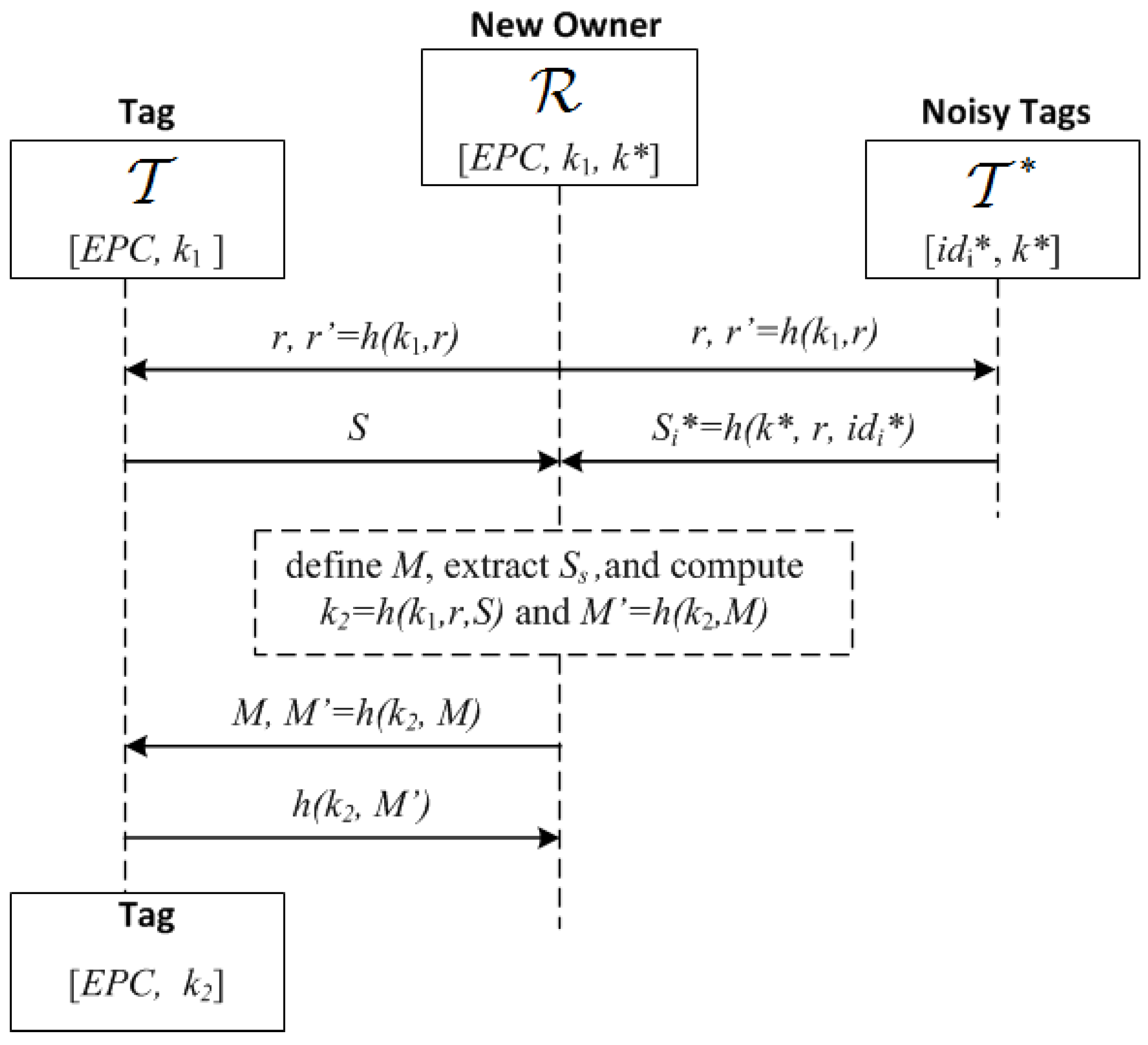
- 1.
- broadcasts , where r is a nonce and :
- 2.
- Upon receiving this, and check that are correct, and if so, generate a random bit string S and the bit strings , of length , where is a guard factor (e.g., ). Then and broadcast these bit strings using a frame for each bit and picking random slots within such frames as described previously (Section 5.1): and and
- 3.
- receives the added signals of S and . First, identifies the frames with irreconcilable collisions (by checking that ) and stores their indices in a list U. Let be the set of frames without irreconcilable collisions. generates a bit string of length with the values of S for the frames with indices in , and a bit string M of length L, whose i-th bit is 0 if and 1 if . Note that the expected value of : , is greater than . However if , then generates another random number r and repeats the first step, extracting a new , and concatenating it to the previous one until . Then, computes , and sends :
- 4.
- generates by taking the bits of S where M is equal to 1, computes and checks the correctness of the received . If this is not correct, then aborts the protocol; otherwise, it computes and sends this to to confirm that the updating was correct:.
- 5.
- checks the received message. If correct, the protocol is completed, and the current owner informs the previous one that the process has been completed. Otherwise, resends the values in Step 3 to checks if has updated its key. If not, the KUP is repeated.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. General Case: , with Irreconcilable Collisions
Appendix A.2. , without Irreconcilable Collisions
Appendix A.3. , without Irreconcilable Collisions
References
- The White House, Office of the Press Secretary. Available online: https://obamawhitehouse.archives.gov/sites/default/files/national_strategy_for_global_supply_chain_security.pdf (accessed on 3 July 2017).
- Paret, D. RFID and Contactless Smart Card Applications; John Wiley & Sons Ltd.: Chichester, UK, 2005. [Google Scholar]
- Liu, H.; Ning, H.; Zhang, Y.; He, D.; Xiong, Q.; Yang, L.T. Grouping-Proofs-Based Authentication Protocol for Distributed RFID Systems. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 1321–1330. [Google Scholar] [CrossRef]
- Burmester, M.; Munilla, J. Chapter RFID Grouping-Proofs in Security and Trends in Wireless Identification and Sensing Platform Tags: Advancements in RFID; Information Science Reference-IGI Gobal: Hershey, PA, USA, 2013; pp. 89–119. [Google Scholar]
- Vullers, P. Secure Ownership and Ownership Transfer in RFID Systems. Master’s Thesis, Eindhoven University, Eindhoven, The Netherlands, 2009. [Google Scholar]
- Kapoor, G.; Piramuthu, S. Single RFID Tag Ownership Transfer Protocols. IEEE Trans. Syst. Man Cybern. Part C 2012, 42, 164–173. [Google Scholar] [CrossRef]
- Osaka, K.; Takagi, T.; Yamazaki, K.; Takahashi, O. An Efficient and Secure RFID Security Method with Ownership Transfer. In Computational Intelligence and Security; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4456, pp. 778–787. [Google Scholar]
- Sundaresan, S.; Doss, R.; Zhou, W.; Piramuthu, S. Secure ownership transfer for multi-tag multi-owner passive RFID environment with individual-owner privacy. Comput. Commun. 2015, 55, 112–124. [Google Scholar] [CrossRef]
- Song, B. RFID Tag Ownership Transfer. In Proceedings of the Workshop on RFID Security—RFIDSec’08, Budapest, Hungary, 9–11 July 2008. [Google Scholar]
- Lei, H.; Cao, T. RFID Protocol Enabling Ownership Transfer to Protect against Traceability and DoS Attacks. In Proceedings of the First International Symposium on Data, Privacy, and E-Commerce, Washington, DC, USA, 1–3 November 2007; pp. 508–510. [Google Scholar]
- Munilla, J.; Burmester, M.; Peinado, A.; Yang, G.; Susilo, W. RFID Ownership Transfer with Positive Secrecy Capacity Channels. Sensors 2017, 17, 53. [Google Scholar] [CrossRef] [PubMed]
- Burmester, M.; Munilla, J. Resilient Grouping Proofs with Missing Tag Identification. In Proceedings of the 10th International Conference on Ubiquitous Computing and Ambient Intelligence, UCAmI 2016, San Bartolomé de Tirajana, Gran Canaria, Spain, 29 November–2 December 2016; pp. 544–555. [Google Scholar]
- Piramuthu, S. On Existence Proofs for Multiple RFID Tags. In Proceedings of the IEEE International Conference on Pervasive Services, Workshop on Security, Privacy and Trust in Pervasive and Ubiquitous Computing—SecPerU, Sydney, Australia, 14–18 March 2006. [Google Scholar]
- Burmester, M.; de Medeiros, B.; Motta, R. Provably Secure Grouping-Proofs for RFID Tags; Grimaud, G., Standaert, F.X., Eds.; (CARDIS 2008); Lecture Notes in Computer Science; Springer: London, UK, 2008; Volume 5189, pp. 176–190. [Google Scholar]
- Huang, H.H.; Ku, C.Y. A RFID Grouping Proof Protocol for Medication Safety of Inpatient. J. Med. Syst. 2009, 33, 467–474. [Google Scholar] [CrossRef] [PubMed]
- Chien, H.Y.; Yang, C.C.; Wu, T.C.; Lee, C.F. Two RFID-based Solutions to Enhance Inpatient Medication Safety. J. Med. Syst. 2011, 35, 369–375. [Google Scholar] [CrossRef] [PubMed]
- Burmester, M.; Munilla, J. Distributed Group Authentication for RFID Supply Management; Technical Report E-Print. International Association for Cryptological Research. Available online: http://eprint.iacr.org/2013/779 (accessed on 3 July 2017).
- Peris-Lopez, P.; Orfila, A.; Hernandez-Castro, J.C.; van der Lubbe, J.C.A. Flaws on RFID grouping-proofs. Guidelines for future sound protocols. J. Netw. Comput. Appl. 2011, 34, 833–845. [Google Scholar] [CrossRef]
- Sato, Y.; Igarashi, Y.; Mitsugi, J.; Nakamura, O.; Murai, J. Identification of missing objects with group coding of RF tags. In Proceedings of the IEEE International Conference on RFID, Orlando, FL, USA, 3–5 April 2012; pp. 95–101. [Google Scholar]
- Sato, Y.; Mitsugi, J.; Nakamura, O.; Murai, J. Theory and performance evaluation of group coding of RFID tags. IEEE Trans. Autom. Sci. Eng. 2012, 9, 458–466. [Google Scholar] [CrossRef]
- Gallager, R.G. Low-density parity-check codes. IRE Trans. Inf. Theory 1962, IT-8, 21–28. [Google Scholar] [CrossRef]
- Su, Y.S.; Lin, J.R.; Tonguz, O.K. Grouping of RFID Tags via Strongly Selective Families. IEEE Commun. Lett. 2013, 17, 1120–1123. [Google Scholar]
- Su, Y.S.; Tonguz, O.K. Using the Chinese Remainder Theorem for the Grouping of RFID Tags. IEEE Trans. Commun. 2013, 61, 4741–4753. [Google Scholar] [CrossRef]
- Su, Y.S. Extended Grouping of RFID Tags Based on Resolvable Transversal Designs. IEEE Signal Process. Lett. 2014, 21, 488–492. [Google Scholar] [CrossRef]
- Ben Mabrouk, N.; Couderc, P. EraRFID: Reliable RFID systems using erasure coding. In Proceedings of the 2015 IEEE International Conference on RFID, Tokyo, Japan, 16–18 September 2015; pp. 121–128. [Google Scholar]
- Burmester, M.; Munilla, J. Tag Memory-Erasure Tradeoff of RFID Grouping Codes. IEEE Commun. Lett. 2016, 20, 1144–1147. [Google Scholar] [CrossRef]
- Burmester, M.; Munilla, J. Performance Analysis of LDPC-Based RFID Group Coding. IEEE Trans. Autom. Sci. Eng. 2017, 14, 398–402. [Google Scholar] [CrossRef]
- Saito, J.; Imamoto, K.; Sakurai, K. Reassignment Scheme of an RFID Tag’s Key for Owner Transfer. In EUC Workshops; Enokido, T., Yan, L., Xiao, B., Kim, D., Dai, Y.S., Yang, L.T., Eds.; Lecture Notes in Computer Science; Springer: Nagasaki, Japan, 2005; Volume 3823, pp. 1303–1312. [Google Scholar]
- Molnar, D.; Soppera, A.; Wagner, D. A Scalable, Delegatable Pseudonym Protocol Enabling Ownership Transfer of RFID Tags. In Proceedings of the Workshop on Selected Areas in Cryptography (SAC 2005), Kingston, ON, Canada, 11–12 August 2005; Volume 3897. [Google Scholar]
- Avoine, G.; Dysli, E.; Oechslin, P. Reducing Time Complexity in RFID Systems. In Proceedings of the 12th International Conference on Selected Areas in Cryptography, Kingston, ON, Canada, 11–12 August 2005; pp. 291–306. [Google Scholar]
- Soppera, A.; Burbridge, T. Secure by default: The RFID acceptor tag (RAT). In Workshop on RFID Security—RFIDSec’06; Ecrypt: Graz, Austria, 2006. [Google Scholar]
- Osaka, K.; Takagi, T.; Yamazaki, K.; Takahashi, O. An Efficient and Secure RFID Security Method with Ownership Transfer. In Proceedings of the 2006 International Conference on Computational Intelligence and Security, Guangzhou, China, 3–6 November 2006; Volume 2, pp. 1090–1095. [Google Scholar]
- Chen, H.B.; Lee, W.B.; Zhao, Y.H.; Chen, Y.L. Enhancement of the RFID Security Method with Ownership Transfer. In Proceedings of the 3rd International Conference on Ubiquitous Information Management and Communication, Suwon, Korea, 15–16 January 2009; pp. 251–254. [Google Scholar]
- Jappinen, P.; Hamalainen, H. Enhanced RFID Security Method with Ownership Transfer. In Proceedings of the International Conference on Computational Intelligence and Security, Suzhou, China, 13–17 December 2008; Volume 2, pp. 382–385. [Google Scholar]
- Yoon, E.J.; Yoo, K.Y. Two Security Problems of RFID Security Method with Ownership Transfer. In Proceedings of the IFIP International Conference on Network and Parallel Computing, Shanghai, China, 18–21 October 2008; pp. 68–73. [Google Scholar]
- Kapoor, G.; Piramuthu, S. Vulnerabilities in some recently proposed RFID ownership transfer protocols. IEEE Commun. Lett. 2010, 14, 260–262. [Google Scholar] [CrossRef]
- Dimitriou, T. rfidDOT: RFID delegation and ownership transfer made simple. In Proceedings of the 4th International Conference on Security and Privacy in Communication Networks, Istanbul, Turkey, 22–25 September 2008; pp. 1–8. [Google Scholar]
- Elkhiyaoui, K.; Blass, E.O.; Molva, R. ROTIV: RFID Ownership Transfer with Issuer Verification. In Proceedings of the 7th International Conference on RFID Security and Privacy, Amherst, MA, USA, 26–28 June 2011; pp. 163–182. [Google Scholar]
- Song, B.; Mitchell, C.J. Scalable RFID security protocols supporting tag ownership transfer. Comput. Commun. 2011, 34, 556–566. [Google Scholar] [CrossRef]
- Ng, C.Y.; Susilo, W.; Mu, Y.; Safavi-Naini, R. Practical RFID Ownership Transfer Scheme. J. Comput. Secur. 2011, 19, 319–341. [Google Scholar] [CrossRef]
- Kapoor, G.; Zhou, W.; Piramuthu, S. Multi-tag and Multi-owner RFID Ownership Transfer in Supply Chains. Decis. Support Syst. 2011, 52, 258–270. [Google Scholar] [CrossRef]
- EPC Global UHF Air Interface Protocol Standard Generation2/Version2. Available online: https://www.gs1.org/epcrfid/epc-rfid-uhf-air-interface-protocol/2-0-1 (accessed on 3 July 2017).
- Chen, C.L.; Lai, Y.L.; Chen, C.C.; Deng, Y.Y.; Hwang, Y.C. RFID Ownership Transfer Authorization Systems Conforming EPCglobal Class-1 Generation-2 Standards. Int. J. Netw. Secur. 2011, 13, 41–48. [Google Scholar]
- Sabaragamu Koralalage, K.H.S.; Reza, S.M.; Miura, J.; Goto, Y.; Cheng, J. POP Method: An Approach to Enhance the Security and Privacy of RFID Systems Used in Product Lifecycle with an Anonymous Ownership Transferring Mechanism. In Proceedings of the 2007 ACM Symposium on Applied Computing, Seoul, Korea, 11–15 March 2007; pp. 270–275. [Google Scholar]
- Chen, C.L.; Huang, Y.C.; Jiang, J.R. A secure ownership transfer protocol using EPCglobal Gen-2 RFID. Telecommun. Syst. 2013, 53, 387–399. [Google Scholar] [CrossRef]
- Munilla, J.; Burmester, M.; Peinado, A. Attacks on ownership transfer scheme for multi-tag multi-owner passive RFID environments. Comput. Commun. 2016, 88, 84–88. [Google Scholar] [CrossRef]
- Roca, V.; Cunche, M.; Lacan, J.; Bouabdallah, A.; Matsuzono, K. Simple Reed-Solomon Forward Error Correction (FEC) Scheme for FECFRAME. Available online: http://www.rfc-editor.org/info/rfc6865 (accessed on 4 July 2017).
- Avoine, G. Adversarial Model for Radio Frequency Identification; Technical Report; Swiss Federal Institute of Technology (EPFL), Security and Cryptography Laboratory (LASEC): Lausanne, Switzerland, 2005. [Google Scholar]
- Juels, A.; Weis, S.A. Defining Strong Privacy for RFID. ACM Trans. Inf. Syst. Secur. 2009, 13. [Google Scholar] [CrossRef]
- Vaudenay, S. On Privacy Models for RFID. In Proceedings of the Advances in Cryptology – ASIACRYPT 2007, Kuching, Malaysia, 2–6 December 2007; Volume 4833, pp. 68–87. [Google Scholar]
- Castelluccia, C.; Avoine, G. Noisy Tags: A Pretty Good Key Exchange Protocol for RFID Tags. In Proceedings of the International Conference on Smart Card Research and Advanced Applications—CARDIS, Tarragona, Spain, 19–21 April 2006; Domingo-Ferrer, J., Posegga, J., Schreckling, D., Eds.; Lecture Notes in Computer Science. Springer: Tarragona, Spain, 2006; Volume 3928, pp. 289–299. [Google Scholar]


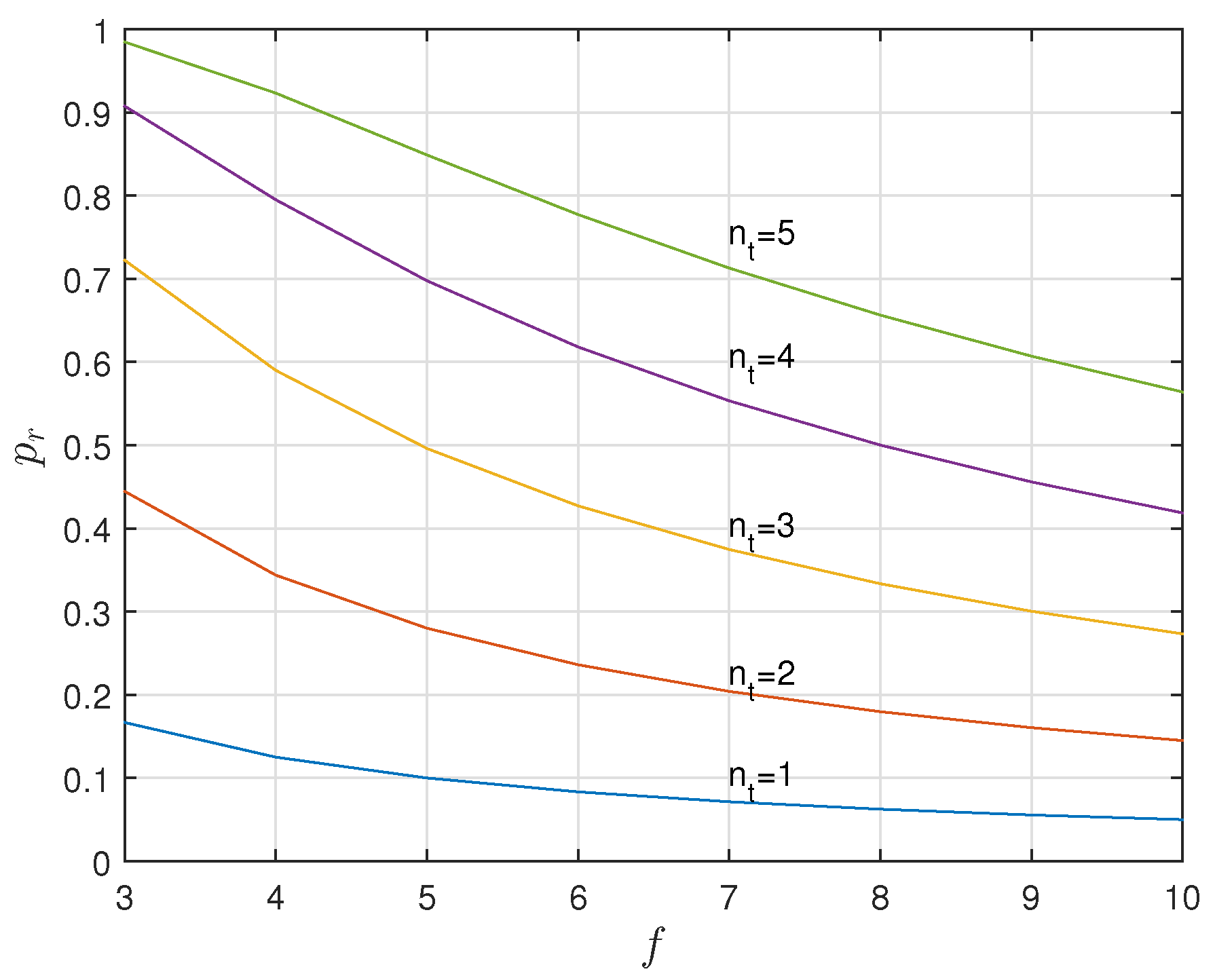
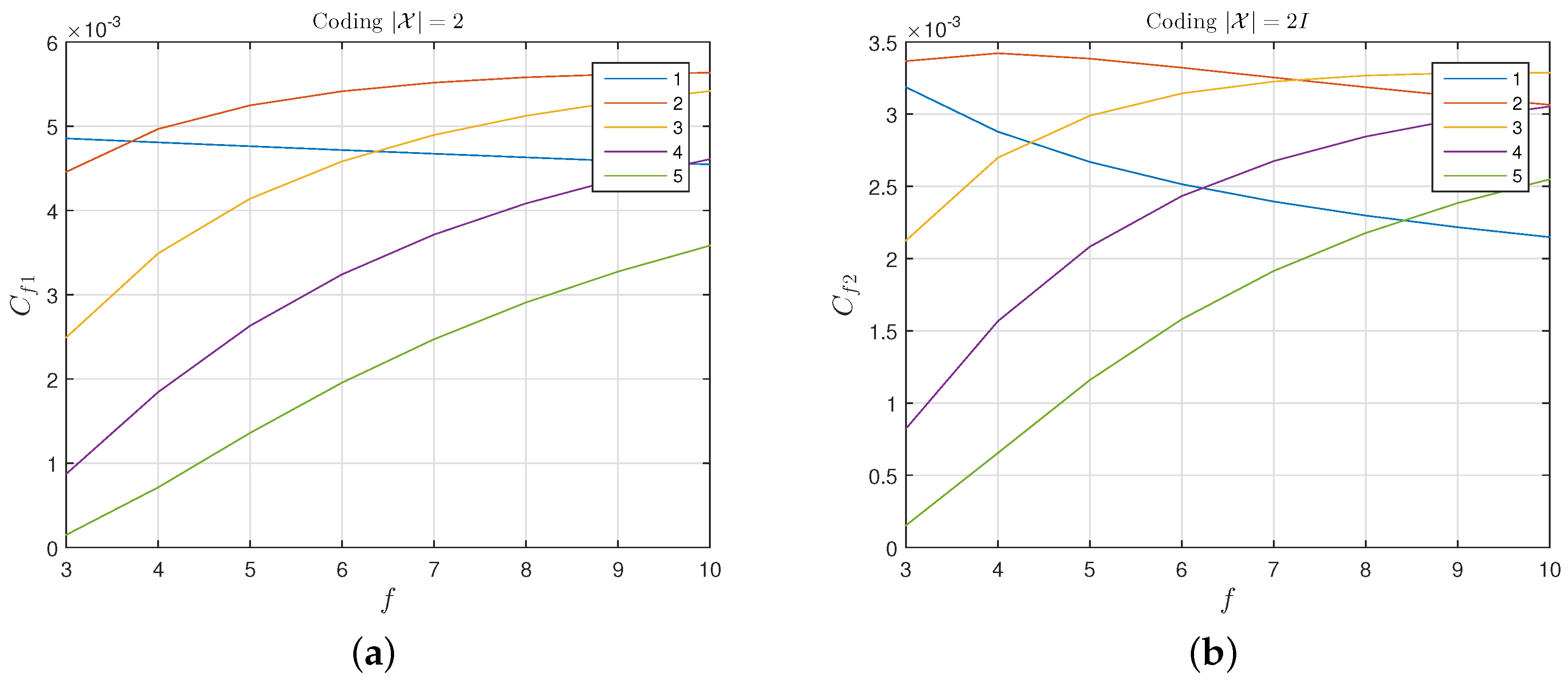
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burmester, M.; Munilla, J.; Ortiz, A.; Caballero-Gil, P. An RFID-Based Smart Structure for the Supply Chain: Resilient Scanning Proofs and Ownership Transfer with Positive Secrecy Capacity Channels. Sensors 2017, 17, 1562. https://doi.org/10.3390/s17071562
Burmester M, Munilla J, Ortiz A, Caballero-Gil P. An RFID-Based Smart Structure for the Supply Chain: Resilient Scanning Proofs and Ownership Transfer with Positive Secrecy Capacity Channels. Sensors. 2017; 17(7):1562. https://doi.org/10.3390/s17071562
Chicago/Turabian StyleBurmester, Mike, Jorge Munilla, Andrés Ortiz, and Pino Caballero-Gil. 2017. "An RFID-Based Smart Structure for the Supply Chain: Resilient Scanning Proofs and Ownership Transfer with Positive Secrecy Capacity Channels" Sensors 17, no. 7: 1562. https://doi.org/10.3390/s17071562
APA StyleBurmester, M., Munilla, J., Ortiz, A., & Caballero-Gil, P. (2017). An RFID-Based Smart Structure for the Supply Chain: Resilient Scanning Proofs and Ownership Transfer with Positive Secrecy Capacity Channels. Sensors, 17(7), 1562. https://doi.org/10.3390/s17071562







